1. Introduction
In recent decades, additive manufacturing (AM) has gained popularity, and the number of users demanding 3DPs has increased each year. Accordingly, Vicari [
1] estimated that the 3D printing industry (3DPI) would continue to grow, and its market share would reach USD 9 billion in 2025. Additive manufacturing is a new technology promising radical changes and transforming traditional production, supply, and logistics systems. Accordingly, it can be used in almost all industries; hence, it has gained popularity in various industries, e.g., aviation, vehicle manufacturing, construction, foodstuffs, pharmaceutical, biomedical, and ornamentation [
2]. Primarily, it can lead to transformational and revolutionary changes in the automotive, textile, and construction industries. Aside from these industries, 3D printing technology is promising for all industries with the potential for digital transformation. The main reason for this is that additive manufacturing has many relative advantages and superiorities over traditional subtractive manufacturing technologies; it can also help accelerate digital transformation for industries and companies.
3DPs used in additive manufacturing processes are cheaper than machinery and equipment used in traditional and classical subtractive manufacturing systems. Thus, these systems have more reasonable and flexible investment and setup costs. Therefore, industries can update their additive manufacturing systems quickly and easily, depending on technological improvements. Industries can gain the ability to meet small and customized orders of customers as additive manufacturing provides for production with smaller economic batch sizes. When its indirect impacts are evaluated, industries can better manage their inventory and produce more flexible and practical strategies. It may even be possible to redesign production networks with a zero-stock approach, shifting from a traditional production strategy to a modern (digital) production strategy for industries [
3]. Industries’ dreams of creating well-operating, agile production and supply chain systems may become a reality. In addition, additive manufacturing can prepare a way to optimize logistics costs, aside from reducing inventory costs. As a result, while additive manufacturing can help create speedy, agile, and lower-cost production, supply, and logistics systems, it also makes it possible to meet the requirements and expectations of customers with better conditions. As a result, additive manufacturing can create more sustainable production systems, protect the environment, and reduce external costs arising from industries’ production activities.
However, additive manufacturing has some limitations and drawbacks despite its many valuable advantages. First, it is a pretty new technology, and the accumulation of knowledge on it has not accomplished a satisfactory level for practitioners in the industries or scholars in academic life. Therefore, additive production is not yet a sufficiently reliable manufacturing system for practitioners and decision-makers in various industries; its manufacturing costs are still relatively high as the production capacity of 3DPs in units of time is deficient. Thus, unit manufacturing costs are still high, and unit products are non-economical. In addition, the supply costs of raw materials used in additive manufacturing processes are relatively high. This causes production costs to remain high compared to the costs of traditional production systems.
Moreover, staff (i.e., blue-collar workers and white-collar workers) in industries have limited or no information about this production technology. Therefore, the production system may become more fragile in an extraordinary situation. At the same time, supply and logistics processes concerning additive manufacturing have not been optimized sufficiently, and good practices have not yet been generated in the industries. This may cause many problems and challenges concerning supply and replenishment. The number of good examples is exceptionally scarce to make benchmarking possible. Hence, a commonly accepted and tested road map does not exist yet for decision-makers in this transformation process; unfortunately, we cannot shed enough light on the matter either.
The hesitancy of decision-makers and practitioners to transform from traditional subtractive production systems to AM may stem from risks related to the limitations and drawbacks of additive manufacturing. These kinds of decisions are perilous because they are irreversible. Inadequate knowledge and the absence of data about 3D printers and printing technology make it challenging to solve these problems. Moreover, evaluating and selecting 3D printers used in additive manufacturing processes is a decision-making problem, as an assessment process has numerous contradictory criteria and complex uncertainties. Therefore, selecting suitable industrial 3DPs is difficult, complex, and laborious for practitioners. Also, Panda et al. [
4] highlighted that 3DP selection is difficult for them, as it is affected by many factors and variables. Moreover, it is necessary to identify the industry requirements for 3DP utilization, and the selected printer should meet these requirements on a vast scale. Available 3DPs have many similar functions and features, which confuses decision-makers. Misevaluation may incur high and severe costs for industries. Also, all supply chain systems, such as production, supply, and logistics, may become unbalanced. Therefore, it causes a decrease in the overall efficiency of value chains. Selecting suitable 3DPs with carefully detailed process management is a critical and managerial decision for industries.
Moreover, a new and unprecedented business paradigm has existed, and industries and supply chains must respond to the requirements generated by this digital business world’s paradigms. Some factors have become more critical and vital in the digitalized business environment compared to the past. For instance, shorter product life cycles, customizing and personalizing the products, and increasing product variety have led to these factors. Industries need more flexible and changeable production systems to respond to these requirements. The traditional subtractive manufacturing systems operate based on scale and mass production economics, and their flexibility level is low. Hence, subtractive production systems have difficulty responding to these requirements on a vast scale. Moreover, novel and innovative technologies emerging in the fourth industrial revolution have considerably increased competition in almost all industries. Correspondingly, industries and supply chains must find new and suitable ways to keep up with these requirements generated by the new and digitalized business environment and survive in the highly competitive business environment.
Aside from digital transformation, shifting to additive manufacturing is a compulsion rather than a preference for industries, at least for the near future. Accordingly, selecting optimal and adequate 3D printers for additive manufacturing processes may be an excellent and effective start for industries in this transformation process. However, there are potent interactions among technologies, partially built on each other, and the maturation levels of these technologies are different [
5]. This transformation process has many significant difficulties and challenges. Thus, a vital, practical, and effective mathematical tool is necessary to handle complicated uncertainties and make the practitioners’ work more accessible. In this connection, the current work proposes an integrated group decision-making model involving the Fermatean Fuzzy Stepwise Weight Assessment Ratio Analysis (FF–SWARA) and the Fermatean Ranking of Alternatives through Functional mapping of criterion sub-intervals into a Single Interval (FF–RAFSI). Moreover, it aggregates the experts’ evaluation by applying the Dombi aggregating operator. The proposed model has been implemented to address a critical decision problem in the car-manufacturing industry by considering two case studies.
The primary motivation of the work is to evaluate 3D printing technologies concerning whether they are working in the manufacturing industry or not. As is known, the automotive industry is severely under pressure from the competition and uncertainties in the relevant sector. Also, the customers expect smooth automobiles produced with excellent and impeccable artistry, aside from offering low and reasonable prices by manufacturers. However, several wastes, losses, and defects can occur in the manufacturing process due to human errors. Even though robotics are used in manufacturing, they perform some definite jobs, e.g., assembling, drilling, and tightening screws, they have significant weaknesses in producing automobile components with no plane surface geometrically. However, the human force used to produce these kinds of components is slow and leads to a deceleration in the production process due to some inherent problems sourcing humanistic factors. Three-dimensional printers have several advantages and superiorities over human force, which may help address this problem in mass production systems.
The remainder is structured as follows. In
Section 2, a detailed literature survey was carried out.
Section 3 presents the suggested FF approach and its execution phases. In
Section 4, the suggested tool was implemented to solve the 3DP selection problem in the automotive industry (AI); a comprehensive validation test consisting of three stages was executed to test the robustness and practicability of the suggested FF implementation. In
Section 5, the results are assessed and examined. In
Section 6, the study is finalized. Moreover, the constraints of the current study and suggestions for future research are pointed out in the final section.
2. Research Background
Additive manufacturing, i.e., 3D printers and 3D printer technologies, a crucial component of the industry 4.0 process, has increasingly become a popular and remarkable topic for practitioners in various industries, scholars, and researchers. There are two significant reasons for that. First, additive manufacturing and 3D printers have a remarkable potential for revolutionary changes in whole supply chains and industries. Hence, it can indirectly lead to changing everything in our lives. Second, there are still substantial and critical gaps in the literature; scholars and practitioners must do something to fill these gaps. Although these gaps lead to increased doubts about the reliability and applicability of additive manufacturing, they cause hesitation in transforming from traditional subtractive production to additive manufacturing. These hesitancies and doubts can be accepted as usual because these transformations and changes require making risky and irreversible decisions.
In practice, different 3D printer technologies can be used in various industries. In addition to the different advantages and disadvantages of each technology, each technology has different capabilities and features. In this respect, comparing these technologies to evaluate and understand 3D printer technologies from a broader perspective is essential.
Table 1 shows the comparison results for existing 3D printer technologies.
Accordingly, encouraging the decision-makers to decide on this digital and industrial transformation depends on filling these gaps in the literature. More research on this issue is required to fill these gaps. However, increasing the amount of research handling additive manufacturing and 3D printer technologies in the literature is promising. When an extensive and elaborate bibliographical review was performed, it was observed that previous studies focused on three crucial topics: AM, 3D printer technologies, and 3D printers’ features and functions.
In addition, when we examined the previous works focusing on the 3DP selection, a focal point of the current study, it was noted that most of these studies focusing on 3DP selection have increased from 2013 to the present. According to the results of the review in the scientific databases, 327 studies are available in the literature. However, the number of previous works has decreased to 39 when we add keywords such as MCDM, decision, and multi-attribute decision-making model. The most crucial reason is to focus on 3D printers’ technical features; most studies deal with 3D printers by performing technical, empirical, and experimental studies rather than selection problems.
In this context, previous studies on the selection of 3DP are presented in
Table 1, and previous studies focusing on the selection of three-dimensional printers and AM technology are presented in
Table 2.
As seen in
Table 2, some of the authors focusing on 3D Printer selection preferred to use decision-making procedures’ extended form based on diverse fuzzy sets in 15 studies existing in the relevant literature. Also, applying the classical frameworks’ objective and subjective forms was suggested in 14 papers to solve the 3DP selection problem. Although fuzzy AHP and classical AHP approaches were used in eight papers and five studies, fuzzy TOPSIS and ANP techniques were implemented in two works. Finally, some procedures, e.g., BWM, EDAS, ELECTRE, F-GRA, F-SAW, IVSFS–ARAS, IVSFS–TOPSIS, PIV, and QFD, were used once in various studies. As is understood, the researchers are aware of the existing uncertainties, and various fuzzy sets were used in many works in the relevant literature. However, most of these researchers preferred the traditional fuzzy set theory (Zadeh, 1965) and the classical AHP method or the extended version of the AHP based on fuzzy set theory. However, these papers have not presented sufficient information about how the researchers overcame the structural problems and limitations of the AHP and F-AHP approaches.
In addition, it is noteworthy that another subjective weighting technique that has been the subject of many studies in the literature is the SWARA approach, and various fuzzy sets-based extensions are widely used to process uncertainties. In this perspective, some of the studies on the SWARA technique in the literature are presented in
Table 3.
When the earlier works employing the extensions of the SWARA method with the help of the various fuzzy sets were evaluated, it was noticed that the researchers mostly preferred to use bipolar q-ROFs and hesitant fuzzy sets. The other fuzzy sets used in the literature can be shown as Hesitant bipolar Fs (2), Pythagorean Fs (2), Spherical Fs (2), Double Hierarchy Bipolar Hesitant Fs (1), Double Hierarchy Hesitant (1), Fermatean Fs (1), Golden Cut-Oriented q-ROFs (1), Picture Fs (1), Picture fuzzy rough sets (1). However, only one study employing the Fermatean fuzzy SWARA has been found in the literature. Ayyildiz [
47] extended the SWARA approach based on FFs to evaluate sustainable development goals. It proves that the members of the research society are unaware of the FF–SWARA method’s advantages even though it provides many precious theoretical and practical contributions.
The SWARA technique Keršulienė et al. (2010) developed has a simple, understandable, and practical algorithm. With a smaller number of calculations and comparisons, it can reach quite reasonable and logical conclusions. In addition, the method incorporates practitioners’ knowledge and experience into the evaluation process [
66,
67]. It also provides a complete consensus between the opinions of different experts, transforming the individual assessments of the experts into the common opinion of the decision-making group [
68]. Its main advantages can be summarized as follows: (i) it ranks the selection criteria according to their importance; (ii) It eliminates unimportant criteria by means of voting; (iii) It assists in setting criteria with full consensus among decision-makers; (iv) It provides the opportunity to evaluate the ranking determined by each decision-maker [
69].
The RAFSI approach is an extremely powerful decision-making model compared to other decision-making tools in the literature. In this respect, its most important advantage is that it is completely resistant to the problem of turning rows thanks to its structural features. This advantage of the procedure also increases the reliability of the model from the point of view of decision-makers. However, RAFSI provides a flexible decision-making environment. The RAFSI method developed by Žižović et al. [
70] has three important advantages that are recommended for further use: (i) its practical algorithm helps in solving complex real-world problems; (ii) the RAFSI method has a novel approach to data normalization that transfers data from the initial decision and converts the matrix into any range suitable for making rational decisions; and (iii) the mathematical formulation of the RAFSI method eliminates the problem of order reversal, which is one of the most significant shortcomings of current MADM methods.
Due to this advantageous structure, the RAFSI technique has been a preferred tool in solving various complex decision problems by many researchers in the literature. These studies are summarized in
Table 4.
Although the RAFSI approach is pretty solid and resilient to the rank-reversal problem, better than many popular MCDM procedures, the number of studies using this framework or its extensions is exceptionally scarce. It means adequate awareness concerning this approach’s critical advantages and theoretical contributions is still unavailable in the research society. However, after three successful examples employing the classical form of the RAFSI technique [
70,
78,
79], the researchers preferred to use extensions of the RAFSI based on various fuzzy sets, e.g., Classical fuzzy sets [
71,
72,
76,
80], Dombi-based fuzzy sets [
77], Q-Rung Orthopair fuzzy sets [
75], Single Interval fuzzy sets [
73], and Type-2 neutrosophic numbers [
74]. Even though this combination has precious potential and practical advantages to address highly complicated problems, no study in the relevant literature proposes the extended form of the RAFSI approach based on the Fermatean fuzzy sets (FFs). In this context, FFs-based multi-criteria decision-making techniques in the literature are summarized in
Table 5 and
Table 6, respectively.
When we survey the relevant literature in detail, there are 143 studies employing various decision-making procedures’ extensions based on the FFs available. Although in 2019, only four papers used FFs-based decision-making frameworks in the literature, the number of studies using FFs increased to 69 in 2022. We demonstrate some of these studies, which are focused on fascinating decision-making problems in
Table 5 and
Table 6. The ever-increasing number of studies employing the Fermatean fuzzy sets proves that awarenesses of the members of the research society concerning the critical and precious advantages and contributions of FF sets has continued to increase.
2.1. Research Gaps
When the literature is evaluated in general, almost all authors in the previous studies dealing with 3DP selection agree that AM has a powerful potential for the industries’ transformation. Also, there is a complete consensus that it cannot be an alternative to traditional subtractive production systems. AM is used in a few industries for prototyping, producing tools, and medical implants, which are exceptionally personalized products [
111]. Moreover, the expectations and requirements of each industry on 3DPTs are different. However, in the literature, only a few studies examined the 3DP selection for a specific industry, such as aviation [
36], educational institutions [
41], and the innovation center of an academic institution [
38]. Studies carried out without considering these different requirements and expectations of industries may cause doubts about whether the results of these studies are proper for actual conditions. Hence, authors of future studies should consider these differences to reach more rational, realistic, and logical results.
When we handle these findings with many works focusing on 3DP selection using decision-making techniques, it can be argued that gaps in the literature generate these situations mentioned above. From this perspective, AM is a novel technology, and decision-makers have insufficient information and experience to make proper and optimal decisions about selecting appropriate 3DPs. Therefore, scholars and researchers have not yet provided decision-makers with sufficient information and data for utilizing the 3DPT in industries. However, the number of studies proposing decision support systems, decision-making tools, and models has recently increased to make the practitioners’ business more easily relevant to the 3DP and printing technology selection.
However, in the literature, traditional and classical MCDM frameworks commonly preferred decision-making techniques such as the Analytic Hierarchy Process, VIKOR, TOPSIS, PROMETHEE [
31], and ELECTREE. However, these approaches cannot handle ambiguities in complex decision-making problems faced in AM. Though the number of papers examining the selection of 3DPs with the help of fuzzy approaches is still low, an increasing number of these studies carried out in recent years may be an indicator that researchers have started to notice that 3DP selection is an extraordinarily complex evaluation problem, which is influenced by a lot of complicated situations and ambiguities. However, the number of papers using classical decision-making approaches is still higher than studies applying fuzzy approaches. Moreover, most of the studies applying fuzzy techniques preferred to use the extended versions of these approaches mentioned above by the fuzzy set theory.
Additionally, the following gap, which was noticed in the literature, is relevant to the criteria applied by the preceding papers. First, it is indefinite how these factors were chosen, and there is no adequate information about frameworks applied to identify the criteria in these studies. Also, it is ambiguous how the experts were selected and which criteria were considered to identify them in some studies conducting a questionnaire to benefit from experts’ evaluations, experiences, and opinions. Furthermore, considering only experts’ opinions makes it challenging to provide objectivity. The authors and researchers did not indicate how they overcame this problem. Another significant indicator of the gap in the criteria is that each author applied different criteria sets; there are no generally recognized factor sets in the literature. It may raise doubts about the validity and compatibility of the criteria and may essentially decrease the trustworthiness of the analyses. Also, most authors did not find it necessary to test the robustness of the approach or model they proposed. However, notably, the Analytic Hierarchy Process technique and many traditional decision-making approaches in these previous papers suffer from rank reversal [
112,
113,
114,
115,
116]. It means the results obtained by applying these approaches may modify dramatically if an option is added to or eliminated from the scope of the evaluation. It is a crucial and essential problem with respect to the reliability of the implemented techniques. Also, these techniques have many drawbacks, limitations, and structural problems. In particular, the AHP has a highly complicated basic algorithm, as it requires many computations and comparisons; these complexities may arise depending on the number of factors and options. Moreover, it needs extra calculations to ascertain the consistency ratio. Consequently, these findings indicate that decision-makers lack a robust, stable, and efficient model for complicated ambiguities. Hence, the requirements for this model also prove another gap related to the decision-making approach.
Finally, most 3DPs evaluated by authors in the previous studies are improper for mass production because their production speed, capacity, and maximum build size are insufficient to respond to the requirements of some industries such as textile, automotive, and machine manufacturing. Thus, these previous studies cannot meet the requirements of these industries concerning the transformation of the production system, as the examined 3DPs by the authors carrying out these studies cannot produce thousands of products with equal quality and standards.
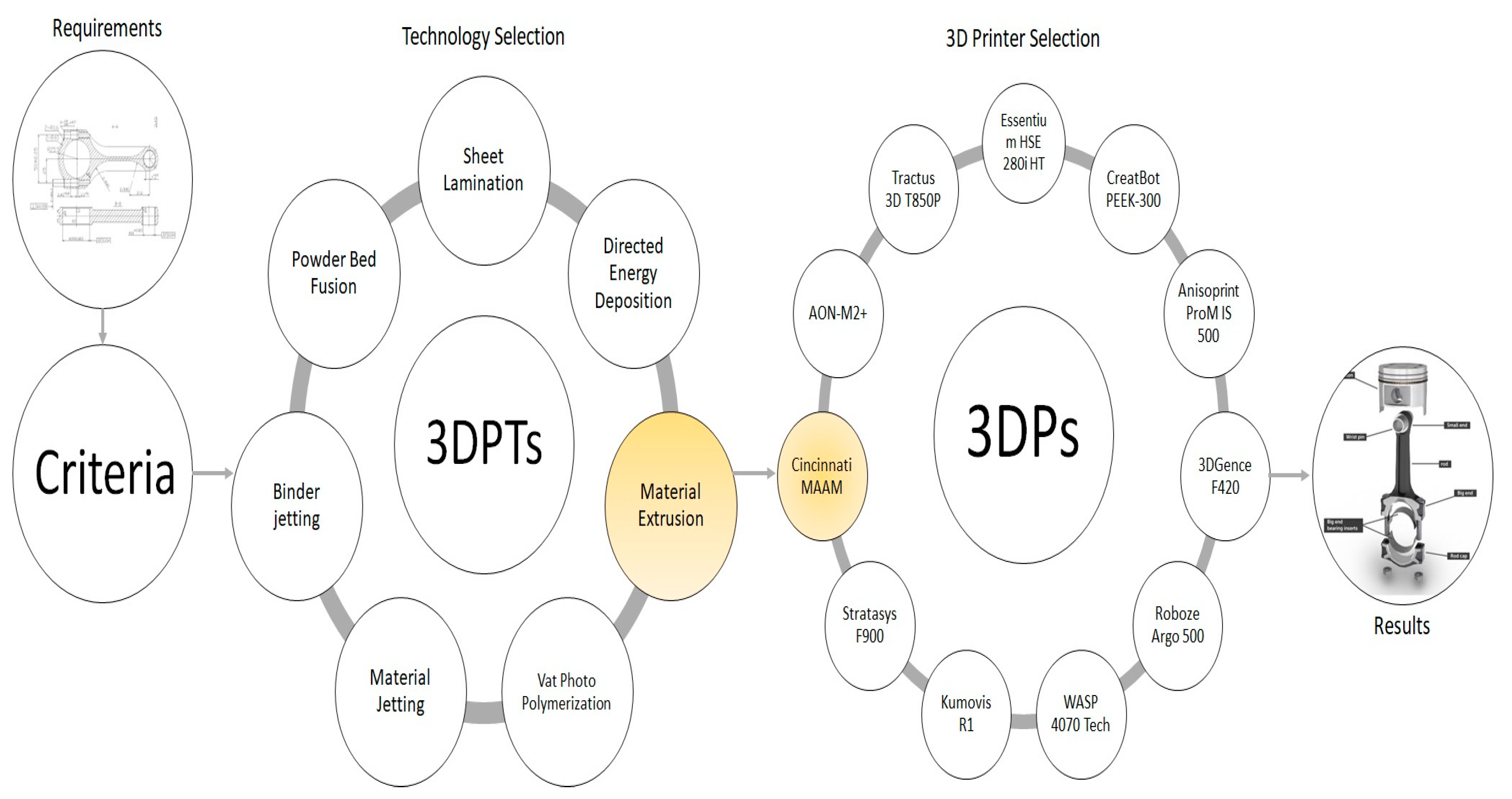
3DPs are classified into seven groups by considering the 3DPTs, their different capabilities, advantages, and disadvantages. These 3DPTs have an incomparable function in identifying relationships between the abilities of 3DPs and the requirements of the industries and lean selection processes. Identifying the appropriate 3DPT alternative can help eliminate the 3DPs using different 3DPTs (i.e., that do not meet the requirements) in the evaluation process. That makes it easier for the practitioners’ business concerning the choice of industrial 3DPs in AI and can help make the production process lean. On the other hand, the authors who carried out the earlier studies dealt with the 3DP selection. Eventually, most of them overlooked the significance of the different 3DPTs. However, selecting 3DPs without identifying the appropriate 3DPT may not provide rational or logical results. Selecting a 3DP alternative at a high rank concerning criteria such as reasonable purchasing cost, production speed, and so on may not be feasible, rational, or logical due to its improper 3DPT for the current industry.
2.2. Motivations of the Work
There are many motivations for the work. First, it is based on a real-world evaluation problem. From this perspective, one of Turkey’s large-scale automotive sub-industrial enterprises had evaluated shifting from a subtractive production system to AM for one of the manufacturing plants producing connecting rods. The company produces approximately 8000 units annually to meet the requirements of a single customer. However, senior executives of this company had no road map to help manage this transformation process, and they did not know what was to be done to reach desirable and expected results. The auto spare part planned to be produced using 3DPT is presented in
Figure 1.
Also, they have limited knowledge about 3DPs and no idea how the best 3DPs can be selected. However, all of them made sure that this decision was compulsory for their company because an international key player producing brake systems was preparing to enter the market soon; it was an essential concern for these top managers. They asked for technical support from us to find a reasonable and efficient resolution for this problem. We noticed that conducting this process as a research process will be better in the first meeting with these executives.
Correspondingly, a research process was designed and carried out (the details of this procedure are demonstrated in the subsequent section) to identify the selection criteria and propose a decision-making model. Therefore, the paper’s first motivation is to generate an optimal, robust, and efficient decision environment for selecting appropriate 3DPT and printers for the company. We noticed critical gaps in the literature and practice when conducting an extensive literature review and pre-examining to collect details and data.
Although many investigations have been performed to demonstrate innovative advancements in 3DP and AM technologies and their adoption in various industries in the relevant literature, the previous works have neglected the potential and possibly practical contributions of selecting the most appropriate 3DP technologies and 3DPs for the manufacturing industries. Most studies evaluated personal and small 3DPs purchased with hobby-aimed by users, but these 3D printers are not proper for mass production of auto parts, and the obtained findings cannot be generalized to the manufacturing industries. Moreover, the relevant literature fails to adequately contribute to the manufacturing industries regarding the selection of the most appropriate 3DPTs and 3DPs. However, the selection of 3DPTs and 3DPs is an extraordinarily complicated decision-making problem affected by highly complex uncertainties. There are two significant reasons for that: first, AM and 3DP technologies are relatively new and high-tech instruments. Second, the technical and operational information of the experts in various manufacturing industries is mostly insufficient concerning these machines. In addition, there are no criteria set that are commonly accepted by practitioners and can be used to assess 3DPTs and 3DPs in industries’ practices. In addition, a wrong decision in the selection of 3DPTs and 3DPs is unrecoverable, as the acquisition costs of these machines are enormously high. Finally, senior executives in the automotive industry mostly consider recommendations of the specialists in the 3DPs manufacturing industry to select a proper 3DP to use in the additive manufacturing process. However, these recommendations may be fallacious for decision-makers since these experts consider their 3DP manufacturer or distributor firm’s benefits and may suggest their products provide higher profits even though they do not fit the manufacturing company’s requirements.
Thus, practitioners who are responsible for assessing and selecting the most proper 3DPTs and 3DPs alternatives in the automotive industry can be motivated to apply a decision-making framework to successfully re-construction their production lines based on AM systems in the manufacturing plants. The current study is motivated by considering gaps and deficiencies in industry practices, briefly demonstrated below.
The members of the research society have neglected the Importance and practical contributions of the selection of 3DPTs and 3DPs in the car-manufacturing industry.
These research gaps influence the industry practices concerning the adoption of 3DP and AM technologies in the relevant industry. Consequently, the research society fails to contribute adequately to appraise the available 3DPs alternatives in the automobile industry.
As 3DP and AM are newly emerging and sophisticated technologies, the accumulation of knowledge of the industry’s professionals on the selection, establishment, usage, and compatibility of these new manufacturing technologies is severely scant.
Decision-makers in the automotive industry face many challenges concerning the appraise of 3DPTs and 3DPs technologies for auto parts manufacturing processes due to a lack of trustworthiness and robust MCDM procedures that can adequately deal with greatly complicated ambiguities in the literature.
No set of identified criteria is commonly accepted by researchers and top managers influencing the assessment process for evaluating and selecting the proper and best 3DPTs and 3DPs.
The current study attempts to find logical answers to the research questions, which helps decision-makers in the automotive industry explore practical and efficient ways to appraise the 3DPs AM technologies. The following research questions are presented:
RQ1. Why do manufacturing companies in the automotive industry require 3DP and AM technologies, and how can these technologies reshape the auto parts manufacturing processes?
RQ2. What are the most critical and influential criteria that should be included in the scope of the 3DPTs and 3DPs selection evaluation?
RQ3. How can these new manufacturing technologies influence production systems’ overall performances and efficiencies?
RQ4. Is it possible to suggest a novel procedure to determine the criteria influencing the selection of 3DPTs and 3DPs?
RQ5. How can the existing ambiguities be dealt with in an appraisal process to identify suitable 3DPTs and 3DPs for the automotive manufacturing industry?
In this connection, the objectives of the study are briefly demonstrated to find reasonable and logical answers to the research questions as follows:
- (a)
Developing a procedure to determine the significant criteria that should be included in the scope of analysis to address the 3DPs selection problem for the car-manufacturing industry.
- (b)
By implementing the suggested procedure, determining the influential criteria to structure the decision-making problem properly.
- (c)
Identifying the best 3DPT and 3DP alternatives by implementing the suggested decision-making approach for the automotive industry.
Accordingly, the current paper’s most significant motivation is proposing a stable, consistent, and practical mathematical tool that can effectively handle intricate unpredictability. The third inducement of the work is to introduce a set of factors that is up-to-date and appropriate to real-world evaluation problems and to identify with a detailed literature review and examination performed together with incredibly skilled executives. The criteria set can inspire practitioners in industries and researchers who conduct future studies on this subject.
2.3. The Motivation for Developing the FFD–SWARA and RAFSI Model
Aside from deficiencies concerning additive manufacturing practices in the automotive industry, we noticed critical research gaps in this field when we investigated the relevant literature carefully. The most crucial gap was related to improper criteria and factors used in the previous studies. Most existing studies dealt with personal 3D printers. The findings of these studies cannot be generalized for the 3D printers employed in the mass production processes because the criteria used in these works are not suitable for the selection of 3DP used in mass production. Furthermore, the approaches involved mostly objective and classical fuzzy sets proposed by these studies could not produce satisfactory solutions due to their structural problems and disadvantages. First, additive manufacturing is a new practice in the automobile manufacturing industry, and practitioners in the relevant industry encounter several challenges concerning decision-making due to significant and critical deficiencies in collecting information and data concerning these implementations. However, the procedures in the literature are not sufficiently reliable for these decision-makers because some of them, using objective approaches, overlooked ambiguities in the car-manufacturing industry. Classical fuzzy sets employed in some studies could not successfully process highly complicated vagueness because the classical fuzzy sets consider only membership functions and overlook non-membership functions. Therefore, practitioners in the automotive sector need a robust, trustworthy, and practical decision-making tool that can handle excessively complex uncertainties to assess the 3DP alternatives employed in the car-manufacturing processes. Considering this requirement, we developed a hybrid decision-making model involving the SWARA and the RAFSI. Also, we extended this combination with the help of the Fermatean fuzzy sets. Each approach has diverse advantages and contributions to addressing decision-making problems, and the suggested integrated model merges these advantages.
First, the SWARA approach helps to compute the criteria weights logically and identifies the relative significance of the criteria more realistically [
66]. In addition, it requires fewer computations and pairwise comparisons than the AHP technique [
118]. The complexness of the SWARA method is relatively low compared to many popular frameworks, which are used to identify the criteria weights. Moreover, experts with various features can work together [
119], and it is not necessary to identify presuppositions to evaluate a decision-making problem. Moreover, it provides an excellent compromise among the experts by considering and associating their assessments and eliminates the impacts of experts’ excessive assessments.
Second, the RAFSI approach has many benefits in addressing complicated decision-making problems. First, this framework has an efficient basic algorithm, and practitioners can apply it without needing advanced mathematical knowledge. Thus, the RAFSI approach’s basic procedure is simple Deveci et al. [
120]. It also eliminates the rank-reversal problem that can be accepted as a big challenge of the MCDM approaches due to the advantages of the new normalization technique applied by this framework [
70,
120]. Therefore, the procedure’s advantages make it a more trustworthy approach for decision-makers to solve extraordinarily complicated decision-making problems.
Moreover, the Fermatean fuzzy sets can define more ambiguities [
121] and describe uncertainties more extensively [
122]. Consequently, due to the advantages of the score function and accurate function, which were defined by Senapati & Yager [
123], the Fermatean fuzzy sets, which are the extended form of the Intuitionistic fuzzy sets IFSs, can deal with more complicated vague information compared to the IFSs and other traditional fuzzy sets.
5. Results and Discussions
AM is a promising production system with many advantages compared to traditional subtractive manufacturing systems [
142]. However, industries still do not dare to transform their production systems because these kinds of decisions are extremely risky and irreversible. Hence, they are concerned about what would happen if anything went wrong. The main reasons for that are a lack of data and insufficient information about this issue. Available information about AM and 3DPs produced in the literature is insufficient to encourage the industry decision-makers about this transformation process. Thus, it is necessary to do much more research to fill the gaps in the literature.
When a broad literature review was performed, we noted significant and severe gaps in the literature. First, A major part of the studies examining the selection of three-dimensional printers did not focus on any industries’ requirements that are related to 3DPs utilization. Consequently, the studies evaluated the selection of 3DPs without considering an industry’s requirements concerning employing 3DPs in manufacturing. However, 3DPs are produced to meet the diverse, special, and different requirements of the last users regarding both industrial and individual usage. For instance, while the automotive industry needs 3DPs, which can be used to produce large-sized auto parts at a higher accuracy level in mass production processes, the medical and health industry requires 3DPs, which can produce at the highest accuracy instead of mass production. Consequently, studies in the relevant literature did not consider the special requirements of diverse industries aside from the different abilities and features of the 3DPs. Second, 3DPs are produced based on diverse three-dimension printer technologies, such as Binder Jetting, Powder Bed Fusion, Material Extrusion, Material Jetting, etc.; each 3DP technology has diverse abilities and features and meets the different requirements of the last users. In this connection, the earlier studies assessed the 3DPs without considering the 3DP technologies and their different features. Therefore, after the 3DP technology, which can meet the requirements of any industry, is identified, evaluating the alternatives produced with this 3DP technology may be more logical and reasonable.
Many studies in the relevant literature evaluated personal 3DP alternatives. Moreover, these papers do not provide sufficient information about industrial 3DPs for industry practitioners, as these printers can be used for individual requirements such as hobbies and prototyping instead of mass production. The second gap is relevant to methodological frames applied in the preceding studies. The author (s) preferred using traditional decision-making approaches such as AHP, TOPSIS, PROMETHEE, VIKOR, and ELECTREE. Aside from structural problems and drawbacks, these approaches may overlook the numerous complicated uncertainties in an assessment process for selecting the best and proper 3DPTs and 3DPs.
Furthermore, there are many unpredictable uncertainties in addition to predictable ambiguities. Therefore, classical fuzzy theory cannot overcome these kinds of uncertainties. Thus, a robust, effective, applicable, and reliable decision tool is required to handle predictable and unpredictable uncertainties to solve highly complicated decision-making problems faced in AM.
By keeping these requirements and motivations of the industry in mind, the present study suggests a novel decision-making model by extending the SWARA and RAFSI combination based on the Fermatean fuzzy sets. The suggested model has numerous helpful conceptual contributions to the literature. These contributions can be outlined as follows.
The suggested integrated model associates the precious advantages of the SWARA approach, the RAFSI technique, and the Fermatean fuzzy sets. Therefore, the suggested model is a robust and efficient decision-making tool that can handle excessively complicated uncertainties.
The SWARA approach, which is part of the suggested hybrid model and employed to identify the weights of the criteria, has many precious advantages. It provides an opportunity to compute the criteria weights more logically and reasonably. Correspondingly, the SWARA approach considers practitioners’ priorities and the requirements of the relevant organization while a decision-making problem is addressed [
66]. Thus, it can produce models based on situations, priorities, and degrees of significance [
143]. In addition, practitioners can leave irrelevant and unimportant criteria and factors out of the assessment, and it allows them to complete the assessment process quickly. Also, it requires fewer pairwise comparisons and computations than some traditional weighting approaches, such as AHP and ANP. Hence, the SWARA technique has a more understandable procedure [
118]. This advantage of the approach makes its basic algorithm more practical and applicable. In addition, it provides an opportunity to crisply evaluate the relative significance of the criteria [
130].
The implementation of the RAFSI approach used to identify the preference ratings of the alternatives is very simple [
120] and has an understandable algorithm. It presents an excellent normalization technique that objectively converts information in the decision matrix to processable data [
70]. Moreover, it is maximally resistant to the rank-reversal problem, which is accepted as a critical structural problem of different decision-making approaches [
70,
120]. Based on its advantages, the RAFSI technique presents a trustworthy decision-making framework at the level of excellence to the decision-makers, and it gives results to the practitioners trying to solve highly complex decision-making problems at a higher level of accuracy.
The Fermatean fuzzy sets have critical and significant advantages compared to other fuzzy sets. In particular, the sum of cubes of membership and non-membership functions takes a value of less than 1 [
121], and there is a relationship between membership and non-membership of an element [
144], and FFs consider this relationship more than other fuzzy sets differently. Thanks to this advantage provided by its structural feature, decision-makers can assign membership and non-membership values from a wider domain [
121]. Correspondingly, FFs can overcome uncertainties better than other fuzzy sets, which are highly complicated. Furthermore, its ability to capture more ambiguities [
123] and process complex and indeterminate information provide advantages to solving highly complex decision-making problems.
In addition to its conceptual contributions, the present paper has many precise managerial findings. These implications can be summarized as:
It presents a novel set of criteria determined by executing extensive fieldwork with broadly skilled experts with vast knowledge of AI and digital transformation and a detailed literature review. Executives can consider these criteria when they face a decision-making problem on 3DP selection in AM. Moreover, they may inspire researchers to conduct further studies on this subject.
Aside from practitioners in the field of AM, designers and engineers in the 3DP manufacturing industry can consider the paper’s findings and use them as a guide to improve their products and technologies. They can focus on more influential criteria to generate a well-designed production system providing more rational resource utilization.
The current paper proposes a basic algorithm that can be used as a roadmap to select appropriate 3DPs for AM. This roadmap can help to select more rational, logical, and reasonable alternatives. Hence, the preferences of the decision-makers may be more optimal.
The current paper presents an algorithm that is different from those of previous studies. It recommends evaluating the proper 3DPTs before selecting 3DPs. Evaluating fewer and more reasonable 3DP options is possible because it can help eliminate some alternatives using 3DPT options. Thus, it makes the evaluation and selection easier for practitioners.
Also, it focuses on industrial 3DPTs and 3DPs, which are proper for mass AM production. Therefore, individual and low-capacity 3DPs are out of the scope of the current study. Hence, the current paper examines the applicability of AM technologies in AI concerning digital transformation.
When the outcomes and findings of the study are evaluated, C1 accuracy in printing is the most influential criterion, as it confirms that each manufactured product is in the same form. Hence, providing standardization in product form also increases the firm’s trustworthiness with the other supply chain stakeholders. The customers (car-manufacturing companies) want to fully rely on the appropriate purchased auto parts, which can be used in manufacturing processes because a slight mistake concerning the accuracy of any auto part’s form can lead to irrevocable results after the manufacturing process starts.
The study’s main finding concerning the most influential criterion confirms the outcomes acquired in the studies carried out by Ghaleb et al. [
23] and Khamhong et al. [
18]. According to these authors, accuracy is the most essential and critical factor for selecting the most appropriate 3DP. According to their study’s findings, Aydoğdu & Gül [
37] indicated that quality is the most critical factor. In some studies, the researchers claimed that the cost of production is the most determinant factor for selecting a three-dimensional printer [
22,
27,
45]. However, the researchers did not associate the outcomes of their studies with any industry’s requirements concerning 3DP utilization. Hence, it is not possible to check the validity of these findings. In addition, each 3DP shows diverse performance in producing different objects. These studies did not illustrate an object as an example that can be produced using additive manufacturing implementations. In the current work, aside from the current study carried out to address a critical decision-making problem in the automotive industry, we also pointed out an object that will be produced in an additive manufacturing process in the automotive manufacturing industry, as illustrated in
Figure 3. Ultimately, printing the connecting rods for heavy trucks by employing 3DPs is pointed out as the main focal point of the paper.