Abstract
Since the discovery of electricity, electric cables have become ubiquitous in human constructions, from machines to buildings. Insulators play a crucial role in ensuring the proper functioning of these cables, so it is important to monitor their possible damage, which can be caused by environmental contamination, severe temperature variations, and electrical and mechanical stress. While shunt conductance is a direct health indicator of cable insulation, measuring the cable average shunt conductance is not sufficient for the detection of localized insulator damage, since localized conductance variations are diluted over a long cable length in such measurements. The objective of this paper is to assess the feasibility of reflectometry techniques for the monitoring of insulator damage in electric cables. To this end, the estimation of localized conductance variations is investigated based on electrical measurements made at one end of a cable. To avoid estimating a large number of discretized conductance values along a long cable, the proposed method relies on sparse regression, which automatically focuses on localized conductance variations at unknown positions caused by accidental insulator damage. In order to efficiently apply sparse regression techniques, the telegrapher’s equations describing electric wave propagation in cables are transformed through several steps into a simple linear regression form. Then, Lasso (Least Absolute Shrinkage and Selection Operator) regression is applied to process the voltage and current data collected at a single end of the monitored cable. Numerical simulations show the potential of this method for fast estimation of localized shunt conductance variations.
1. Introduction
Since the discovery of electricity, electric cables have become ubiquitous in human constructions, from machines to buildings [1,2]. These cables have often been considered reliable and are ignored by fault diagnosis systems. Today, the reliability of some cable connections is becoming increasingly critical due to the importance of power supply and telecommunication, and some research activities have emerged to investigate this issue, such as [3,4,5,6,7,8]. Most of these studies concern the monitoring of cable impedance. In contrast, the present paper is focused on distributed shunt conductance, which is a direct health indicator of cable insulation [9]. There exist also other insulator monitoring methods relying on fiber-optic sensors incorporated into cables [10], whereas the present study is only based on electric voltage and current measurements made at one end of the monitored cable, for wide applicability to most electric cables.
Playing an important role in cables, insulators are subject to different causes of degradation and failure: temperature variations, environmental contamination, and electrical, mechanical, and chemical stress. Currently, the average shunt conductance assessed from direct current (DC) measurements is widely used in the industry for the evaluation of cable insulation. This method is efficient for the monitoring of cable aging, resulting in degradation well spread over the whole length of a cable, but is not suitable for localized failures, which would be diluted over a long cable when the average shunt conductance is tested. It is thus important to develop methods for the detection and the diagnosis of localized failures, which are typically caused by accidental events.
Compared to cable impedance, relatively few studies on shunt conductance monitoring have been reported [11,12,13,14,15], and they often assume constant conductance per unit length along the whole cable. Non-uniform shunt conductance has been considered in [13,15]. To estimate a large number of discretized shunt conductance values along a long cable with sufficient accuracy (shunt conductance is typically at the order of Siemens/meter), large data sets have to be processed, requiring considerable computer memory and computation time. In order to reduce the number of unknowns to be estimated, this paper assumes that the shunt conductance varies only at a few positions along the cable, in order to address the case of localized failures. Of course, the positions of localized failures are unknown. To efficiently solve such a particular parameter estimation problem, sparse regression techniques will be applied [16,17,18]. To increase the numerical efficiency, sparse regression will be used in association with some particular transformations of dynamic systems [19]. To our knowledge, this proposed solution is the only electrical measurement-based method for the efficient detection, location, and quantification of localized insulator failures.
Insulation failure diagnosis by shunt conductance monitoring has the advantage of being non-destructive, since it is essentially based on voltage and current measurements. However, such measurements can only be made at one or two ends of a cable, whereas localized failures may appear anywhere along the cable at unknown positions. This is the main cause of difficulty in this approach. By analyzing electrical waves involving different frequencies based on a mathematical model of wave propagation, it is possible to extract information about localized failures from measurements made at the ends of a cable [1]. The particularity of the reported work is the automatic focus on localized shunt conductance variations with the efficient application of sparse regression techniques.
The solution of embedding fiber-optic sensors (FOS) in between copper wires of high-voltage phases or within insulator cross-linked polyethylene (XPLE) has been suggested in the literature [9,10], and the FOS placement strategy targets the fine bending monitoring of phases. The embedding of FOS within the XPLE or in between copper wires is technologically challenging due to the risk of breaking the sensors. This risk exists regardless of the area of placement of the FOS (embedded along the central copper wire and/or helically wound the same way as other copper wires). Indeed, extensive inter-copper-wire sliding/friction can arise with a high failure probability and risk of breaking the FOS. The option of embedding the FOS within thermoplastic materials is an alternative, although it would lead to the underestimation of the magnitude of the thermal parameters of the cables. Whether the error is constant or increasing, when shifting the positioning of the FOS between the copper section and the edge of the insulator, this is a key question that must be answered properly. It is worth noting that FOS embedding requires the special design and fabrication of cables with built-in fiber-optic sensors, which are themselves subject to possible failures. In contrast, the method proposed in this paper is based on electrical measurements made from the cable ends, without requiring any embedded sensor in the monitored cables.
This paper is organized as follows. Section 2 formulates the considered problem and summarizes the proposed solution. Section 3 presents the perturbation analysis and space-time discretization. Section 4 focuses on Kalman pre-filtering. Section 5 discusses Lasso sparse estimation. Section 6 presents the numerical results. Finally, Section 7 concludes the paper.
2. Problem Formulation and Solution Summary
In this section, the studied problem is first formulated, before a summary of the proposed solution is presented.
2.1. Cable Equations
In this work, electrical waves propagated in a cable are characterized by the well-known telegrapher’s equations [1,20,21]. They can be derived either from Maxwell’s equations under appropriate assumptions or from the equivalent circuit of a cable, as illustrated in Figure 1. See, e.g., [1,20]. Let be the time, be the cable longitudinal coordinate, and and be the distributed voltage and current along the cable at instant t and at position x; the telegrapher’s equations are
where , and denote, respectively, the series resistance, inductance, capacitance, and shunt conductance per unit length of the cable at the position x. The cable left end () is connected to a source with impedance and to an instrument so that the current is measured. Then,
At the other end () with a load of impedance , the boundary condition is
or, alternatively, if it is open-circuited,

Figure 1.
Equivalent circuit model of telegrapher’s equations.
From the system point of view, the input is
and the output is
In an electric cable with normal dielectric properties, the shunt conductance per unit length is very low, typically at the order of Siemens/meter. Gradual or sudden increments in the shunt conductance may occur due to degradation or damage to the dielectric properties of the insulator. The diagnostic method presented in this paper is based solely on electrical measurements made at one end of a cable, since it is more difficult to simultaneously measure at the two ends of a long cable, it is and not realistic to perform measurements along the entire length of the cable. To ease the presentation, the instruments are said to be connected at the left end of the cable where , whereas the right end corresponds to .
2.2. Shunt Conductance Estimation from Measurements
The method proposed in this paper for the monitoring of insulation damage consists of estimating the distributed shunt conductance from electric voltage–current measurements collected from one end of the cable only.
At first view, an obvious difficulty of this considered problem is due to the fact that, in the telegrapher’s Equation (1), the voltage and the current are unknown, except at the left end of the cable, where . This is not the only difficulty, as summarized below.
- The unknown distributed along the whole cable length is to be estimated from measurements at one cable end.
- The measurements have very weak sensitivity to small variations of .
- In the term of Equation (1), and are both unknown except at the point . This leads to a bilinear estimation problem.
2.3. Summary of the Proposed Method
After some transformations of the telegrapher’s equations, sparse estimation techniques will be applied, in order to automatically focus the estimation of on cable segments where the shunt conductance has deviated from its nominal value. The positions of such segments are unknown.
The essential steps are summarized as follows.
- In (1b), the bilinear term is linearized by perturbation analysis.
- The partial differential equations are discretized in x and in t in order to approximate the original infinite-dimensional system by a finite-dimensional discrete-time system.
- The Kalman filter is applied to pre-filter the voltage and current signals, assuming that throughout the cable, for some nominal conductance value . The effect of ignored by the Kalman filter then additively appears in the Kalman innovation.
- Lasso regression is then applied to estimate the unknown by analyzing the Kalman innovation sequence, under the assumption that deviates from its nominal value at some unknown positions.
3. Perturbation Analysis and Space-Time Discretization
This section summarizes the transformations of the telegrapher’s equations by perturbation analysis and space-time discretization, leading to state-space equations in order to apply Kalman pre-filtering followed by sparse regression.
Assume that, in system (1), the shunt conductance has deviated from the nominal profile in such a way that
with some unknown and . Then, the perturbation analysis linearizes the bilinear term and yields two fictive systems: the zero-order system characterizing the nominal behavior corresponding to , and the first-order system describing the small deviation from the nominal behavior. See [15] for the details of the perturbation analysis in the particular case of . See also the footnote at the bottom of this page.
The space variable x is then discretized, leading to discretized current and voltage as illustrated in Figure 1. These discretized variables are then collected in the state vector
The zero-order and first-order systems have, respectively, their state vectors denoted by and .
The continuous-time state-space equations for the zero-order system are
and, similarly, for the first-order system,
The input and output of the zero-order system are
The matrices and are detailed in Appendix A at the end of this paper (Usually, state-space equations are written with the notations . Here, are used instead of to avoid confusion with the capacitance notation in the (discretized) telegrapher’s equations.). The term is composed as
in which are discretized , is the zero matrix, the input of the first-order system is
and spans a vector to a diagonal matrix. The output of the first-order system is
The state of the zero-order system is computed by solving the zero-order state Equation (9). For the purpose of insulator monitoring, will be estimated from , , , and . Notice that the state vector of the first-order system is also unknown.
The continuous-time state-space Equation (10) is then discretized in time, with the time stepsize :
where, for notational simplicity, means , and, similarly, for other occurrences of “”,
while are added for various modeling measurement errors. Note that the right-hand side of (15) is expressed with the matrix exponential [22].
4. Kalman Pre-Filtering
Let the covariance matrices of in (14) be denoted by Q and R, respectively. The pre-filtering consists of applying the Kalman filter to (14) by setting the unknown to zero, so that the term is ignored. Of course, this Kalman filter ignoring the term produces biased results. The analysis of this bias will lead to a simple linear regression equation for the estimation of , as presented below. Well-known results of Kalman filtering can be found in [23,24,25].
The resulting Kalman filter is
where is the state prediction (usually with the double index in the Kalman filter literature), and is the Kalman gain computed as follows:
The variance of the measurement noise is based on the measurement instrument’s data sheet, whereas the covariance of the modeling noise is used as a tuning parameter chosen by experimental trials.
The innovation (prediction error) of the Kalman filter is computed as
If the assumption made for Kalman pre-filtering was true, then the resulting Kalman innovation ( in this particular case) would behave as a zero mean noise sequence. However, if the insulator conductance has deviated from the nominal value. This discrepancy between the reality and the filter, which assumes , implies a bias in the innovation . More precisely, the biased Kalman innovation behaves as follows.
Proposition 1.
Let be the zero mean Kalman innovation in the particular case of system (14). The innovation corresponding to is related to by the following equation:
where the matrix is recursively defined as
A similar result regarding the updated filter error was presented in [19], in a case where the Kalman innovation does not exist because of the involvement of unknown inputs. In what follows, direct proof of (20) and (21) is presented.
Proof.
Let us start the proof by deriving the state estimation error dynamics. The state estimation error will be denoted by
It then follows from (14) and (17) that
and
Then, the last result is rearranged as
Applying this recursion from to the current value of k, we have
with the state transition matrix defined, for , as
and, for , as
Gathering (19), (23), and (26) yields
The notation was introduced directly before (20) for the particular case . In (29), it corresponds to when . Then,
and, by combining (29) and (30),
Following the iterations defined in (21), it is straightforward to check, with the notation defined in (27) and (28), that
and (31) becomes
which is exactly (20). This result is thus proven. □
In the linear regression (20), the innovation is computed through Kalman pre-filtering, is a known matrix, is obtained from (21), and is a noise term (a zero mean Kalman innovation). In principle, it is possible to estimate the unknown parameter vector with the classical least squares method [26,27,28,29,30] based on (20).
However, in the linear regression Equation (20), the vector contains a large number of unknowns, which correspond to the shunt conductance discretized along a cable. The estimation of all these unknowns would require a huge amount of data in order to achieve sufficient accuracy for the very small conductance values, typically at the order of Siemens/meter. To avoid this difficulty, sparse regression will be applied in the next section in order to automatically focus the estimation on the discretized shunt conductance values that deviate from the nominal conductance value.
5. Sparse Estimation by Lasso
From a data set collected at discrete time instants , a matrix and a vector are built as
where and are as in (20). Then, according to (20),
with the error vector
Based on the linear regression Equation (35), sparse regression algorithms can be applied for the estimation of by assuming that has a small number of non-zero values. The Lasso algorithm is given in [17,18]. Other algorithms could also be applied—for instance, stability selection [31], the Danzig selector [32], orthogonal pursuit [33], and CoSaMP [34]. The resulting Lasso estimation is
with and denoting the norm and norm, and being a weighting parameter determined by cross-validation [16] (section 5.1).
6. Numerical Simulation Results
A cable of 800 m is numerically simulated, with R = 1 m/m, L = 0.1 H/m, C = 5 pF/m. The nominal shunt conductance value Siemens/m. At some small segments of the cable, the conductance has the abnormal conductance value G = Siemens/m. The simulations are based on the well-known telegrapher’s equations [1].
For the voltage and current data collected at one end of the simulated cable, the sampling period is 10 ns. Each simulation is made for the duration of 20 ms, yielding 2,000,000 sampled data points. White Gaussian noise is added to the sampled data such that the signal-to-noise rate is 80 dB.
The right end of the cable is open-circuited. At the left end, a multi-sinusoidal voltage is injected and the resulting current signal is measured. The voltage and current signals are then processed with the method presented in this paper to estimate the conductance profile .
In the simulation result displayed in Figure 2, the blue line represents simulated conductance profile , and the red dotted line represents the estimated conductance profile, both in Siemens/m. Notice that the vertical axis (ordinate) is at the scale of . In this example, the Lasso regression has correctly detected most positions where the conductance deviates from the nominal value. The estimation error is less than Siemens/m.
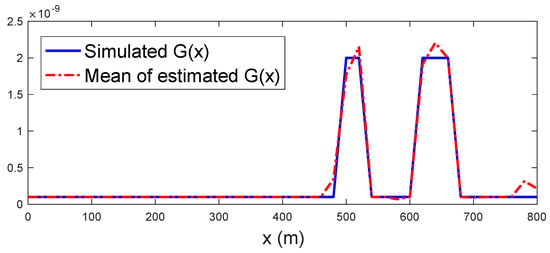
Figure 2.
Result 1 of shunt conductance profile estimation in one simulation. Abscissa: position along the cable in meters. Ordinate: shunt conductance in Siemens/meter. Blue line: simulated conductance profile , red dotted line: estimated conductance profile.
In another simulation result shown in Figure 3, the algorithm has over-detected the conductance at more positions. Nevertheless, the estimation error remains below Siemens/m.
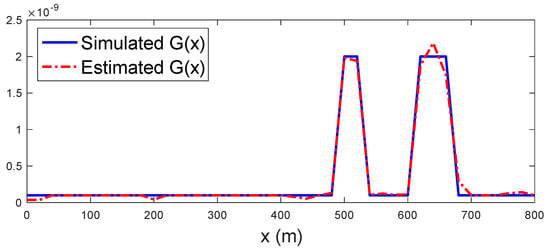
Figure 3.
Result 2 of shunt conductance profile estimation in one simulation. Abscissa: position along the cable in meters. Ordinate: shunt conductance in Siemens/meter. Blue line: simulated conductance profile , red dotted line: estimated conductance profile.
To evaluate the statistical properties of this estimation method, the simulation is then repeated 100 times with different random noise realizations, and the conductance profile is estimated for each of these simulations. The results are summarized in Figure 4: the blue line gives the simulated conductance profile , the red line shows the estimated conductance profile averaged over 100 simulations, and the pink area indicates the uncertainty of the estimated profile corresponding to the standard deviation around the estimated mean profile. The root mean squared error (RMSE) and mean absolute percentage error (MAPE) of these results are presented in Table 1.
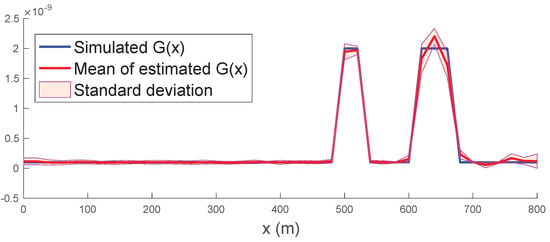
Figure 4.
Results of shunt conductance profile estimation based on 100 simulations. Abscissa: position along the cable in meters. Ordinate: shunt conductance in Siemens/meter. Blue line: simulated conductance profile , red line: estimated conductance profile averaged over 100 simulations, pink area: uncertainty of the estimated profile corresponding to the standard deviation around the estimated average profile.

Table 1.
Root mean squared error (RMSE) and mean absolute percentage error (MAPE) of the results of shunt conductance estimation based on 100 realizations. The unit of RMSE is nano ( Siemens/meter. MAPE is a percentage (×100%).
These results show that the distributed conductance estimation error is generally below Siemens/m. The accuracy of the estimation method based on the processing of 2,000,000 sampled data points appears sufficient to detect and characterize localized conductance variations at the order of Siemens/m. To our knowledge, this is the first reported method for distributed shunt conductance estimation automatically focusing on localized conductance variations at unknown positions. It provides an electrical measurement-based method for the efficient detection, location, and quantification of localized insulator failures. Despite the very small conductance values and the resulting weak sensitivity of electric measurements made at one end of a cable, the automatic focus on localized conductance variations makes possible the monitoring of localized insulator damage by processing sensor data with a computational time of about 10 s on a notebook computer. This computational efficiency is due to the transformations of the telegrapher’s equations to a linear regression form, from Equation (1) to Equation (20).
7. Conclusions
The shunt conductance directly reflects the insulator quality of a cable, since it is proportional to the leakage current in the insulator. Good cables have a very small nominal conductance value. Even if it is locally multiplied by a factor of 10, the effects of the variation on the cable may be barely perceptible from electrical measurements. Nevertheless, the spatially localized growth of can reveal inadvertent cable degradation, as an early sign of failure. The proposed method of this paper offers direct information about localized damage that should attract the attention of cable operators. In addition, by periodically estimating , the temporal evolution of provides important information for damage prognosis.
The diagnosis of localized insulator damage has been investigated in the reported work. Numerical simulations have shown the potential for future developments, particularly the ability of sparse regression to automatically focus on localized variations in the shunt conductance profile. Based on this exploratory numerical study, the encouraging results will open the door to experimental validation. In the near future, we plan to evaluate the performance of other sparse regression techniques applied to the considered problem. We will also work on different types of cables.
Author Contributions
Conceptualization, Q.Z.; methodology, Q.Z.; software, Q.Z.; validation, Q.Z. and M.D.-H.; formal analysis, Q.Z.; investigation, Q.Z.; resources, M.D.-H. and Q.Z.; data curation, Q.Z.; writing—original draft preparation, Q.Z.; writing—review and editing, Q.Z. and M.D.-H.; visualization, Q.Z. and M.D.-H.; supervision, Q.Z.; project administration, M.D.-H. and Q.Z.; funding acquisition, Q.Z. and M.D.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the FLOW CAM project of MarTERA ERA-NET COFUND.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Telegrapher’s Equations Space Discretization
The telegrapher’s equations (1) approximated by the circuit in Figure 1 correspond to the discretization of (1) in x, with the size of the discretization step
and (The positions are at the nodes in Figure 1).
Define the state vector for the discretized telegrapher equations
Similarly, the state vectors of the zero-order and first-order systems are, respectively, denoted by and . Then, the state-space equations of the zero-order and first-order systems are
and
where the matrices
with (the unspecified entries are zeros)
and
where and are the zero and identity matrices.
References
- Paul, C.R. Analysis of Multiconductor Transmission Lines; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Ulaby, F.T.; Michielssen, E.; Ravaioli, U. Fundamentals of Applied Electromagnetics, 6th ed; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Auzanneau, F. Wire troubleshooting and diagnosis: Review and perspectives. Prog. Electromagn. Res. B 2013, 49, 253–279. [Google Scholar] [CrossRef]
- Bawart, M.; Marzinotto, M.; Mazzanti, G. Diagnosis and location of faults in submarine power cables. IEEE Electr. Insul. Mag. 2016, 32, 24–37. [Google Scholar] [CrossRef]
- Chen, C.; Guan, Q.; Guan, Q.; Jin, X.; Shi, Z. A wavenumber domain reflectometry approach to locate and image line-like soft faults in cables. IEEE Trans. Instrum. Meas. 2023, 72, 6011012. [Google Scholar] [CrossRef]
- Furse, C.M.; Kafal, M.; Razzaghi, R.; Shin, Y.-J. Fault diagnosis for electrical systems and power networks: A review. IEEE Sens. J. 2020, 21, 888–906. [Google Scholar] [CrossRef]
- Huo, Y.; Prasad, G.; Atanackovic, L.; Lampe, L.; Leung, V.C. Cable diagnostics with power line modems for smart grid monitoring. IEEE Access 2019, 7, 60206–60220. [Google Scholar] [CrossRef]
- Lee, H.M.; Lee, G.S.; Kwon, G.-Y.; Bang, S.S.; Shin, Y.-J. Industrial applications of cable diagnostics and monitoring cables via time–frequency domain reflectometry. IEEE Sens. J. 2020, 21, 1082–1091. [Google Scholar] [CrossRef]
- Miceli, M.; Carvelli, V.; Drissi-Habti, M. Modelling electro-mechanical behaviour of an XPLE insulation layer for hi-voltage composite power cables: Effect of voids on onset of coalescence. Energies 2023, 16, 4620. [Google Scholar] [CrossRef]
- Drissi-Habti, M.; Abhijit, N.; Sriharsha, M.; Carvelli, V.; Bonamy, P.-J. Concept of placement of fiber-optic sensor in smart energy transport cable under tensile loading. Sensors 2022, 22, 2444. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, A.B.; Neves, W.L.; Costa, E.G.; Cavalcanti, M.N. The effect of the shunt conductance on transmission line models. In Proceedings of the International Conference on Power Systems Transients, Rio de Janeiro, Brazil, 24–28 June 2001; pp. 49–54. [Google Scholar]
- Fernandes, A.B.; Neves, W.L.; Costa, E.G.; Cavalcanti, M.N. Transmission line shunt conductance from measurements. IEEE Trans. Power Deliv. 2004, 19, 722–728. [Google Scholar] [CrossRef]
- Jing, L.; Wang, W.; Li, Z.; Murch, R.D. Detecting impedance and shunt conductance faults in lossy transmission lines. IEEE Trans. Antennas Propag. 2018, 66, 3678–3689. [Google Scholar] [CrossRef]
- Yu, T.-C. Influences of frequency-dependent shunt admittances on underground cable systems. IEEE Trans. Power Deliv. 2008, 23, 2385–2391. [Google Scholar]
- Zhang, Q.; Tang, H. Diagnosis of inhomogeneous insulation degradation in electric cables by distributed shunt conductance estimation. Control Eng. Pract. 2013, 21, 1195–1203. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2021. [Google Scholar]
- Liu, H.; Yu, B. Asymptotic properties of Lasso+mLS and Lasso+Ridge in sparse high-dimensional linear regression. Electron. J. Stat. 2013, 7, 3124–3169. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zhang, Q. Dynamic system fault diagnosis under sparseness assumption. IEEE Trans. Signal Process. 2021, 69, 2499–2508. [Google Scholar] [CrossRef]
- Dworsky, L.N. Modern Transmission Line Theory and Applications; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Sadiku, M.N.O. Elements of Electromagnetics; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Leonard, I. The matrix exponential. SIAM Rev. 1996, 38, 507–512. [Google Scholar] [CrossRef]
- Anderson, B.D.O.; Moore, J.B. Optimal Filtering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory; Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Kailath, T.; Sayed, A.H.; Hassibi, B. Linear Estimation; Prentice-Hall: New York, NY, USA, 2000. [Google Scholar]
- Björck, A. Numerical Methods for Least Squares Problems; SIAM: Philadephia, PA, USA, 1996. [Google Scholar]
- Kariya, T.; Kurata, H. Generalized Least Squares; Wiley: Chichester, UK, 2004. [Google Scholar]
- Rao, C.R.; Toutenburg, H. Linear Models: Least Squares and Alternatives, 2nd ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Strutz, T. Data Fitting and Uncertainty: A Practical Introduction to Weighted Least Squares and Beyond; Vieweg and Teubner: Wiesbaden, Germany, 2010. [Google Scholar]
- Wolberg, J. Data Analysis Using the Method of Least Squares: Extracting the Most Information from Experiments; Springer: Berlin, Germany, 2005. [Google Scholar]
- Meinshausen, N.; Buhlmann, P. Stability selection. J. R. Stat. Soc. Ser. B 2010, 72, 417–473. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. Rejoinder: The Dantzig selector: Statistical estimation when p is much larger than n. Ann. Stat. 2007, 35, 2392–2404. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).