An Optimal Hierarchical Control Strategy for 4WS-4WD Vehicles Using Nonlinear Model Predictive Control
Abstract
:1. Introduction
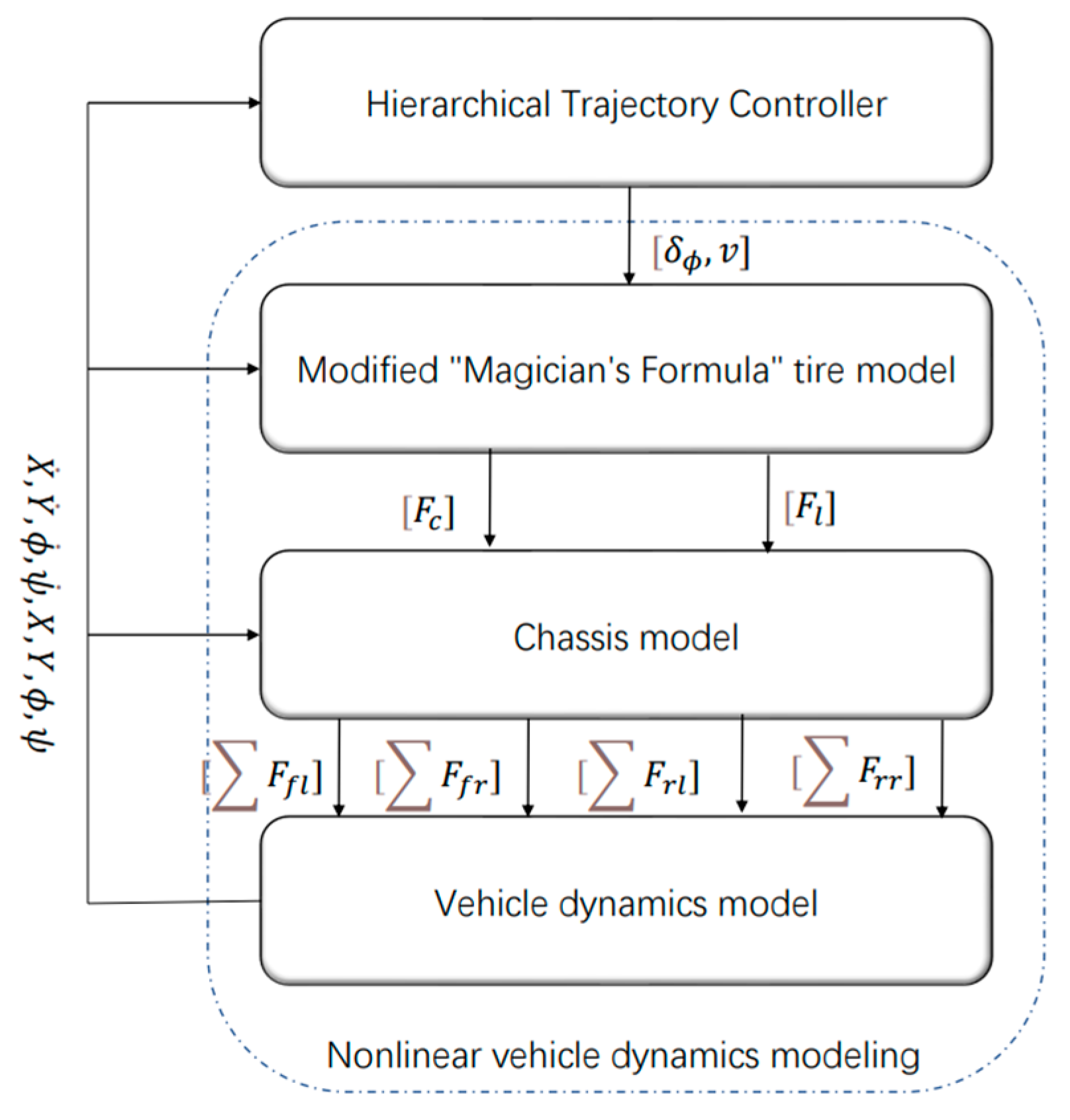
2. Nonlinear Three-Dimensional Pose-Varying Vehicle Model
2.1. Model Assumptions
- Autonomous driving takes place on a flat road surface, i.e., there is no vertical freedom of the chassis due to the unevenness of the vertical road surface, and the change in the gravitational potential energy of the vehicle due to the displacement of the vertical road surface is neglected.
- The overall structure of autonomous driving is rigid, and the body stiffness is large enough.
- Assuming that the steering system is rigid and ignoring the local degrees of freedom due to the deformation of the steering column, the input from the steering wheel can be applied directly and proportionally to the steering wheel.
- The effects of drag and vehicle aerodynamics can be ignored.
- The role of tire return torque can be ignored.
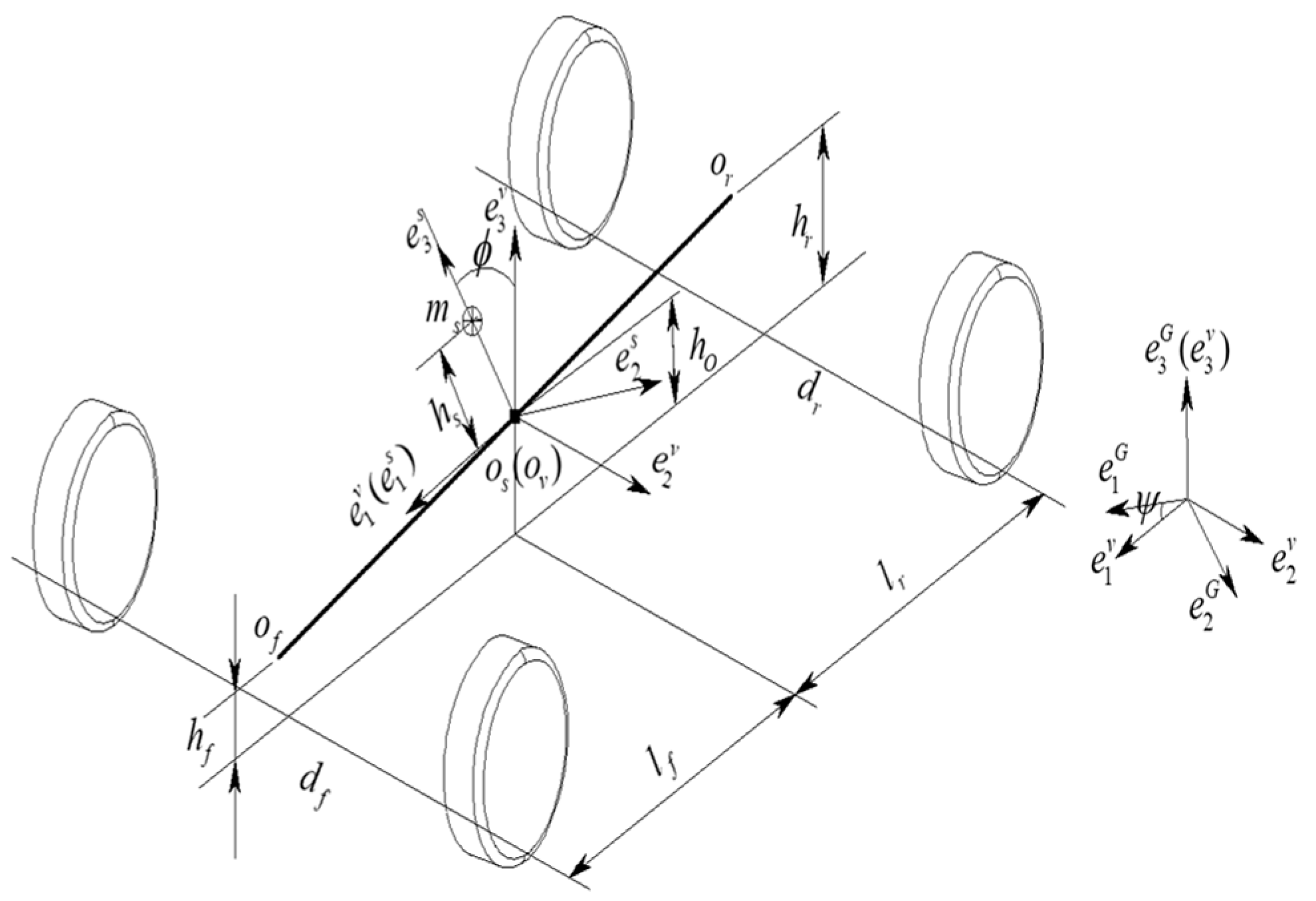
2.2. Kinematic Analysis of the Vehicle
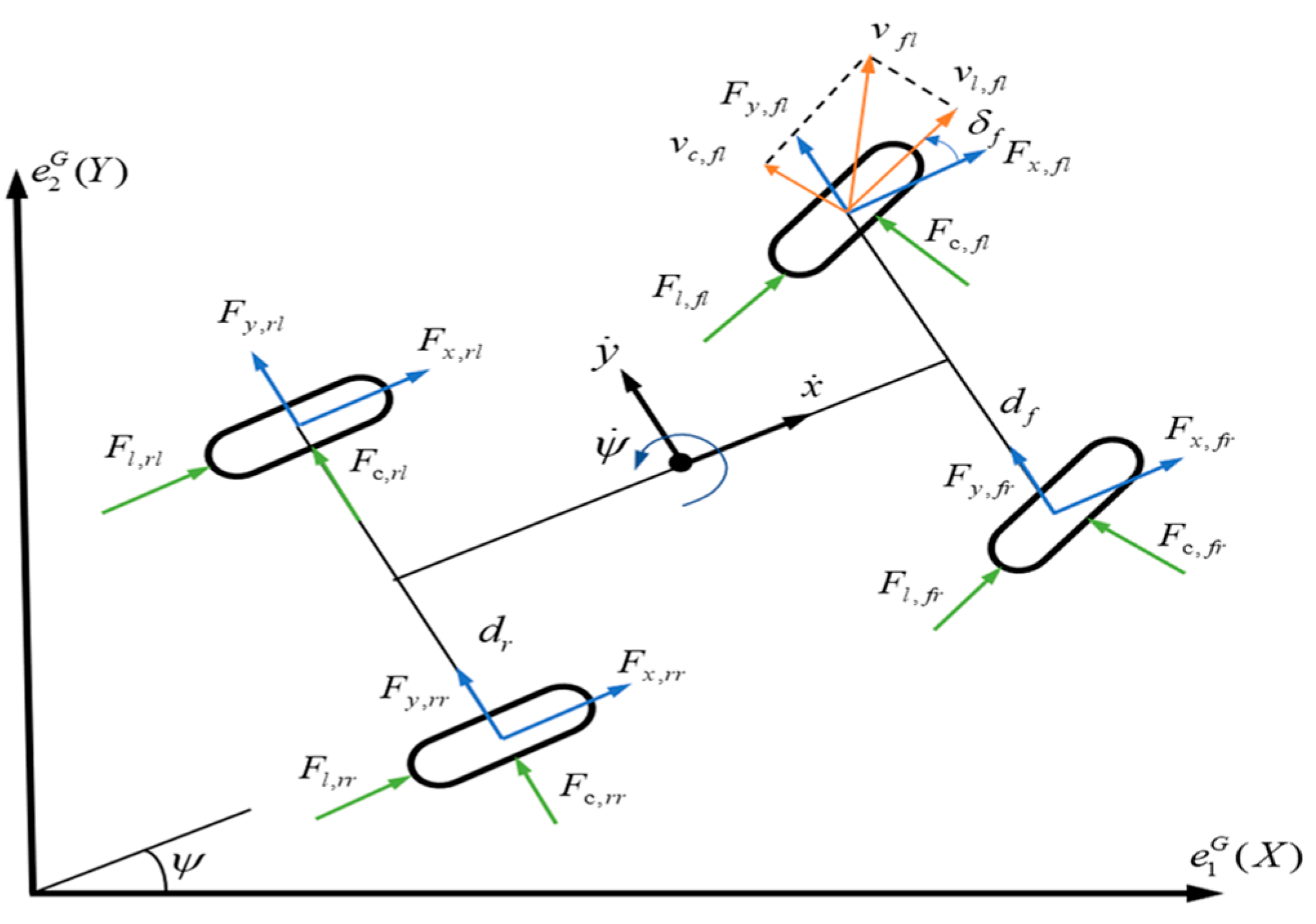
2.3. Vehicle Dynamics Model
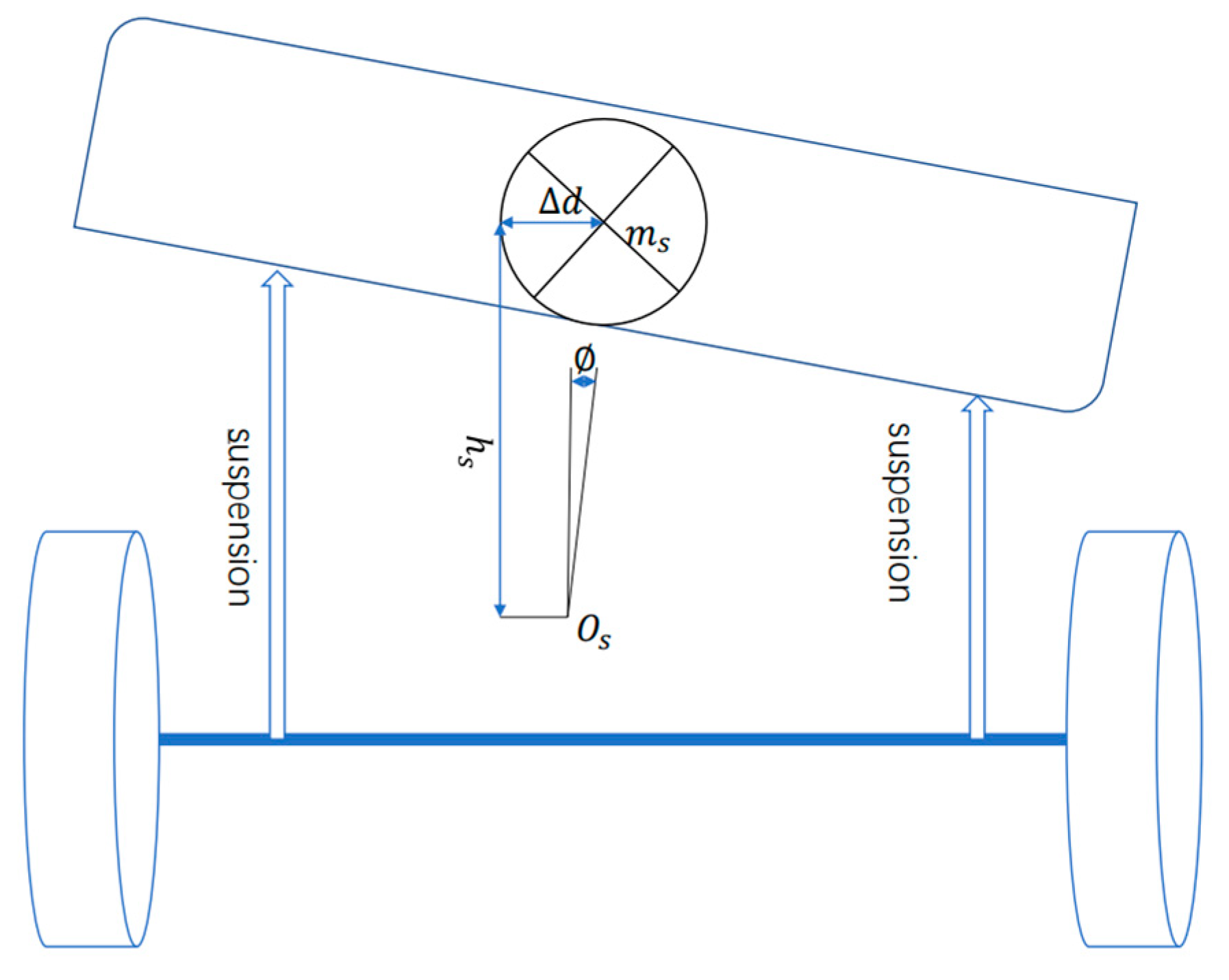
2.4. Chassis Dynamics Model
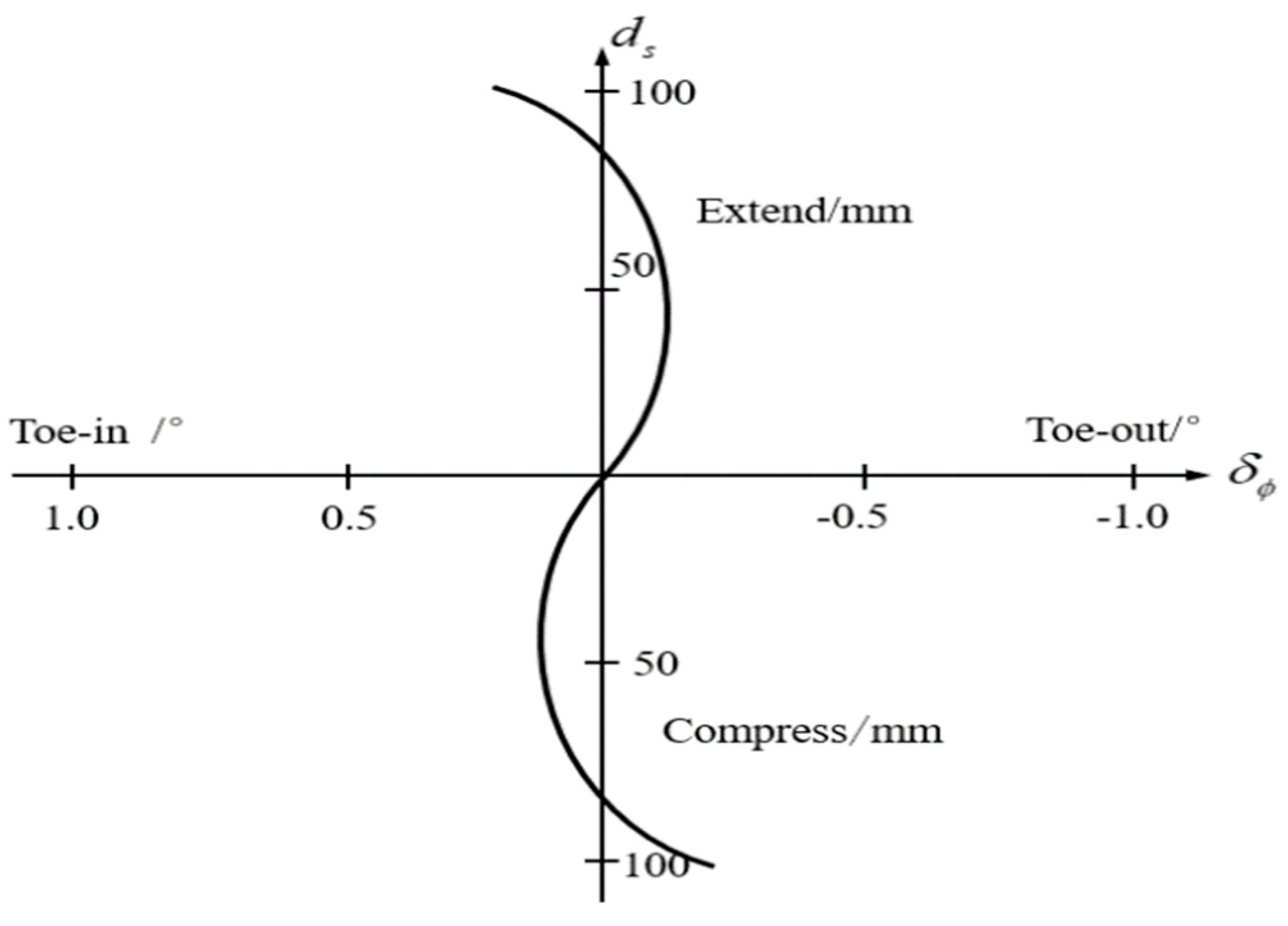
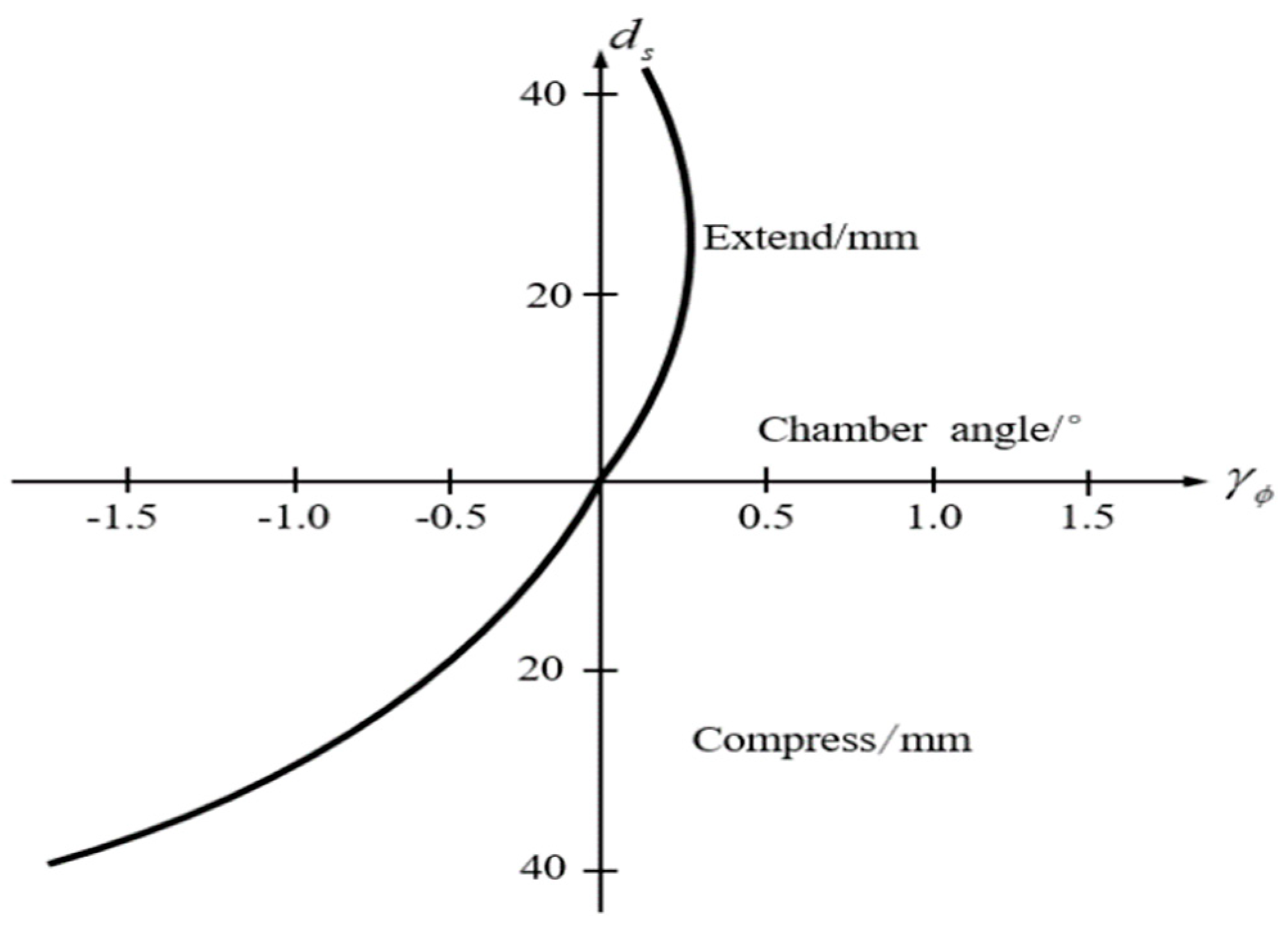
2.5. Modified “Magic Formula” Tire Model
3. Upper Trajectory Tracking Controller
3.1. Predictive Model
3.2. Constraints
3.3. Cost Function
3.4. Solutions
4. Lower Decoupling-Controller
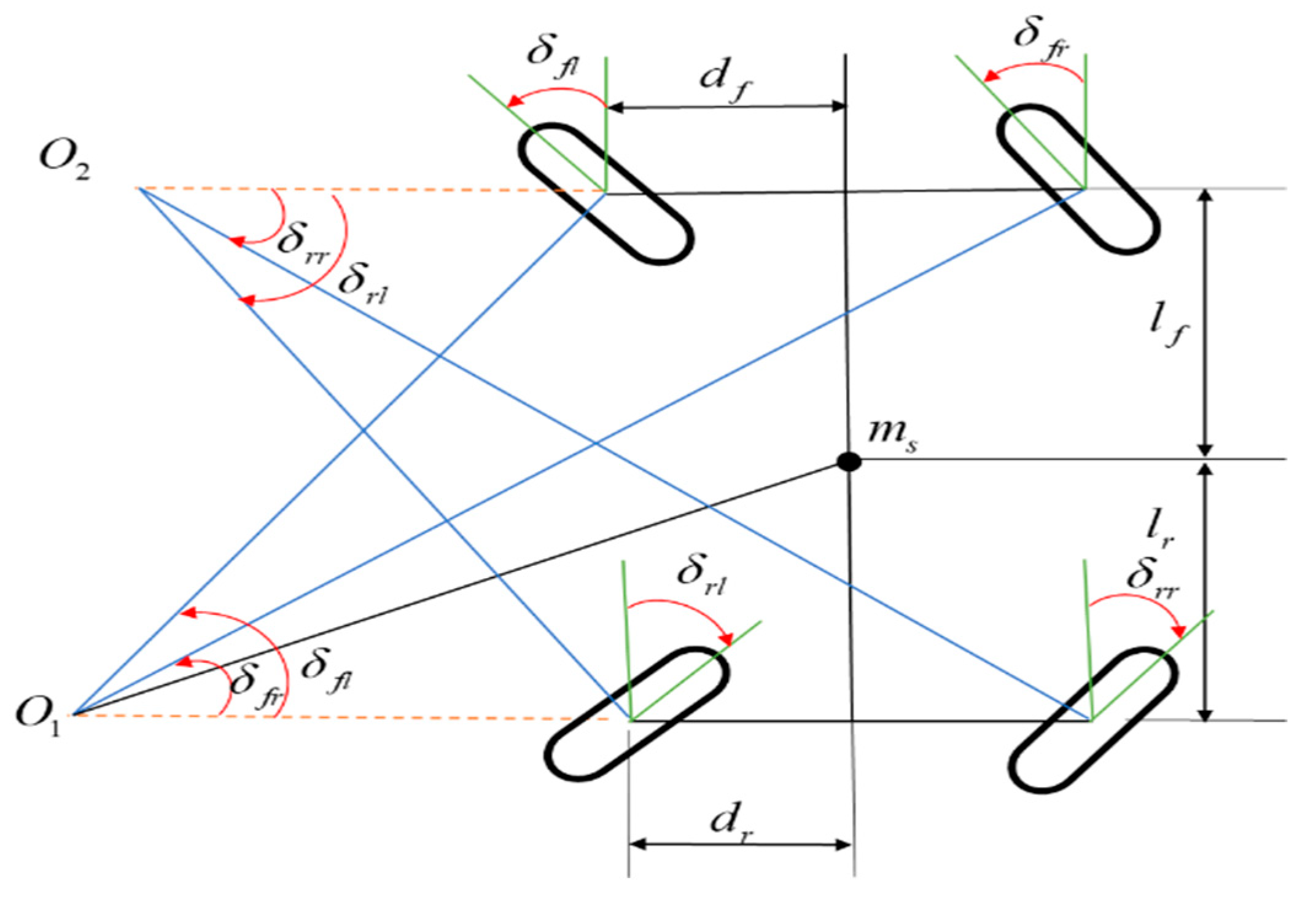
4.1. Four-Wheel Angle Decoupling Control Scheme
4.2. Four-Wheel Torque Decoupling Control Scheme
4.2.1. Four-Wheel Torque Control Variables Variation
4.2.2. Upper Control Variable Difference
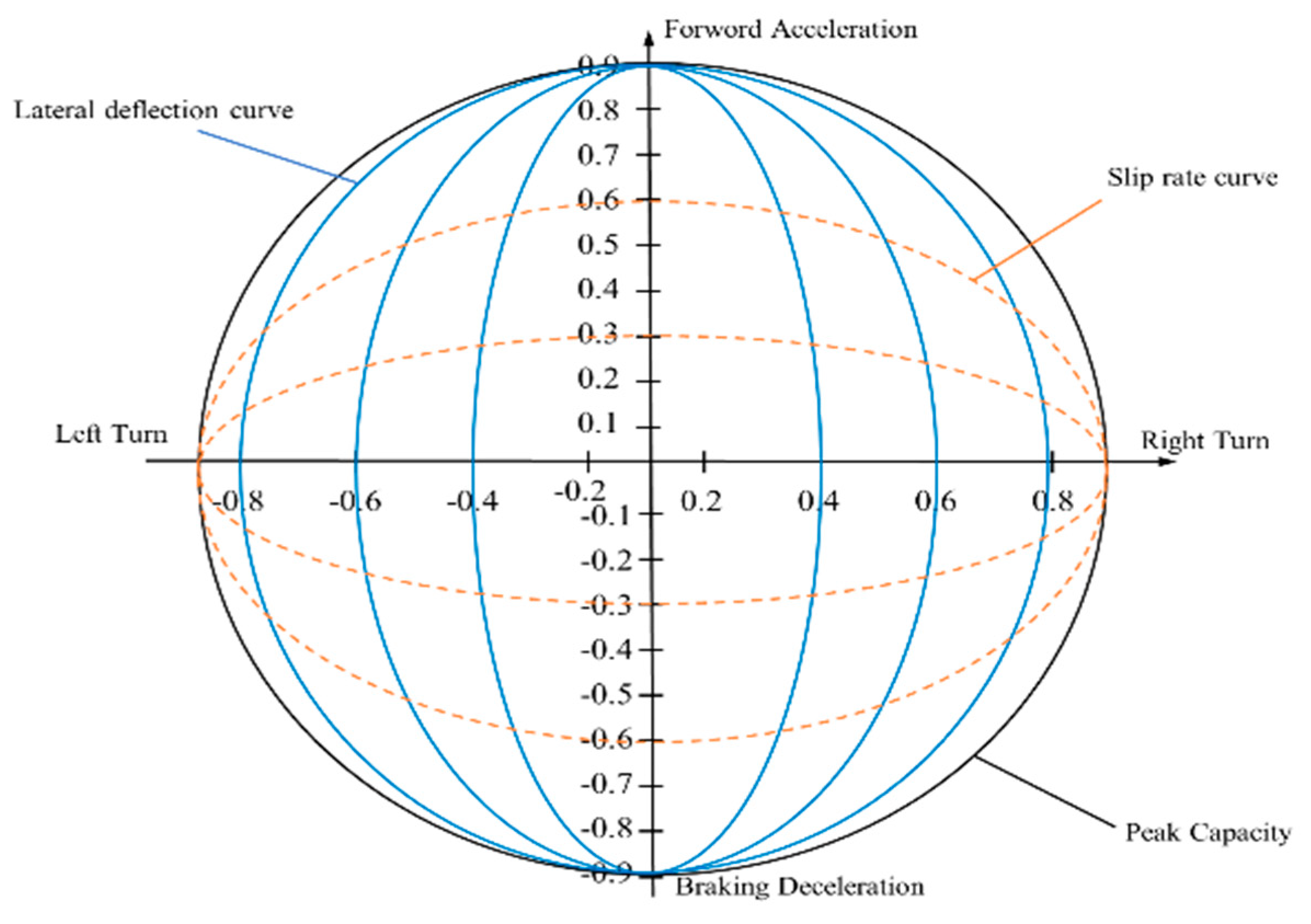
4.2.3. Tire Adhesion Limit
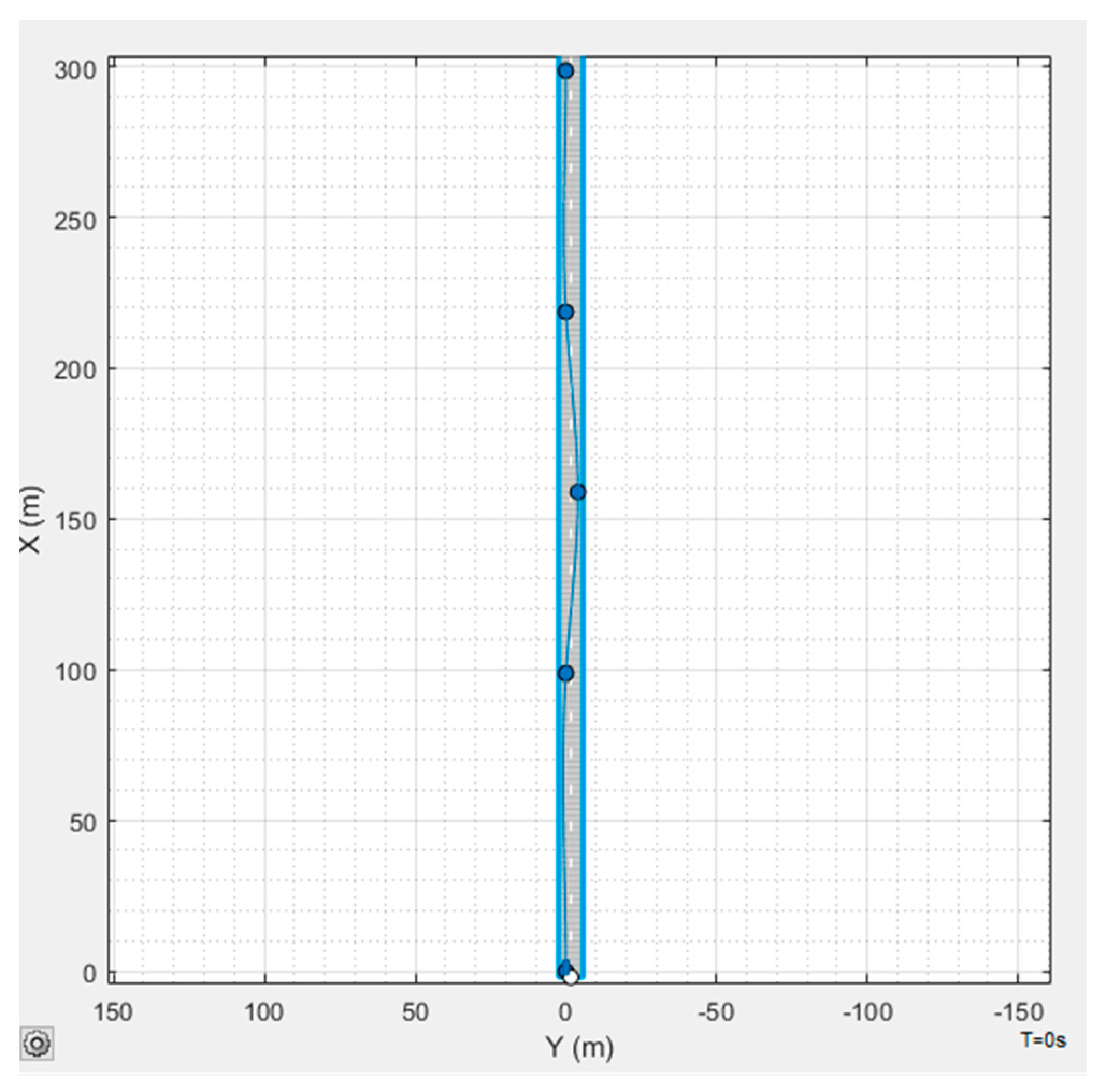
5. Simulation and Analysis
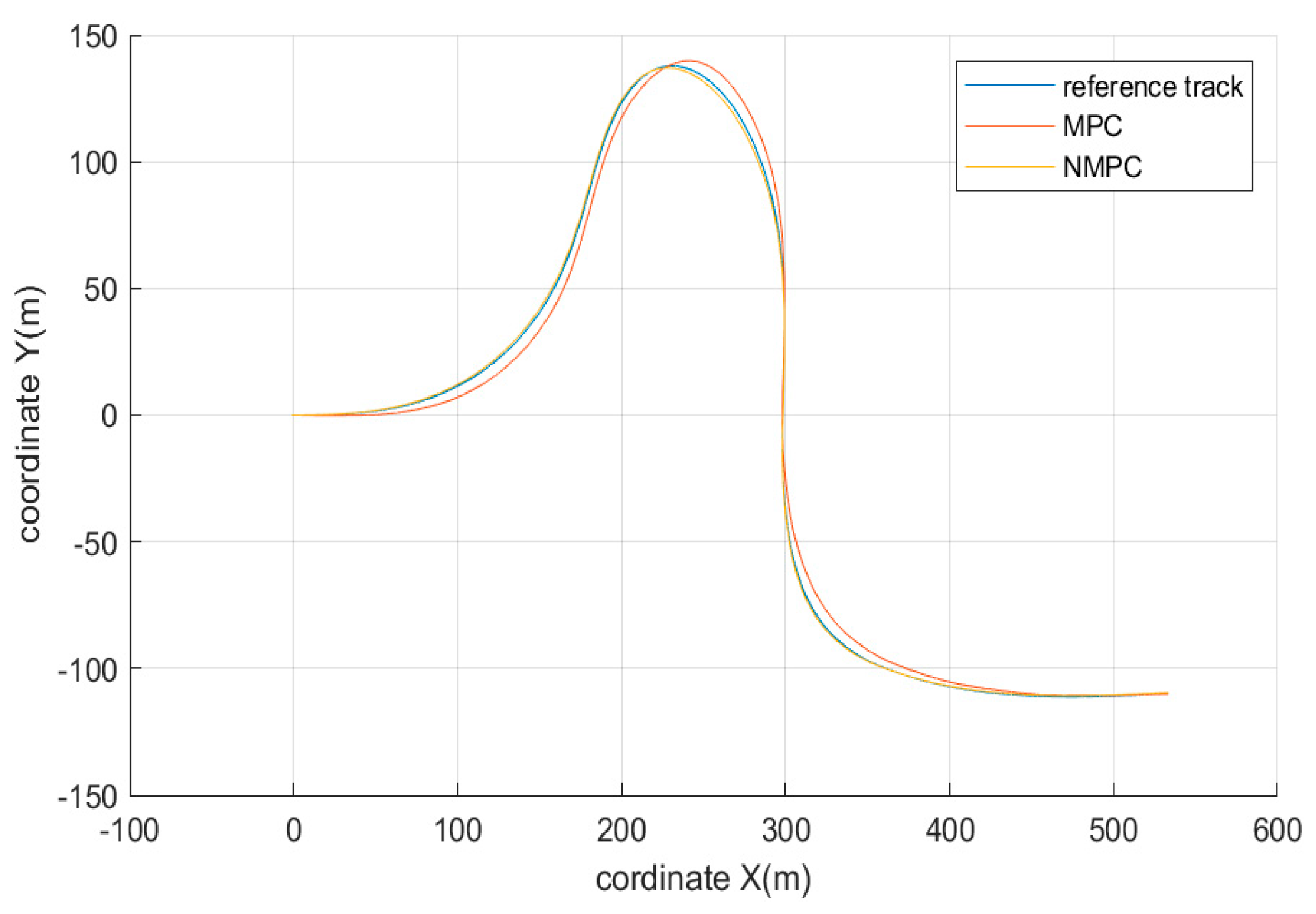
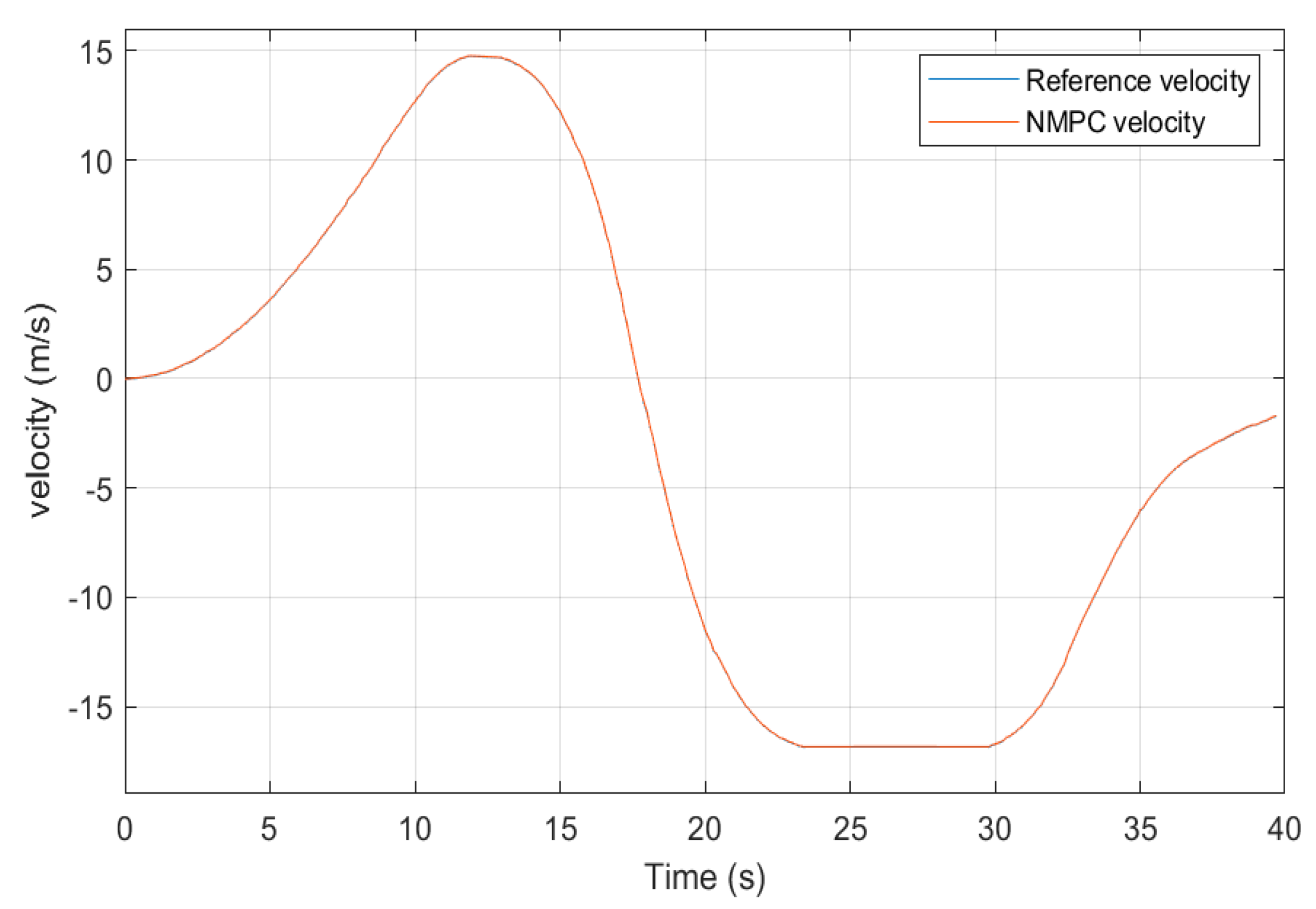
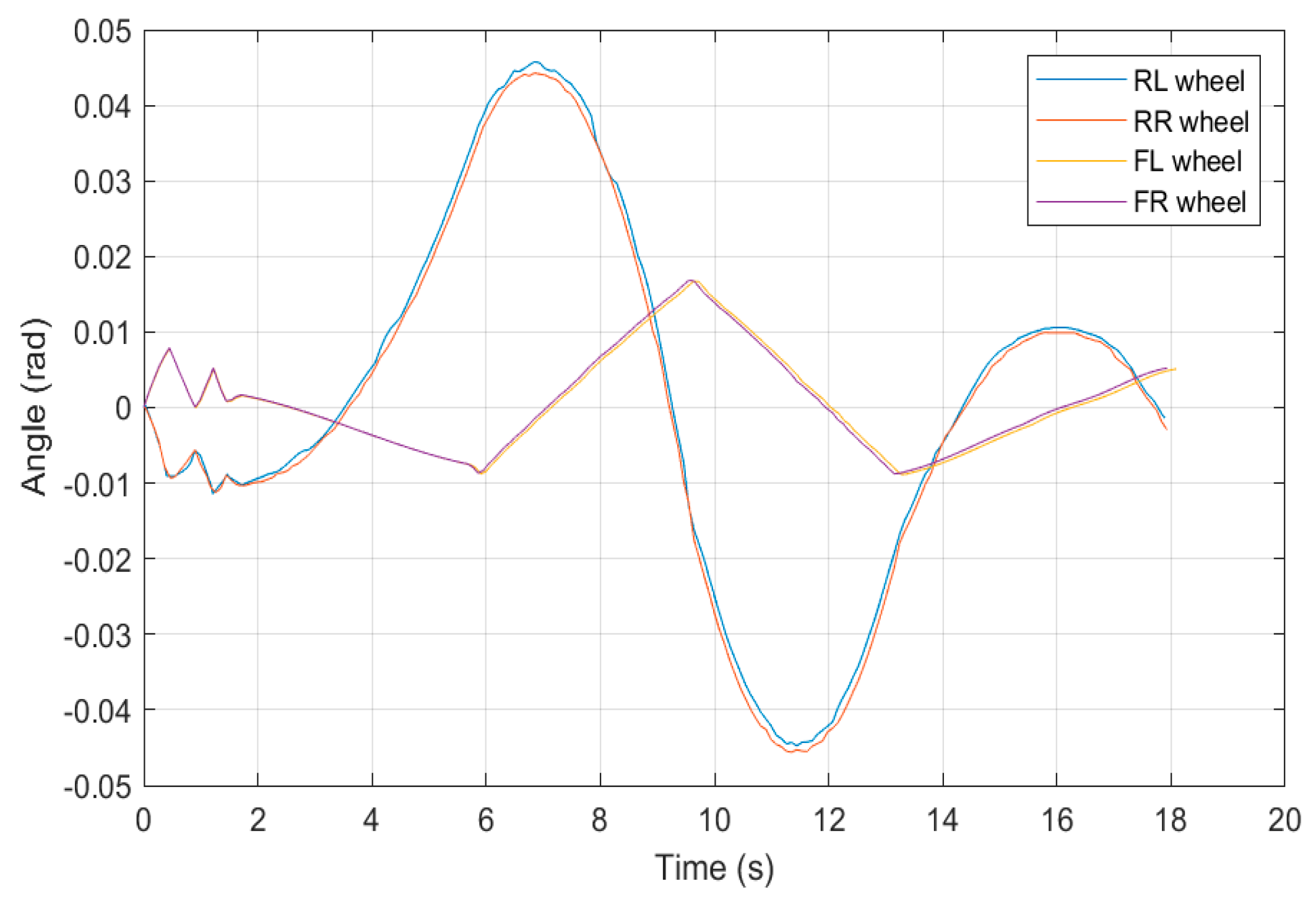
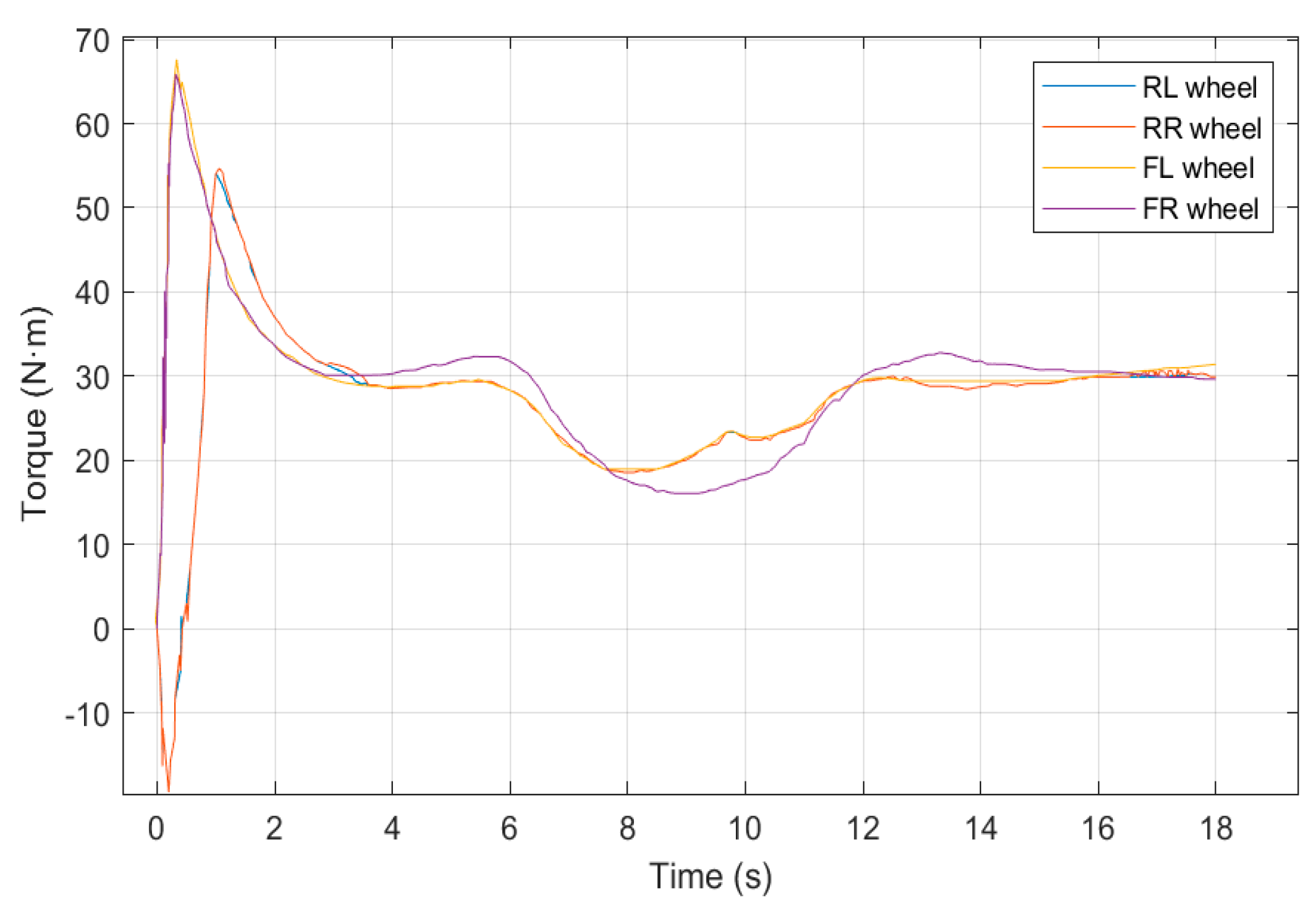
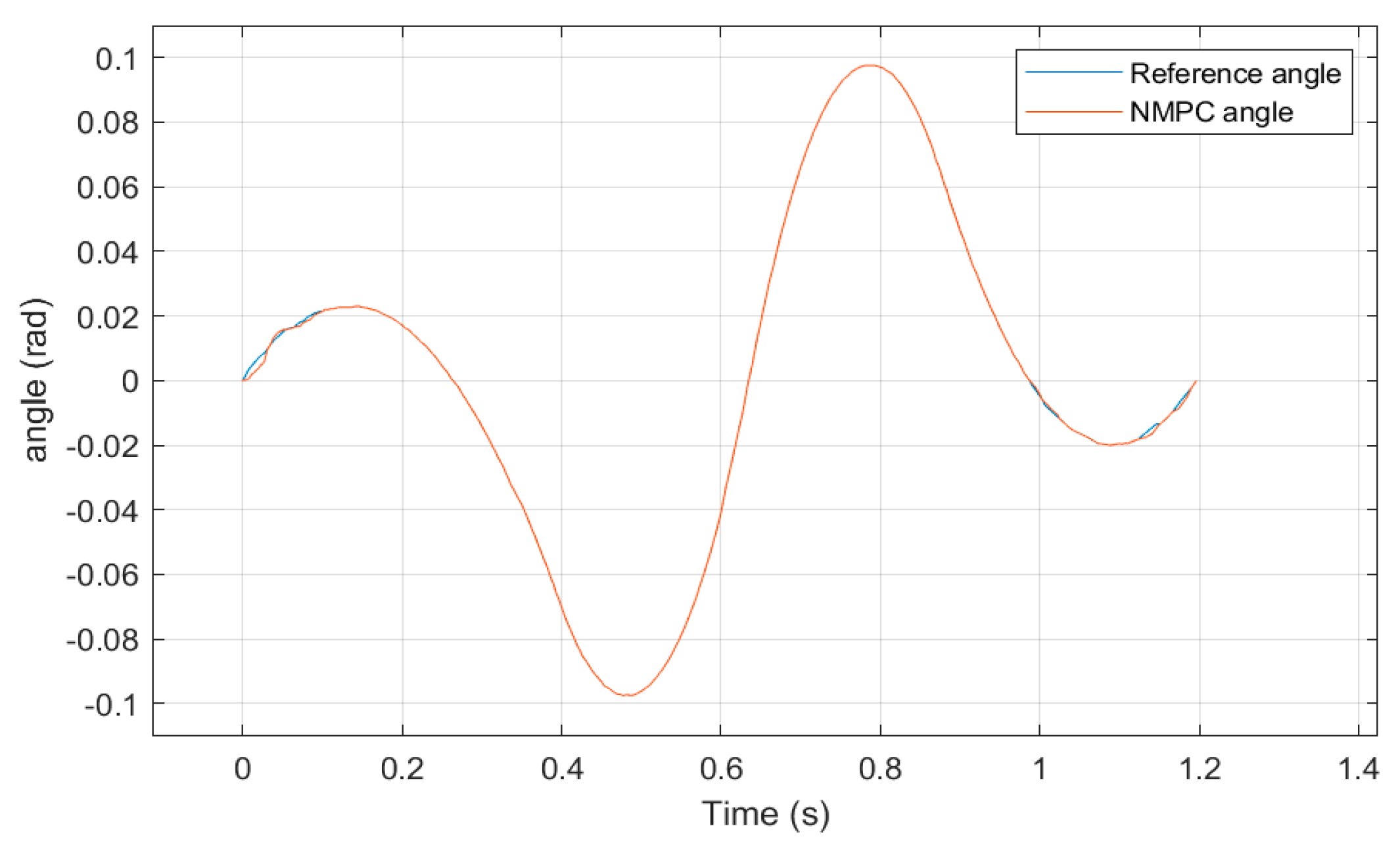
5.1. Simulation of High-Speed Serpentine Working Conditions
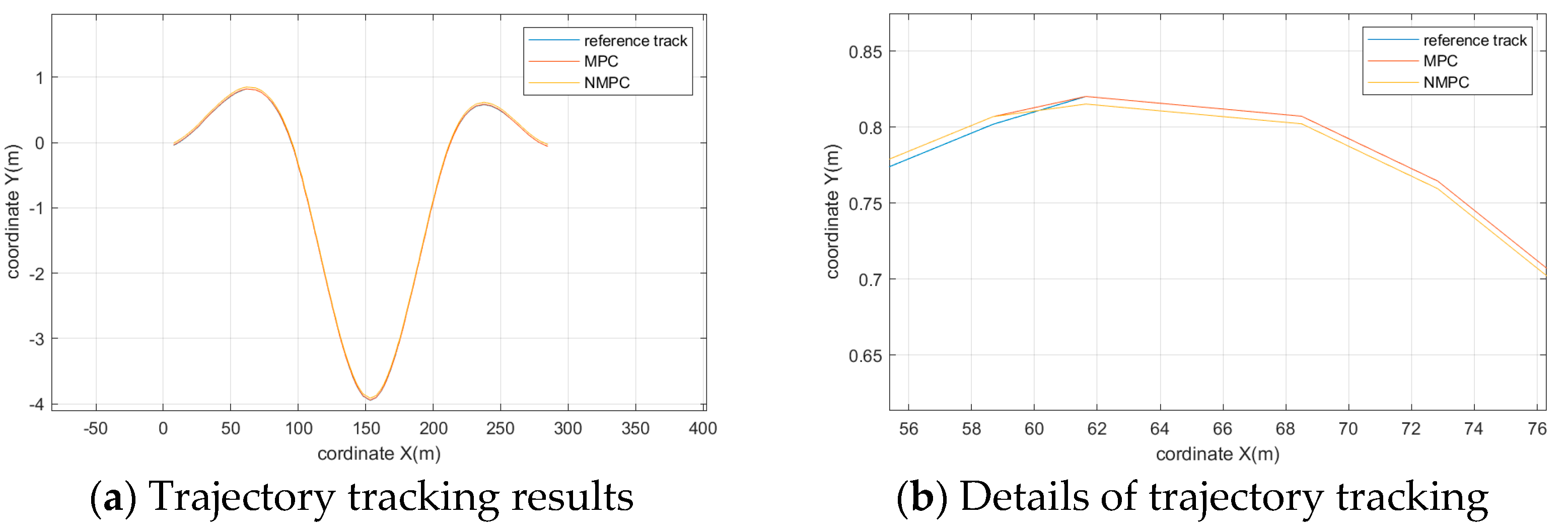
5.2. Simulation of Double-Shifted Line Working Condition
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter Name | Parameter | Numeric |
|---|---|---|
| Sampling Period | 0.01 | |
| Prediction Time Domain | 10 | |
| Control Time Domain | 4 | |
| Weighting Matrix | [1,1,0.1,0.2,1,1,0,1] | |
| Weight Matrix | [0.6,0.6] | |
| Weight matrix | [0.1,0.1,0,0,0.1,0.1,0,0] | |
| Weight Coefficients | 1000 | |
| Weighting Matrix | [0.3,0.3,0.8,0.8] | |
| Weight Coefficients | [0.3 1 0.6] |
References
- Silva, D.S.; Csiszár, C.; Földes, D. Autonomous vehicles and urban space management. Sci. J. Silesian Univ. Technol. Ser. Transp. 2021, 110, 169–181. [Google Scholar]
- Dudziak, A.; Stoma, M.; Kuranc, A.; Caban, J. Assessment of Social Acceptance for Autonomous Vehicles in Southeastern Poland. Energies 2021, 14, 5778. [Google Scholar] [CrossRef]
- Caban, J.; Nieoczym, A.; Dudziak, A.; Krajka, T.; Stopková, M. The Planning Process of Transport Tasks for Autonomous Vans—Case Study. Appl. Sci. 2022, 12, 2993. [Google Scholar] [CrossRef]
- Bartuska, L.; Labudzki, R. Research of basic issues of autonomous mobility. Transp. Res. Procedia 2020, 44, 356–360. [Google Scholar] [CrossRef]
- Farkaš, P.; Szőke, L.; Aradi, S. Defining metrics for scenario-based evaluation of autonomous vehicle models. In Proceedings of the 2022 IEEE 1st International Conference on Cognitive Mobility (CogMob), Budapest, Hungary, 12–13 October 2022; pp. 155–160. [Google Scholar]
- Kosobudzki, M.; Zajac, P.; Gardyński, L. A Model-Based Approach for Setting the Initial Angle of the Drive Axles in a 4 × 4 High Mobility Wheeled Vehicle. Energies 2023, 16, 1938. [Google Scholar] [CrossRef]
- Nieoczym, A.; Caban, J.; Dudziak, A.; Stoma, M. Autonomous vans—The planning process of transport tasks. Open Eng. 2020, 10, 18–25. [Google Scholar] [CrossRef]
- Czech, P.; Turoń, K.; Barcik, J. Autonomous Vehicles: Basic Issues. Sci. J. Silesian Univ. Technol. Ser. Transp. 2018, 100, 15–22. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, F. A Novel Simulation-Based Optimization Method for Autonomous Vehicle Path Tracking with Urban Driving Application. Mathematics 2023, 11, 4762. [Google Scholar] [CrossRef]
- Weilin, L.; Bo, C. Disturbance suppression and NN compensation based trajectory tracking of underactuated AUV. Ocean Eng. 2023, 288, 116172. [Google Scholar]
- Han, Y.; Ma, X.; Wang, B.; Zhang, H.; Zhang, Q.; Chen, G. A Strategy for Integrated Multi-Demands High-Performance Motion Planning Based on Nonlinear MPC. Appl. Sci. 2023, 13, 12443. [Google Scholar] [CrossRef]
- Wei, L.; Xiang, G.; Ma, C.; Jiang, X.; Dian, S. Trajectory Tracking Control of Transformer Inspection Robot Using Distributed Model Predictive Control. Sensors 2023, 23, 9238. [Google Scholar] [CrossRef]
- Si, Y.; Zhang, L. Research on Path Planning and Trajectory Tracking of Autonomous Vehicle. Autom. Mach. Learn. 2023, 4, 47–54. [Google Scholar]
- Hui, S.; Dayi, Q.; Haibing, G.; Kekun, Z.; Tao, W. Lane-Changing Trajectory Tracking and Simulation of Autonomous Vehicles Based on Model Predictive Control. Sustainability 2022, 14, 13272. [Google Scholar]
- Stano, P.; Montanaro, U.; Tavernini, D.; Tufo, M.; Fiengo, G.; Novella, L.; Sorniotti, A. Model predictive path tracking control for automated road vehicles: A review. Annu. Rev. Control 2023, 55, 194–236. [Google Scholar] [CrossRef]
- Manav, K.; Sharifuddin, M. Recent developments on target tracking problems: A review. Ocean Eng. 2021, 236, 109558. [Google Scholar]
- Shilp, D.; Saber, F.; Umberto, M.; Mehrdad, D.; Alan, S.; Francis, M.; Alexandros, M. Trajectory planning and tracking for autonomous overtaking: State-of-the-art and future prospects. Annu. Rev. Control 2017, 45, 76–86. [Google Scholar]
- Zhou, L.; Wang, G.; Sun, K.; Li, X. Trajectory Tracking Study of Track Vehicles Based on Model Predictive Control. Stroj. Vestn. J. Mech. Eng. 2019, 65, 329–342. [Google Scholar] [CrossRef]
- Wang, S.; Guo, J.; Mao, Y.; Wang, H.; Fan, J. Research on the Model Predictive Trajectory Tracking Control of Unmanned Ground Tracked Vehicles. Drones 2023, 7, 496. [Google Scholar] [CrossRef]
- Wang, J.; Chu, L.; Zhang, Y.; Mao, Y.; Guo, C. Intelligent Vehicle Decision-Making and Trajectory Planning Method Based on Deep Reinforcement Learning in the Frenet Space. Sensors 2023, 23, 9819. [Google Scholar] [CrossRef]
- Peng, H.; Xinbo, C. Towards Autonomous Driving: Review and Perspectives on Configuration and Control of Four-Wheel Independent Drive/Steering Electric Vehicles. Actuators 2021, 10, 184. [Google Scholar]
- Chowdhri, N.; Ferranti, L.; Iribarren, F.S.; Shyrokau, B. Integrated nonlinear model predictive control for automated driving. Control Eng. Pract. 2021, 106, 104654. [Google Scholar] [CrossRef]
- Ritschel, R.; Schrödel, F.; Hädrich, J.; Jäkel, J. Nonlinear Model Predictive Path-Following Control for Highly Automated Driving. IFAC Pap. 2019, 52, 350–355. [Google Scholar] [CrossRef]
- Chen, T.; Chen, L.; Xu, X.; Cai, Y.; Jiang, H.; Sun, X. Passive fault-tolerant path following control of autonomous distributed drive electric vehicle considering steering system fault. Mech. Syst. Signal Process. 2019, 123, 298–315. [Google Scholar] [CrossRef]
- Várszegi, B.; Takács, D.; Orosz, G. On the nonlinear dynamics of automated vehicles—A nonholonomic approach. Eur. J. Mech. A Solids 2018, 74, 371–380. [Google Scholar] [CrossRef]
- Van, N.D.; Sualeh, M.; Kim, D.; Kim, G. A Hierarchical Control System for Autonomous Driving towards Urban Challenges. Appl. Sci. 2020, 10, 3543. [Google Scholar] [CrossRef]
- Logan, S.; Lucian, N.; Eric, K. An efficient method for maximal area coverage in the context of a hierarchical controller for multiple unmanned aerial vehicles. Eur. J. Control 2023, 74, 100850. [Google Scholar]
- Nie, Y.; Liu, Y.; Cheng, S.; Mei, M.; Xiao, L. Unified Brake Service by a Hierarchical Controller for Active Deceleration Control in an Electric and Automated Vehicle. Energies 2017, 10, 2052. [Google Scholar] [CrossRef]
- Rafael, G.S.J.; Ramón, S.O.; Salvador, T.M.; Celso, M.S.; Manuel, H.G.V.; Mayra, A.C.; Gilberto, S.O.; Hind, T. Tracking Control for Mobile Robots Considering the Dynamics of All Their Subsystems: Experimental Implementation. Complexity 2017, 2017, 5318504. [Google Scholar]
- Qu, T.; Zhao, J.W.; Gao, H.H.; Cai, K.Y.; Chen, H.; Xu, F. Multi-mode switching-based model predictive control approach for longitudinal autonomous driving with acceleration estimation. IET Intell. Transp. Syst. 2020, 14, 2102–2112. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J. (Eds.) Nonlinear Model Predictive Control. In Nonlinear Model Predictive Control: Theory and Algorithms; Springer: London, UK, 2011; pp. 43–66. [Google Scholar]
- Minh, V.T.; Reza, M.; Jindrich, C.; Jaroslav, H. Model Predictive Control for Autonomous Driving Vehicles. Electronics 2021, 10, 2593. [Google Scholar]
- Hannes, W.; Frieder, G.; Oliver, S. Near Time Optimal Trajectory Generation for Over-Actuated Vehicles using Nonlinear Model Predictive Controller. IFAC Pap. 2020, 53, 15626–15631. [Google Scholar]
- Wang, J.; Liu, Z.; Chen, H.; Zhang, Y.; Zhang, D.; Peng, C. Trajectory Tracking Control of a Skid-Steer Mobile Robot Based on Nonlinear Model Predictive Control with a Hydraulic Motor Velocity Mapping. Appl. Sci. 2024, 14, 122. [Google Scholar] [CrossRef]
- Wu, Y.L.; Li, S.M.; Zhang, Q.J.; Sun-Woo, K.; Yan, L.Y. Route Planning and Tracking Control of an Intelligent Automatic Unmanned Transportation System Based on Dynamic Nonlinear Model Predictive Control. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16576–16589. [Google Scholar] [CrossRef]
- Bejarano, G.; Manzano, J.M.; Salvador, J.R.; Limon, D. Nonlinear model predictive control-based guidance law for path following of unmanned surface vehicles. Ocean Eng. 2022, 258, 111764. [Google Scholar] [CrossRef]
- Zou, K.; Cai, Y.F.; Chen, L.; Sun, X.Q. Event-triggered nonlinear model predictive control for trajectory tracking of unmanned vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 2474–2483. [Google Scholar] [CrossRef]
- Dawood, M.; Abdelaziz, M.; Ghoneima, M.; Hammad, S. A nonlinear model predictive controller for autonomous driving. In Proceedings of the 2020 International Conference on Innovative Trends in Communication and Computer Engineering (ITCE), Aswan, Egypt, 8–9 February 2020; pp. 151–157. [Google Scholar]
- Qin, S.J.; Badgwell, T.A. An Overview of Nonlinear Model Predictive Control Applications; Allgöwer, F., Zheng, A., Eds.; Birkhäuser: Basel, Switzerland, 2000; pp. 369–392. [Google Scholar]
- Rawlings, J.B.; Meadows, E.S.; Muske, K.R. Nonlinear Model Predictive Control: A Tutorial and Survey. IFAC Proc. Vol. 1994, 27, 185–197. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Bakker, E. The Magic Formula Tyre Model. Veh. Syst. Dyn. 2007, 21, 1–18. [Google Scholar] [CrossRef]
- Tian, M.; Gabor, S.; Denes, T.; Nan, C. Vehicle Shimmy Modeling with Pacejka’s Magic Formula and the Delayed Tire Model. J. Comput. Nonlinear Dyn. 2020, 15, 031005. [Google Scholar]
- Bardawil, C.; Daher, N.; Shammas, E. Applying the Similarity Method on Pacejka’s Magic Formula to Estimate the Maximum Longitudinal Tire-Road Friction Coefficient. In Proceedings of the American Control Conference 2020, Denver, CO, USA, 1–3 July 2020; pp. 218–223. [Google Scholar]
- Shi, P.; Zhao, Q.; Zhang, R.; Ye, L. The Simulation of Tire Dynamic Performance Based on “Magic Formula”. In Proceedings of the 2nd International Conference on Automation, Mechanical Control and Computational Engineering (AMCCE 2017), Beijing, China, 25–26 March 2017. [Google Scholar]
- Besselink, I.J.M.; Schmeitz, A.J.C.; Pacejka, H.B. An improved Magic Formula/Swift tyre model that can handle inflation pressure changes. Veh. Syst. Dyn. 2010, 48, 337–352. [Google Scholar] [CrossRef]
- Lu, C.Y.; Shih, M.C. Application of the Pacejka Magic Formula Tyre Model on a Study of a Hydraulic Anti-Lock Braking System for a Light Motorcycle. Veh. Syst. Dyn. 2010, 41, 431–448. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Wang, K.; Li, Q.; Yang, J. An Optimal Hierarchical Control Strategy for 4WS-4WD Vehicles Using Nonlinear Model Predictive Control. Machines 2024, 12, 84. https://doi.org/10.3390/machines12010084
Xu X, Wang K, Li Q, Yang J. An Optimal Hierarchical Control Strategy for 4WS-4WD Vehicles Using Nonlinear Model Predictive Control. Machines. 2024; 12(1):84. https://doi.org/10.3390/machines12010084
Chicago/Turabian StyleXu, Xuan, Kang Wang, Qiongqiong Li, and Jiafu Yang. 2024. "An Optimal Hierarchical Control Strategy for 4WS-4WD Vehicles Using Nonlinear Model Predictive Control" Machines 12, no. 1: 84. https://doi.org/10.3390/machines12010084
APA StyleXu, X., Wang, K., Li, Q., & Yang, J. (2024). An Optimal Hierarchical Control Strategy for 4WS-4WD Vehicles Using Nonlinear Model Predictive Control. Machines, 12(1), 84. https://doi.org/10.3390/machines12010084







