An Optimization Method for Green Permutation Flow Shop Scheduling Based on Deep Reinforcement Learning and MOEA/D
Abstract
1. Introduction
- Secondly, the optimization goal of most research is to minimize completion time, with little consideration given to other objectives such as energy consumption, machine utilization, and delivery time. However, as an essential aspect of manufacturing, energy consumption has become increasingly significant due to its dual impact on production costs and the environment. Therefore, implementing an effective energy-saving strategy in production scheduling not only helps to reduce production costs and enhance the competitiveness of enterprises, but also reduces carbon emissions. It aligns with the global green environmental trend and promotes the achievement of sustainable development goals.
- Furthermore, in existing research, the state of the environment for RL algorithms is typically constructed as a set of performance indicators, with each indicator usually mapped to a specific feature. However, the intricate correlations among these performance indicators lead to a complex internal structure of the environmental state, which may contain a large amount of redundant information. This complexity not only increases the difficulty of convergence for neural networks, but may also negatively impact the decision-making process of the agent, reducing the accuracy and efficiency of its decisions.
- Finally, in existing research, the action space of the agent is often limited to a series of heuristic rules based on experience. While these rules are easy to understand and implement, they may restrict the exploration of the agent, preventing it from fully uncovering and executing more complex and efficient scheduling strategies.
- Firstly, for the existing end-to-end deep reinforcement learning network, which is difficult to apply to different scales of the green permutation flow shop scheduling problem (GPFSP) considering energy consumption, we designed a network model based on DRL (DRL-PFSP) to solve PFSP. This network model does not require any high-quality labeled data and can flexibly handle PFSPs of various sizes, directly outputting the corresponding scheduling solutions, which greatly enhances the practicality and usability of the algorithm.
- Secondly, the DRL-PFSP model is trained using the actor–critic RL method. After the model is trained, it can directly generate scheduling solutions for PFSPs of various sizes in a very short time.
- Furthermore, in order to significantly enhance the quality of solutions produced by the MOEA/D algorithm, this study innovatively employs solutions generated by the DRL-PFSP model as the initial population for MOEA/D. This approach not only provides MOEA/D with a high-quality starting point, but also accelerates the convergence of the algorithm and improves the performance of the final solutions. Additionally, to further optimize the energy consumption target, a strategy of job postponement for energy saving is proposed. This strategy reduces the machine’s idle time without increasing the completion time, thereby achieving further optimization of energy consumption.
- Eventually, through comparative analysis of simulation experiments with the unimproved MOEA/D, NSGA-II, MPA, SSA, AHA, and SOA, the GDRL-MOEA/D model algorithm constructed in this study demonstrated superior performance. The experimental results reveal that the solution quality of GDRL-MOEA/D was superior to the other six algorithms in all 24 test cases. In terms of solution speed, GDRL-MOEA/D was not significantly different from the other algorithms, and the difference was within an acceptable range.
2. Multi-Objective Optimization Model for the GPFSP
2.1. Problem Description
- All jobs are mutually independent and can be processed at the initial moment;
- Only one job can be processed on each machine at any given time;
- Each job needs to be processed on each machine exactly once;
- All jobs have the same processing sequence on each machine;
- The job cannot be interrupted once it starts processing on a machine;
- The transportation and setup times of jobs between different machines are either disregarded or incorporated into the processing time of the jobs.
2.2. Notations
2.3. Optimization Objectives
2.3.1. Makespan
2.3.2. Total Energy Consumption
3. The Solution Framework of the GDRL-MOEA/D
- First, with the objective of minimizing the maximum completion time, we applied an end-to-end deep reinforcement learning strategy (DRL-PFSP) to model the PFSP problem in Section 3.1 and systematically trained the model using the actor–critic algorithm. Once the DRL-PFSP model is trained, it can efficiently provide high-quality solutions for PFSP instances of varying sizes and complexities.
- Next, in Section 3.2, these solutions are used as the initial population for MOEA/D to further optimize the scheduling results, forming the DRL-MOEA/D approach. This integrated method improves the efficiency and adaptability of the solving process while maintaining the optimization quality of the solutions.
- Finally, in order to further reduce energy consumption without increasing the completion time, an innovative energy-saving strategy is proposed in Section 3.3. This strategy optimizes the energy consumption of the scheduling plans generated by DRL-MOEA/D, aiming to achieve more environmentally friendly and efficient workshop scheduling.
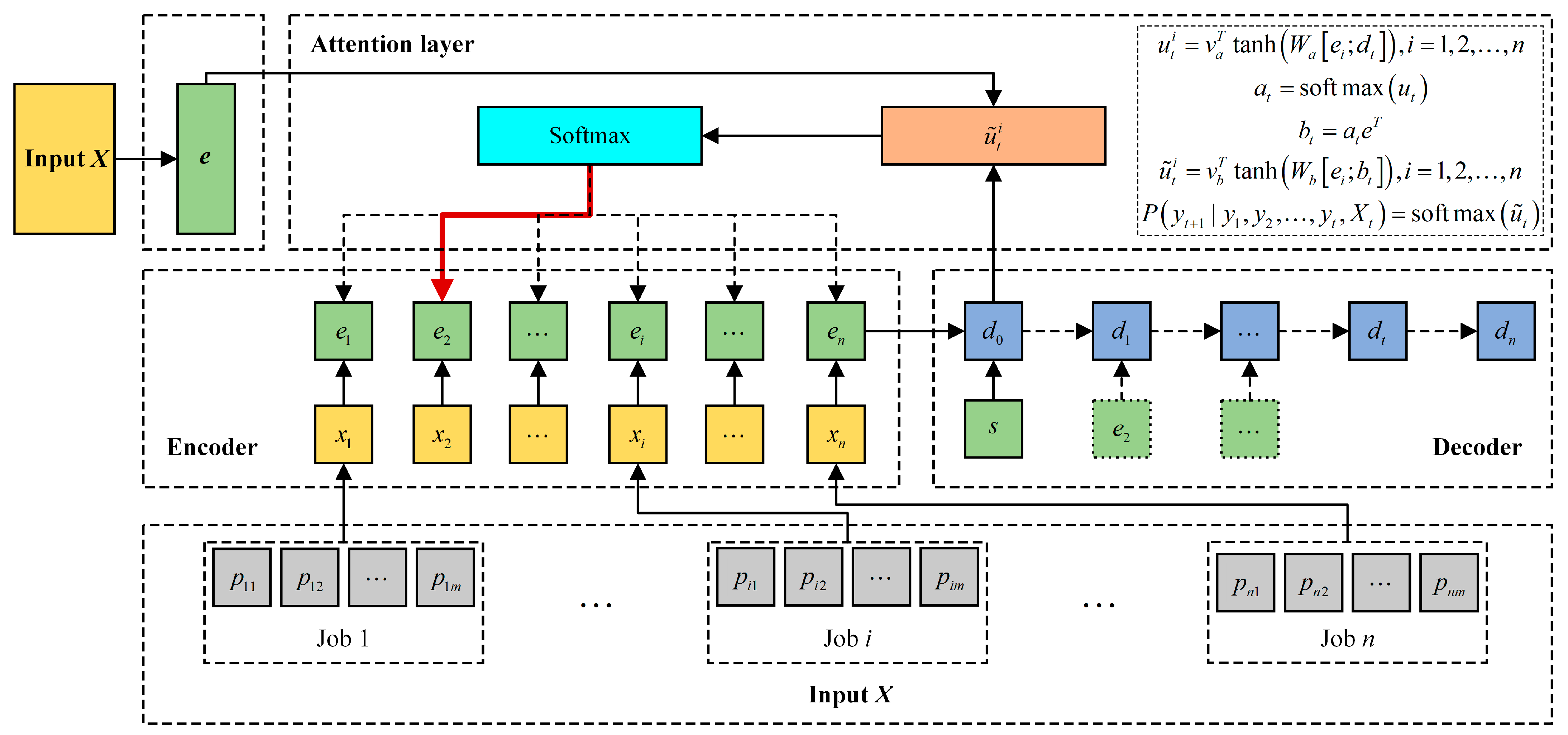
3.1. The Structure of the DRL-PFSP
3.1.1. Input Layer
3.1.2. Encoding Layer
3.1.3. Decoding Layer
3.1.4. Attention Layer
3.1.5. The Training Method for PFSP
| Algorithm 1: The Framework of the Actor–Critic Training Algorithm. | ||||
| Input: : the parameters of the actor network; : the parameters of the critic network | ||||
| Output: The optimal parameters , | ||||
| 1 | for do | |||
| 2 | Generate instances based on PFSP | |||
| 3 | for do | |||
| 4 | ||||
| 5 | while the jobs have not been fully accessed do | |||
| 6 | select the next job according to | |||
| 7 | and update | |||
| 8 | end while | |||
| 9 | compute the reward : | |||
| 10 | end for | |||
| 11 | Calculate the strategy gradient of actor network and critic network: | |||
| 12 | ||||
| 13 | ||||
| 14 | Optimize the network parameters of actor network and critic network based on strategy gradient: | |||
| 15 | ||||
| 16 | ||||
| 17 | return | |||
| 18 | end for | |||
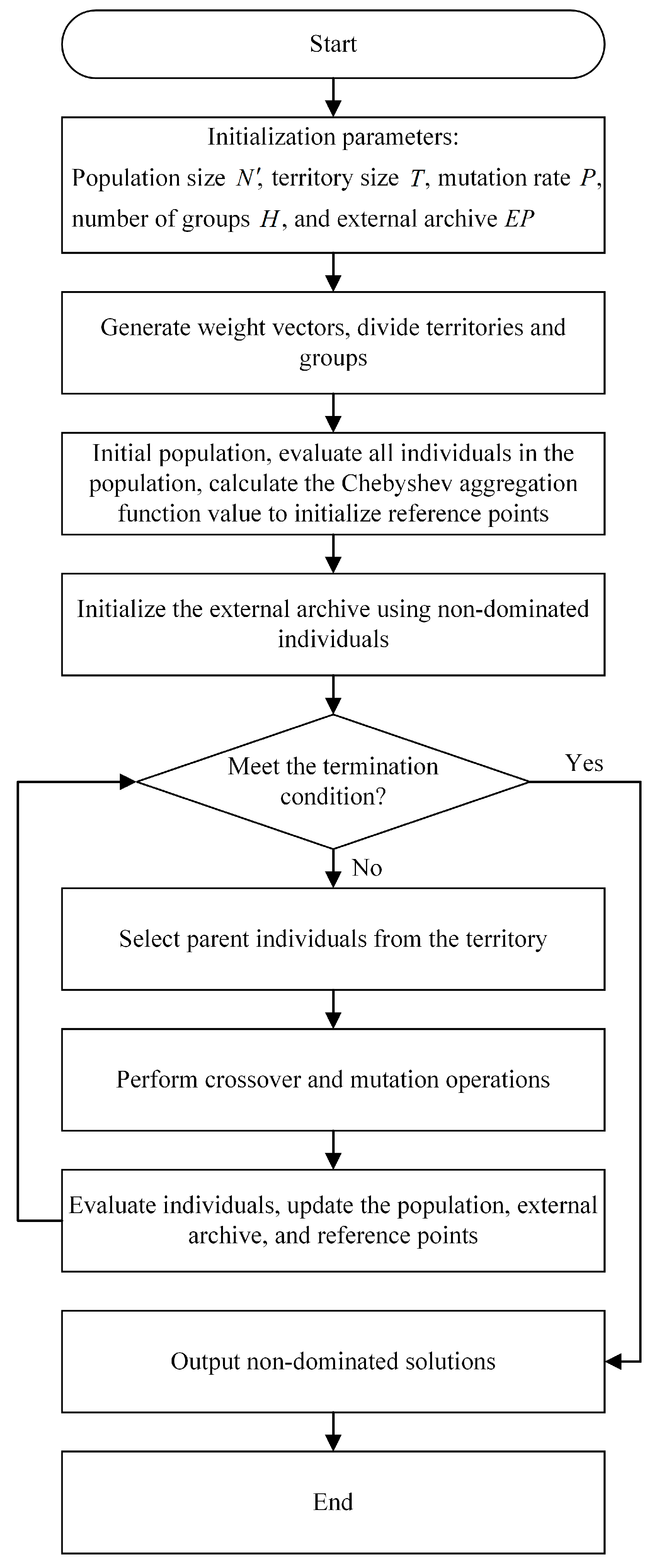
3.2. The Algorithm of MOEA/D
3.2.1. Evaluation of Adaptation Values
3.2.2. Weight Vectors
3.2.3. Neighborhood
3.2.4. The Process of MOEA/D
- Refine the initialization of uniformly distributed reference weight vectors , and then calculate the Euclidean geometric distance between vector and each of these weight vectors. Subsequently, filter out the weight vectors with the smallest Euclidean distances as the neighborhood of and store the neighborhood information in the neighborhood matrix, i.e., the neighborhood of weight vector is represented as , ;
- Initialize population based on the DRL-PFSP model, and calculate the fitness value for each , ;
- Initialize reference points , where , .
- Select two random individuals from the neighborhood of individual , and generate a descendant individual using crossover and mutation operations.
- If , then update the reference point , .
- Update the neighborhood solutions, that is, for , if , then , .
3.3. The Energy-Saving Strategy
4. Numerical Experiments
4.1. Experimental Settings
4.2. Parameter Settings of the DRL-PFSP Model
4.3. Experimental Results and Discussions
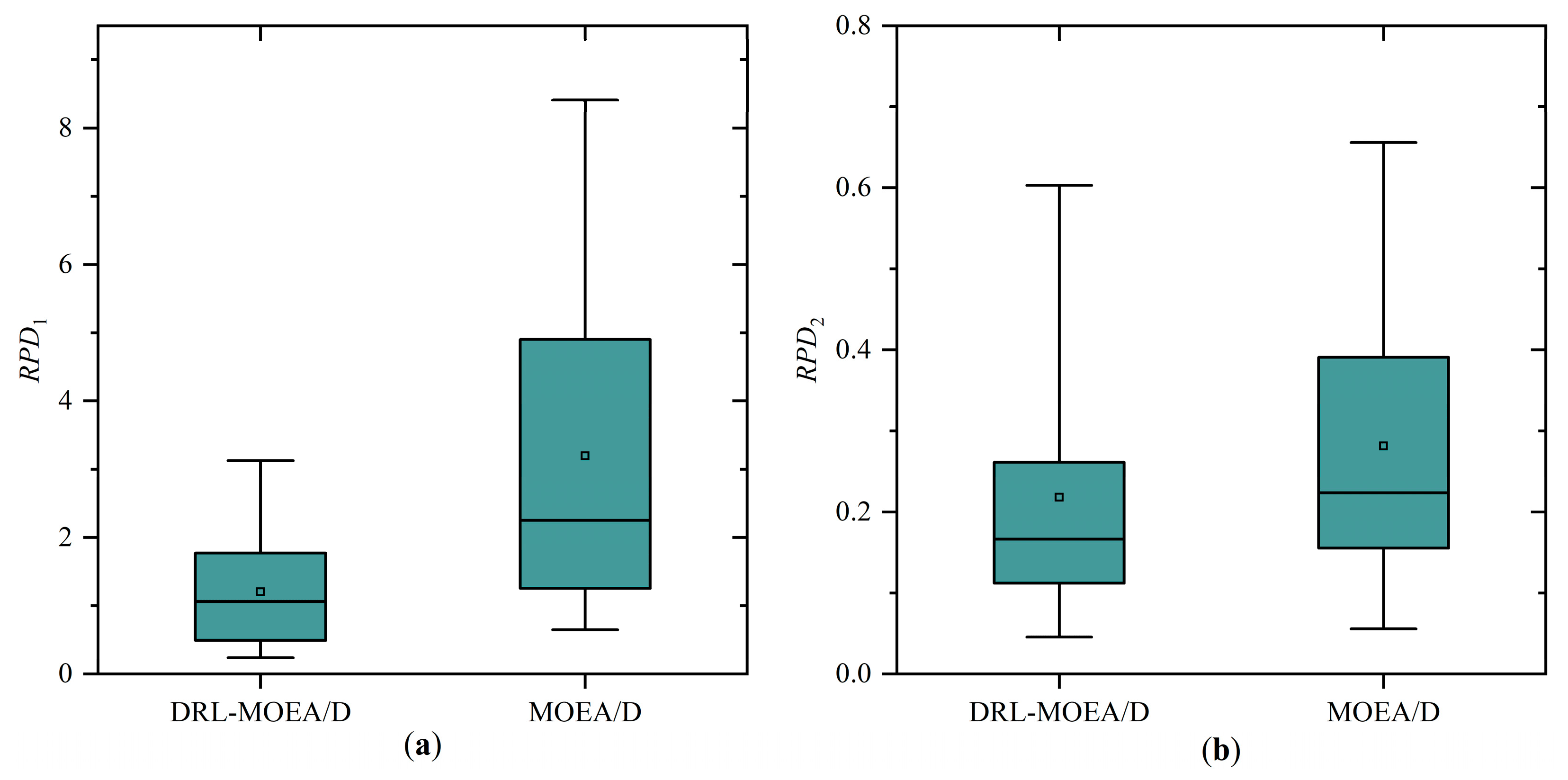
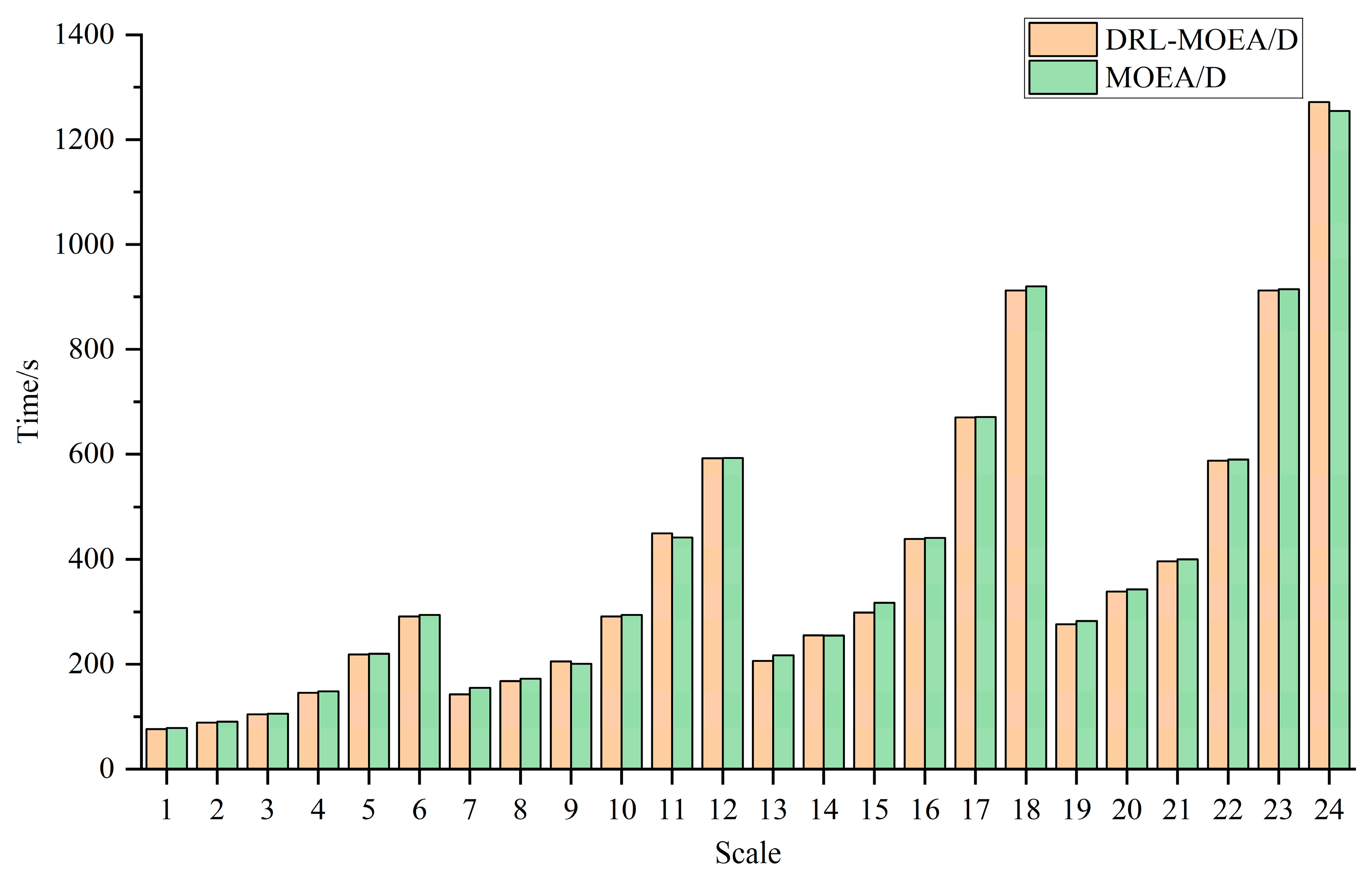
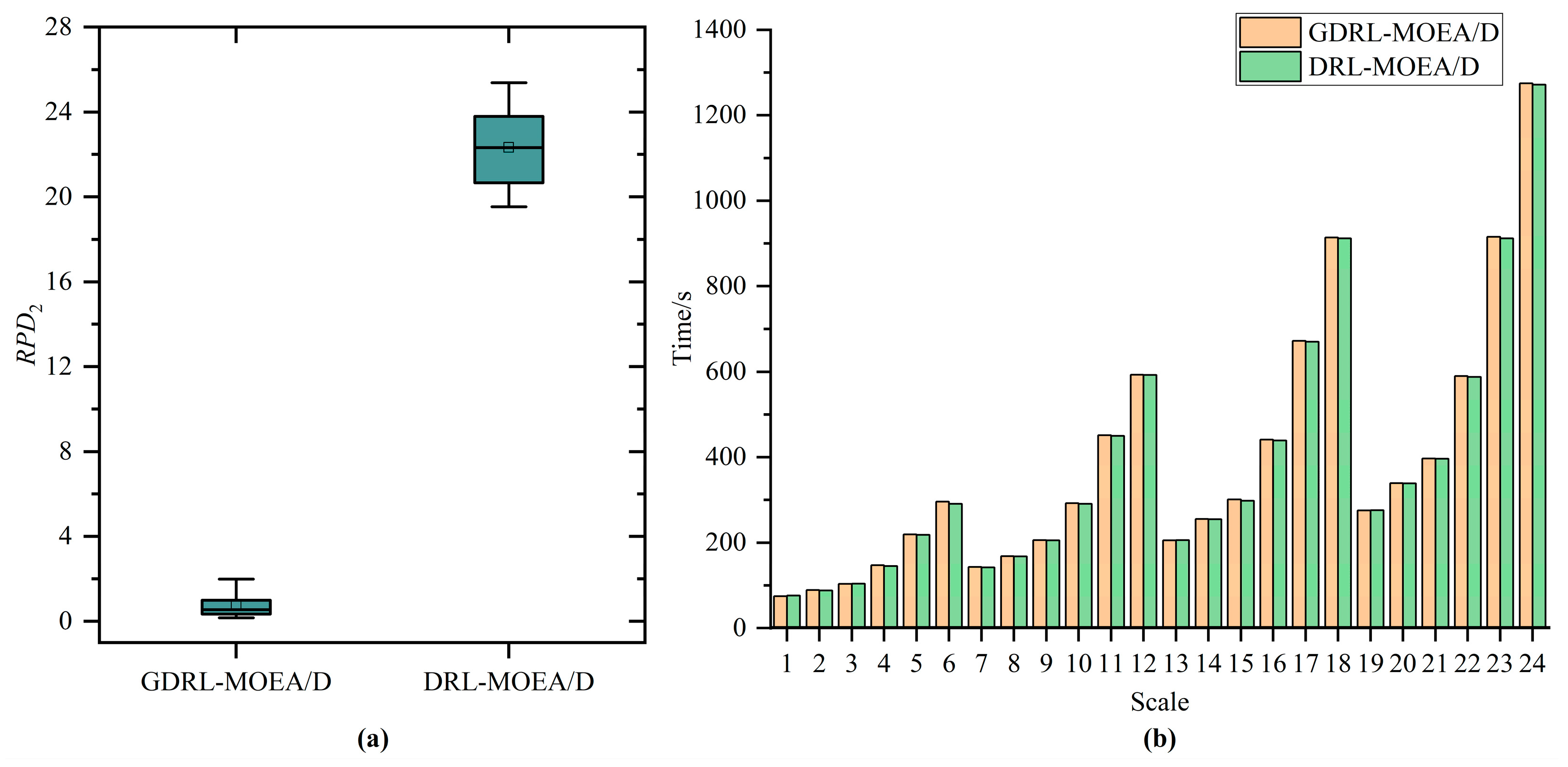
4.3.1. The Effectiveness of Initializing the Population Based on DRL-PFSP
4.3.2. The Effectiveness of the Energy-Saving Strategy
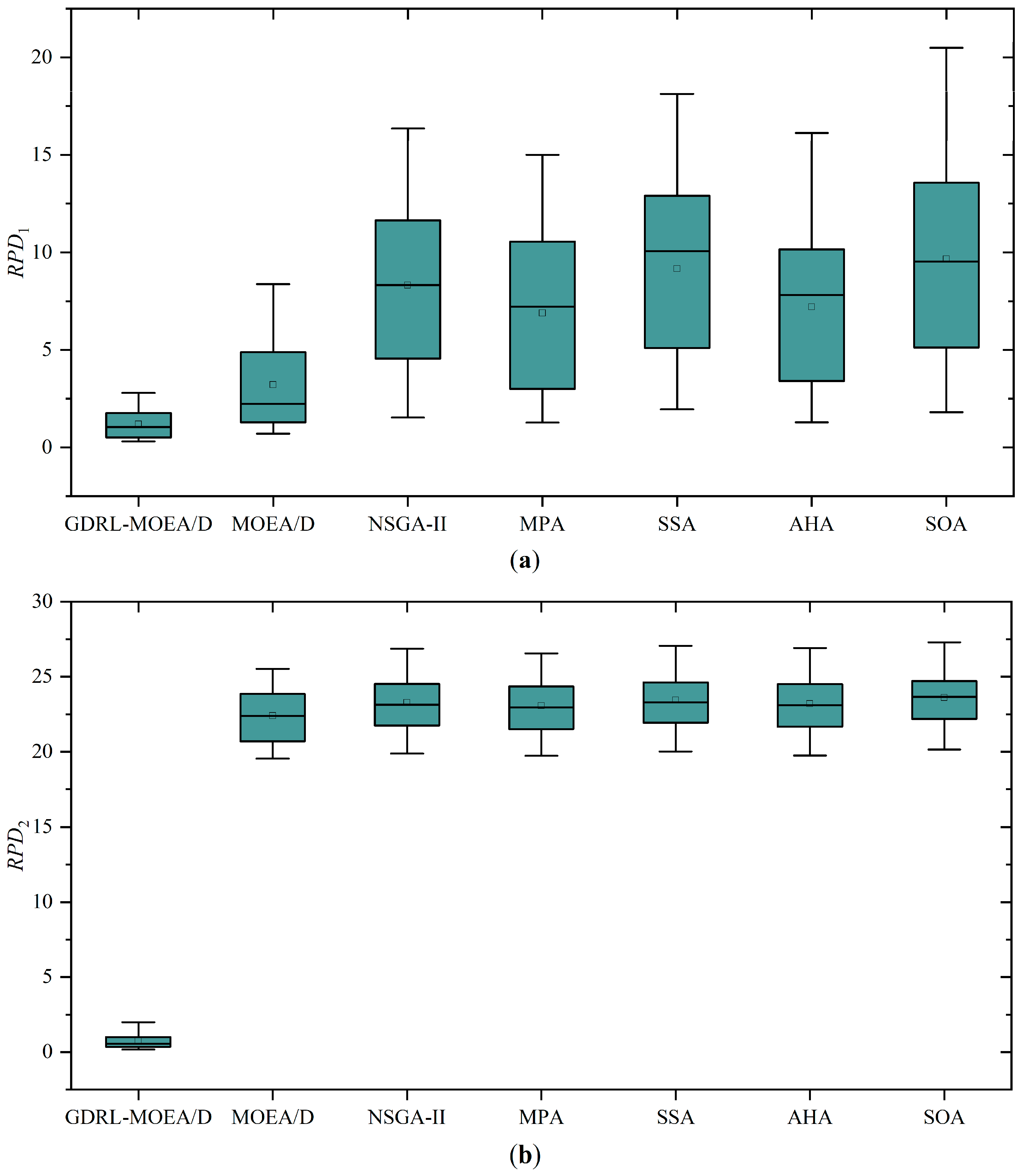
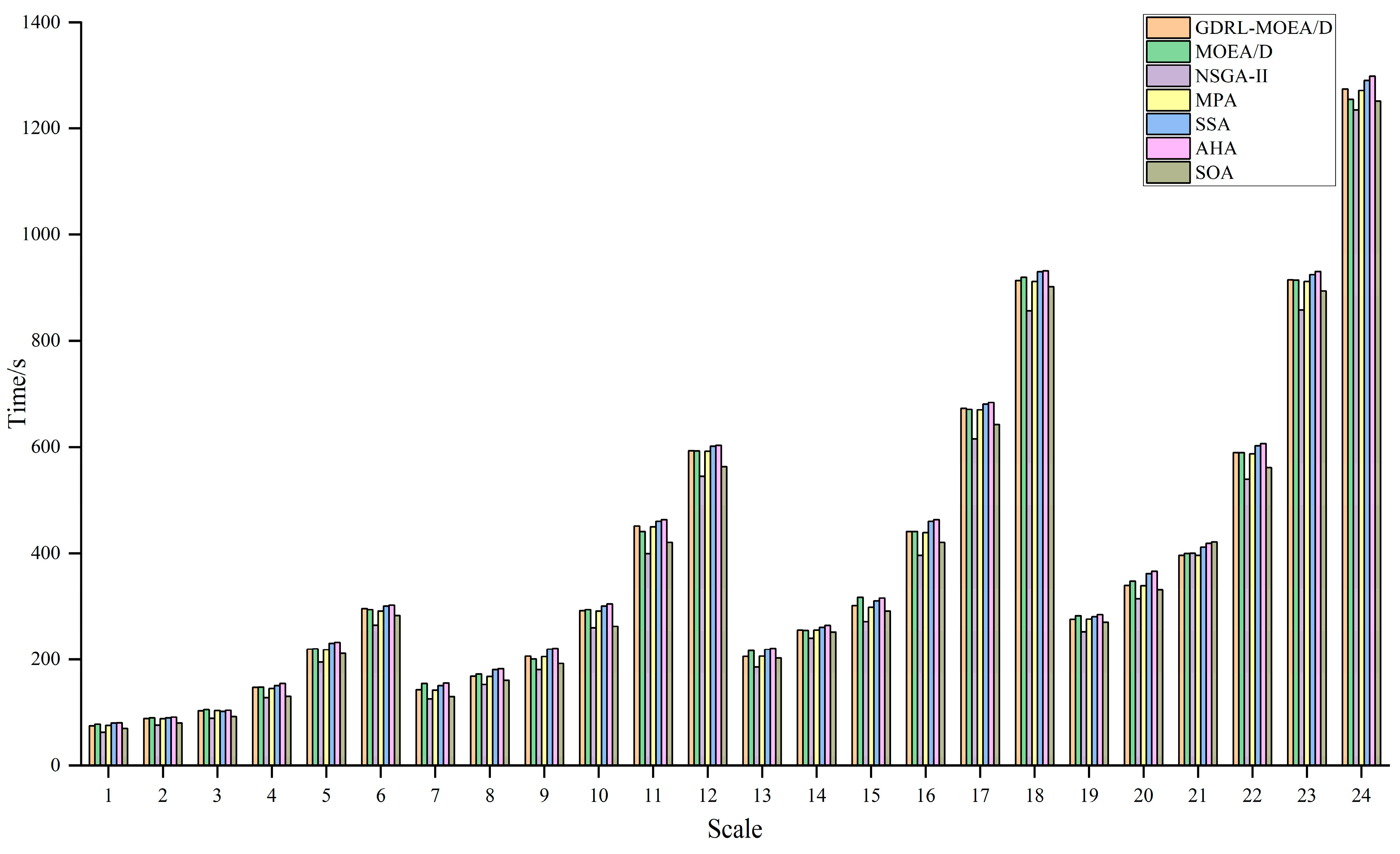
4.3.3. Comparison with Other Algorithms
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McMahon, G.; Burton, P. Flow-shop scheduling with the branch-and-bound method. Oper. Res. 1967, 15, 473–481. [Google Scholar] [CrossRef]
- Yavuz, M.; Tufekci, S. Dynamic programming solution to the batching problem in just-in-time flow-shops. Comput. Ind. Eng. 2006, 51, 416–432. [Google Scholar] [CrossRef]
- Ronconi, D.P.; Birgin, E.G. Mixed-Integer Programming Models for Flowshop Scheduling Problems Minimizing the Total Earliness and Tardiness. In Just-in-Time Systems; Springer: Berlin/Heidelberg, Germany, 2012; pp. 91–105. [Google Scholar]
- Campbell, H.G.; Dudek, R.A.; Smith, M.L. A heuristic algorithm for the n job, m machine sequencing problem. Manag. Sci. 1970, 16, B-630–B-637. [Google Scholar]
- Gupta, J.N. A functional heuristic algorithm for the flowshop scheduling problem. J. Oper. Res. Soc. 1971, 22, 39–47. [Google Scholar] [CrossRef]
- Nawaz, M.; Enscore, E.E., Jr.; Ham, I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. Omega 1983, 11, 91–95. [Google Scholar] [CrossRef]
- Johnson, S.M. Optimal two-and three-stage production schedules with setup times included. Nav. Res. Logist. Q. 1954, 1, 61–68. [Google Scholar] [CrossRef]
- Puka, R.; Duda, J.; Stawowy, A.; Skalna, I. N-NEH+ algorithm for solving permutation flow shop problems. Comput. Oper. Res. 2021, 132, 105296. [Google Scholar] [CrossRef]
- Puka, R.; Skalna, I.; Duda, J.; Stawowy, A. Deterministic constructive vN-NEH+ algorithm to solve permutation flow shop scheduling problem with makespan criterion. Comput. Oper. Res. 2024, 162, 106473. [Google Scholar] [CrossRef]
- Puka, R.; Skalna, I.; Łamasz, B.; Duda, J.; Stawowy, A. Deterministic method for input sequence modification in NEH-based algorithms. IEEE Access 2024, 12, 68940–68953. [Google Scholar] [CrossRef]
- Zhang, J.; Dao, S.D.; Zhang, W.; Goh, M.; Yu, G.; Jin, Y.; Liu, W. A new job priority rule for the NEH-based heuristic to minimize makespan in permutation flowshops. Eng. Optim. 2023, 55, 1296–1315. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, Y. A hybrid bat algorithm for solving the three-stage distributed assembly permutation flowshop scheduling problem. Appl. Sci. 2021, 11, 10102. [Google Scholar] [CrossRef]
- Chen, S.; Zheng, J. Hybrid grey wolf optimizer for solving permutation flow shop scheduling problem. Concurr. Comput. Pract. Exp. 2024, 36, e7942. [Google Scholar] [CrossRef]
- Tian, S.; Li, X.; Wan, J.; Zhang, Y. A novel cuckoo search algorithm for solving permutation flowshop scheduling problems. In Proceedings of the 2021 IEEE International Conference on Recent Advances in Systems Science and Engineering (RASSE), Tainan, Taiwan, 7–10 November 2021; pp. 1–8. [Google Scholar]
- Khurshid, B.; Maqsood, S.; Omair, M.; Sarkar, B.; Ahmad, I.; Muhammad, K. An improved evolution strategy hybridization with simulated annealing for permutation flow shop scheduling problems. IEEE Access 2021, 9, 94505–94522. [Google Scholar] [CrossRef]
- Razali, F.; Nawawi, A. Optimization of Permutation Flowshop Schedulling Problem (PFSP) using First Sequence Artificial Bee Colony (FSABC) Algorithm. Prog. Eng. Appl. Technol. 2024, 5, 369–377. [Google Scholar]
- Qin, X.; Fang, Z.; Zhang, Z. Hybrid symbiotic organisms search algorithm for permutation flow shop scheduling problem. J. Zhejiang Univer. Eng. Sci. 2020, 54, 712–721. [Google Scholar]
- Rui, Z.; Jun, L.; Xingsheng, G. Mixed No-Idle Permutation Flow Shop Scheduling Problem Based on Multi-Objective Discrete Sine Optimization Algorithm. J. East China Univ. Sci. Technol. 2022, 48, 76–86. [Google Scholar]
- Yan, H.; Tang, W.; Yao, B. Permutation flow-shop scheduling problem based on new hybrid crow search algorithm. Comput. Integr. Manuf. Syst. 2024, 30, 1834. [Google Scholar]
- Yang, L. Unsupervised machine learning and image recognition model application in English part-of-speech feature learning under the open platform environment. Soft Comput. 2023, 27, 10013–10023. [Google Scholar] [CrossRef]
- Mohi-Ud-Din, G.; Marnerides, A.K.; Shi, Q.; Dobbins, C.; MacDermott, A. Deep COLA: A deep competitive learning algorithm for future home energy management systems. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 5, 860–870. [Google Scholar] [CrossRef]
- Dudhane, A.; Patil, P.W.; Murala, S. An end-to-end network for image de-hazing and beyond. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 6, 159–170. [Google Scholar] [CrossRef]
- Bai, X.; Wang, X.; Liu, X.; Liu, Q.; Song, J.; Sebe, N.; Kim, B. Explainable deep learning for efficient and robust pattern recognition: A survey of recent developments. Pattern Recognit. 2021, 120, 108102. [Google Scholar] [CrossRef]
- Aurangzeb, K.; Javeed, K.; Alhussein, M.; Rida, I.; Haider, S.I.; Parashar, A. Deep Learning Approach for Hand Gesture Recognition: Applications in Deaf Communication and Healthcare. Comput. Mater. Contin. 2024, 78, 127–144. [Google Scholar] [CrossRef]
- Malik, N.; Altaf, S.; Tariq, M.U.; Ahmed, A.; Babar, M. A Deep Learning Based Sentiment Analytic Model for the Prediction of Traffic Accidents. Comput. Mater. Contin. 2023, 77, 1599–1615. [Google Scholar] [CrossRef]
- Vinyals, O.; Fortunato, M.; Jaitly, N. Pointer networks. arXiv 2015, arXiv:1506.03134. [Google Scholar]
- Ling, Z.; Tao, X.; Zhang, Y.; Chen, X. Solving optimization problems through fully convolutional networks: An application to the traveling salesman problem. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 7475–7485. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, C.; Cao, Z.; Song, W.; Tan, P.S.; Zhang, J.; Wen, B.; Dauwels, J. Learning to solve multiple-TSP with time window and rejections via deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2022, 24, 1325–1336. [Google Scholar] [CrossRef]
- Luo, J.; Li, C.; Fan, Q.; Liu, Y. A graph convolutional encoder and multi-head attention decoder network for TSP via reinforcement learning. Eng. Appl. Artif. Intell. 2022, 112, 104848. [Google Scholar] [CrossRef]
- Bogyrbayeva, A.; Yoon, T.; Ko, H.; Lim, S.; Yun, H.; Kwon, C. A deep reinforcement learning approach for solving the traveling salesman problem with drone. Transp. Res. Part C Emerg. Technol. 2023, 148, 103981. [Google Scholar] [CrossRef]
- Gao, H.; Zhou, X.; Xu, X.; Lan, Y.; Xiao, Y. AMARL: An attention-based multiagent reinforcement learning approach to the min-max multiple traveling salesmen problem. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 9758–9772. [Google Scholar] [CrossRef]
- Wang, Q.; Hao, Y.; Zhang, J. Generative inverse reinforcement learning for learning 2-opt heuristics without extrinsic rewards in routing problems. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101787. [Google Scholar] [CrossRef]
- Pan, W.; Liu, S.Q. Deep reinforcement learning for the dynamic and uncertain vehicle routing problem. Appl. Intell. 2023, 53, 405–422. [Google Scholar] [CrossRef]
- Wang, Q.; Hao, Y. Routing optimization with Monte Carlo Tree Search-based multi-agent reinforcement learning. Appl. Intell. 2023, 53, 25881–25896. [Google Scholar] [CrossRef]
- Xu, Y.; Fang, M.; Chen, L.; Xu, G.; Du, Y.; Zhang, C. Reinforcement learning with multiple relational attention for solving vehicle routing problems. IEEE Trans. Cybern. 2021, 52, 11107–11120. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Mao, M.; Zhao, X.; Zou, J. A hybrid of deep reinforcement learning and local search for the vehicle routing problems. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7208–7218. [Google Scholar] [CrossRef]
- Si, J.; Li, X.; Gao, L.; Li, P. An efficient and adaptive design of reinforcement learning environment to solve job shop scheduling problem with soft actor-critic algorithm. Int. J. Prod. Res. 2024, 1–16. [Google Scholar] [CrossRef]
- Chen, R.; Li, W.; Yang, H. A deep reinforcement learning framework based on an attention mechanism and disjunctive graph embedding for the job-shop scheduling problem. IEEE Trans. Ind. Inform. 2022, 19, 1322–1331. [Google Scholar] [CrossRef]
- Shao, C.; Yu, Z.; Tang, J.; Li, Z.; Zhou, B.; Wu, D.; Duan, J. Research on flexible job-shop scheduling problem based on variation-reinforcement learning. J. Intell. Fuzzy Syst. 2024, 1–15. [Google Scholar] [CrossRef]
- Han, B.; Yang, J. A deep reinforcement learning based solution for flexible job shop scheduling problem. Int. J. Simul. Model. 2021, 20, 375–386. [Google Scholar] [CrossRef]
- Yuan, E.; Wang, L.; Cheng, S.; Song, S.; Fan, W.; Li, Y. Solving flexible job shop scheduling problems via deep reinforcement learning. Expert Syst. Appl. 2024, 245, 123019. [Google Scholar] [CrossRef]
- Wan, L.; Cui, X.; Zhao, H.; Li, C.; Wang, Z. An effective deep actor-critic reinforcement learning method for solving the flexible job shop scheduling problem. Neural Comput. Appl. 2024, 36, 11877–11899. [Google Scholar] [CrossRef]
- Peng, S.; Xiong, G.; Yang, J.; Shen, Z.; Tamir, T.S.; Tao, Z.; Han, Y.; Wang, F.-Y. Multi-Agent Reinforcement Learning for Extended Flexible Job Shop Scheduling. Machines 2023, 12, 8. [Google Scholar] [CrossRef]
- Wu, X.; Yan, X.; Guan, D.; Wei, M. A deep reinforcement learning model for dynamic job-shop scheduling problem with uncertain processing time. Eng. Appl. Artif. Intell. 2024, 131, 107790. [Google Scholar] [CrossRef]
- Liu, R.; Piplani, R.; Toro, C. A deep multi-agent reinforcement learning approach to solve dynamic job shop scheduling problem. Comput. Oper. Res. 2023, 159, 106294. [Google Scholar] [CrossRef]
- Gebreyesus, G.; Fellek, G.; Farid, A.; Fujimura, S.; Yoshie, O. Gated-Attention Model with Reinforcement Learning for Solving Dynamic Job Shop Scheduling Problem. IEEJ Trans. Electr. Electron. Eng. 2023, 18, 932–944. [Google Scholar] [CrossRef]
- Wu, X.; Yan, X. A spatial pyramid pooling-based deep reinforcement learning model for dynamic job-shop scheduling problem. Comput. Oper. Res. 2023, 160, 106401. [Google Scholar] [CrossRef]
- Su, C.; Zhang, C.; Xia, D.; Han, B.; Wang, C.; Chen, G.; Xie, L. Evolution strategies-based optimized graph reinforcement learning for solving dynamic job shop scheduling problem. Appl. Soft Comput. 2023, 145, 110596. [Google Scholar] [CrossRef]
- Liu, C.-L.; Huang, T.-H. Dynamic job-shop scheduling problems using graph neural network and deep reinforcement learning. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6836–6848. [Google Scholar] [CrossRef]
- Zhu, H.; Tao, S.; Gui, Y.; Cai, Q. Research on an Adaptive Real-Time Scheduling Method of Dynamic Job-Shop Based on Reinforcement Learning. Machines 2022, 10, 1078. [Google Scholar] [CrossRef]
- Tiacci, L.; Rossi, A. A discrete event simulator to implement deep reinforcement learning for the dynamic flexible job shop scheduling problem. Simul. Model. Pract. Theory 2024, 134, 102948. [Google Scholar] [CrossRef]
- Zhang, L.; Feng, Y.; Xiao, Q.; Xu, Y.; Li, D.; Yang, D.; Yang, Z. Deep reinforcement learning for dynamic flexible job shop scheduling problem considering variable processing times. J. Manuf. Syst. 2023, 71, 257–273. [Google Scholar] [CrossRef]
- Chang, J.; Yu, D.; Zhou, Z.; He, W.; Zhang, L. Hierarchical reinforcement learning for multi-objective real-time flexible scheduling in a smart shop floor. Machines 2022, 10, 1195. [Google Scholar] [CrossRef]
- Zhou, T.; Luo, L.; Ji, S.; He, Y. A Reinforcement Learning Approach to Robust Scheduling of Permutation Flow Shop. Biomimetics 2023, 8, 478. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.; Wang, L.; Wang, J.; Lu, J. Deep reinforcement learning based optimization algorithm for permutation flow-shop scheduling. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 7, 983–994. [Google Scholar] [CrossRef]
- Wang, Z.; Cai, B.; Li, J.; Yang, D.; Zhao, Y.; Xie, H. Solving non-permutation flow-shop scheduling problem via a novel deep reinforcement learning approach. Comput. Oper. Res. 2023, 151, 106095. [Google Scholar] [CrossRef]
- Jiang, E.-D.; Wang, L. An improved multi-objective evolutionary algorithm based on decomposition for energy-efficient permutation flow shop scheduling problem with sequence-dependent setup time. Int. J. Prod. Res. 2019, 57, 1756–1771. [Google Scholar] [CrossRef]
- Rossit, D.G.; Nesmachnow, S.; Rossit, D.A. A Multiobjective Evolutionary Algorithm based on Decomposition for a flow shop scheduling problem in the context of Industry 4.0. Int. J. Math. Eng. Manag. Sci. 2022, 7, 433–454. [Google Scholar]
- Nazari, M.; Oroojlooy, A.; Snyder, L.; Takác, M. Reinforcement learning for solving the vehicle routing problem. arXiv 2018, arXiv:1802.04240. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]




| References | Type of Problem | Objectives | Approach | Approach Type |
|---|---|---|---|---|
| [1] | PFSP | Makespan | Branch and bound | Exact algorithms |
| [2] | PFSP | Makespan | Dynamic programming | |
| [3] | PFSP | Makespan | Integer programming | |
| [4] | PFSP | Makespan | Campbell Dudek Smith algorithm | Heuristic methods |
| [5] | PFSP | Makespan | Gupta algorithm | |
| [6,7,8,9,10,11] | PFSP | Makespan | Nawaz Enscore Ham algorithm | |
| [12] | PFSP | Makespan | Hybrid bat optimization algorithm | Metaheuristic methods |
| [13] | PFSP | Makespan | Hybrid grey wolf algorithm | |
| [14] | PFSP | Makespan, total energy consumption | Cuckoo search algorithm | |
| [15] | PFSP | Makespan | Hybrid Evolution Strategy | |
| [16] | PFSP | Makespan | Artificial Bee Colony algorithm | |
| [17] | PFSP | Makespan | Hybrid cooperative coevolutionary search algorithm | |
| [18] | PFSP | Makespan, maximum tardiness | Discrete sine optimization method | |
| [19] | PFSP | Makespan | Hybrid crow search algorithm | |
| [37] | JSSP | Makespan | Soft actor–critic algorithm | Reinforcement learning methods |
| [38] | JSSP | Makespan | Deep reinforcement learning | |
| [39] | FJSSP | Makespan | Hybrid deep reinforcement learning | |
| [40] | FJSSP | Makespan | Deep reinforcement learning | |
| [41] | FJSSP | Makespan | Deep reinforcement learning | |
| [42] | FJSSP | Makespan | Deep actor–critic reinforcement learning | |
| [43] | FJSSP | Makespan | Multi-agent reinforcement learning | |
| [44] | DJSSP | Makespan | Deep reinforcement learning | |
| [45] | DJSSP | Makespan | Deep multi-agent reinforcement learning | |
| [46] | DJSSP | Makespan | Gated-attention model with reinforcement learning | |
| [47] | DJSSP | Makespan | Deep reinforcement learning | |
| [48] | DJSSP | Makespan | Graph reinforcement learning | |
| [49] | DJSSP | Makespan | Graph neural network and deep reinforcement learning | |
| [50] | DJSSP | Makespan | Deep reinforcement learning | |
| [51] | DFJSSP | Makespan | Deep reinforcement learning | |
| [52] | DFJSSP | Makespan | Proximal Policy Optimization algorithm | |
| [53] | DFJSSP | Makespan | The combination of a double deep Q-network (DDQN) and a dueling DDQN | |
| [54] | PFSP | Makespan | Deep reinforcement learning | |
| [55] | PFSP | Makespan | Deep reinforcement learning | |
| [56] | PFSP | Makespan | Deep reinforcement learning |
| Notations | Definition |
|---|---|
| The total number of jobs | |
| The total number of machines or the total number of job operations | |
| and | |
| The number of operations for job | |
| operation of job | |
| The processing time of job | |
| The completion time of job | |
| , is the index of machines | |
| , is the index of machines | |
| , is the index of machines | |
| The total energy consumption of all machines | |
| The maximum completion time | |
| , is the index of machines | |
| if job is the immediate predecessor operation of job | |
| The learnable parameters of the DRL-PFSP model | |
| The context vectors output by the encoder | |
| The decoding vector from the decoder at time step | |
| The “attention” mask for the inputs at time step | |
| The context vector at time step | |
| , represents the jobs that have been selected at time step represents the jobs available at time step | |
| The network parameters of the actor network | |
| The network parameters of the critic network | |
| The actual reward value yielded by the actor network, for in-stance, | |
| The total number of training instances | |
| The expected reward of the critic network for each instance | |
| The individuals of the population | |
| The population size | |
| The weight vectors of the current subproblem, where is the number of objectives for the problem | |
| The reference points | |
| The subdivision level for each objective coordinate | |
| The Chebyshev aggregation function; represents an individual in the population | |
| The maximum percentage deviation of the maximum completion time | |
| The maximum percentage deviation of the energy consumption | |
| obtained by all compared algorithms | |
| The best obtained by all compared algorithms | |
| The average value of |
| Actor Network (Pointer Network) | Critic Network |
|---|---|
| Encoder: 1D-Conv(, 128, kernel size = 1, stride = 1) | 1D-Conv (, 128, kernel size = 1, stride = 1) |
| 1D-Conv (128, 20, kernel size = 1, stride = 1) | |
| Decoder: GRU (hidden size = 128, number of layers = 1) Attention (No hyper parameters) | 1D-Conv (20, 20, kernel size = 1, stride = 1) |
| 1D-Conv (20, 1, kernel size = 1, stride = 1) |
| (n, m) | The Average RPD Value for Each Algorithm | The Computation Time of Algorithm/s | ||||
|---|---|---|---|---|---|---|
| DRL-MOEA/D | MOEA/D | DRL-MOEA/D | MOEA/D | |||
| RPD1 | RPD2 | RPD1 | RPD2 | |||
| (50, 5) | 0.5174 | 0.6032 | 0.6480 | 0.6559 | 76.2302 | 78.3117 |
| (50, 6) | 1.1057 | 0.1115 | 1.7287 | 0.1775 | 88.5214 | 90.2976 |
| (50, 7) | 1.9905 | 0.2166 | 3.6439 | 0.2200 | 104.2893 | 105.8324 |
| (50, 10) | 1.7088 | 0.1298 | 2.2966 | 0.4152 | 145.2546 | 148.1882 |
| (50, 15) | 2.5123 | 0.5662 | 8.4098 | 0.5736 | 218.6872 | 219.9746 |
| (50, 20) | 3.1292 | 0.5978 | 6.6061 | 0.6120 | 291.0637 | 294.0099 |
| (100, 5) | 0.2683 | 0.1329 | 1.1107 | 0.1424 | 142.1222 | 154.5248 |
| (100, 6) | 0.5515 | 0.1939 | 0.9147 | 0.1727 | 168.0217 | 172.2160 |
| (100, 7) | 1.4165 | 0.1718 | 2.2110 | 0.1727 | 205.3689 | 200.6013 |
| (100, 10) | 1.5976 | 0.1872 | 4.2494 | 0.2198 | 291.2315 | 293.9304 |
| (100, 15) | 1.8348 | 0.2842 | 5.0751 | 0.3575 | 450.0200 | 441.8432 |
| (100, 20) | 2.2150 | 0.4492 | 7.2053 | 0.4710 | 592.2356 | 592.6549 |
| (150, 5) | 0.3271 | 0.1142 | 0.8654 | 0.1200 | 206.2297 | 216.773 |
| (150, 6) | 0.4795 | 0.1093 | 1.2698 | 0.1323 | 255.2442 | 254.7261 |
| (150, 7) | 1.0168 | 0.0675 | 2.0241 | 0.2564 | 298.3484 | 316.9811 |
| (150, 10) | 0.4252 | 0.1607 | 1.2371 | 0.1682 | 439.0293 | 441.1019 |
| (150, 15) | 1.3355 | 0.1544 | 4.7322 | 0.3040 | 669.9642 | 670.6341 |
| (150, 20) | 1.6796 | 0.2939 | 5.1543 | 0.3693 | 912.1419 | 920.1188 |
| (200, 5) | 0.5483 | 0.0517 | 0.8484 | 0.0765 | 276.1188 | 282.2372 |
| (200, 6) | 0.2385 | 0.0458 | 1.3282 | 0.0558 | 338.6582 | 342.7295 |
| (200, 7) | 0.5096 | 0.0638 | 1.6252 | 0.0943 | 396.4272 | 400.0306 |
| (200, 10) | 0.4651 | 0.1128 | 2.6457 | 0.2268 | 587.6343 | 589.5134 |
| (200, 15) | 0.9884 | 0.2387 | 4.6916 | 0.4121 | 912.2259 | 914.6555 |
| (200, 20) | 2.0133 | 0.1796 | 6.2465 | 0.3529 | 1271.5979 | 1254.9765 |
| AVG | 1.2031 | 0.2182 | 3.1987 | 0.2816 | 389.0278 | 391.5359 |
| (n, m) | The Average RPD Value for Each Algorithm | The Computation Time of Each Algorithm/s | ||
|---|---|---|---|---|
| GDRL-MOEA/D | DRL-MOEA/D | GDRL-MOEA/D | DRL-MOEA/D | |
| RPD2 | RPD2 | |||
| (50, 5) | 1.6924 | 20.1261 | 75.1254 | 76.2302 |
| (50, 6) | 1.6876 | 24.3180 | 89.2452 | 88.5214 |
| (50, 7) | 1.9866 | 24.5283 | 103.5411 | 104.2893 |
| (50, 10) | 0.9362 | 19.7679 | 147.3512 | 145.2546 |
| (50, 15) | 0.8797 | 24.7655 | 219.5412 | 218.6872 |
| (50, 20) | 0.4857 | 20.6822 | 295.6234 | 291.0637 |
| (100, 5) | 0.4237 | 19.5342 | 143.2415 | 142.1222 |
| (100, 6) | 1.4500 | 23.6355 | 168.6145 | 168.0217 |
| (100, 7) | 0.3360 | 22.3653 | 206.1235 | 205.3689 |
| (100, 10) | 0.3590 | 20.6560 | 292.2514 | 291.2315 |
| (100, 15) | 0.6011 | 25.3751 | 451.3547 | 450.0200 |
| (100, 20) | 0.3944 | 21.6173 | 593.1045 | 592.2356 |
| (150, 5) | 0.9851 | 20.5960 | 205.6841 | 206.2297 |
| (150, 6) | 1.2060 | 21.8462 | 255.4562 | 255.2442 |
| (150, 7) | 0.7356 | 23.7286 | 301.2514 | 298.3484 |
| (150, 10) | 0.3196 | 22.4336 | 441.0145 | 439.0293 |
| (150, 15) | 0.3807 | 22.2747 | 672.5241 | 669.9642 |
| (150, 20) | 0.1680 | 23.8685 | 913.8121 | 912.1419 |
| (200, 5) | 0.9916 | 19.6915 | 275.6581 | 276.1188 |
| (200, 6) | 0.4009 | 21.2566 | 339.2514 | 338.6582 |
| (200, 7) | 0.7289 | 22.9484 | 396.5412 | 396.4272 |
| (200, 10) | 0.2848 | 21.9042 | 589.5418 | 587.6343 |
| (200, 15) | 0.2600 | 25.3070 | 915.2564 | 912.2259 |
| (200, 20) | 0.1676 | 22.8183 | 1274.4514 | 1271.5979 |
| AVG | 0.7442 | 22.3352 | 390.2317 | 389.5359 |
| Algorithms | Descriptions | Characteristic | Application Scenarios |
|---|---|---|---|
| NSGA-II | An advanced genetic algorithm for solving multi-objective optimization problems, which introduces improvements such as fast non-dominated sorting, crowding distance estimation, and elitist strategies based on NSGA, significantly enhancing the algorithm’s efficiency and solution quality. | NSGA-II achieves precise sorting of solutions with lower computational complexity and maintains population diversity through crowding distance. | Production scheduling, engineering design, path planning, power system optimization, etc. |
| MPA | A metaheuristic algorithm designed based on the predatory behavior of marine predators, which simulates the dynamic behavior of predators during the processes of hunting and migration to balance global search and local exploitation. | MPA excels at handling optimization problems with complex search spaces, effectively avoiding local optima and demonstrating strong global optimization capabilities. | Engineering design, logistics optimization, production scheduling, etc. |
| SSA | A metaheuristic algorithm based on sparrow foraging behavior, aimed at solving complex optimization problems by simulating the collaboration and decision-making mechanisms of sparrows during the foraging process. | SSA is simple in structure and easy to implement, with good optimization ability and convergence speed. | Production scheduling, resource allocation, etc. |
| AHA | A metaheuristic algorithm that simulates behaviors such as guiding foraging, area foraging, and migratory foraging of hummingbirds. | AHA demonstrates high adaptability, allowing it to dynamically adjust search strategies based on the scale and complexity of the problem, exhibiting good flexibility and robustness. | Production scheduling, path planning, multi-objective decision making, etc. |
| SOA | A metaheuristic algorithm based on the migration and predatory behavior of seagulls, aimed at solving complex global optimization problems. | SOA is characterized by simplicity and ease of implementation, strong global search capabilities, and broad applicability. | Engineering optimization, data mining, production scheduling, image processing, etc. |
| (n, m) | The Average RPD Value for Each Algorithm | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GDRL-MOEA/D | MOEA/D | NSGA-II | MPA | SSA | AHA | SOA | ||||||||
| RPD1 | RPD2 | RPD1 | RPD2 | RPD1 | RPD2 | RPD1 | RPD2 | RPD1 | RPD2 | RPD1 | RPD2 | RPD1 | RPD2 | |
| (50, 5) | 0.5349 | 1.6924 | 0.6952 | 20.1942 | 4.0498 | 20.8703 | 3.1144 | 20.7063 | 6.0056 | 21.2036 | 4.1135 | 20.8055 | 7.2949 | 21.3956 |
| (50, 7) | 0.7269 | 1.6876 | 1.7416 | 24.4001 | 4.6646 | 24.8379 | 2.8409 | 24.6383 | 5.2277 | 24.9639 | 3.0602 | 24.7468 | 6.9934 | 25.1091 |
| (50, 10) | 2.1224 | 1.9866 | 3.6366 | 24.5325 | 11.5032 | 25.3896 | 9.1224 | 25.2037 | 13.9339 | 25.6607 | 11.0271 | 25.7350 | 15.9728 | 26.1701 |
| (50, 15) | 1.7289 | 0.9362 | 2.2645 | 20.1093 | 10.4516 | 21.4295 | 7.5891 | 21.1843 | 11.2122 | 21.5983 | 9.8977 | 21.1774 | 12.8126 | 21.9546 |
| (50, 20) | 2.4884 | 0.8797 | 8.3774 | 24.7746 | 16.3570 | 26.5221 | 14.9996 | 25.9764 | 18.1457 | 26.7899 | 16.1320 | 26.4391 | 20.4967 | 27.3059 |
| (100, 5) | 2.7940 | 0.4857 | 6.5506 | 20.6979 | 13.8905 | 22.7676 | 12.5223 | 22.4634 | 14.1222 | 23.0694 | 10.8028 | 22.4707 | 14.2957 | 23.8263 |
| (100, 6) | 0.4932 | 0.4237 | 1.0922 | 19.5454 | 4.4411 | 19.8794 | 2.8800 | 19.7333 | 5.0479 | 20.1175 | 2.9957 | 19.7542 | 5.5589 | 20.3161 |
| (100, 7) | 0.3513 | 1.4500 | 0.8593 | 23.6094 | 5.0790 | 24.2241 | 3.3404 | 24.0738 | 5.1484 | 24.2105 | 3.4077 | 24.2649 | 4.6836 | 24.0524 |
| (100, 10) | 1.2530 | 0.3360 | 2.2087 | 22.3664 | 8.0974 | 23.1223 | 7.3630 | 23.0017 | 10.3049 | 23.2399 | 8.6940 | 23.2307 | 9.4021 | 23.9177 |
| (100, 15) | 1.6883 | 0.3590 | 4.2494 | 20.6953 | 12.6673 | 21.9838 | 10.6005 | 21.6971 | 13.3050 | 22.2634 | 9.8033 | 21.8840 | 13.4569 | 22.4374 |
| (100, 20) | 1.3746 | 0.6011 | 5.0405 | 25.4667 | 13.1514 | 26.8720 | 11.5269 | 26.5528 | 14.1177 | 27.0574 | 11.9604 | 26.9201 | 14.3532 | 27.0540 |
| (150, 5) | 2.1456 | 0.3944 | 7.1890 | 21.6437 | 13.6901 | 23.0835 | 12.1343 | 22.9091 | 14.3731 | 23.3640 | 12.8380 | 23.1266 | 15.0228 | 23.3508 |
| (150, 6) | 0.5595 | 0.9851 | 1.3563 | 20.6030 | 3.3165 | 20.8377 | 2.5156 | 20.7410 | 4.3366 | 20.8875 | 2.8546 | 20.7496 | 3.1512 | 20.8535 |
| (150, 7) | 0.4932 | 1.2060 | 1.2673 | 21.8742 | 4.0876 | 22.2464 | 2.8358 | 22.1585 | 3.7450 | 22.2795 | 3.3969 | 22.2003 | 4.3025 | 22.4164 |
| (150, 10) | 1.0679 | 0.7356 | 2.0229 | 23.7572 | 4.9376 | 24.1118 | 3.8312 | 24.0326 | 4.8591 | 24.1931 | 3.4368 | 24.1881 | 4.6581 | 24.3320 |
| (150, 15) | 0.6039 | 0.3196 | 1.2337 | 22.4428 | 6.0427 | 23.1658 | 4.8818 | 22.9335 | 6.9101 | 23.2386 | 5.2370 | 23.1630 | 7.4584 | 23.3205 |
| (150, 20) | 1.5000 | 0.3807 | 4.7201 | 22.4572 | 11.1145 | 23.4994 | 9.0835 | 23.0333 | 11.9827 | 23.7174 | 8.3422 | 23.0910 | 12.1749 | 23.8704 |
| (200, 5) | 1.7873 | 0.1680 | 5.1543 | 23.9617 | 11.6012 | 25.2615 | 10.6978 | 25.4128 | 12.3295 | 25.5058 | 10.1595 | 25.4325 | 13.6903 | 25.5540 |
| (200, 6) | 0.4653 | 0.9916 | 0.8325 | 19.7213 | 1.5293 | 20.0045 | 1.2729 | 19.8921 | 1.9503 | 20.0221 | 1.2842 | 19.8486 | 1.8093 | 20.1448 |
| (200, 7) | 0.3032 | 0.4009 | 1.3001 | 21.2688 | 2.6068 | 21.5087 | 1.8491 | 21.3293 | 3.3536 | 21.5723 | 1.9924 | 21.4549 | 3.9930 | 21.8319 |
| (200, 10) | 0.4383 | 0.7289 | 1.6349 | 22.9860 | 5.5199 | 23.4555 | 3.6985 | 23.1576 | 6.2797 | 23.4693 | 4.5586 | 23.0760 | 6.5712 | 23.5114 |
| (200, 15) | 0.5598 | 0.2848 | 2.6148 | 22.0431 | 8.5497 | 22.8128 | 7.0618 | 22.5205 | 9.8386 | 22.9871 | 7.2791 | 22.4929 | 9.6581 | 22.9751 |
| (200, 20) | 1.0207 | 0.2600 | 4.6460 | 25.5237 | 10.6289 | 26.6426 | 8.9969 | 26.5614 | 10.9768 | 26.7788 | 9.5384 | 26.6343 | 11.2898 | 26.7975 |
| AVG | 2.0876 | 0.1676 | 6.2365 | 23.0307 | 11.6794 | 24.1396 | 10.4965 | 23.8991 | 12.5157 | 24.2843 | 10.1338 | 23.9889 | 12.8426 | 24.2816 |
| (n, m) | The Computation Time of Each Algorithm/s | ||||||
|---|---|---|---|---|---|---|---|
| GDRL-MOEA/D | MOEA/D | NSGA-II | MPA | SSA | AHA | SOA | |
| (50, 5) | 75.1254 | 78.3117 | 63.4386 | 76.2302 | 80.4125 | 81.1252 | 70.5412 |
| (50, 6) | 89.2452 | 90.2976 | 76.7797 | 88.5214 | 90.5412 | 91.5241 | 80.4224 |
| (50, 7) | 103.5411 | 105.8324 | 89.2609 | 104.2893 | 102.4125 | 104.6321 | 92.4125 |
| (50, 10) | 147.3512 | 148.1881 | 128.1632 | 145.2546 | 150.5412 | 154.5214 | 130.5418 |
| (50, 15) | 219.5412 | 219.9746 | 194.9998 | 218.6872 | 230.4512 | 232.1745 | 211.2156 |
| (50, 20) | 295.6234 | 294.0099 | 264.4712 | 291.0637 | 300.4124 | 302.4512 | 282.9541 |
| (100, 5) | 143.2415 | 154.5248 | 125.7052 | 142.1222 | 150.5416 | 155.5412 | 130.1445 |
| (100, 6) | 168.6145 | 172.2160 | 152.7174 | 168.0217 | 180.9841 | 182.4152 | 160.7841 |
| (100, 7) | 206.1235 | 200.6013 | 180.8117 | 205.3689 | 219.5412 | 220.7451 | 192.5412 |
| (100, 10) | 292.2514 | 293.9304 | 259.8535 | 291.2315 | 300.7451 | 304.5415 | 262.3562 |
| (100, 15) | 451.3547 | 441.1938 | 399.5518 | 450.0200 | 460.4152 | 463.1278 | 420.7412 |
| (100, 20) | 593.1045 | 592.6549 | 544.2545 | 592.2356 | 601.5471 | 603.4985 | 563.6482 |
| (150, 5) | 205.6841 | 216.7729 | 185.8298 | 206.2297 | 218.8471 | 220.7894 | 202.3541 |
| (150, 6) | 255.4562 | 254.7261 | 240.0422 | 255.2442 | 260.4841 | 264.3456 | 251.5624 |
| (150, 7) | 301.2514 | 316.9811 | 271.1553 | 298.3484 | 310.4514 | 315.4514 | 291.2481 |
| (150, 10) | 441.0145 | 441.1019 | 396.4780 | 439.0293 | 460.4152 | 463.3972 | 420.7892 |
| (150, 15) | 672.5241 | 670.6341 | 615.5960 | 669.9642 | 680.5123 | 683.7456 | 642.4874 |
| (150, 20) | 913.8121 | 920.1188 | 856.0781 | 912.1419 | 930.2457 | 932.1789 | 902.1872 |
| (200, 5) | 275.6581 | 282.2372 | 252.1723 | 276.1188 | 280.7451 | 284.4152 | 270.4671 |
| (200, 6) | 339.2514 | 347.0803 | 314.1157 | 338.6582 | 361.5141 | 365.8741 | 331.3416 |
| (200, 7) | 396.5412 | 400.0306 | 400.3811 | 396.4272 | 411.7452 | 418.8415 | 421.7412 |
| (200, 10) | 589.5418 | 589.5134 | 539.3509 | 587.6343 | 602.4578 | 606.7456 | 561.5715 |
| (200, 15) | 915.2564 | 914.6555 | 858.1994 | 912.2259 | 924.7451 | 930.6481 | 894.3251 |
| (200, 20) | 1274.4514 | 1254.9765 | 1235.4191 | 1271.5979 | 1290.4514 | 1298.3458 | 1251.8413 |
| AVG | 390.2317 | 391.6902 | 360.2011 | 389.0278 | 400.0483 | 403.3782 | 376.6758 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Yuan, Y.; Sitahong, A.; Chao, Y.; Wang, Y. An Optimization Method for Green Permutation Flow Shop Scheduling Based on Deep Reinforcement Learning and MOEA/D. Machines 2024, 12, 721. https://doi.org/10.3390/machines12100721
Lu Y, Yuan Y, Sitahong A, Chao Y, Wang Y. An Optimization Method for Green Permutation Flow Shop Scheduling Based on Deep Reinforcement Learning and MOEA/D. Machines. 2024; 12(10):721. https://doi.org/10.3390/machines12100721
Chicago/Turabian StyleLu, Yongxin, Yiping Yuan, Adilanmu Sitahong, Yongsheng Chao, and Yunxuan Wang. 2024. "An Optimization Method for Green Permutation Flow Shop Scheduling Based on Deep Reinforcement Learning and MOEA/D" Machines 12, no. 10: 721. https://doi.org/10.3390/machines12100721
APA StyleLu, Y., Yuan, Y., Sitahong, A., Chao, Y., & Wang, Y. (2024). An Optimization Method for Green Permutation Flow Shop Scheduling Based on Deep Reinforcement Learning and MOEA/D. Machines, 12(10), 721. https://doi.org/10.3390/machines12100721






