Acoustoelastic Theory and Mode Analysis of Bolted Structures Under Preload
Abstract
1. Introduction
2. Analytic Theory
2.1. The Preload of Bolted Structure
2.2. Acoustoelastic Theory
3. Results and Discussion
- (1)
- Boundary conditions: Using the solid mechanics physical field, the upper surface of the square steel is set as a fixed constraint, and the bottom end of the screw is set as a specified displacement.
- (2)
- Mesh division: Tetrahedral mesh division is used for the bolt head and nut, and the sweeping division method is used for the bolt rod and square steel.
- (3)
- Post-processing: Steady-state analysis and characteristic frequency analysis are adopted to import the simulation data related to frequency and strain into Origin for data processing and draw the correlation curve.
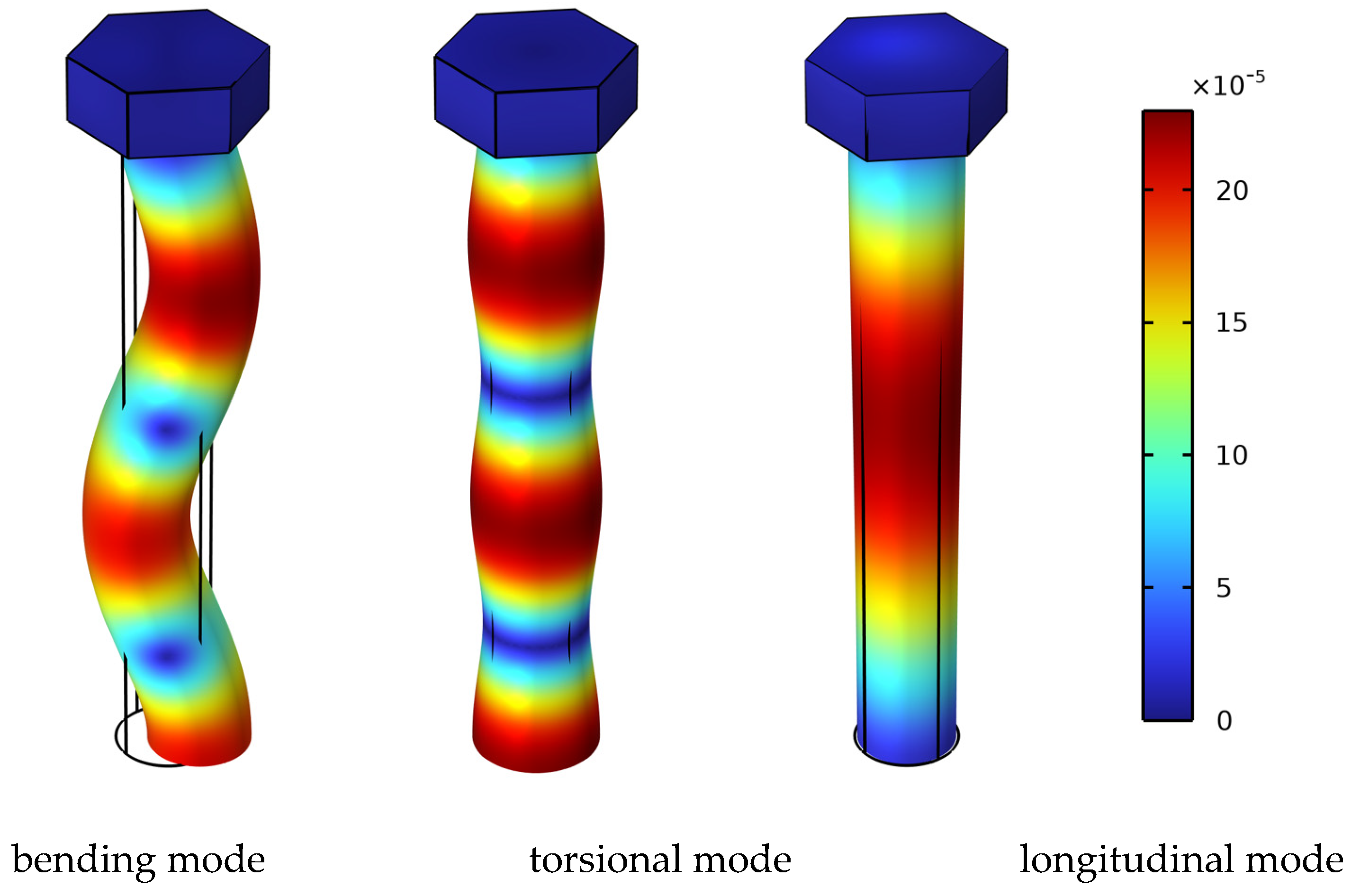
3.1. Modes Analysis of Preload on Bolted Structure
3.1.1. The Modes of the Bolted Structure Under the Non-Stress Conditions
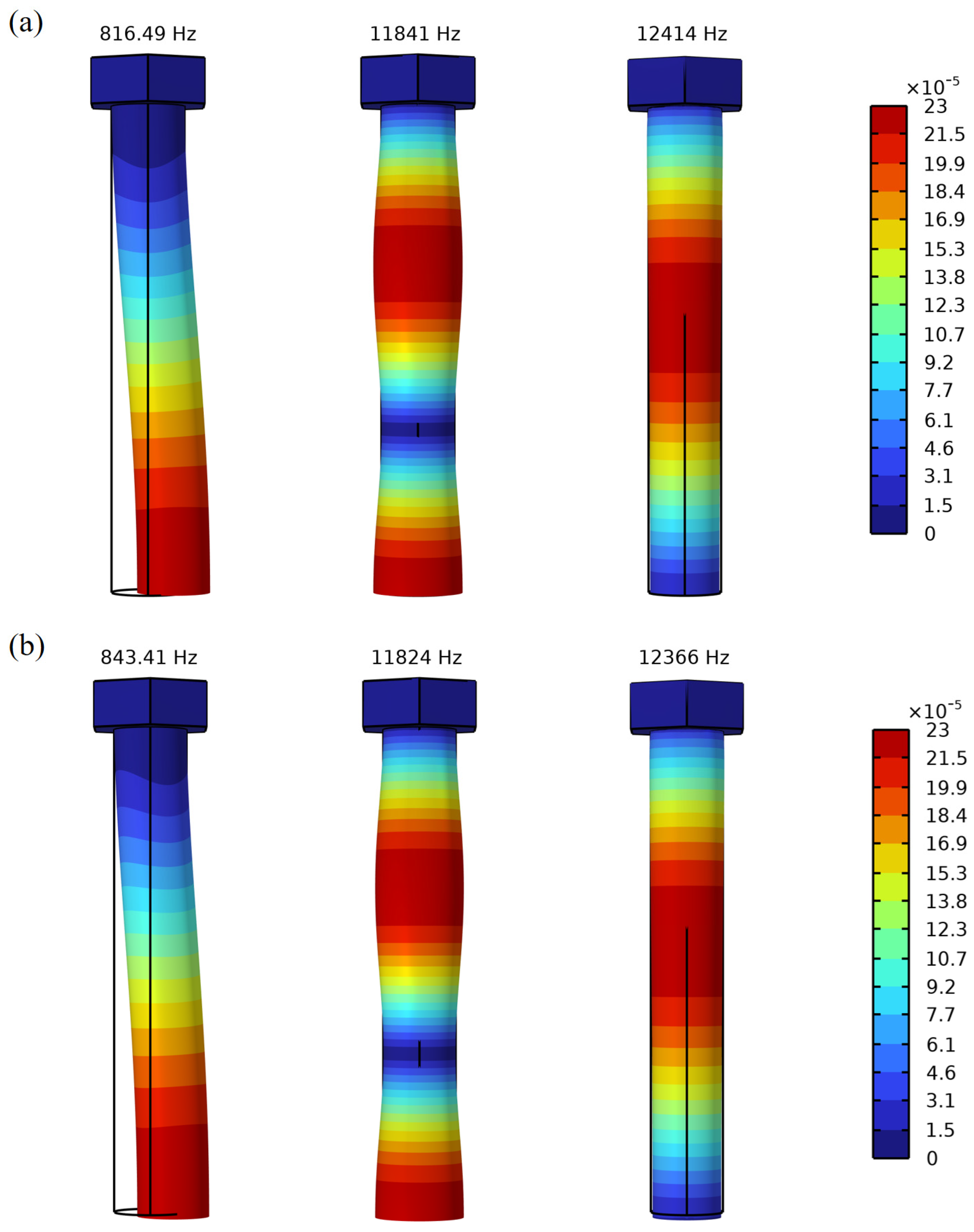
3.1.2. Verification of the Characteristic Frequency and Preload
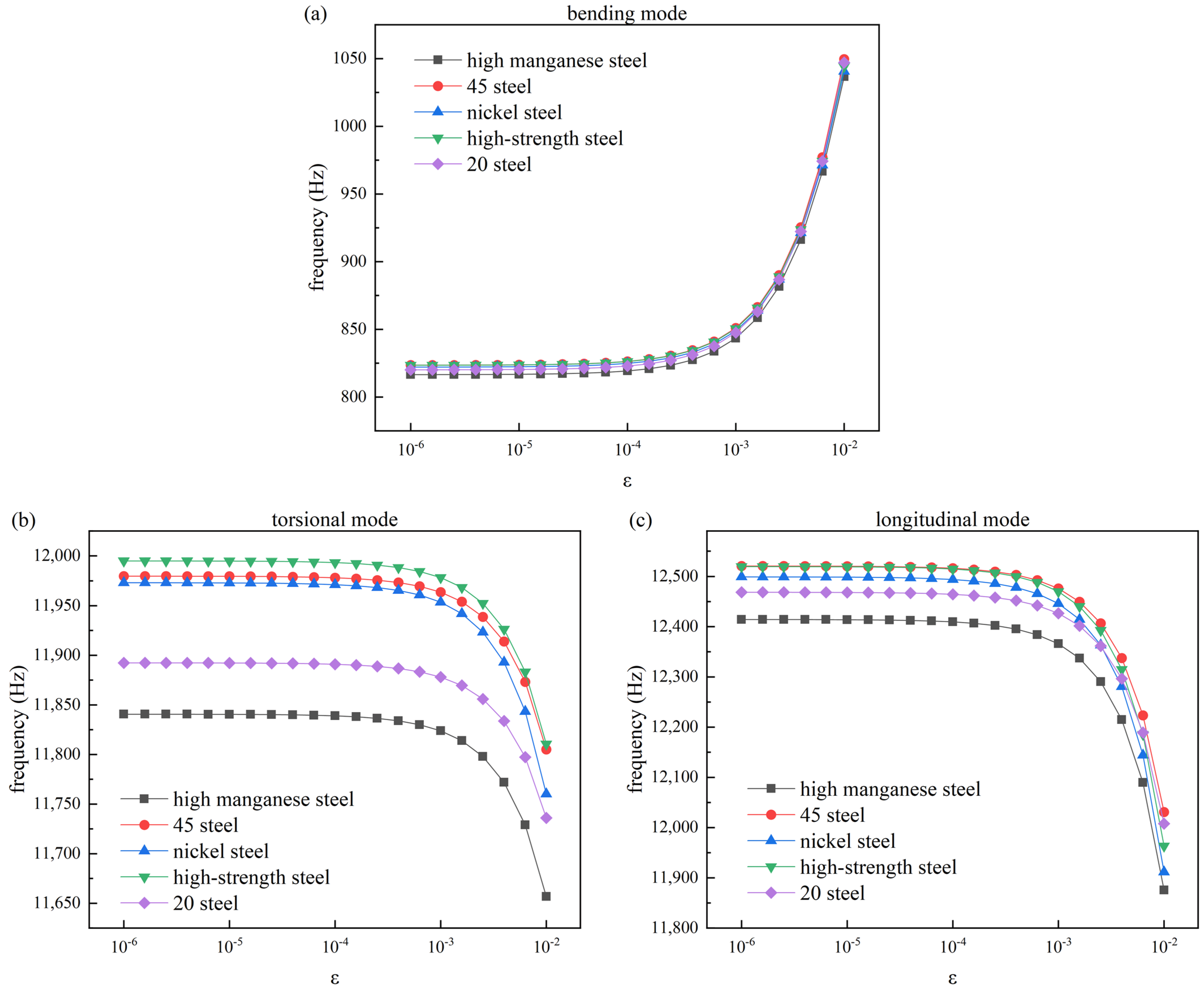
3.2. Influence of Material and Structural Parameters
3.2.1. Influence of Bolt Material Parameters on Natural Frequency Characteristics
3.2.2. Influence of Bolted Structure Parameters on Natural Frequency Characteristics
4. Conclusions
- (i)
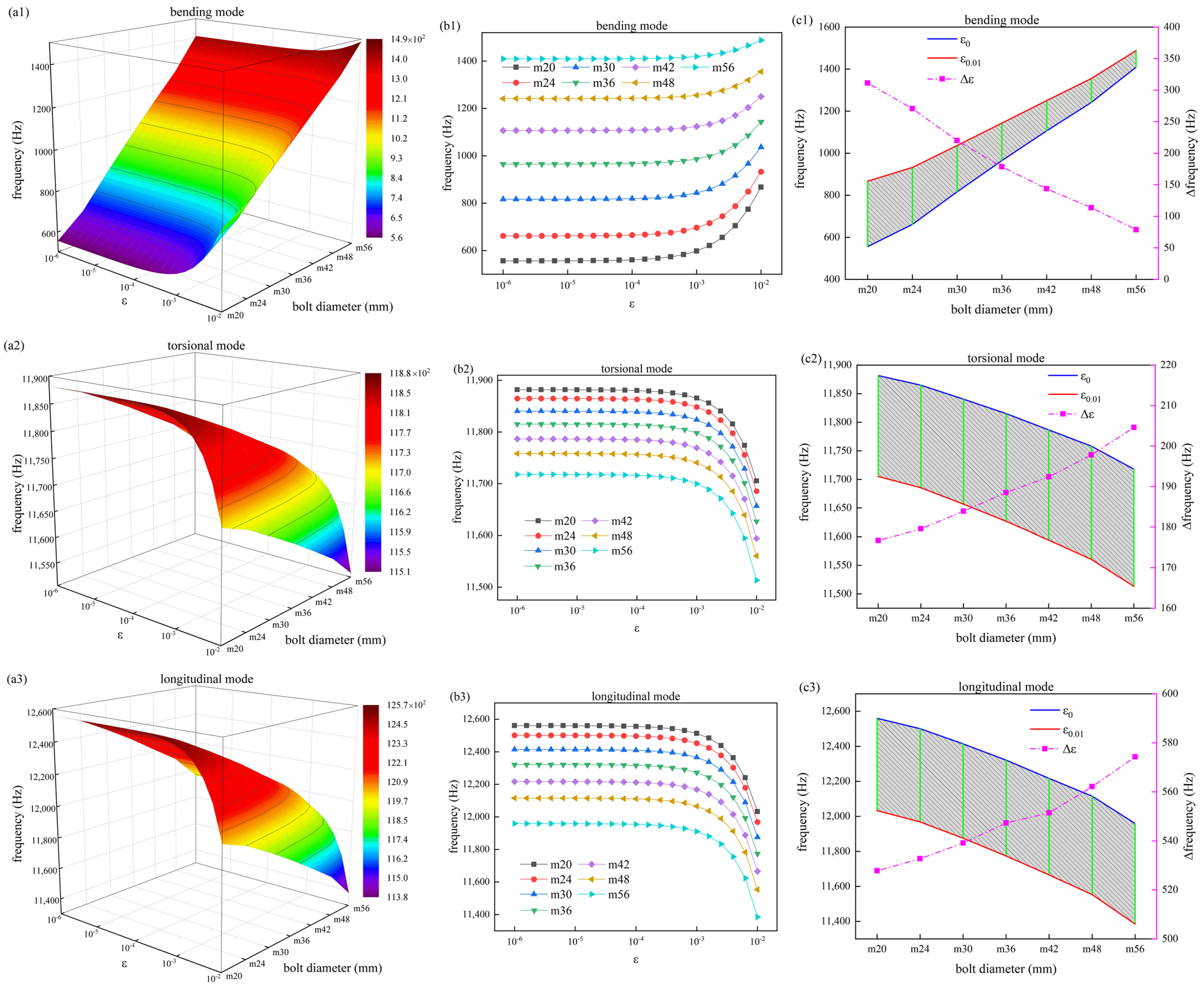
- The study of bolts made of various materials shows that the general change trend is the same, and the natural frequency under different structural modes has an obvious change trend under different preloading forces. Specifically, the bending mode frequency demonstrates an augmentation with increasing preload, whereas the torsional and longitudinal mode frequencies display a reduction.
- (ii)
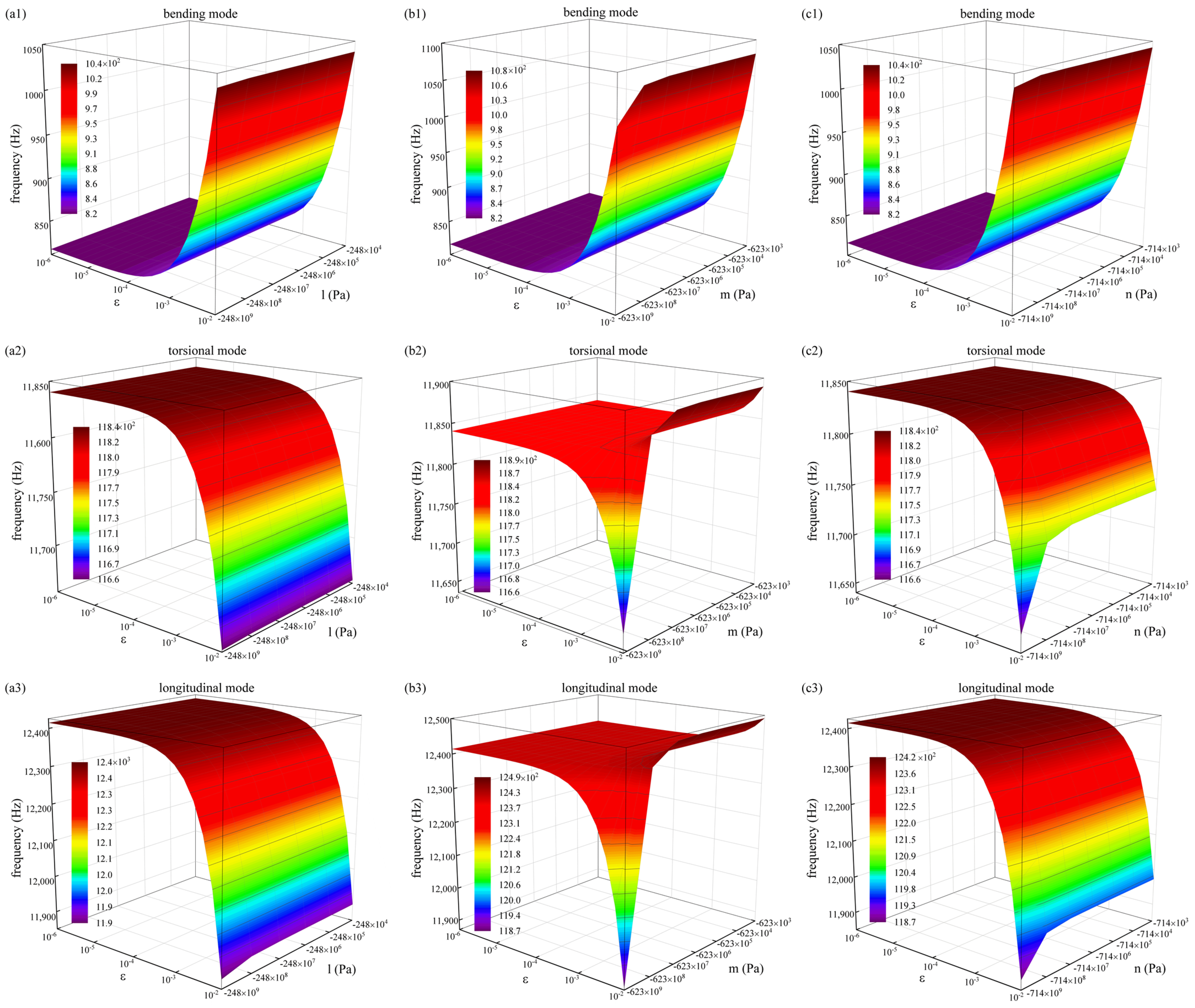
- The parameters of high manganese steel were chosen as the base research parameters to investigate the variation in bolt natural frequency with preloads when altering the Lame elastic constants in this study. For , the bending mode frequency increases with an increase in preload. While the torsional and longitudinal modes decrease when changes in a small range, as reaches a large value, the effect of preload on frequency becomes less pronounced. In contrast, there is no significant overall change in the frequencies of the three modes with increasing preload for .
- (iii)
- The parametric studies of Murnaghan’s third-order elastic constants , show that the change in the elastic constants is weaker than the pattern of change in the fundamental frequency of the structure embodied in the preload force, and the frequency of in bending mode increases with preload, while the frequency of in torsional and longitudinal modes decreases with preload. As for , the frequency in the bending mode increases with preload, while the frequencies in the torsional and longitudinal modes mainly increase with preload. However, when , the frequency decreases with increasing preload. In the case of , the bending mode frequency increases with preload, whereas the frequencies in the torsional and longitudinal modes decrease with increasing preload.
- (iv)
- The structure parameters of bolts are studied in this paper. It is observed that the bending mode frequency increases with an increase in preload, while the torsional mode frequency and longitudinal mode frequency decrease with an increase in preload. In the bending mode, the frequency value of initially increases and then decreases with an increase in bolt length. It decreases with an increase in bolt diameter. In the torsion mode and longitudinal mode, the frequency value of decreases with an increase in bolt length and increases with an increase in bolt diameter.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, H.B.; Zhang, X.; Liu, Y.K.; Wang, Y.Q. Research on electromagnetic ultrasonic unidirectional stress transverse and longitudinal wave joint measurement method. Mech. Des. Manuf. 2021, 9, 241–246. [Google Scholar] [CrossRef]
- Zhang, X. EMAT-Based Unidirectional Stress Transverse and Longitudinal Wave Joint Measurement Method. Master’s Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar] [CrossRef]
- Lian, J.; Qian, Y.; Dong, L. Research on the effect of assembly process on the preload force of ultra-high-speed test shaft system. Aerosp. Manuf. Technol. 2018, 2, 52–56. [Google Scholar]
- Xin, J. Ultrasonic Non-Destructive Testing and Calibration Technique for Gear Tooth Root Residual Stress. Master’s Thesis, Beijing University of Technology, Beijing, China, 2015. [Google Scholar]
- Lv, Y.; Zhang, X.; Gao, J.; Song, G.; He, C. Method and system for axial stress detection of bolts based on acoustoelastic effect. Nondestruct. Test. 2023, 45, 11–15. [Google Scholar]
- Lv, Y.; Xie, L.; Song, G.; He, C.; Cheng, J.; Ji, S. A method for axial stress detection of bolts based on acoustoelastic effect. J. Beijing Inst. Technol. 2022, 48, 920–927. [Google Scholar]
- Gao, S. Research on Electromagnetic Ultrasonic Detection of Wind Turbine Bolt Stress. Master’s Thesis, Shenyang University of Technology, Shenyang, China, 2022. [Google Scholar] [CrossRef]
- Lee, S.-H. Research on the Measurement Technique of High Tensile Bolt Pre-Tension by Ultrasonic Double Wave Method. Master’s Thesis, Beijing University of Architecture, Beijing, China, 2023. [Google Scholar] [CrossRef]
- Pan, Q.; Chang, M.; Pan, R.; Xu, X.; Li, S.; Zhang, Y. Research on nonlinear ultrasonic detection technology of bolt axial stress. J. Mech. Eng. 2021, 57, 88–95. [Google Scholar]
- Feng, S. Research on Ultrasonic Detection Method of Axial Stress in High Strength Bolts. Master’s Thesis, Hubei University of Technology, Wuhan, China, 2022. [Google Scholar] [CrossRef]
- Feng, S.; Tu, J.; Wei, S.; Chi, Y.; Zhang, X.; Song, X. Ultrasonic testing of axial stress of high strength bolts for bridges. Int. J. Appl. Electromagn. Mech. 2020, 64, 685–692. [Google Scholar] [CrossRef]
- Crecraft, D.I. Ultrasonic measurement of stresses. Ultrasonics 1968, 6, 117–121. [Google Scholar] [CrossRef]
- Kwaśniewki, J. Influence of acoustoelastic coefficient on wave time of flight in stress measurement in piezoelectric self-excited system. Mech. Syst. Signal Process. 2016, 78, 143–155. [Google Scholar] [CrossRef]
- Zhao, X.-X.; Li, Y.-M.; Liu, X.-G.; Yao, K. Ultrasonic measurement on axial force of high-strength bolt in service. J. Low Freq. Noise Vib. Act. Control. 2020, 39, 596–603. [Google Scholar] [CrossRef]
- Kelardeh, S.M.; Hosseini, S.V.; Heidari, M.; Parvaz, H. An investigation of the effect of bolt tightening stress on ultrasonic velocity in cylinder head and main bearing cap bolts of diesel engine. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 375. [Google Scholar] [CrossRef]
- Mills, B.; Javadi, Y.; Abad, F.; Lotfian, S.; MacLeod, C.; Mehmanparast, A.; Pierce, G.; Gachagan, A. Inspection of wind turbine bolted connections using the ultrasonic phased array system. Heliyon 2024, 10, e34579. [Google Scholar] [CrossRef]
- Leng, J.; Tian, H.; Zhou, G.; Wu, Z. A review of research on dynamic damage diagnosis methods for in-service offshore platforms. Chin. J. Saf. Sci. 2017, 27, 79–85. [Google Scholar] [CrossRef]
- Zhao, G.; Jin, X.; Cui, Y.; Feng, Z.; Wang, T.; Xiong, Z. A contact stiffness identification method based on modal strain energy. J. Mech. Eng. 2020, 56, 147–153. [Google Scholar]
- Gou, B.; Lu, Q.; Wang, B.; Wang, S. Detection of bolt tightening force using intrinsic frequency outlier analysis. Vib. Shock 2015, 34, 77–82. [Google Scholar]
- An, W.W.; Guo, B.; Gong, Z.R. A dynamic stiffness identification method for bolted joints based on modal experiments. Mech. Des. Manuf. 2015, 2, 1–3+7. [Google Scholar]
- Zhao, G.; Wang, B.; Yu, G.; Yang, H.; Huang, X. Study on the influence law of bolt preload on the characteristic parameters of bolt bonding surface. Mech. Strength 2018, 40, 392–397. [Google Scholar] [CrossRef]
- Zhao, G.; Xiong, Z.; Jin, X.; Hou, L.; Gao, W. Prediction of contact stiffness in bolted interface with natural frequency experiment and FE analysis. Tribol. Int. 2018, 127, 157–164. [Google Scholar] [CrossRef]
- Sah, S.M. Estimating bolt tightness using transverse natural frequencies. J. Sound Vib. 2018, 431, 137–149. [Google Scholar] [CrossRef]
- Bonisoli, E.; Marcuccio, G. Venturini, Interference fit estimation through stress-stiffening effect on dynamics. Mech. Syst. Signal Process. 2021, 160, 107919. [Google Scholar] [CrossRef]
- de Faria, A.R.; Donadon, M.V. The use of piezoelectric stress stiffening to enhance buckling of laminated plates. Lat. Am. J. Solids Struct. 2009, 7, 167–183. [Google Scholar] [CrossRef][Green Version]
- Han, X. Study on the Dynamic Characteristics of Bolted Flange Connection Structures Considering the Connection State. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2021. [Google Scholar] [CrossRef]
- Michael, W. Bolted Joint Preload Distribution from Torque Tightening. Stroj. Časopis-J. Mech. Eng. 2021, 71, 329–342. [Google Scholar] [CrossRef]
- Egle, D.M.; Bray, D.E. Measurement of acoustoelastic and third-order elastic constants for rail steel. J. Acoust. Soc. Am. 1976, 60, 741–744. [Google Scholar] [CrossRef]

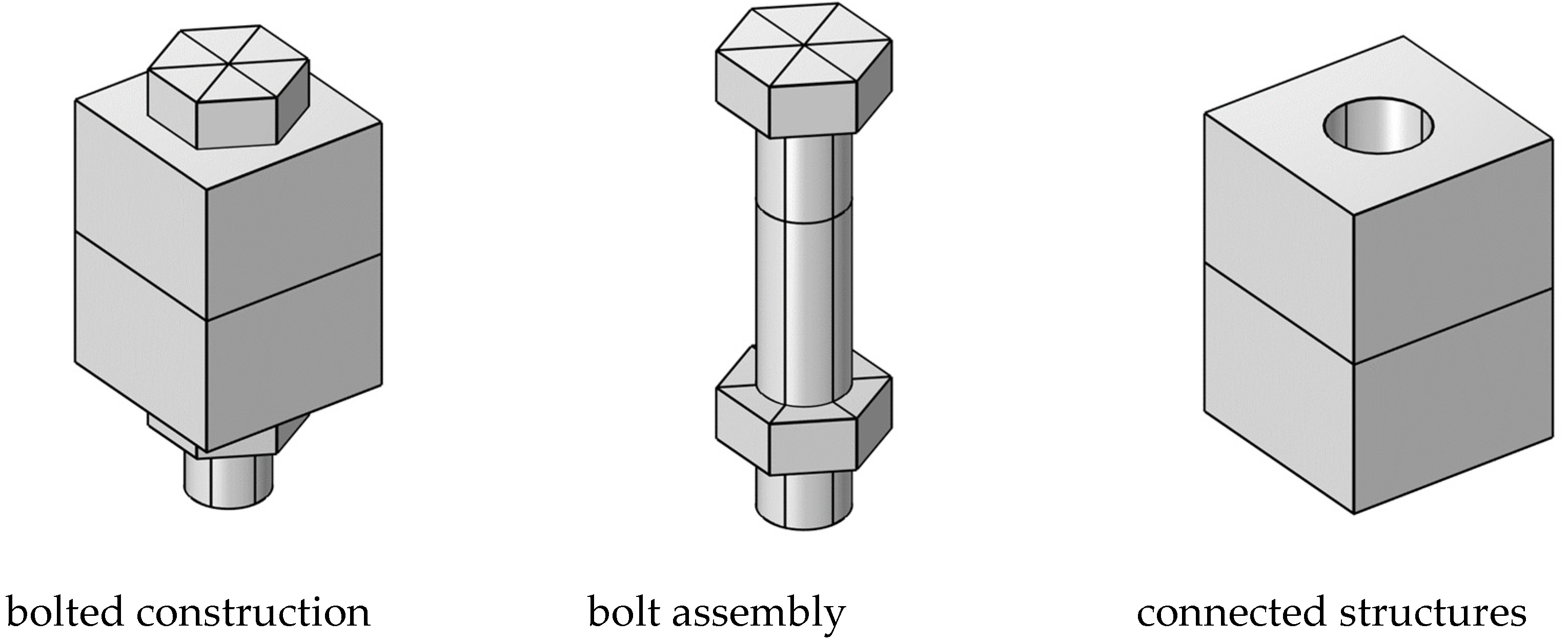


| Parameters | Bolts and Nuts | Connected Structures | |
|---|---|---|---|
| Density (kg/m3) | 7850 | 7850 | |
| Young’s modulus (GPa) | / | 205 | |
| Poisson’s ratio | / | 0.28 | |
| Lame constants (GPa) | 115.8 | / | |
| 79.9 | / | ||
| Murnaghan constants (GPa) | −248 | / | |
| −623 | / | ||
| −714 | / | ||
| Materials | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) |
|---|---|---|---|---|---|
| high manganese steel | 115.8 | 79.9 | −248 | −623 | −714 |
| 45 steel | 111.59 | 81.79 | −81.25 | −583.1 | −782.85 |
| nickel steel | 109 | 81.7 | −56 | −671 | −785 |
| high-strength steel | 109 | 82 | −426 | −619 | −708 |
| 20 steel | 116.8 | 80.6 | −69 | −574 | −670 |
| Modes | Bolt Length (mm) | ||||||
|---|---|---|---|---|---|---|---|
| 0 | |||||||
| bending mode | 160 | 1251.1052 | 1251.1310 | 1251.3626 | 1253.6743 | 1276.3310 | 1462.4871 |
| 180 | 999.6774 | 999.7043 | 999.9459 | 1002.3572 | 1025.9347 | 1217.7101 | |
| 200 | 816.4894 | 816.5171 | 816.7656 | 819.2445 | 843.4099 | 1036.5595 | |
| 220 | 679.0554 | 679.0836 | 679.3371 | 681.8648 | 706.4184 | 898.8077 | |
| 240 | 573.2732 | 573.3018 | 573.5590 | 576.1223 | 600.9244 | 791.1777 | |
| 260 | 490.3680 | 490.3969 | 490.6568 | 493.2466 | 518.1976 | 705.3551 | |
| torsional mode | 160 | 14,758.2860 | 14,758.2647 | 14,758.0733 | 14,756.1568 | 14,736.7916 | 14,521.3192 |
| 180 | 13,139.7706 | 13,139.7520 | 13,139.5841 | 13,137.9032 | 13,120.9241 | 12,932.7591 | |
| 200 | 11,840.5873 | 11,840.5707 | 11,840.4212 | 11,838.9246 | 11,823.8100 | 11,656.6958 | |
| 220 | 10,774.1496 | 10,774.1346 | 10,773.9998 | 10,772.6499 | 10,759.0183 | 10,608.4617 | |
| 240 | 9883.7275 | 9883.7139 | 9883.5914 | 9882.3652 | 9869.9843 | 9733.5249 | |
| 260 | 9129.2540 | 9129.2415 | 9129.1291 | 9128.0043 | 9116.6478 | 8991.5975 | |
| longitudinal mode | 160 | 15,366.3660 | 15,366.3057 | 15,365.7626 | 15,360.3260 | 15,305.3337 | 14,680.9919 |
| 180 | 13,737.3769 | 13,737.3234 | 13,736.8418 | 13,732.0213 | 13,683.2901 | 13,134.8923 | |
| 200 | 12,414.3921 | 12,414.3440 | 12,413.9115 | 12,409.5820 | 12,365.8280 | 11,875.3106 | |
| 220 | 11,322.5266 | 11,322.4830 | 11,322.0902 | 11,318.1582 | 11,278.4294 | 10,833.7621 | |
| 240 | 10,405.5042 | 10,405.4644 | 10,405.1054 | 10,401.5126 | 10,365.2200 | 9960.6934 | |
| 260 | 9625.6932 | 9625.6564 | 9625.3258 | 9622.0160 | 9588.5866 | 9216.4303 | |
| Modes | Bolt Diameter (mm) | ||||||
|---|---|---|---|---|---|---|---|
| 0 | |||||||
| bending mode | m20 | 556.0075 | 556.0515 | 556.4473 | 560.3864 | 597.9781 | 867.2763 |
| m24 | 661.7927 | 661.8287 | 662.1521 | 665.3746 | 696.4897 | 932.5279 | |
| m30 | 816.4706 | 816.4982 | 816.7468 | 819.2257 | 843.3908 | 1036.5284 | |
| m36 | 964.8648 | 964.8866 | 965.0829 | 967.0414 | 986.2233 | 1143.3586 | |
| m42 | 1106.5374 | 1106.5548 | 1106.7115 | 1108.2758 | 1123.6285 | 1250.2272 | |
| m48 | 1241.7633 | 1241.7773 | 1241.9032 | 1243.1599 | 1255.4958 | 1355.3737 | |
| m56 | 1409.4438 | 1409.4542 | 1409.5472 | 1410.4757 | 1419.5657 | 1488.2257 | |
| torsional mode | m20 | 11,881.8176 | 11,881.8016 | 11,881.6569 | 11,880.2087 | 11,865.5911 | 11,705.0988 |
| m24 | 11,864.9056 | 11,864.8893 | 11,864.7427 | 11,863.2756 | 11,848.4636 | 11,685.3448 | |
| m30 | 11,840.5147 | 11,840.4981 | 11,840.3486 | 11,838.8522 | 11,823.7392 | 11,656.6415 | |
| m36 | 11,815.2532 | 11,815.2363 | 11,815.0838 | 11,813.5572 | 11,798.1335 | 11,626.7273 | |
| m42 | 11,786.5573 | 11,786.5401 | 11,786.3852 | 11,784.8344 | 11,769.1594 | 11,594.1859 | |
| m48 | 11,758.2861 | 11,758.2686 | 11,758.1104 | 11,756.5275 | 11,740.5192 | 11,560.4818 | |
| m56 | 11,717.8232 | 11,717.8052 | 11,717.6434 | 11,716.0230 | 11,699.6249 | 11,513.2325 | |
| longitudinal mode | m20 | 12,560.5105 | 12,560.4628 | 12,560.0340 | 12,555.7417 | 12,512.4062 | 12,032.7104 |
| m24 | 12,501.1768 | 12,501.1290 | 12,500.6986 | 12,496.3903 | 12,452.8744 | 11,968.4747 | |
| m30 | 12,414.3149 | 12,414.2668 | 12,413.8343 | 12,409.5048 | 12,365.7510 | 11,875.2266 | |
| m36 | 12,321.2757 | 12,321.2275 | 12,320.7931 | 12,316.4446 | 12,272.4644 | 11,773.9822 | |
| m42 | 12,216.9599 | 12,216.9117 | 12,216.4777 | 12,212.1327 | 12,168.1574 | 11,665.5454 | |
| m48 | 12,115.4487 | 12,115.4007 | 12,114.9690 | 12,110.6510 | 12,065.6764 | 11,553.3148 | |
| m56 | 11,959.0018 | 11,958.9538 | 11,958.5215 | 11,954.1922 | 11,910.2540 | 11,384.7374 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Kuang, R.; Tian, G.; Shi, X.; Sun, L. Acoustoelastic Theory and Mode Analysis of Bolted Structures Under Preload. Machines 2024, 12, 822. https://doi.org/10.3390/machines12110822
Zhao L, Kuang R, Tian G, Shi X, Sun L. Acoustoelastic Theory and Mode Analysis of Bolted Structures Under Preload. Machines. 2024; 12(11):822. https://doi.org/10.3390/machines12110822
Chicago/Turabian StyleZhao, Lei, Rui Kuang, Guizhong Tian, Xiaona Shi, and Li Sun. 2024. "Acoustoelastic Theory and Mode Analysis of Bolted Structures Under Preload" Machines 12, no. 11: 822. https://doi.org/10.3390/machines12110822
APA StyleZhao, L., Kuang, R., Tian, G., Shi, X., & Sun, L. (2024). Acoustoelastic Theory and Mode Analysis of Bolted Structures Under Preload. Machines, 12(11), 822. https://doi.org/10.3390/machines12110822






