Modeling and Characteristic Test for a Crank-Connecting Rod Mem-Inerter Device

Abstract

This paper presents a mechanical crank-connecting rod mem-inerter device, with its output and memory characteristics being investigated and validated. Previous research suggests that a hydraulic mem-inerter generates a sizeable damping force, practically transforming it into a mem-dashpot. This greatly influences a system’s vibration characteristics when using a hydraulic mem-inerter. In contrast, the proposed crank-connecting rod inerter exhibits negligible damping force, addressing the issue of excessive damping in hydraulic inerters and potentially enhancing the actual isolation effect. We successfully developed a prototype of the trial production device, and a bench characteristic test was conducted. Our quasi-static test results indicate that frictional resistance during device operation can be negligible. Our dynamic characteristic test results reveal that the characteristic curves of the device on the momentum–velocity plane can be displayed as a pinched hysteresis loop. Our results are in agreement with the simulation outcomes, which proves that the crank-connecting rod inerter is a physical realization of a mem-inerter device.

1. Introduction

The inerter is a mechanical shock-absorbing element introduced by Smith [1]. Inerter-based devices play a crucial role in high-performance vibration control systems with different characteristics [2,3]. As a novel two-terminal mechanical element, the inerter suppresses undesired structural vibrations, characterized by the apparent mass effect of employing lightweight gravitational mass [4,5]. Due to its compact size and mass, the inerter has garnered extensive research on suspension [6] and significant attention in the engineering and construction fields [7,8]. Additionally, the negative stiffness effect is another characteristic of inerter elements during dynamic excitations that can be utilized to enhance structural vibration absorption [4,9]. One of its distinctive features is the inerter’s ability to generate a force that aids motion, contrasting with the conventional positive stiffness system where the force opposes motion. This property enables the inerter to be employed in reducing the natural frequency of a vibration system. Moreover, the conceptualization of the inerter has driven the transformation of mechanical networks, shifting from a mass–spring–damper configuration to an inerter–spring–damper arrangement. A mechanical network can be matched to an electrical network through the utilization of the proposed inerter. Incorporating both spring and damping elements in conjunction with the inerter facilitates enhanced damping effects [10,11], contributing to the formation of a more efficient mechanical network for vibration control systems. Leveraging these advantages, the inerter has found widespread application in diverse fields, including automotive engineering [12,13], aerospace engineering [14,15], civil engineering [16,17], and vibration energy harvesting [18,19]. Scholars have demonstrated the promise and efficiency of inerter-based devices for mitigating structural vibrations.

Classified according to the medium used for inertance encapsulation, inerters are primarily categorized into mechanical and hydraulic types [20]. Smith et al. [21] proposed a gear rack inerter, which leverages the speed-increasing effect of gears to amplify the rotational inertance of a flywheel, thereby encapsulating a larger inertial force. Saito et al. [22] and Ikago et al. [23,24] proposed a ball screw mechanism that converts linear motion into rapid rotation of the flywheel to fabricate an inerter device. They demonstrated through experimental tests the apparent mass effect and the efficient structural response mitigation effect of this inerter device, which has been the inerter system adopted in practical building structures, to date. Wang et al. [25] proposed a hydraulic inerter, employing liquid flow to drive hydraulic motor rotation and generate the apparent mass effect. However, the inertance provided by each of the aforementioned inerters is constant and cannot change with the relative displacement of the two terminals; thus, it is unable to adapt to complex and variable vibration conditions. During the design phase, these components are optimized for specific working conditions, limiting their adaptability to dynamic and intricate vibration scenarios. This inadequacy hinders the fulfillment of performance requirements for vibration reduction systems. Presently, a discernible trend in both electronic and mechanical elements is the transition from parameter-immutable to parameter-mutable characteristics [26,27].

It is well known that active and semi-active devices can provide variable stiffness or damping and are particularly promising at suppressing system vibration [28]. However, the dependence on external power supply, sensing, and feedback systems also makes active isolation techniques more complex, costly, and difficult, and semi-active inerters are no exception. Conversely, passive-variable parameter elements, such as memory elements, are widely accepted in the field of shock and vibration-control engineering, due to their simplicity and high reliability. During the early 1970s, Chua [29] introduced a new circuit element called the memristor. It is a nonlinear memory element that relates flux linkage and charge. This led to the development of mathematical theories for nonlinear memory elements in electrical circuits. Chua and Kang [30] later generalized the memristor concept to a nonlinear dynamical system. They created a mathematical theory for memristive systems. Di Ventra et al. [31] extended this theory, to include memcapacitive and meminductive systems. Oster and Auslander [32] introduced a simple physical example of a tapered dashpot as a mem-dashpot. Jeltsema et al. [33] and Biolek et al. [34] proposed two other physical examples of the mem-dashpot: the cable-reel and the yoyo-toy, respectively. Pei et al. introduced the concept of mem-spring [35], using the mem-spring model to represent origin-crossing material behaviors. In 2018, Zhang et al. [36] proposed a triangular table of elementary mechanical memory elements. The table was based on the triangular periodic table of elementary circuit elements and force–current analogies, as shown in Figure 1. The figure illustrates the position of each element and its corresponding device. Furthermore, Zhang presented a hydraulic mem-inerter implementation device corresponding to the memcapacitor based on the structural principle of the hydraulic inerter [36]. After applying the hydraulic mem-inerter to vehicle suspension, the investigation showed that suspension equipped with the mem-inerter could naturally self-adjust its inertance based on the vehicle load, providing better ride comfort than the linear inerter [37]. Such adaptivity was possible due to the memory elements’ learning ability, which had been revealed in some preliminary research [38,39]. However, the device produced large parasitic damping while in operation, causing the damping force to be much greater than the inertial force. At present, this viscous parasitic damping force is a major shortcoming of almost all hydraulic inerters. This issue transforms the hydraulic mem-inerter into a corresponding “mem-dashpot” element in the triangular element periodic table, which greatly affects its practical application effects.

The primary research objective of this paper was to demonstrate through modeling and characteristic testing that the proposed crank-connecting rod inerter device is a memory element. The conventional hydraulic mem-inerter generates a sizeable parasitic damping force, which can convert it into a mem-dashpot during practical applications, thereby affecting its actual performance. Through modeling on the constitutive-relation plane, this paper demonstrates that the proposed crank-connecting rod inerter is an ideal realization of a mem-inerter. With negligible damping force, it does not alter the element’s position in the periodic table, providing a significant advantage over the hydraulic mem-inerter. Firstly, the corresponding constitutive model is derived to describe the mechanical behavior of the device. The relationship between its structure parameters and the output characteristics is studied. Secondly, according to the constitutive relation, it is proved that the device is a variable parameter memory element, which can provide different inertance according to the relative displacement of its two terminals. On this basis, a prototype of a crank-connecting rod mem-inerter was designed and fabricated for experimental research. A series of dynamic tests on the device were conducted, to verify the constitutive model.

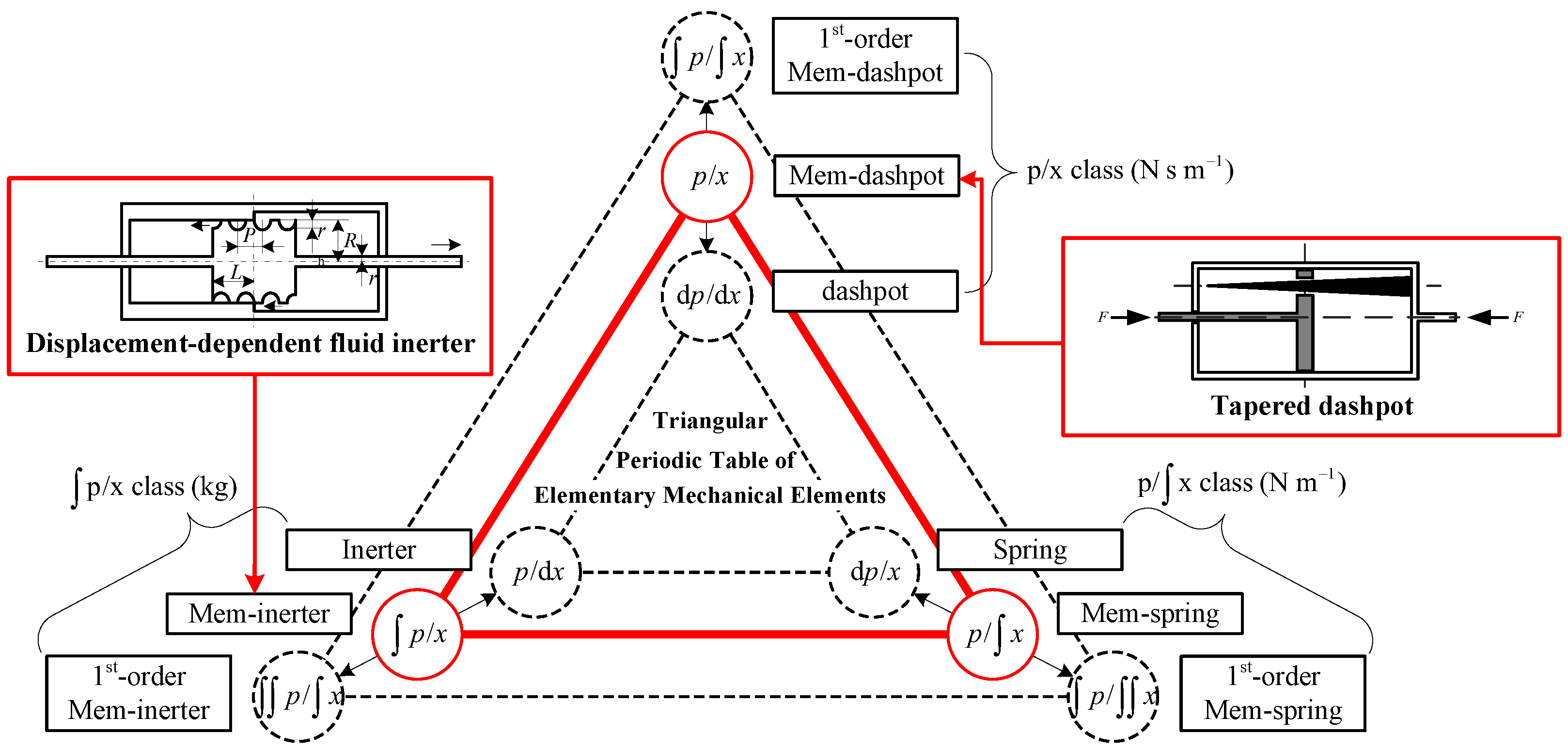
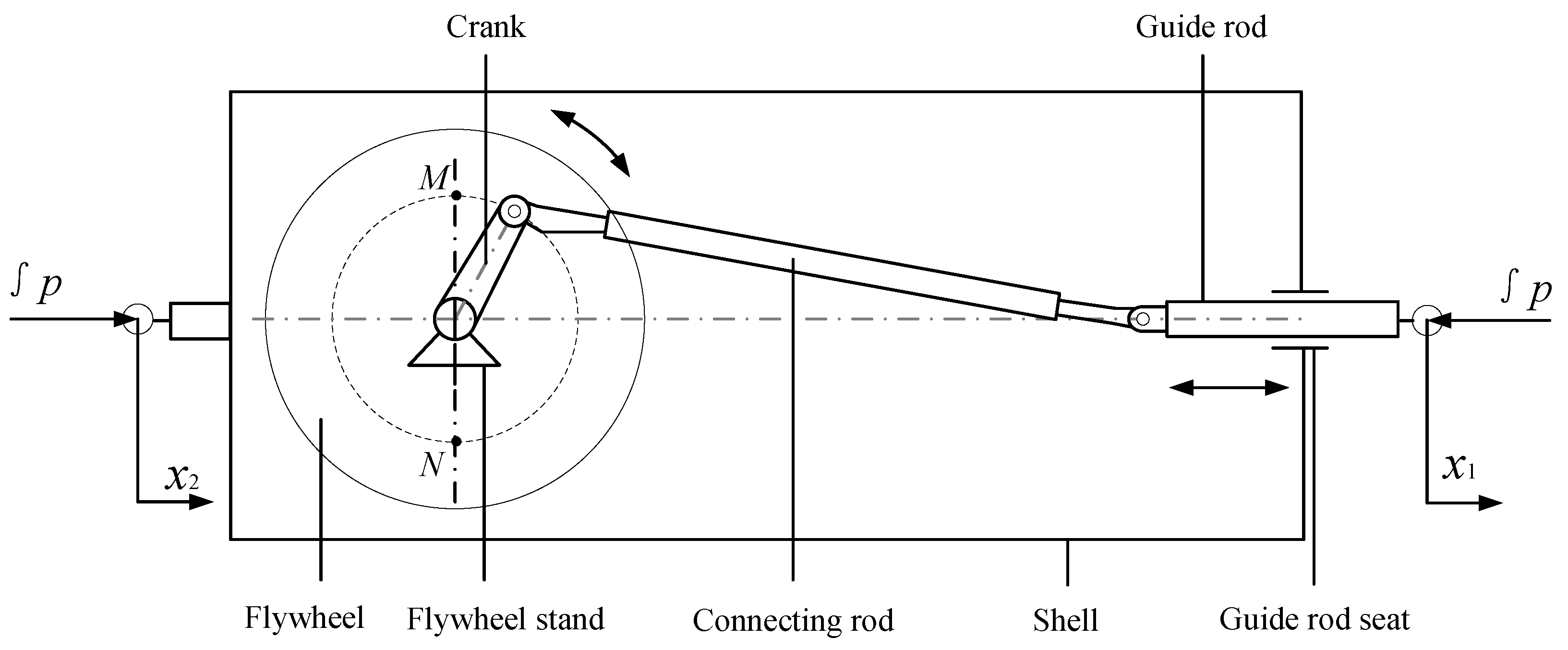
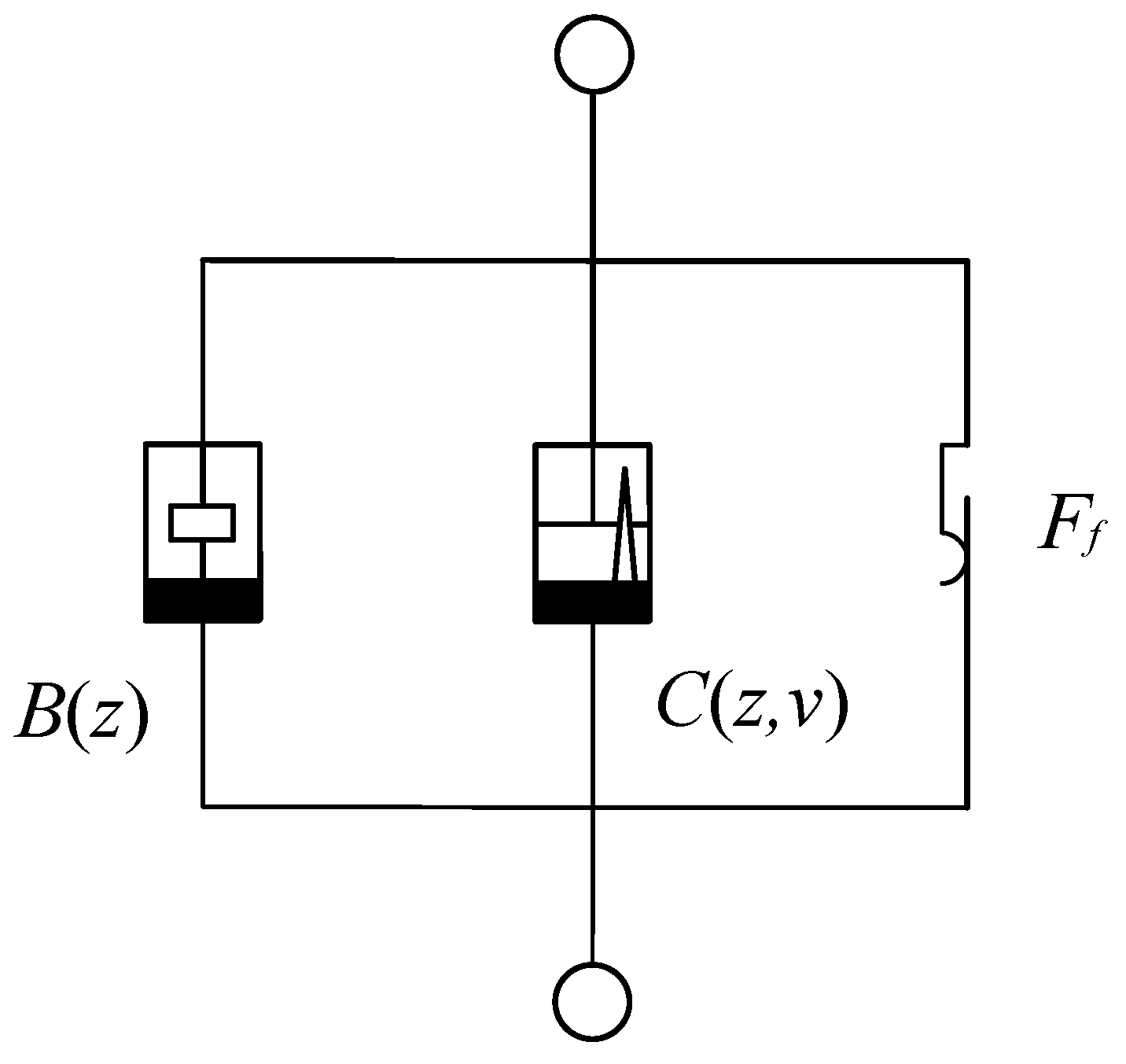
2. Crank-Connecting Rod Mem-Inerter Device

2.1. Structural Design and Working Principle

This section describes our design for a crank-connecting rod mem-inerter device, mainly composed of a mass flywheel, a crank-connecting rod mechanism, and a guiding mechanism. The guide rod, as one of the independent movement terminals, slides and fits with the guide rod seat, moving in a straight line along the guide rod seat, which is fixedly connected to the shell. The flywheel stand is fixedly connected to the shell and serves as another independent movement terminal together with the shell. The flywheel and the crank are concentrically installed on the flywheel stand, and the crank swings back and forth between the top dead-center M and bottom dead-center N, driving the flywheel to rotate. The connecting rods are hinged with the crank and the guide rod, respectively. The specific structure is shown in Figure 2.

The guide rod is the first independent terminal, and the flywheel stand connected to the shell serves as the second independent terminal together with the shell. The device converts the linear motion of the guide rod into the rotational motion of the flywheel through a crank-connecting rod mechanism, thereby converting the energy input at two terminals of the device into the kinetic energy of the flywheel. The first terminal stores energy when moving closer to the second terminal and, vice versa, releases energy. The inertance generated by the rotation of the flywheel changes with the relative displacement of the two terminals, overcoming the disadvantage of traditional linear inerter devices with constant inertance. When the two terminals are connected to the system, they can control mechanical force, momentum, and integrated momentum to absorb the vibration energy between the two platforms and isolate the relative vibration between them.

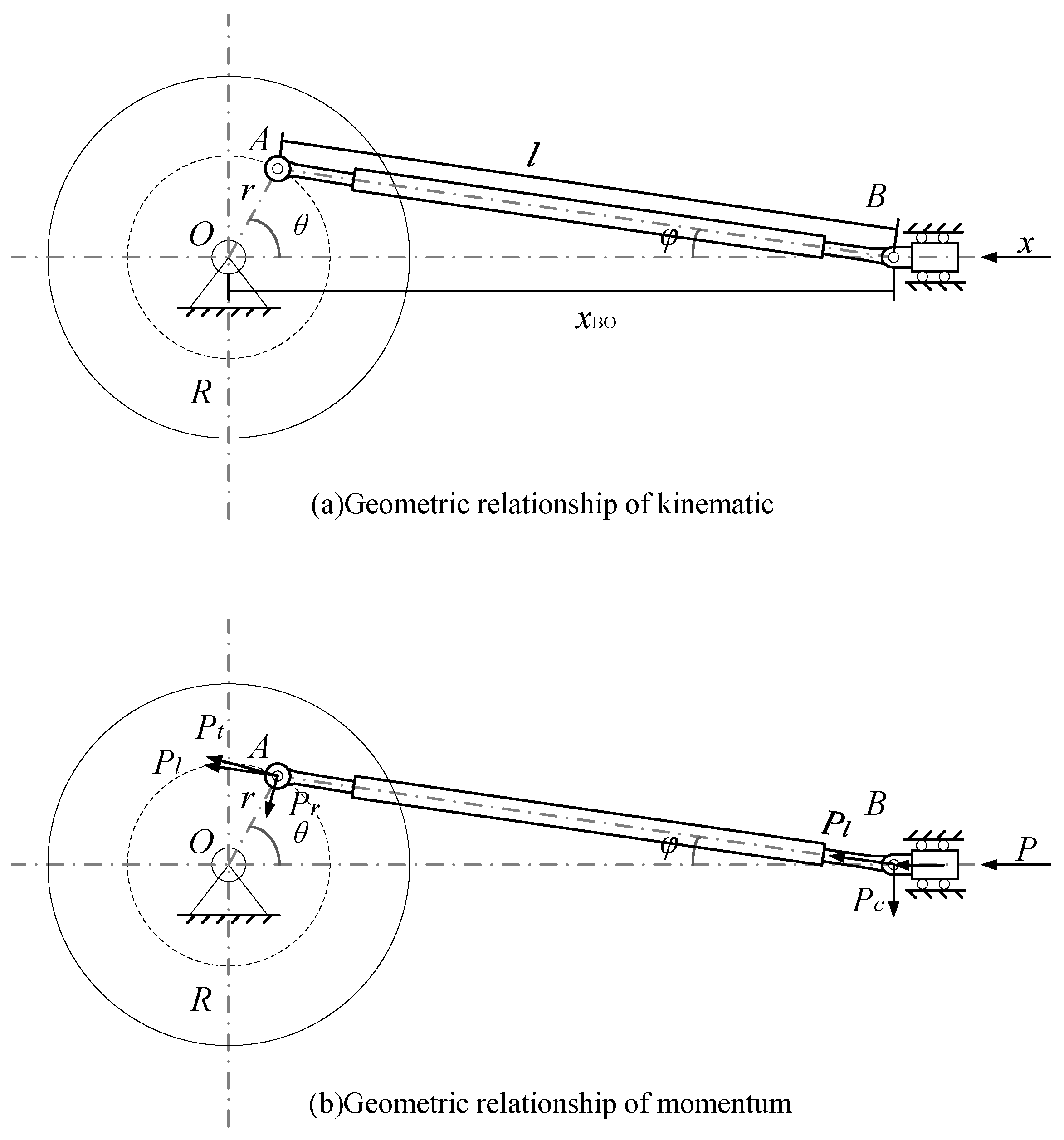
2.2. Modeling

2.2.1. Model Assumptions

To facilitate analysis and mastery of performance characteristics, the following simplified assumptions are made when establishing a mathematical model of a crank-connecting rod mem-inerter:

• The mass distribution of the flywheel is uniform and its moment of inertia always remains constant;
• The crank-connecting rod mechanism is tightly connected and sufficiently rigid, without any gaps or deformations and the inertance of the device is not affected by the mass of the mechanism itself;
• The indirect contact surfaces of each component of the device are smooth and the frictional resistance can be ignored.

2.2.2. Mathematics Modeling

According to the above, the inertance coefficient of a crank-connecting rod mem-inerter is related to the axial displacement of the guide rod. With reference to the triangular periodic table of mechanical elements, it is preliminarily assumed that the device is a displacement-dependent mem-inerter and that its constitutive relation is described by the curve in the integrated momentum $\delta \left(t\right)$—the corresponding displacement $x\left(t\right)$ plane. In order to facilitate the definition of the constitutive relation of the mem-inerter, in this section, analysis is based on the kinematics geometric relationship of the device, and the corresponding geometric relationship at the momentum level is established. Finally, the inertance and constitutive relation expression of the mem-inerter device are obtained.

As shown in Figure 3a, R is the radius of the flywheel, r is the length of the crank, and l is the length of the connecting rod. The initial distance between the flywheel stand point O and one end point B of the guide rod is $x_{BO}$, the horizontal displacement of the guide rod is x, the angle between the crank and the horizontal axis is $\theta$, and the angle between the connecting rod and the horizontal axis is $\phi$. From this, the instantaneous distance $x_B$ between point O of the flywheel stand and point B of one end of the guide rod can be expressed as

$$x_B=x_{BO}-x$$

(1)

We assume that the guide rod’s horizontal axis passes through point O and that the crank is perpendicular to the horizontal axis as the initial state, with the horizontal direction to the left being defined as the positive direction. Since the inerter is constantly subjected to a repetitive motion working state, in order to avoid the device reaching its limit state and causing the locking mechanism to fail, the guide rod’s horizontal displacement must satisfy $x\in (-r,r)$.

According to the kinematics geometric relationship shown in Figure 3a, the instantaneous distance $x_B$ between the flywheel stand point O and the guide rod endpoint B can also be expressed as

$$x_B=rcos\theta +lcos\phi$$

(2)

The relationship between crank length r, the connecting rod length l, the included angle $\theta$, and $\phi$ can be represented as

$$rsin\theta =lsin\phi$$

(3)

Through the trigonometric function theory, the positive and cosine formulas of the included angle $\theta$ and $\phi$ can be represented as follows:

$$cos\theta ={\displaystyle \frac{x_B^2+r^2-l^2}{2x_{B}r}}$$

(4)

$$sin\theta =\sqrt{(1-{cos}^2\theta )}={\displaystyle \frac{\sqrt{2l^2(r^2+x_B^2)-{(r^2-x_B^2)}^2-l^4}}{2x_{B}r}}$$

(5)

$$cos\phi ={\displaystyle \frac{x_B^2-r^2+l^2}{2x_{B}l}}$$

(6)

and

$$sin\phi ={\displaystyle \frac{\sqrt{2l^2(r^2+x_B^2)-{(r^2-x_B^2)}^2-l^4}}{2x_{B}l}}$$

(7)

In the geometric relationship of momentum shown in Figure 3b, according to the parallelogram rule the relationship between the momentum P on one end of the device and the momentum $P_l$ on the connecting rod is as follows:

$$P=P_{l}cos\phi$$

(8)

The relationship between the momentum $P_l$ received by the connecting rod and the tangential momentum $P_t$ transmitted by the crank to the flywheel is expressed as

$$P_t=P_{l}sin(\phi +\theta )$$

(9)

According to the law of conservation of angular momentum, the relationship between the angular velocity of the flywheel $\dot{\theta }$ and $P_t$ can be established as follows:

$$I\dot{\theta }=r{P}_t$$

(10)

Combining Equation (8) with Equation (10), the expression for momentum P can be obtained as

$$P={\displaystyle \frac{Icos\phi \dot{\theta }}{rsin(\phi +\theta )}}$$

(11)

Assuming a time-dependent displacement excitation $x\left(t\right)$ is applied to the guide rod, the distance $x_B\left(t\right)$ between points $OB$ can be expressed as

$$x_B\left(t\right)=x_{BO}-x_t$$

(12)

According to Equation (12), the first- and second-order differential relationship between $x\left(t\right)$ and $x_B\left(t\right)$ concerning time can be obtained:

$$\begin{array}{c}\hfill {\dot{x}}_B\left(t\right)=-{\dot{x}}_t\\ \hfill {\ddot{x}}_B\left(t\right)=-{\ddot{x}}_t\end{array}$$

(13)

where $\dot{x}$(t) is the axial velocity of the guide rod and $\ddot{x}$(t) is the axial acceleration of the guide rod.

Substituting Equations (12) and (13) into Equation (4) yields

$$\dot{\theta }={\displaystyle \frac{r^2-x_B^2-l^2}{2r{x_B}^{2}sin\theta }}{\dot{x}}_B$$

(14)

$$\ddot{\theta }={\displaystyle \frac{2(l^2-r^2){{\dot{x}}_B}^2+(r^2-x_B^2-l^2)x_B{\ddot{x}}_B}{2r{x}_B^{3}sin\theta }}-{\displaystyle \frac{{\dot{\theta }}^{2}cos\theta }{sin\theta }}$$

(15)

where $\dot{\theta }$ is the angular velocity of the crank rotation and $\ddot{\theta }$ is the angular acceleration for the crank rotation.

Combining the above, the expression for momentum P is expressed as

$$P=B\left(x\right)\dot{x}$$

(16)

where $B\left(x\right)$ is the inertance of the device, as follows:

$$B\left(x\right)={\displaystyle \frac{m{R}^2{(l^2-r^2+{(x_{BO}-x)}^2)}^2}{2(x_{BO}-x)\left(2l^2(r^2+{(x_{BO}-x)}^2)\right)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4}}$$

(17)

From Equation (17), it can be found that the inertance of the device is non-linear related to the relative displacement between the two terminals, which means that the crank-connecting rod mem-inerter is a displacement-dependent non-linear inerter.

By taking the derivative on both sides of Equation (16), we can obtain the expression for the output force at the two terminals of the device as

$$\begin{array}{cc}\hfill F& ={\displaystyle \frac{Icos\phi \ddot{\theta }}{rsin(\phi +\theta )}}\hfill \\ \hfill & =-{\displaystyle \frac{m{R}^2{(r^2-l^2-{(x_{BO}-x)}^2)}^2\ddot{x}}{2{(x_{BO}-x)}^2(2l^2(r^2+{(x_{BO}-x)}^2)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4)}}\hfill \\ & +[{\displaystyle \frac{m{R}^2{(r^2-l^2-{(x_{BO}-x)}^2)}^2(r^2+l^2-{(x_{BO}-x)}^2)}{{(2l^2(r^2+{(x_{BO}-x)}^2)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4)}^2}}\hfill \\ & -{\displaystyle \frac{m{R}^2(r^2-l^2-{(x_{BO}-x)}^2)(-r^2+l^2-{(x_{BO}-x)}^2}{2{(x_{BO}-x)}^2(2l^2(r^2+{(x_{BO}-x)}^2)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4)}}]{\dot{x}}^2\hfill \end{array}$$

(18)

From the above equation, it can be seen that the expression for the output force of the mem-inerter mainly consists of two functions related to relative acceleration and relative velocity. This indicates that the output force of the mem-inerter device can be equivalent to the superposition of nonlinear inertial force and nonlinear damping force. Therefore, the expression for the output force of the device can also be rewritten as

$$F=F_B+F_C=B\left(x\right)\ddot{x}+C(x,\dot{x})\dot{x}$$

(19)

where $F_B$ is the inertial force, $F_C$ is the damping force, $B\left(x\right)$ is the inertance, and $C(x,\dot{x})$ is the damping coefficient and can be expressed as

$$\begin{array}{cc}\hfill & B\left(x\right)=-{\displaystyle \frac{m{R}^2{(r^2-l^2-{(x_{BO}-x)}^2)}^2}{2{(x_{BO}-x)}^2\left(2l^2(r^2+{(x_{BO}-x)}^2)\right)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4)}}\hfill \\ \hfill & C(x,\dot{x})=[{\displaystyle \frac{m{R}^2{(r^2-l^2-{(x_{BO}-x)}^2)}^2(r^2+l^2-{(x_{BO}-x)}^2)}{{(2l^2(r^2+{(x_{BO}-x)}^2)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4)}^2}}\hfill \\ & -{\displaystyle \frac{m{R}^2(r^2-l^2-{(x_{BO}-x)}^2)(-r^2+l^2-{(x_{BO}-x)}^2}{2{(x_{BO}-x)}^2(2l^2(r^2+{(x_{BO}-x)}^2)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4)}}]{\dot{x}}^2\hfill \end{array}$$

(20)

The constitutive relation generally refers to a set of algebraic relations that map one-to-one between dependent variables and independent variables. The traditional linear elements can be defined and described on any plane. For example, for a linear inerter, suppose that the inertial force generated by its motion is f, the relative acceleration at two terminals of the device is a, and the inertance is a constant b. Then, the linear inerter can be defined on the f-a plane [1]:

$$f=b·a$$

(21)

By integrating Equation (21), the definition relationship of the linear inerter on the p-v plane can be expressed by [40]

$$p={\int }_{-\infty }^{t}f\mathrm{d}\tau =b·v$$

(22)

where p is the momentum of the linear inerter and v is the relative velocity at the two terminals.

Similarly, the linear inerter can also be defined on the integrated momentum plane and other planes, and the theoretical relationship obtained is a one-to-one correspondence relationship. The crank-connecting rod mem-inerter shown in Figure 2 cannot be defined on the plane of force or momentum.

As shown in Equations (16) and (18), the above two expressions both contain three variables [$P,x,\dot{x}$] that do not conform to the standard of the one-to-one correspondence relationship of two constitutive equation variables. To obtain the constitutive equation of the crank-connecting rod mem-inerter, we integrate Equation (16) in the time domain:

$$\begin{array}{cc}\hfill & \delta ={\int }_{-\infty }^{t}P\mathrm{d}\tau \hfill \\ \hfill & ={\displaystyle \frac{m{R}^{2}l(ln(x_{BO}-x+l-r)-ln(x_{BO}-x-l+r))}{4r(l-r)}}\hfill \\ & +{\displaystyle \frac{m{R}^{2}l(ln(x_{BO}-x-l-r)-ln(x_{BO}-x+l+r))}{4r(l+r)}}-{\displaystyle \frac{m{R}^2}{2(x_{BO}-x)}}\hfill \end{array}$$

(23)

where $\delta$ is the integrated momentum of the crank-connecting rod mem-inerter.

From this, it can be seen that Equation (23) only includes $\delta$,x two variables and that the two variables are one-to-one correspondence relationships, which conforms to the definition of constitutive relation. This indicates that the dynamic characteristics of the crank-connecting rod mem-inerter can be studied on the $\delta$-x plane. Equation (16) can be derived from Equation (23) and can also accurately describe the dynamic characteristics of this device.

2.3. Characteristic Analysis

In order to explore the relevant characteristics of the mem-inerter, a cosine displacement excitation of x = Acos(2$\pi$$ft$) was applied to one terminal of the device and the other terminal was a fixed installation. The maximum vibration amplitude A of the excitation was 0.05 m and the frequency f was 2 Hz. The set device parameters are shown in

Table 1. Simulation parameters of device characteristic test analysis.

Parameter	Value	Unit
Flywheel radius R	0.3	$\mathrm{m}$
Crank length r	0.07	$\mathrm{m}$
Connecting rod length l	0.3	$\mathrm{m}$
Flywheel mass m	10	$\mathrm{kg}$
Initial position $x_{BO}$	0.2	$\mathrm{m}$

.

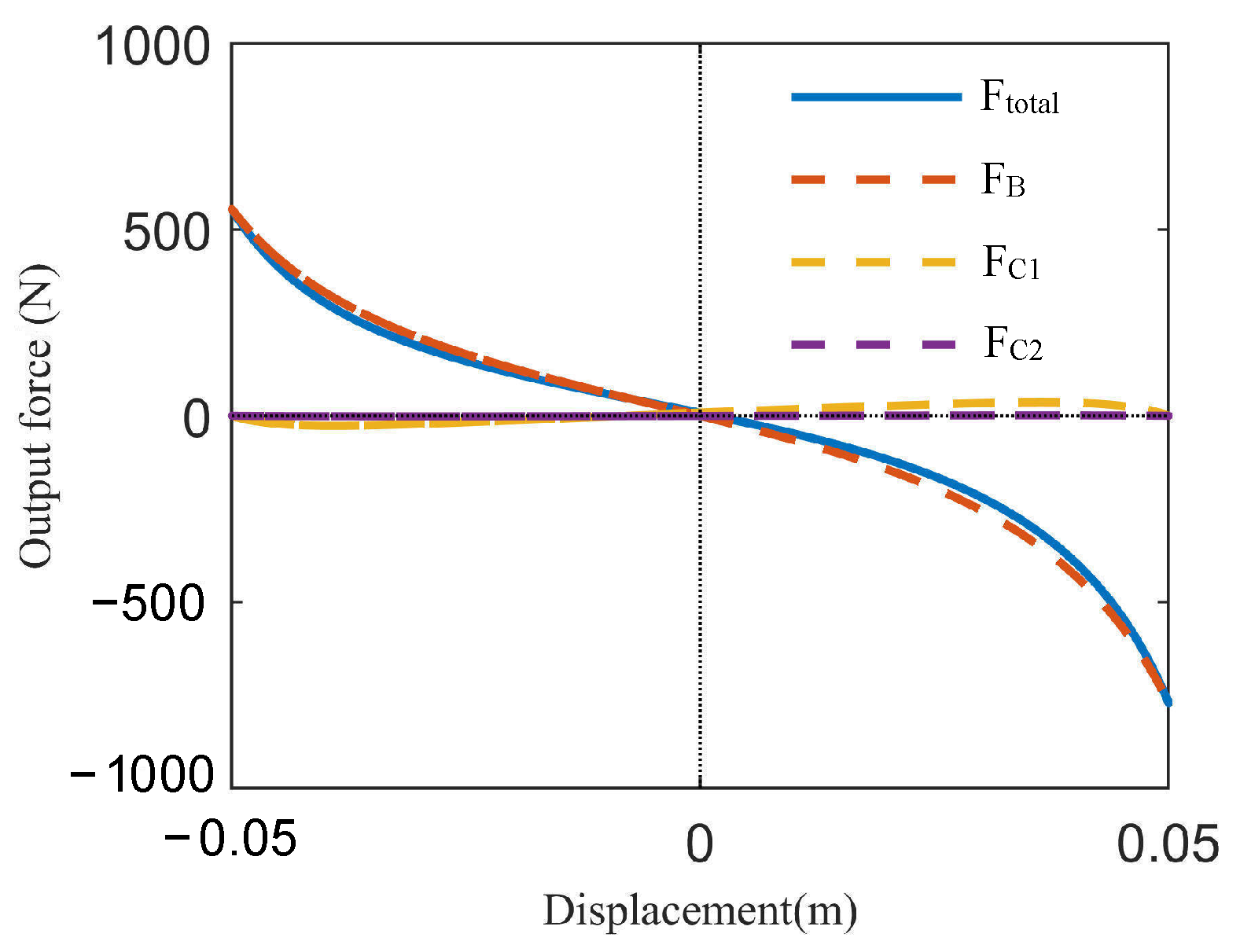
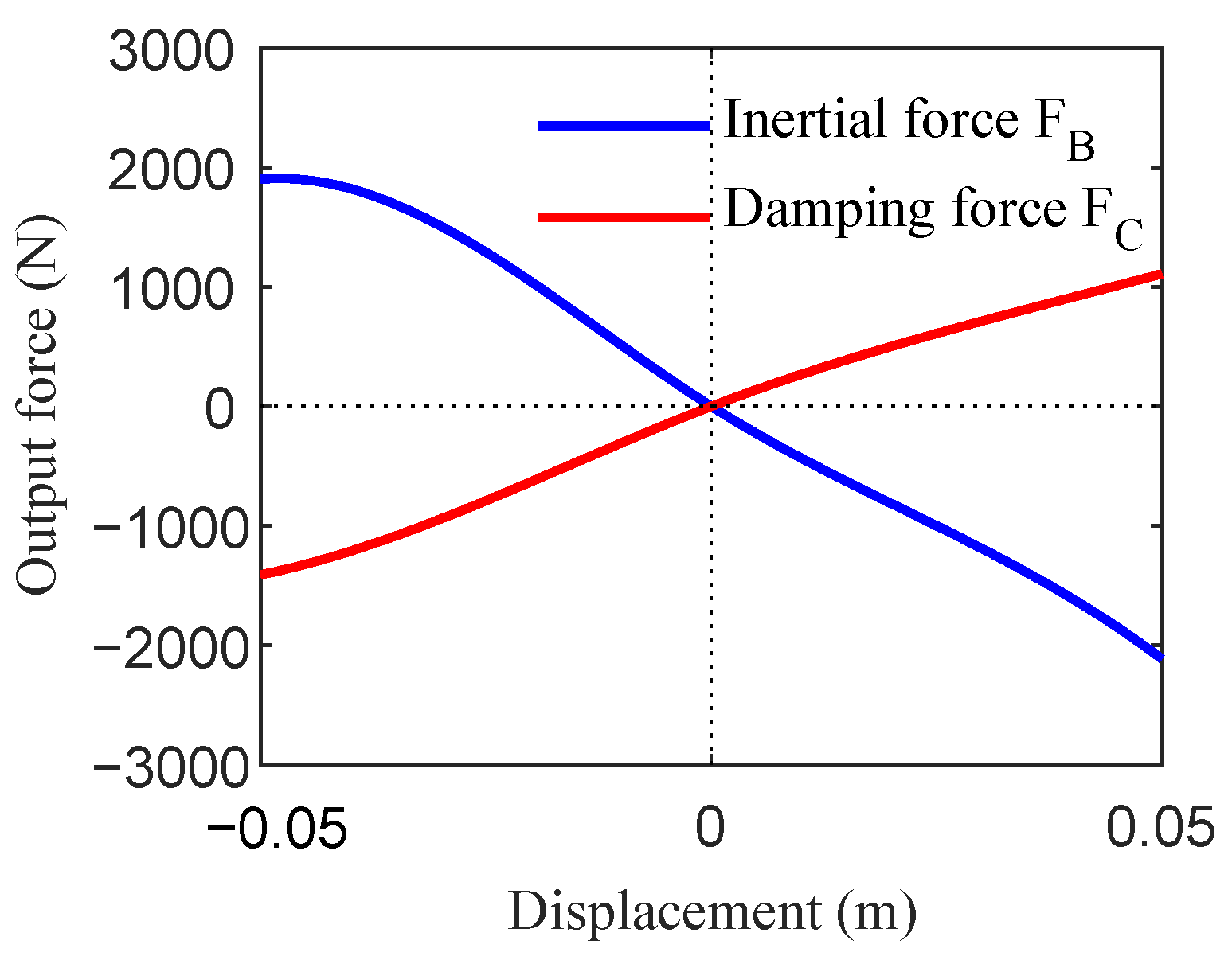
2.3.1. Output Force Characteristics

According to the output force formula of the crank-connecting rod mem-inerter derived from the above section, the force at the two terminals of the device included the inertial force related to the relative acceleration and the damping force related to the relative velocity. To explore the composition of these two forces with different properties in the working state of the device, a simulation analysis was carried out to obtain the characteristic curves related to the total output force, inertial force, and damping force and displacement, as shown in Figure 4, where the total output force of the device is expressed as $F_{total}$, the inertial force is $F_B$ and the damping force is divided into two terms, $F_{C1}$ and $F_{C2}$, as shown below:

$$\begin{array}{cc}\hfill & F_B=-{\displaystyle \frac{m{R}^2{(r^2-l^2-{(x_{BO}-x)}^2)}^2\ddot{x}}{2{(x_{BO}-x)}^2(2l^2(r^2+{(x_{BO}-x)}^2)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4)}}\hfill \\ \hfill & F_{C1}={\displaystyle \frac{m{R}^2{(r^2-l^2-{(x_{BO}-x)}^2)}^2(r^2+l^2-{(x_{BO}-x)}^2)\dot{x}}{{(2l^2(r^2+{(x_{BO}-x)}^2)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4)}^2}}\hfill \\ \hfill & F_{C2}=-{\displaystyle \frac{m{R}^2(r^2-l^2-{(x_{BO}-x)}^2)(-r^2+l^2-{(x_{BO}-x)}^2\dot{x}\ddot{x}}{2{(x_{BO}-x)}^2(2l^2(r^2+{(x_{BO}-x)}^2)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4)}}{\dot{x}}^2\hfill \end{array}$$

(24)

From Figure 4, it can be found that the inertial force of the device dominated the total output force, and the direction of the damping force and inertial force was opposite. In the two damping forces, it can be found that compared to force $F_{C1}$, force $F_{C2}$ can be ignored. Therefore, the output force calculation formula of the crank-connecting rod mem-inerter can be approximately expressed as

$$\begin{array}{cc}\hfill & F=B\left(x\right)\dot{x}\ddot{x}+C(x,\dot{x})x\hfill \\ \hfill & =-{\displaystyle \frac{m{R}^2{(r^2-l^2-{(x_{BO}-x)}^2)}^2\ddot{x}}{2{(x_{BO}-x)}^2\left(2l^2{(r^2+x_{BO}-x)}^2\right)-{(r^2-x_{BO}-x^2)}^2-l^4}}\hfill \\ & +{\displaystyle \frac{m{R}^2{(r^2-l^2-{(x_{BO}-x)}^2)}^2(r^2+l^2-{(x_{BO}-x)}^2){\dot{x}}^2}{2l^2(r^2+{(x_{BO}-x)}^2)-{(r^2-{(x_{BO}-x)}^2)}^2-l^4}}\hfill \end{array}$$

(25)

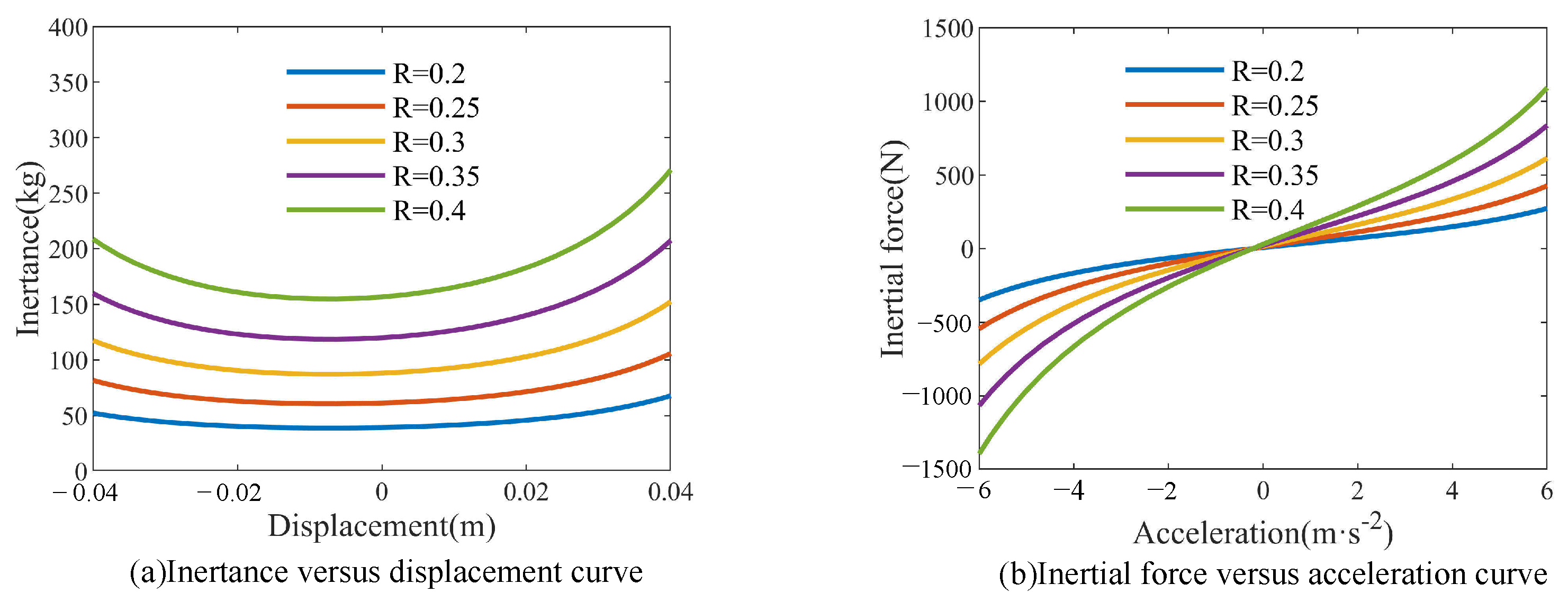
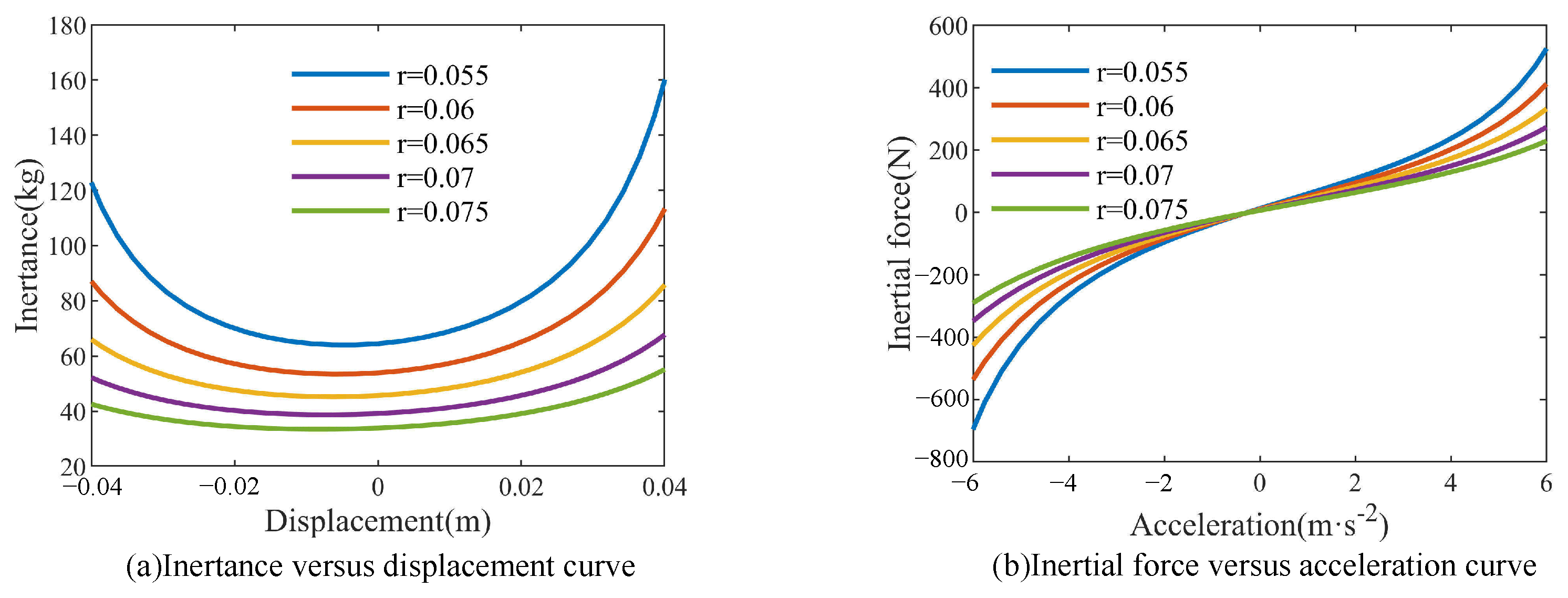
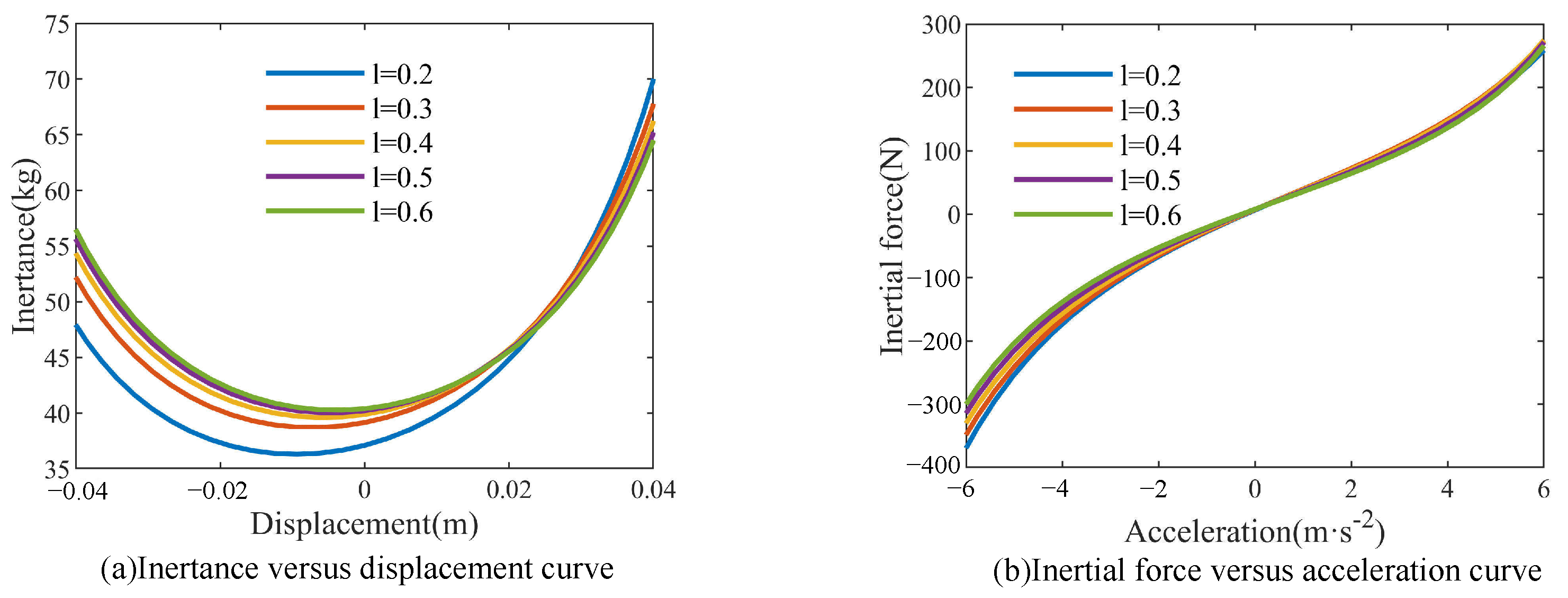
2.3.2. Structural Parameter Characteristics

The inertance, which is the characteristic parameter of the device, is not a constant but rather varies with displacement. Alternatively, the inertance is a function of displacement, which is influenced by the flywheel radius R, crank length r, connecting rod length l, and flywheel mass m. The essence of the influence of the flywheel radius R and flywheel mass m on the inertance is the moment of the inertia I of the flywheel. To explore the influence of the above parameters on the inertance, Table 1 was taken as the reference parameter, and the control variable method was used to change a parameter, to observe the influence of the structural parameters of the device on it.

(1)

Flywheel radius R

With the flywheel radius R taken as different values, the inertance and inertial force curves of the crank-connecting rod mem-inerter are shown in Figure 5. From Figure 5a, it can be concluded that the inertance of the mem-inerter is a horseshoe-shaped curve with an opening upwards. In the initial displacement state, the inertance of the device is small, and it increases with the increase of the motion amplitude. In addition, when the displacement x is the same, the inertance of the inerter increases with the increase of the flywheel radius, and the larger the flywheel radius the more obvious the nonlinear characteristics will be. From Figure 5b, it can be found that the inertial force of the device is directly proportional to the acceleration, and that the inertial force will increase with the increase of the flywheel radius.

(2)

Crank length r

The inertance and inertial force curves of the mem-inerter under different crank lengths r are shown in Figure 6. From Figure 6a, it can be concluded that the inertance of the inerter decreases with the increase of the crank length. Figure 6b shows that the inertial force of the inerter also decreases with the increase of the crank length.

(3)

Connecting rod length l

With the connecting rod length l being taken as different values, the inertance and inertial force curves of the crank-connecting rod mem-inerter are shown in Figure 7. From Figure 7a, it can be found that the shape of the inertance curve of the device is the same as the previous horseshoe curve with an opening upwards. However, the difference is that when the connecting rod length l changes, the inertance exhibits different symmetries throughout the entire working stroke. When the connecting rod length l is short, this asymmetry is more pronounced. As the connecting rod length l increases, the inertance is greatly reduced. Figure 7b shows that the inertial force of the inerter decreases with the increase of the connecting rod length, and it is also asymmetrical with the change of the connecting rod length. In summary, no matter how the structural parameters of the crank-connecting rod inerter change, its inertance curve always shows a horseshoe-shaped curve with an opening upward, maintaining a small inertance in the initial state of device motion and increasing with the intensification of motion. And its inertial force curve can reflect strong nonlinearity.

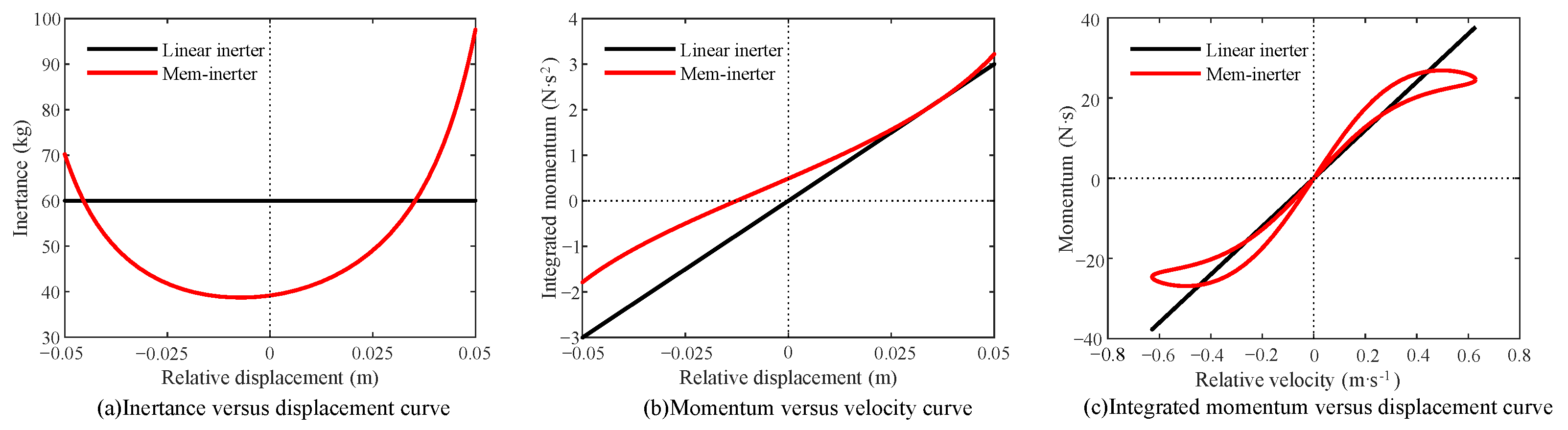
2.3.3. Memory Characteristics

Taking the initial position of the device $x_{BO}$ = 0.3 m, we compared and analyzed the linear inerter with an inertance of b = 120 kg. By using Equations (16), (17) and (23), the characteristic curves of the linear inerter and the crank-connecting rod mem-inerter could be drawn, as shown in Figure 8.

It can be found from Figure 8a that the crank-connecting rod mem-inerter has obvious nonlinearity. Compared with the linear inerter with constant inertance, its value changes nonlinearly with the change of displacement, which indicates that the device is a displacement-dependent nonlinear element. Figure 8b further proves that the crank-connecting rod inerter is a memory element, and on the momentum–velocity plane the characteristic curve of the device is a pinched hysteresis loop passing through the first and the third quadrants. To define a memory element, we find its constitutive relation, as shown in Figure 8c. The characteristic curve of the device on the integrated momentum–displacement plane is a one-to-one correspondence relationship. For a linear inerter, we also find that the characteristic curve is a straight line passing through the origin on both the velocity and the displacement planes, further proving that linear elements can be defined on any plane.

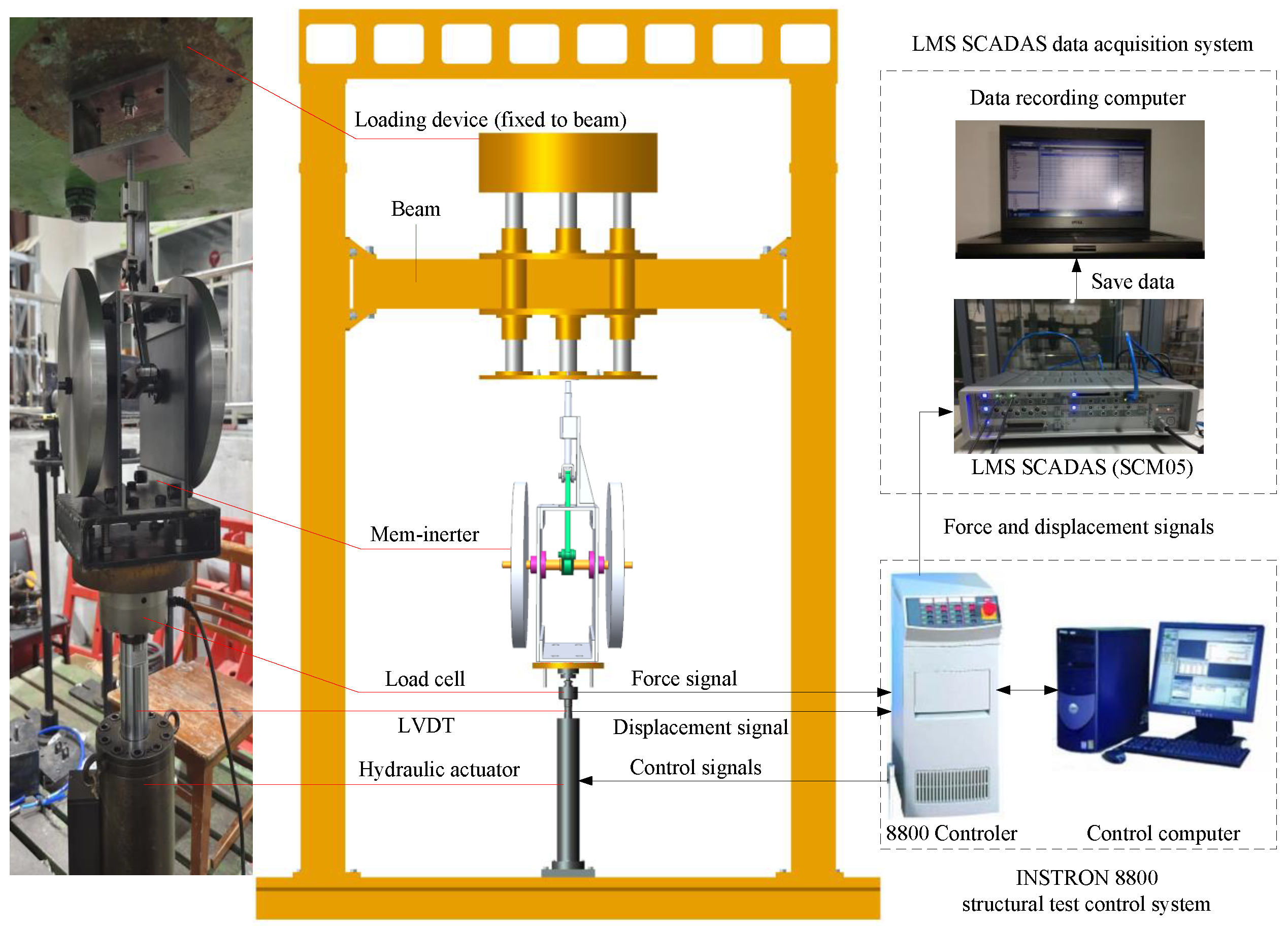
3. Bench Test

3.1. Engineering Model

From Equation (25), it can be found that the total output force of the crank-connecting rod mem-inerter device includes the acceleration-dependent inertial force and the velocity-dependent nonlinear damping force. In the process of engineering application, due to the complexity of the device structure, the joints of various components will be subject to contact friction during operation. Hence, it is imperative to take into account the influence of frictional resistance. Subsequently, the engineering model for the crank-connecting rod mem-inerter can be regarded as a vibration-reduction apparatus operating in parallel with the mem-inerter, nonlinear damper, and dry friction, as illustrated in Figure 9:

3.1.1. Dry Friction Model

Because there are many kinematic pairs in the crank-connecting rod mem-inerter, it is inevitably affected by dry friction, which is mainly manifested in nonlinear factors such as the crank-connecting mechanism and bearing movement. The direction of the dry-friction force $F_f$ is opposite to the direction of motion of the inerter, and its magnitude remains unchanged, which can be expressed as

$$F_f=-f_0·sign\left(v\right)$$

(26)

where $f_0$ is the actual value of the friction, and where the direction is always positive.

3.1.2. Parasitic Damping Model

From Equation (25), it can be found that the device had a nonlinear damper, and the expression of its parasitic damping force was a function related to velocity v and displacement x. To further analyze the parasitic damping of the device, for this section we applied a cosine displacement excitation expressed as x = Acos(2$\pi$$ft$) to one terminal of the device, using the parameters of the crank-connecting rod mem-inerter in

Table 2. Parameters of the parasitic damping model analysis.

Parameter	Value	Unit
Flywheel mass m	10	$\mathrm{kg}$
Flywheel radius R	0.2	$\mathrm{m}$
Crank length r	0.08	$\mathrm{m}$
Connecting rod length l	0.2	$\mathrm{m}$
Initial position $x_{BO}$	0.2	$\mathrm{m}$

, and the other terminal was fixed and installed. We set the frequency f to 2 Hz and the amplitude A to 0.05 m.

Through simulation analysis, the characteristic curves were discernible that depicted the damping force $F_C$ and the inertial output force $F_B$ of the crank-connecting rod mem-inerter, relative to the displacement x, as presented in Figure 10. Furthermore, a comparative assessment of the damping and inertial force relationship within the hydraulic mem-inerter in previous studies [41], under consistent excitation conditions, is illustrated in Figure 11. To provide a clearer illustration of the relationship between the two forces, the absolute value of the ratio of the damping force to the inertial force is defined as $\alpha$. Herein, ${\alpha }_1$ signifies the relationship between the two forces in the crank-connecting rod mem-inerter, while ${\alpha }_2$ represents the same in the hydraulic mem-inerter. The values of ${\alpha }_1$, ${\alpha }_2$ at various displacements are tabulated in

Table 3. Relationship between displacement x and $\alpha$ in the two devices .

Displacement x (m)	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$
−0.01	0.0218	0.7421
−0.02	0.0237	0.6702
−0.03	0.0380	0.6269
−0.04	0.0315	0.6051
−0.05	4.4398 × ${10}^{-33}$	0.5984
0.01	0.2040	0.6185
0.02	0.1090	0.6159
0.03	0.0773	0.5973
0.04	0.0324	0.5639
0.05	4.4529 × ${10}^{-33}$	0.5248

. By comparing the data analysis, it can be concluded that the damping force of the hydraulic mem-inerter device constitutes a non-negligible component of the output force. However, the damping force of the crank-connecting rod mem-inerter is minimal, exerting almost negligible impact on the total output force, rendering it ignorable. Ultimately, the engineering model of the crank-connecting rod mem-inerter device can be simplified as a vibration-reduction apparatus operating in parallel with the inerter and dry friction.

3.2. Prototype Trial Production

According to the 3D model drawings, on the premise of meeting the design requirements and processing technology, the physical device of the crank-connecting rod mem-inerter was processed and manufactured. The final assembly diagram and the corresponding structure of the device are shown in Figure 12. The device is about 440 mm in overall design height, with a guide rod stroke of ±50 mm.The horizontal working stroke of the equipment satisfies the range specified previously. Additionally, the ±5 mm vertical stroke can limit the movement range of the crank, preventing it from reaching the top or bottom dead-center positions. Overall, it can be observed that the device does not produce any motion interference during its operation. This ensures the smooth operation of the device. The specifications of the crank-connecting rod mem-inerter device are shown in

Table 4. Specifications of the crank-connecting rod mem-inerter device.

Description	Value	Unit
Crank length r	80	$\mathrm{mm}$
Connecting rod length l	200	$\mathrm{mm}$
Flywheel radius R	140	$\mathrm{mm}$
Flywheel mass m	10	$\mathrm{kg}$
Initial position $x_{BO}$	200	$\mathrm{mm}$
Stroke	±50	$\mathrm{mm}$
Overall height	440.8	$\mathrm{mm}$

.

3.3. Characteristic Test of Mem-Inerter Device

The main content of this experiment included the following two parts: quasi-static triangular wave input test and dynamic sine wave input test.

3.3.1. Triangular Wave Input Quasi-Static Test

Purpose: There are many kinematic pairs in the crank-connecting rod mem-inerter, such as the mutual rotation of the crank-connecting rod, and the rotation of each part of the bearing will produce friction. In order to accurately analyze the dynamic performance of the mem-inerter and obtain precise test results, it is crucial to measure the friction force present in the device during testing.

Test plan: Install the device vertically on the vibration table, set the height of the vibration table to reach the set initial position, and use a triangular wave displacement input with a frequency of 0.01 Hz and an amplitude of 0.03 m. At this time, the operating speed of the vibration table is extremely low, which can be regarded as a static state. Repeat the test three times to obtain the final test data.

3.3.2. Sine Wave Input Dynamic Characteristics Test

Purpose: To measure the total output force of the mem-inerter device, where the output force of the device includes frictional force and inertial force. By using MATLAB(2022b) data processing, the frictional resistance measured in quasi-static tests can be separated to obtain the inertial force of the device and draw the characteristic curve.

Test plan: Install the device vertically on the vibration table, set the height of the vibration table to reach the set initial position, use a sine wave displacement input with an amplitude of 0.03 m, set the frequency to 1–4 Hz, with a frequency step of 1 Hz, and repeat the test three times at each frequency to obtain the final data.

3.3.3. Signal Acquisition

This test was mainly divided into two parts: a quasi-static test and a dynamic characteristic test. During the experiment, one end of the excitation table was fixed. Therefore, the main signals required for the experiment were: (1) the displacement signal of the excitation table; (2) the excitation table force signal. The above two types of signals could be directly obtained from the force and displacement sensors included in the excitation table.

3.4. Working Principle and Layout Installation of the Test Bench

This experiment used the INSTRON8800 CNC hydraulic (Instron Corporation, Canton, MA, USA) servo excitation table as the excitation source. Due to the built-in displacement and force sensors of the excitation table, and the ability to synchronously collect two types of signals through the operating system’s built-in data-acquisition system (LMS), there was no need to set up an additional specialized data-acquisition system in the experiment. The working principle of the excitation table is as follows: first, set the required inputs (waveform, frequency, balance position, number of cycles, etc.) on the PC operating system. The microcomputer system sends out the input signal, which is converted in a digital-to-analog converter. Then, the controller controls the servo valve, to drive the hydraulic vibration exciter to obtain the required input (the input signal can be displacement input or force input). At the same time, the force and displacement sensors on the excitation table can collect corresponding output signals in real time. After signal amplification, they are transmitted to the microcomputer system, forming a control loop, allowing the system to control the movement of the vibration exciter in real time while collecting data. The layout of the characteristic test of the mem-inerter on the platform is shown in Figure 13. The mem-inerter was vertically fixed on the excitation table through upper and lower fixtures, and the loading device of the excitation table was relatively fixed, with the beam using the fixed fixture matched with the excitation table. At this time, the upper end of the excitation table could be regarded as absolutely fixed. During the test process, the displacement input was mainly provided by the lower end of the excitation table, and displacement and force signals were collected.

4. Experimental Results and Analysis

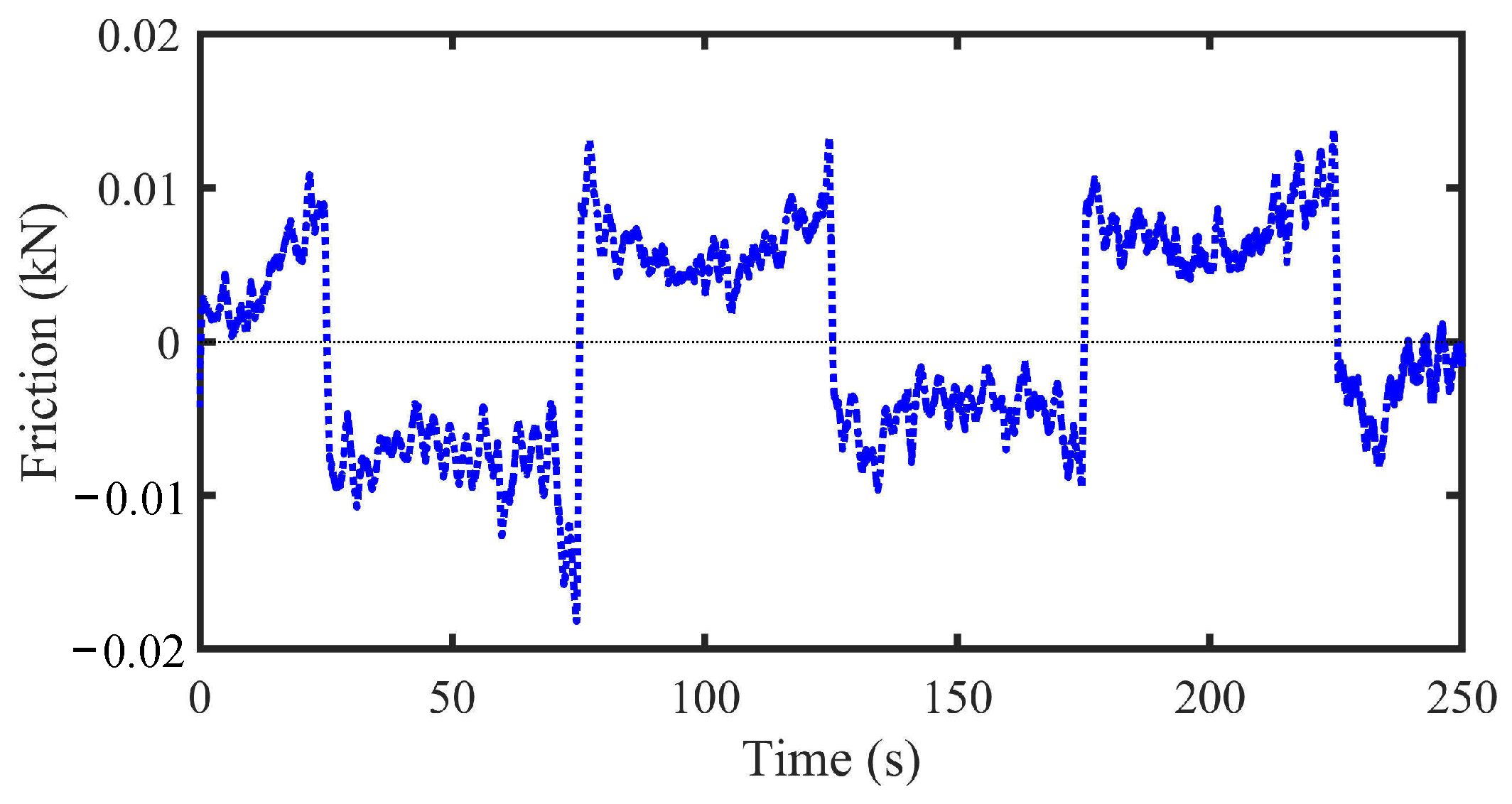
4.1. Dry Friction Separation

The triangular wave input can be considered as a constant velocity motion in the smooth running section. In the quasi-static test, we used a triangular wave input with a frequency of 0.01 Hz and an amplitude of 0.03 m, and it can be calculated that the input speed of the vibration exciter at this time was about 1.2 × ${10}^{-3}$ m ${\mathrm{s}}^{-1}$, which can be considered as a quasi-static state (it can be considered as a quasi-static state when the speed is less than 0.01 m ${\mathrm{s}}^{-1}$). At this point, the inertial force generated by the device could be ignored, and the value measured by the force-sensing signal could be regarded as the magnitude of the frictional resistance. The friction force and the fitting curve of the experimental device are shown in Figure 14.

From Figure 13, it can be found that the frictional resistance of the device was relatively small, mostly less than 10 N, and that the direction was opposite to the motion direction of the inerter.

4.2. Characteristic Analysis of Mem-Inerter

Referring to the experimental plan, we applied a sinusoidal displacement input x = Asin(2$\pi$$ft$) to one terminal of the device, where the amplitude A was 0.03 m and the frequency f was 1–4 Hz. By processing the experimental data, the characteristic curves of the device at 1 Hz, 2 Hz, 3 Hz, and 4 Hz could be obtained, as shown in Figure 15.

By analyzing the four momentum–velocity–time diagrams in the left column, the following observations can be made: Under four different frequencies, the momentum curves and relative velocity curves of the crank-connecting rod inerter were both sinusoidal. Both curves shared the same period and crossed the zero point at the same time. This phenomenon is known as the “coincident zero-crossing characteristic” of memory elements. And it serves as a fundamental condition for determining whether a particular element is a memory element.

Examining the four momentum–velocity plane diagrams in the right column reveals the following conclusions: (1) At various frequencies, the characteristic curves of the device on the momentum–velocity plane formed a pinched hysteresis loop traversing the first and third quadrants. In electrical engineering, this characteristic is recognized as a signature of circuit elements with memory, further confirming that the crank-connecting rod inerter functions as a physical realization of a mem-inerter. (2) The hysteresis loop curves exhibited some irregularities, with deviations from smoothness and asymmetry about the origin in the first and third quadrants. These discrepancies can be attributed to sampling errors from the excitation table and the processing inaccuracies of the device. Despite these imperfections, the evidence still supports the classification of the device as a mechanical memory element. (3) The intersection point of the hysteresis loop curves deviated from the coordinate origin when the frequency was at 1 Hz and 2 Hz. As the frequency increased, i.e., at 3 Hz and 4 Hz, the intersection point of the hysteresis loop curves gradually approached the coordinate origin. This was due to the presence of a relatively small parasitic damping force within the device, where the impact of increasing frequency on the inertial force outweighed that of the damping force, rendering the latter negligible at higher frequencies. This behavior further underscores the advantages of the crank-connecting rod inerter over hydraulic inerters at elevated frequencies. As the frequency decreases, the proportion of the parasitic damping force in the total output force increases, causing the intersection point of the hysteresis loop curves to gradually deviate from the origin. However, this deviation remains relatively small and is generally considered negligible within acceptable error margins.

5. Conclusions

This article demonstrates, through modeling and characteristic testing, that the crank-connecting rod inerter serves as an ideal inerter implementation device with negligible damping. The main work and conclusions are summarized as follows:

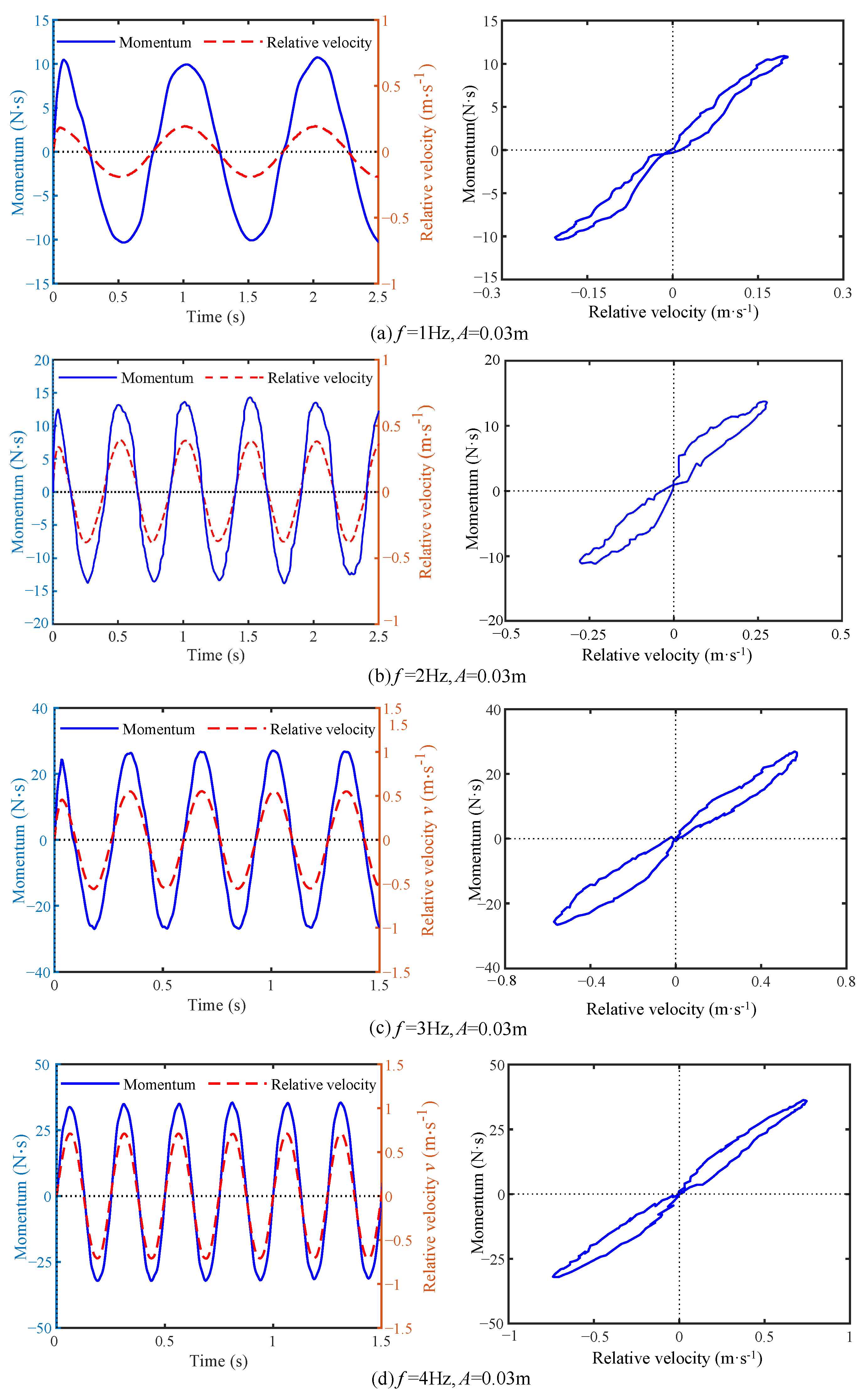
• Firstly, the research established a mathematical model for the proposed device and derived its inertance expression and constitutive relation. The findings indicated the characteristic curve on the momentum–velocity plane, displaying a pinched hysteresis loop. On the integrated momentum–displacement plane, a one-to-one correspondence relationship was observed, which served as evidence for the memory characteristics of the crank-connecting rod inerter. Therefore, it was classified as a displacement-dependent mem-inerter.
• Secondly, this study established a practical engineering model for the crank-connecting rod mem-inerter, and a prototype of the trial production device was successfully developed. The results of the simulation and the bench test indicated that the damping force constituted a relatively small proportion of the mem-inerter’s output force. Quasi-static tests further confirmed the device’s low frictional resistance. Consequently, the parasitic damping and frictional resistance could be disregarded.
• Thirdly, the dynamic characteristic test results demonstrated consistent pinched hysteresis loop characteristic curves on the momentum–velocity plane at various frequencies. Notably, the time domain curves of momentum and velocity intersected the time axis, providing conclusive evidence that the proposed device serves as an ideal physical realization of a mem-inerter.

In future research, we will apply the crank-connecting rod mem-inerter device to specific vibration isolation systems. We will conduct a comparative analysis to identify the differences between this device and the original hydraulic mem-inerter, emphasizing their effects on vibration isolation performance. Based on the results presented in this paper, we will then delve into detailed research and analysis.