Improved Synchronous Sampling and Its Application in High-Speed Railway Bearing Damage Detection
Abstract
:1. Introduction
2. Synchronous Resampling Method Based on Inverse Function Interpolation
2.1. Basic Principles of Synchronous Resampling
2.2. Synchronous Time-Point Calculation Based on Inverse Function Interpolation
2.3. Implementation of Synchronous Resampling Based on Inverse Function Interpolation
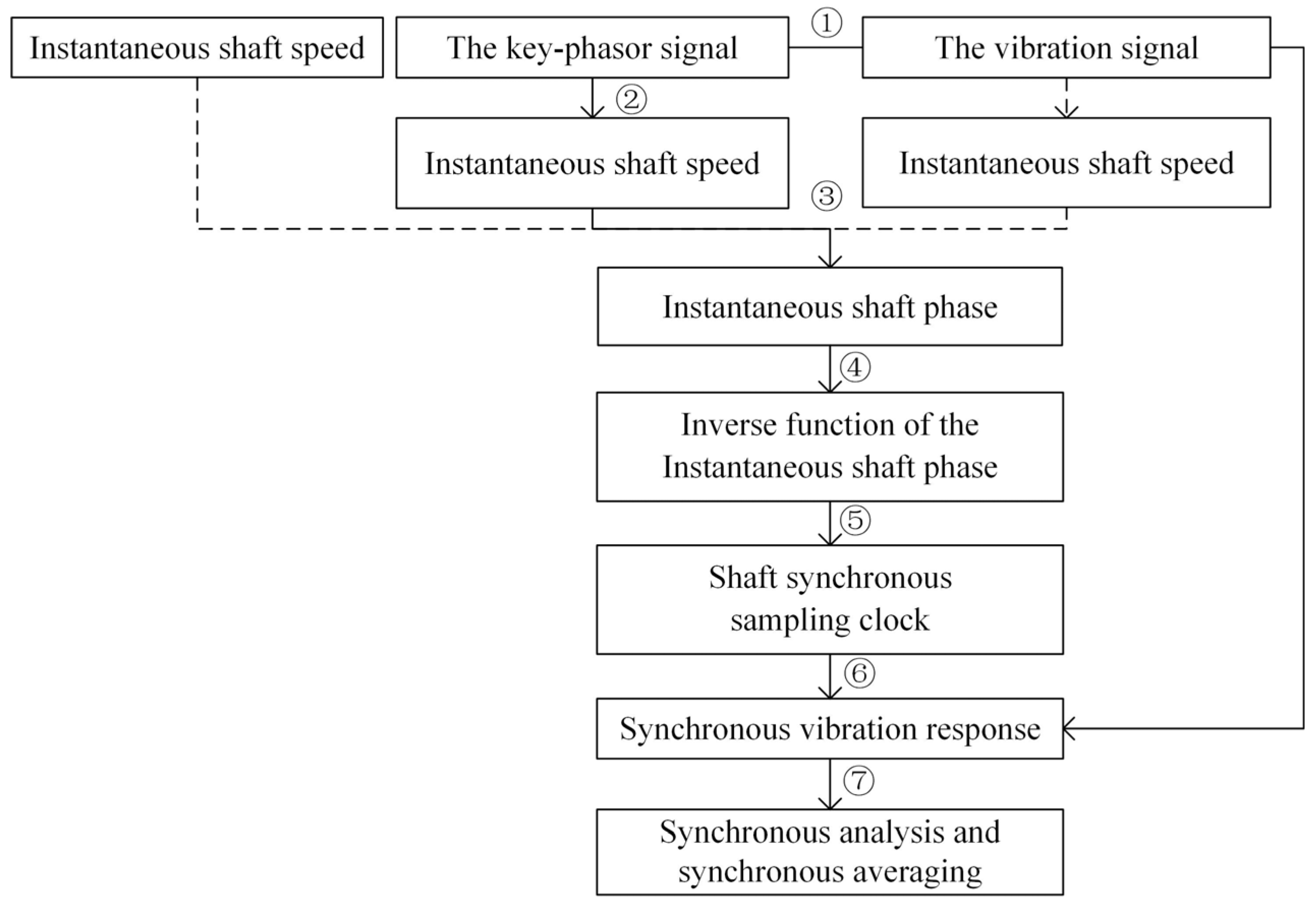
- Signal acquisition. It is assumed that both the vibration signal and the key-phasor signal are obtained simultaneously and are digitized at a high sampling frequency with high resolution, as shown in Figure 1.
- Instantaneous shaft speed recognition. If the shaft speed information is provided in the form of a pulse train, the corresponding instantaneous shaft speed can be obtained by conventional signal processing [25]. The instantaneous shaft speed can also be extracted by processing the vibration signal if the shaft speed information is not available [26,27].
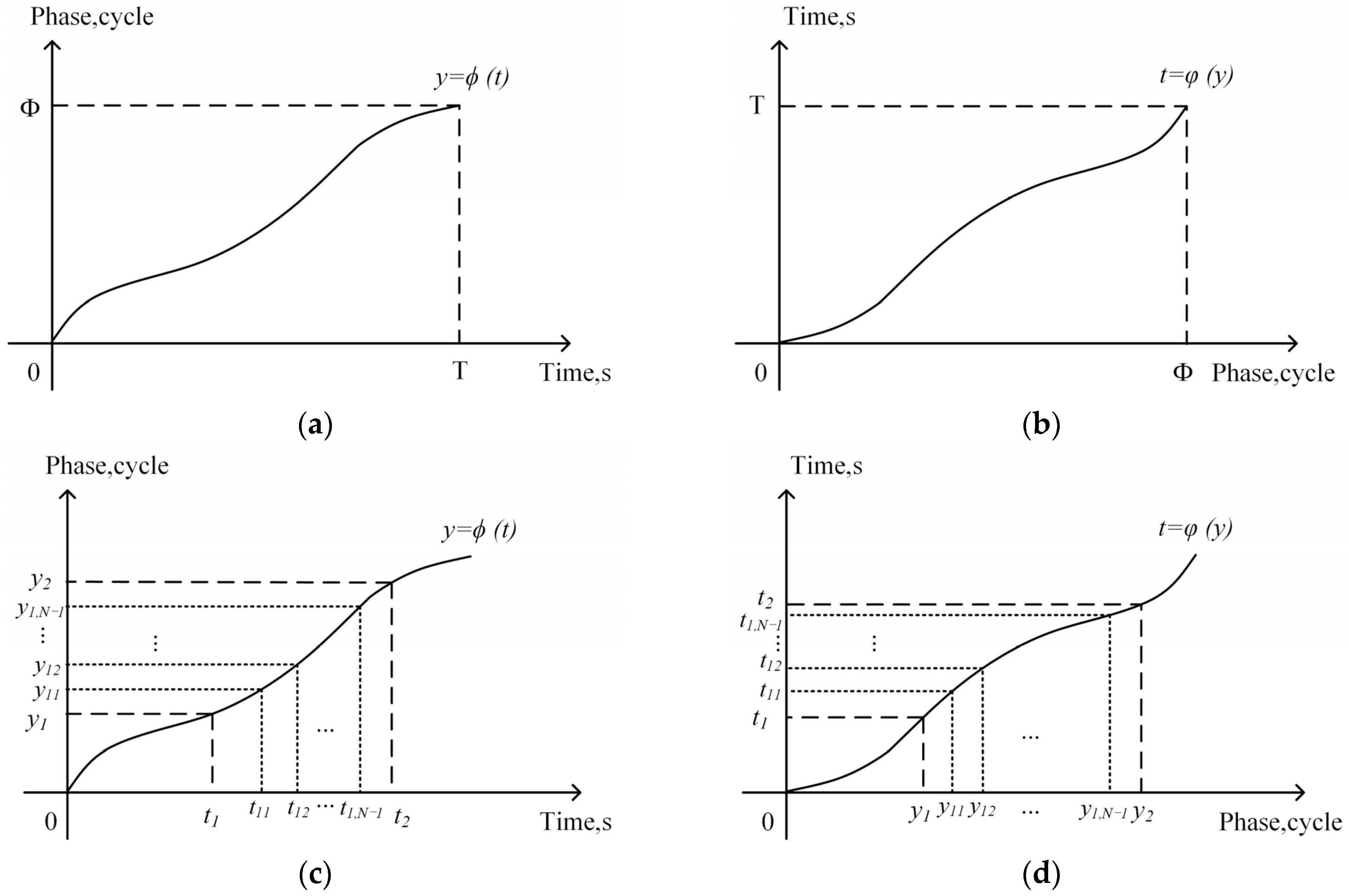
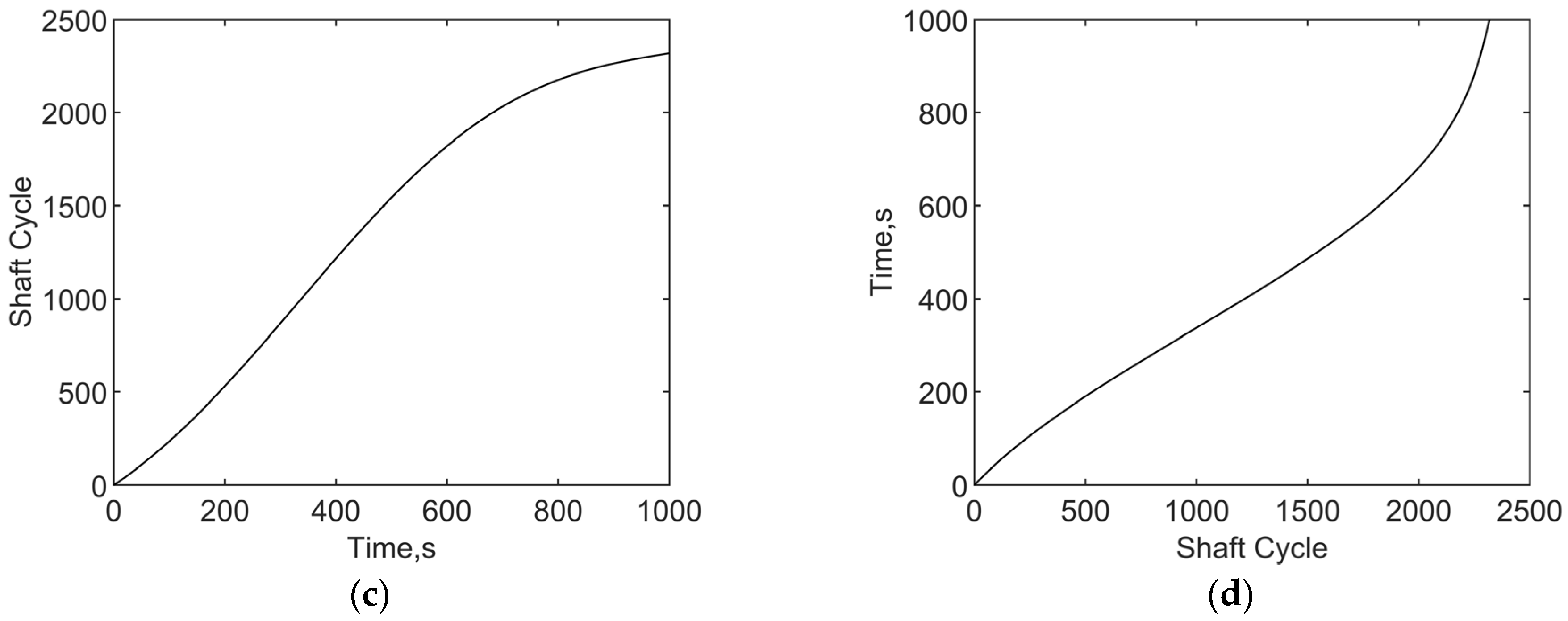
- Instantaneous phase recognition. Relative instantaneous phase function is obtained by numerical integration of the instantaneous shaft speed. Without losing the generality, the phase is set to 0 at initial time. The obtained relation between the phase of shaft rotation and time, , is as shown in Figure 3a.
- Inverse function conversion of the instantaneous phase. Find the inverse function of the instantaneous phase identified in step 3, as shown in Figure 3b.
- Shaft synchronous resampling clock evaluation. Using the interpolation algorithm on the inverse function , the synchronous resampling timestamps , are determined quickly by evaluation from the inverse function for given .
- Vibration response resampling. According to the synchronous sampling clock, the vibration response signal is resampled synchronously to obtain the synchronous response signal in the equal shaft angle domain.
- Synchronous analysis and synchronous averaging. The synchronously resampled vibration response signal is analyzed and the results are used to diagnose the health condition of the rotation machinery.
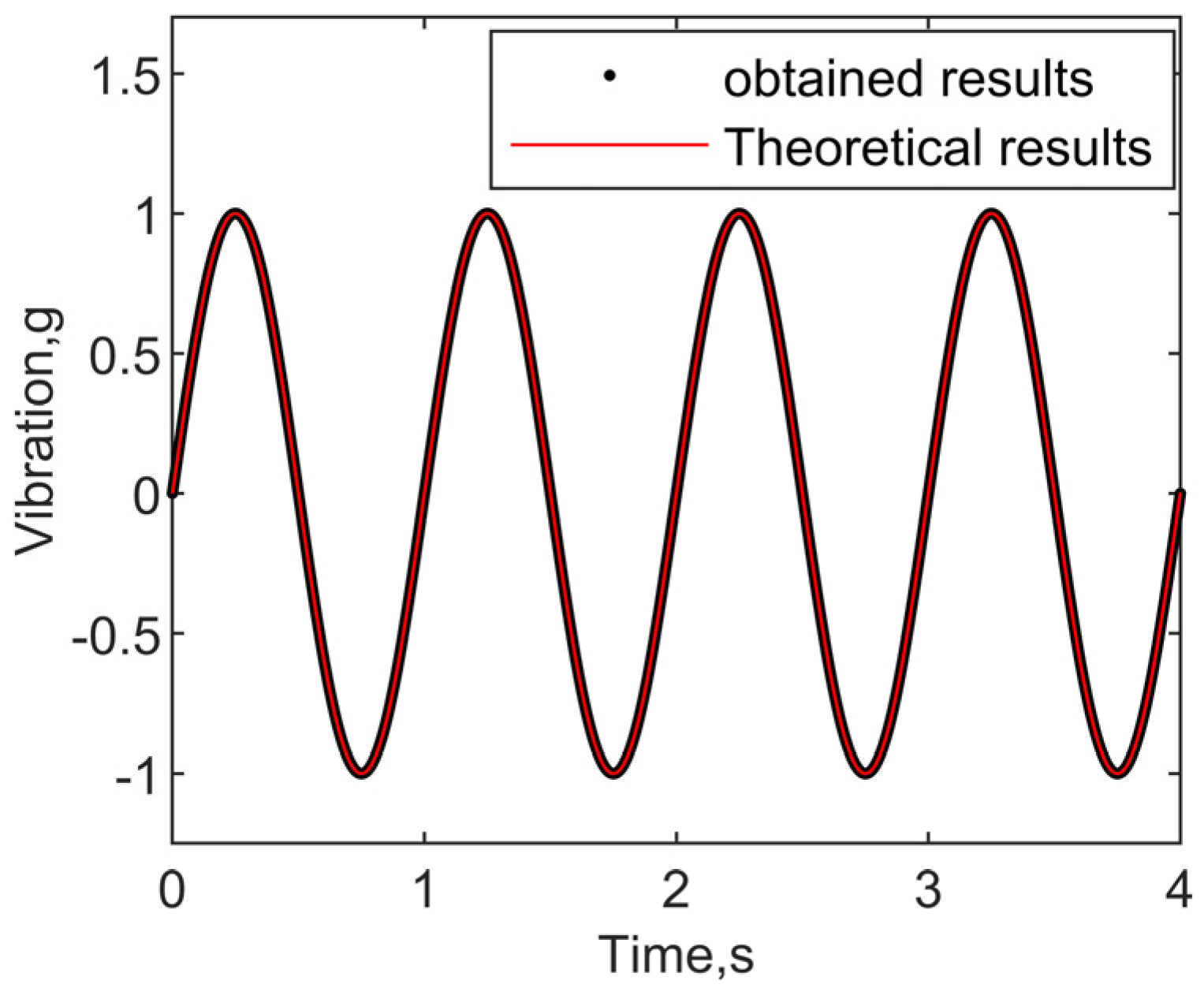
3. Validation
4. Applications on Railway Bearing Damage Detection
4.1. Test Setup
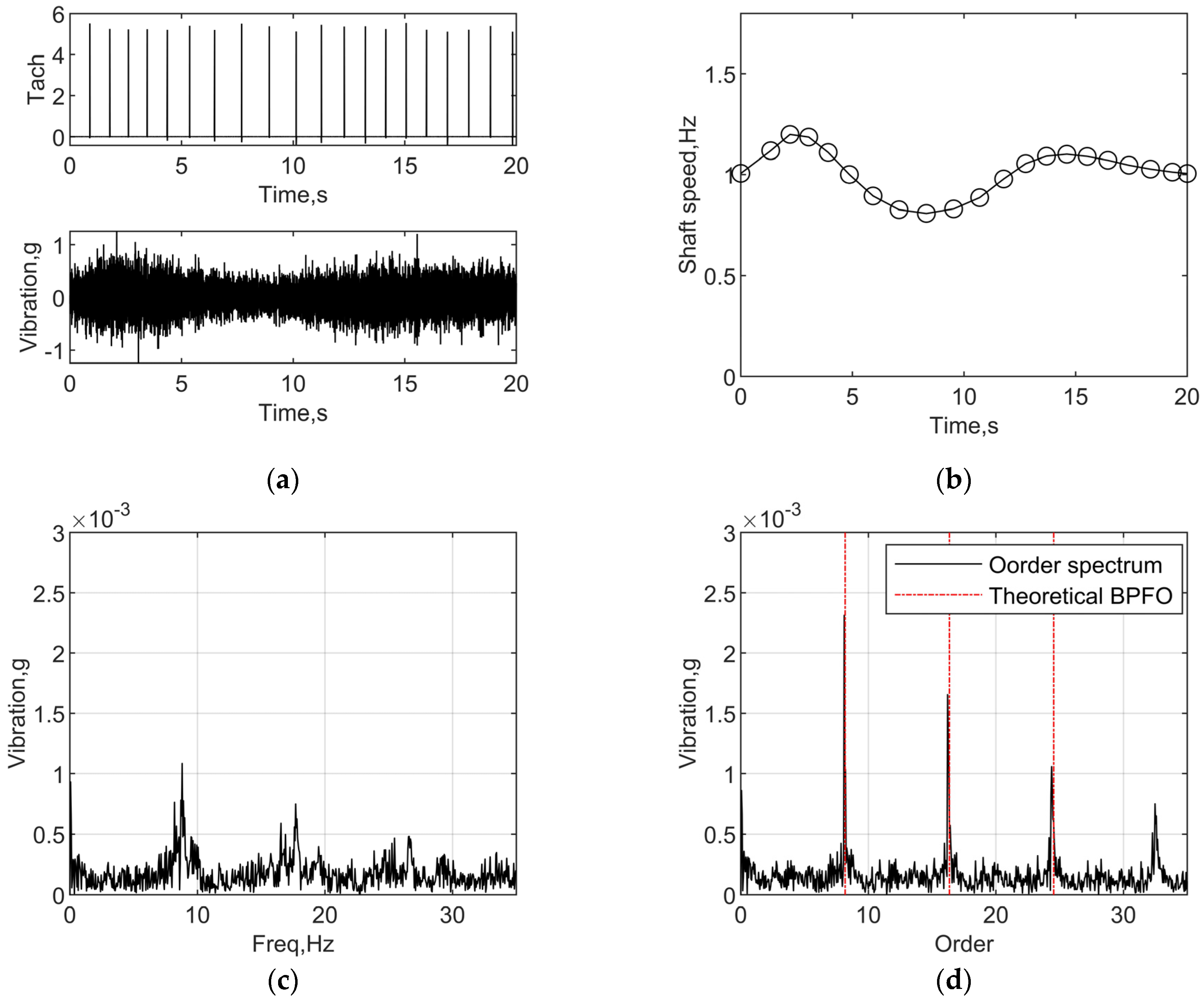
4.2. Extraction of Bearing Outer Race Spalling Damage Features
4.3. Extraction of Bearing Outer Race Indentation Damage Features
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gawde, S.; Patil, S.; Kumar, S.; Kamat, P.; Kotecha, K.; Abraham, A. Multi-fault diagnosis of Industrial Rotating Machines using Data-driven approach: A review of two decades of research. Eng. Appl. Artif. Intell. 2023, 123, 106139. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Y.Q.; Xu, M.Q.; Huang, W.H. A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery. Entropy-Switz 2019, 21, 409. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A Review on Vibration-Based Condition Monitoring of Rotating Machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.C.; Ni, Q.; Beer, M. A review of vibration-based gear wear monitoring and prediction techniques. Mech. Syst. Signal Process. 2023, 182, 109605. [Google Scholar] [CrossRef]
- Zhou, P.; Chen, S.Q.; He, Q.B.; Wang, D.; Peng, Z.K. Rotating machinery fault-induced vibration signal modulation effects: A review with mechanisms, extraction methods and applications for diagnosis. Mech. Syst. Signal Process. 2023, 200, 110489. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.C.; Wang, K.; Wei, D.; Zhou, C.; Ni, Q. A novel order spectrum-based Vold-Kalman filter bandwidth selection scheme for fault diagnosis of gearbox in offshore wind turbines. Ocean. Eng. 2022, 266, 112920. [Google Scholar] [CrossRef]
- Schmidt, S.; Heyns, P.S.; de Villiers, J.P. A tacholess order tracking methodology based on a probabilistic approach to incorporate angular acceleration information into the maxima tracking process. Mech. Syst. Signal Process. 2018, 100, 630–646. [Google Scholar] [CrossRef]
- Yeh, T.-C.; Pan, M.-C.; Ho, C.-Y.; IEEE. DSP-Base Adaptive Angular-Velocity VKF Order Tracking for Online Real-Time Monitoring System. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 1813–1819. [Google Scholar]
- Camerini, V.; Coppotelli, G.; Bendisch, S.; Kiehn, D. Impact of pulse time uncertainty on synchronous average: Statistical analysis and relevance to rotating machinery diagnosis. Mech. Syst. Signal Process. 2019, 129, 308–336. [Google Scholar] [CrossRef]
- Yin, N.; Meng, Z.; Guan, Y.; Fan, F.J. An adaptive multiple time domain synchronous averaging method and its application in vibration signal feature enhancement. Meas. Sci. Technol. 2022, 33, 055004. [Google Scholar] [CrossRef]
- Wang, L.; Hu, M.H.; Ma, B.; Jiang, Z.N. Time Synchronous Averaging Based on Cross-power Spectrum. Chin. J. Mech. Eng. 2023, 36, 51. [Google Scholar] [CrossRef]
- Huang, Z.F.; Sun, K.C.; Wei, D.H.; Mao, H.L.; Li, X.N.; Qian, X. Improved time domain synchronous averaging based on the moving interpolation and kurtosis criterion searching. Meas. Sci. Technol. 2021, 32, 105010. [Google Scholar] [CrossRef]
- Zhang, B.Q.; Zhang, F.H.; Luo, H.G. Virtual shaft-based synchronous analysis for bearing damage detection and its application in wind turbines. Wind Energy 2022, 25, 1252–1269. [Google Scholar] [CrossRef]
- Huang, Y.K.; Zhang, W.Y.; Wang, K.; Zhang, B.Q.; Zhang, F.H.; Luo, H.G. Fault diagnosis of low-speed rolling bearing based on weighted reconstruction of vibration envelopes. Wind Energy 2023, 26, 637–649. [Google Scholar] [CrossRef]
- Mcfadden, P.D.; Smith, J.D. Vibration Monitoring of Rolling Element Bearings by the High-Frequency Resonance Technique—A Review. Tribol. Int. 1984, 17, 3–10. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R.B. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mech. Syst. Signal Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics-A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Luo, H.G.; Qiu, H.; Ghanime, G.; Hirz, M.; van der Merwe, G. Synthesized Synchronous Sampling Technique for Differential Bearing Damage Detection. J. Eng. Gas Turb. Power 2010, 132, 072501. [Google Scholar] [CrossRef]
- Liu, W.; He, D.; Zhao, T.; Liu, D.; IEEE. DSP Based Module for Processing Vibration Signals of Rotation Machinery. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1700–1705. [Google Scholar]
- Liu, T.; Cui, L.; Zhang, C. Study on Fault Diagnosis Method of Planetary Gearbox Based on Turn Domain Resampling and Variable Multi-Scale Morphological Filtering. Symmetry 2021, 13, 51. [Google Scholar] [CrossRef]
- Potter, R.; Gribler, M. Computed order tracking obsoletes older methods. SAE Trans. 1989, 98, 1099–1103. [Google Scholar]
- Bossley, K.M.; Mckendrick, R.J.; Harris, C.J.; Mercer, C. Hybrid computed order tracking. Mech. Syst. Signal Process. 1999, 13, 627–641. [Google Scholar] [CrossRef]
- Fyfe, K.R.; Munck, E.D.S. Analysis of computed order tracking. Mech. Syst. Signal Process. 1997, 11, 187–205. [Google Scholar] [CrossRef]
- Saavedra, P.N.; Rodriguez, C.G. Accurate assessment of computed order tracking. Shock Vib. 2006, 13, 13–32. [Google Scholar] [CrossRef]
- Peeters, C.; Leclère, Q.; Antoni, J.; Lindahl, P.; Donnal, J.; Leeb, S.; Helsen, J. Review and comparison of tacholess instantaneous speed estimation methods on experimental vibration data. Mech. Syst. Signal Process. 2019, 129, 407–436. [Google Scholar] [CrossRef]
- Lu, S.L.; Yan, R.Q.; Liu, Y.B.; Wang, Q.J. Tacholess Speed Estimation in Order Tracking: A Review With Application to Rotating Machine Fault Diagnosis. IEEE T Instrum. Meas. 2019, 68, 2315–2332. [Google Scholar] [CrossRef]
- Yan, G.X.; Chen, J.; Bai, Y.; Yu, C.Q.; Yu, C.M. A Survey on Fault Diagnosis Approaches for Rolling Bearings of Railway Vehicles. Processes 2022, 10, 724. [Google Scholar] [CrossRef]
- Wang, J.H.; Yang, J.W.; Bai, Y.L.; Zhao, Y.; He, Y.P.; Yao, D.C. A comparative study of the vibration characteristics of railway vehicle axlebox bearings with inner/outer race faults. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2021, 235, 1035–1047. [Google Scholar] [CrossRef]
- Sahu, D.; Dewangan, R.K.; Matharu, S.P.S. An Investigation of Fault Detection Techniques in Rolling Element Bearing. J. Vib. Eng. Technol. 2023. [Google Scholar] [CrossRef]
- Li, X.Y.; Cai, Z.K.; Zhang, W.Y.; Wu, T.H.; Zhang, B.Q.; Luo, H.G. Tachometer-Less Synchronous Sampling for Large Speed Fluctuations and Its Application in the Monitoring of Wind Turbine Drive Train Condition. Machines 2023, 11, 942. [Google Scholar] [CrossRef]



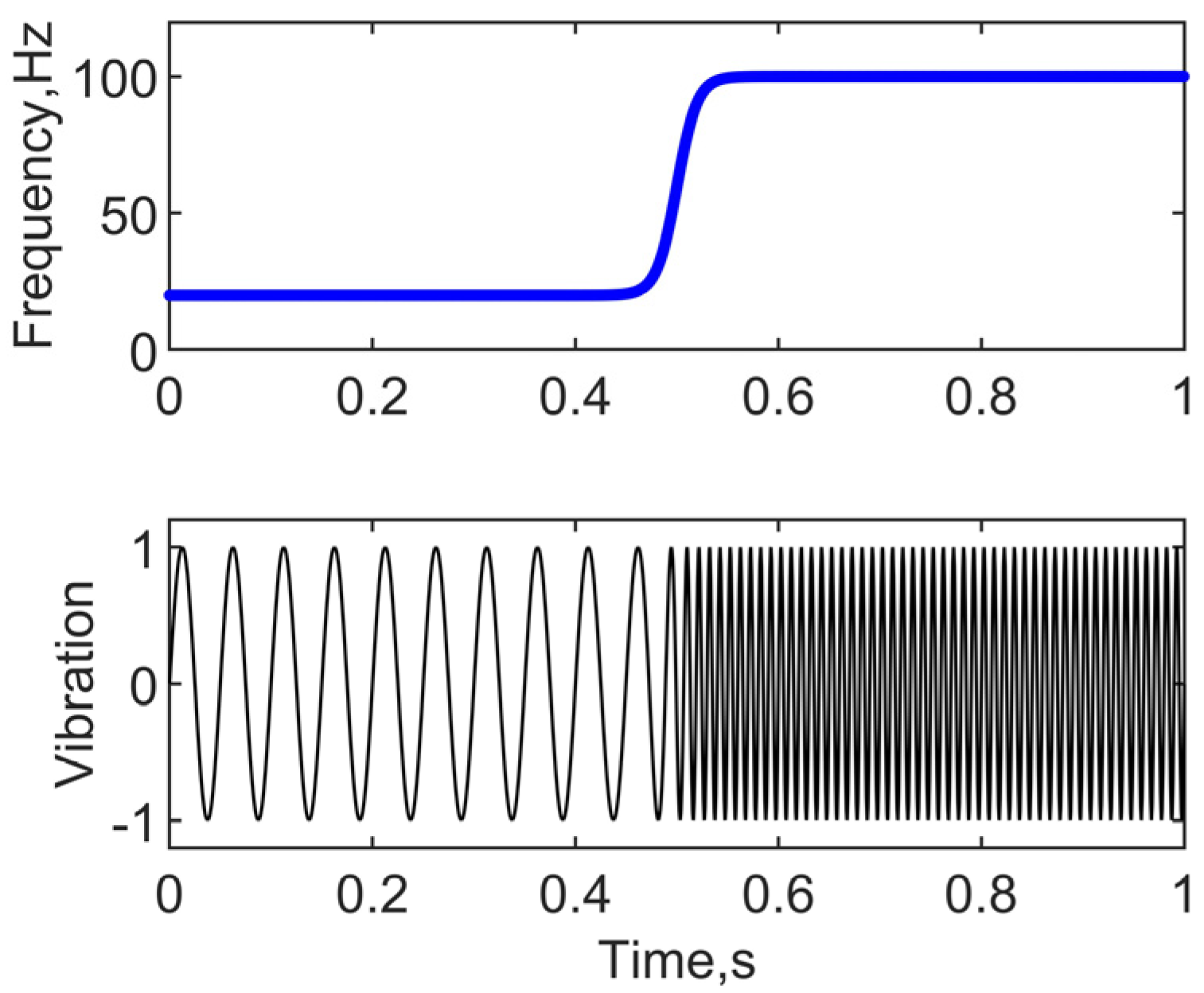
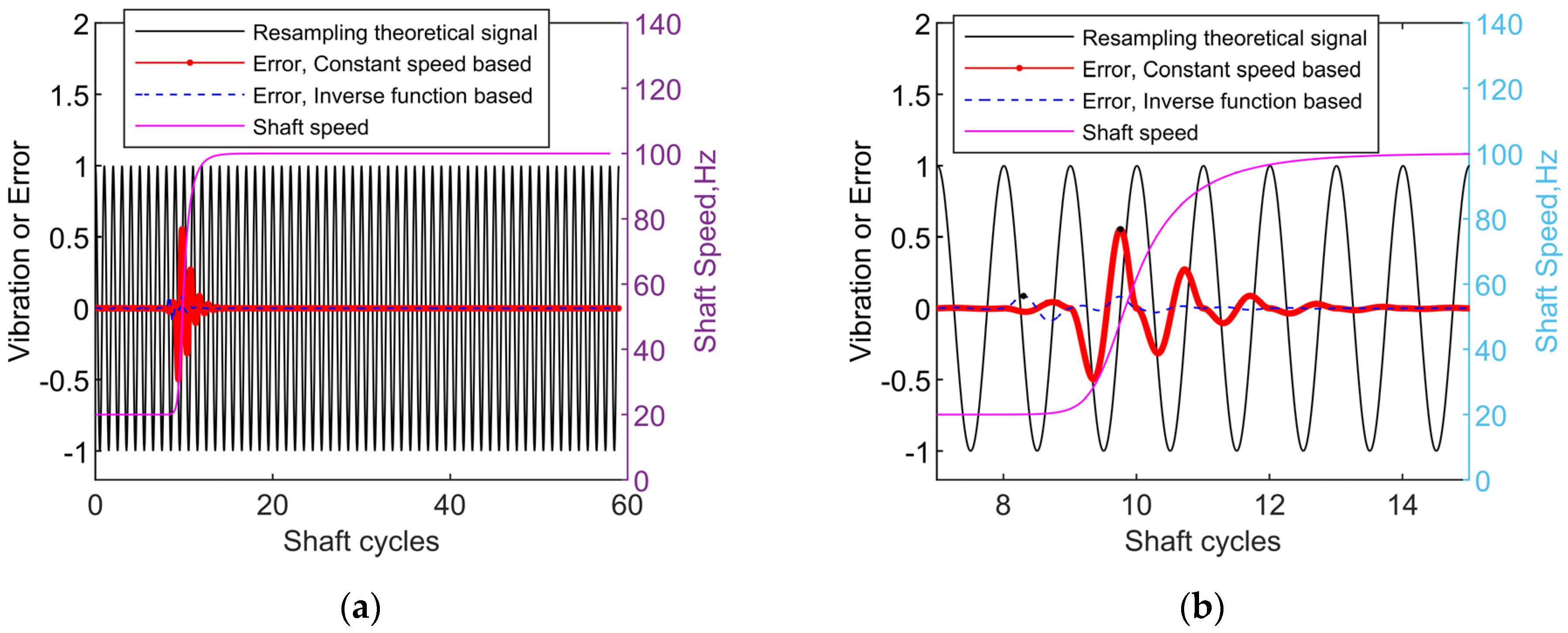


| Resampling Methods | Synchronization Time Calculation Duration | MSE |
|---|---|---|
| Inverse function based | 0.008881 s | 9.3385 × 10−7 |
| Traditional iteration based | 0.049916 s | 1.1263 × 10−6 |
| With constant shaft-speed assumption within each cycle | 0.024069 s | 1.1719 × 10−6 |
| Maximum Error, % | ||
|---|---|---|
| Constant Speed-Based | Inverse Function-Based | |
| 200 | 79.0 | 23.8 |
| 100 | 55.5 | 8.8 |
| 50 | 30.0 | 3.4 |
| 20 | 12.0 | 0.5 |
| 10 | 5.8 | 0.3 |
| Pitch Diameter (mm) | Rolling Diameter (mm) | Number of Rollers | Contact Angle (Deg) |
|---|---|---|---|
| 183.929 | 26 | 19 | 10 |
| the outer race damage order | the inner race damage order | the roller damage order | the cage damage order |
| 8.177 | 10.822 | 3.468 | 0.429 |
| Method Used | Amplitude | |||
|---|---|---|---|---|
| 1st Order Damage Feature | 2rd Order Damage Feature | 3th Order Damage Feature | ||
| Conventional AEA | 3.016 × 10−4 | 2.535 × 10−4 | 1.923 × 10−4 | 17.077 |
| AEA based on proposed method | 4.770 × 10−4 | 3.832 × 10−4 | 3.395 × 10−4 | 42.261 |
| Method Used | Amplitude | |||
|---|---|---|---|---|
| 1st Damage Feature | 2rd Damage Feature | 3th Damage Feature | ||
| Conventional AEA | 1.085 × 10−3 | 7.481 × 10−4 | 4.672 × 10−4 | 36.352 |
| AEA based on proposed method | 2.312 × 10−3 | 1.656 × 10−3 | 1.058 × 10−3 | 157.579 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Huang, Y.; Zhang, B.; Luo, H.; Yu, X.; Chen, D.; Zhang, Z. Improved Synchronous Sampling and Its Application in High-Speed Railway Bearing Damage Detection. Machines 2024, 12, 101. https://doi.org/10.3390/machines12020101
Wang K, Huang Y, Zhang B, Luo H, Yu X, Chen D, Zhang Z. Improved Synchronous Sampling and Its Application in High-Speed Railway Bearing Damage Detection. Machines. 2024; 12(2):101. https://doi.org/10.3390/machines12020101
Chicago/Turabian StyleWang, Kun, Yukun Huang, Baoqiang Zhang, Huageng Luo, Xiang Yu, Dawei Chen, and Zhiqiang Zhang. 2024. "Improved Synchronous Sampling and Its Application in High-Speed Railway Bearing Damage Detection" Machines 12, no. 2: 101. https://doi.org/10.3390/machines12020101
APA StyleWang, K., Huang, Y., Zhang, B., Luo, H., Yu, X., Chen, D., & Zhang, Z. (2024). Improved Synchronous Sampling and Its Application in High-Speed Railway Bearing Damage Detection. Machines, 12(2), 101. https://doi.org/10.3390/machines12020101






