Synchronization of Dual Induction Motor Multi-Frequency Control Based on Fixed Speed Ratio
Abstract
:1. Introduction
2. Electromechanical Coupling Model for Vibrating Systems
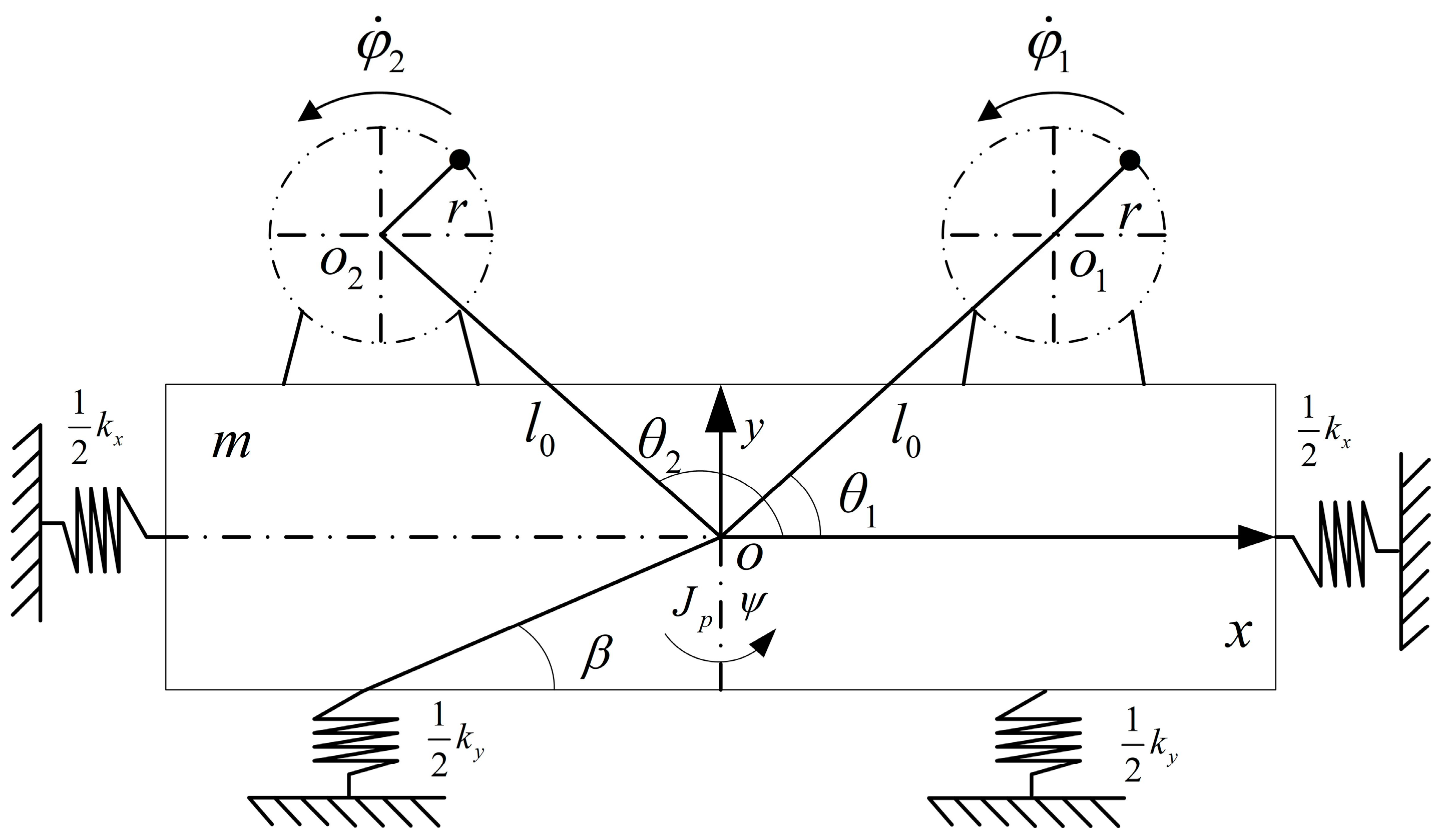
2.1. Dynamic Model of Dual Induction Motor Vibration System
2.2. Model of Asynchronous Motor
2.3. Controlled Synchronization Response Analysis
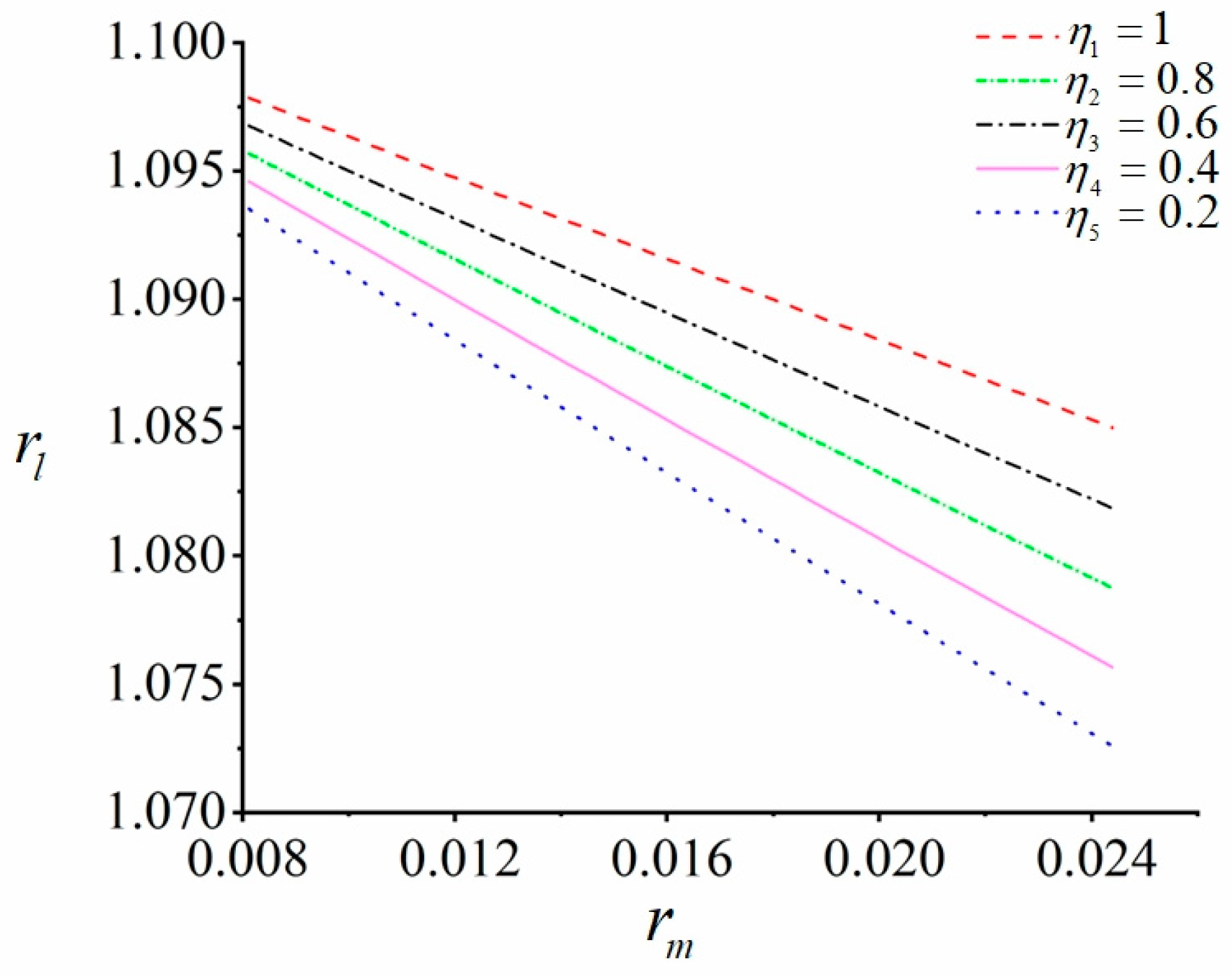
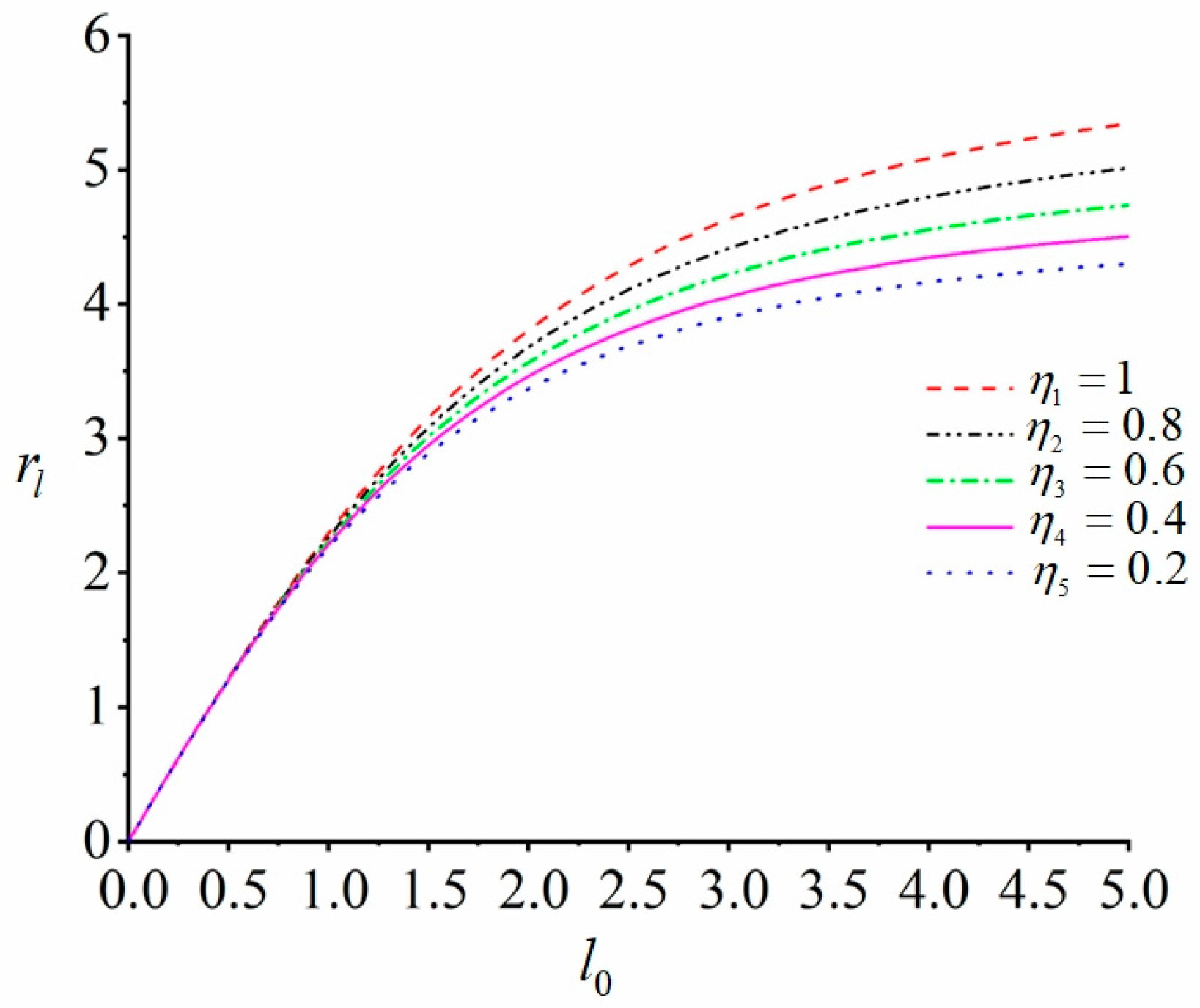
2.4. Motion Characteristics Analysis of Vibrating Systems
3. Design of the Control System
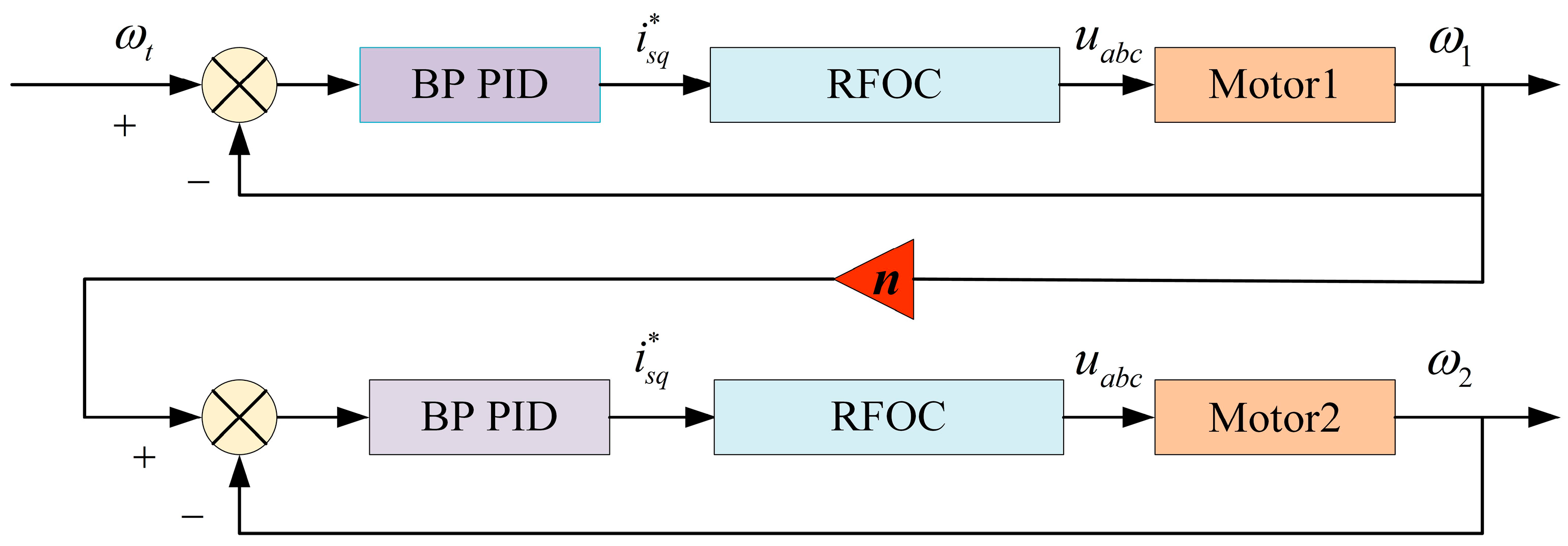
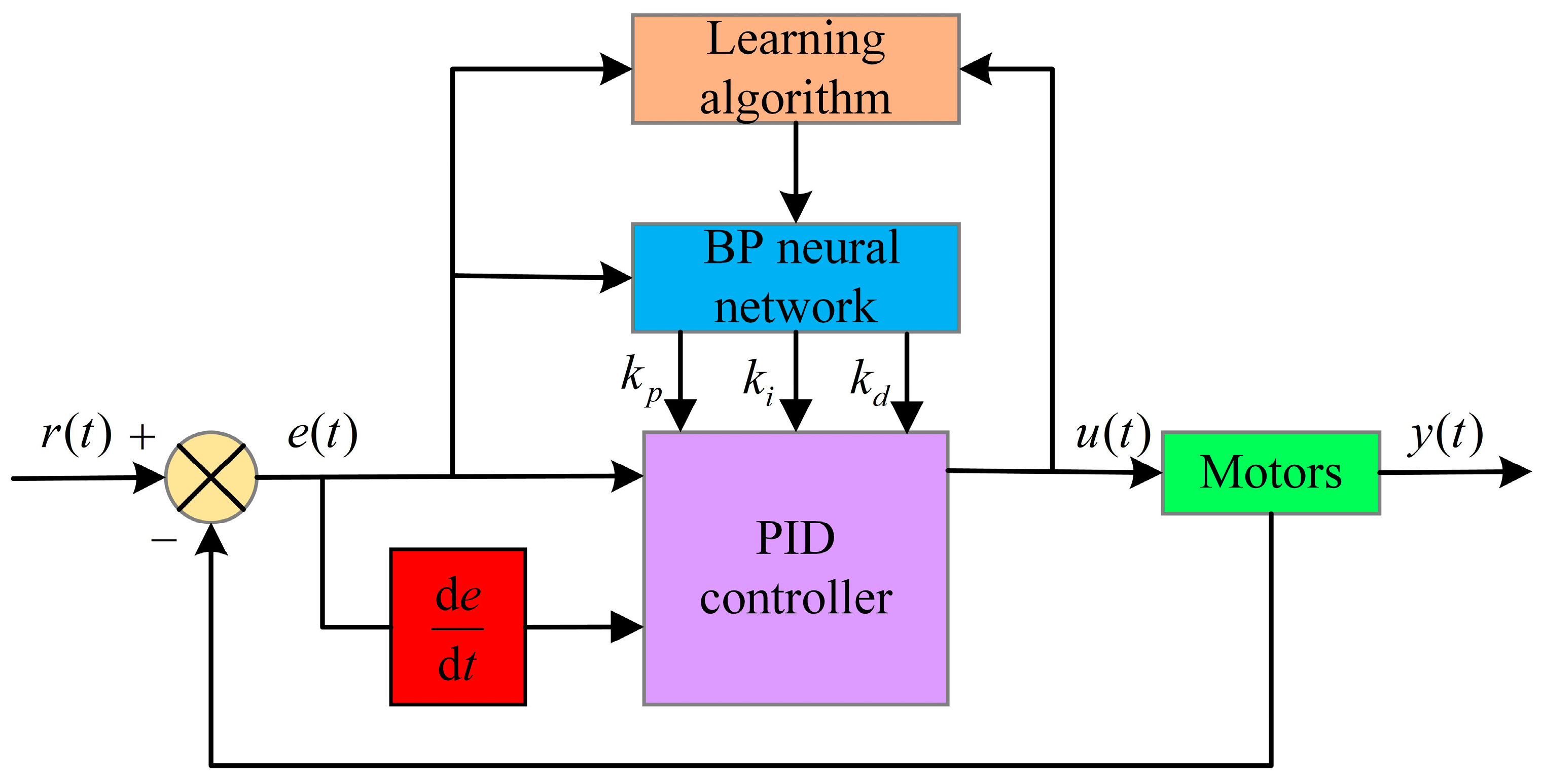
3.1. Design of the Electromechanical Coupling System
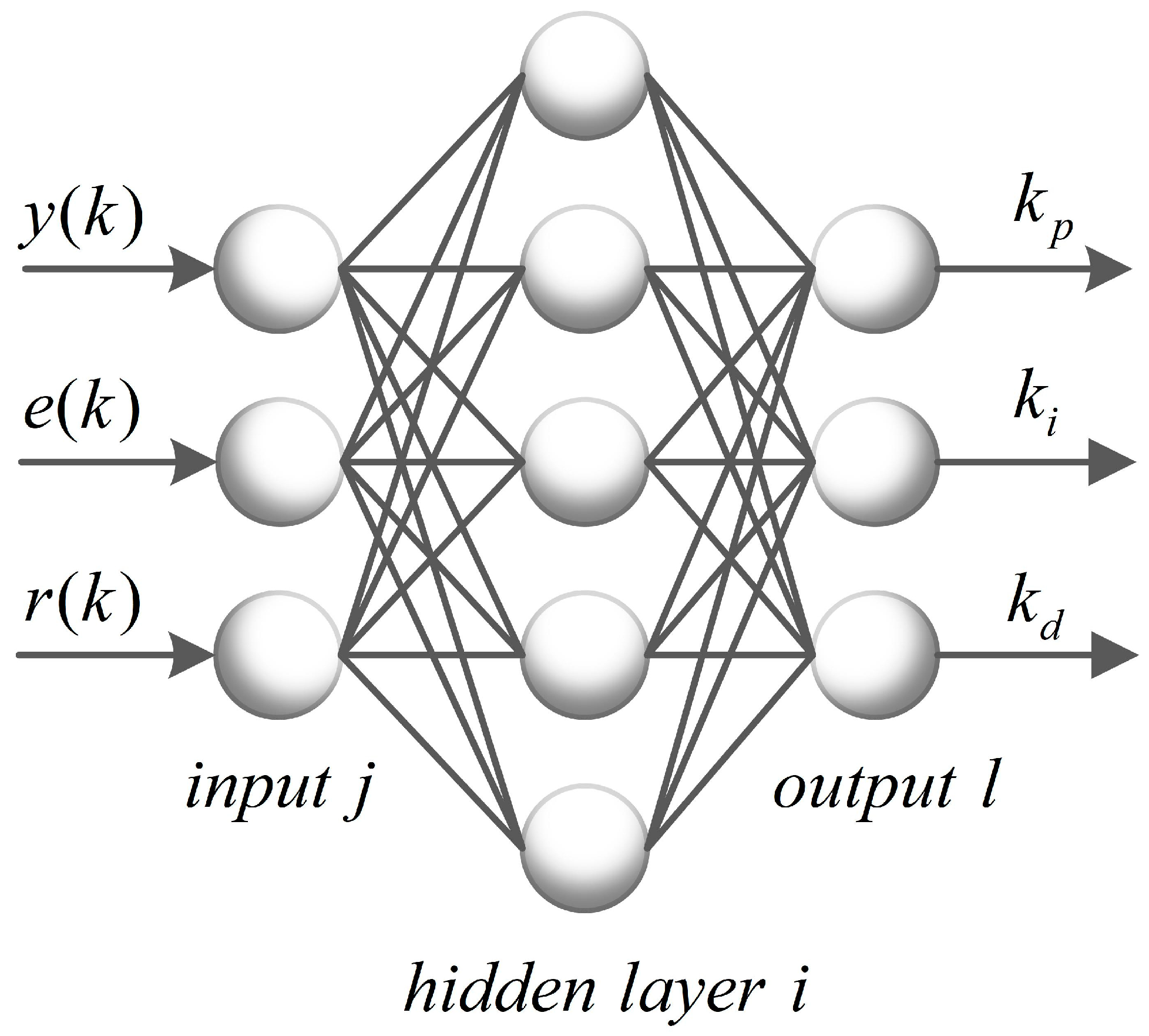
3.2. Design of the BP PID Method
3.3. Step Summary of BP PID Control Algorithm
- (1)
- Combined with the control object to determine the structure of the BP neural network, we obtained the number of nodes in input layer and hidden layer. We selected a set of initial random values (0, 0.5) for the connection weight of the hidden layer and the connection weight of the output layer. The inertia coefficient and the autonomous learning rate of neural network were determined.
- (2)
- We sampled the system setting value and the actual output value at the time, then calculated .
- (3)
- We sampled , , and , respectively, as inputs into the BP neural network.
- (4)
- According to the Formulas (18)–(20), we calculated the inputs and outputs of each layer of the neural network. Finally, the output values , , and of the BP neural network were obtained.
- (5)
- According to Formula (21), the output of the incremental PID could be obtained, i.e., the control quantity accepted by the induction motor.
- (6)
- According to Formula (27), we adjusted the connection weight of the output layer.
- (7)
- According to Formula (28), we adjusted the connection weights of the implicit layer.
- (8)
- According to the Formula (22), if the performance index function was less than the set value and the three parameters of the BP neural network satisfied the requirements of the PID controller, we terminated the learning process. On the contrary, if , we would have returned to step (2) and continued the learning process again.
4. Results and Discussion
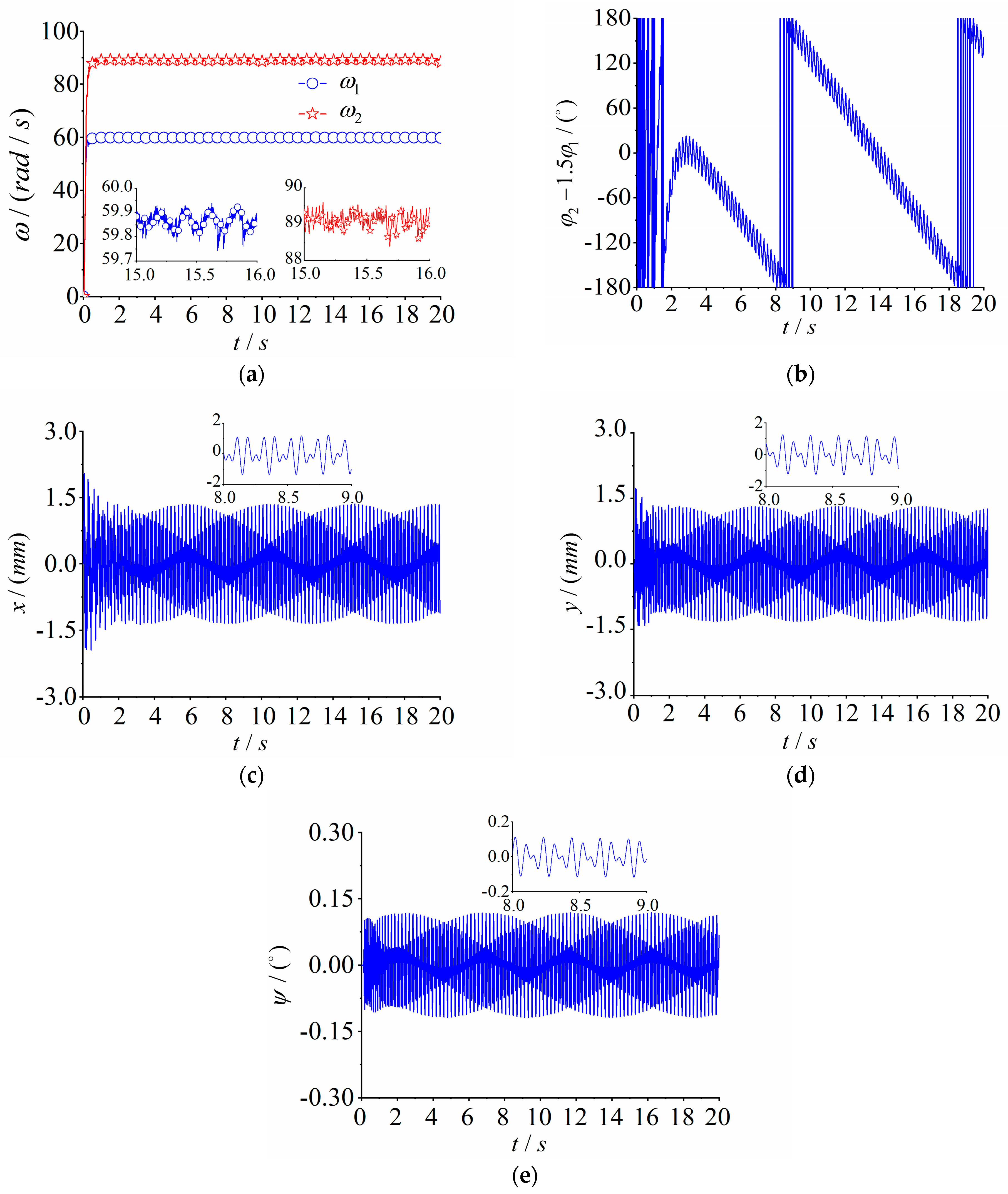
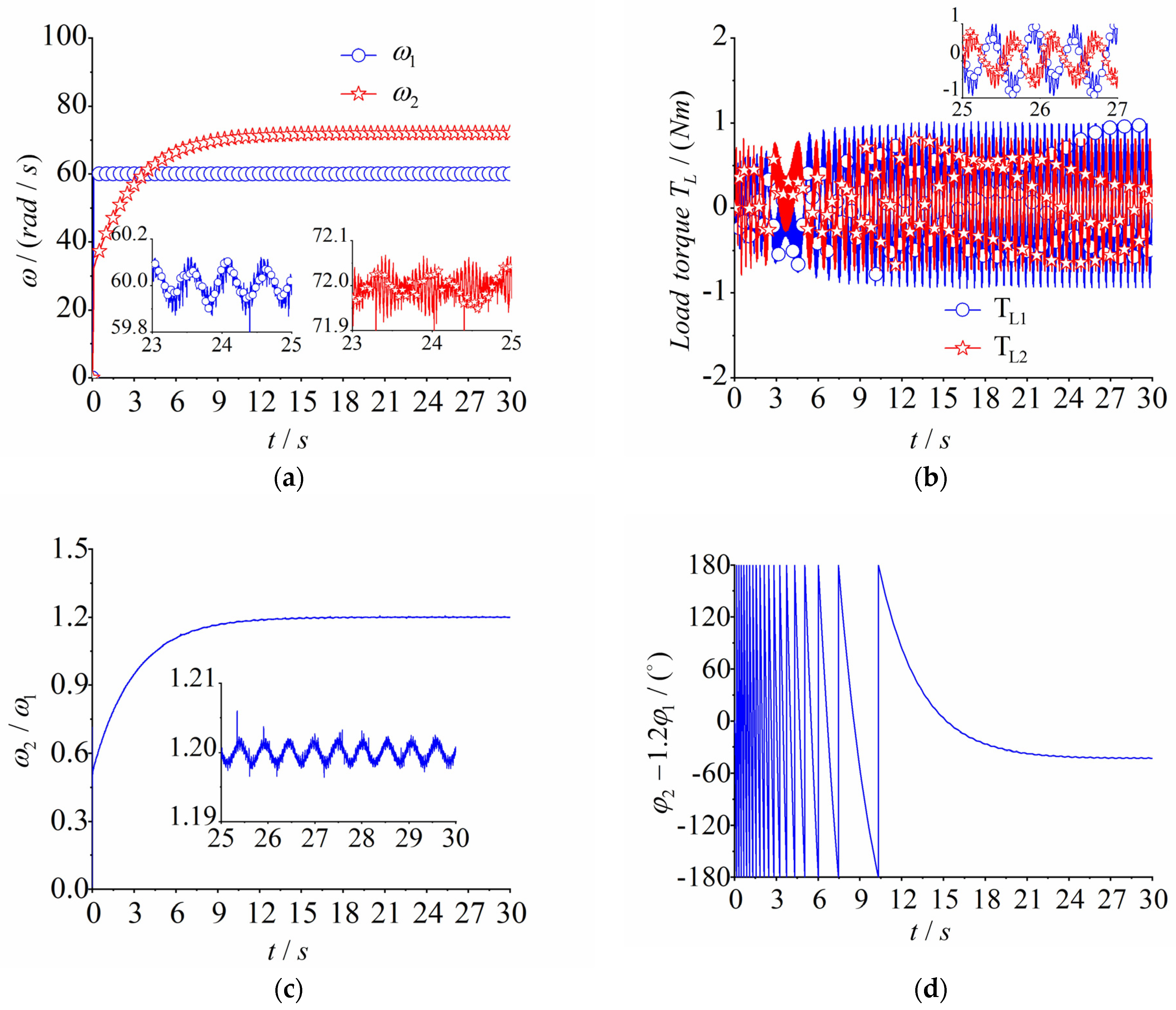
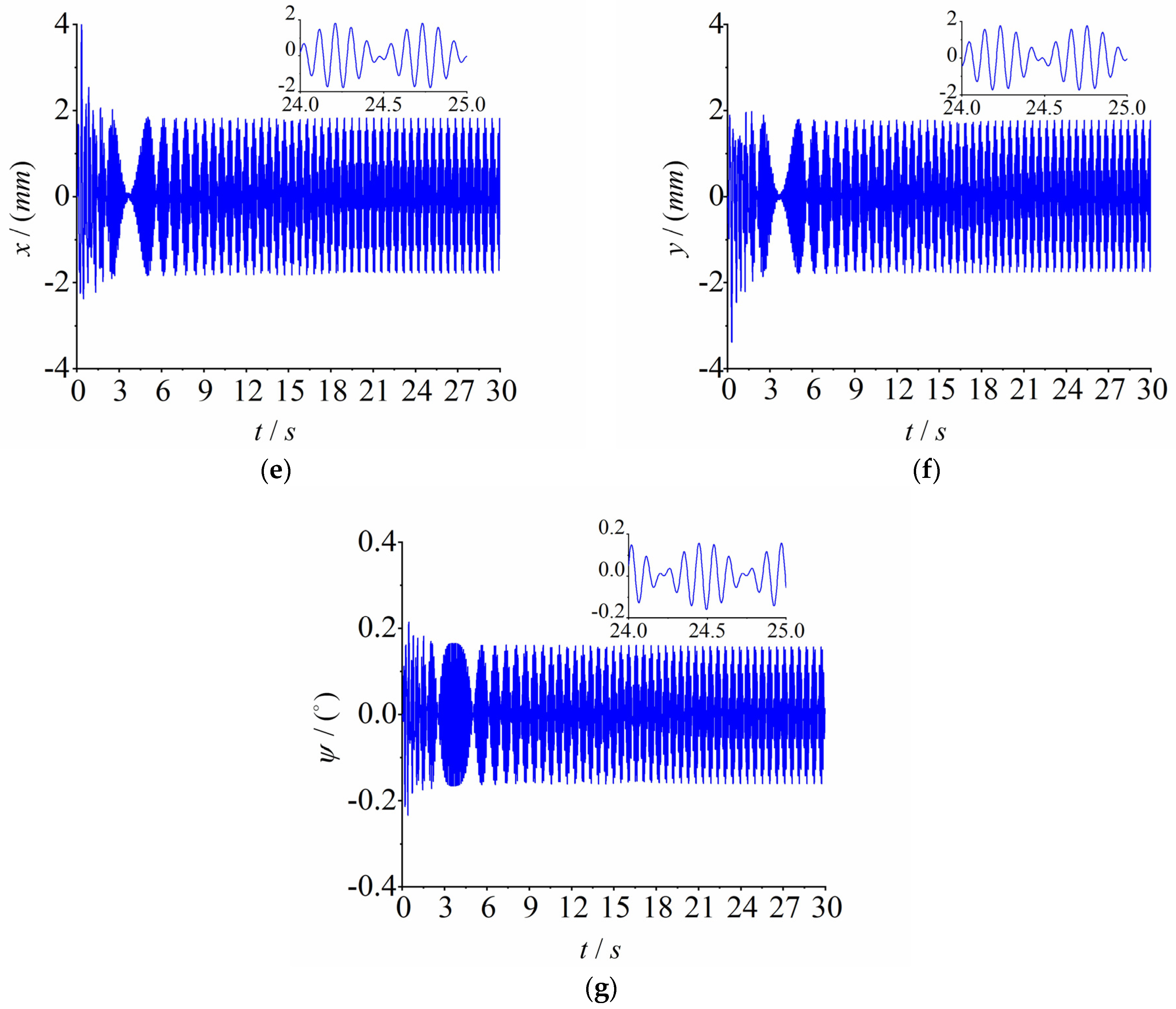
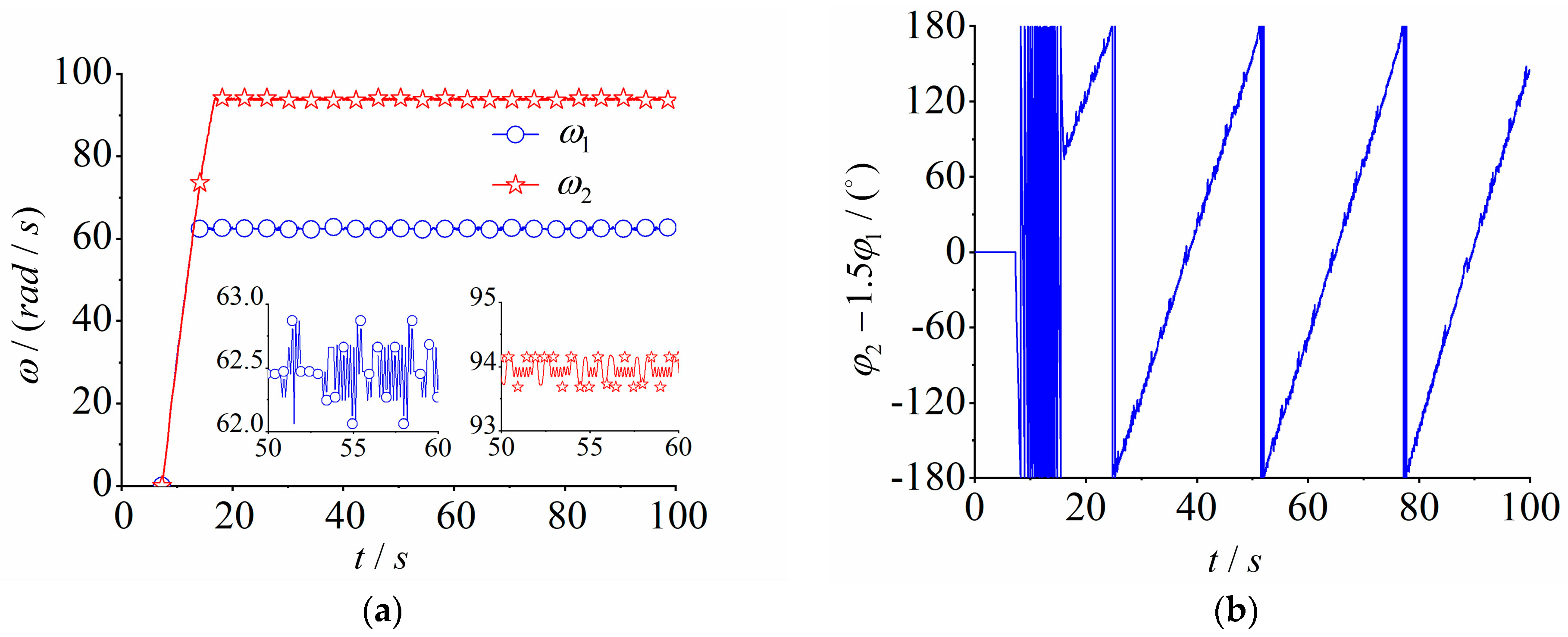
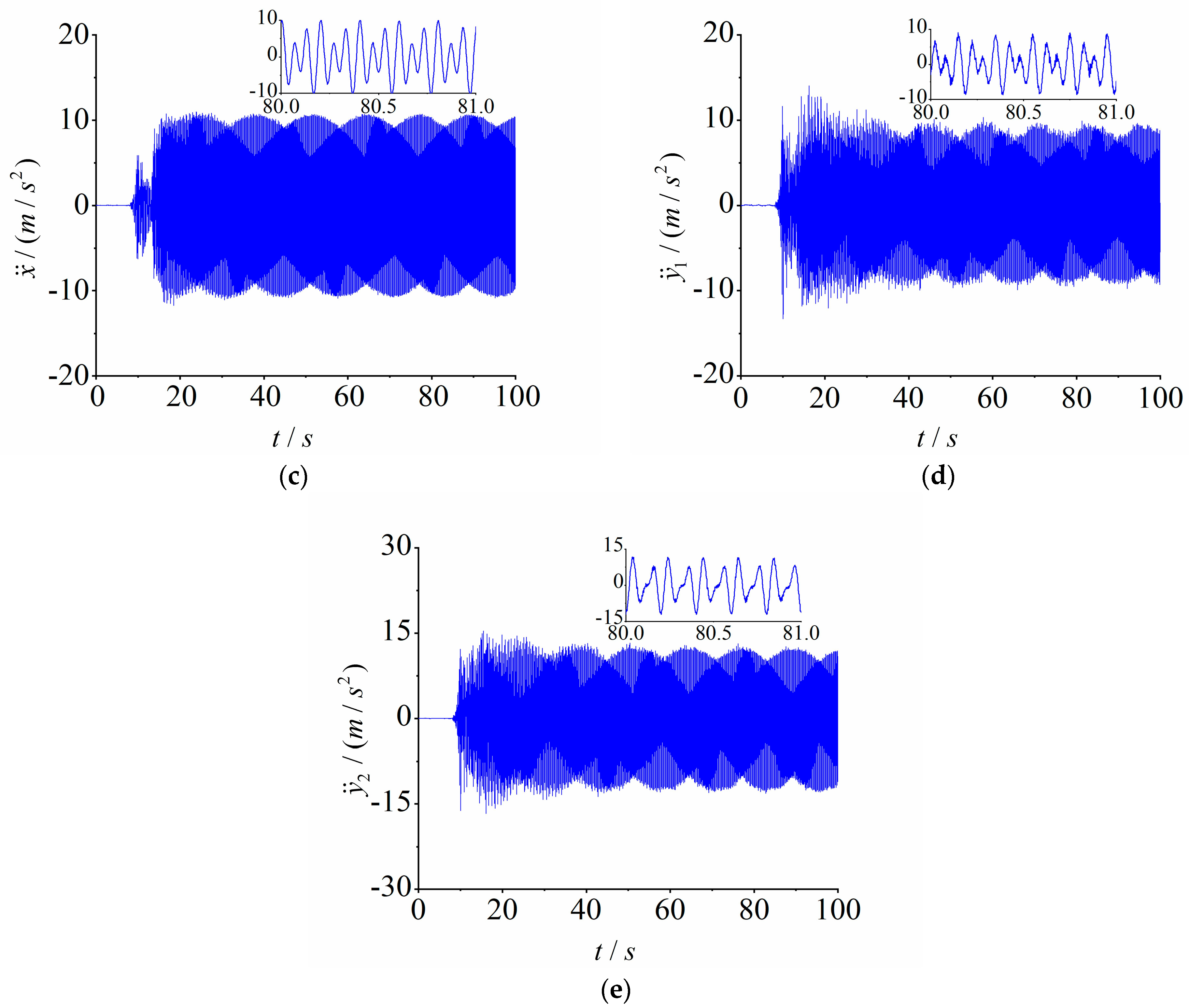
4.1. Numerical Simulation of the Multifrequency Self-Synchronization
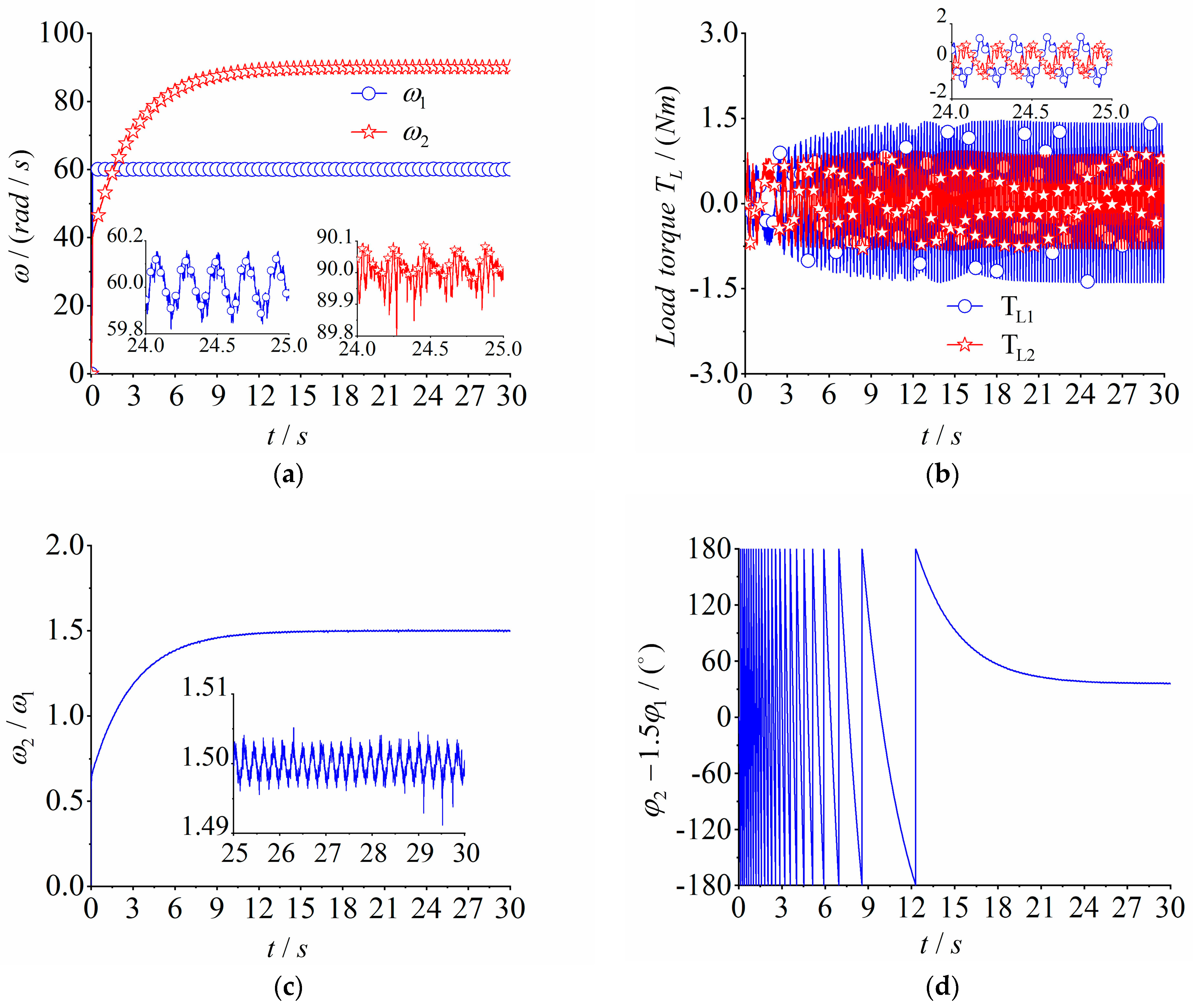
4.2. Numerical Simulation of the Multifrequency Composite Synchronization
4.3. Experimental Verification
4.3.1. Experiment of Multifrequency Self-Synchronization
4.3.2. Experiment of Multifrequency Control Synchronization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rodriguez, C.G.; Moncada, M.A.; Dufeu, E.E.; Razeto, M.I. Nonlinear Model of Vibrating Screen to Determine Permissible Spring Deterioration for Proper Separation. Shock Vib. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Li, J.; Yu, W.; Kong, L.R. Synchronization characteristics of two vibrators in a novel hydraulic coupling system. Alex. Eng. J. 2022, 61, 11663–11676. [Google Scholar] [CrossRef]
- Hartig, J.; Shetty, A.; Conklin, D.R.; Weimer, A.W. Aeration and cohesive effects on flowability in a vibrating powder conveyor. Powder Technol. 2022, 408, 117724. [Google Scholar] [CrossRef]
- Wen, B.C.; Liu, S.Y.; He, Q. Theory and Dynamic Design Method of Vibrating Machinery; China Machine Press: Beijing, China, 2001. [Google Scholar]
- Wen, B.C.; Fan, J.; Zhao, C.Y.; Xiong, W.L. Vibratory Synchronization and Controlled Synchronization in Engineering; Science Press: Beijing, China, 2009. [Google Scholar]
- Klemiato, M.; Czubak, P. Event driven control of vibratory conveyors operating on the frahm’s eliminator basis. Arch. Metall. Mater. 2015, 60, 19–25. [Google Scholar] [CrossRef]
- Shagniev, O.B.; Tomchina, O.P.; Fradkov, A.L. Learning Speed-Gradient Synchronization Control of the Two-Rotor Vibration Setup. IFAC Pap. 2022, 55, 144–148. [Google Scholar] [CrossRef]
- Barathiraja, K.; Devaradjane, G.; Paul, J.; Rakesh, S.; Jamadade, G. Analysis of automotive transmission gearbox synchronizer wear due to torsional vibration and the parameters influencing wear reduction. Eng. Fail. Anal. 2019, 105, 427–443. [Google Scholar]
- Shen, G.; Chen, Z.; Wu, X.; Li, Z.; Tong, X. Stepwise shape optimization of the surface of a vibrating screen. Particuology 2021, 58, 26–34. [Google Scholar] [CrossRef]
- Blekman, I.I. Synchronization in Science and Technology; ASME Press: New York, NY, USA, 1988. [Google Scholar]
- Wen, B.C.; Guan, L.Z. Synchronization Theory and Debugging Method of Self-synchronous Vibration Motor. Min. Mach. 1979, 5, 35–45. [Google Scholar]
- Wen, B.C.; Zhang, H.; Liu, S.Y.; He, Q.; Zhao, C.Y. Theory and Techniques of Vibration Machinery and Their Applications; Science Press: Beijing, China, 2010. [Google Scholar]
- Inoue, J.C. On the Self-Synchronization of Mechanical Vibrators: Part 5, Shock Vibrator. J. Jpn. Soc. Mech. Eng. 1967, 70, 35–42. [Google Scholar] [CrossRef]
- Zhao, C.; Zhu, H.; Zhang, Y.; Wen, B. Synchronization of two coupled exciters in a vibrating system of spatial motion. Acta Mech. Sin. 2010, 26, 477–493. [Google Scholar] [CrossRef]
- Li, Y.; Ren, T.; Zhang, J.; Zhang, M. Synchronization of two eccentric rotors driven by one motor with two flexible couplings in a spatial vibration system. Math. Probl. Eng. 2019, 2019, 2969687. [Google Scholar] [CrossRef]
- Fang, P.; Wang, Y.; Hou, Y.; Wu, Y. Synchronous control of multi-motor coupled with pendulum in a vibration system. IEEE Access 2020, 8, 51964–51975. [Google Scholar] [CrossRef]
- Fang, P.; Hou, Y. Synchronization characteristics of a rotor-pendula system in multiple coupling resonant systems. Proc. Inst. Mech. Eng. Part C 2018, 232, 1802–1822. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, X.; Chen, X.; Wen, B.; Wang, B. Synchronization analysis and control of three eccentric rotors in a vibration system using adaptive sliding mode control algorithm. Mech. Syst. Signal Process. 2016, 72-73, 432–450. [Google Scholar] [CrossRef]
- Kong, X.X.; Chen, C.Z.; Wen, B.C. Composite synchronization of three eccentric rotors driven by induction motors in a vibration system. Mech. Syst. Signal Process. 2018, 102, 158–179. [Google Scholar] [CrossRef]
- Kong, X.X.; Zhou, C.; Wen, B.C. Composite synchronization of four exciters driven by induction motors in a vibration system. Meccanica 2020, 55, 2107–2133. [Google Scholar] [CrossRef]
- Huang, Z.; Song, G.; Li, Y.; Sun, M. Synchronous control of two counter-rotating eccentric rotors in nonlinear coupling vibration system. Mech. Syst. Signal Process. 2019, 114, 68–83. [Google Scholar] [CrossRef]
- Huang, Z.; Song, G.; Zhang, Z.; Zhang, X. Control synchronization of two nonidentical homodromy exciters in nonlinear coupled vibration system. IEEE Access 2019, 7, 109934–109944. [Google Scholar] [CrossRef]
- Jin, C.; Cai, M.; Xu, Z. Dual-Motor Synchronization Control Design Based on Adaptive Neural Networks Considering Full-State Constraints and Partial Asymmetric Dead-Zone. Sensors 2021, 21, 4261. [Google Scholar] [CrossRef]
- Jia, L.; Wang, C.; Liu, Z.L. Multifrequency controlled synchronization of four inductor motors by the fixed frequency ratio method in a vibration system. Sci. Rep. 2023, 13, 2467. [Google Scholar] [CrossRef]
- Jia, L.; Liu, Z.L. Multifrequency composite synchronization of three inductor motors with the method of fixed speed ratio in a vibration system. Proc. Inst. Mech. Eng. 2023, 237, 254–268. [Google Scholar] [CrossRef]
- Zhang, X.L.; Wen, B.C.; Zhan, C.Y. Synchronization of three non-identical coupled exciters with the same rotating directions in a far-resonant vibrating system. J. Sound Vib. 2013, 332, 2300–2317. [Google Scholar] [CrossRef]
- Chen, J. Mathematical Model and Speed Adjustment System of Alternating Motors; National Defense Industry Press: Beijing, China, 1989. [Google Scholar]






| Symbol | Explanation |
|---|---|
| M | The total mass of the vibration system |
| m | The mass of the rigid body |
| m1, m2 | The eccentric rotor mass of 1 and 2 motors |
| r | The radius of eccentric rotor |
| l0 | The distance between the center of the body and the rotation center of the eccentric rotor |
| le | The equivalent rotation radius of the vibration system |
| J | The moment of inertia of the vibration system |
| JP | The moment of inertia of the rigid body |
| J1, J2 | The moment of inertia of two eccentric rotors |
| fx, fy, fψ | The stiffness coefficients of the vibration system in the x, y, and ψ |
| f1, f2 | The damping coefficient of two induction motors |
| kx, ky kψ | The spring stiffness of the vibration system in the x, y, and ψ directions |
| Te1, Te2 | The electromagnetic torque of two induction motors |
| TL1, TL2 | The load torque of two induction motors |
| Subscript s | Stator |
| Subscript r | Rotor |
| d-, q- | The d- and q- axes in rotor field-oriented coordinate |
| i, u, R | The current, the voltage, and the resistance |
| Ls | Self-inductance of the stator |
| Lr | Self-inductance of the rotor |
| Lm | Mutual inductance of the stator and rotor |
| Tr | A rotor time constant |
| Lks | Stator leakage inductance |
| Rks | Equivalent stator resistance |
| np | Pole logarithm of induction motor |
| θ | Synchronous flux angle |
| ω | Mechanical angular velocity |
| ωs | Synchronous electrical angular velocity |
| Parameters | Motor 1 | Motor 2 |
|---|---|---|
| Rated power P/kW | 1.1 | 1.1 |
| Pole pairs np | 3 | 3 |
| Rated frequency f0/Hz | 50 | 50 |
| Rated voltage U/V | 220 | 220 |
| Rated speed n/(r/min) | 950 | 950 |
| Stator resistance Rs/Ω | 40.4 | 40.5 |
| Rotor resistance referred Rr/Ω | 12 | 12.813 |
| Stator inductance Ls/H | 3.92 | 3.92 |
| Rotor inductance referred Lr/H | 1.222 | 1.222 |
| Mutual inductance Lm/H | 1.116 | 1.116 |
| Rated flux linkage /Wb | 0.98 | 0.98 |
| Damping coefficients f1,2/(Nms/rad) | 0.005 | 0.005 |
| Parameters | Value |
|---|---|
| M/kg | 246 |
| Jp/(kg.m2) | 43.3 |
| kx/(N/m) | 129,332 |
| ky/(N/m) | 105,334 |
| kψ/(Nm/rad) | 30,715 |
| fx/(Ns/m) | 615.5 |
| fy/(Ns/m) | 618 |
| fψ/(Nsm/rad) | 180.2 |
| l0/m | 0.5 |
| α/(°) | 0 |
| θ1/(°) | 30 |
| θ2/(°) | 150 |
| m0/kg | 4 |
| r/m | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Jia, L. Synchronization of Dual Induction Motor Multi-Frequency Control Based on Fixed Speed Ratio. Machines 2024, 12, 97. https://doi.org/10.3390/machines12020097
Zhang X, Jia L. Synchronization of Dual Induction Motor Multi-Frequency Control Based on Fixed Speed Ratio. Machines. 2024; 12(2):97. https://doi.org/10.3390/machines12020097
Chicago/Turabian StyleZhang, Xin, and Lei Jia. 2024. "Synchronization of Dual Induction Motor Multi-Frequency Control Based on Fixed Speed Ratio" Machines 12, no. 2: 97. https://doi.org/10.3390/machines12020097





