An Analysis of the Kinematical Characteristics of an Eccentric Curve-Face Gear Pair with Compound Motion
Abstract
:1. Introduction
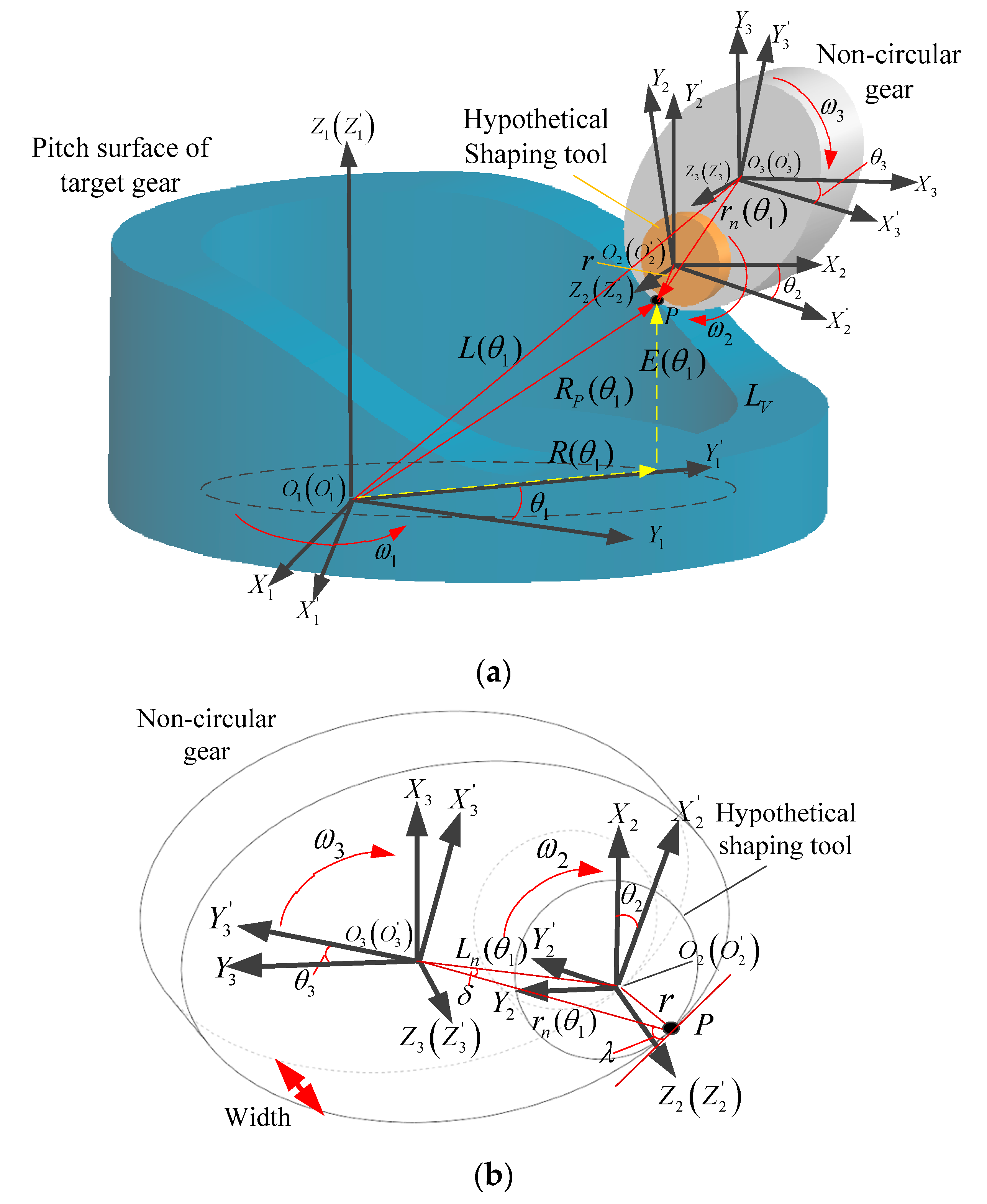
2. Transmission Model of Eccentric Curve-Face Gear Pair
2.1. Equation of Engagement Tooth Surface with Complex Motion
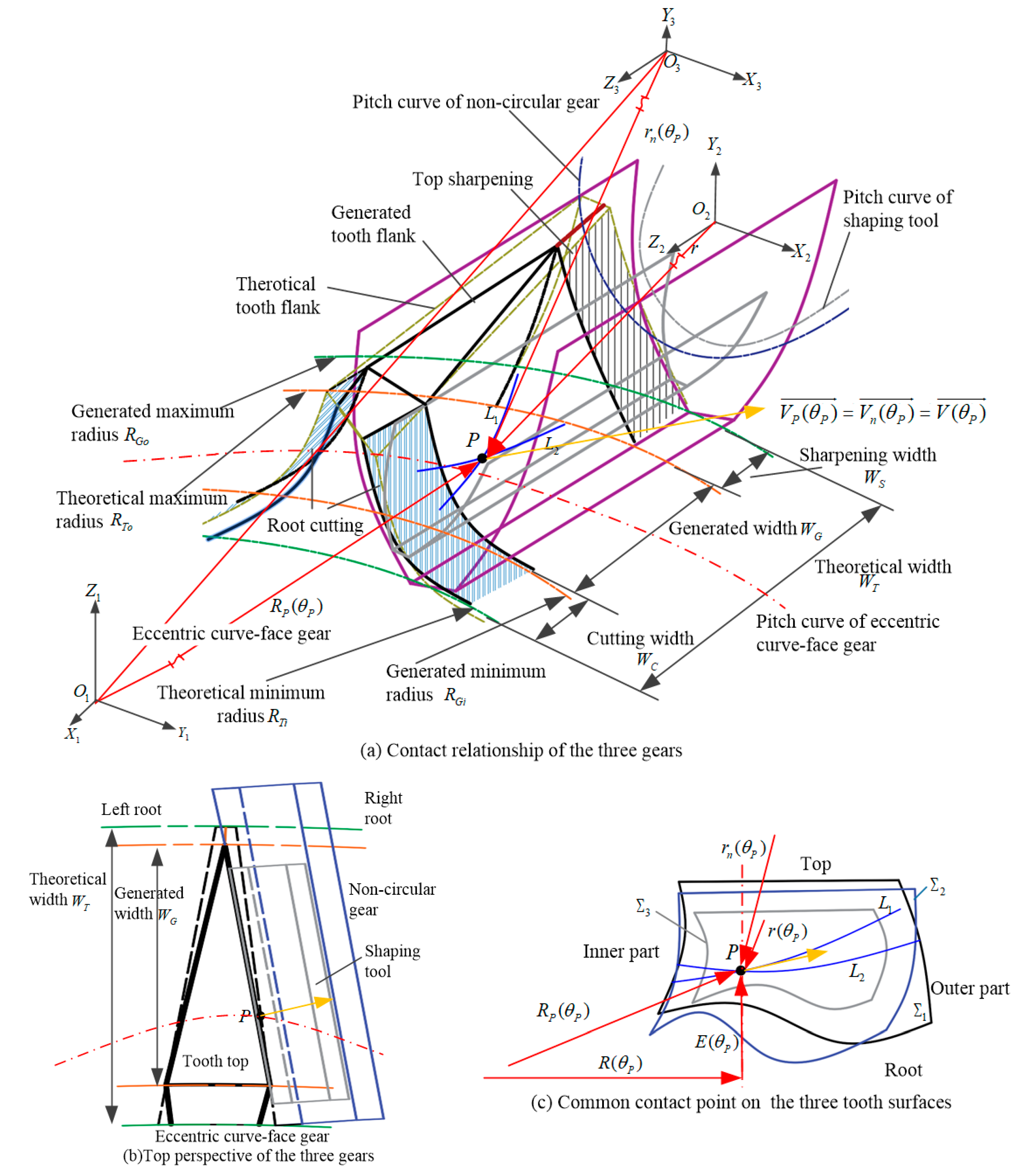
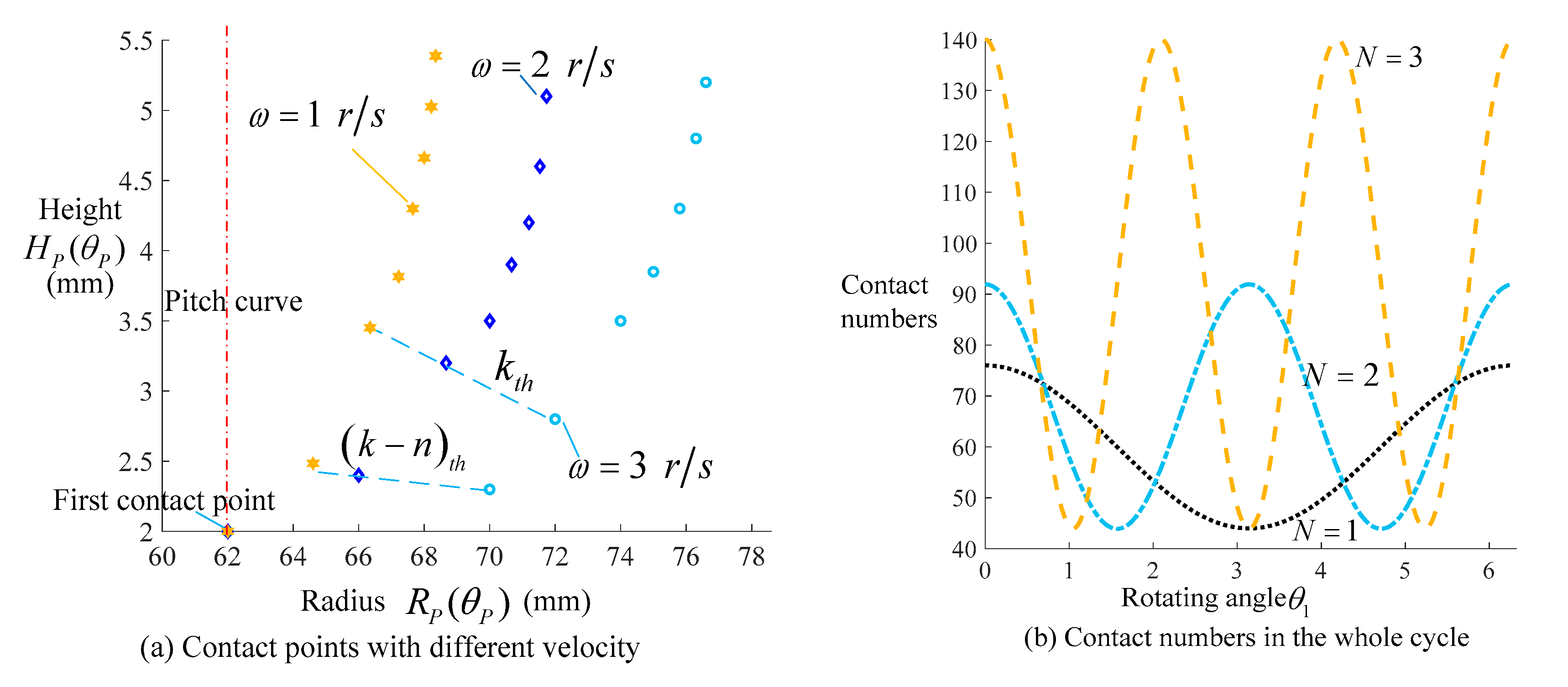
2.2. Effective Surface with Eccentric Pitch Curve
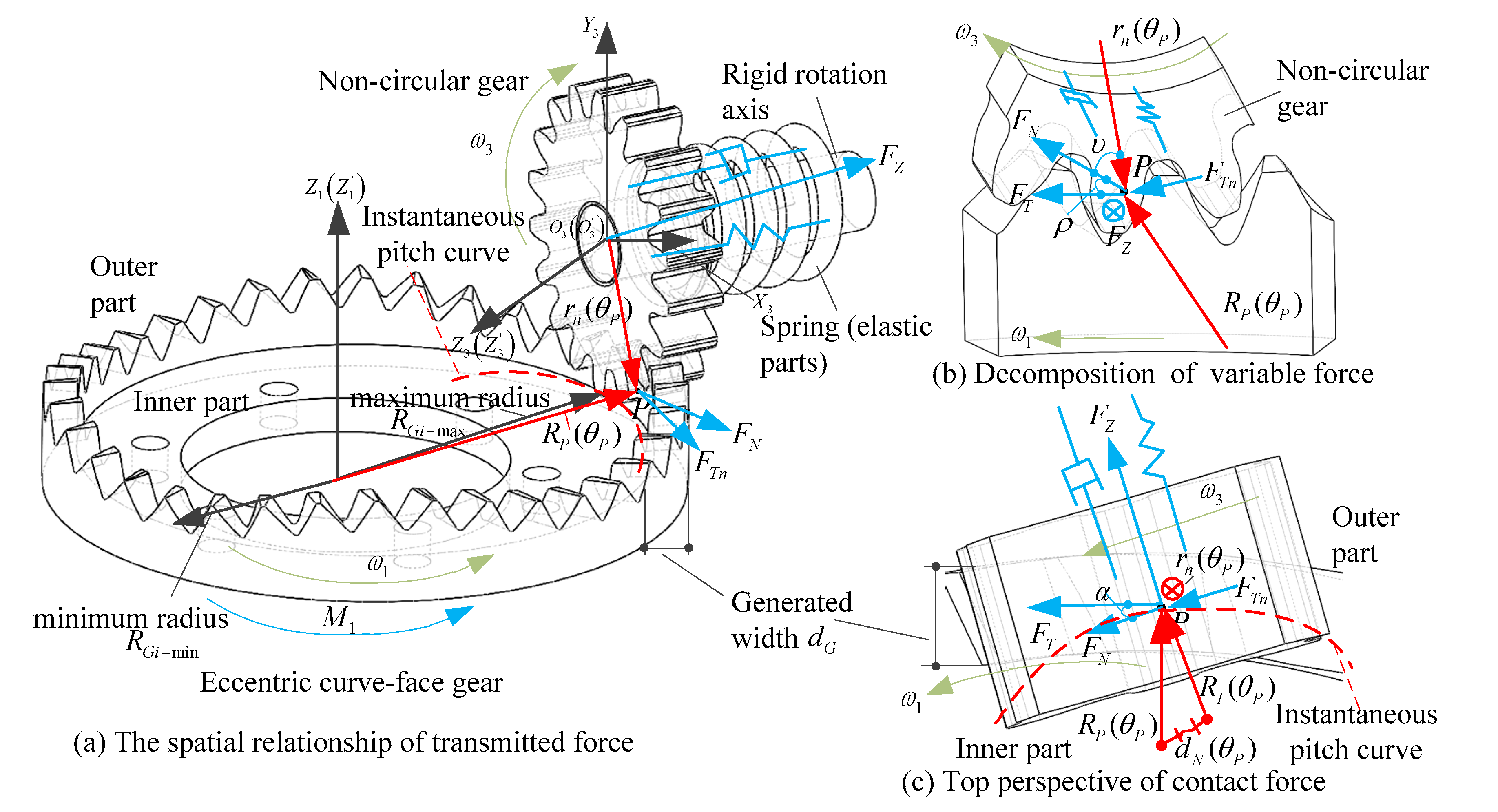
3. Kinematic Characteristics of Rigid–Flexible Coupling Gear System
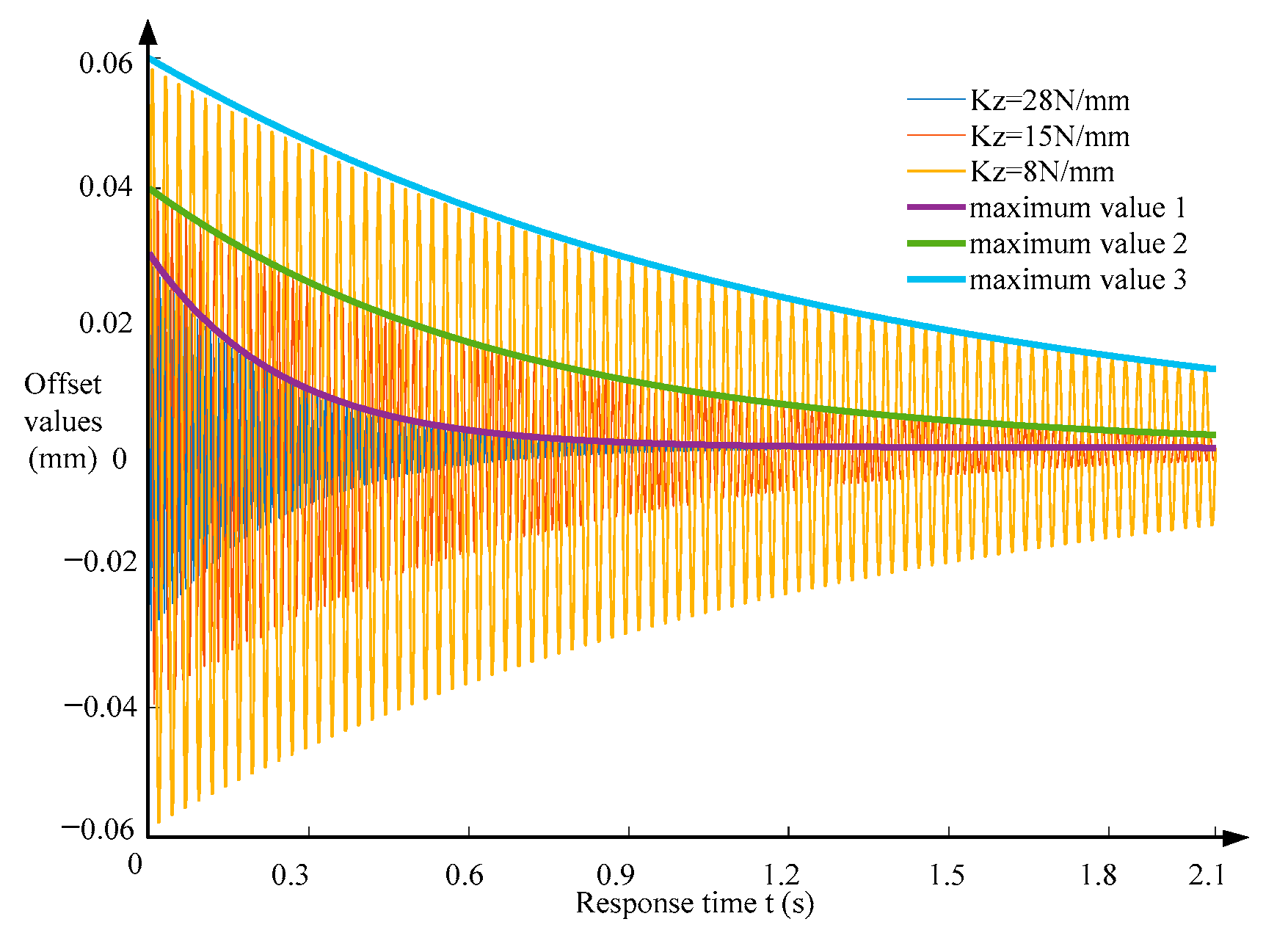
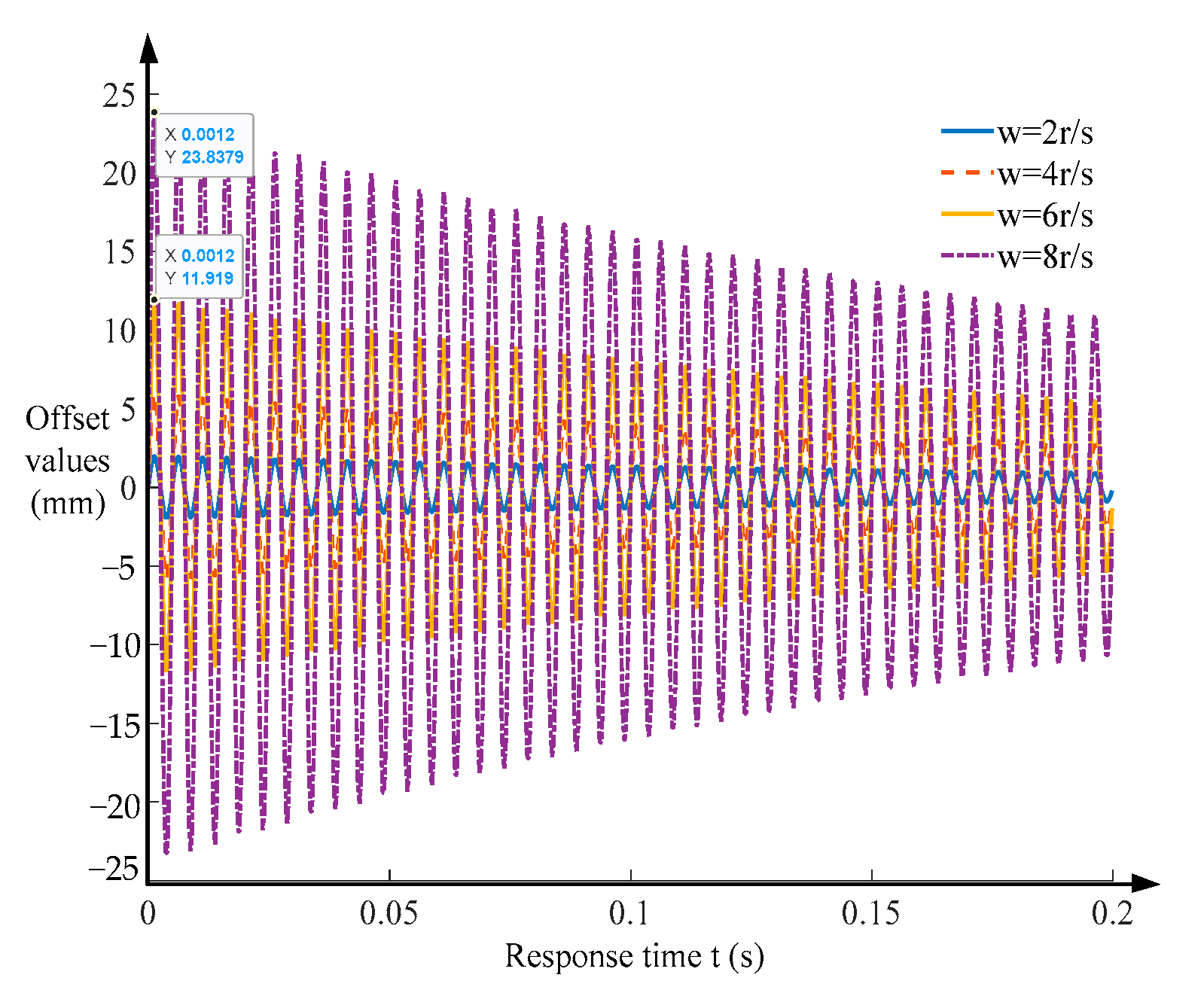
3.1. Response Equation of Rigid–Flexible Coupling System
3.2. Interval-Separated Transmission Characteristics
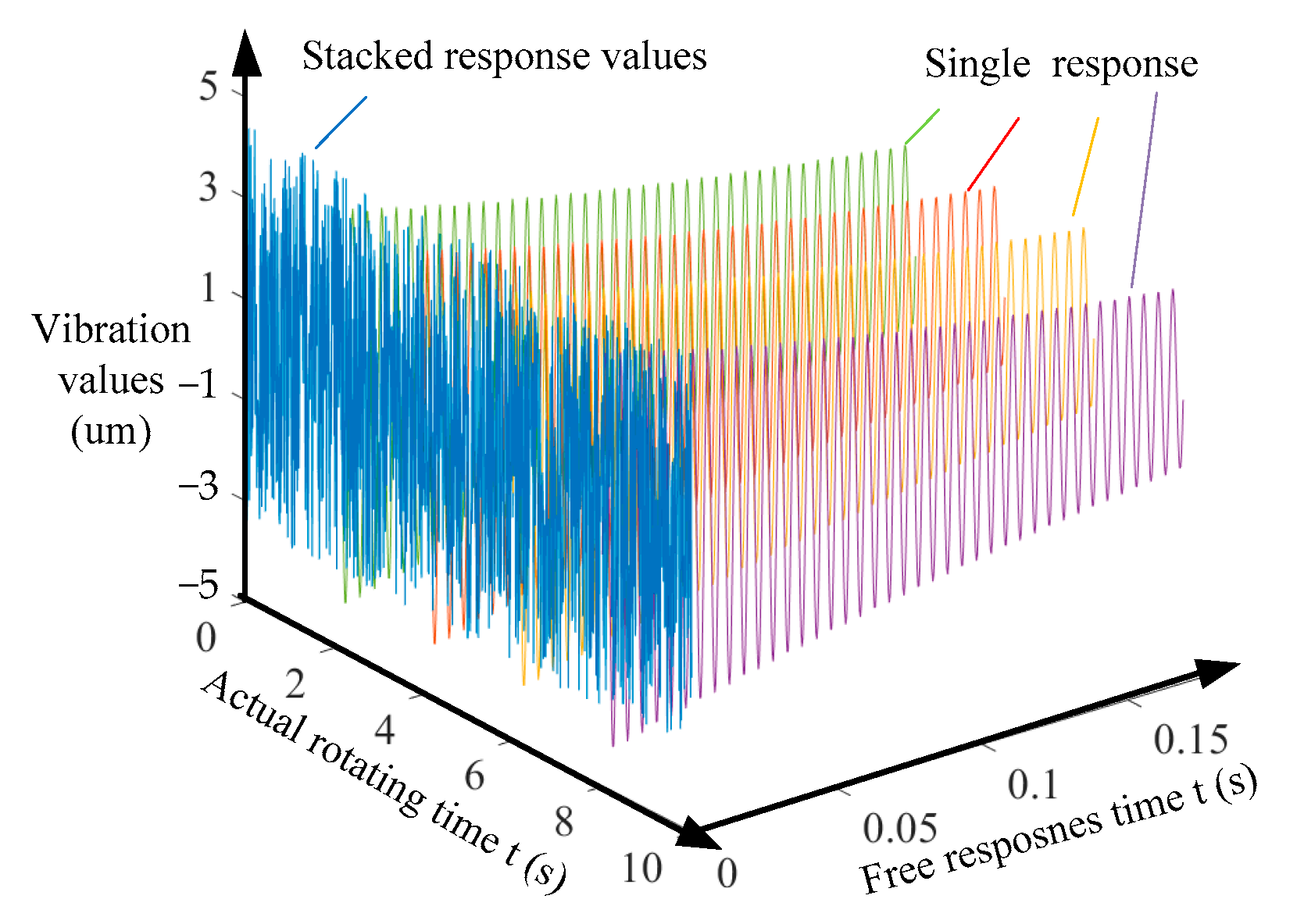
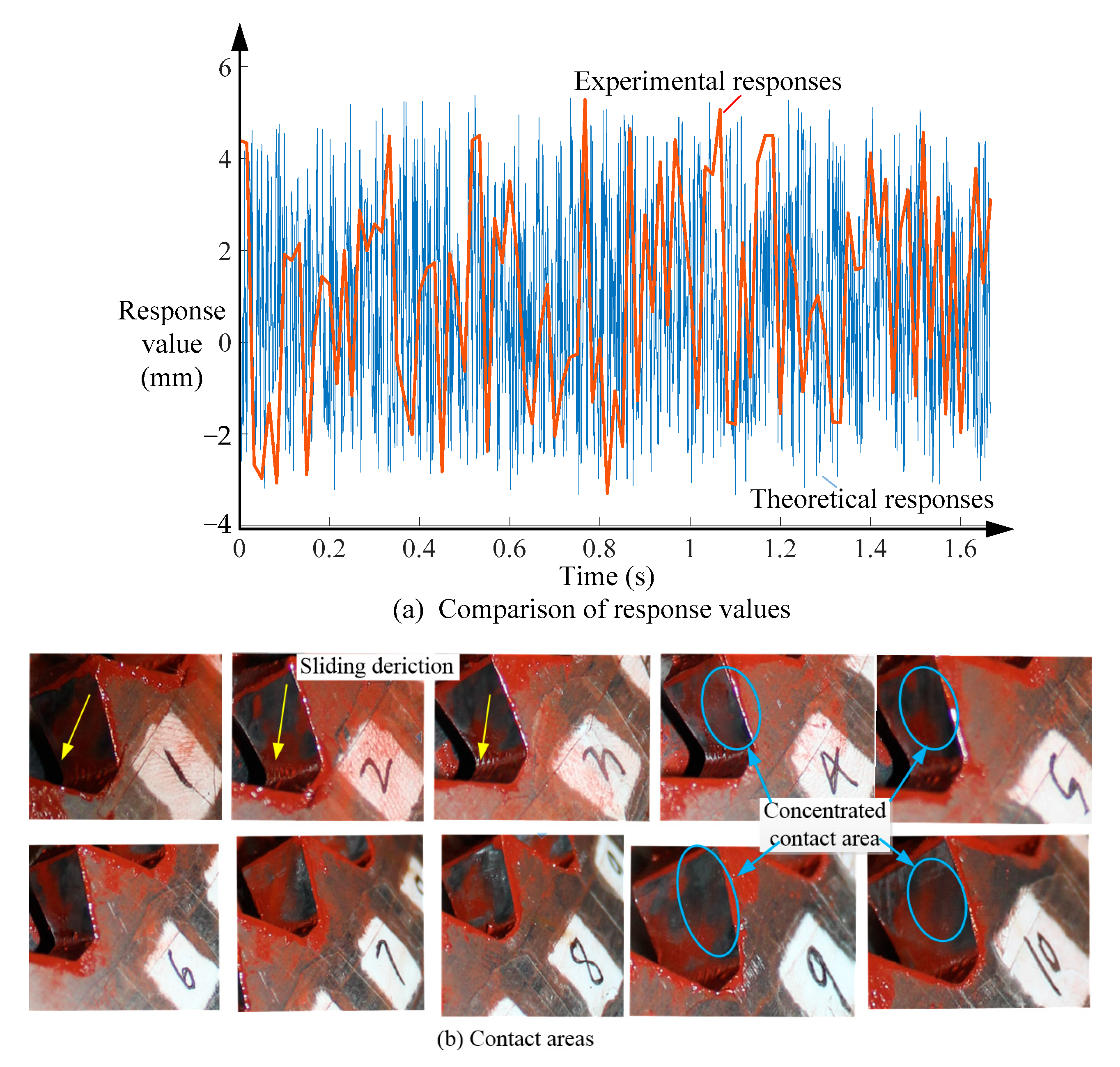
4. Experiments
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nirala, A.; Kumar, N.; Singh, D.B.; Singh, A.K.; Sharma, S.K.; Yadav, J.K.; Prasad, H.; Chandan, S.; Shrivastava, A.K. Simulation analysis of composite helical spring for compression, torsional and transverse mode. Mater. Today-Proc. 2020, 28, 2263–2267. [Google Scholar] [CrossRef]
- Michalczyk, K. Natural transverse vibrations of helical springs in sections covered with elastic coatings. Bull. Pol. Acad. Sci.-Tech. Sci. 2018, 65, 949–959. [Google Scholar] [CrossRef]
- Gu, Z.W.; Hou, X.N.; Ye, J.Q. Design and analysis method of nonlinear helical springs using a combining technique: Finite element analysis, constrained Latin hypercube sampling and genetic programming. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2021, 235, 5917–5930. [Google Scholar] [CrossRef]
- Yang, C.J.; Zhang, W.H.; Ren, G.X.; Liu, X.Y. Modeling and dynamics analysis of helical spring under compression using a curved beam element with consideration on contact between its coils. Meccanica 2014, 49, 907–917. [Google Scholar] [CrossRef]
- Hamza, A.; Ayadi, S.; Hadj-Taieb, E. Propagation of strain waves in cylindrical helical springs. J. Vib. Control 2015, 21, 1914–1929. [Google Scholar] [CrossRef]
- Renno, J.M.; Mace, B.R. Vibration modelling of helical springs with non-uniform ends. J. Sound Vib. 2012, 331, 2809–2823. [Google Scholar] [CrossRef]
- Zhou, C.J.; Hu, B.; Chen, S.Y.; He, L.P. An enhanced flexible dynamic model and experimental verification for a valve train with clearance and multi-directional deformations. J. Sound Vib. 2017, 410, 249–268. [Google Scholar] [CrossRef]
- Pawar, H.B.; Desale, D.D. Optimization of Three Wheeler Front Suspension Coil Spring. Procedia Manuf. 2018, 20, 428–433. [Google Scholar] [CrossRef]
- Gu, Z.W.; Hou, X.N.; Keating, E.; Ye, J.Q. Non-linear finite element model for dynamic analysis of high-speed valve train and coil collisions. Int. J. Mech. Sci. 2020, 173, 105476. [Google Scholar] [CrossRef]
- Baran, R.; Michalczyk, K.; Warzecha, M. Experimental Analysis of Transverse Distribution Stiffness of Helical Compression Springs. Acta Mech. Autom. 2023, 17, 95–103. [Google Scholar] [CrossRef]
- Lin, C.; Liu, Y. Characteristic analysis and application of composite motion curve-face gear pair. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1797–1804. [Google Scholar] [CrossRef]
- Lin, C.; Liu, Y.; Gu, S.J. Analysis of nonlinear twisting vibration characteristics of orthogonal curve-face gear drive. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 1499–1505. [Google Scholar] [CrossRef]
- He, C.J.; Lin, C. Analysis of loaded characteristics of helical curve-face gear. Mech. Mach. Theory 2017, 115, 267–282. [Google Scholar] [CrossRef]
- Liu, D.W.; Ren, T.Z.; Jin, X. Geometrical model and tooth analysis of undulating face gear. Mech. Mach. Theory 2015, 86, 140–155. [Google Scholar] [CrossRef]
- Temirkhan, M.; Bin, T.H.; Spitas, V.; Spitas, C. Parametric design of straight bevel gears based on a new tooth contact analysis model. Arch. Appl. Mech. 2023, 93, 4181–4196. [Google Scholar] [CrossRef]
- Temirkhan, M.; Spitas, C.; Wei, D.M. A computationally robust solution to the contact problem of two rotating gear surfaces in space. Meccanica 2023, 58, 2455–2466. [Google Scholar] [CrossRef]
- Shaabidov, S.A.; Irgashev, B.A. Computational Procedure of a Gearing Module of Spur Gear Transmissions on Wear Resistance of Gearwheel Teeth. J. Frict. Wear 2019, 40, 431–436. [Google Scholar] [CrossRef]
- Xiao, Z.M.; Cao, J.X.; Yu, Y.X. Mathematical Modeling and Dynamic Analysis of Planetary Gears System with Time-Varying Parameters. Math. Probl. Eng. 2020, 2020, 3185624. Available online: https://www.hindawi.com/journals/mpe/2020/3185624/ (accessed on 16 March 2020). [CrossRef]
- Jasem, M.A.; Krauinsh, P.Y. Introduction of a wave face kinematic reducer in pumping technologies for the extraction of high-viscous oil in extreme conditions. Bull. Tomsk. Polytech. Univ.-Geo Assets Eng. 2022, 333, 45–53. [Google Scholar]
- Xie, C.Y.; Yu, W. Gear dynamic modelling based on the concept of dynamic mesh stiffness: Theoretical study and experimental verification. J. Mech. Sci. Technol. 2022, 36, 4953–4965. [Google Scholar] [CrossRef]
- Wang, Q.B.; Ma, H.B.; Kong, X.G. A distributed dynamic mesh model of a helical gear pair with tooth profile errors. J. Central South Univ. 2018, 25, 287–303. [Google Scholar] [CrossRef]
- Wang, Z.G.; Lo, C.C.; Chen, Y.C. Comparison and Verification of Dynamic Simulations and Experiments for a Modified Spur Gear Pair. Machines 2022, 10, 191. [Google Scholar] [CrossRef]
- He, Z.Y.; Lin, T.J.; Chen, C.J. Mathematical models and dynamic contact analysis of involute/noninvolute beveloid gears. J. Vibroeng. 2014, 16, 2946–2961. [Google Scholar]
- He, X.Z.; Zhou, X.Q.; Xue, Z.; Hou, Y.X.; Liu, Q.; Wang, R.Q. Effects of gear eccentricity on time-varying mesh stiffness and dynamic behavior of a two-stage gear system. J. Mech. Sci. Technol. 2019, 33, 1019–1032. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.Y.; Li, H.G.; Wu, S.J. Nonlinear characteristics of gear pair considering fractal surface dynamic contact as internal excitation. Int. J. Non-Linear Mech. 2022, 143, 104027. [Google Scholar] [CrossRef]
- He, C.Y.; Chen, Z.G.; Zhai, W.M.; Jiang, J.Z.; Wang, K.Y. A spatial dynamics model for heavy-haul electric locomotives considering the dynamic coupling effect of gear transmissions. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2019, 233, 961–973. [Google Scholar] [CrossRef]
- Spitas, C.; Spitas, V. Coupled multi-DOF dynamic contact analysis model for the simulation of intermittent gear tooth contacts, impacts and rattling considering backlash and variable torque. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2016, 230, 1022–1047. [Google Scholar] [CrossRef]
- Marjanovic, N.; Ivkovic, B.; Blagojevic, M.; Stojanovic, B. Experimental determination of friction coefficient at gear drives. J. Balk. Tribol. Assoc. 2010, 16, 517–526. [Google Scholar]
- Litvin, F.L. Gear Geometry and Applied Theory, 2nd ed.; Cambridge University: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Lin, C.; Wu, X.Y. Calculation and Characteristic Analysis of Tooth Width of Eccentric Helical Curve-Face Gear. Iran. J. Sci. Technol.-Trans. Mech. Eng. 2019, 43, 781–797. [Google Scholar] [CrossRef]


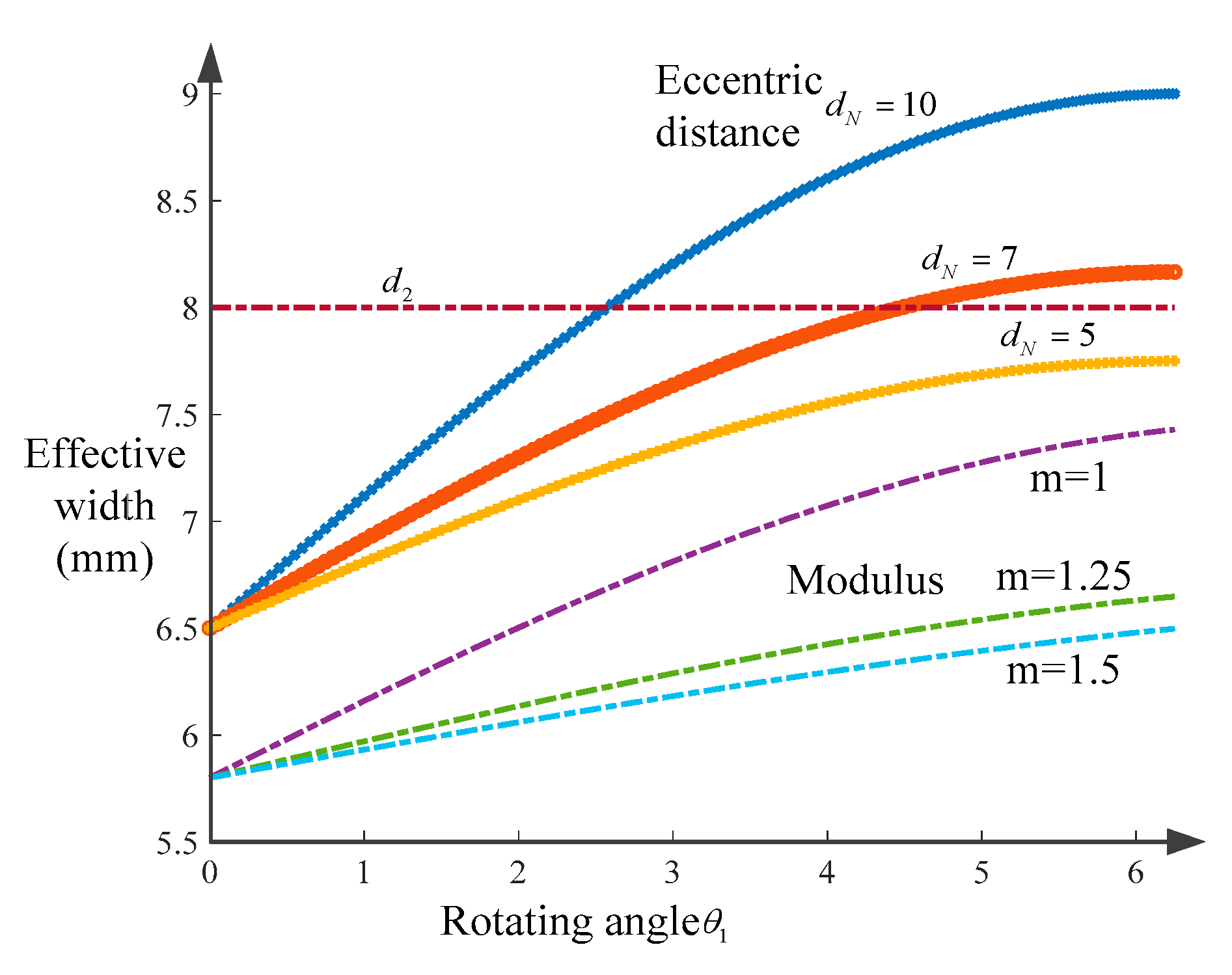



| Parameter | Range | Parameter | Range |
|---|---|---|---|
| (mm) | 70–72 | Eccentricity times | 1, 2, 3 |
| Width of eccentric curve-face gear (mm) | 8–20 | Eccentricity distance (mm) | 5–10 |
| Undulating times | 2, 3, 4 | Range of height (mm) | 6–12 |
| Tooth number of shaping tool | 18, 20, 22 | Modulus | 1, 1.25, 1.5 |
| Radius of shaping tool (mm) | 18–44 | Width of shaping tool (mm) | 8–20 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Minimum base radius (mm) | 60 | Eccentricity times | 1 |
| Undulating times | 4 | Eccentricity distance (mm) | 7 |
| Tooth number of shaping tool | 18 | Range of height (mm) | 8 |
| Width of shaping tool (mm) | 20 | Modulus (mm) | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Zhang, J.; Lin, C. An Analysis of the Kinematical Characteristics of an Eccentric Curve-Face Gear Pair with Compound Motion. Machines 2024, 12, 162. https://doi.org/10.3390/machines12030162
He C, Zhang J, Lin C. An Analysis of the Kinematical Characteristics of an Eccentric Curve-Face Gear Pair with Compound Motion. Machines. 2024; 12(3):162. https://doi.org/10.3390/machines12030162
Chicago/Turabian StyleHe, Chunjiang, Jinxu Zhang, and Chao Lin. 2024. "An Analysis of the Kinematical Characteristics of an Eccentric Curve-Face Gear Pair with Compound Motion" Machines 12, no. 3: 162. https://doi.org/10.3390/machines12030162
APA StyleHe, C., Zhang, J., & Lin, C. (2024). An Analysis of the Kinematical Characteristics of an Eccentric Curve-Face Gear Pair with Compound Motion. Machines, 12(3), 162. https://doi.org/10.3390/machines12030162





