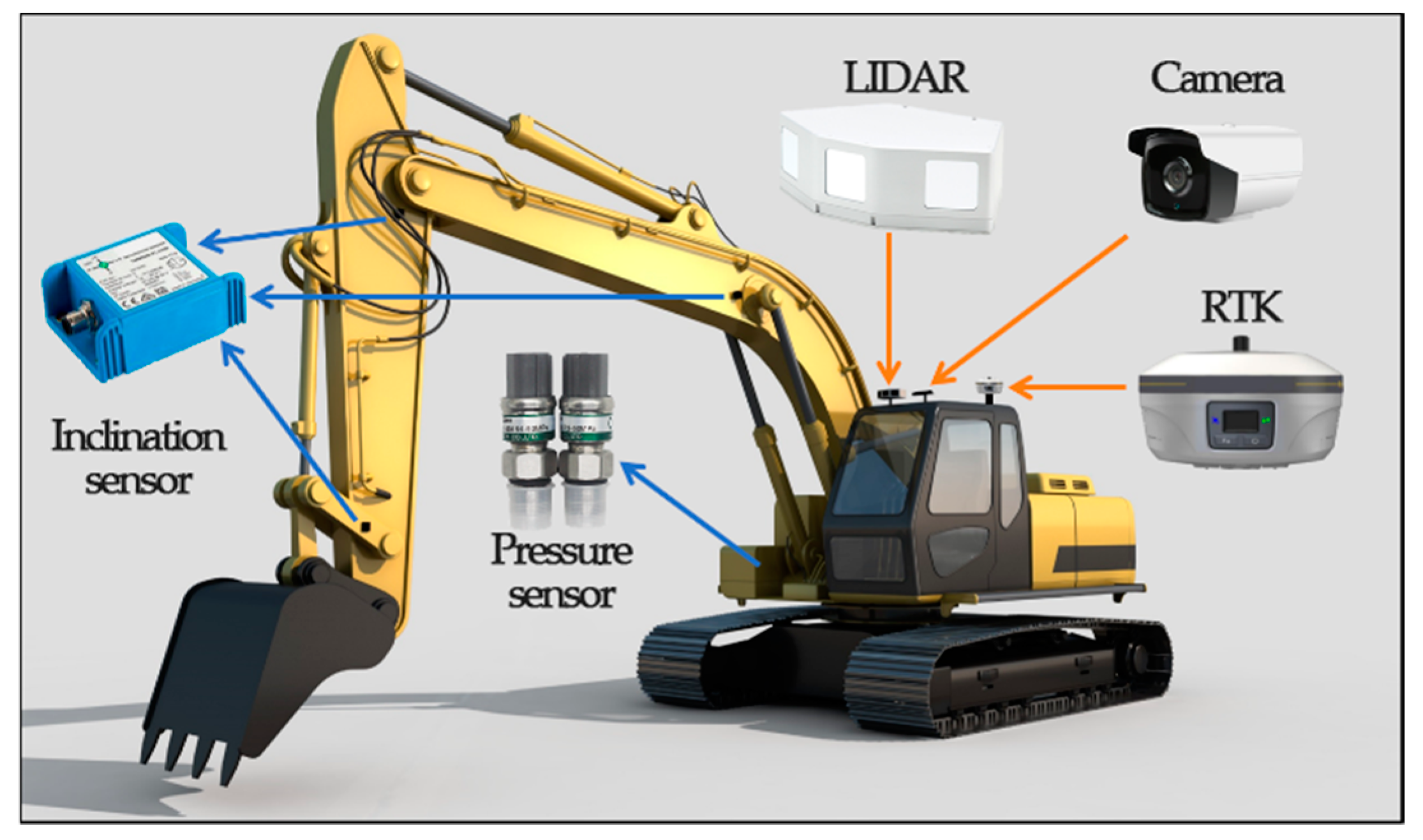
1. Introduction
In the field of excavators, unmanned excavators, as automated and intelligent tools, are gradually gaining widespread attention and application [
1,
2]. In recent years, China’s unmanned excavator industry has been developing rapidly, but due to the variety of different models and brands in the unmanned excavator market, professionals and decision makers in the field of excavators are unable to fully and objectively understand the various aspects of unmanned excavators to make an informed choice [
3,
4]. For example, decision makers are often unable to choose the right unmanned excavator for projects that require a large number of excavation operations or when operations need to be completed in a limited amount of time, resulting in inefficiencies and severe energy consumption. The comprehensive performance evaluation of unmanned excavators can help decision makers select the most suitable model for their needs [
5]. By considering different indicators and criteria, such as work efficiency, operation technology, energy consumption, etc., decision makers can select the most suitable unmanned excavator according to their specific needs to improve work efficiency and save costs [
6]. It also provides a scientific and objective evaluation framework for professionals, thus promoting the application and development of unmanned excavator technology and optimizing the performance and efficiency of unmanned excavators [
7]. Therefore, the comprehensive performance evaluation of unmanned excavators is of paramount importance.
Many scholars have made important contributions regarding the evaluation of the comprehensive performance of unmanned vehicles [
8,
9]. John M. Dolan [
10] proposed an evaluation framework based on perception, decision making, and control to comprehensively examine the integrated performance of unmanned vehicles in their research. They provide a powerful method for the performance evaluation of unmanned vehicles in different scenarios by deeply analyzing the performance of the sensor system, the effect of the decision-making algorithm, and the overall control performance of the vehicle. Jane Q. Public [
11] also focused on the safety and interaction performance of unmanned vehicles, proposing a series of quantitative and qualitative evaluation metrics to gain a comprehensive understanding of the performance of unmanned vehicles in their interactions with the environment and other traffic participants. The work of these scholars has laid a solid foundation for the development of the unmanned vehicle field and contributed to the continuous improvement of comprehensive performance evaluation methods [
12,
13]. However, there has been relatively limited research evaluating the comprehensive performance of unmanned construction machinery [
14,
15,
16]. As crucial equipment in engineering machinery, the application of unmanned excavators in the engineering field cannot be ignored. Therefore, a comprehensive evaluation of unmanned excavators is particularly urgent to gain a deeper understanding of their performance and potential advantages in engineering tasks, to provide strong support for the further development of the field.
The selection of appropriate methods for evaluating criteria helps professionals and decision makers to effectively assess and identify the best alternatives [
17,
18,
19]. Consideration of conflict factors becomes critical when applying criteria to select from a range of alternatives. An overview diagram of the unmanned excavator hardware system is shown in
Figure 1. The unmanned excavator system uses a variety of sensor fusion and sensing algorithms. The sensing module supports the unmanned operation of the unmanned excavator in different working conditions and harsh environments. It also ensures the operational efficiency, robustness, and generalization capability of the unmanned excavator system. The operation and motion planning module integrates data-driven learning algorithms and optimization algorithms, which can effectively calculate the digging position and the trajectory of the excavator bucket to ensure operation efficiency [
20,
21]. The high-precision motion control system effectively achieves precise motion control of each mechanism of the excavator. For example, two criteria used to select an unmanned excavator with good communication performance may be transmission distance and signal stability. These two criteria conflict with each other because increasing the transmission distance leads to a decrease in signal stability. Consequently, a multi-criteria strategy should be used to overcome this problem [
22,
23]. A multi-stage process is involved in multi-criteria decision making, which entails the following steps: (i) Defining the objective; (ii) Choosing the criteria to measure the objective; (iii) Defining the alternatives; (iv) Giving the criteria weights; (v) Using an appropriate mathematical algorithm to rank the alternatives [
24].
Numerous techniques have been put out in the literature and used to navigate a variety of multi-criteria decision making situations [
25]. The Technique of Order Preference Based on Similarity of Ideal Solutions (TOPSIS) was created in 1981 by Hwang [
26]. TOPSIS compares each choice with ideal and unacceptable solutions in order to determine which is the greatest option. But, the approach can fall short of capturing the complexity of uncertain settings [
27,
28]. In multi-criteria decision making, cluster analysis is a potent technique that groups similar alternatives according to their attributes or performance across various criteria. It is an unsupervised learning technique made to find naturally occurring clusters or groupings within a dataset without the requirement for any pre-established labels or desired results [
29]. It is crucial to remember that cluster analysis does not offer a clear ranking of options or information on preferences. Artificial neural networks (ANNs) have demonstrated potential and are being used as an effective tool for multi-criteria decision making [
30]. Note that adequate and pertinent data are frequently needed for the effective application of neural networks in multi-criteria decision making. The analytic hierarchy process (AHP) is a popular method for making decisions based on several variables and has been effectively utilized in break performance decision making scenarios. AHP was used by Hendre [
31] to assess the crucial characteristics of a novel brake pad material. The primary benefits of AHP are its ability to handle both qualitative and quantitative data effectively, cope with various criteria, and ease of comprehension. On the other hand, factor comparisons frequently entail some subjectivity and ambiguity [
32]. For instance, an expert can be aware that one aspect is more significant than another, but they might not be able to offer a precise scale for the comparison because they are unsure of the significance of each factor. The presence of imprecise or insufficient comparisons necessitates the abandonment of the traditional AHP technique in this situation [
33]. The three primary techniques in use are the fuzzy composite judgment approach, the Monte Carlo method, and the current AHP. Intelligent algorithms based on neural network prediction and other techniques have become widely employed in risk assessment with the emergence of artificial intelligence networks [
34]. Measuring the effect of a particular risk factor on an unmanned excavator is challenging during its test period, when it is subject to interference from a variety of sources. Conventional approaches to risk assessment use quantitative studies that are sensitive to subjectivity and uncertainty and risk assessment scoring procedures that depend on human subjectivity [
35]. The neural network risk assessment approach has high requirements for the robustness and stability of the algorithm, and while it can reduce the impact of subjectivity to some extent, it still requires a significant number of training samples [
36]. A proper evaluation analysis approach is, therefore, required. The fuzzy analytic hierarchy process (FAHP), which was first presented by Laarhoven and Pedrycz, is a potent technique for handling ambiguity in decision-making situations where the available data is lacking or unclear [
37]. FAHP considers the interdependencies among the criteria and assists in identifying the impact of modifying one criterion based on the other criteria. This characteristic facilitates a deeper analysis of the decision problem and clarifies the causal connections among the criteria [
38]. Numerous domains have employed it, such as artificial intelligence, control engineering, management science, and multi-criteria decision making.
However, the evaluation findings cannot be seen using the aforementioned methods, the significance of each element is not explained in detail, and ranking the results for several objects with comparable complete performance is challenging [
39]. A multivariate comprehensive evaluation and analysis method is the radar chart method. In order to more fully portray the assessment item’s comprehensive strength, it might take into account not only the overall benefits of the object but also the coordinated development of all areas [
40]. The radar chart’s ability to graphically represent the state of the object under evaluation is its most crucial attribute. Nonetheless, the arrangement of each indicator determines the form of the radar chart, resulting in evaluation outcomes that are not distinct [
41]. Furthermore, the radar chart’s angles, which represent the indices’ weights, are equal, meaning they do not accurately depict the degree to which the indices used to assess the particular object had an impact [
42]. As a result, this study suggests a technique that integrates multivariate picture area analysis with the fuzzy analytic hierarchy process, integrating indicator weights and values for qualitative assessment.
The study uses a combination of fuzzy analytic hierarchy process and multivariate image area analysis in order to obtain a more effective comprehensive performance evaluation of unmanned excavators. For this purpose, evaluation indexes are extracted based on signal stability. Five main criteria and fifteen sub-criteria are proposed to construct the hierarchy of performance evaluation based on two main aspects of unmanned excavators. And, three types of unmanned excavators were evaluated. Performance tests were conducted on three types of unmanned excavators to obtain the evaluation value sets of the corresponding criteria. Then, the fuzzy analytic hierarchy process was applied to calculate the weights of the evaluation criteria; imprecise decision makers’ judgments were expressed as fuzzy numbers instead of precise values. In addition, multivariate image area analysis is used to analyze each performance index of unmanned excavators and compare the performance indexes of different models of unmanned excavators. This study further provides a scientific basis for the optimal design and improvement of unmanned excavators and provides a reference for future research in this field.
The study is organized as follows:
Section 2 describes the establishment of a comprehensive evaluation index system based on signal stability extraction for unmanned excavators. In
Section 3, the content and process of the evaluation method are described. In
Section 4, the proposed method is illustrated using case studies of three unmanned excavators. In
Section 5, the main conclusions, limitations, and future work are summarized.
2. Establishing the Comprehensive Evaluation Index System
The evaluation of unmanned excavators is mainly oriented towards ontology and phenomenology. The comprehensive performance of the unmanned excavator is completed by evaluating the comprehensive performance of the excavator. The test of the unmanned excavator is the main way to realize the scientific and fair evaluation of the key technology research level of the unmanned excavator. With the proposal and development of the concept of a mechatronic excavator, the intelligent construction technology of unmanned excavators has also been developed rapidly. The development of intelligent construction technology and wireless communication technology provides a platform for the development of automatic control technology of unmanned excavators, and robotization and intelligence become the focus of future research in the field of excavator control. The following is mainly from excavator intelligent construction technology and excavator wireless communication technology for unmanned excavator evaluation index research.
2.1. Intelligent Technology
The data analysis capabilities of the intelligent technology of unmanned excavators are realized by combining sensors, cameras, lidars, and other devices, as well as machine learning algorithms. These technologies allow excavators to capture large amounts of data and turn it into useful information. The data analysis process includes data collection, processing, and interpretation, using machine learning algorithms to identify patterns, anomalies, and risks and make intelligent work decisions.
Specifically,
Figure 2 shows a schematic diagram of the intelligent construction topology of the unmanned excavator. The intelligent construction technology of the unmanned excavator integrates advanced 3D terrain scanning, automatic elevation angle adjustment, real-time construction monitoring and analysis, and the ability to work in collaboration with autonomous transport vehicles. These technologies enable excavators to accurately perform excavation, loading, and transportation tasks, optimize construction processes, and improve operational efficiency, while reducing manpower requirements and operational risks, providing an efficient, safe, and environmentally resilient solution for modern engineering and construction.
2.2. Wireless Communication Technology
Wireless communication technology plays a vital role in optimizing workflows, increasing efficiency, and reducing costs.
Figure 3 shows the overall communication scheme. It covers five objects, including the mining process operation site, the cloud platform, the company’s service center and the user, and the operation equipment uploads the relevant parameters to the cloud platform through the base station network. The cloud platform calculates and stores the model, displays the data on the monitoring screen of the operating equipment, and transmits it to the user and the company’s internal platform at the same time to achieve a full range of management functions.
The wireless communication system of the unmanned excavator usually adopts radio frequency communication technology, such as Wi-Fi, Bluetooth, LTE, etc., and its transmission distance can reach hundreds of meters to thousands of meters, depending on the communication technology and equipment power. To ensure the stability of data transmission and reception, optimized antenna design, signal processing techniques, and measures to avoid signal interference, such as frequency hopping techniques and signal encryption, are employed.
Unmanned excavators require low-latency and interference-resistant communication in applications to ensure real-time data transmission and accurate control. Communication technologies with high bandwidth and low latency are usually used, and a series of measures are taken to improve immunity, such as frequency spread spectrum, signal coding, and multi-antenna technology. At home and abroad, Komatsu’s KOMTRAX system, JCB Construction Machinery Company’s GlobalT-RACS system, the Tianyuan Group, the Shenyang Institute of Automation, the Chinese Academy of Sciences, the Shanghai Jiao Tong University, and other units developed construction machinery wireless communication systems, all providing reliable solutions for remote management and information exchange of construction machinery
2.3. Evaluation Index System Establishment
The evaluation of an unmanned excavator is a multi-level comprehensive evaluation problem, which should be divided into different evaluation levels according to the complexity of each key technical decision of an unmanned excavator. As the evaluation indexes are more complicated, according to the principle of comprehensiveness, the initial selection of indexes allows the existence of difficult-to-operate indexes and only seeks the whole rather than the best and then gradually optimizes them in the process of further analysis. For the comprehensive evaluation of such a complex nonlinear system as an unmanned excavator, the core indexes are used as the network output, and other indexes are used as the network input to establish a forward neural network model, through which the correlation between the inputs and outputs is portrayed, to reasonably select the required index variables and exclude the unreasonable index variables. As the technology is constantly developing, an evaluation level that can scientifically, objectively, and as comprehensively as possible reflect the target characteristics of the object should be determined using the idea of hierarchical evaluation; consequently, the unmanned excavator evaluation index system and the recursive hierarchical relationship are established.
The hierarchical analysis structure is shown in
Figure 4. This evaluation system is a performance evaluation system for unmanned excavators, which includes two main parts: mechanical characteristics and intelligent characteristics. Each part is equipped with a goal level, a criterion level, and an index level to facilitate a comprehensive performance evaluation of the driverless excavator.
The indicators in the comprehensive evaluation system of unmanned excavators are crucial for the evaluation of unmanned excavators, because they cover the key performance requirements that excavators need to meet in actual operations. In terms of mechanical characteristics, the maximum digging force refers to the maximum force that the unmanned excavator can exert during excavation operations, which directly affects the excavator’s operating efficiency and ability to adapt to different soil qualities. Maximum digging depth refers to the maximum digging depth that an unmanned excavator can achieve, which determines its applicability in a specific project. The maximum speed reflects the maximum moving speed of the excavator on flat ground, which affects the operation efficiency and the convenience of transferring the site. Operational precision refers to the ability of an excavator to perform precise tasks, such as precise positioning and digging. This is essential for engineering projects that require high-precision operations. Load sensing capability refers to the excavator’s ability to perceive the weight of the load, which is important to ensure the safety and efficiency of the operation. Automated movement control capability refers to the ability of an excavator to move autonomously without human intervention, which helps to improve the level of automation of operations. Among the intelligent features, obstacle detection accuracy reflects the excavator’s detection accuracy of surrounding obstacles, which is important for avoiding collisions and ensuring work safety. Terrain sensing capability reflects the excavator’s ability to perceive the terrain, which helps the excavator adapt to different terrain conditions. Weather condition sensing refers to the excavator’s ability to perceive changes in the weather, which is important for maintaining operational safety and efficiency in adverse weather conditions. Single machine intelligent operation capability refers to the intelligent operation capability of the excavator as an independent unit, including autonomous navigation and operation. Machine group intelligent construction capability refers to the ability of multiple unmanned excavators to work together, which is essential for the efficiency and coordination of large-scale engineering projects. Data analysis capacity refers to the ability of an excavator to collect and analyze data, which helps to optimize work processes and improve decision-making efficiency. Transmission distance refers to the maximum distance between the unmanned excavator and its communication equipment to maintain effective communication. The transmission distance directly affects the operating range and flexibility of the unmanned excavator, which is especially important for the unmanned excavator operating in a wide or remote area. The transmission distance refers to the maximum range that can achieve effective communication between the unmanned excavator and the control center. It determines how far away the excavator can operate and is essential for the expansion of the operating area and operational flexibility. Signal stability reflects the reliability of the communication connection. It plays a decisive role in ensuring that the unmanned excavator receives accurate operation instructions and real-time data feedback, which directly affects the continuity and safety of the operation. The delay and anti-interference ability jointly determine the response speed of the unmanned excavator to the operation command and the communication reliability in complex environments. This has a significant impact on improving operational efficiency, avoiding potential risks, and achieving precise control.
These indicators together constitute a comprehensive evaluation system of unmanned excavators, which not only reflect the basic performance of excavators but also cover the level of intelligence and automation. Through the comprehensive evaluation of these indicators, the performance of the unmanned excavator can be fully understood, so as to provide a basis for engineering selection, operation optimization, and technology research and development.
3. Study on the Comprehensive Evaluation Method of Unmanned Excavators
3.1. Fuzzy Analytic Hierarchy Process
The fuzzy analytic hierarchy process is a multi-criteria decision-making method for decision making and evaluation of complex problems. It is a method that combines the analytic hierarchy process with fuzzy theory. In the fuzzy analytic hierarchy process, the problem is also decomposed into a hierarchy including objective, criterion, and index levels. Each level can have multiple factors or criteria, forming a tree structure. The objective layer represents the final goal of the decision, the criterion level is the criteria for evaluating the program, and the index level contains the evaluation indexes. The fuzzy analytic hierarchy process introduces fuzzy numbers and fuzzy language to describe the decision maker’s evaluation of uncertainty and ambiguity. Through the weighting calculation of fuzzy numbers and consistency tests, the weights or scores of each scheme are finally determined. Experts need to make judgments based on their expertise and compare each factor in pairs in the corresponding parts of the structure in the hierarchy. These experts’ preferences are then converted into a fuzzy numerical evaluation matrix. De-fuzzification is used to convert the fuzzy scales into clear scales and priority weights are calculated. The basic steps are as follows:
Analyze the relationship between the factors in the system and construct a hierarchical structure model, as shown in
Figure 4;
Derive the two factors’ comparison affiliation degree and construct fuzzy comparison matrix A. The fuzzy scale table and its meaning are shown in
Table 1;
- 3.
Let
be an object set and
be a goal set. According to the method of Chang’s extent analysis [
43], each object is taken and extent analysis for each goal is performed, respectively. Therefore, m extent analysis values for each object can be obtained using the following signs:
In Equation (1), all the
values are triangular fuzzy numbers expressed as a triple
. Here
and
are the mean, the lower, and the upper bounds, respectively. A fuzzy set is defined by its membership function as shown in Equation (2):
The procedure of FAHP is described as follows:
Perform extent analysis for each goal, respectively. The fuzzy synthetic extent concerning an object is defined as shown in Equation (3):
Evaluate the degree of possibility for
, fuzzily restricted to belong to
M, to be greater than
fuzzily restricted to belong to
M. The degree of possibility is defined as shown in Equation (4):
In addition, it can be equivalently expressed as shown in Equation (5):
where
d is the ordinate of the highest intersection point
D between
and
, as shown in
Figure 5. To compare
and
we need both the values of
and
.
Calculate the priority weights of the criteria. The degree of possibility for a convex fuzzy number to be greater than the
k convex fuzzy number
can be defined using Equation (6):
Assume that Equation (7) holds
For
. Then, the weight vector is given by
In Equation (8), are n elements.
The normalized weight vector is calculated as
In Equation (9),
is a non-fuzzy vector.
In Equation (10), n is the order of the fuzzy matrix R, .
If
is scaled according to
Table 1 and
is satisfied, then R is the fuzzy matrix. To ensure that the inconsistency of the fuzzy matrix is within the allowable range, the consistency test formula is given, as shown in Equation (11):
where
is the maximum eigenvalue of the pairwise comparison matrix, and RI is the random consistency index, which is related to n only, and can be found by looking up the table. At this time, the normalized eigenvector of
can be used as the weights
. As shown in Equation (12),
satisfies:
- 4.
Comprehensive scoring of unmanned excavator using multivariate image area analysis method.
3.2. Multivariate Image Area Analysis Method
According to the fuzzy analytic hierarchy process, the weights of each index in the index layer can be obtained, and these different weights are constructed on a radar chart. The specific evaluation score of the unmanned excavator is derived by calculating the area of the radar chart.
When calculating the evaluation score determined by using the area of the radar chart, there is no direct calculation method because the radar chart is an irregular graph. Therefore, this study adopts the method of dividing triangles to find the area and calculates the overall area through the combination of triangles. Because different factors are weighted differently in the evaluation, the decomposed triangle is not regular. In the calculation, regular triangles cannot be directly used for calculation but need to be converted into ordinary triangles for calculation. The area of the triangle is calculated to obtain the evaluation score represented by the area of the polygon by converting the polygon area calculations into the triangle area summation.
As can be seen from
Figure 6, the coordinate origin and any two vertices adjacent to the polygon form a triangle, and the area of the triangle can be obtained by cross-multiplying the two plane vectors formed by the three vertices. Then, the formula for the area of the polygon is shown in Equation (13).
where Ω is an n-edge polygon with vertices
aligned positively along the boundary. The coordinates are in order:
.
S creates a vector diagram of the area of the polygon of Ω. From
Figure 6, it can be seen that the coordinate origin and any two adjacent vertices of the polygon form a triangle, and the area of the triangle can be obtained from the outer product of the two plane vectors formed by the three vertices.
Adding up the triangle areas gives the area of the polygon. Through this calculation formula, the evaluation score of the unmanned excavator performance evaluation system based on fuzzy comprehensive hierarchical analysis can be specified. A specific evaluation score can be obtained by calculating these different triangle areas, and the whole calculation process can be simplified by using MATLAB R2023a.
In the software, we use quantitative manipulation and functional programming to improve the efficiency and readability of the code. First, a fuzzy comparison matrix is defined to represent the relative importance of indicators at each level. Use the FAHP function to calculate the weight vector for each level. Then, set the parameters of the radar chart and input the weights and polar points of each indicator that have been calculated before. The angle and radius of each primary edge are repeated through vectorization operations to construct a complete polar point. The area of the triangle on each primary edge is calculated by looping through each primary edge and weighted according to the corresponding weights. Finally, the weighted areas of all triangles are added to obtain the total area of the radar chart, and the results are displayed.
Figure 7 illustrates the comprehensive evaluation process. This flowchart details the process of building an evaluation model using the fuzzy analytic hierarchy process. Firstly, a multi-level decision-making structure is constructed, including the criterion layer, the scheme layer, and the sub-criterion layer. Emphasize the importance of experts in the parameter assignment; they assign parameter values based on expertise and experience. The relative importance of factors is determined by establishing a priority relationship matrix, and the uncertainty is dealt with by converting it into a fuzzy uniform matrix. The local importance weights of each factor are calculated and integrated into the overall goal to align the weights. It is recommended to draw a radar chart to visually display the weights and use multivariate image area analysis to quantify the evaluation results. The final evaluation results are usually calculated with the help of professional calculation tools and MATLAB programming programs, and comprehensive evaluation results are obtained to support decision making.
4. Application Analysis of Comprehensive Performance Evaluation of Unmanned Excavators
The Komatsu PC210LCi-11 is a technologically advanced unmanned excavator with automation capabilities, intelligent controls, and efficient performance designed to improve the efficiency and quality of earthmoving and excavation operations. The manufacturer of Komatsu PC210LCi-11 is Komatsu Corporation, which is headquartered in Japan with the city of Tokyo and the country of Japan. As shown in
Figure 8a. In terms of automation capabilities, the PC210LCi-11 utilizes Komatsu’s iMC (intelligent machine control) technology, which allows for highly automated excavation operations. This technology allows the excavator to sense and control digging depth, slope gradient, and bucket position in real-time, without the need for manual operator intervention. This lowers errors while simultaneously increasing building efficiency. Regarding intelligent control, this excavator has a system in place that automatically modifies work parameters based on the demands of the excavation task. Digging efficiency is increased as a result of optimizing bucket bar action to maintain the ideal working posture during the procedure. Regarding environmental awareness, the PC210LCi-11 has several sensors, such as inertial navigation systems, GPS, and LIDAR. The excavator can sense its surroundings in real-time, including the working surface’s condition, impediments, and topography, thanks to these sensors. This enables the excavator to operate precisely in difficult terrain, reduces the risk of crashes, and increases worker safety. When it comes to effective operation, this excavator has a strong diesel engine that delivers exceptional power performance to handle a range of excavation work situations. It is capable of trench digging, soil excavation, and other civil engineering duties with efficiency. Regarding wireless connectivity, the PC210LCi-11 is additionally outfitted with a feature that enables remote connection monitoring and control. Real-time access to the excavator’s status allows the operator to keep an eye on the work’s progress and take remote action as needed.
Through automation, intelligent control, and environmentally conscious technology, the Komatsu PC210LCi-11 unmanned excavator offers efficient, accurate, and safe digging capabilities for a variety of earthmoving and construction operations. This cutting-edge technology contributes to lower construction costs, fewer mistakes, increased productivity, and more environmentally friendly building solutions.
With a high level of automation, environmental awareness, and wireless communication capabilities, the LIUGONG 922F unmanned excavator is a versatile tool for a range of construction and earthmoving applications. The manufacturer of LIUGONG 922F is Liugong Group, it is headquartered in China, the city is Liuzhou, and the country is China. As shown in
Figure 8b, it facilitates the completion of jobs in challenging situations, lowers risk, and increases construction efficiency. Regarding power performance, high-performance diesel engines with exceptional power performance often drive LIUGONG 922F unmanned excavators, enabling them to handle a variety of excavation operations. This guarantees the excavator’s ability to function well in a variety of engineering settings. Regarding load operation automation capability, LIUGONG’s in-house “i-LIUGONG” intelligent control technology, which boasts a high level of automation capability, is incorporated into the 922F. The excavating, loading, and unloading processes can be automatically controlled via the system. The excavator may enhance loading efficiency by modifying the position and attitude of the bucket bar in real-time, utilizing sophisticated sensors and intelligent control algorithms. Regarding environmental sensing, the LIUGONG 922F autonomous excavator has multiple sensors, including GPS, LIDAR, and cameras, that allow it to sense its surroundings in real-time. These sensors aid in obstacle avoidance, construction process safety, and increased accuracy in difficult-to-work-in terrain. Regarding intelligent capabilities, the 922F is capable of intelligent planning and path selection based on operational requirements thanks to LIUGONG’s intelligent control system. To increase construction efficiency and quality, the excavator can autonomously assess terrain data and automatically modify the digging method. Regarding wireless communication capability, the LIUGONG 922F unmanned excavator has a feature that enables remote monitoring and operation via a wireless connection. Through a cloud connection, the operator can remotely control and intervene in real-time by keeping an eye on the excavator’s status, location, and work progress.
The cutting-edge XCMG XE950DA unmanned excavator boasts superior performance and technological capabilities. The manufacturer of XCMG XE950DA is XCMG Group, headquartered in China, city is Xuzhou, and the country is China. As shown in
Figure 8c. In terms of power performance, the XCMG XE950DA unmanned excavator has a strong diesel engine that typically produces a lot of power, allowing it to perform exceptionally well in a variety of digging and earthmoving tasks. This makes it capable of handling various soil and rock kinds and completing a wide range of engineering tasks. Regarding load operation automation, the XE950DA makes use of XCMG’s proprietary intelligent control technology, which has a high level of automation capacity. To enhance the automation performance of loading and unloading, the system enables the excavator to sense the working environment and task needs in real-time and automatically modify the digging depth, bucket attitude, and other working factors. This lowers errors and boosts productivity. The XCMG XE950DA autonomous excavator has a range of sensors, including LIDAR, cameras, GPS, and other environmental awareness devices, as part of its environmental awareness capabilities. The excavator can perceive its surroundings in real time thanks to these sensors, which can identify changes in the terrain, obstructions, and working surfaces. This enhances worker safety, lessens the chance of collisions, and guarantees accurate excavation operations. When it comes to intelligent capabilities, the XE950DA has an intelligent control system that can evaluate and plan excavation jobs on its own, such as route planning and terrain data processing. To increase the productivity and quality of work, the excavator can autonomously modify its work plan based on the requirements of the digging operation. Regarding wireless communication, the excavator has wireless communication technology installed so that it may be remotely monitored and controlled. Operators can remotely monitor the excavator’s status, position, and work progress, as well as remotely operate and make adjustments, thus improving the efficiency of production management. The XCMG XE950DA unmanned excavator is a typical high-performance and advanced technology machine designed to improve construction efficiency, reduce risk, and provide highly automated and intelligent solutions for earthmoving and excavation tasks.
4.1. Establishing the Hierarchical Model
For the comprehensive evaluation of unmanned excavators, the hierarchical model used in this study is divided into three levels:
The first level represents the goal of the problem to be solved and is called the goal level, denoted as level . For the unmanned excavator comprehensive evaluation problem, the goal is to obtain the performance evaluation and intelligent evaluation of the unmanned excavator;
The second level represents the intermediate links involved in realizing the predetermined goal, which is called the criterion level, denoted as level . Based on the comprehensive evaluation index system of unmanned excavators constructed in the previous section, the evaluation of unmanned excavators is divided into five aspects: mechanical capability, load handling automation capability, environmental perception, intelligence capability, and wireless communication capability, as comprehensive evaluation criteria;
The third level represents multiple evaluation indexes established for each unmanned excavator criterion level, which is called the index level, denoted level
. According to the different focuses considered in each criterion, different sets of evaluation indexes are selected, as shown in
Figure 4.
4.2. Constructing the Fuzzy Matrix and Calculating the Weights
It is proposed to select unmanned excavator data as the premise of the analysis and select three different groups of construction machinery type data for the establishment of the evaluation system; the selected data is as in
Table 2.
After six experienced unmanned excavator evaluators fully understand the judgment matrix construction method, based on the hierarchical analysis structure model, the indexes of each level are compared in pairs and averaged to construct a fuzzy consistent judgment matrix, and then the weights of the indexes of each level were calculated through hierarchical single sorting. Goal level weights:
. Criterion level weights:
. The weights of the index level are shown in
Table 3.
From the comparative analysis of the weight coefficients of the index level, it can be seen that, relative to unmanned excavators, the maximum digging depth and the machine group intelligent construction capability are the most important, with a weight coefficient of 0.10, followed by the maximum speed and the single machine intelligent operation capability, with a weight coefficient of 0.09. Through the comparative analysis of the weight coefficients of the criterion level, it can be seen that the indexes of the mechanical capability and the intelligent capability are relatively important. It shows that people’s subjective feelings about the above indexes are more sensitive and need to be focused on when evaluating unmanned excavators.
4.3. Multivariate Image Area Calculation Score
The comprehensive score, calculated using the index radar chart, is a representation of the three excavators as shown in
Figure 9, each with a side length representing the weight of a certain index, i.e., the weight that each index should occupy in the overall rating. Since the weights represented by different indexes are not the same, the polygon is irregular and, when calculating the evaluation scores represented by the 15-sided region, it needs to be regularized into 15 irregular triangular regions for calculation. In this study, MATLAB is used to calculate the specific value of the evaluation score represented by an irregular triangle and then obtain the specific value of the evaluation score represented by 15 irregular triangles. The irregular polygon composed of these 15 irregular triangles is used to determine the comprehensive performance evaluation score of each model as follows: G1 = 78.53; G2 = 57.97; and G3 = 69.49.
From the score, it can be seen that the comprehensive performance of Komatsu PC210LCi-11 is relatively strong and meets the requirements, while XCMG’s XE950DA and LIUGONG’s 922F have relatively weak comprehensive performance. From the evaluation indexes, the maximum digging depth and the machine group intelligent construction capability are the main indexes affecting the comprehensive performance of the whole unmanned excavator. In the future, XCMG’s XE950DA and LIUGONG’s 922F should focus on these aspects to improve the comprehensive performance of the unmanned excavator.
As shown in
Figure 10, in the evaluation process of the three unmanned excavators of Komatsu, LIUGONG, and XCMG, it can be concluded that there is a difference between the evaluation results of the traditional evaluation method AHP and those of the evaluation method FAHP of this study. The results of the traditional evaluation method AHP are Komatsu PC210LCi-11 scoring 59.9 points, LIUGONG 922F scoring 69.6 points, and XCMG XE950DA scoring 76.28 points. The evaluation results of the evaluation method FAHP in this study are 78.53 points for Komatsu PC210LCi-11, 57.97 points for Liu Gong 922F, and 69.49 points for XCMG XE950DA. According to the comparison of actual analysis and evaluation results, Komatsu PC210LCi-11 has better comprehensive performance, which shows that the evaluation method of this study is more comprehensive and reasonable.
This can verify the validity and feasibility of the evaluation method in this study. The fuzzy analytic hierarchy process method can deal with the ambiguity and uncertainty between evaluation indicators. Through expert opinion and fuzzy mathematics operations, the subjective evaluation can be transformed into relative weights, and the indicators can be divided and ranked hierarchically. This method can provide more objective and scientific evaluation results. Compared with the traditional subjective evaluation method, the fuzzy analytic hierarchy process method introduces the concept of fuzzy mathematics into the evaluation process and pays more attention to the accurate assessment of the weight and importance of each evaluation index. It can help decision makers better clarify the evaluation hierarchy and avoid subjective bias and unreasonable weight settings. The multivariate image area analysis method can intuitively display the comprehensive results of multiple evaluation indicators. Drawing radar charts and graphically displaying the evaluation results of different indicators can help to quickly compare and understand the comprehensive performance of different unmanned excavators and discover their strengths and weaknesses. Compared with the traditional evaluation methods of weighted average or weighted sum, the multivariate image area analysis method pays more attention to the comprehensive analysis and comparison of multiple indicators. It can highlight the performance of different excavators against different indicators and provide an intuitive graphical display to facilitate the judgment of decision makers.