Enhancing Real-Time Kinematic Relative Positioning for Unmanned Aerial Vehicles
Abstract
:1. Introduction
- GNSS Measurements Time Synchronization between UAVs;
- Cycle slip detection strategy for a UAV;
- Adopting Dual Kalman filter (KF) structure to cope with ratio test failures owing to relatively inaccurate estimates of newly added states.
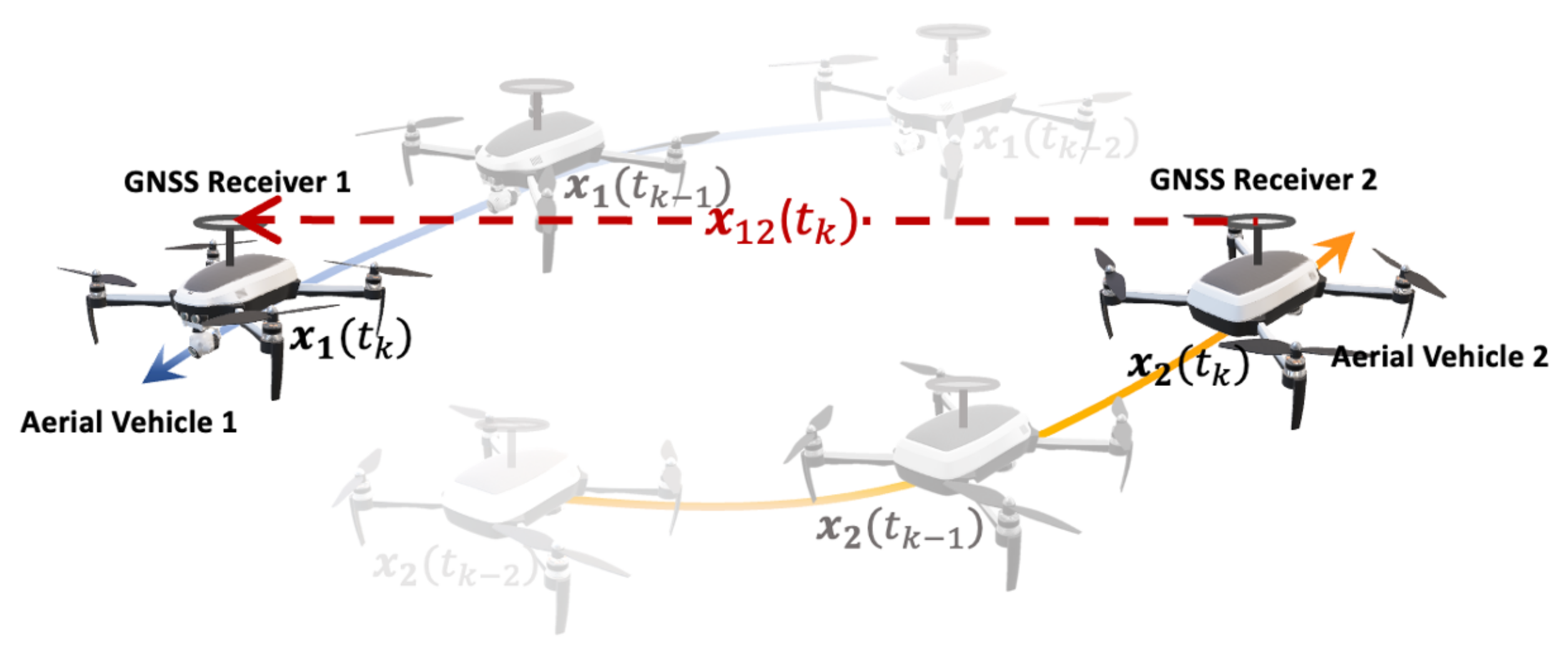
2. Gnss Measurements Pre-Processing and Time Synchronization
3. Cycle Slip Detection Strategy for a UAV
- Time-Differenced Dual-Frequency carrier phase Combination (TDDFC);
- Doppler-Aided Cycle Slip Detection (DACSD);
- Time-Differenced Single-Frequency carrier phase Measurements (TDSFM);
3.1. Time-Differenced Dual-Frequency Carrier Phase Combination (TDDFC)
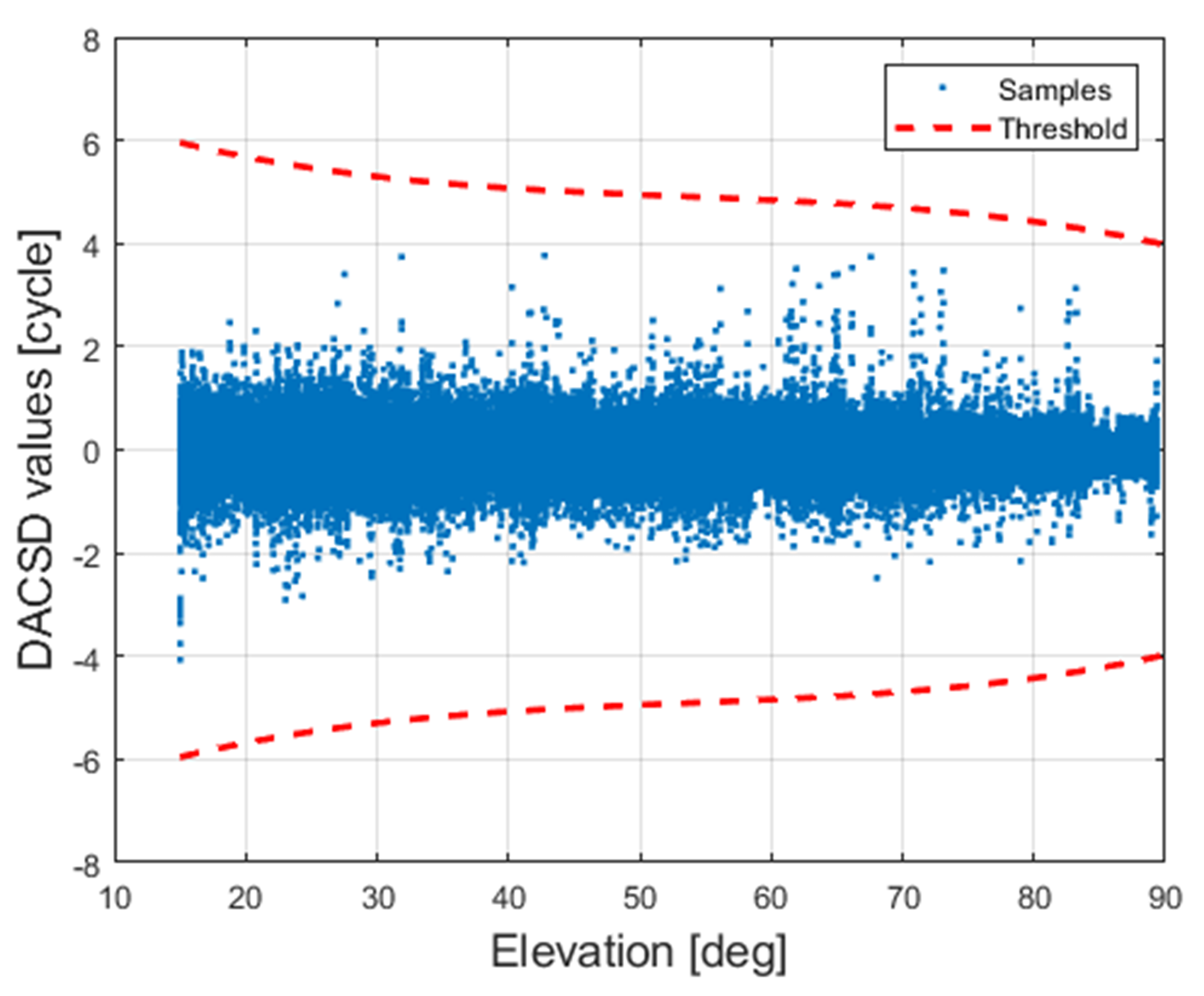
3.2. Doppler-Aided Cycle Slip Detection (DACSD)
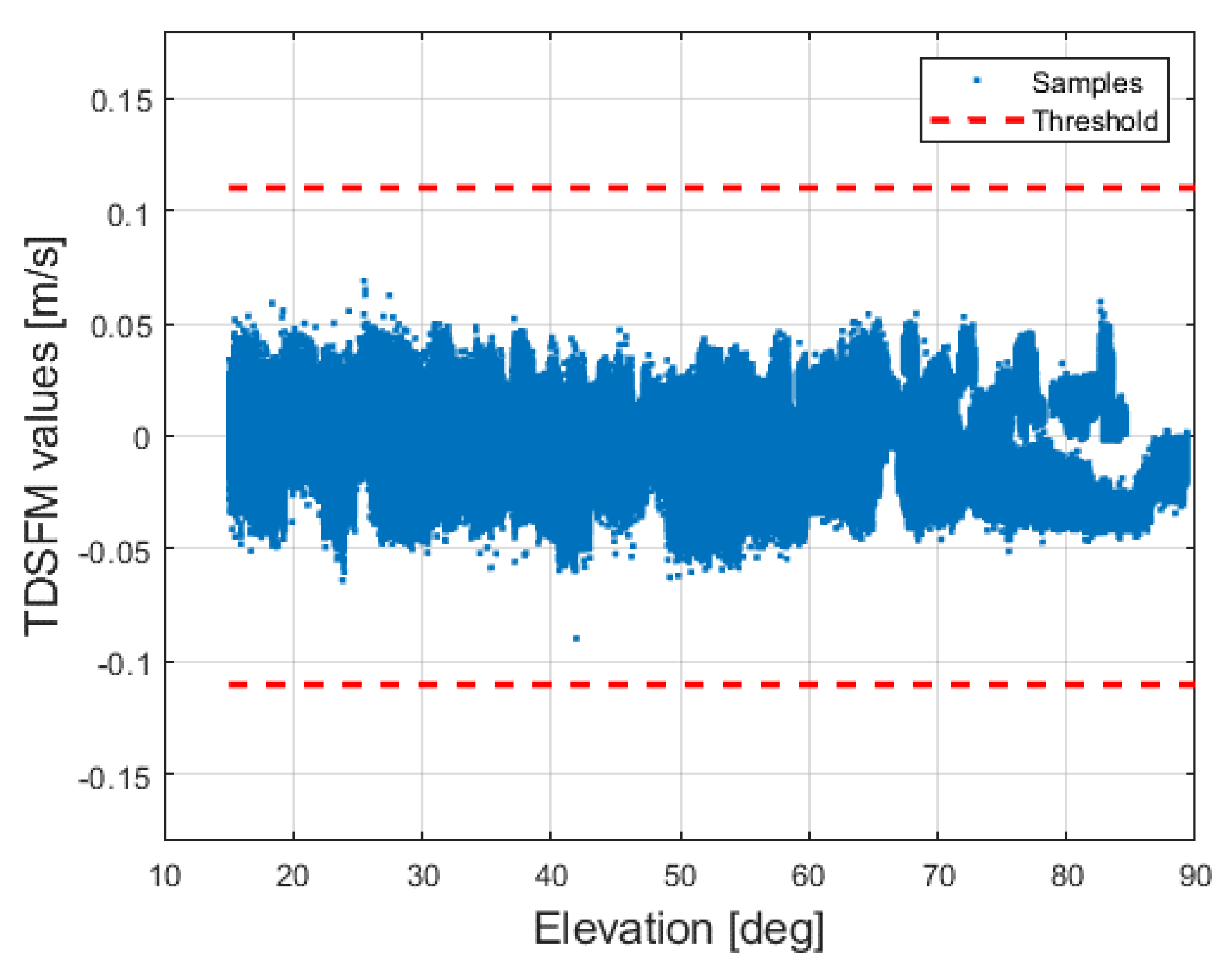
3.3. Time-Differenced Single-Frequency Carrier Phase Measurements (TDSFM)
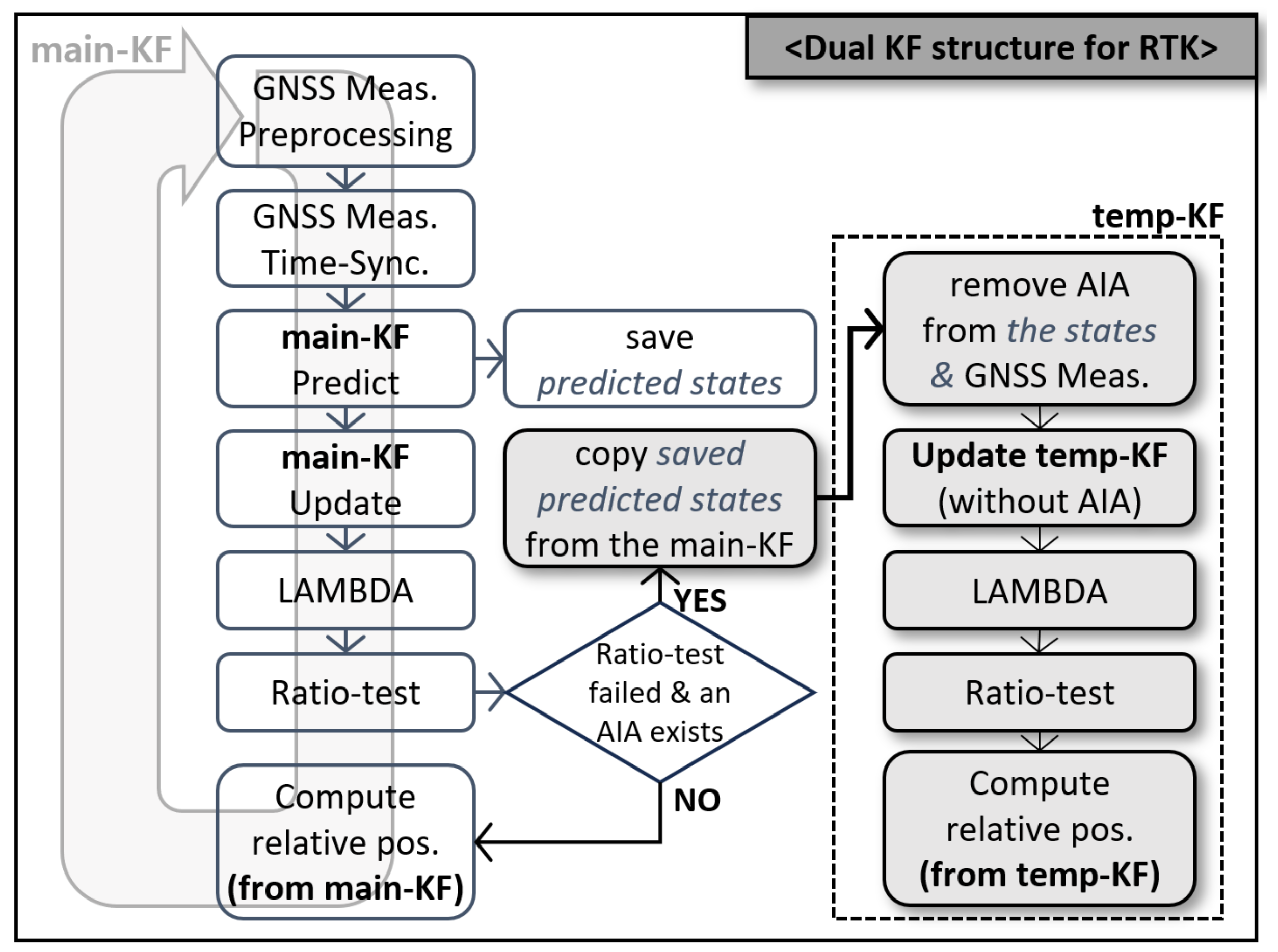
4. Proposed Dual Kalman Filter Structure for RTK and Its Rationales
4.1. Conventional Kalman Filter Based RTK Approach
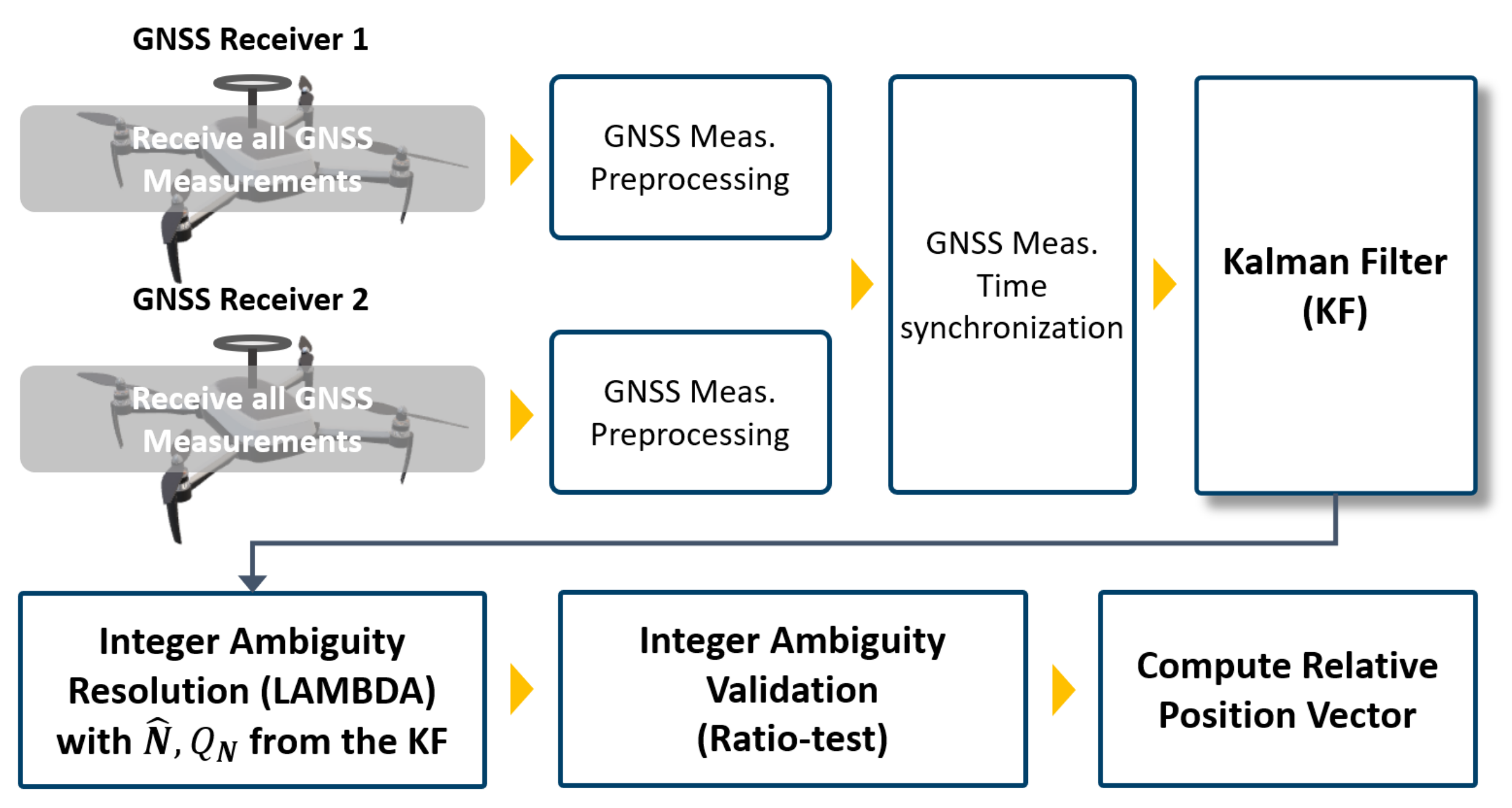
4.2. Dual Kalman Filter Structure
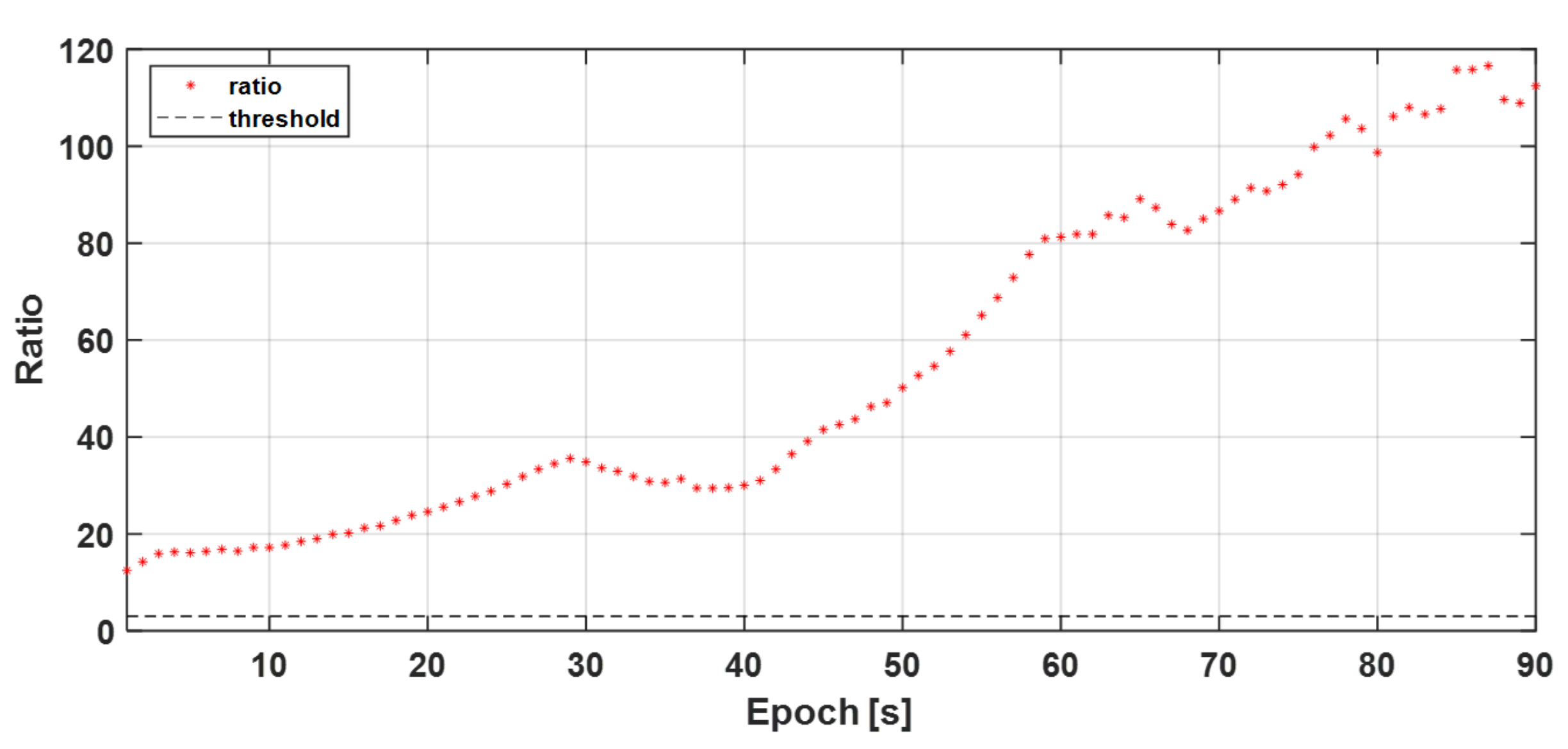
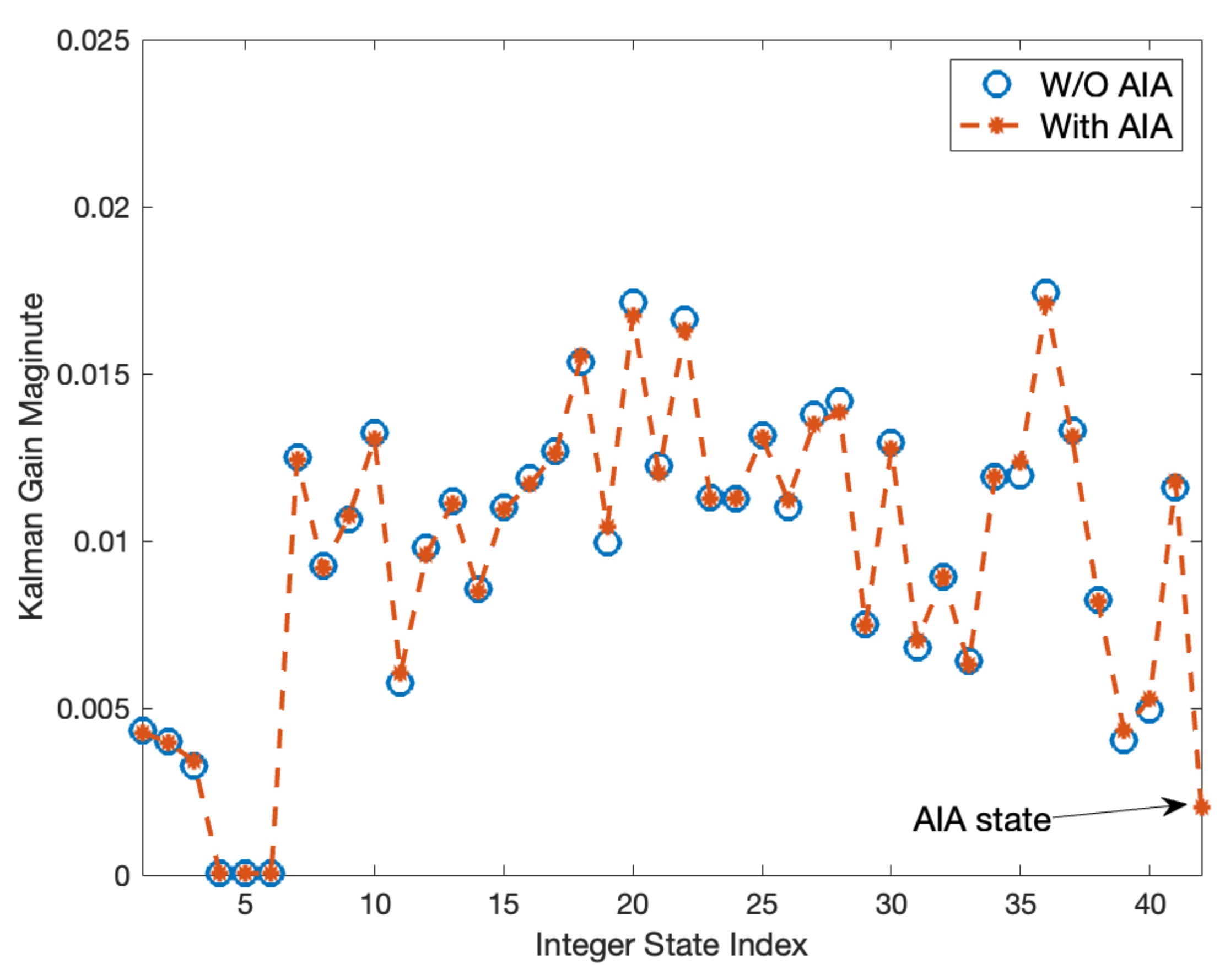
4.2.1. Analysis of the Effect of a Newly Risen Satellite on the KF and Integer Ambiguity Resolution in LAMBDA
4.2.2. Dual KF Structure Development Strategy
5. Results
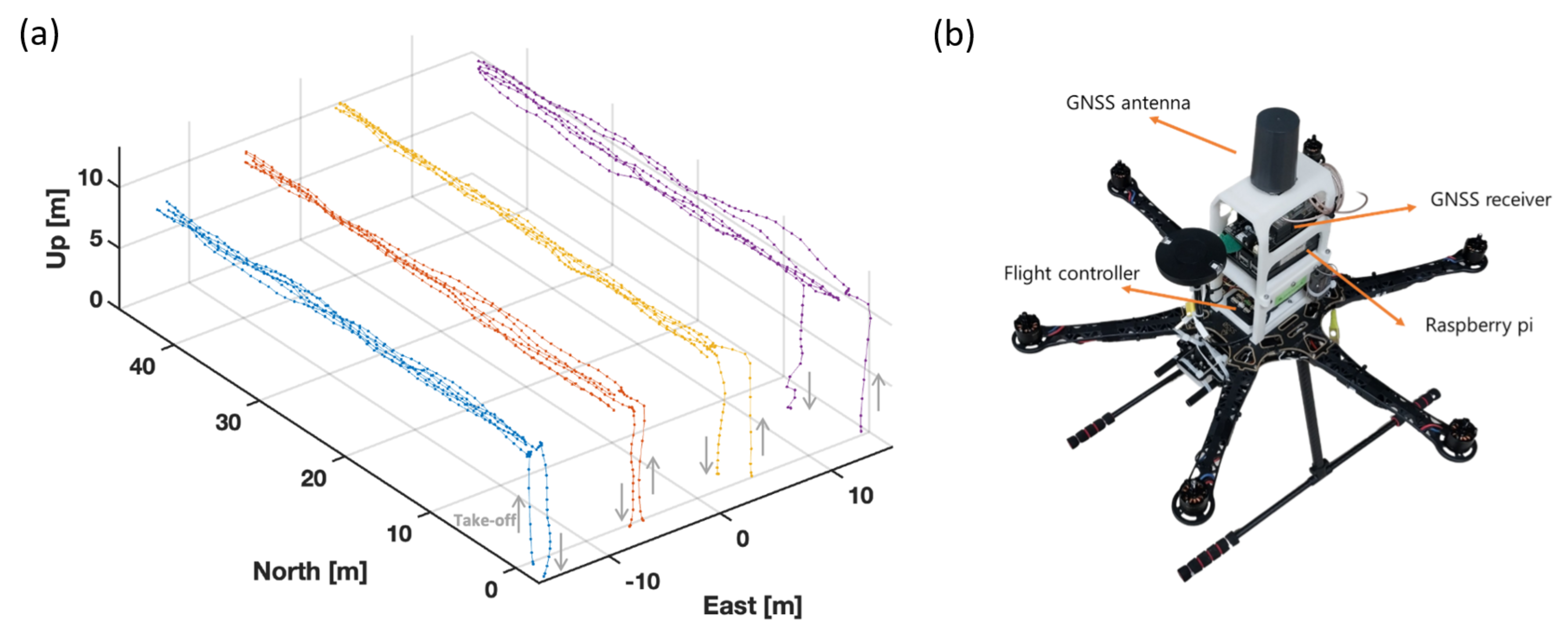
5.1. Experimental Set-Up and Methods
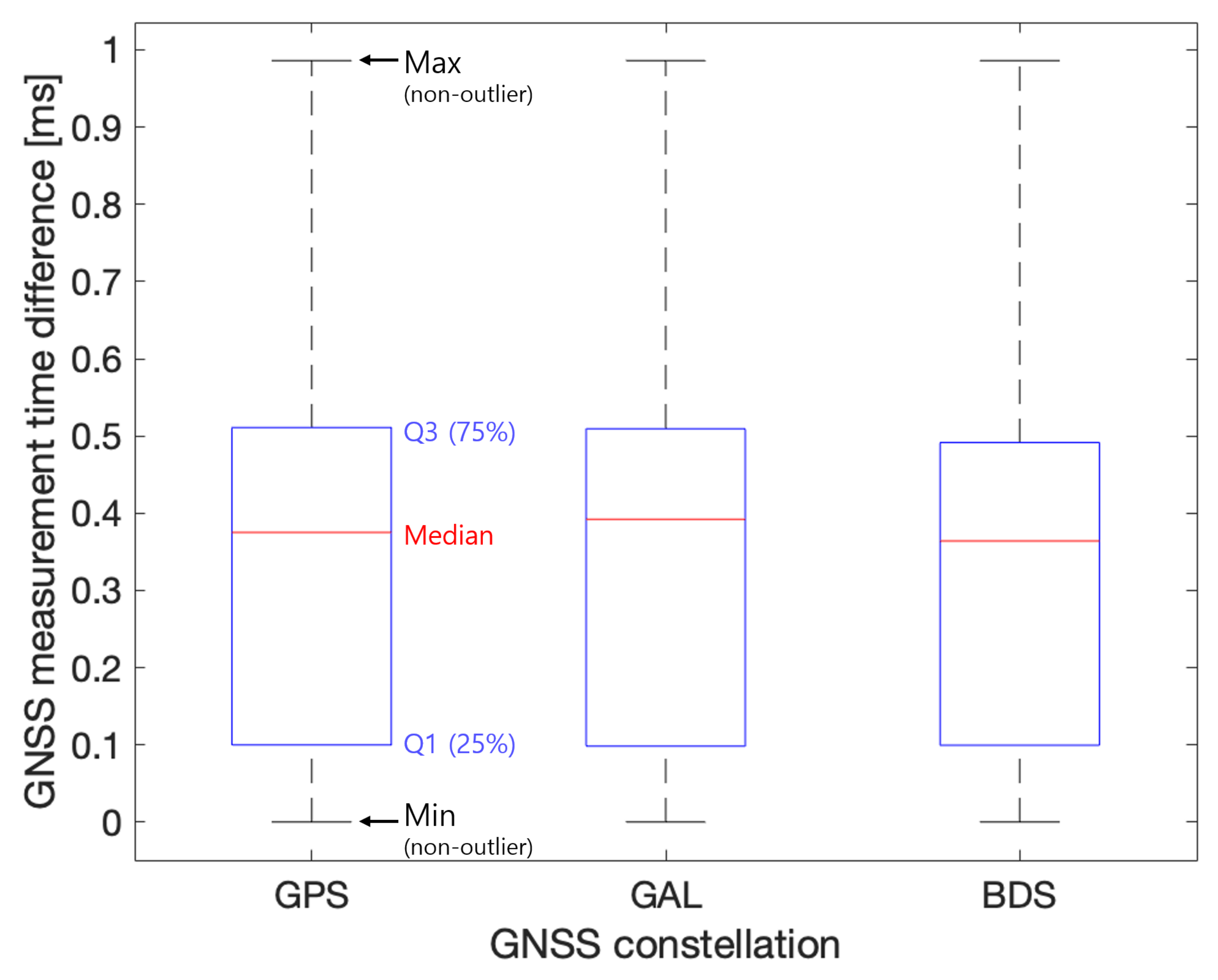
5.2. Performance Improvement through Synchronization of Measurement Times
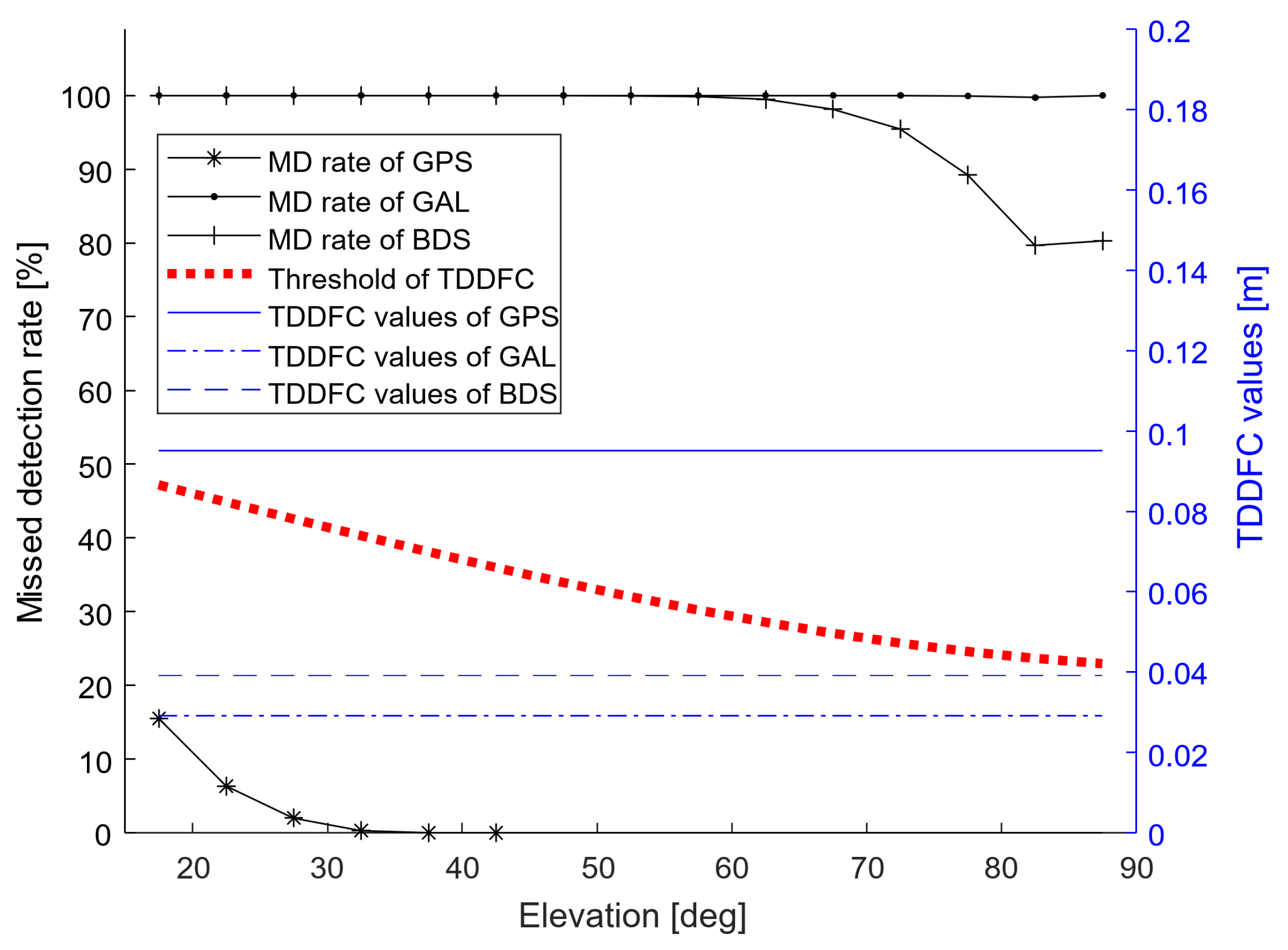
5.3. Performance Improvement via Proposed Cycle Slip Detection Strategy for a UAV
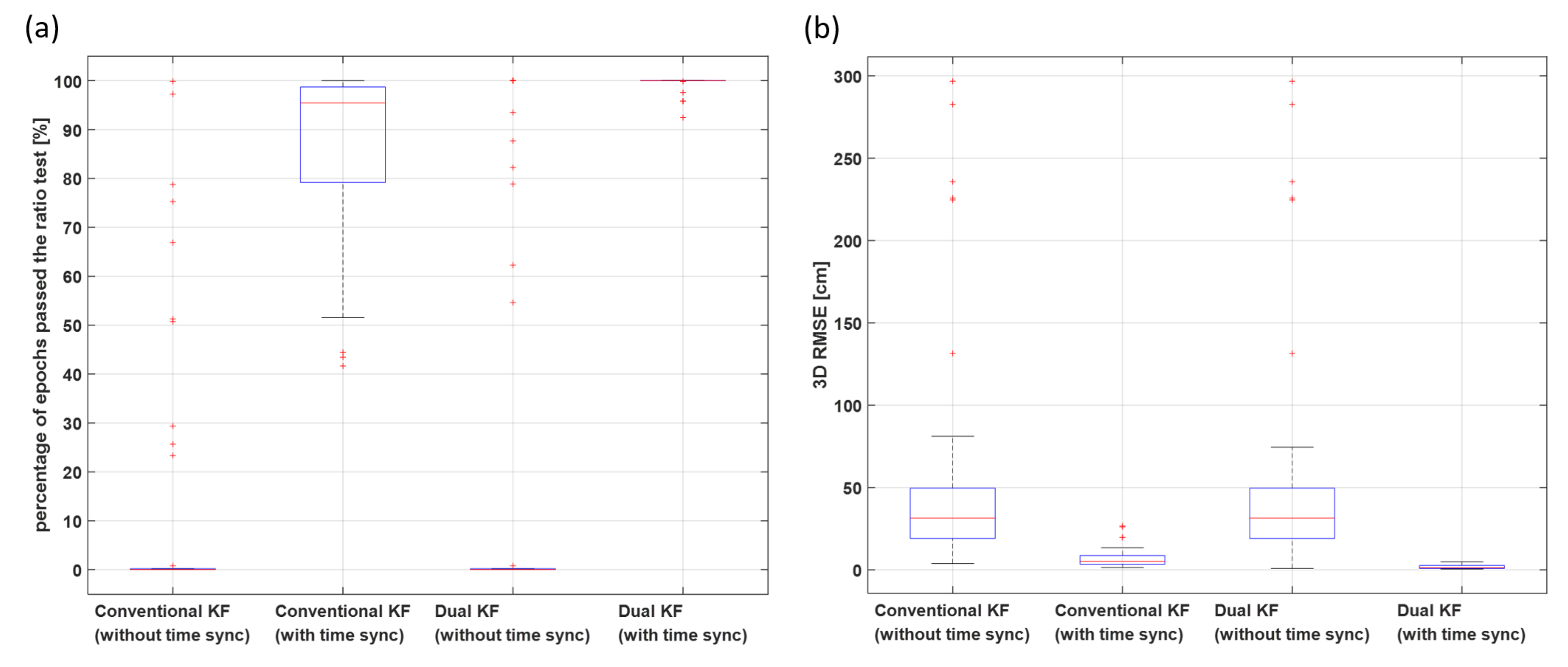
5.4. Performance Improvement via Dual Kalman Filter Structure
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, H.; Slaughter, D.C.; Ruiz, M.P.; Gliever, C.; Upadhyaya, S.K.; Smith, R.F. RTK GPS mapping of transplanted row crops. Comput. Electron. Agric. 2010, 71, 32–37. [Google Scholar] [CrossRef]
- Varbla, S.; Puust, R.; Ellmann, A. Accuracy assessment of RTK-GNSS equipped UAV conducted as-built surveys for construction site modelling. Surv. Rev. 2020, 53, 477–492. [Google Scholar] [CrossRef]
- Tamura, Y.; Matsui, M.; Pagnini, L.; Ishibashi, R.; Yoshida, A. Measurement of wind-induced response of buildings using RTK-GPS. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1783–1793. [Google Scholar] [CrossRef]
- Meguro, J.; Hashizume, T.; Takiguchi, J.; Kurosaki, R. Development of an autonomous mobile surveillance system using a network-based RTK-GPS. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3096–3101. [Google Scholar] [CrossRef]
- Zhao, S.; Cui, X.; Guan, F.; Lu, M. A Kalman Filter-Based Short Baseline RTK Algorithm for Single-Frequency Combination of GPS and BDS. Sensors 2014, 14, 15415–15433. [Google Scholar] [CrossRef] [PubMed]
- Verhagen, S. Integer ambiguity validation: An open problem? GPS Solut. 2004, 8, 36–43. [Google Scholar] [CrossRef]
- Li, T.; Wang, J. Some remarks on GNSS integer ambiguity validation methods. Surv. Rev. 2012, 44, 230–238. [Google Scholar] [CrossRef]
- Jonge, P.D.; Tiberius, C. Integer ambiguity estimation with the lambda method. In GPS Trends in Precise Terrestrial, Airborne, and Spaceborne Applications; Springer: Berlin/Heidelberg, Germany, 1996; pp. 280–284. [Google Scholar] [CrossRef]
- Jonge, P.D.; Tiberius, C. The LAMBDA method for integer ambiguity estimation: Implementation aspects. Publ. Delft Comput. Cent. LGR Ser. 1996, 12, 1–47. [Google Scholar]
- Verhagen, S.; Li, B.; Geodesy, M. LAMBDA Software Package: Matlab Implementation, Version 3.0; Delft University of Technology and Curtin University: Perth, Australia, 2012. [Google Scholar]
- Pervan, B.; Chan, F.C.; Gebre-Egziabher, D.; Pullen, S.A.M.; Enge, P.E.R.; Colby, G. Performance Analysis of Carrier-Phase DGPS Navigation for Shipboard Landing of Aircraft. Navigation 2003, 50, 181–191. [Google Scholar] [CrossRef]
- Pervan, B.; Chan, F.C. System concepts for cycle ambiguity resolution and verification for aircraft carrier landings. In Proceedings of the 14th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2001), Salt Lake City, UT, USA, 11–14 September 2001; pp. 1228–1237. [Google Scholar]
- Heo, M.B.; Pervan, B. Carrier phase navigation architecture for shipboard relative GPS. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 670–679. [Google Scholar]
- Khanafseh, S.; Pervan, B. New approach for calculating position domain integrity risk for cycle resolution in carrier phase navigation systems. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 296–307. [Google Scholar] [CrossRef]
- Khanafseh, S.; Langel, S.; Pervan, B. H1-integrity of carrier phase navigation algorithms using multiple reference receivers. In Proceedings of the 2009 International Technical Meeting of The Institute of Navigation, Anaheim, CA, USA, 26–28 January 2009; pp. 236–247. [Google Scholar]
- Rife, J.; Khanafseh, S.; Pullen, S.; de Lorenzo, D.; Kim, U.-S.; Koenig, M.; Chiou, T.-Y.; Kempny, B.; Pervan, B. Navigation, interference suppression, and fault monitoring in the sea-based joint precision approach and landing system. Proc. IEEE 2008, 96, 1958–1975. [Google Scholar] [CrossRef]
- Kim, G.; Park, W.; Park, B. Moving Baseline RTK-based Ground Vehicle-Drone Combination System. In Proceedings of the 2024 International Technical Meeting of the Institute of Navigation, Long Beach, CA, USA, 22–25 January 2024; pp. 630–636. [Google Scholar]
- Sridhara, H.S.; Kubo, N.; Kikuchi, R. Single-Frequency Multi-GNSS RTK Positioning for Moving Platform. In Proceedings of the 2015 International Technical Meeting of the Institute of Navigation, Dana Point, CA, USA, 26–28 January 2015; pp. 504–511. [Google Scholar]
- Xi, R.; Jiang, W.; Xuan, W.; Xu, D.; Yang, J.; He, L.; Ma, J. Performance Assessment of Structural Monitoring of a Dedicated High-Speed Railway Bridge Using a Moving-Base RTK-GNSS Method. Remote Sens. 2023, 15, 3132. [Google Scholar] [CrossRef]
- Herrera, A.M.; Suhandri, H.F.; Realini, E.; Reguzzoni, M.; De Lacy, M.C. goGPS: Open-source MATLAB software. GPS Solut. 2016, 20, 595–603. [Google Scholar] [CrossRef]
- Takasu, T.; Yasuda, A. Development of the low-cost RTK-GPS receiver with an open source program package RTKLIB. In Proceedings of the International Symposium on GPS/GNSS, International Convention Center, Jeju, Republic of Korea, 4–6 November 2009; pp. 1–6. [Google Scholar]
- Baroni, L.; Kuga, H.K. Analysis of navigational algorithms for a real time differential GPS system. In Proceedings of the 18th International Congress of Mechanical Engineering, Ouro Preto, Brazil, 6–11 November 2005. [Google Scholar]
- Yujin, S.; Euiho, K. GNSS-based Short Baseline Relative Positioning of Moving Vehicles and Evaluation on its Positioning Performance. In Proceedings of the 2021 IPNT Conference, Gangneung, Republic of Korea, 3–5 November 2021. [Google Scholar]
- Zhao, J.; Hernández-Pajares, M.; Li, Z.; Wang, L.; Yuan, H. High-rate Doppler-aided cycle slip detection and repair method for low-cost single-frequency receivers. GPS Solut. 2020, 24, 80. [Google Scholar] [CrossRef]
- Li, Y.G.; Li, Z. Cycle slip detection and ambiguity resolution algorithms for dual-frequency GPS data processing. Mar. Geod. 1999, 22, 169–181. [Google Scholar] [CrossRef]
- Bisnath, S.B. Efficient, automated cycle-slip correction of dual-frequency kinematic GPS data. In Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000; pp. 145–154. [Google Scholar]
- Bastos, L.; Landau, H. Fixing cycle slips in dual-frequency kinematic GPS-applications using Kalman filtering. Manuscripta Geod. 1988, 13, 249–256. [Google Scholar]
- Kim, D.; Langley, R.B. Instantaneous real-time cycle-slip correction of dual frequency GPS data. In Proceedings of the International Symposium on Kinematics Systems in Geodesy, Geomaticsand Navigation, Banff, AB, Canada, 5–8 June 2001; pp. 255–264. [Google Scholar] [CrossRef]
- Chen, D.; Ye, S.; Zhou, W.; Liu, Y.; Jiang, P.; Tang, W.; Yuan, B.; Zhao, L. A double-differenced cycle slip detection and repair method for GNSS CORS network. GPS Solut. 2016, 20, 439–450. [Google Scholar] [CrossRef]
- Liu, Z. A new automated cycle slip detection and repair method for a single dual-frequency GPS receiver. J. Geod. 2011, 85, 171–183. [Google Scholar] [CrossRef]
- Dai, Z. MATLAB software for GPS cycle-slip processing. GPS Solut. 2012, 16, 267–272. [Google Scholar] [CrossRef]
- Lee, C.; Kim, E. Cycle Slip Detection of Single-Frequency Measurements in Drone Platforms. Eng. Proc. 2023, 54, 13. [Google Scholar] [CrossRef]
- Zanetti, R.; DeMars, K.J. Joseph formulation of unscented and quadrature filters with application to consider states. J. Guid. Control. Dyn. 2013, 36, 1860–1864. [Google Scholar] [CrossRef]
- Takasu, T. RTKLIB: Open Source Program Package for RTK-GPS. 2009. Available online: https://www.rtklib.com (accessed on 10 February 2024).
- Trimble Business Center User Guide, 2nd ed.; Trimble Inc.: Dayton, OH, USA, 2008.
- Jiang, Y.; Gao, Y.; Ding, W.; Liu, F.; Gao, Y. An Improved Ambiguity Resolution Algorithm for Smartphone RTK Positioning. Sensors 2023, 23, 5292. [Google Scholar] [CrossRef]




| GPS | Galileo | BeiDou | ||
|---|---|---|---|---|
| Band | L1 | E1 | B1 | |
| Wavelength [m] | 0.19029 | 0.19029 | 0.19204 | |
| Band | L2 | E5b | B2b | |
| Wavelength [m] | 0.24421 | 0.24835 | 0.24835 | |
| TDDFC Values [m] 1 | ||||
|---|---|---|---|---|
| (1,1) | (77,60) | (39,30) | (13,10) | |
| GPS | −0.05392 | 1.7763 | 0.09515 | 0.03172 |
| Galileo | −0.05806 | −0.24835 | −0.02903 | −0.00968 |
| BeiDou | −0.05631 | −0.11392 | 0.03906 | 0.01302 |
| Method | Polynomial Coefficients | |||
|---|---|---|---|---|
| 3rd-Order | 2nd-Order | 1st-Order | Constant | |
| TDDFC [m] | +4.1162 | −1.9358 | −8.2256 | +0.1013 |
| DACSD [cyc] | −1.1586 | +1.8570 | −0.1093 | +7.2164 |
| TDSFM [m/s] | - | - | - | +0.1160 |
| Flight Test Idx | 3D RMSE [cm] (Position Error) | 3D RMSE Reduction Rate [%] | Percentage of Epochs That Passing the Ratio Test [%] | Increase Rate in Passing the Ratio Test [%] | ||
|---|---|---|---|---|---|---|
| Conventional KF | Dual KF | Conventional KF | Dual KF | |||
| 1 | 2.79 | 2.03 | 27.40 | 96.98 | 100.00 | 3.12 |
| 2 | 8.29 | 2.34 | 71.80 | 85.93 | 100.00 | 16.37 |
| 3 | 19.77 | 2.29 | 88.42 | 82.04 | 100.00 | 21.89 |
| 4 | 8.61 | 1.59 | 81.52 | 80.39 | 100.00 | 24.39 |
| 5 | 13.43 | 1.24 | 90.75 | 79.47 | 100.00 | 25.83 |
| 6 | 8.97 | 1.69 | 81.14 | 78.34 | 100.00 | 27.66 |
| 7 | 26.64 | 4.33 | 83.76 | 58.65 | 100.00 | 70.50 |
| 8 | 5.76 | 3.12 | 45.76 | 94.01 | 100.00 | 6.37 |
| 9 | 26.10 | 2.92 | 88.80 | 59.48 | 100.00 | 68.12 |
| 10 | 8.35 | 1.35 | 83.81 | 92.48 | 100.00 | 8.13 |
| 11 | 12.03 | 0.74 | 93.88 | 71.39 | 100.00 | 40.07 |
| 12 | 4.54 | 0.86 | 80.96 | 93.93 | 99.84 | 6.29 |
| 13 | 19.69 | 0.96 | 95.13 | 70.51 | 100.00 | 41.83 |
| 14 | 5.38 | 0.60 | 88.92 | 90.58 | 100.00 | 10.39 |
| 15 | 3.64 | 0.89 | 75.40 | 95.43 | 100.00 | 4.79 |
| 16 | 4.44 | 1.53 | 65.62 | 96.77 | 100.00 | 3.34 |
| 17 | 3.88 | 1.47 | 62.06 | 99.54 | 100.00 | 0.47 |
| 18 | 4.38 | 0.69 | 84.19 | 98.85 | 100.00 | 1.17 |
| 19 | 3.47 | 0.77 | 77.77 | 98.95 | 100.00 | 1.06 |
| 20 | 4.05 | 1.09 | 73.13 | 98.69 | 100.00 | 1.33 |
| 21 | 5.25 | 2.60 | 50.46 | 97.65 | 100.00 | 2.41 |
| 22 | 2.26 | 0.78 | 65.63 | 99.86 | 100.00 | 0.14 |
| 23 | 2.69 | 0.64 | 76.14 | 98.47 | 100.00 | 1.56 |
| 24 | 4.46 | 0.87 | 80.46 | 97.77 | 100.00 | 2.28 |
| 25 | 1.77 | 1.28 | 27.45 | 99.41 | 100.00 | 0.60 |
| 26 | 2.51 | 1.03 | 58.99 | 99.11 | 100.00 | 0.90 |
| 27 | 3.47 | 1.57 | 54.77 | 98.36 | 100.00 | 1.66 |
| 28 | 5.66 | 0.95 | 83.29 | 92.65 | 100.00 | 7.94 |
| 29 | 2.15 | 0.57 | 73.64 | 98.74 | 100.00 | 1.28 |
| 30 | 5.71 | 0.72 | 87.42 | 94.32 | 100.00 | 6.03 |
| 31 | 2.34 | 2.17 | 7.19 | 94.76 | 95.81 | 1.11 |
| 32 | 1.42 | 0.48 | 65.87 | 98.32 | 100.00 | 1.71 |
| 33 | 3.39 | 0.73 | 78.47 | 98.75 | 100.00 | 1.27 |
| 34 | 9.69 | 4.61 | 52.37 | 51.54 | 100.00 | 94.03 |
| 35 | 11.12 | 4.28 | 61.56 | 52.70 | 100.00 | 89.76 |
| 36 | 9.30 | 4.16 | 55.27 | 52.32 | 100.00 | 91.13 |
| 37 | 5.55 | 1.08 | 80.61 | 98.00 | 100.00 | 2.04 |
| 38 | 7.47 | 0.96 | 87.21 | 95.48 | 100.00 | 4.74 |
| 39 | 4.65 | 0.75 | 83.95 | 97.51 | 100.00 | 2.56 |
| 40 | 10.30 | 4.12 | 60.04 | 41.64 | 95.82 | 130.10 |
| 41 | 7.12 | 4.23 | 40.58 | 43.45 | 92.44 | 112.73 |
| 42 | 7.49 | 4.93 | 34.24 | 44.46 | 97.57 | 119.45 |
| 43 | 2.98 | 2.00 | 33.00 | 99.06 | 100.00 | 0.95 |
| 44 | 4.42 | 4.42 | 0.00 | 100.00 | 100.00 | 0.00 |
| 45 | 4.31 | 4.31 | 0.00 | 100.00 | 100.00 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, Y.; Lee, C.; Kim, E. Enhancing Real-Time Kinematic Relative Positioning for Unmanned Aerial Vehicles. Machines 2024, 12, 202. https://doi.org/10.3390/machines12030202
Shin Y, Lee C, Kim E. Enhancing Real-Time Kinematic Relative Positioning for Unmanned Aerial Vehicles. Machines. 2024; 12(3):202. https://doi.org/10.3390/machines12030202
Chicago/Turabian StyleShin, Yujin, Chanhee Lee, and Euiho Kim. 2024. "Enhancing Real-Time Kinematic Relative Positioning for Unmanned Aerial Vehicles" Machines 12, no. 3: 202. https://doi.org/10.3390/machines12030202
APA StyleShin, Y., Lee, C., & Kim, E. (2024). Enhancing Real-Time Kinematic Relative Positioning for Unmanned Aerial Vehicles. Machines, 12(3), 202. https://doi.org/10.3390/machines12030202





