Research on Predicting Welding Deformation in Automated Laser Welding Processes with an Enhanced DEWOA-BP Algorithm

Abstract

Welding stands as a critical focus for the intelligent and digital transformation of the machinery industry, with automated laser welding playing a pivotal role in the sector’s technological advancement. The management of welding deformation in such operations is fundamental, relying on advanced analysis and prediction methods. The endeavor to accurately analyze welding deformation in practical applications is compounded by the interplay of numerous variables, a pronounced coupling effect among these factors, and a reliance on expert intuition. Thus, effective deformation control in automated laser welding operations necessitates the gathering of pre-test laser welding data to develop a predictive approach that accurately reflects real-world conditions and is characterized by improved reliability and stability. To address the technological evolution in automated laser welding, a predictive model based on neural network technology is proposed to map the intricate relationship between process variables and the resulting deformation. At the heart of this approach is the formulation of a predictive model utilizing a back-propagation neural network (BP), with an emphasis on four essential welding parameters: speed, peak power, duty cycle, and defocusing amount. The model’s predictive accuracy is then honed through the application of the whale optimization algorithm (WOA) and the differential evolutionary (DE) algorithm. Finally, extensive testing in an automated laser welding experimental setup is conducted to validate the accuracy and reliability of the proposed prediction model. It is demonstrated through these experiments that the deformation prediction model, enhanced by the DEWOA-BP neural network, accurately forecasts the relationship between laser welding parameters and the induced deformation, maintaining a prediction error margin of ±0.1mm. The model is employed to fulfill the requirements for a pre-welding quality evaluation, thereby facilitating a more calculated and informed approach to welding operations. This method of intelligent prediction is not only crucial for the intelligent transformation of laser welding but also holds significant implications for traditional machining technologies such as milling, grinding, and spraying. It offers innovative ideas and methods that are pivotal for the industrial revolution and technological advancement of the traditional machining industry.

1. Introduction

Welding is recognized as a pivotal technology in the machinery manufacturing industry, playing an essential role in enhancing automation and transforming manufacturing practices [1,2]. Among the various welding methods, laser welding stands out for its use of laser radiation as a power source. This technology is notable for its highly concentrated energy, adjustable and precisely controllable power delivery, and the benefit of non-contact operation. As a result, laser welding has surpassed traditional welding techniques, becoming widely adopted for its capabilities in high-speed processing and precision applications [3].

The evolution of laser welding technology has been marked by the integration of various technological approaches into a cohesive framework that combines artificial intelligence capabilities—such as fuzzy logic control, neural network algorithms, and expert system approaches—with the cross-disciplinary synergy of mechanical, electronic, material, and physical sciences. This advanced framework aims to automate the welding process by emulating human sensory capabilities like visual, tactile, and auditory perceptions to replicate the nuanced human assessments involved in examining weld seams and melt pool dynamics. Laser welding technology, comprising predictive, control, and interactive intelligence, faces challenges in replacing human expertise and sensory responses with algorithm-driven systems and mechanical analogues [4]. Traditional welding’s reliance on manual skill and procedural manuals often introduces biases and complexities that intelligent laser welding seeks to overcome through robotic systems that can acquire quasi-experiential knowledge and make decisions mirroring human cognition [5]. This technology is primarily focused on predicting weld quality under various conditions and identifying and rectifying potential defects to maintain compliance with quality standards.

Building on these advancements in intelligent laser welding, recent research has further refined the predictive capabilities within this domain. In the realm of predictive quality assessment, Tang et al. have devised a method utilizing machine vision coupled with the Hidden Markov Model to simplify the evaluation of welding quality [6]. Sassi and colleagues have employed deep learning techniques, bolstered by transfer learning, for the efficient training of networks to monitor weld quality, yielding high accuracy with a limited dataset [7]. Further research by Praveen Kumar R et al. has explored machine learning for defect recognition in welding, employing classification algorithms to categorize defects captured through machine vision [8]. Guo Jinjin and colleagues have implemented a system integrating fuzzy control and neural networks for high-accuracy welding quality classification [9]. Necip Fazil and co-researchers have used artificial neural networks (ANNs) among other methods, achieving a high precision rate in predicting the ultimate tensile strength of welded joints [10]. SenthilKumar V et al. have proposed a genetic algorithm for optimizing laser cutting parameters, demonstrating a meticulous evaluation of the effects on the quality of cuts [11].

Extending these technological advancements to address the physical outcomes of the welding process, significant efforts are underway to predict and control welding-induced deformations—a critical topic within intelligent prediction. The aim is to anticipate and mitigate part distortions post-welding through simulations that consider heat transfer and material responses. Current methodologies often employ finite element analysis (FEA) to predict these deformations. Ninshu Ma et al. combine finite element analysis with experimental validation to understand and counteract the undesirable effects of weld deformation [12]. Jiangchao Wang et al. have applied elastic finite element methods to predict deformations in structural welding applications, developing optimization strategies to minimize these effects [13]. Yu Cao et al. have introduced an approach tailored for shipbuilding, integrating thermoelastic–plastic finite element methods with inherent deformation theory, to preemptively address deformation concerns [14]. These investigations highlight the ongoing efforts to bridge the gap between theoretical models and practical production needs, with the ultimate goal of enhancing the precision and reliability of laser welding processes.

In the field of mechanical engineering, the utility of deformation prediction methodologies in real-world production scenarios is somewhat constrained. The limited applicability is attributed to the simplified assumptions used within idealized model frameworks. Discrepancies in material quality parameters, the intricacies of on-site conditions, and the multitude of influential factors serve to compound the complexity of analyses. Thus, principles extrapolated from simulations under ideal conditions frequently fall short in practical processing environments. Additionally, the exigencies of production timelines and operational conditions often obviate the development and implementation of economically viable predictive models. Consequently, on-site technicians traditionally depend on empirical knowledge accrued over time for rudimentary inferential assessments.

The essence of the presented study is the formulation of a robust deformation prediction model for laser welding, which is congruent with the realities of processing environments and assimilates the empirical experience of technical staff. The research commences with the establishment of a deformation evaluation criterion, pertinent to actual production activities and intelligible to practitioners. At the heart of the investigation is the deployment of process parameter-driven approaches, coupled with intelligent algorithms and assorted optimization heuristics. The innovative aspect of the methodology lies in its foundation upon the tangible conditions of the processing environment and the specific parameters of the laser welding process. The objective is to derive a predictive model for laser welding deformation, predicated on these parameters, which provides a streamlined yet efficacious means of forecasting welding deformation on-site. This enables operators to refine and enhance production processes, leading to improved operational efficiency. The intelligent prediction algorithm proposed in this paper uses laser welding as an example to conduct the theoretical analysis and model construction, but the algorithmic ideas embodied in it are not limited to the laser welding scene, which is only used as a presentation mode of the algorithm and has no substantive significance. Therefore, this method can reflect a more prominent role in the actual production than the content of this paper and has a wide range of applicability. The prediction model proposed in this paper transcends the resolution of discrete processing issues within enterprises. It endeavors to furnish an advanced intelligent solution to the machining industry, addressing the challenges presented by predominantly manual and experiential procedures. Furthermore, the model offers strategic direction for the intelligent evolution and refinement of the sector as a whole.

2. Analysis of Problems

Welding deformation is predominantly induced via thermal expansion, contraction upon cooling, and the accumulation of residual stresses throughout the welding process [15]. Given its high energy density and the relatively small extent of the heat-affected zone, laser welding is particularly susceptible to significant heat output and excessive temperature gradients at the welded joints, compared to traditional welding methods. Such conditions exacerbate the extent of welding deformation. Consequently, the control of welding deformation is accorded heightened significance in the context of laser welding.

The extent of deformation in laser welding is significantly influenced by various factors such as the welding process parameters, properties of the welding plates, and methodologies for positioning and securing components, with process parameters being the primary contributors to deformation. In conventional laser welding operations, where plate parameters and positioning fixtures are often standardized, the focus is notably on how changes in welding speed, power, and focal point adjustment impact deformation [16]. Welding speed, which determines the linear velocity of the welding head’s movement over the surface, directly affects the heat input and size of the heat-affected zone. A higher welding speed reduces the heat input and the heat-affected zone, thus minimizing deformation. The power of the laser welding dictates the energy level discharged by the laser beam onto the welding surface, where increased power leads to higher thermal energy absorption, enhancing welding efficiency and penetration depth. Given the high output of continuous wave lasers, pulse width modulation (PWM) is used for precise power management, splitting laser power into peak power and duty cycle [17]. Peak power controls the maximum output in a cycle, influencing the energy density essential for material melting, while the duty cycle, representing the percentage of the laser’s operating time within a cycle, affects the heat input and material melting. Additionally, the defocusing amount, or the position of the laser beam’s focal point relative to the workpiece surface, significantly alters the laser beam’s focusing properties and the resulting weld morphology. This combination of factors requires careful adjustment and control to optimize welding outcomes and minimize deformation.

Laser welding distortion assessment involves measuring and analyzing changes in the geometry and dimensions of components that undergo stress during welding, typically using methods like geometric measurements, finite element analysis, or numerical simulation [18]. Due to the need for quick assessments in real-time production settings, conducting detailed analyses of welds, stress levels, and dimensions is often impractical and cost-prohibitive. To address this, an innovative approach using differences in flatness tolerance as a metric for assessing welding deformation has been developed. Flatness is measured by the variation in distance between points on a surface and a reference plane. This method evaluates the flatness of both the unwelded base material and the welded component, with the unwelded material acting as the reference. This allows for quick data collection on how the surface morphology of the joints changes before and after welding, enabling fast and effective predictions of welding deformation.

In automated laser welding operations, controlling welding deformation is a fundamental requirement, with strategies for managing this deformation reliant upon the analysis and prediction of distortions. Traditionally, deformation analysis has been predicated on empirical methods, whereby technicians draw upon their extensive experience from repeated manual welding to deduce the effects of varying welding process parameters and their interrelations. However, the variability and subjectivity inherent in human judgment render this approach less reliable for the automated control of laser welding deformation. A more stable and accurate method for predicting welding deformation is necessitated, one that is grounded in pre-experimental data reflective of actual operational conditions.

The adoption of a neural network offers a more sophisticated and apt solution for predicting parameter-induced deformations in automated laser welding settings. Neural networks, renowned for their robust nonlinear fitting and generalization capabilities, can effectively map complex, multi-dimensional data relationships, thus enabling the development of a predictive model for multi-dimensional, nonlinearly coupled data based solely on empirical observations [19]. The neural network-based model for predicting the impact of laser welding process parameters on welding deformation represents an optimal solution. This approach leverages pre-existing welding pre-test data and the neural network’s nonlinear fitting prowess to unearth patterns among welding parameters, culminating in a predictive model that aligns closely with empirical data, thereby facilitating intelligent predictions of parameter effects. Nonetheless, the predictive accuracy of traditional neural networks can be compromised by the substantial variability and complexity of pre-experimental data, often leading to suboptimal iterative efficiency. To address these challenges, meta-heuristic algorithms are employed to enhance the neural network model, optimizing initial parameters to avoid local minima and augment global search capabilities.

An enhanced BP neural network model (DEWOA-BP), optimized through the integration of differential evolution and whale optimization algorithms, is introduced. This model establishes a predictive linkage between critical welding parameters—welding speed, peak power, duty cycle, and defocusing amount—and the extent of welding deformation, achieving an accurate mapping of process parameters to deformation outcomes. For automated laser welding operations, the feasibility of the proposed improved neural network prediction model is affirmed. Through algorithmic modeling, a concise set of pre-experimental data and judicious parameter settings yield a stable and reliable law of deformation, providing a straightforward and dependable method for deformation prediction. This foundational work paves the way for future advancements in intelligent welding technologies.

3. DEWOA-BP

3.1. BP

Artificial neural networks (ANNs), often shortened to neural networks, mimic the structural and functional characteristics of the human brain [20]. These networks are founded on the principles of distributed and parallel computation and utilize a variety of weight-learning algorithms to achieve nonlinear generalized mapping for discrete datasets. The essential computational, recognition, and control logic is derived from and assimilated based on data samples from the neural network. The development of an artificial neural network involves three core components: the establishment of connection methodologies, the selection of neuron nodes, and the formulation of learning algorithms. Among the diverse spectrum of artificial neural networks, the back-propagation neural network, or BP neural network, is recognized for its prevalence and advanced development [21]. The architecture of the BP neural network, depicted in Figure 1, showcases its structured approach to processing and learning from input data, thereby enabling effective pattern recognition and data approximation capabilities.

BP neural networks are characterized by their ability to adapt to complex control problems through the augmentation of network layers, particularly within large-scale and multivariate systems, where high stability and effectiveness are demonstrated. This capability is essential for constructing nonlinear mapping models that necessitate a high degree of discretization. Given an adequate dataset, deep dynamic features can be learned by BP neural networks, thereby enhancing their adaptability to new conditions and unknown perturbations. In comparison to other neural network types, such as RBF networks and GRNN networks, a broader range of application benefits is offered by BP networks in complex prediction tasks, where superior generalization capabilities and high response efficiency are exhibited.

3.1.1. Connection Method

The common BP neural network adopts the three-layer structure of “n-m-1”, with n nodes in the input layer, m nodes in the hidden layer, and one node in the output layer, and each layer is fully connected to the next layer.

3.1.2. Node Selection

N parameters $\left(x_1,x_2,x_3,\dots ,x_N\right)$ of the input layer represent the N input parameters of the prediction model.

Output layer one parameter y, where y is the modified predicted value.

Kolmogorov’s theorem yields that since there are n nodes in the input layer and one node in the output layer, the number of implied nodes in the intermediate layer satisfies the following relation:

$$m=(\sqrt{a+b}+c),0\le c\le 10$$

(1)

And, the hidden layer results and output layer results can be expressed by the following formulas:

$$a_i^{(l+1)}=g({\displaystyle \sum _{j=0}{\theta }_{ij}^l{x}_j)}$$

(2)

$$y_m=g({\displaystyle \sum _{j=0}{\theta }_{ij}^l{a}_j)}$$

(3)

In the formulas, $a_i^{(l+1)}$ represents the i-th activation unit of the i + 1-th layer; $y_m$ represents the m-th output of the system; ${\theta }_{ij}^l$ represents the weight of the i-th layer mapped to the l + 1-th layer; and function g(x) represents the nonlinear calculation result of linear mapping.

3.1.3. Learning Algorithms

The BP network employs the back-propagation algorithm for parameter updates. Initially, the loss function is computed, followed by a layer-by-layer calculation of the partial derivatives of the loss function. The network is then updated using the gradient descent algorithm. The parameter update algorithm for the output layer is as follows.

$$\frac{\partial }{\partial {\theta }_{ij}^l}J(\theta )=\frac{\partial J(\theta )}{\partial y_i}\times \frac{\partial y_i}{\partial ne{t}_i^l}\times \frac{\partial ne{t}_i^l}{\partial {\theta }_{ij}^l}$$

(4)

$$ne{t}_i^l={\displaystyle \sum _{j=0}{\theta }_{ij}^l{a}_j}$$

(5)

$${\theta }_{ij}^{l-1}={\theta }_{ij}^l-\alpha \frac{\partial }{\partial {\theta }_{ij}^l}J(\theta )$$

(6)

where $J(\theta )$ represents the loss function of the BP neural network; $y_i$ is the network output; and $\alpha$ is the learning rate.

3.2. WOA

The whale optimization algorithm (WOA) is a bio-inspired heuristic search algorithm [22]. It models its search patterns on the intricate hunting strategies of whales, encompassing three distinct phases: encircling prey, deploying bubble-net attacks, and foraging. The underlying mathematical principles guiding the algorithm’s logic are elucidated below.

3.2.1. Phase 1: Surrounding the Prey

Generate a random initialization community $x_i$ within the search range.

Suppose that in d-dimensional space, the current position of the best whale individual $X^{*}$ is $(X_1^{*},X_2^{*},\dots ,X_{\mathrm{d}}^{*})$, and the position of the whale individual $X^j$ is $(X_1^j,X_2^j,\dots ,X_{\mathrm{d}}^j)$. Then, the formula for the next generation $X^{j+1}$ position $(X_1^{j+1},X_2^{j+1},\dots ,X_{\mathrm{d}}^{j+1})$ of whale $X^j$ under the influence of the best whale individual is

$$X_k^{j+1}=X_k^{*}-A_1\times D_k,$$

(7)

$$D_k=\left|C_1\times X_k^{*}-X_k^j\right|,$$

(8)

$$C_1=2r_2,$$

(9)

$$A_1=2a\times r_1-a,$$

(10)

where $x_i$ is the location of the search agent, $lb$ is the lower bound of the variable, $ub$ is the upper bound of the variable, $X_k^{j+1}$ denotes the $k_{th}$ component of the spatial coordinate $X^{j+1}$, $a$ is a linear decrease from 2 to 0 as the number of iterations increases, and $r_1$ and $r_2$ are a random number from 0 to 1.

3.2.2. Phase 2: Foam-net Attack

The bubble-net attack simulates the humpback whale’s characteristic behavior of spitting bubbles while feeding and includes two mathematical models, contraction encircling and spiral position updating.

This contraction encircling behavior is essentially the same as the encirclement of prey behavior described above, with the difference being the range of values for $A_1$. The difference between the two actions is the range of values for $A$. The value of $A$ is adjusted from $\left[-a,a\right]$ to $\left[-1,1\right]$ because the meaning of contraction encirclement is to move the whale in the current position closer to the whale in the best position at the current position.

Spiral position updating. The individual whale at the current position spirals closer to the best individual whale at the current position.

$$X_k^{j+1}=X_k^{*}+D_k\times e^{bl}\times \cos (2\pi l),$$

(11)

$$D_k=\left|X_k^{*}-X_k^j\right|,$$

(12)

where $b$ is the logarithmic spiral shape constant and $l$ is a random number between −1 and 1.

When hunting, humpback whales not only need to shrink and surround but also need to spiral towards the prey. Therefore, each chooses the foam-net attack mode with a probability of 50%. That is, the mathematical model is as follows:

$$X_k^{j+1}=\left\{\begin{array}{c}{X}_k^{*}-A_1\times D_k,p<0.5\\ X_k^{*}+D_k\times e^{bl}\times \cos (2\pi l),p\ge 0.5\end{array}\right.,$$

(13)

3.2.3. Phase 3: Search and Predation

Assuming that the position of a random whale individual $X^{rand}$ in d-dimensional space is $(X_1^{rand},X_2^{rand},\dots ,X_d^{rand})$, and the position of the current whale individual $X^j$ is $(X_1^j,X_2^j,\dots ,X_{\mathrm{d}}^j)$, the mathematical model of search and predation is

$$X_k^{j+1}=X_k^{rand}-A_1\times D_k,$$

(14)

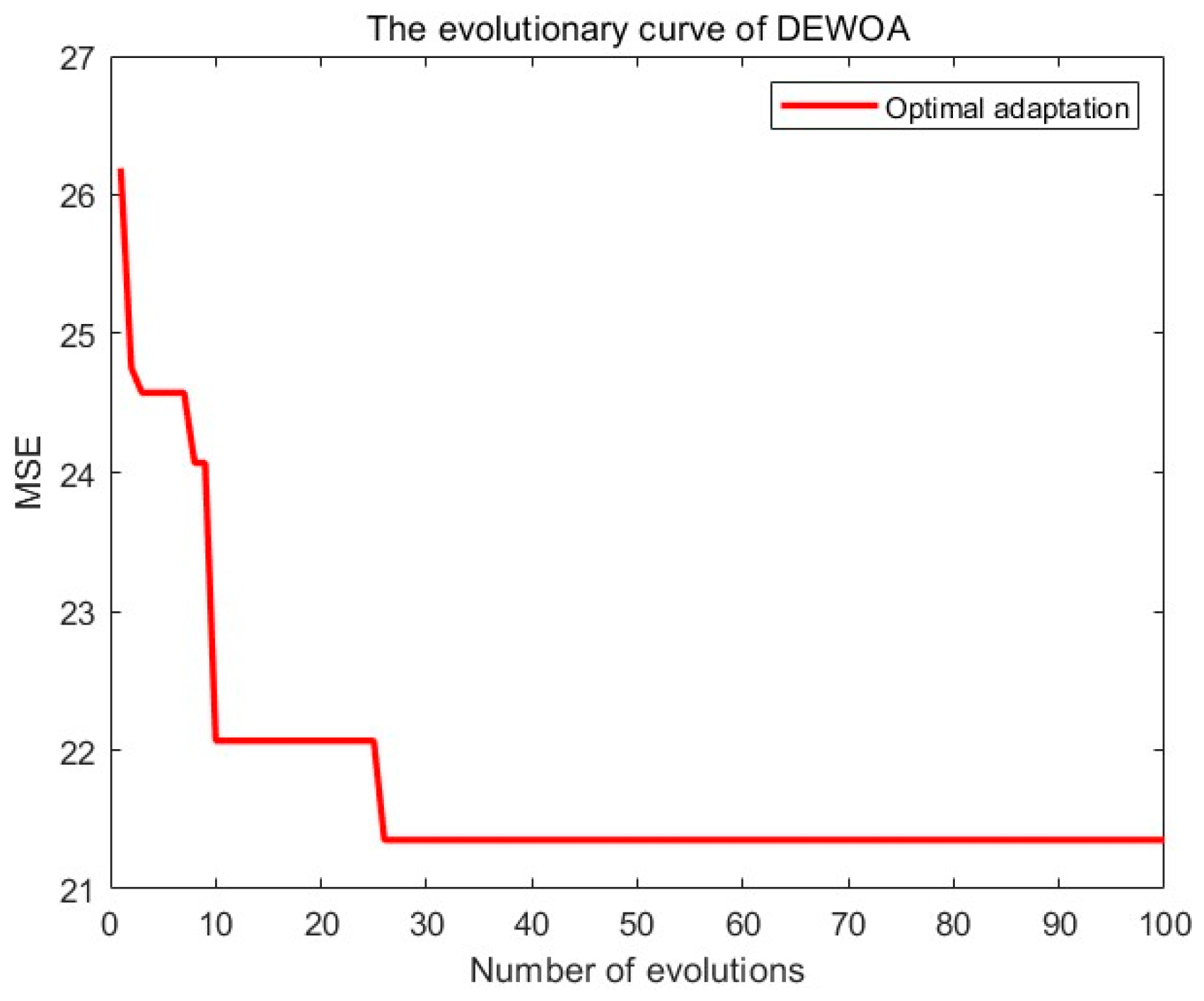
3.3. Algorithmic Improvement Methods

Despite the BP neural network’s capacity for accurate intelligent mapping in complex data systems, owing to its formidable nonlinear fitting and generalization capabilities, its performance, notably prediction accuracy and iteration efficiency, is heavily contingent upon the model’s initial parameters. Moreover, it is susceptible to entrapment in local optima amidst complex data scenarios. This research introduces an innovative enhancement method for the BP neural network by integrating the global optimization prowess and rapid iteration capabilities of the whale optimization algorithm (WOA), aiming to refine the prediction accuracy and speed of the BP neural network. The approach designates the initial weights and biases of the BP neural network as target parameters for the WOA, aligning the WOA’s fitness function with the error function of the BP neural network. Utilizing the evolutionary mechanisms of the WOA to update these parameters, a reduction in the overall error of the BP neural network is achieved, thereby facilitating the effective optimization of weights and biases. This optimization enhances the convergence velocity and global optimization efficiency of the network model, particularly in complex scenarios, yielding a prediction network of heightened accuracy and augmented generalization capacity for nonlinear and intricate problems.

However, the efficacy of WOA optimization is discovered to be significantly influenced by the choice of initial population, with traditional WOA algorithms typically generating this population randomly, thus not ensuring the optimality of the initial group. Furthermore, when faced with extensive search domains, the convergence rate of the WOA diminishes, prolonging the problem resolution time. To address these challenges, this study integrates the differential evolution (DE) algorithm for a secondary optimization of the WOA, thereby enhancing its efficiency. The DE algorithm, a heuristic search mechanism predicated on population differences, when combined with the WOA, leverages DE’s early-stage global solution identification capabilities and introduces diversity to avert local optima entrapment [23]. This synthesis not only harnesses the complementary strengths of both algorithms to simultaneously augment global search efficiency and local optimization capability but also bolsters algorithmic robustness and adaptability. Consequently, the resultant improved DEWOA-BP neural network establishes a prediction network characterized by accelerated convergence, superior prediction accuracy, and enhanced generalization ability, thereby enabling the intelligent prediction of welding deformation in automated laser welding operations.

4. Method

4.1. Overview of the Method

The amount of weld distortion in automated laser welding operations is affected by the coupling of welding speed, peak power, duty cycle, and defocusing amount in actual welding operations, with the following influence equation:

$$\Delta x\in D=\left\{D\left|D\left(x\right)=f\left(V,P_{peak},DC,S\right)\right.\right\}$$

(15)

where $\Delta x$ is the flatness difference in the form of laser welding deformation; D indicates the laser welding deformation obeys the distribution model, and D and laser welding process parameters have a close relationship; V indicates the welding speed, using the unit of mm/min; $P_{peak}$ indicates the peak power, using the unit of %; DC indicates the duty cycle, using the unit of %; S denotes the amount of defocusing in mm. Due to the existence of the coupling effect of welding process parameter action, and the role of the effect of the expression is more complex, it is more difficult to solve the above distribution model through the explicit formula method. For the above obeying model, the data samples from the pre-experiment can be used to fit the data to the above multifactor molecule’s action relationship and generate the prediction model of welding process parameters V, $P_{peak}$, DC, and S to the welding deformation Δx.

In the context of advancements in laser welding process control, a “4-input–1-output” neural network prediction model based on the enhanced DEWOA-BP neural network is presented. This model is designed to forecast laser welding deformation by employing actual welding process parameters as inputs. The nonlinear mapping model correlates these parameters with the resultant welding deformation to produce predictive outputs. Further enhancements to the model’s accuracy and iteration speed are achieved through a proposed quadratic optimization method, which utilizes the improved WOA algorithm refined with the DE algorithm. This method capitalizes on the crossover and mutation processes of the differential evolutionary algorithm to globally optimize the initial whale population of the WOA, thereby securing an optimal starting group. Subsequently, the synergistic capabilities of the DE algorithm’s global search and the WOA algorithm’s local optimization are employed to refine the initial weights and biases of the BP neural network efficiently. This optimization yields a parameter set characterized by optimal prediction accuracy and enhanced iterative efficiency, culminating in the accurate prediction of laser welding deformation. This quadratic optimization approach significantly elevates the predictive model’s accuracy and enhances the autonomy of parameter settings, making it highly applicable and versatile across complex datasets.

4.2. Model

The intelligent prediction model of weld distortion for automated laser welding proposed in this paper is shown in Figure 2 below.

5. Experiment

5.1. Experimental Settings

Experimental validation was carried out on 0.5mm-thick stainless steel sheets. For the welding experiments, a uniform batch of 304 stainless steel sheets, measuring 100 mm × 50 mm × 0.5 mm and subjected to surface deoxidation and decontamination, was selected. The JM-HG2000 laser welding machine, developed by a company based in Wuhan, was chosen for its capabilities. This machine, equipped with an IPG 2000W fiber-coupled laser and a four-axis CNC table, met the specific requirements set forth for the experiments. Furthermore, a custom welding table was employed to aid the welding procedures. As depicted in Figure 3a, this table comprised a simple horizontal fixture table and four rapid horizontal work clamps, engineered to securely hold flat parts in place during the welding process.

In addition to the welding apparatus, the Hexagon Absolute Arm, a six-axis handheld measuring arm, in combination with Ployworks MS 2020 measurement software, was utilized to assess the flatness of the weldments, as shown in Figure 3b. This involved manually maneuvering the handheld arm to touch feature points on the surface of the 304 stainless steel plate, generating multiple sets of three-dimensional spatial coordinate information. The flatness value of the stainless steel sheet was then determined by calculating the discrepancies among these planes. This approach enabled a precise and thorough measurement of the welded sheet’s flatness, significantly enhancing the experimental results’ accuracy.

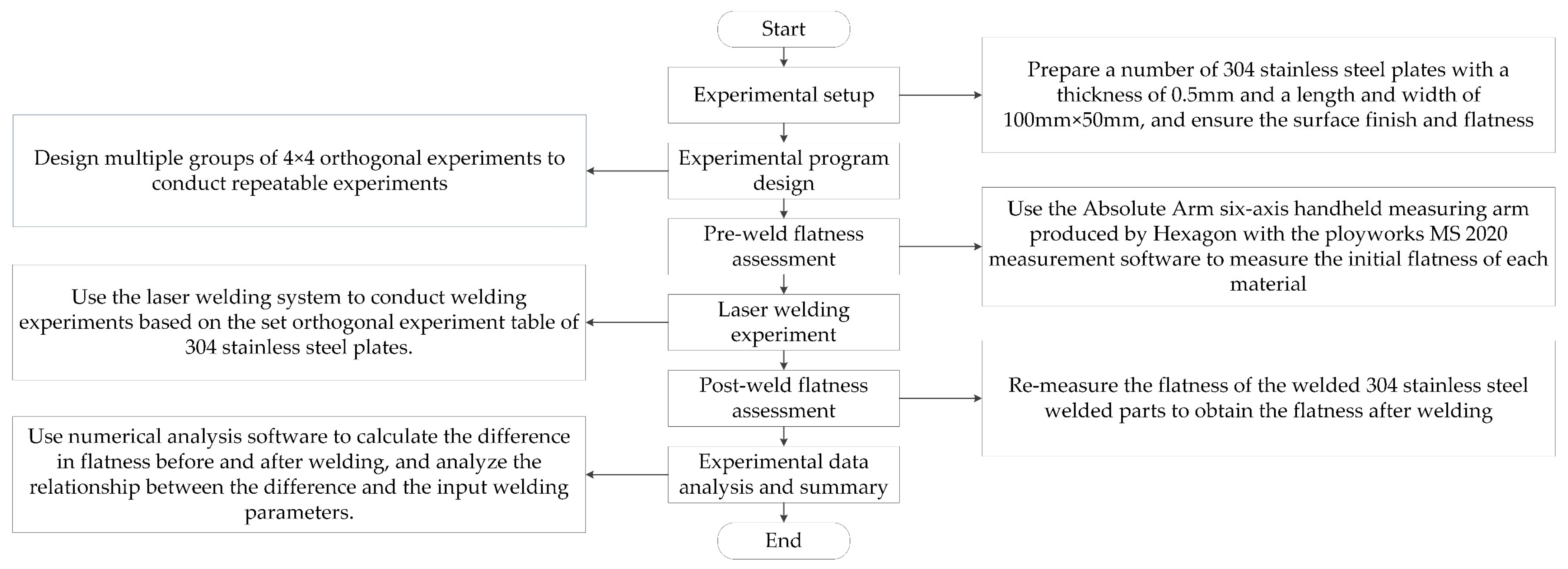
5.2. Data Acquisition Experiment

To construct a nonlinear mapping model correlating welding speed, peak power, duty cycle, defocusing amount, and welding deformation, this study orchestrates a series of laser welding experiments on 304 stainless steel sheets, employing various welding process parameters of an automated laser welding machine. Subsequent to these experiments, a six-joint hand-held measuring arm is utilized for determining the flatness pre- and post-welding, employing the disparity in flatness as a proximate measure for characterizing laser welding deformation. This facilitates the aggregation of a dataset delineating the impact of multiple welding process parameters on welding deformation.

To compile a dataset elucidating the interrelation between welding process parameters and welding deformation, this paper proposes a design for repetitive single-factor experiments on 0.5 mm 304 stainless steel sheets using laser welding, based on four welding process parameters: welding speed, peak power, duty cycle, and focal offset. The parameter values for these single-factor experiments are cataloged in

Table 1. Table of Single-Factor Experimental Parameters.

SN/Parameter	Factor 1: Welding Speed (mm/min)	Factor 2: Peak Power (%)	Factor 3: Duty Cycle (%)	Factor 4: Defocusing Amount (mm)
1	20	30	30	0
2	25	35	35	+1
3	30	40	40	+2
4	40	50	50	+5

. Aiming to mitigate the influence of random errors, each set of experimental parameters is subjected to thrice-repeated laser welding experiments, with the mean of the outcomes deemed as the final result for each parameter set. The selection of experimental parameters with reference to the mature semi-automated laser welding process parameter table, selecting the same optimal range of process parameters with the mature process, and then the optimal range combined with the existing commonly used process parameter combinations were set up for four process parameters of equidistant sampling points. This sampling method cannot include all possible parameter combinations under the welding process parameters, but through the four equidistant sampling points that approximate the discussion of all possible process parameter effects, which ensures that the data collection experiments can be obtained to cover all the welding effects of the data samples. Since the purpose of the experiment is to collect data for subsequent prediction model validation experiments, it is feasible to use this simple sampling method to design the experimental program for laser welding process parameter data collection experiments under the premise of ensuring the number of samples.

The designed experimental workflow for data acquisition is illustrated in Figure 4, encompassing a total of six phases: experimental setup, experimental program design, pre-weld flatness assessment, the execution of laser welding experiments, post-weld flatness assessment, and the subsequent data analysis and synthesis.

5.3. Model Validation Experiment

To assess the reliability of the DEWOA-BP neural network-based prediction model for laser welding deformation, the 256 experimental samples collected in this study were randomly shuffled and segregated into two subsets: 236 training samples and 20 test samples, arranged in no particular order. The DEWOA-BP prediction network was then established using the 236 training samples, and its reliability was evaluated by employing the 20 test samples. Meanwhile, to highlight the enhanced performance of the DEWOA-BP prediction network introduced in this study, comparative analyses were conducted. The traditional BP neural network, traditional RBF neural network, traditional GRNN neural network, and statistical methods were utilized to construct prediction models using the same training dataset, thereby forming an experimental control group. Predictive comparisons were then carried out among the constructed improved DEWOA-BP prediction model, traditional BP prediction model, traditional RBF prediction model, traditional GRNN prediction model, and the model generated via statistical methods. These comparisons were conducted using the same test sample set to ascertain the predictive outcomes of each model. This methodology ensured that the enhanced capabilities of the DEWOA-BP network could be effectively measured against established techniques under identical testing conditions.

The construction of a “4-input–1-output” laser welding deformation model was carried out using MATLAB R2022b, with the initial model parameters set as detailed in

Table 2. Values of initial parameters of the DEWOA-BP prediction algorithm.

Parameter		Value
BP	Number of input layer nodes	4
	Number of output layer nodes	1
	Number of hidden layer nodes	3–12 (adaptive choices)
	Number of training sessions	1000
	Learning rate	0.01
WOA	Minimum error of training target	0.00001
	Maximum number of iterations	100
	Population size	50
	Upper bound	3
	Lower bound	−3
DE	Population size	50
	Variation factor	0.75
	Crossing probability	0.9

. The evolution curve of the DEWOA-BP prediction model developed herein is depicted in Figure 5.

6. Results and Discussion

By analyzing and calculating the prediction results from the improved DEWOA-BP prediction model, the traditional BP prediction model, the traditional RBF prediction model, the traditional GRNN prediction model, and the prediction model generated via the statistical method, comparison plots for each model’s prediction results and prediction errors were obtained, as illustrated in Figure 6 and Figure 7, respectively. In addition to these graphical comparisons, the superiority of the DEWOA-BP prediction model was further elucidated through a detailed statistical analysis of the mean absolute error (MAE), mean squared error (MSE), root-mean-squared error (RMSE), and mean absolute percentage error (MAPE) for each model. These statistical measures are presented in

Table 3. Comparison of MAE, MSE, RMSE, and MAPE of the improved DEWOA-BP prediction model, the traditional BP prediction model, the traditional RBF prediction model, the traditional GRNN prediction model, and the prediction model generated via the statistical method.

Type	DEWOA-BP	BP	RBF	GRNN	Statistical Methods
MAE	0.07	0.2175	0.2376	0.287	0.5189
MSE	0.0109	0.0687	0.0833	0.0985	0.3567
RMSE	0.1043	0.2621	0.2887	0.3138	0.5973
MAPE	42.5292	312.2395	357.6041	358.3177	821.0032

, providing a more accurate and intuitive representation of the comparative performance of the models.

Incorporating both the graphical and tabular data, a detailed analysis and discussion are presented as follows:

(1)

From Figure 6 and Figure 7, it is demonstrated that the prediction effectiveness of the model employing statistical methods is significantly lacking. Specifically, a consistent prediction deviation greater than 0.8 mm is observed across 20 test samples, with an error rate exceeding 100%. As detailed in Table 3, the mean absolute error (MAE) is recorded at 0.5189, the mean squared error (MSE) at 0.3567, the root-mean-squared error (RMSE) at 0.5973, and the mean absolute percentage error (MAPE) at 821.0032. These metrics substantially underperform compared to those of alternative neural network-based prediction models. The inefficacy of statistical methods in scenarios such as laser welding, characterized by high levels of data discretization and significant noise interference, renders them unsuitable for applications requiring high precision. The principal limitation of the statistical approach is attributed to its reliance on predetermined functional models, which fail to accommodate the variability and noise prevalent in discrete laser welding data samples.

(2)

From Figure 6 and Figure 7, it can be found that the traditional general regression neural network (GRNN) is shown to inadequately reflect effective predictions on the test data samples, with minimal variation observed across the 20 test results. The data presented in Table 3 indicate an average MAE of 0.287, an MSE of 0.0985, an RMSE of 0.3138, and a MAPE of 358.3177. These results suggest that the GRNN model does not produce a viable prediction under the tested conditions. The inherent design of the GRNN, which is based on probability density functions and demonstrates a lack of sensitivity to data distribution, is found to be ineffective against test samples marked by high sparsity and severe data noise, leading to poor predictive performance in precision-critical applications.

(3)

From Figure 6 and Figure 7, it can be found that the data trends of the traditional BP and RBF prediction neural networks are essentially consistent with the actual data, indicating a certain level of prediction feasibility. However, large prediction deviations are still present in some of the test samples. As a result, the prediction outcomes of the traditional BP and RBF neural networks can be seen as approximations of the welding deformation change rules, but due to significant error fluctuations, they are not suitable for practical welding site applications. As shown in Table 3, the average mean absolute error (MAE) of the BP prediction neural network is 0.2175, the mean squared error (MSE) is 0.0687, the root-mean-squared error (RMSE) is 0.2621, and the mean absolute percentage error (MAPE) is 312.2395. Similarly, the RBF prediction neural network displays an average MAE of 0.2376, MSE of 0.0833, RMSE of 0.2887, and MAPE of 357.6041. Although both models demonstrate some effectiveness, significant accuracy issues remain. The primary reason for the challenges faced by the BP prediction neural network is that its training relies on optimization algorithms such as gradient descent, which carry the risk of converging to local minima rather than the global optimal solution. In the case of the RBF neural network, its prediction mechanism involves mapping the input to a high-dimensional space through a radial basis function and then applying a linear model for regression or classification, which can be slightly inadequate as sample complexity increases. After thoroughly analyzing the deficiencies of the two models, it is suggested that the prediction performance of the BP neural network could be optimized by improving the initial parameter settings, preventing convergence to local minima, and striving for the global optimum. Such improvements would allow the traditional BP neural network to maintain its predictive capabilities in the face of complex problems and nonlinear models while reducing prediction fluctuations and enhancing prediction stability. Therefore, selecting the BP neural network for model optimization in this study is deemed reasonable.

(4)

From Figure 6 and Figure 7, it can be found that the DEWOA-BP prediction neural network achieves higher prediction accuracy under error allowance conditions when compared with the BP and RBF prediction neural networks. The results from 20 test samples are generally consistent with the actual sample data, with the prediction error for 10 samples within 0.05 mm and for 18 test samples within 0.1 mm, thus meeting the demands of actual laser welding operations. As presented in Table 3, the average mean absolute error (MAE) for the DEWOA-BP network is 0.07, which is 67.82% lower than that of the traditional BP network and 70.54% lower than that of the traditional RBF network. The mean squared error (MSE) is noted at 0.0109, which is 84.13% lower than that of the traditional BP network and 86.91% lower than that of the traditional RBF network. Additionally, the root-mean-squared error (RMSE) is recorded at 0.1043, 60.21% lower than the BP network and 63.87% lower than the RBF network. The mean absolute percentage error (MAPE) stands at 42.5292, which is 86.38% lower than the BP network and 88.14% lower than the RBF network. Due to factors such as uneven plate quality and environmental variables, occasional errors are introduced in the welding sample data, typically resulting in large fluctuations in welding prediction results, which in turn contribute to high MAPE values. However, from the perspective of practical requirements, the DEWOA-BP prediction neural network proposed in this study is shown to satisfactorily meet operational needs and exhibit a significant degree of reliability. The enhanced global optimization capability of the DEWOA-BP model, in comparison with the traditional BP and RBF models, allows for a more thorough analysis and synthesis of the complex relationships within the sample data. This culminates in the generation of more accurate and reliable predictive rules, effectively meeting the requirements for setting automated laser welding process parameters.

7. Conclusions

(1)

Despite the complexity of laser welding deformation during laser welding operations, the data from the laser welding process are compiled and analyzed in this study, and combined with neural network technology, a novel method for predicting welding deformation is proposed. This method enables intelligent predictions from laser welding process parameters to laser-induced deformation. The prediction accuracy and stability of the model are found to generally meet the requirements of the welding process. An analysis and assessment of welding quality based on welding process parameters can be conducted prior to actual welding operations, thereby determining the appropriateness of the set laser welding process parameters.

(2)

A BP prediction neural network based on the differential progress optimization algorithm and enhanced via secondary optimization using the whale optimization algorithm is introduced in this paper. This approach is employed for predicting laser welding deformation from laser welding process parameters. By utilizing the DEWOA algorithm to optimize the BP neural network, traditional limitations such as local optimization inefficiency or poor convergence are effectively overcome, significantly enhancing the global optimization capabilities of the BP neural network. As a result, the neural network’s capacity for complex data fitting and mapping is substantially improved. The predictive performance of this model is shown to be superior to that of the traditional BP prediction model, the traditional RBF prediction model, the traditional GRNN prediction model, and models generated via statistical methods. This advancement meets the requirements of actual automated laser welding operations and exhibits strong predictive reliability.

(3)

The integration and advancement of intelligent algorithms with traditional machining technology represent a crucial aspect of the intelligent and digital transformation of the machinery industry. This paper proposes the implementation of an intelligent prediction algorithm, which is significant not only for the intelligent transformation of laser welding but also provides strong guidance for traditional machining technologies like milling, grinding, and spraying, which are labor-intensive and operate in harsh environments with stringent requirements for processing quality and stability. Departing from traditional simulation methods and utilizing actual processing data, modern computational technologies such as neural networks are employed to construct a nonlinear mapping model. The generalization and nonlinear fitting abilities of neural networks are harnessed to uncover deep data relationships that traditional data models cannot reveal. This enables predictions and analyses based on deep data connections and facilitates seamless integration with other automation units and intelligent modules for collaborative operations and system integration. Ultimately, this approach contributes to building a genuinely significant factory environment and realizing the industrial revolution and technological upgrading of the traditional machining industry.