Investigation of Torque and Reduction of Torque Ripples through Assisted-Poles in Low-Speed, High-Torque Density Spoke-Type PMSMs
Abstract
1. Introduction
2. Machine Topology and Structural Designs
3. Air-Gap Flux Density Distribution
3.1. Air-Gap Flux Density Harmonics
3.2. Flux Density Harmonics and Average Torque Production Mechanism
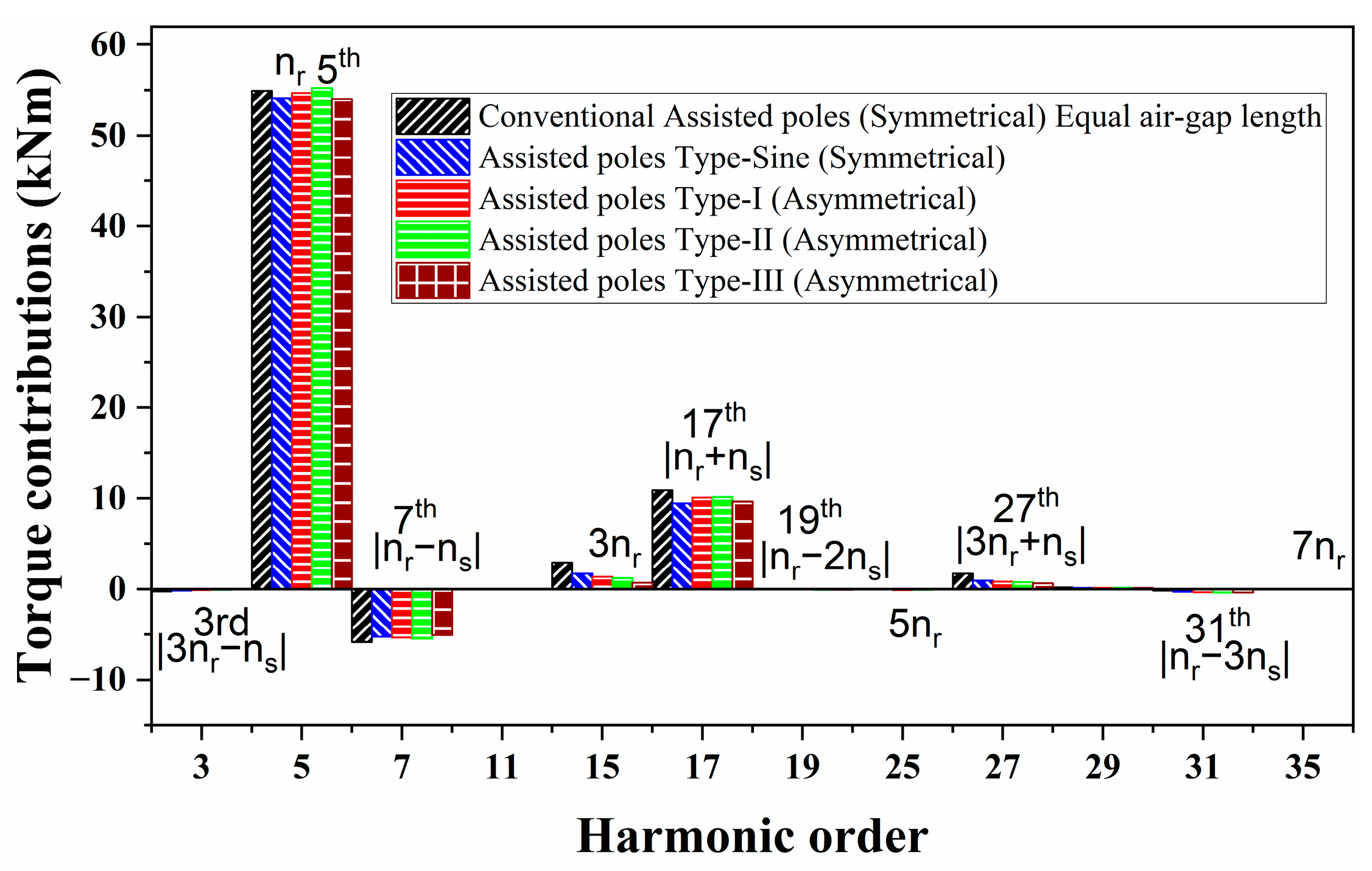
3.3. Stator and Rotor MMFs and Torque Ripple Response
3.4. FEA Validation
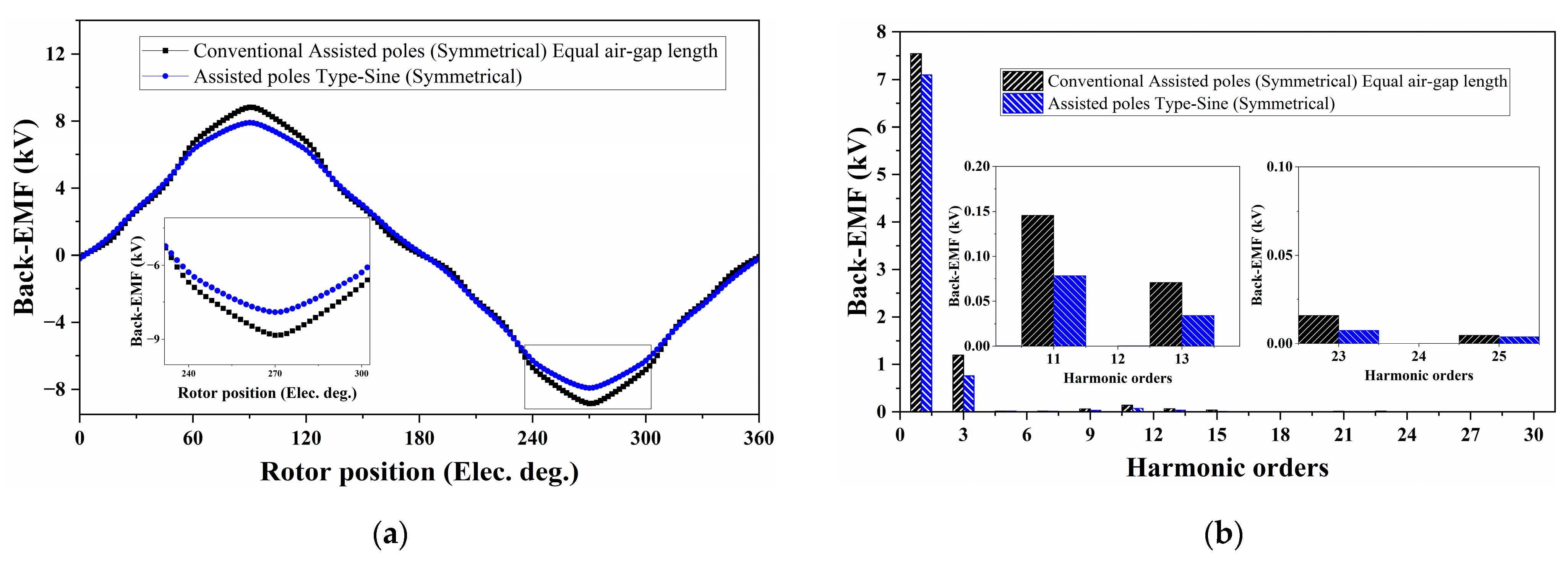
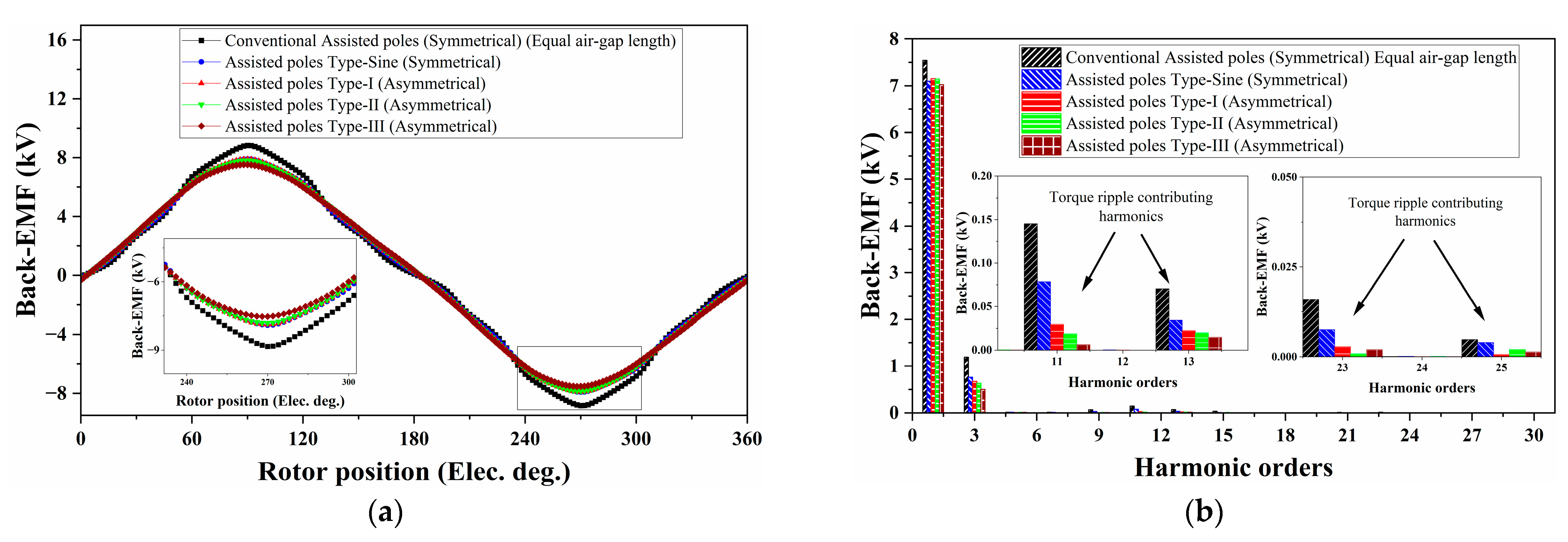
3.5. Back-EMF Response
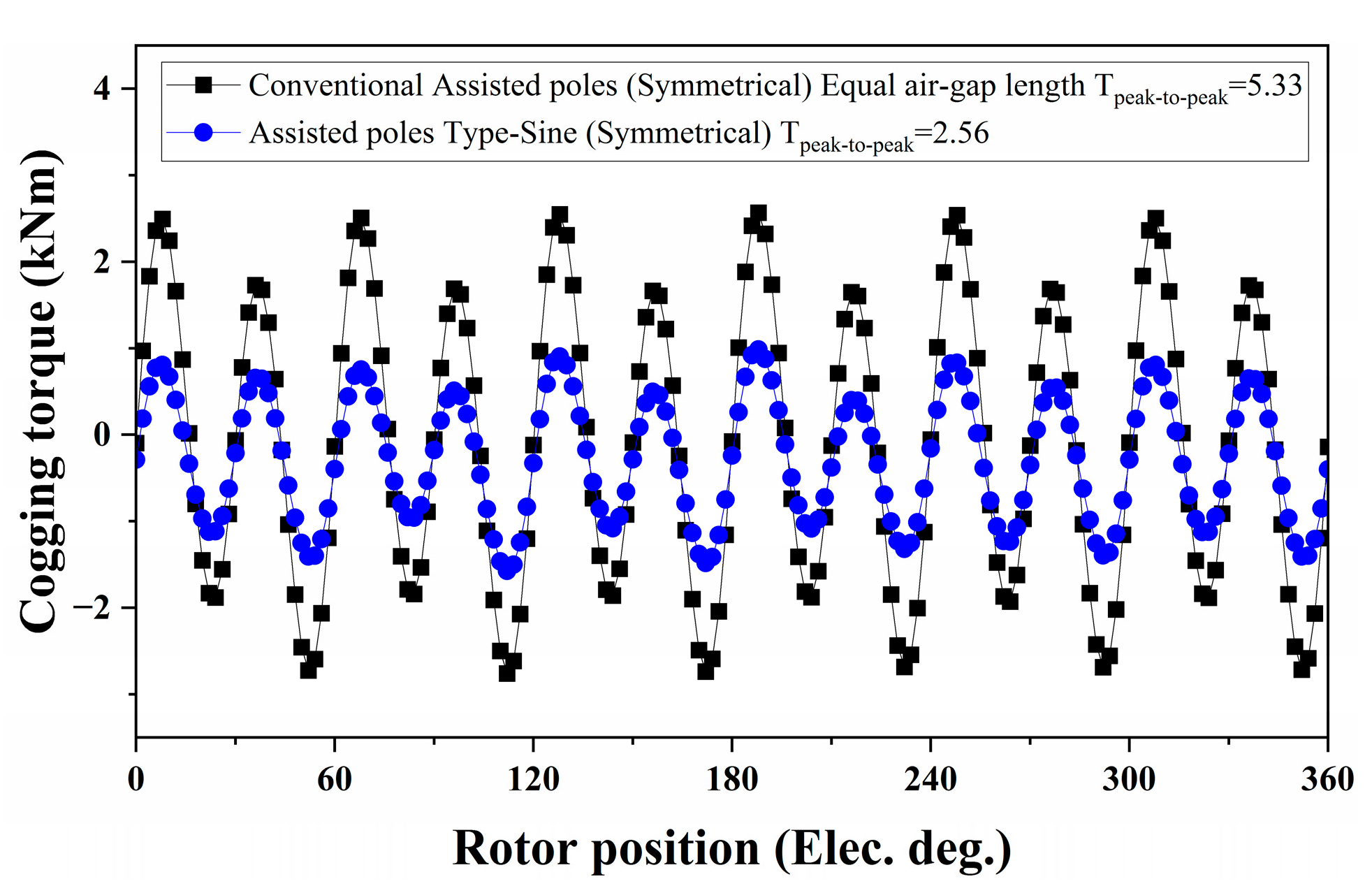
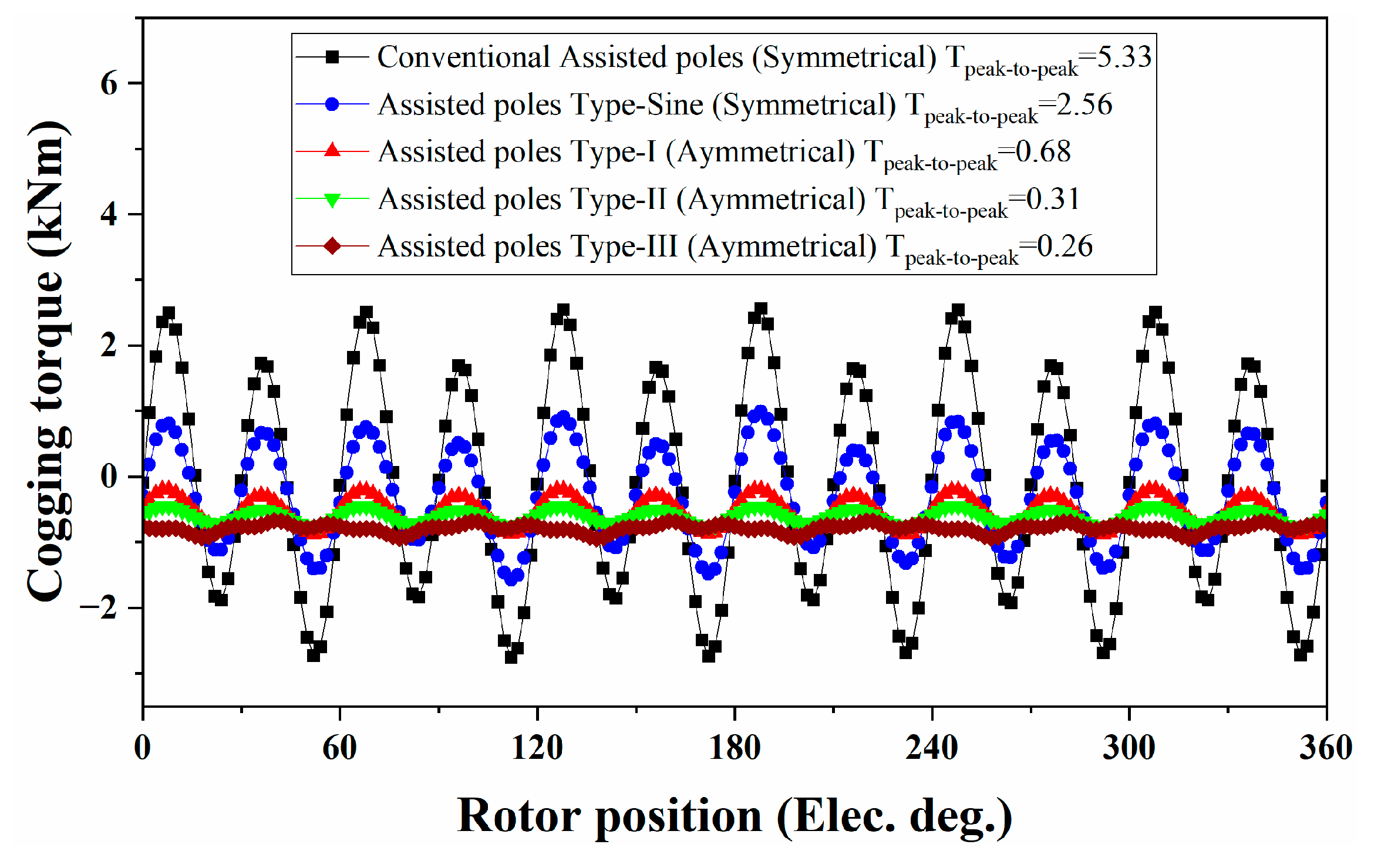
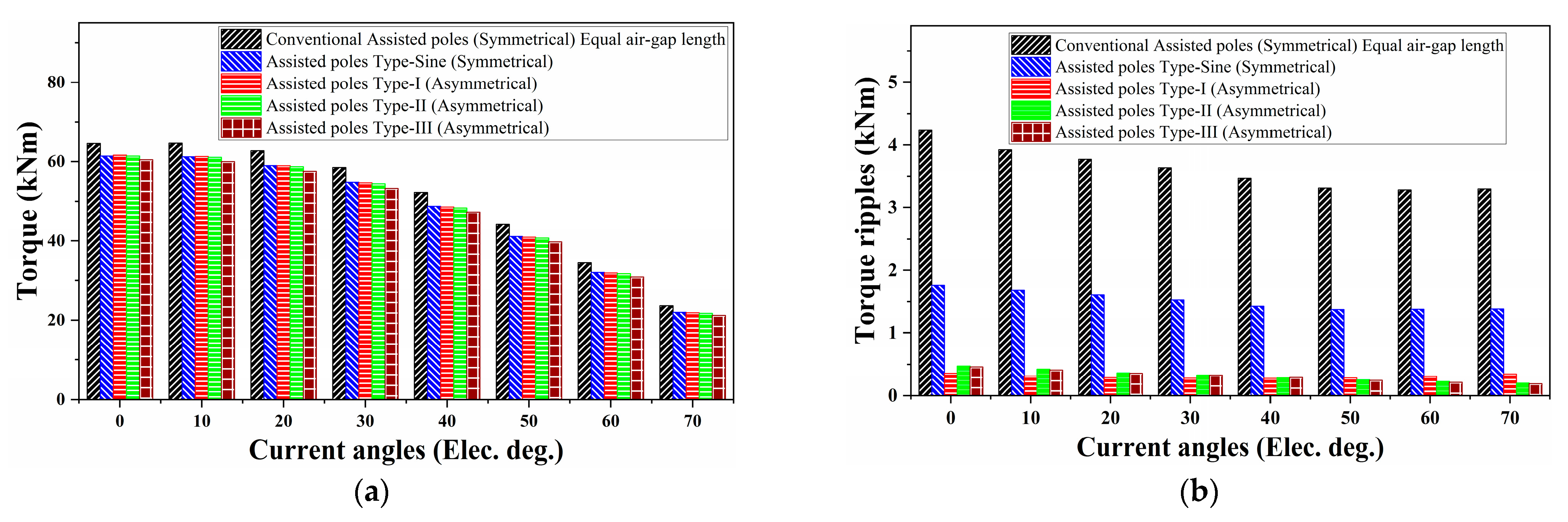
3.6. Generated Torque and Torque Ripple Comparison
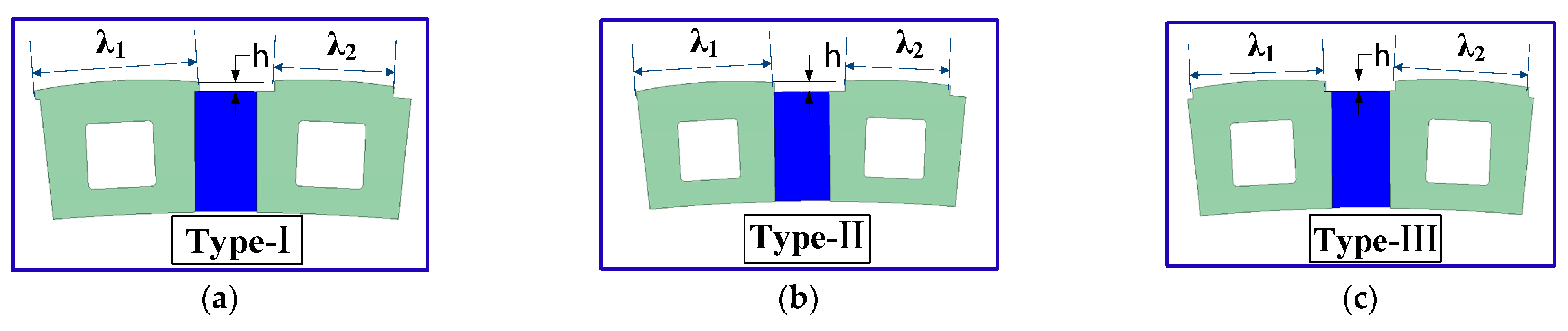
4. Torque Ripple Reduction through Asymmetrically Designed Assisted-Poles
5. Validation of Torque Ripple Reduction through Asymmetrically Designed Assisted Poles
6. FEA Validation and Comparative Analysis of Machine Designs with Symmetrical and Asymmetrical Assisted-Poles
6.1. Air-Gap Flux Density and Average Torque Response
6.2. Back-EMF Response Analysis
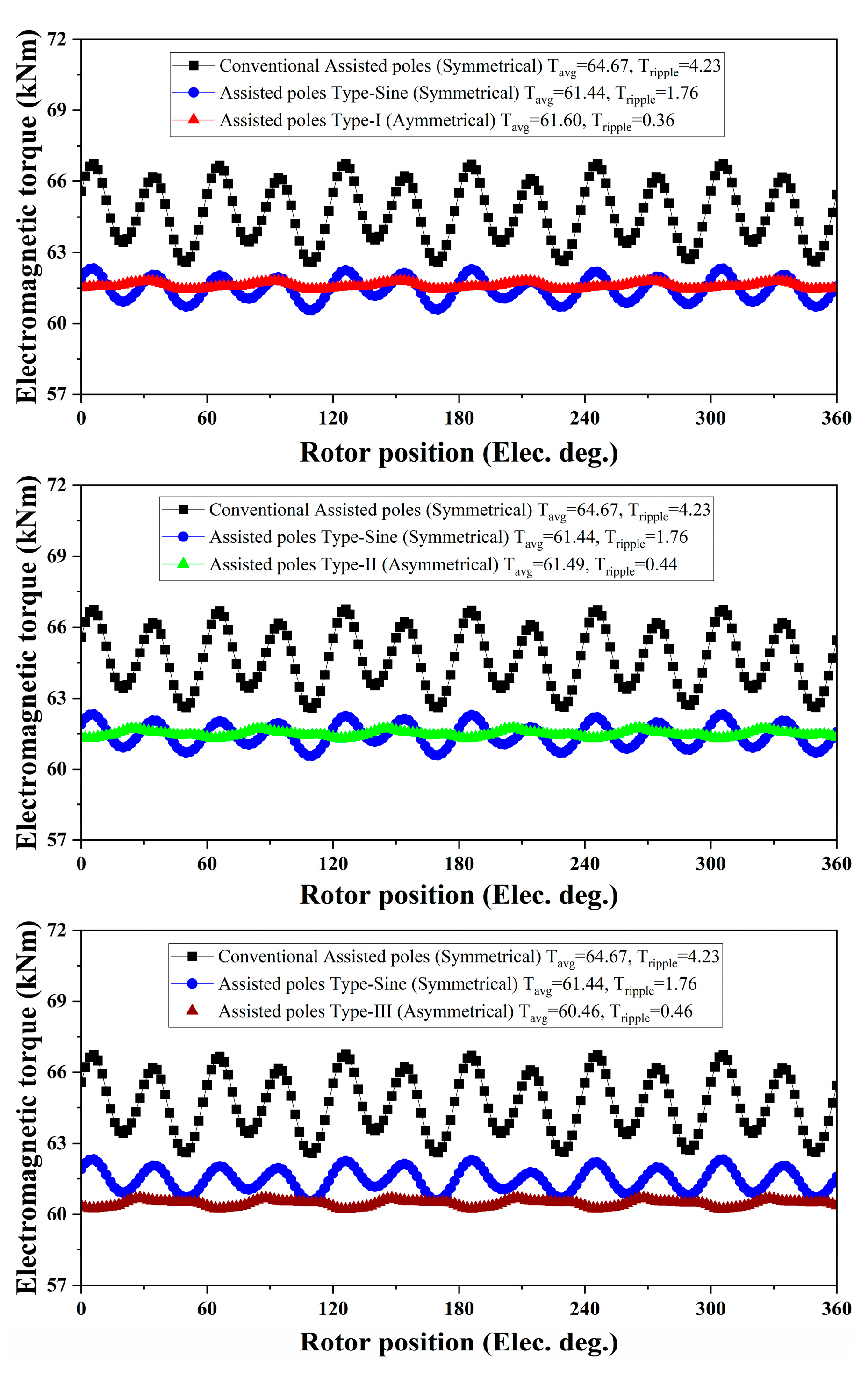
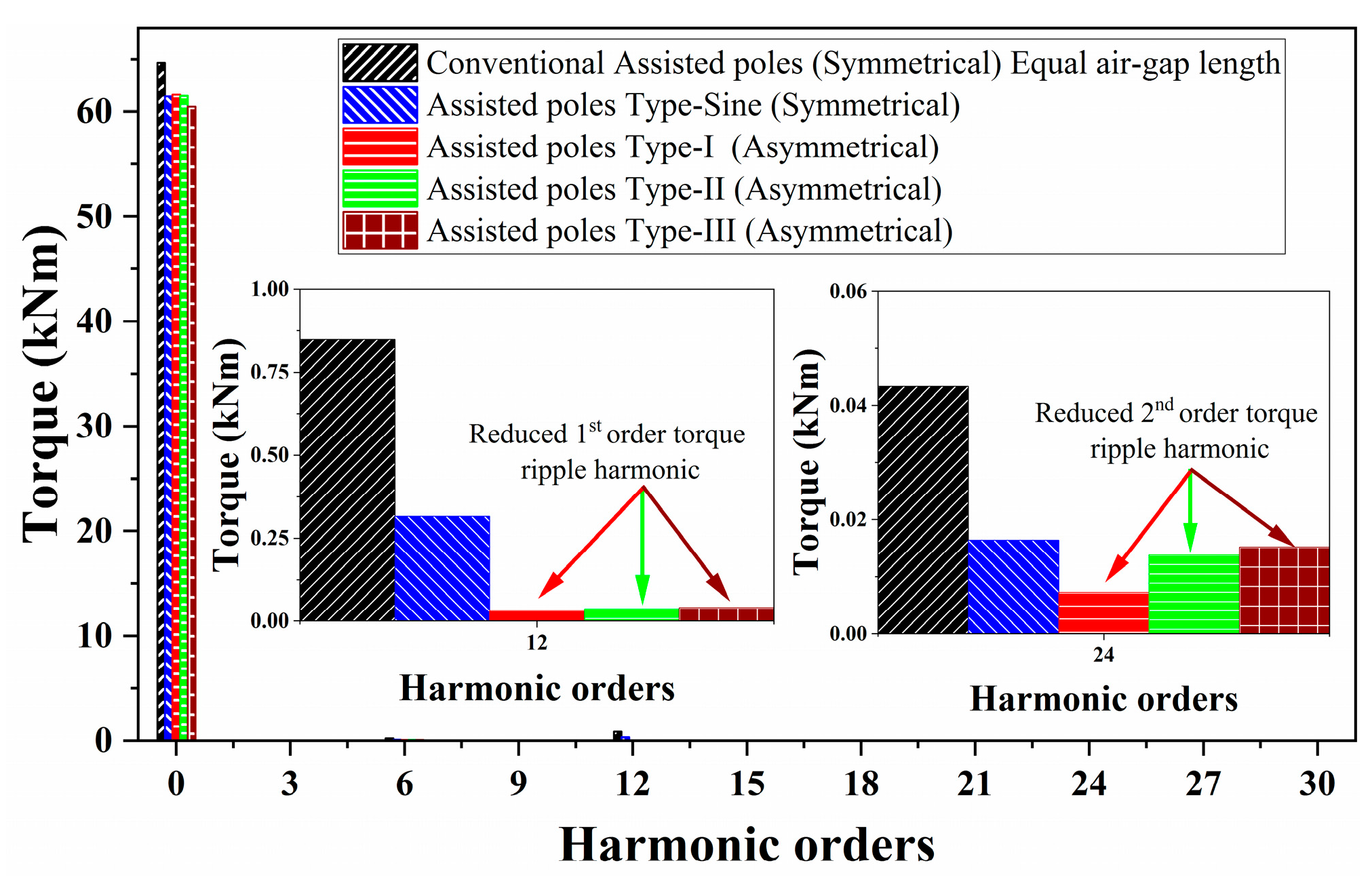
6.3. Torque Response Analysis
7. Conclusions
- (1)
- The air-gap magnetic flux density harmonic order (nr), equal to the number of pole pairs, is the main (air-gap flux density and torque producing) harmonic component for the spoke-type PMSM having symmetrical and asymmetrical designs of the assisted-poles and having FSCW configuration. Additionally, modulated air-gap magnetic field harmonics, which contribute a considerable portion to overall air-gap flux density distribution and torque production, are also explored.
- (2)
- By analyzing the assisted-poles geometries (symmetrical and asymmetrical) for the machine prototype, it has been established that the pole–arc ratio in the case of asymmetrically designed assisted-poles can be varied to obtain optimized values, which can eliminate the corresponding torque ripple producing rotor-MMF harmonics resulting in reduced torque ripples and cogging torque.
- (3)
- The proposed generalized torque ripple reduction technique can be applied to different designs of the machine prototype having asymmetrically designed assisted-poles to reduce the corresponding torque ripples through the proposed pole–arc ratio selection technique.
- (4)
- In further research, the impact of asymmetrical assisted-poles designs on the radial forces, vibration, and noise response will be investigated to analyze the machine prototype for its vibro-acoustic behavior.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boldea, I.; Tutelea, L.N.; Parsa, L.; Dorrell, D.G. Automotive Electric Propulsion Systems with Reduced or No Permanent Magnets: An Overview. IEEE Trans. Ind. Electron. 2014, 61, 5696–5711. [Google Scholar] [CrossRef]
- El-Refaie, A. Fractional-slot Concentrated-windings Synchronous Permanent Magnet Machines: Opportunities and Challenges. IEEE Trans. Ind. Electron. 2010, 57, 107–121. [Google Scholar] [CrossRef]
- Morimoto, S.; Ooi, S.; Inoue, Y.; Sanada, M. Experimental Evaluation of a Rare-earth-free Pmasynrm with Ferrite Magnets for Automotive Applications. IEEE Trans. Ind. Electron. 2014, 61, 5749–5756. [Google Scholar] [CrossRef]
- Kim, S.-I.; Park, S.-H.; Park, T.; Cho, J.; Kim, W.-H.; Lim, S. Investigation and Experimental Verification of a Novel Spoke-type Ferrite-magnet Motor for Electric-vehicle Traction Drive Applications. IEEE Trans. Ind. Electron. 2014, 61, 5763–5770. [Google Scholar] [CrossRef]
- Liu, G.; Zhipeng, L.; Zhao, W.; Chen, Q.; Xu, G. Third Harmonic Current Injection in Fault-tolerant Five-phase Permanent-magnet Motor Drive. IEEE Trans. Power Electron. 2018, 33, 6970–6979. [Google Scholar] [CrossRef]
- Jia, H.; Cheng, M.; Hua, W.; Zhao, W.; Li, W. Torque Ripple Suppression in Flux-switching PM Motor by Harmonic Current Injection Based on Voltage Space-vector Modulation. IEEE Trans. Magn. 2010, 46, 1527–1530. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, W.; Liu, G.; Zhipeng, L. Extension of Virtual-signal-injection-based MTPA Control for Five-phase IPMSM into Fault-tolerant Operation. IEEE Trans. Ind. Electron. 2019, 66, 944–955. [Google Scholar] [CrossRef]
- Carraro, E.; Bianchi, N.; Zhang, S.; Koch, M. Design and Performance Comparison of Fractional Slot Concentrated Winding Spoke Type Synchronous Motors with Different Slot-pole Combinations. IEEE Trans. Ind. Appl. 2018, 54, 2276–2284. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Gong, W.; Qu, L.; Zhao, W.; Shen, Y. Design of a Spoke-type Permanent-magnet Motor with Optimal Winding Configuration for Electric Vehicle Applications. J. Appl. Phys. 2012, 111, 07E710. [Google Scholar] [CrossRef]
- Zhao, W.; Lipo, T.A.; Kwon, B.-I. Dual-stator Two-phase Permanent Magnet Machines with Phase-group Concentrated-coil Windings for Torque Enhancement. IEEE Trans. Magn. 2015, 51, 8112404. [Google Scholar] [CrossRef]
- Hwang, K.-Y.; Rhee, S.-B.; Yang, B.-Y.; Kwon, B.-I. Rotor Pole Design in Spoke-type Brushless DC Motor by Response Surface Method. IEEE Trans. Magn. 2007, 43, 1833–1836. [Google Scholar] [CrossRef]
- Liu, F.; Zhu, X.; Wu, W.; Quan, L.; Xiang, Z.; Hua, Y. Design and Analysis of an Interior Permanent Magnet Synchronous Machine with Multiflux-barriers Based on Flux-intensifying Effect. IEEE Trans. Appl. Supercond. 2018, 28, 5201005. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Zhao, W.; Mingming, S.; Liu, Z. Design and Analysis of the New High-reliability Motors with Hybrid Permanent Magnet Material. IEEE Trans. Magn. 2014, 50, 8207010. [Google Scholar] [CrossRef]
- Liang, P.; Chai, F.; Yu, Y.; Chen, L. Analytical Model of a Spoke-type Permanent Magnet Synchronous In-wheel Motor with Trapezoid Magnet Accounting for Tooth Saturation. IEEE Trans. Ind. Electron. 2019, 66, 1162–1171. [Google Scholar] [CrossRef]
- Zhao, W.; Kwon, J.-W.; Wang, X.; Lipo, T.A.; Kwon, B.-I. Optimal Design of a Spoke-type Permanent Magnet Motor with Phase-group Concentrated-coil Windings to Minimize Torque Pulsations. IEEE Trans. Magn. 2017, 53, 8104604. [Google Scholar] [CrossRef]
- Zhang, P.; Sizov, G.Y.; Ionel, D.M.; Demerdash, N.A.O. Establishing the Relative Merits of Interior and Spoke-type Permanent-magnet Machines with Ferrite or Ndfeb Through Systematic Design Optimization. IEEE Trans. Ind. Appl. 2015, 51, 2940–2948. [Google Scholar] [CrossRef][Green Version]
- Zhao, W.; Ma, A.; Ji, J.; Chen, X.; Yao, T. Multiobjective Optimization of a Double-side Linear Vernier PM Motor Using Response Surface Method and Differential Evolution. IEEE Trans. Ind. Electron. 2020, 67, 80–90. [Google Scholar] [CrossRef]
- Ge, X.; Zhu, Z.-Q.; Li, J.; Chen, J.T. A Spoke-type IPM Machine with Novel Alternate Airspace Barriers and Reduction of Unipolar Leakage Flux by Step-staggered Rotor. IEEE Trans. Ind. Appl. 2016, 52, 4789–4797. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, G.; Zhai, F.; Liu, G. A Novel Spoke-type PM Motor with Auxiliary Salient Poles for Low Torque Pulsation. IEEE Trans. Ind. Electron. 2020, 67, 4762–4773. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, G.; Liu, G.; Zhao, W.; Liu, L.; Lin, Z. Torque Ripple Reduction in Five-phase IPM Motors by Lowering Interactional MMF. IEEE Trans. Ind. Electron. 2018, 65, 8520–8531. [Google Scholar] [CrossRef]
- Fornasiero, E.; Bianchi, N.; Bolognani, S. Slot Harmonic Impact on Rotor Losses in Fractional-slot Permanent-magnet Machines. IEEE Trans. Ind. Electron. 2012, 59, 2557–2564. [Google Scholar] [CrossRef]
- Shah, S.H.; Wang, Y.; Shi, D.; Shen, J.-X. Investigation of Air-gap Magnetic Field Harmonics and Generated Torque in Low-speed High-power Density Spoke-type FSCW Pmsms. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 4269–4274. [Google Scholar] [CrossRef]
- Shah, S.H.; Wang, Y.; Shi, D.; Zhu, Z.; Shen, J.-X. Investigation of Low-speed High-power Density Spoke-type FSCW PMSM with Similar PM Volume and Different Shapes Considering Magnetic Gearing Effect. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 4660–4665. [Google Scholar] [CrossRef]





| Specifications | Symmetric Design | Asymmetric Design | |||
|---|---|---|---|---|---|
| Conventional Design | Type-Sine | Type-I | Type-II | Type-III | |
| Slots/poles | 72/60 | ||||
| Stator outer diameter | 1610 (mm) | ||||
| Stator inner diameter | 1360 (mm) | ||||
| Rotor outer diameter | 1354 (mm) | ||||
| Rotor inner diameter | 1264 (mm) | ||||
| λ1 pole–arc ratio | 0.87 | 0.87 | 0.84 | 0.77 | |
| λ2 pole–arc ratio | 0.87 | 0.69 | 0.66 | 0.59 | |
| λ1 − λ2 | - | - | 0.18 | 0.18 | 0.18 |
| PM width | 20 (mm) | ||||
| PM height | 40 (mm) | ||||
| Machine speed | 60 (rpm) | ||||
| Rated power | 400 (kW) | ||||
| Air-gap length | 3 (mm) | ||||
| PM Air-Gap Magnetic Flux Density | AR Air-Gap Magnetic Flux Density | ||
|---|---|---|---|
| Harmonics | Mechanical speed of rotation | Harmonics | Mechanical speed of rotation |
| , | |||
| , | |||
| Machine Designs | Back-EMF Harmonics (kV) | ||||
|---|---|---|---|---|---|
| 1st | 11th | 13th | 23rd | 25th | |
| Conventional Assisted-poles (Symmetrical) | 7.54 | 0.145 | 0.070 | 0.016 | 0.004 |
| Assisted-poles Type-Sine (Symmetrical) | 7.099 | 0.078 | 0.034 | 0.007 | 0.003 |
| Machine Designs | Tavg (kNm) | Tripples (kNm) | Tcogging (Peak-to-Peak) (kNm) |
|---|---|---|---|
| Conventional Assisted-poles (Symmetrical) | 64.67 | 4.23 | 5.33 |
| Assisted-poles Type-Sine (Symmetrical) | 61.44 | 1.76 | 2.56 |
| Assisted-Poles–Arc Ratio | Tavg (kNm) | Tripples (kNm) | Tcogging (Peak-to-Peak) (kNm) | ||
|---|---|---|---|---|---|
| λ1 | λ2 | λ1 − λ2 | |||
| 0.87 | 0.82 | 0.04 | 62.00 | 1.657 | 2.528 |
| 0.79 | 0.87 | 0.08 | 61.95 | 1.36 | 2.19 |
| 0.76 | 0.87 | 0.11 | 61.85 | 0.96 | 1.70 |
| 0.72 | 0.87 | 0.14 | 61.74 | 0.62 | 1.15 |
| 0.69 | 0.87 | 0.18 | 61.60 | 0.36 | 0.68 |
| 0.66 | 0.87 | 0.21 | 61.43 | 0.42 | 0.41 |
| 0.62 | 0.87 | 0.24 | 61.24 | 0.59 | 0.40 |
| 0.59 | 0.87 | 0.28 | 61.02 | 0.74 | 0.73 |
| 0.56 | 0.87 | 0.31 | 60.77 | 1.10 | 1.24 |
| 0.52 | 0.87 | 0.34 | 60.50 | 1.80 | 1.99 |
| 0.49 | 0.87 | 0.38 | 60.18 | 2.0 | 2.42 |
| 0.46 | 0.87 | 0.41 | 59.84 | 2.31 | 2.74 |
| 0.42 | 0.87 | 0.44 | 59.48 | 2.33 | 2.80 |
| Assisted-Poles–Arc Ratio | Tavg (kNm) | Tripples (kNm) | Tcogging (Peak-to-Peak) (kNm) | ||
|---|---|---|---|---|---|
| λ1 | λ2 | λ1 − λ2 | |||
| 0.79 | 0.84 | 0.04 | 61.92 | 1.17 | 1.92 |
| 0.76 | 0.84 | 0.08 | 61.83 | 0.80 | 1.46 |
| 0.72 | 0.84 | 0.11 | 61.72 | 0.51 | 0.95 |
| 0.69 | 0.84 | 0.14 | 61.59 | 0.50 | 0.51 |
| 0.66 | 0.84 | 0.18 | 61.49 | 0.44 | 0.31 |
| 0.62 | 0.84 | 0.21 | 61.24 | 0.49 | 0.28 |
| 0.59 | 0.84 | 0.24 | 61.03 | 0.58 | 0.59 |
| 0.56 | 0.84 | 0.28 | 60.79 | 0.90 | 1.06 |
| 0.52 | 0.84 | 0.31 | 60.52 | 1.35 | 1.67 |
| 0.49 | 0.84 | 0.34 | 60.22 | 1.77 | 2.19 |
| 0.46 | 0.84 | 0.38 | 59.89 | 2.05 | 2.50 |
| 0.24 | 0.84 | 0.41 | 59.54 | 2.14 | 2.54 |
| 0.39 | 0.84 | 0.44 | 59.17 | 1.878 | 2.82 |
| Assisted-Poles–Arc Ratio | Tavg (kNm) | Tripples (kNm) | Tcogging (Peak-to-Peak) (kNm) | ||
|---|---|---|---|---|---|
| λ1 | λ2 | λ1 − λ2 | |||
| 0.72 | 0.77 | 0.04 | 61.09 | 1.09 | 0.81 |
| 0.69 | 0.77 | 0.08 | 60.97 | 0.68 | 0.10 |
| 0.66 | 0.77 | 0.11 | 60.81 | 0.77 | 0.27 |
| 0.62 | 0.77 | 0.14 | 60.65 | 0.69 | 0.28 |
| 0.59 | 0.77 | 0.18 | 60.46 | 0.46 | 0.26 |
| 0.56 | 0.77 | 0.21 | 60.20 | 0.55 | 0.65 |
| 0.52 | 0.77 | 0.24 | 59.95 | 0.97 | 1.19 |
| 0.49 | 0.77 | 0.28 | 59.67 | 1.36 | 1.65 |
| 0.46 | 0.77 | 0.31 | 59.37 | 1.56 | 1.93 |
| 0.42 | 0.77 | 0.34 | 59.07 | 1.57 | 1.88 |
| 0.39 | 0.77 | 0.38 | 58.73 | 1.31 | 1.62 |
| 0.36 | 0.77 | 0.41 | 58.35 | 0.73 | 1.06 |
| 0.32 | 0.77 | 0.44 | 57.93 | 0.79 | 0.49 |
| Machine Designs | Back-EMF Harmonics (kV) | ||||
|---|---|---|---|---|---|
| 1st | 11th | 13th | 23rd | 25th | |
| Conventional Assisted-poles (Symmetrical) | 7.54 | 0.145 | 0.070 | 0.016 | 0.004 |
| Assisted-poles Type-Sine (Symmetrical) | 7.099 | 0.078 | 0.034 | 0.007 | 0.003 |
| Assisted-poles Type-I (Asymmetrical) | 7.155 | 0.029 | 0.022 | 0.002 | 0.0007 |
| Assisted-poles Type-II (Asymmetrical) | 7.144 | 0.018 | 0.019 | 0.0008 | 0.002 |
| Assisted-poles Type-III (Asymmetrical) | 7.025 | 0.006 | 0.014 | 0.002 | 0.001 |
| Machine Designs | Tavg (kNm) | Tripples (kNm) | Tcogging (Peak-to-Peak) (kNm) |
|---|---|---|---|
| Conventional Assisted-poles (Symmetrical) | 64.67 | 4.23 | 5.33 |
| Assisted-poles Type-Sine (Symmetrical) | 61.44 | 1.76 | 2.56 |
| Assisted-poles Type-I (Asymmetrical) | 61.60 | 0.36 | 0.68 |
| Assisted-poles Type-II (Asymmetrical) | 61.43 | 0.48 | 0.25 |
| Assisted-poles Type-III (Asymmetrical) | 60.46 | 0.46 | 0.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, S.H.; Wang, Y.-C.; Shi, D.; Shen, J.-X. Investigation of Torque and Reduction of Torque Ripples through Assisted-Poles in Low-Speed, High-Torque Density Spoke-Type PMSMs. Machines 2024, 12, 327. https://doi.org/10.3390/machines12050327
Shah SH, Wang Y-C, Shi D, Shen J-X. Investigation of Torque and Reduction of Torque Ripples through Assisted-Poles in Low-Speed, High-Torque Density Spoke-Type PMSMs. Machines. 2024; 12(5):327. https://doi.org/10.3390/machines12050327
Chicago/Turabian StyleShah, Sayyed Haleem, Yun-Chong Wang, Dan Shi, and Jian-Xin Shen. 2024. "Investigation of Torque and Reduction of Torque Ripples through Assisted-Poles in Low-Speed, High-Torque Density Spoke-Type PMSMs" Machines 12, no. 5: 327. https://doi.org/10.3390/machines12050327
APA StyleShah, S. H., Wang, Y.-C., Shi, D., & Shen, J.-X. (2024). Investigation of Torque and Reduction of Torque Ripples through Assisted-Poles in Low-Speed, High-Torque Density Spoke-Type PMSMs. Machines, 12(5), 327. https://doi.org/10.3390/machines12050327







