Multi-Response Optimization of Electrochemical Machining Parameters for Inconel 718 via RSM and MOGA-ANN
Abstract
:1. Introduction
1.1. Critical Issues and Scopes
1.2. State-of-the-Art Review of Electrochemical Machining Inconel 718
2. Materials and Methods
2.1. Workpiece Material and Tool
2.2. Experimental Planning and Methods
2.3. Multi-Response Optimization
2.3.1. Response Surface Methodology
2.3.2. Desirability Function Analysis (DFA)
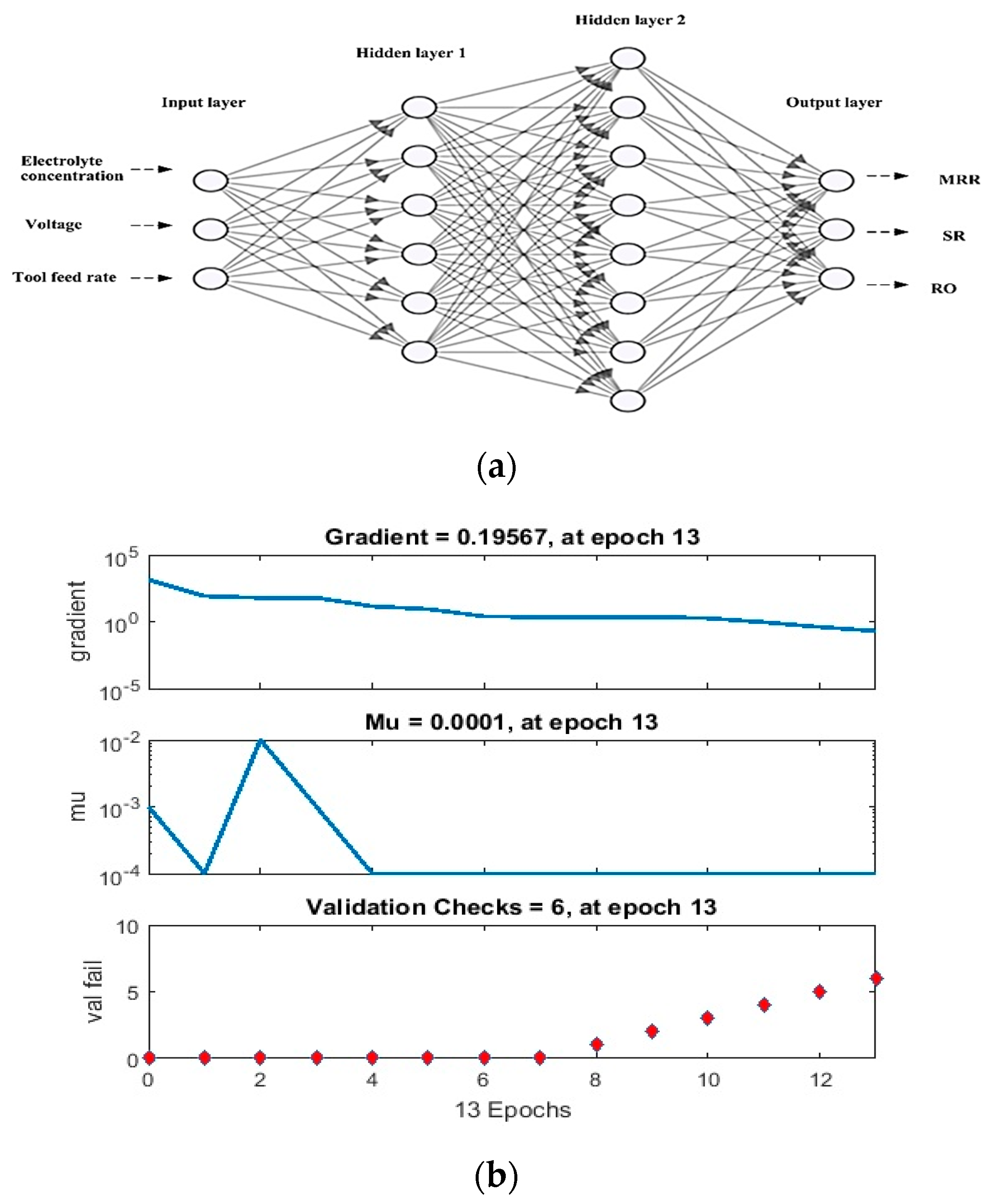
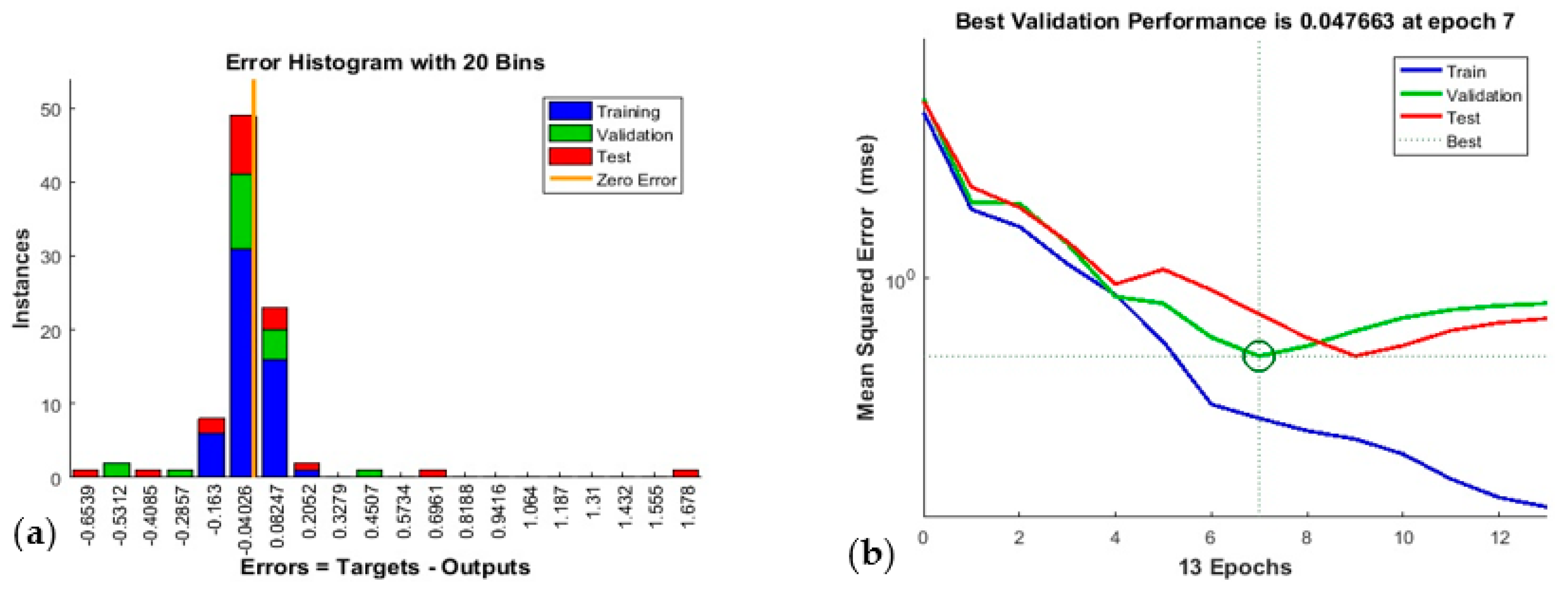
2.3.3. Artificial Neural Networks (ANN)
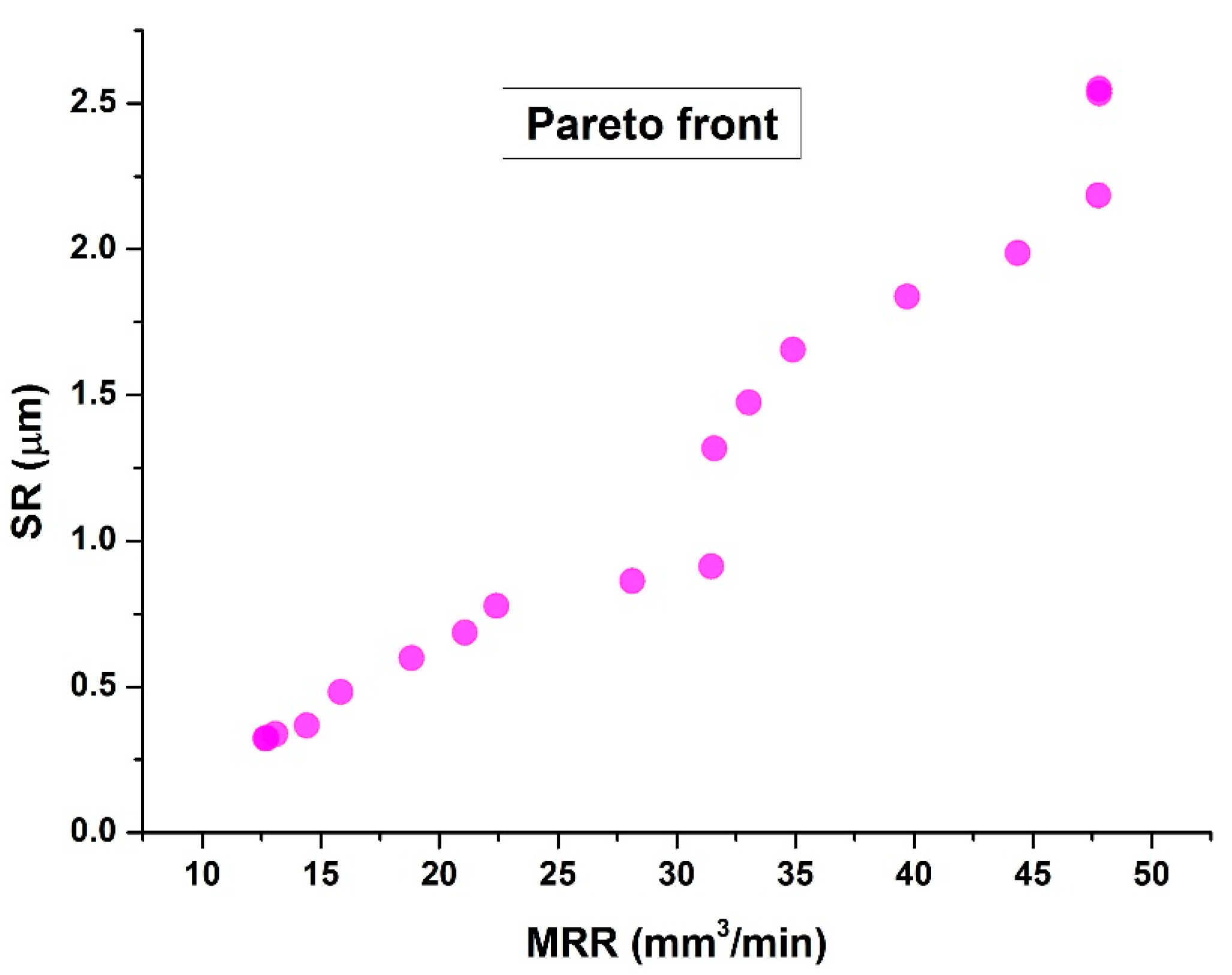
2.3.4. MOGA Analysis
3. Results and Discussion
3.1. Machined Surface Morphology Analysis
3.2. Characterization of Machined Debris or Cake
4. Conclusions
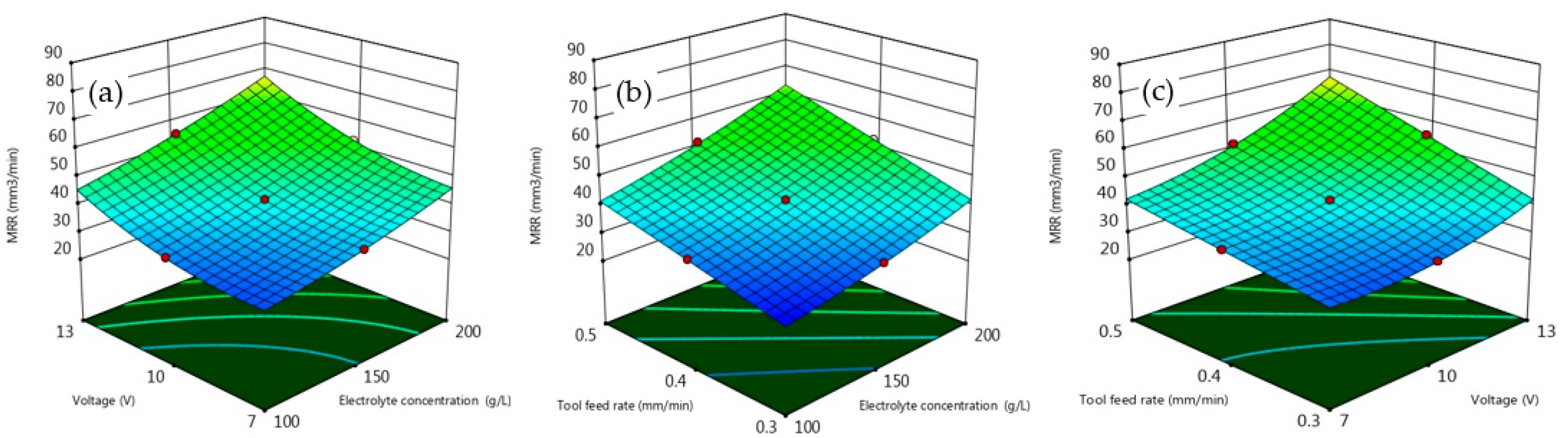
- MRR is found to be maximum for all the higher-level values of inputs, that is, electrolyte concentration (200 g/L), tool feed rate (0.5 mm/min), and voltage (13 volts).
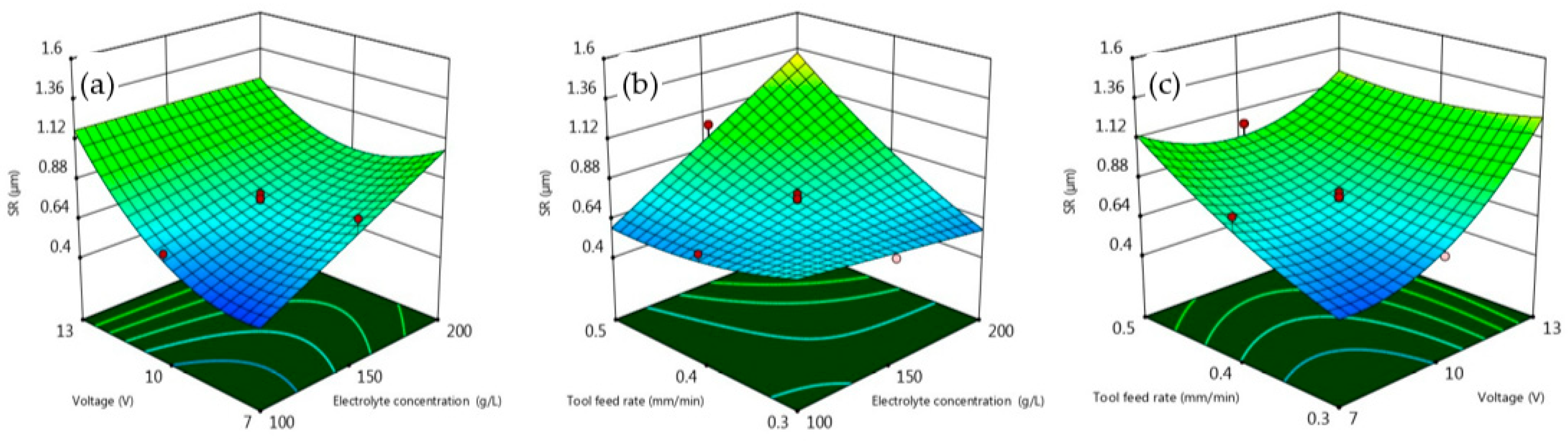
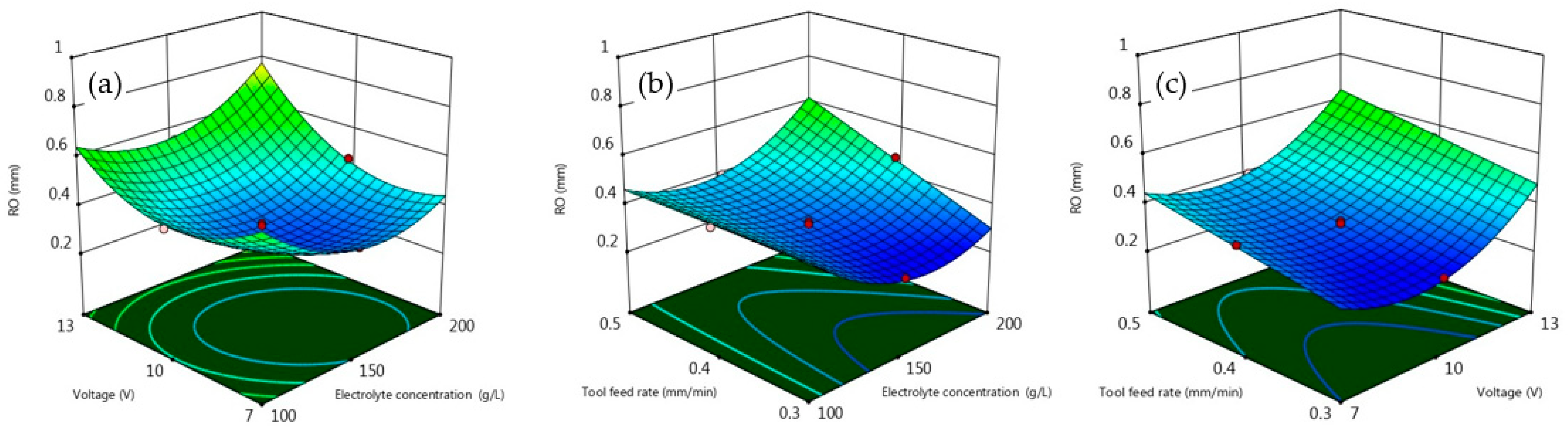
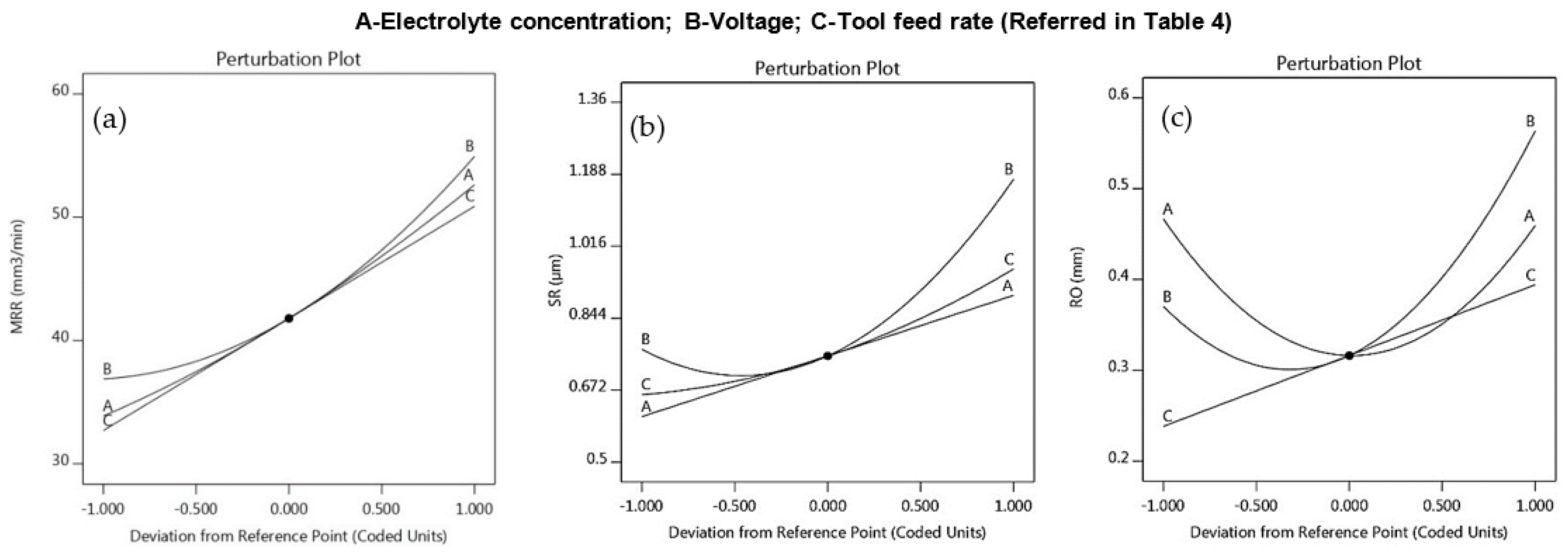
- Surface roughness is found to be low at a voltage of 7 volts and an electrolyte concentration of 100 g/L when the tool feed rate is kept constant. On the other hand, the radial overcut is at its minimum at a voltage of 10 volts and an electrolyte concentration of 150 g/L when the tool feed rate remains constant.
- With the help of the desirability approach, the optimal input parameters are found at an electrolyte concentration of 200 g/L, a voltage of 11.7466 volts, a tool feed rate of 0.3909 mm/min, and a corresponding desirability of 0.927.
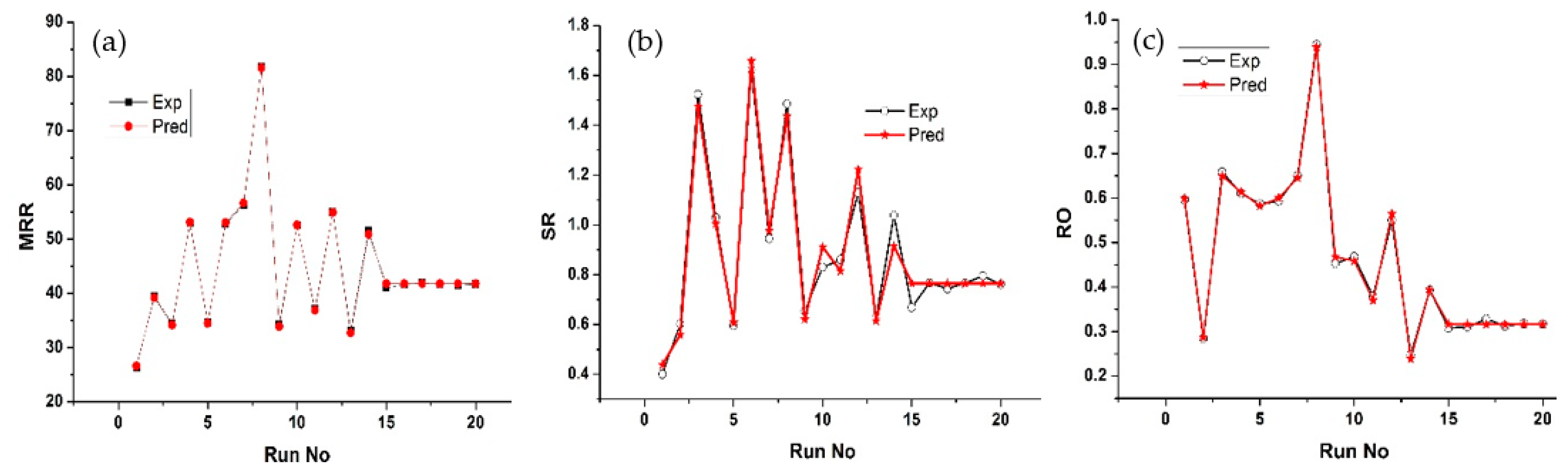
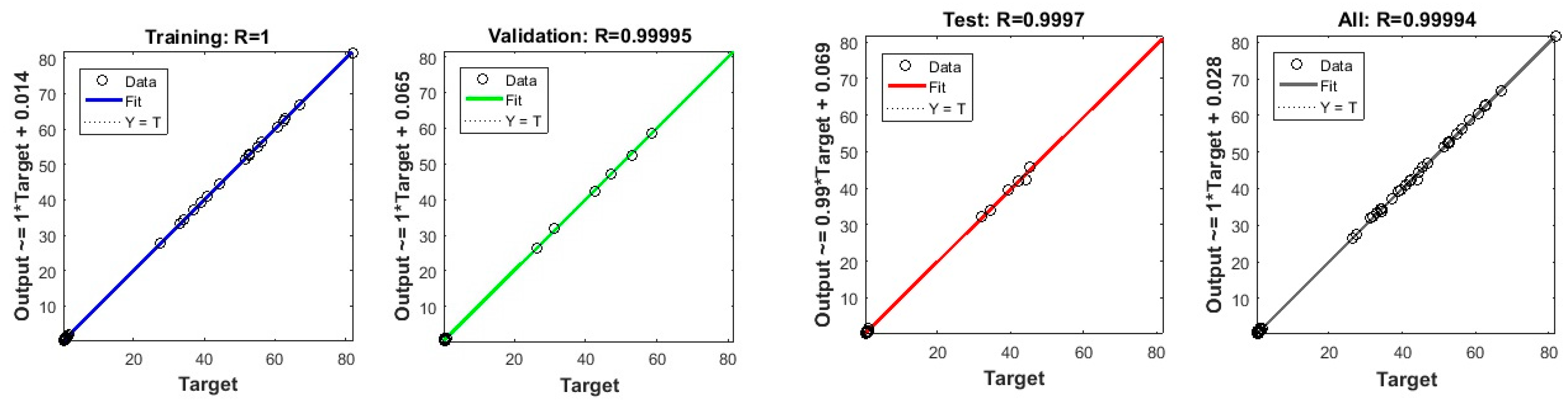
- The predicted values for MRR, SR, and RO are determined to be 59.066 mm3/min, 0.98 μm, and 0.5926 mm, respectively, at the maximum desirability of 0.9276. Judging by the R values, the ANN tool demonstrates superior fitting or performance in predicting outcomes compared to RSM, with R values of 0.99994 and 0.9276, respectively.
- The balanced optimal outcomes attained through the MOGA-ANN hybrid technique are outlined as follows (listed as serial number 1 in Table 8): The input parameters at their optimal values are EC: 100.099 g/L; V: 8.815 volts; and TFR: 0.3 mm/min. The corresponding output values are 47.59 mm3/min, 0.0317µm, and 0.276 mm for MRR, SR, and RO, respectively.
- It can be concluded that the MOGA-ANN hybrid approach for multi-optimization proves to be a more effective method compared to RSM for achieving maximum MRR while minimizing SR and RO in the electrochemical machining process for Inconel 718.
- Elevated machining voltage results in detrimental effects on the machined surface, such as the formation of micro-holes attributed to hydrogen liberation, surface irregularities caused by sticky debris, and the adherence of stubborn residues due to burning.
- The debris is full of nano/micro particulate Inconel 718. Further investigation can be initiated to separate pure Inconel 718 as an explicit byproduct for additive manufacturing industries.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhadeshia, H.K.D.H. Nickel Based Superalloys. Available online: https://www.phase-trans.msm.cam.ac.uk/2003/Superalloys/superalloys.html (accessed on 7 October 2023).
- Choudhury, I.A.; El-Baradie, M.A. Machining nickel base superalloys: Inconel 718. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 1998, 212, 195–206. [Google Scholar] [CrossRef]
- Klocke, F.; Zeis, M.; Klink, A.; Veselovac, D. Experimental research on the Electrochemical Machining of modern titanium- and nickel-based alloys for aero engine components. Procedia CIRP 2013, 6, 368–372. [Google Scholar] [CrossRef]
- Van Riel, T.; Qian, J.; Lauwers, B. Exploratory study of wire based ECM finishing of 316L stainless steel, implemented within a hybrid wire EDM-ECM platform. Procedia CIRP 2022, 113, 465–470. [Google Scholar] [CrossRef]
- ASM Handbook Committee. ASM Handbook Volume 16: Machining; ASM Handbook Committee, Ed.; ASM International: Materials Park, OH, USA, 1989; ISBN 978-1-62708-188-7. [Google Scholar]
- Crichton, I.M.; McGeough, J.A.; Munro, W.; White, C. Comparative studies of ecm, edm and ecam. Precis. Eng. 1981, 3, 155–160. [Google Scholar] [CrossRef]
- Ghosh, A.; Mallik, A.K. Manufacturing Science, 2nd ed.; East-West Press Pvt Ltd.: New Delhi, India, 2010; ISBN 9780470203125. [Google Scholar]
- Liu, J.; Liu, Y.; Zhang, Z.; Wang, H. Parameter Optimization and Experimental Study on Tool-Vibration-Assisted Pulsed Electrochemical Machining of γ-TiAl TNM Blades. Appl. Sci. 2022, 12, 8042. [Google Scholar] [CrossRef]
- Jadhav, D.B.; Jadhav, P.V.; Bilgi, D.S.; Sawant, A.A. Experimental Investigation of MRR on Inconel 600 using Ultrasonic Assisted Pulse Electrochemical Machining. IOP Conf. Ser. Mater. Sci. Eng. 2018, 377, 012095. [Google Scholar] [CrossRef]
- Jiang, X.; Li, D.; Xu, Z. Simulation and Experimental Analyses of Multi-field Coupling in Electrochemical Machining. Int. J. Electrochem. Sci. 2022, 17, 220932. [Google Scholar] [CrossRef]
- Rajurkar, K.P.; Zhu, D.; MacGeough, J.A.; Kozak, J.; De Silva, A. New Developments in Electro-Chemical Machining. CIRP Ann. 1999, 48, 567–579. [Google Scholar] [CrossRef]
- Pingale, A.D.; Owhal, A.; Katarkar, A.S.; Belgamwar, S.U.; Rathore, J.S. Recent researches on Cu-Ni alloy matrix composites through electrodeposition and powder metallurgy methods: A review. Mater. Today Proc. 2021, 47, 3301–3308. [Google Scholar] [CrossRef]
- Lee, K.J.; Lee, J.S. Synthesis of nano metal powder by electrochemical reduction of metal oxides. Mater. Sci. Forum 2004, 449–452, 1137–1140. [Google Scholar] [CrossRef]
- Zhao, L.Y.; Siu, A.C.; Pariag, L.J.; He, Z.H.; Leung, K.T. Electrochemical deposition of chromium core-shell nanostructures on H-Si(100): Evolution of spherical nanoparticles to uniform thin film without and with atop hexagonal microrods. J. Phys. Chem. C 2007, 111, 14621–14624. [Google Scholar] [CrossRef]
- Rai, V.; Liu, D.; Xia, D.; Jayaraman, Y.; Gabriel, J.C.P. Electrochemical approaches for the recovery of metals from electronic waste: A critical review. Recycling 2021, 6, 53. [Google Scholar] [CrossRef]
- Benedict, G.F. Nontraditional Manufacturing Processes, 1st ed.; Taylor & Francis: Abingdon, UK, 1987; ISBN 0824773527. [Google Scholar]
- Reed, R.C. The Superalloys as High-Temperature Materials; Cambridge University Press: Cambridge, UK, 2006; ISBN 9780521859042. [Google Scholar]
- Klocke, F.; Zeis, M.; Harst, S.; Klink, A.; Veselovac, D.; Baumgärtner, M. Modeling and simulation of the electrochemical machining (ECM) material removal process for the manufacture of aero engine components. Procedia CIRP 2013, 8, 265–270. [Google Scholar] [CrossRef]
- Geethapriyan, T.; Kalaichelvan, K.; Muthuramalingam, T. Influence of Coated Tool Electrode on Drilling Inconel Alloy 718 in Electrochemical Micro Machining. Procedia CIRP 2016, 46, 127–130. [Google Scholar] [CrossRef]
- Geethapriyan, T.; Kalaichelvan, K.; Muthuramalingam, T. Multi performance optimization of electrochemical micro-machining process surface related parameters on machining Inconel 718 using Taguchi-grey relational analysis. Metall. Ital. 2016, 108, 13–19. [Google Scholar]
- Zhu, D.; Yu, L.; Zhang, R. Dissolution Effects with Different Microstructures of Inconel 718 on Surface Integrity in Electrochemical Machining. J. Electrochem. Soc. 2018, 165, E872–E878. [Google Scholar] [CrossRef]
- Klocke, F.; Herrig, T.; Zeis, M.; Klink, A. Experimental Investigations of Cutting Rates and Surface Integrity in Wire Electrochemical Machining with Rotating Electrode. Procedia CIRP 2018, 68, 725–730. [Google Scholar] [CrossRef]
- Wang, D.; He, B.; Cao, W. Enhancement of the localization effect during electrochemical machining of inconel 718 by using an alkaline solution. Appl. Sci. 2019, 9, 690. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, J. Experimental Research on the Counter-Rotating Electrochemical Machining of 304 Stainless Steel and Inconel 718 Alloy. Int. J. Electrochem. Sci. 2019, 14, 9741–9754. [Google Scholar] [CrossRef]
- Madhankumar, S.; Kumaar, K.A.; Arunachalam, S.; Suhirtharaj, J.B.; Anek Anil, K.; Aadhavan, P.; Hari Narayanan, K.R.; Akshey, P.B. Assessments and comparison of Inconel 625 and Inconel 718 alloys from overcut in micro ECM. Mater. Today Proc. 2021, 45, 6459–6464. [Google Scholar] [CrossRef]
- Madhankumar, S.; Rajesh, S.; Balamurugan, R.; Tharun Sri Ram, N.; Venuprasath, S.; Tazmeel Ahamed, S. Optimization of Material Removal Rate and Surface Roughness for Micro ECM of Inconel 718 alloy utilizing Grey Relational Technique. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1059, 012008. [Google Scholar] [CrossRef]
- Rajesh, S.; Antony Prabu, D.; Gobikrishnan, U.; Lokesh Kumar, P.J.; Selvan, T.A.; Ramesh, A.; Madhankumar, S. Surface roughness assessments and comparative study of Inconel 625 and Inconel 718 alloys after micro electrochemical machining. Mater. Today Proc. 2022, 62, 938–943. [Google Scholar] [CrossRef]
- Kong, W.; Zeng, Y.; Liu, Z.; Hu, X.; Kong, H. Helical wire electrochemical discharge machining on large-thickness Inconel 718 alloy in low-conductivity salt-glycol solution. Chin. J. Aeronaut. 2023, 36, 522–533. [Google Scholar] [CrossRef]
- Leo Kumar, S.P.; Jerald, J.; Kumanan, S.; Aniket, N. Process parameters optimization for micro end-milling operation for CAPP applications. Neural Comput. Appl. 2014, 25, 1941–1950. [Google Scholar] [CrossRef]
- Beruvides, G.; Castaño, F.; Quiza, R.; Haber, R.E. Surface roughness modeling and optimization of tungsten-copper alloys in micro-milling processes. Meas. J. Int. Meas. Confed. 2016, 86, 246–252. [Google Scholar] [CrossRef]
- Agrawal, S.; Agrawal, S.; Kumar Kasdekar, D. Optimization of MRR and electrolyte coating thickness of ECM parameters using PCA based GRA. Mater. Today Proc. 2018, 5, 18956–18965. [Google Scholar] [CrossRef]
- Majumder, H.; Paul, T.R.; Dey, V.; Dutta, P.; Saha, A. Use of PCA-grey analysis and RSM to model cutting time and surface finish of Inconel 800 during wire electro discharge cutting. Meas. J. Int. Meas. Confed. 2017, 107, 19–30. [Google Scholar] [CrossRef]
- Adak, D.K.; Pal, V.; Das, S.; Ghara, T.; Joardar, H.; Alrasheedi, N.; Haldar, B. Surface Preparation for Coating and Erosion MRR of SS 304 Using Silicon Carbide Abrasive Jet. Lubricants 2023, 11, 10. [Google Scholar] [CrossRef]
- Haldar, B.; Joardar, H.; Louhichi, B.; Alsaleh, N.A.; Alfozan, A. A Comparative Machinability Study of SS 304 in Turning under Dry, New Micro-Jet, and Flood Cooling Lubrication Conditions. Lubricants 2022, 10, 359. [Google Scholar] [CrossRef]
- Karumuri, S.; Haldar, B.; Pradeep, A.; Karanam, S.A.K.; Sri, M.N.S.; Anusha, P.; Sateesh, N.; Subbiah, R.; Vijayakumar, S. Multi-objective optimization using Taguchi based grey relational analysis in friction stir welding for dissimilar aluminium alloy. Int. J. Interact. Des. Manuf. 2023, 18, 1627–1644. [Google Scholar] [CrossRef]
- Winiczenko, R.; Kaleta, A.; Górnicki, K. Application of a moga algorithm and ann in the optimization of apple drying and rehydration processes. Processes 2021, 9, 1415. [Google Scholar] [CrossRef]
- Pramanick, A.; Kumar, R.; Mandal, S.; Dey, P.P.; Das, P.K. Modeling and multi-objective optimization of WEDM of spark plasma sintered boron carbide considering preferences of users. IOP Conf. Ser. Mater. Sci. Eng. 2018, 377, 012094. [Google Scholar] [CrossRef]
- Bhaumik, M.; Maity, K.; Mohapatra, K. Das Multi-Objective Optimization ff EDM Process Parameters Using Rsm-Based GRA and Topsis Method For Grade 6 Titanium Alloy. Surf. Rev. Lett. 2021, 28, 4–5. [Google Scholar] [CrossRef]
- Rajamanickam, S.; Prasanna, J. Multi objective optimization during small hole electrical discharge machining (EDM) of Ti-6Al-4V using TOPSIS. Mater. Today Proc. 2019, 18, 3109–3115. [Google Scholar] [CrossRef]
- Prakash, C.; Kansal, H.K.; Pabla, B.S.; Puri, S. Multi-objective optimization of powder mixed electric discharge machining parameters for fabrication of biocompatible layer on β-Ti alloy using NSGA-II coupled with Taguchi based response surface methodology. J. Mech. Sci. Technol. 2016, 30, 4195–4204. [Google Scholar] [CrossRef]
- Kumar, L.; Kumar, K.; Chhabra, D. Experimental investigations of electrical discharge micro-drilling for Mg-alloy and multi-response optimization using MOGA-ANN. CIRP J. Manuf. Sci. Technol. 2022, 38, 774–786. [Google Scholar] [CrossRef]
- Hosamo, H.; Hosamo, M.H.; Nielsen, H.K.; Svennevig, P.R.; Svidt, K. Digital Twin of HVAC system (HVACDT) for multiobjective optimization of energy consumption and thermal comfort based on BIM framework with ANN-MOGA. Adv. Build. Energy Res. 2023, 17, 125–171. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Y.; Liang, D.; Ivanov, M. Performances of regression model and artificial neural network in monitoring welding quality based on power signal. J. Mater. Res. Technol. 2020, 9, 1231–1240. [Google Scholar] [CrossRef]
- Nalbant, M.; Gokkaya, H.; Toktaş, I. Comparison of regression and artificial neural network models for surface roughness prediction with the cutting parameters in CNC turning. Model. Simul. Eng. 2007, 2007, 092717. [Google Scholar] [CrossRef]









| Characteristics: | EDM | ECM | Hybrid EDM-ECM |
|---|---|---|---|
| Mechanism: | Spark erosion (current density is the main factor) | Atomic dissolution (Current density and atomic number are the main factors) | Hybrid (initially EDM and fishing by ECM) |
| Material removal rate (MRR): | ~4350 mm3/min per 400 A | ~650 to 4400 mm3/min per 1000 A [5] | Higher than both |
| Heat affected zone (HAZ): | Yes [6] | No [6] | Removed by ECM |
| Stress-concentration: | Yes | No | Removed by ECM |
| Tool wear: | Yes | No | Yes |
| Surface quality: |
|
| Better than EDM |
| Shape flexibility: | Restricted | Better than EDM and Hybrid EDM-ECM | Restricted |
| Dimensional accuracy: | Generally, ±0.013 to ±0.005 mm can be obtained Wire-EDM [5] | Upto ±0.025 mm [5] | Better than ECM |
| Power requirement: | 0.5 and 400 A and 40 to 400 V DC | 50 to 4000 A and 5 to 30 V DC | Hybrid mode |
| Fluid and flow pressure: | Di-electric pressure ia about 2 kg/cm2 | High electrolyte pressure (14 kg/cm2) is unfavourable for soft/thin metallic parts | unfavourable for soft/thin metallic parts |
| Maintenance: | Regular | Regular and highly essential | Regular and highly essential |
| Process Parameters | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Electrolyte concentration (g/L), EC | 100 | 150 | 200 |
| Voltage (V), V | 7 | 10 | 13 |
| Tool feed rate (mm/min), TFR | 0.3 | 0.4 | 0.5 |
| Exp No. | Electrolyte Concentration (g/L) | Voltage (V) | Tool Feed Rate (mm/min) | Material Removal Rate (mm3/min) | Surface Roughness (µm) | Radial Overcut (mm) |
|---|---|---|---|---|---|---|
| 01 | 100 | 7 | 0.3 | 26.321 | 0.401 | 0.596 |
| 02 | 100 | 7 | 0.4 | 32.153 | 0.672 | 0.462 |
| 03 | 100 | 7 | 0.5 | 34.595 | 0.595 | 0.587 |
| 04 | 100 | 10 | 0.3 | 27.473 | 0.503 | 0.299 |
| 05 | 100 | 10 | 0.4 | 34.199 | 0.654 | 0.453 |
| 06 | 100 | 10 | 0.5 | 44.38 | 0.998 | 0.379 |
| 07 | 100 | 13 | 0.3 | 34.392 | 1.865 | 0.658 |
| 08 | 100 | 13 | 0.4 | 42.125 | 1.059 | 0.432 |
| 09 | 100 | 13 | 0.5 | 56.325 | 0.945 | 0.65 |
| 10 | 150 | 7 | 0.3 | 31.34 | 0.793 | 0.35 |
| 11 | 150 | 7 | 0.4 | 37.084 | 0.86 | 0.402 |
| 12 | 150 | 7 | 0.5 | 44.159 | 1.006 | 0.919 |
| 13 | 150 | 10 | 0.3 | 33.056 | 0.628 | 0.248 |
| 14 | 150 | 10 | 0.4 | 41.018 | 0.669 | 0.338 |
| 15 | 150 | 10 | 0.5 | 51.56 | 1.038 | 0.393 |
| 16 | 150 | 13 | 0.3 | 47.008 | 0.807 | 0.448 |
| 17 | 150 | 13 | 0.4 | 55 | 1.129 | 0.55 |
| 18 | 150 | 13 | 0.5 | 66.952 | 0.706 | 0.582 |
| 19 | 200 | 7 | 0.3 | 39.479 | 0.602 | 0.284 |
| 20 | 200 | 7 | 0.4 | 42.532 | 0.891 | 0.427 |
| 21 | 200 | 7 | 0.5 | 52.7 93 | 1.622 | 0.593 |
| 22 | 200 | 10 | 0.3 | 45.381 | 0.495 | 0.453 |
| 23 | 200 | 10 | 0.4 | 52.56 | 0.83 | 0.468 |
| 24 | 200 | 10 | 0.5 | 58.405 | 1.145 | 0.627 |
| 25 | 200 | 13 | 0.3 | 52.94 | 1.029 | 0.61 |
| 26 | 200 | 13 | 0.4 | 62.882 | 1.256 | 0.374 |
| 27 | 200 | 13 | 0.5 | 81.807 | 1.486 | 0.944 |
| Source | MRR | SR | RO | |||
|---|---|---|---|---|---|---|
| F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |
| Linear vs. Mean | 48.34 | <0.0001 | 3.74 | 0.0327 | 5.83 | 0.0182 |
| 2FI vs. Linear | 4.71 | 0.0195 | 9.52 | 0.0014 | 3.17 | 0.0012 |
| Quadratic vs. 2FI | 241.43 | <0.0001 | 25.93 | <0.0001 | 478.00 | <0.0001 |
| Cubic vs. Quadratic | 0.7757 | 0.5792 | 4.89 | 0.0426 | 2.99 | 0.1115 |
| Source | MRR | SR | RO | |||
|---|---|---|---|---|---|---|
| F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |
| Model | 1896.03 | <0.0001 | 61.98 | <0.0001 | 789.98 | <0.0001 |
| A-Electrolyte concentration | 4770.66 | <0.0001 | 51.76 | <0.0001 | 1.44 | 0.2551 |
| B-Voltage | 4415.70 | <0.0001 | 101.76 | <0.0201 | 980.49 | <0.0001 |
| C-Tool feed rate | 4484.51 | <0.0001 | 55.54 | <0.0001 | 638.95 | <0.0001 |
| AB | 108.99 | <0.0001 | 43.00 | <0.0001 | 412.74 | <0.0001 |
| AC | 97.29 | <0.0001 | 106.70 | <0.0001 | 559.49 | <0.0001 |
| BC | 579.02 | <0.0001 | 54.93 | <0.0001 | 1.52 | 0.2431 |
| A2 | 36.70 | <0.0001 | 37.92 | <0.0001 | 725.10 | <0.0001 |
| B2 | 294.30 | <0.0001 | 2.64 | 0.1326 | 765.18 | <0.0001 |
| Lack of Fit | 2.38 | 0.1803 | 3.18 | 0.1128 | 2.54 | 0.1631 |
| not significant | not significant | not significant | ||||
| R² | 0.9993 | 0.9783 | 0.9983 | |||
| Adjusted R² | 0.9987 | 0.9625 | 0.9970 | |||
| Predicted R² | 0.9953 | 0.8447 | 0.9904 | |||
| Comparison | MRR (mm3/min) | SR (µm) | RO (mm) |
|---|---|---|---|
| Predicted | 59.066 | 0.98 | 0.5926 |
| Experimental | 60.106 | 0.956 | 0.5844 |
| % Variation | <2% | <3% | <2% |
| Sl No | Input Parameter | Output | ||||
|---|---|---|---|---|---|---|
| EC | V | TFR | MRR | SR | RO | |
| 1 | 100.099 | 8.815 | 0.300 | 47.59 | 0.317 | 0.276 |
| 2 | 100.001 | 12.983 | 0.500 | 12.14 | 2.163 | 0.738 |
| 3 | 100.001 | 9.711 | 0.500 | 47.60 | 0.318 | 0.274 |
| 4 | 100.009 | 12.259 | 0.476 | 11.79 | 2.498 | 0.503 |
| 5 | 100.020 | 9.914 | 0.315 | 47.56 | 0.318 | 0.279 |
| 6 | 100.005 | 12.800 | 0.464 | 13.39 | 1.993 | 0.686 |
| 7 | 100.002 | 12.909 | 0.482 | 23.41 | 1.156 | 0.400 |
| 8 | 100.037 | 12.697 | 0.425 | 33.31 | 0.610 | 0.129 |
| 9 | 100.099 | 8.815 | 0.300 | 19.68 | 1.470 | 0.502 |
| 10 | 100.009 | 10.472 | 0.322 | 29.79 | 0.841 | 0.198 |
| 11 | 100.001 | 12.507 | 0.488 | 11.79 | 2.498 | 0.503 |
| 12 | 100.008 | 9.413 | 0.439 | 45.66 | 0.324 | 0.225 |
| 13 | 100.018 | 12.965 | 0.326 | 36.99 | 0.482 | 0.020 |
| 14 | 100.008 | 12.262 | 0.474 | 14.85 | 1.879 | 0.622 |
| 15 | 100.002 | 10.602 | 0.499 | 22.89 | 1.371 | 0.332 |
| 16 | 100.007 | 11.695 | 0.463 | 31.78 | 0.680 | 0.170 |
| 17 | 100.001 | 11.483 | 0.500 | 40.48 | 0.446 | 0.103 |
| 18 | 100.009 | 12.989 | 0.488 | 17.38 | 1.626 | 0.574 |
| Sl No | Input Parameter | Output Responses | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Predicted Values | Experimental Values | ||||||||
| EC | V | TFR | MRR | SR | RO | MRR | SR | RO | |
| 1 | 100.099 | 8.815 | 0.300 | 47.59 | 0.317 | 0.276 | 48.54 | 0.329 | 0.288 |
| 5 | 100.020 | 9.914 | 0.315 | 47.56 | 0.318 | 0.279 | 48.92 | 0.321 | 0.292 |
| 10 | 100.009 | 10.47 | 0.322 | 29.79 | 0.841 | 0.198 | 29.49 | 0.864 | 0.192 |
| 15 | 100.002 | 10.60 | 0.499 | 22.89 | 1.371 | 0.332 | 23.69 | 1.439 | 0.338 |
| 18 | 100.009 | 12.98 | 0.488 | 17.38 | 1.626 | 0.574 | 18.07 | 1.941 | 0.584 |
| Element | Weight % | Atomic % | Error % | Net Int. |
|---|---|---|---|---|
| C K | 0.1 | 0.2 | 100.0 | 0.0 |
| Na K | 37.6 | 64.8 | 10.1 | 75.6 |
| Cl K | 0.6 | 0.7 | 65.4 | 1.8 |
| Ti K | 0.5 | 0.4 | 64.1 | 0.8 |
| Cr K | 1.6 | 1.2 | 50.7 | 2.0 |
| Fe K | 9.2 | 6.5 | 16.1 | 8.4 |
| Ni K | 20.2 | 13.6 | 14.0 | 11.2 |
| Nb L | 4.1 | 1.7 | 18.1 | 5.7 |
| Mo L | 26.0 | 10.7 | 8.3 | 35.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, S.; Mondal, A.K.; Čep, R.; Joardar, H.; Haldar, B.; Kumar, A.; Alsalah, N.A.; Ataya, S. Multi-Response Optimization of Electrochemical Machining Parameters for Inconel 718 via RSM and MOGA-ANN. Machines 2024, 12, 335. https://doi.org/10.3390/machines12050335
Saha S, Mondal AK, Čep R, Joardar H, Haldar B, Kumar A, Alsalah NA, Ataya S. Multi-Response Optimization of Electrochemical Machining Parameters for Inconel 718 via RSM and MOGA-ANN. Machines. 2024; 12(5):335. https://doi.org/10.3390/machines12050335
Chicago/Turabian StyleSaha, Subhadeep, Arpan Kumar Mondal, Robert Čep, Hillol Joardar, Barun Haldar, Ajay Kumar, Naser A. Alsalah, and Sabbah Ataya. 2024. "Multi-Response Optimization of Electrochemical Machining Parameters for Inconel 718 via RSM and MOGA-ANN" Machines 12, no. 5: 335. https://doi.org/10.3390/machines12050335
APA StyleSaha, S., Mondal, A. K., Čep, R., Joardar, H., Haldar, B., Kumar, A., Alsalah, N. A., & Ataya, S. (2024). Multi-Response Optimization of Electrochemical Machining Parameters for Inconel 718 via RSM and MOGA-ANN. Machines, 12(5), 335. https://doi.org/10.3390/machines12050335










