Kinematic Parameter Identification and Error Compensation of Industrial Robots Based on Unscented Kalman Filter with Adaptive Process Noise Covariance
Abstract
:1. Introduction
- (1)
- An unscented Kalman filter with Adaptive Process Noise Covariance (APNC-UKF) algorithm for robot kinematic parameter identification is proposed to address the loss of high-order system information of conventional kinematic parameter identification algorithms and improve the identification accuracy.
- (2)
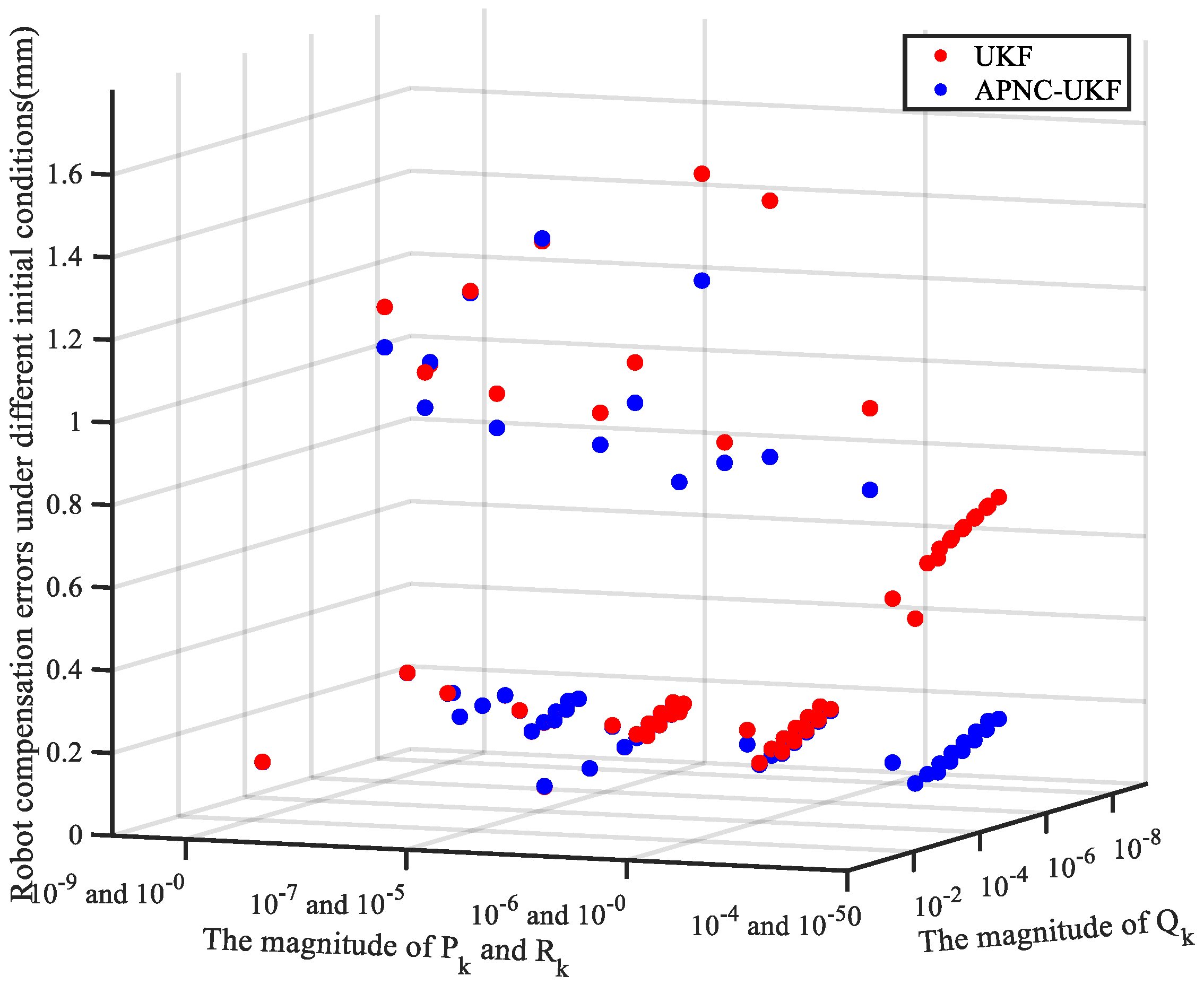
- By comparing the conventional UKF and the APNC-UKF with different initial parameters, the stability of APNC-UKF parameter identification is proved, which can effectively reduce the number of adjustments of initial parameters.
- (3)
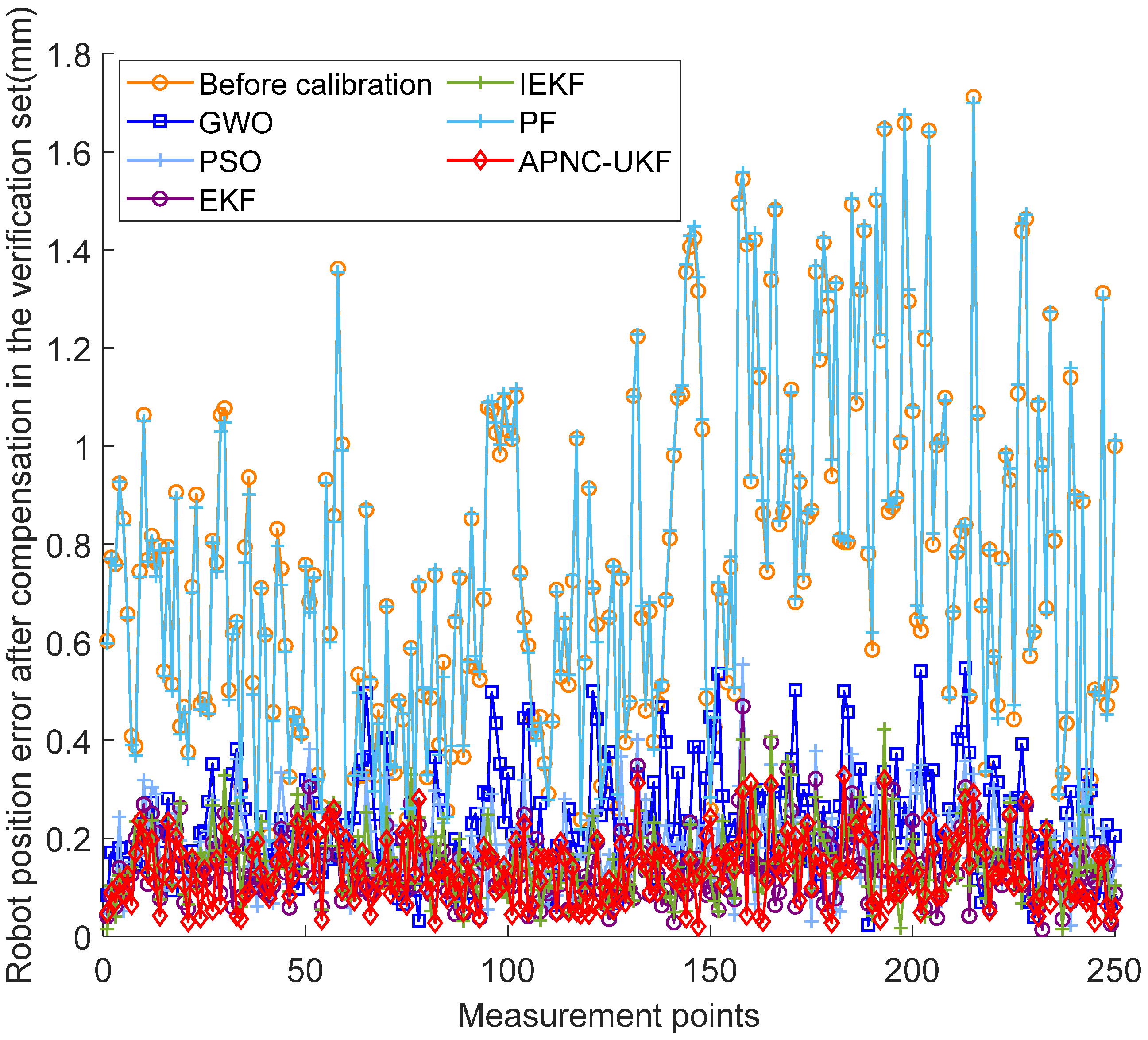
- Compared with the EKF, IEKF, PF, PSO, and GWO algorithms commonly used in robot calibration, the APNC-UKF proposed in this paper has advantages in the three indicators of maximum, average value, and standard deviation, and the robot compensation accuracy is higher.
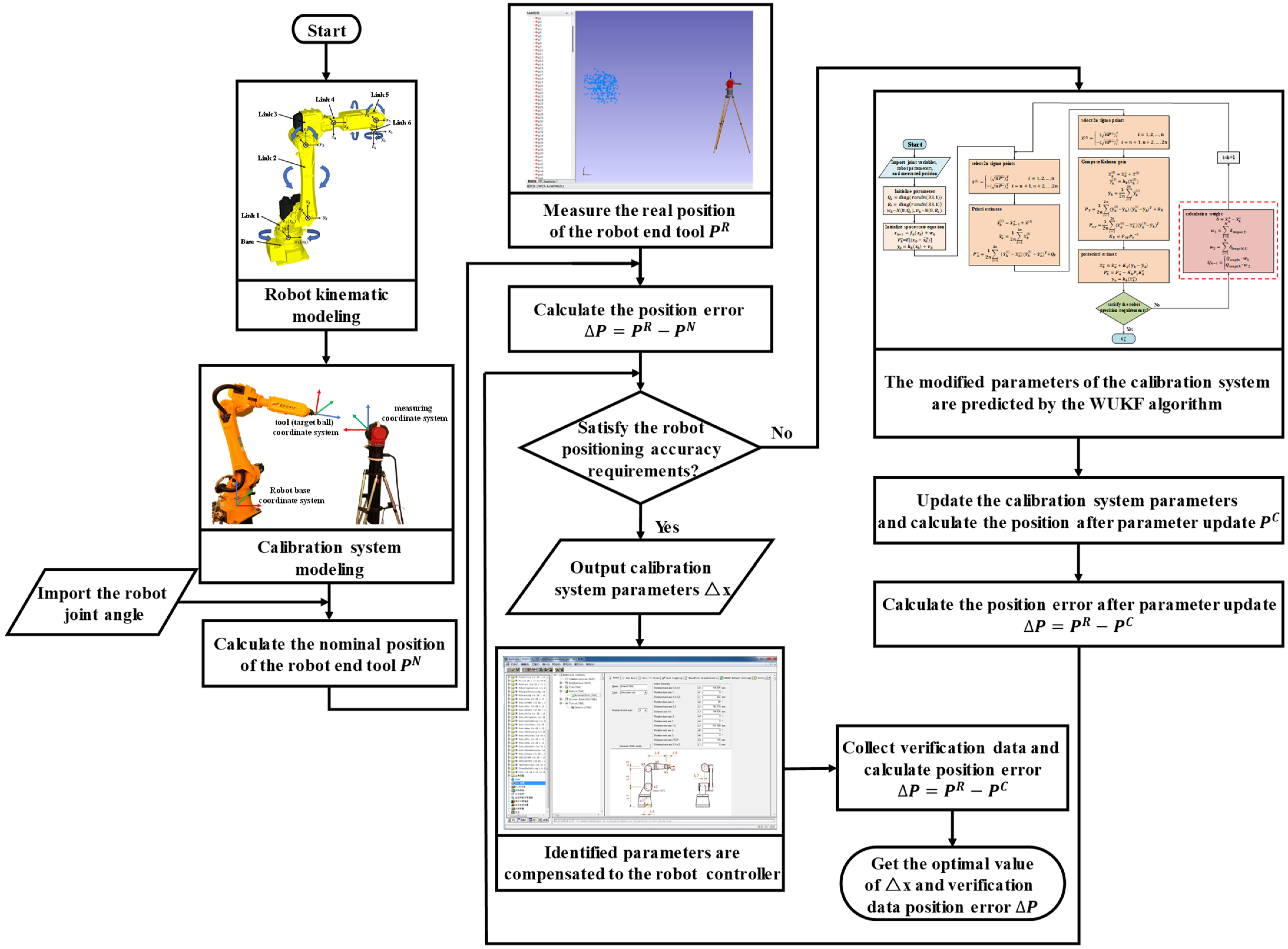
2. Modeling and Problem Formulation
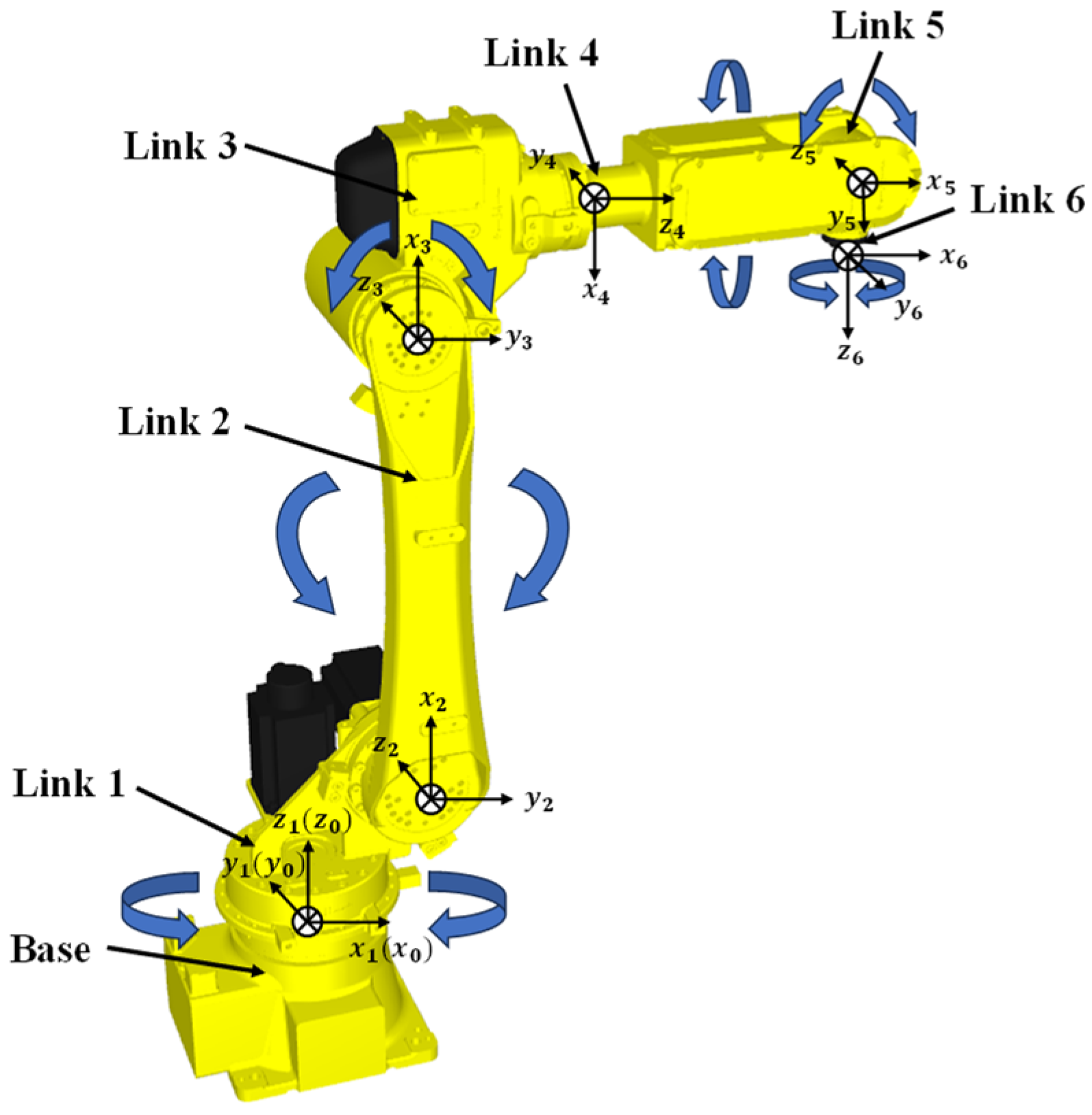
2.1. Robot Kinematic Modeling
2.2. Calibration System Modeling
3. Calibration System Parameter Identification Based on APNC-UKF
3.1. Parameter Identification Based on UKF
- (1)
- Initialization:
- (2)
- Cycle k = 1, 2, …, n, and completes the following steps.
- Select 2n sigma points and obtain 2n priori estimates by non-linear system equations:
- b.
- Calculate the prior estimation and prior estimation error covariance:
- c.
- Select 2n sigma points and obtain 2n measured predicted values through the non-linear measurement equation:
- d.
- Calculate measurement estimation, measurement estimation covariance, and cross-covariance:
- e.
- Update posterior state estimation and posterior estimation covariance:
3.2. Limitation Analysis of UKF Used in Robot Calibration
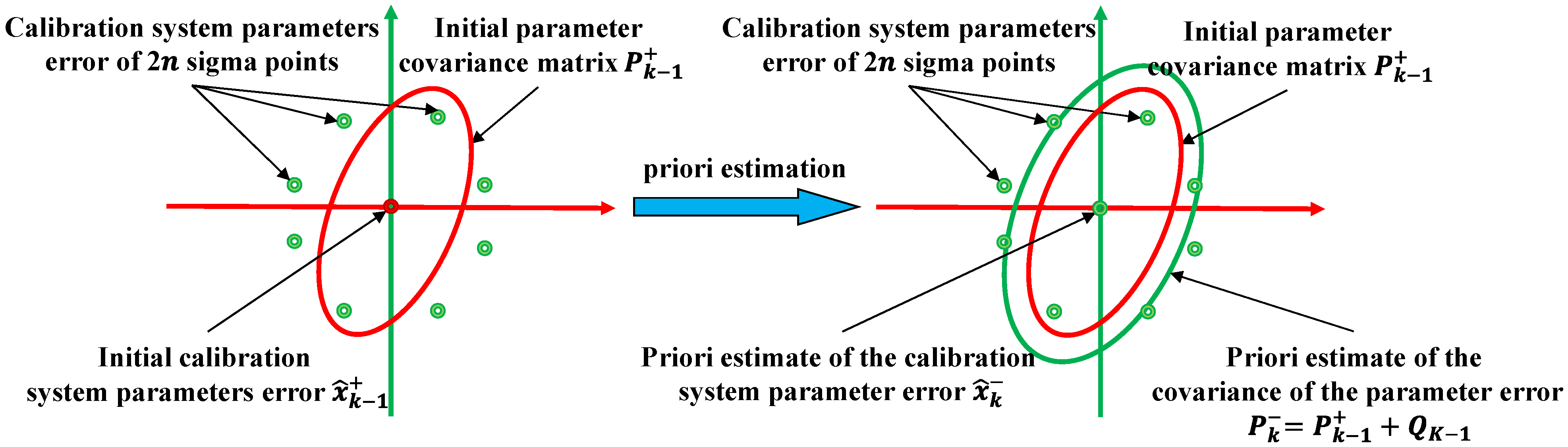
3.3. APNC-UKF
| Algorithm 1 APNC-UKF | |
| /∗Initialization∗/ | |
| 1 Initialize P0, Q0 and R0 | |
| 2 Initialize and | |
| 3 Initialize | |
| /∗ APNC-UKF Step∗/ | |
| for k = 1, 2, …n | |
| select prior sigma points via (7) | |
| Calculate base on (9) | |
| Calculate base on (24) | |
| Calculate base on (10) and Updated Qk | |
| select posterior sigma points via (11) | |
| Calculate , and base on (13) | |
| Update , and with (14) | |
| Calculate , and base on (19) (20) (21) | |
| end for | |
4. Experiments
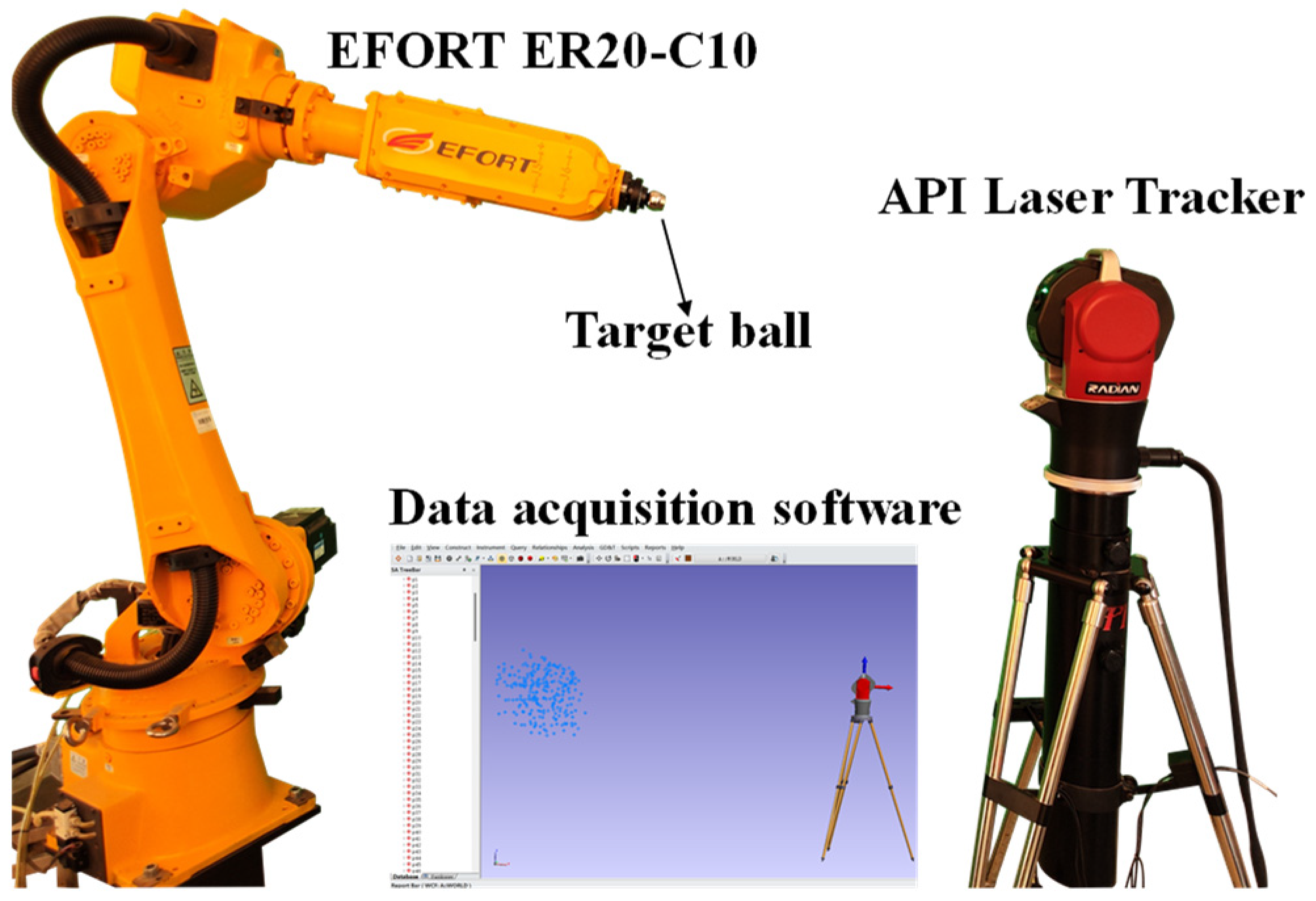
4.1. Experimental Settings
- Data Acquisition.
- b.
- Experimental steps.
- (1)
- The position of the robot’s TCP is collected by the laser tracker and Spatial Analyzer (SA) of version 2017.08.11_29326(x64), and the joint angle of the robot is exported by the robot controller.
- (2)
- Fifty sets of joint angles and positions are selected as the identification set data, and the parameter error obtained by parameter identification is compensated to the controller of the robot. Then, the parameters of the robot are corrected, and the accuracy of the robot is improved.
- (3)
- The laser tracker and SA software are used to collect the remaining 250 sets of data, and the robot accuracy before and after kinematic parameter identification and compensation is compared.
- c.
- Evaluation protocol.
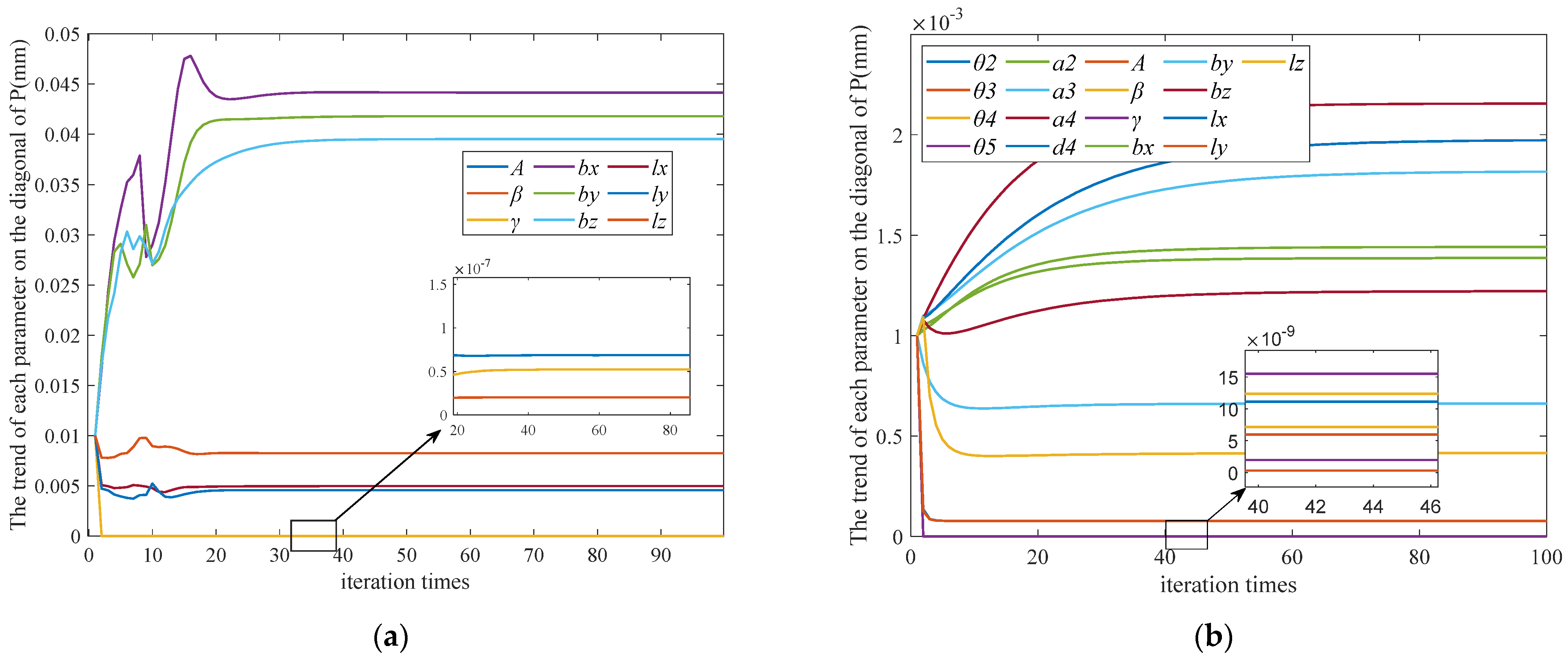
4.2. Adaptive Strategy Validation
4.3. Performance Evaluation
- (1)
- M1: GWO is widely used in non-linear non-Gaussian dynamical systems for robot calibration [12].
- (2)
- M2: PSO is a classical optimization algorithm widely applied to solve various engineering problems [11].
- (3)
- M3: The EKF is used to solve non-linear state estimation problems and has been successfully applied to non-linear robot calibration systems [15].
- (4)
- M4: The IEKF algorithm is an improved version of the Kalman filter used for state estimation in non-linear systems [16].
- (5)
- M5: The PF is a probabilistic and statistical method that is mainly used to solve uncertainty problems. It is a sample-based filtering method that estimates the state of a system by generating a large number of random particles. [14].
- (6)
- M6: The APNC-UKF algorithm proposed in this study.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Magnitude of Pk | Magnitude of Qk | Magnitude of Rk | Positioning Error by UKF (Validation Set Data) | Positioning Error by APNC-UKF (Validation Set Data) | The Percentage Increase in the Effect of APNC-UKF |
|---|---|---|---|---|---|
| 1.00 × 10−1 | 1.00 × 10−4 | 1.00 × 10−1 | 1.095222294 | 0.897481668 | 18.05% |
| 1.00 × 10−2 | 1.00 × 10−4 | 1.00 × 10−2 | 0.609642194 | 0.212950275 | 65.07% |
| 1.00 × 10−3 | 1.00 × 10−4 | 1.00 × 10−3 | 0.536938932 | 0.137954447 | 74.31% |
| 1.00 × 10−4 | 1.00 × 10−4 | 1.00 × 10−3 | 0.658531114 | 0.140398137 | 78.68% |
| 1.00 × 10−4 | 1.00 × 10−4 | 1.00 × 10−4 | 0.645238624 | 0.134456923 | 79.16% |
| 1.00 × 10−5 | 1.00 × 10−4 | 1.00 × 10−3 | 0.675880759 | 0.140818089 | 79.17% |
| 1.00 × 10−5 | 1.00 × 10−4 | 1.00 × 10−4 | 0.654208082 | 0.134458464 | 79.45% |
| 1.00 × 10−6 | 1.00 × 10−4 | 1.00 × 10−3 | 0.677695171 | 0.140862985 | 79.21% |
| 1.00 × 10−6 | 1.00 × 10−4 | 1.00 × 10−4 | 0.655137334 | 0.134458641 | 79.48% |
| 1.00 × 10−7 | 1.00 × 10−4 | 1.00 × 10−3 | 0.677877167 | 0.140867506 | 79.22% |
| 1.00 × 10−7 | 1.00 × 10−4 | 1.00 × 10−4 | 0.655230562 | 0.134458659 | 79.48% |
| 1.00 × 10−8 | 1.00 × 10−4 | 1.00 × 10−3 | 0.677895372 | 0.140867958 | 79.22% |
| 1.00 × 10−8 | 1.00 × 10−4 | 1.00 × 10−4 | 0.655239828 | 0.134458661 | 79.48% |
| 1.00 × 10−9 | 1.00 × 10−4 | 1.00 × 10−3 | 0.677897193 | 0.140868003 | 79.22% |
| 1.00 × 10−9 | 1.00 × 10−4 | 1.00 × 10−4 | 0.655240699 | 0.134458661 | 79.48% |
| 1.00 × 100 | 1.00 × 10−5 | 1.00 × 10−2 | 0.364474976 | 0.921471299 | −60.45% |
| 1.00 × 10−1 | 1.00 × 10−5 | 1.00 × 10−1 | 1.643268261 | 1.384727987 | 15.73% |
| 1.00 × 10−2 | 1.00 × 10−5 | 1.00 × 10−2 | 0.968604444 | 0.919025931 | 5.12% |
| 1.00 × 10−3 | 1.00 × 10−5 | 1.00 × 10−3 | 0.247654211 | 0.213092469 | 13.96% |
| 1.00 × 10−4 | 1.00 × 10−5 | 1.00 × 10−3 | 1.504733096 | 0.884518188 | 41.22% |
| 1.00 × 10−4 | 1.00 × 10−5 | 1.00 × 10−4 | 0.142341742 | 0.137953044 | 3.08% |
| 1.00 × 10−5 | 1.00 × 10−5 | 1.00 × 10−4 | 0.144549185 | 0.140393993 | 2.87% |
| 1.00 × 10−5 | 1.00 × 10−5 | 1.00 × 10−5 | 0.150457437 | 0.134456858 | 10.63% |
| 1.00 × 10−6 | 1.00 × 10−5 | 1.00 × 10−4 | 0.144935628 | 0.140814276 | 2.84% |
| 1.00 × 10−6 | 1.00 × 10−5 | 1.00 × 10−5 | 0.150222634 | 0.134458389 | 10.49% |
| 1.00 × 10−7 | 1.00 × 10−5 | 1.00 × 10−4 | 0.144980877 | 0.140859368 | 2.84% |
| 1.00 × 10−7 | 1.00 × 10−5 | 1.00 × 10−5 | 0.150200583 | 0.134458566 | 10.48% |
| 1.00 × 10−8 | 1.00 × 10−5 | 1.00 × 10−4 | 0.144985512 | 0.140863911 | 2.84% |
| 1.00 × 10−8 | 1.00 × 10−5 | 1.00 × 10−5 | 0.150198437 | 0.134458584 | 10.48% |
| 1.00 × 10−9 | 1.00 × 10−5 | 1.00 × 10−4 | 0.144985977 | 0.140864366 | 2.84% |
| 1.00 × 10−9 | 1.00 × 10−5 | 1.00 × 10−5 | 0.150198232 | 0.134458586 | 10.48% |
| 1.00 × 10−1 | 1.00 × 10−6 | 1.00 × 10−2 | 0.140810964 | 0.142626411 | −1.27% |
| 1.00 × 10−3 | 1.00 × 10−6 | 1.00 × 10−3 | 0.998557151 | 0.921307232 | 7.74% |
| 1.00 × 10−3 | 1.00 × 10−6 | 1.00 × 10−4 | 0.136522803 | 0.136668409 | −0.11% |
| 1.00 × 10−4 | 1.00 × 10−6 | 1.00 × 10−4 | 0.216529599 | 0.213182093 | 1.55% |
| 1.00 × 10−5 | 1.00 × 10−6 | 1.00 × 10−4 | 1.070292318 | 0.972590499 | 9.13% |
| 1.00 × 10−5 | 1.00 × 10−6 | 1.00 × 10−5 | 0.137528637 | 0.137951441 | −0.31% |
| 1.00 × 10−6 | 1.00 × 10−6 | 1.00 × 10−5 | 0.140435883 | 0.140392345 | 0.03% |
| 1.00 × 10−6 | 1.00 × 10−6 | 1.00 × 10−6 | 0.143326354 | 0.134456838 | 6.19% |
| 1.00 × 10−7 | 1.00 × 10−6 | 1.00 × 10−5 | 0.140942991 | 0.140815203 | 0.09% |
| 1.00 × 10−7 | 1.00 × 10−6 | 1.00 × 10−6 | 0.143333755 | 0.134458381 | 6.19% |
| 1.00 × 10−8 | 1.00 × 10−6 | 1.00 × 10−5 | 0.140997429 | 0.140860636 | 0.10% |
| 1.00 × 10−8 | 1.00 × 10−6 | 1.00 × 10−6 | 0.143334617 | 0.134458559 | 6.19% |
| 1.00 × 10−9 | 1.00 × 10−6 | 1.00 × 10−5 | 0.141002912 | 0.140865213 | 0.10% |
| 1.00 × 10−9 | 1.00 × 10−6 | 1.00 × 10−6 | 0.143334704 | 0.134458577 | 6.19% |
| 1.00 × 10−4 | 1.00 × 10−7 | 1.00 × 10−4 | 1.006016995 | 0.922846429 | 8.27% |
| 1.00 × 10−5 | 1.00 × 10−7 | 1.00 × 10−5 | 0.214656552 | 0.213931648 | 0.34% |
| 1.00 × 10−6 | 1.00 × 10−7 | 1.00 × 10−5 | 1.325771168 | 1.332520163 | −0.51% |
| 1.00 × 10−6 | 1.00 × 10−7 | 1.00 × 10−6 | 0.137735691 | 0.137948881 | −0.15% |
| 1.00 × 10−7 | 1.00 × 10−7 | 1.00 × 10−6 | 0.140218817 | 0.140391658 | −0.12% |
| 1.00 × 10−7 | 1.00 × 10−7 | 1.00 × 10−7 | 0.133529813 | 0.134456834 | −0.69% |
| 1.00 × 10−8 | 1.00 × 10−7 | 1.00 × 10−6 | 0.140646299 | 0.140811874 | −0.12% |
| 1.00 × 10−8 | 1.00 × 10−7 | 1.00 × 10−7 | 0.133531414 | 0.134458373 | −0.69% |
| 1.00 × 10−9 | 1.00 × 10−7 | 1.00 × 10−6 | 0.140692021 | 0.140856727 | −0.12% |
| 1.00 × 10−9 | 1.00 × 10−7 | 1.00 × 10−7 | 0.133531601 | 0.134458551 | −0.69% |
| 1.00 × 10−5 | 1.00 × 10−8 | 1.00 × 10−5 | 1.021945114 | 0.936464331 | 8.36% |
| 1.00 × 10−6 | 1.00 × 10−8 | 1.00 × 10−6 | 0.220689693 | 0.220015883 | 0.31% |
| 1.00 × 10−7 | 1.00 × 10−8 | 1.00 × 10−6 | 1.169518525 | 1.164537173 | 0.43% |
| 1.00 × 10−7 | 1.00 × 10−8 | 1.00 × 10−7 | 0.137875563 | 0.137948014 | −0.05% |
| 1.00 × 10−8 | 1.00 × 10−8 | 1.00 × 10−7 | 0.140292458 | 0.140388792 | −0.07% |
| 1.00 × 10−9 | 1.00 × 10−8 | 1.00 × 10−7 | 0.140708765 | 0.140809297 | −0.07% |
| 1.00 × 10−2 | 1.00 × 10−9 | 1.00 × 10−3 | 0.141797638 | 0.140898062 | 0.63% |
| 1.00 × 10−6 | 1.00 × 10−9 | 1.00 × 10−6 | 1.148368859 | 1.050760485 | 8.50% |
| 1.00 × 10−7 | 1.00 × 10−9 | 1.00 × 10−7 | 0.238380739 | 0.237686562 | 0.29% |
| 1.00 × 10−8 | 1.00 × 10−9 | 1.00 × 10−7 | 0.959804783 | 0.965616414 | −0.60% |
| 1.00 × 10−9 | 1.00 × 10−9 | 1.00 × 10−8 | 0.140301339 | 0.140388535 | −0.06% |
References
- Fu, P.; Miao, Y.; Wang, Y.; Jiang, X.; Xu, C.; Liu, L.; Zhou, L. A Review of Research Progress and Key Technologies of Robotic Drilling in Aviation. CAAI Trans. Intell. Syst. 2022, 17, 874–885. [Google Scholar]
- Gao, G.; Niu, J.; Liu, F.; Na, J. Positioning Error Compensation of 6-Dof Robots Based on Anisotropic Error Similarity. Opt. Precis. Eng. 2022, 30, 1955–1967. [Google Scholar] [CrossRef]
- Zhang, C.T.; Wang, Y. Research on Online Calibration Method of Six-Axis Force Sensor for Industrial Robot. J. Electron. Meas. Instrum. 2021, 35, 161–168. [Google Scholar]
- Feng, L.M.; Yu, J.H.; Wang, Y.Y. Research on Calibration of Absolute Positioning Accuracy of 6-Dof Cooperative Robot. Manuf. Autom. 2022, 44, 25–28. [Google Scholar]
- Ni, H.K.; Yang, Z.Y.; Yang, Y.F. Robot Kinematics Calibration Method Considering Base Frame Error. China Mech. Eng. 2021, 33, 647–655. [Google Scholar]
- Sun, T.; Liu, C.Y.; Lian, B.B. Calibration for Precision Kinematic Control of an Articulated Serial Robot. IEEE Trans. Ind. Electron. 2021, 68, 6000–6009. [Google Scholar] [CrossRef]
- Guo, Y.L.; Zou, L.; Wang, Z.L. A Novel Kinematic Parameters Calibration Method for Industrial Robot Based on Levenberg-Marquardt and Differential Evolution Hybrid Algorithm. Robot. Comput.-Integr. Manuf. 2021, 71, 161–165. [Google Scholar]
- Ping, Y.; Guo, Z.G.; Yang, B.K. Plane Kinematic Calibration Method for Industrial Robot Based on Dynamic Measurement of Double Ball Bar. Precis. Eng. 2021, 62, 265–272. [Google Scholar]
- Jiang, Z.Z.; Zhou, J.; Han, H.Q. A Novel Robot Hand-Eye Calibration Method to Enhance Calibration Accuracy Based on the Poe Model. Adv. Robot. 2023, 37, 1052–1062. [Google Scholar] [CrossRef]
- Bai, M.; Zhang, M.L.; Zhang, H. Calibration Method Based on Models and Least-Squares Support Vector Regression Enhancing Robot Position Accuracy. IEEE Access 2021, 9, 136060–136070. [Google Scholar] [CrossRef]
- Wang, W.D.; Song, H.J.; Yan, Z.Y. A Universal Index and an Improved Pso Algorithm for Optimal Pose Selection in Kinematic Calibration of a Novel Surgical Robot. Robot. Comput.-Integr. Manuf. 2021, 50, 90–101. [Google Scholar] [CrossRef]
- Peng, T.C.; Zhang, T.; Sun, Z.J. Research on Robot Accuracy Compensation Method Based on Modified Grey Wolf Algorithm. In Proceedings of the 2023 8th Asia-Pacific Conference on Intelligent Robot Systems, Xi’an, China, 7–9 July 2023; pp. 1–6. [Google Scholar]
- Lv, H.Y. Application of Process Noise Recursive Least Squares Method. China Instrum. 2021, 1, 1–6. [Google Scholar]
- Deng, X.; Ge, L.; Li, R.; Liu, Z. Research on the Kinematic Parameter Calibration Method of Industrial Robot Based on Lm and Pf Algorithm. 2020. Available online: https://www.semanticscholar.org/paper/Research-on-the-kinematic-parameter-calibration-of-Deng-Ge/fdf9bf2b7c0beece8302fdd9ce5140a648700d2f (accessed on 22 August 2020).
- Le, N.V.; Caverly, R.J. Cable-Driven Parallel Robot Pose Estimation Using Extended Kalman Filtering with Inertial Payload Measurements. IEEE Robot. Autom. Lett. 2021, 6, 3615–3622. [Google Scholar]
- Lee, K.; Kwon, H.; You, K. Iterative Solution of Relative Localization for Cooperative Multi-Robot Using Iekf. Univers. J. Mech. Eng. 2017, 5, 15–19. [Google Scholar] [CrossRef]
- Du, G.L.; Shao, H.K.; Chen, Y.J. An Online Method for Serial Robot Self-Calibration with Cmac and Ukf. Robot. Comput.-Integr. Manuf. 2016, 42, 39–48. [Google Scholar] [CrossRef]
- Urrea, C.; Agramonte, R. Evaluation of Parameter Identification of a Real Manipulator Robot. Symmetry 2022, 14, 1446. [Google Scholar] [CrossRef]
- Geetha, S.; Natarajan, U. Kinematic Parameter Estimation of Vrt 6 Robot Using Unscented Kalman Filter with Adaptive Choice of Scaling Parameter. J. Balk. Tribol. Assoc. 2018, 24, 123–140. [Google Scholar]
- Huang, T.; Zhao, D.; Yin, F.W. Kinematic Calibration of a 6-Dof Hybrid Robot by Considering Multicollinearity in the Identification Jacobian. Mech. Mach. Theory 2019, 131, 371–384. [Google Scholar] [CrossRef]
- Li, M.Y.; Du, Z.J.; Ma, X.X. A Robot Hand-Eye Calibration Method of Line Laser Sensor Based on 3d Reconstruction. Robot. Comput.-Integr. Manuf. 2021, 71, 102–106. [Google Scholar] [CrossRef]
- Li, Z.B.; Li, S.; Bamasag, O.O. Diversified Regularization Enhanced Training for Effective Manipulator Calibration. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 8778–8790. [Google Scholar] [CrossRef] [PubMed]
| Algorithms | Characteristics |
|---|---|
| PSO | PSO and GWO search for optimal solutions without the need for linearization and lack of noise resistance. |
| GWO | |
| EKF | EKF and IEKF can resist noise but require linearization, resulting in the loss of high-order information. |
| IEKF | |
| PF | PF enables the estimation of the state of a non-linear system by approximating the probability density function by using a set of randomly sampled state particles |
| UKF | The UKF can resist noise without linearization, approximating non-linear functions by sampling on the Gaussian distribution, thus preserving high-order information. |
| i | αi−1 (°) | ai−1 (mm) | di (mm) | θi (°) |
|---|---|---|---|---|
| 1 | 0 | 0 | 540.000 | θ1 |
| 2 | −90 | 166.605 | 0 | θ2 |
| 3 | 0 | 782.270 | 0 | θ3 |
| 4 | −90 | 138.826 | 761.350 | θ4 |
| 5 | 90 | 0 | 0 | θ5 |
| 6 | 0 | 0 | 125.000 | θ6 |
| x-Direction (mm) | y-Direction (mm) | z-Direction (mm) | |
|---|---|---|---|
| max value | 1350 | 800 | 950 |
| min value | 750 | 200 | 350 |
| Algorithms | Before Calibration | GWO | PSO | EKF | IEKF | PF | APNC -UKF | |
|---|---|---|---|---|---|---|---|---|
| Metrics | ||||||||
| Max (mm) | 1.7117 | 0.5466 | 0.5547 | 0.4694 | 0.4227 | 1.6986 | 0.3282 | |
| Mean (mm) | 0.7558 | 0.2306 | 0.1832 | 0.1405 | 0.1544 | 0.7581 | 0.1347 | |
| Std (mm) | 0.3479 | 0.1049 | 0.0826 | 0.0702 | 0.0723 | 0.3518 | 0.0669 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, G.; Guo, X.; Li, G.; Li, Y.; Zhou, H. Kinematic Parameter Identification and Error Compensation of Industrial Robots Based on Unscented Kalman Filter with Adaptive Process Noise Covariance. Machines 2024, 12, 406. https://doi.org/10.3390/machines12060406
Gao G, Guo X, Li G, Li Y, Zhou H. Kinematic Parameter Identification and Error Compensation of Industrial Robots Based on Unscented Kalman Filter with Adaptive Process Noise Covariance. Machines. 2024; 12(6):406. https://doi.org/10.3390/machines12060406
Chicago/Turabian StyleGao, Guanbin, Xinyang Guo, Gengen Li, Yuan Li, and Houchen Zhou. 2024. "Kinematic Parameter Identification and Error Compensation of Industrial Robots Based on Unscented Kalman Filter with Adaptive Process Noise Covariance" Machines 12, no. 6: 406. https://doi.org/10.3390/machines12060406
APA StyleGao, G., Guo, X., Li, G., Li, Y., & Zhou, H. (2024). Kinematic Parameter Identification and Error Compensation of Industrial Robots Based on Unscented Kalman Filter with Adaptive Process Noise Covariance. Machines, 12(6), 406. https://doi.org/10.3390/machines12060406







