Young’s Modulus and Hardness Identification of Extruded Aluminum by Scratching Damper
Abstract
:1. Introduction
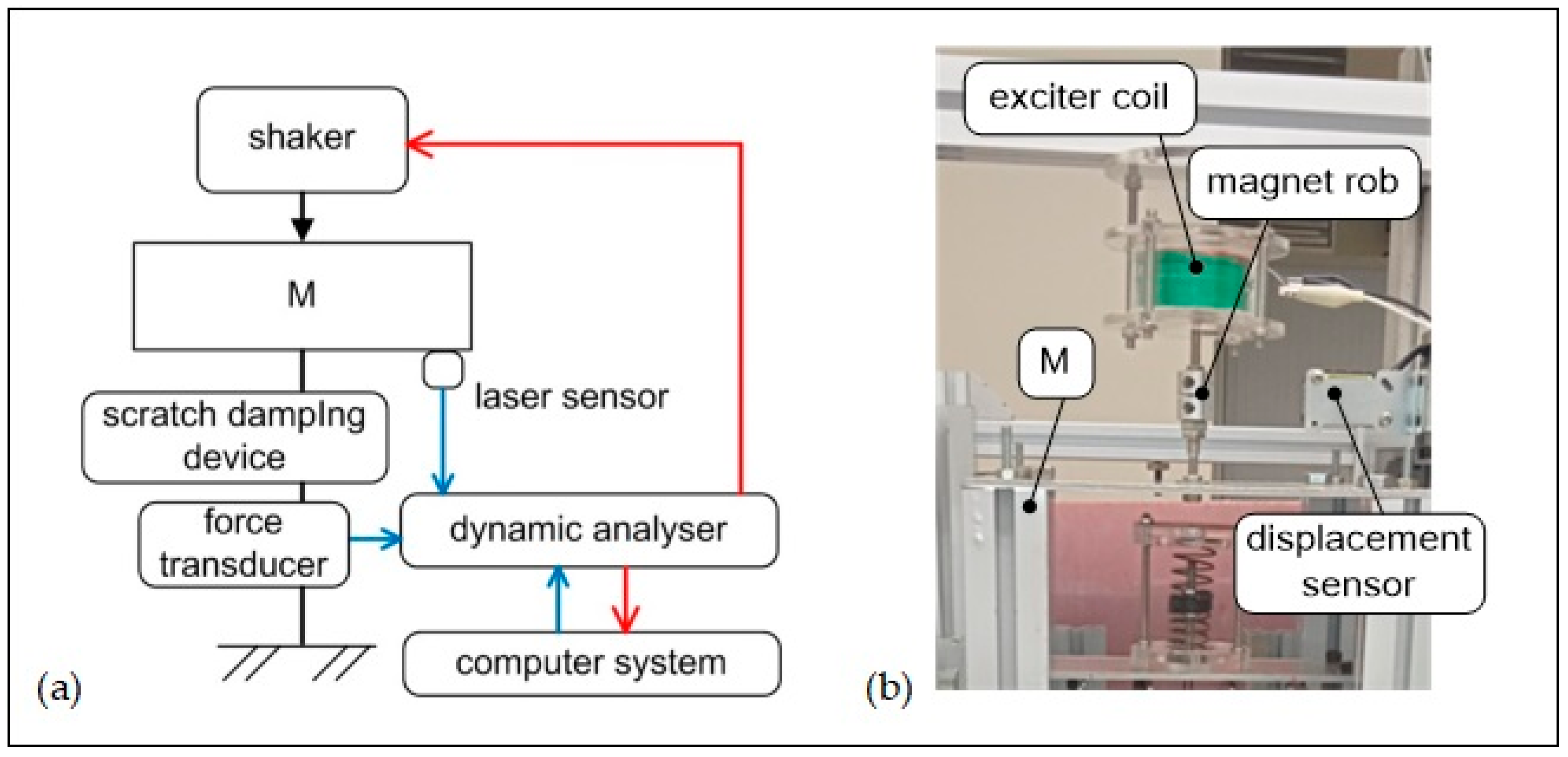
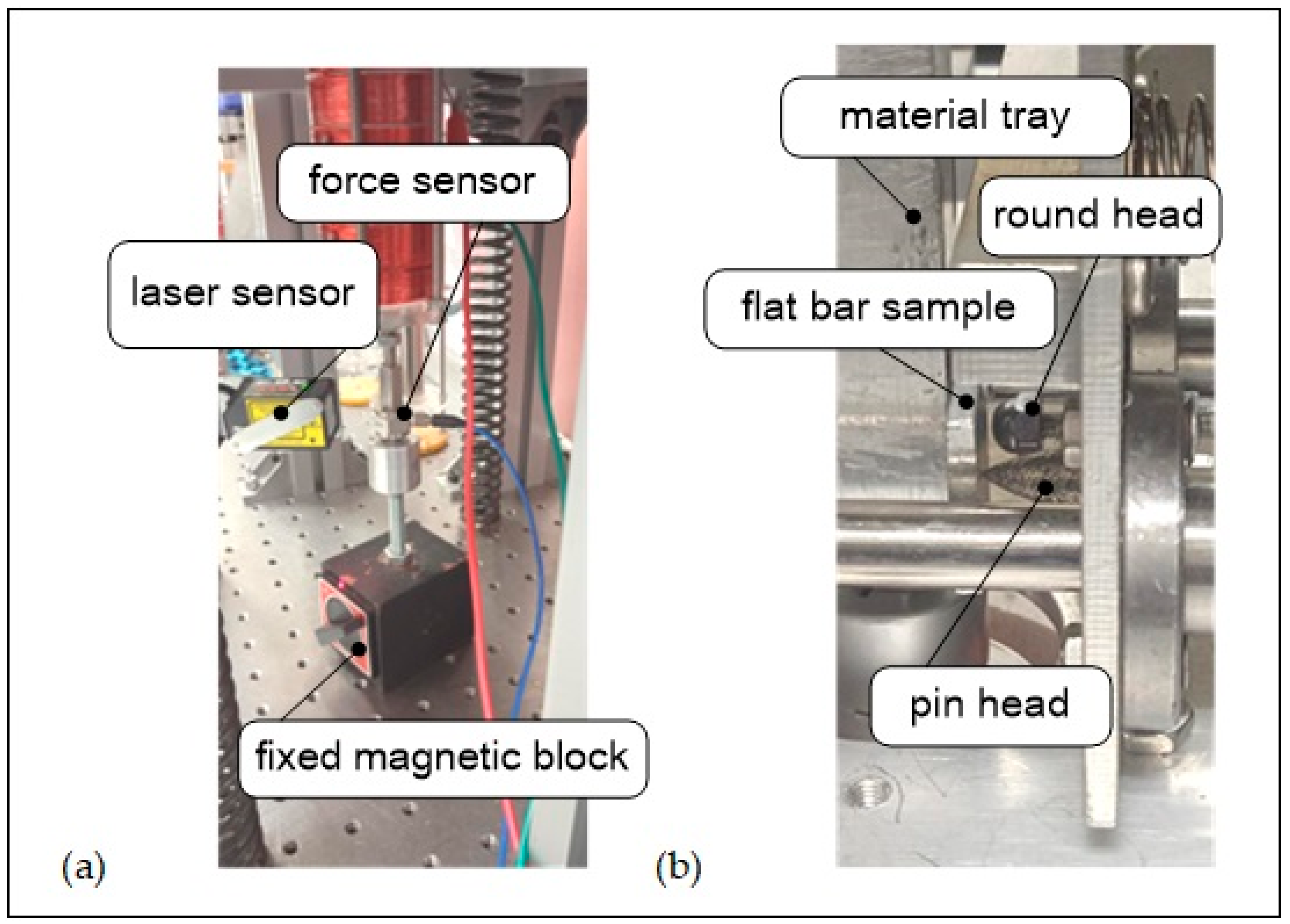
2. Design and Working Principle of Scratching Damper
3. Results and Discussion
3.1. Young’s Modulus of Extruded Aluminum Flat Bar
3.2. Hardness Estimation and Brinell Test
3.3. Dimension Inspection and Performance Evaluation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kamplade, K.; Biermann, D. Examination of the Material Removal of unreinforced, thermoplastic Polymers by Scratch Tests. Prod. Eng. 2019, 13, 713–719. [Google Scholar] [CrossRef]
- Varga, M.; Leroch, S.; Rojacz, H.; Ripoll, M.R. Study of wear mechanisms at high temperature scratch testing. Wear 2017, 388–389, 112–118. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Yang, X. Numerical study of liquid sloshing using smoothed particle hydrodynamics with adaptive spatial resolution. Eng. Anal. Bound. Elem. 2024, 159, 272–287. [Google Scholar] [CrossRef]
- Akono, A.; Ulm, F. An improved technique for characterizing the fracture toughness crack growth. Wear 2014, 313, 117–124. [Google Scholar] [CrossRef]
- Torabi, A.R.; Shahbazian, B. Notch tip plastic zone determination by extending Irwin’s model. Theor. Appl. Fract. Mech. 2020, 108, 102643. [Google Scholar] [CrossRef]
- Souza, J.M.; Yoshimura, H.N.; Peres, F.M.; Schön, C.G. Effect of sample pre-cracking method and notch geometry in plane strain fracture toughness tests as applied to a PMMA resin. Polym. Test. 2012, 31, 834–840. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, Y.; Zhou, M.; Wang, Q.; Ling, L. Material deformation and removal mechanism of SiCp/Al composites in ultrasonic vibration assisted scratch test. Ceram. Int. 2018, 44, 15133–15144. [Google Scholar] [CrossRef]
- Qiu, Z.; Liu, C.; Wang, H.; Yang, X.; Fang, F.; Tang, J. Crack propagation and the material removal mechanism of glass–ceramics by the scratch test. Mechnical Behav. Biomed. Mater. 2016, 64, 75–85. [Google Scholar] [CrossRef]
- Al Wakeel, S.; Hubler, M.H. Introducing heterogeneity into the micro-scratch test fracture toughness relation for brittle particle composites. Exp. Mech. 2018, 58, 1237–1247. [Google Scholar] [CrossRef]
- Akono, A.; Ulm, F. Fracture scaling relations for scratch tests of axisymmetric shape. Mech. Phys. Solids 2012, 60, 379–390. [Google Scholar] [CrossRef]
- Su, M.; Young, B. Material properties of normal and high strength aluminium alloys at elevated temperatures. Thin-Walled Struct. 2019, 137, 463–471. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress–Strain Curves by Three Parameters. NACA Tech. Note 902, 1943. Available online: https://ntrs.nasa.gov/citations/19930081614 (accessed on 10 June 2024).
- Janeczek, A.; Fydrych, D. The Influence of Tool Shape and Process Parameters on the Mechanical Properties of AW-3004 Aluminium Alloy Friction Stir Welded Joints. Materials 2021, 14, 3244. [Google Scholar] [CrossRef] [PubMed]
- Rockenhäuser, C.; Hartrott, P.; Skrotzki, B. Brinell-Hardness data (HBW 2.5/62.5) of aluminum alloy EN AW-2618A after different aging times and temperatures. Data Brief 2023, 46, 108830. [Google Scholar] [CrossRef] [PubMed]
- DIN EN ISO 6506-1:2015-02; Metallic Materials—Brinell Hardness Test—Part 1: Test Method. Beuth Verlag GmbH: Berlin, Germany, 2015.
- Sun, R.; Wong, W.; Cheng, L. Tunable electromagnetic shunt damper with opposing magnets configuration. Smart Mater. Struct. 2020, 29, 115034. [Google Scholar] [CrossRef]
- Tamadon, A.; Baghestani, A.; Bajgholi, M.E. Influence of WC-based pin tool profile on microstructure and mechanical properties of AA1100 FSW welds. Technologies 2020, 8, 34. [Google Scholar] [CrossRef]
- Kovacik, J.; Simancik, F. Aluminium foam—Modulus of elasticity and electrical conductivity according to percolation theory. Scr. Mater. 1998, 39, 239–246. [Google Scholar] [CrossRef]
- Isichenko, M. Percolation Statistical Topography and Transport in Random Media. Rev. Mod. Phys. 1992, 64, 961. [Google Scholar] [CrossRef]
- Kováčik, J. The tensile behaviour of porous metals made by GASAR process. Acta Mater. 1998, 46, 5413–5422. [Google Scholar] [CrossRef]
- Su, H.; Xue, L.; Wu, C. Optimizing the tool pin with three flats in friction stir welding of aluminum alloy. Int. J. Adv. Manuf. Technol. 2020, 108, 721–733. [Google Scholar] [CrossRef]
- Eyvazian, A.; Hamouda, A.M.; Aghajani, H. Study on the effects of tool tile angle, offset and plunge depth on friction stir welding of poly(methyl methacrylate)T-joint. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 234, 773–787. [Google Scholar] [CrossRef]
- Hemmouche, L.; Chicot, D.; Amrouche, A.; Iost, A.; Belouchrani, M.A.; Decoopman, X.; Louis, G.; Puchi-Cabrera, E.S. An analysis of the elastic properties of a porous aluminium oxide film by means of indentation techniques. Mater. Sci. Eng. A 2013, 585, 155–164. [Google Scholar] [CrossRef]
- Sharmaa, N.; Siddiqueea, A.N.; Khana, Z.A. Material stirring during FSW of Al–Cu: Effect of pin profile. Mater. Manuf. Process. 2018, 33, 786–794. [Google Scholar] [CrossRef]
- Shah, P.H.; Badheka, V.J. Friction stir welding of aluminium alloys: An overview of experimental findings—Process, variables, development and applications. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2017, 233, 1191–1226. [Google Scholar] [CrossRef]
- Aluminum Association (AA). Aluminum Design Manual (ADM); Aluminum Association (AA): Washington, DC, USA, 2015. [Google Scholar]
- European Committee for Standardization, Eurocode 9: Design of aluminum structures—Part 1-2: Structural fire design, BS EN 1999-1-2, Brussels, 2007. Available online: https://www.phd.eng.br/wp-content/uploads/2014/11/en.1999.1.2.2007.pdf (accessed on 29 April 2024).
- Ali, M.M.; Omran, A.N.M.; Mohamed, M.A. Prediction the correlations between hardness and tensile properties of aluminium-silicon alloys produced by various modifiers and grain refineries using regression analysis and an artificial neural network model. Eng. Sci. Technol. 2021, 24, 105–111. [Google Scholar]
- International Alloy Designations and Chemical Composition Limits for Wrought Aluminum and Wrought Aluminum Alloys; The Aluminum Association: Washington, DC, USA, 2018; ISSN 2377-6692.
- Li, Q.; Zhang, X.; Wang, L.; Qiao, J. The Effect of Extrusion and Heat Treatment on the Microstructure and Tensile Properties of 2024 Aluminum Alloy. Materials 2022, 15, 7566. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Liu, C.; Miao, K. Effects of cooling rate and cryogenic temperature on the mechanical properties and deformation characteristics of an Al-Mg-Si-Fe-Cr alloy. J. Alloys Compd. 2023, 947, 169559. [Google Scholar] [CrossRef]
- Wang, Y.; Xiong, L.; Feng, D. Investigation of the penetration performance of the radial forging process for Wrought Aluminium Alloy. Materials 2024, 17, 2065. [Google Scholar] [CrossRef]
- Wang, Y.G.Y.; Zhao, S. Experimental investigation and optimization of the semisolid multicavity squeeze casting process for wrought aluminum alloy scroll. Materials 2020, 13, 5278. [Google Scholar] [CrossRef]

 curve fit and test data of ,
curve fit and test data of ,  curve fit and test data of ,
curve fit and test data of ,  curve fit and test data of ).
curve fit and test data of ).
 curve fit and test data of ,
curve fit and test data of ,  curve fit and test data of ,
curve fit and test data of ,  curve fit and test data of ).
curve fit and test data of ).


| Data\Dial Division | 2 | 3 | 4 |
|---|---|---|---|
| Normal force (N) | 0.16 | 0.24 | 0.32 |
| Total energy (J) | 35.2 | 56.5 | 78.8 |
| Damping motion energy (J) | 24.8 | 47.8 | 70.3 |
| Scratch energy (J) | 10.4 | 8.69 | 8.51 |
| Scratch performance (%) | 29.5 | 15.4 | 10.8 |
| Young’s modulus (GPa) | 54.6 | 56.2 | 56.8 |
| Hardness | 73.4 | 76.1 | 77.5 |
| Scratch depth (mm) | 0.193 | 0.176 | 0.180 |
| Scratch length (mm) | 3.38 | 3.10 | 2.92 |
| Scratch volume (mm3) | 0.183 | 0.160 | 0.141 |
| Scratch energy factor (GJ/m3) | 56.8 | 54.5 | 60.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wong, C.-N.; Vyas, A.; Wong, W.-O.; Sun, R. Young’s Modulus and Hardness Identification of Extruded Aluminum by Scratching Damper. Machines 2024, 12, 413. https://doi.org/10.3390/machines12060413
Wong C-N, Vyas A, Wong W-O, Sun R. Young’s Modulus and Hardness Identification of Extruded Aluminum by Scratching Damper. Machines. 2024; 12(6):413. https://doi.org/10.3390/machines12060413
Chicago/Turabian StyleWong, Chun-Nam, Anand Vyas, Wai-On Wong, and Ruqi Sun. 2024. "Young’s Modulus and Hardness Identification of Extruded Aluminum by Scratching Damper" Machines 12, no. 6: 413. https://doi.org/10.3390/machines12060413
APA StyleWong, C.-N., Vyas, A., Wong, W.-O., & Sun, R. (2024). Young’s Modulus and Hardness Identification of Extruded Aluminum by Scratching Damper. Machines, 12(6), 413. https://doi.org/10.3390/machines12060413










