Topology Analysis and Structural Optimization of Air Suspension Mechanical-Vibration-Reduction Wheels
Abstract
:1. Introduction
2. Materials and Methods
2.1. Design and Development of Air Suspension Mechanical-Vibration-Reduction Wheel
2.2. Topology Optimization Analysis Method
2.3. Topology Optimization Analysis Process
3. Analysis Process and Optimization Results
3.1. Inner Rim
3.1.1. Establish a Topology Optimization Analysis Model
Supporting Reaction Force of Inner Rim
Setting Mesh
Constraints and Optimization Areas
Optimization Analysis Parameters
3.1.2. Optimization Results and Analysis
3.1.3. Structural Improvement Design Scheme
3.2. Outer Rim
3.2.1. Establish a Topology Optimization Analysis Model
Supporting Reaction Force of Outer Rim
Setting Mesh
Constraints and Optimization Areas
Optimization Analysis Parameters
3.2.2. Optimization Results and Analysis
3.2.3. Structural Improvement Design Scheme
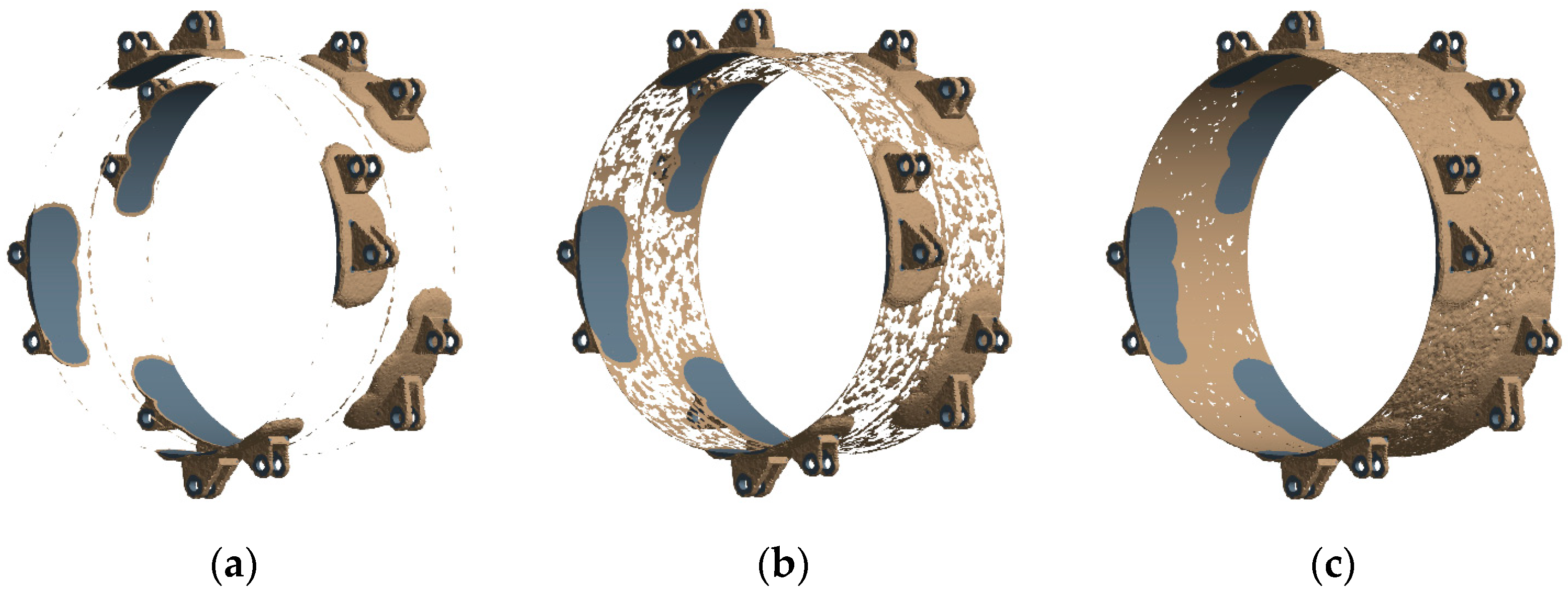
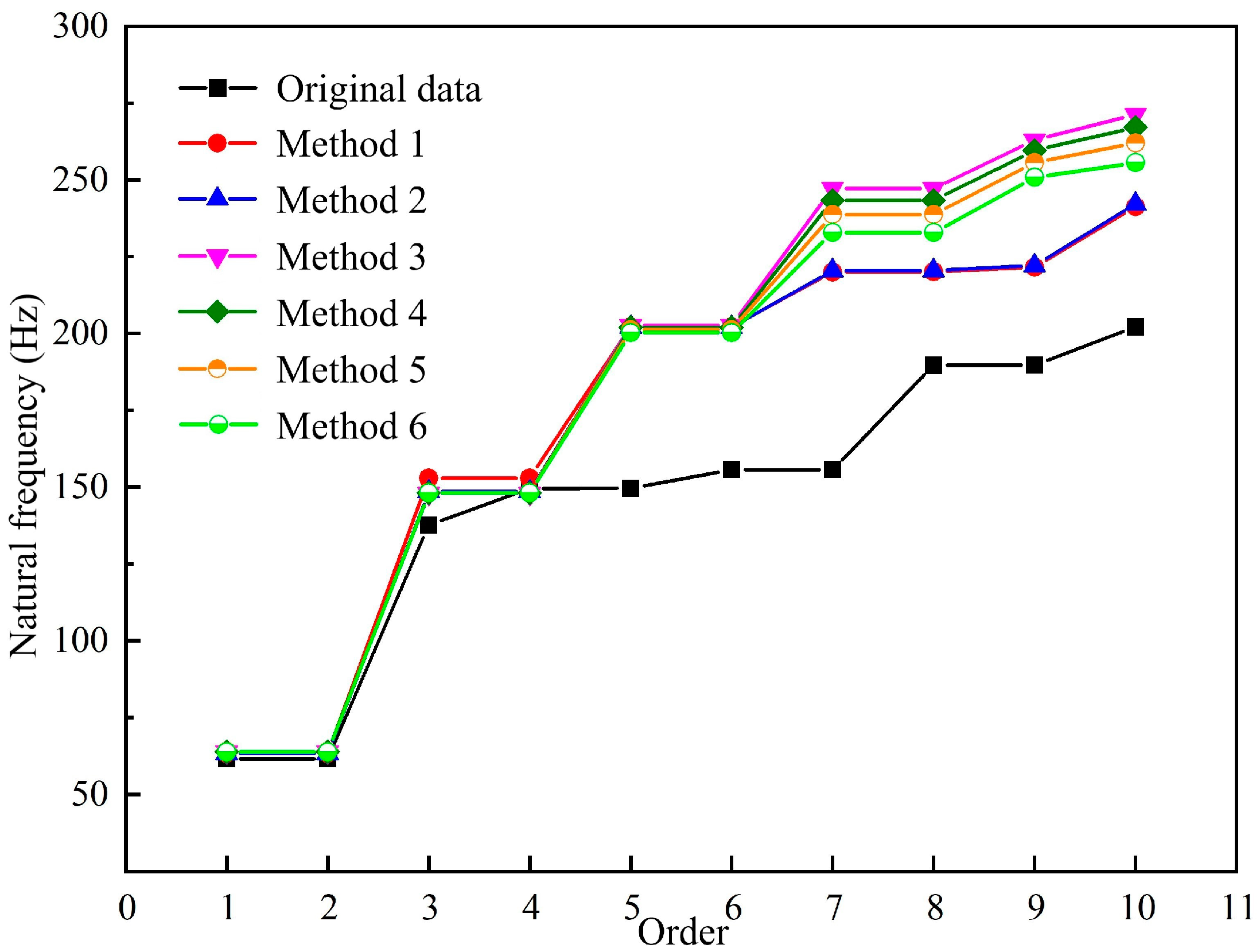
4. Verification of Structural Optimization Results
4.1. Inner Rim
4.2. Outer Rim
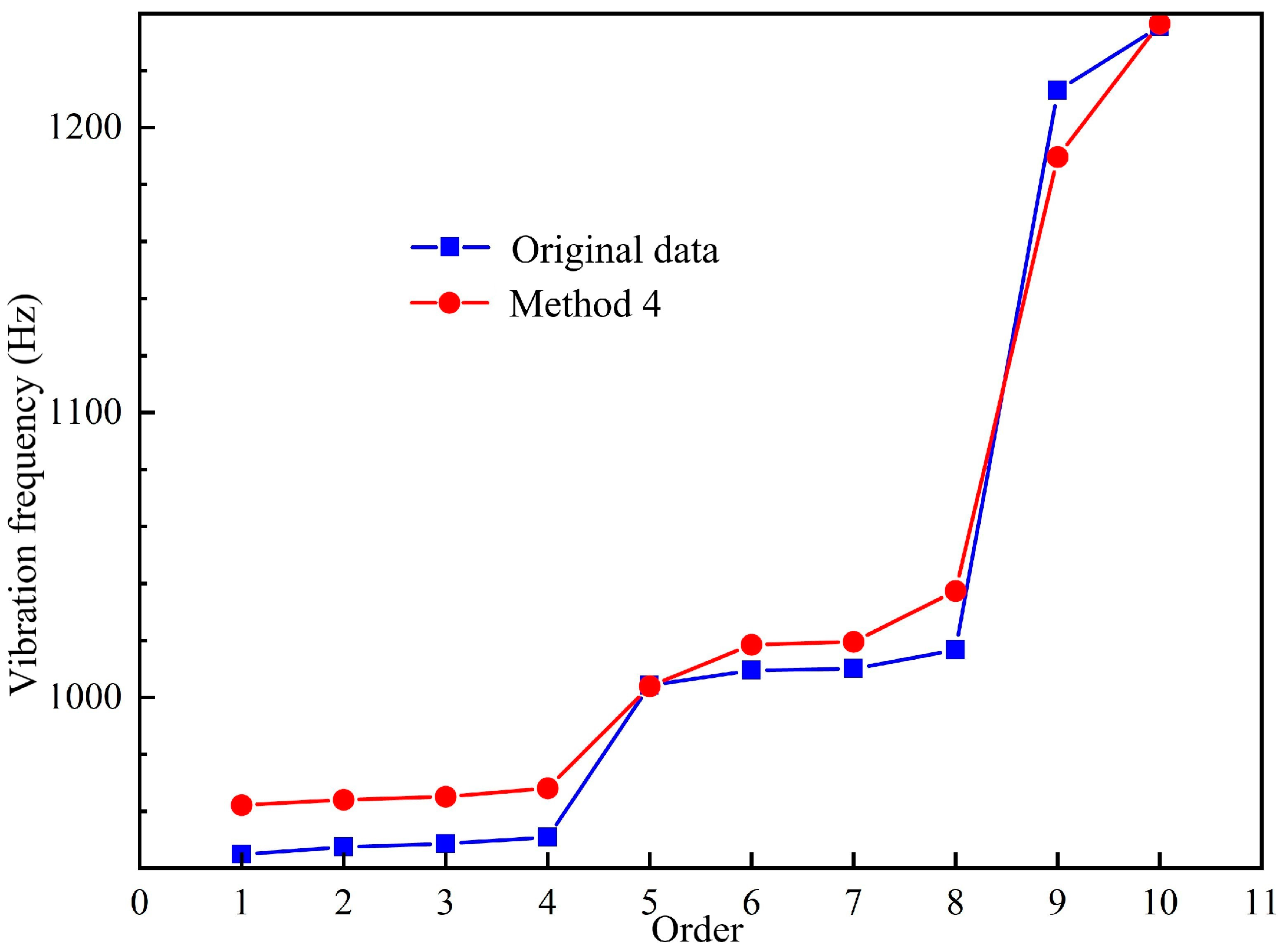
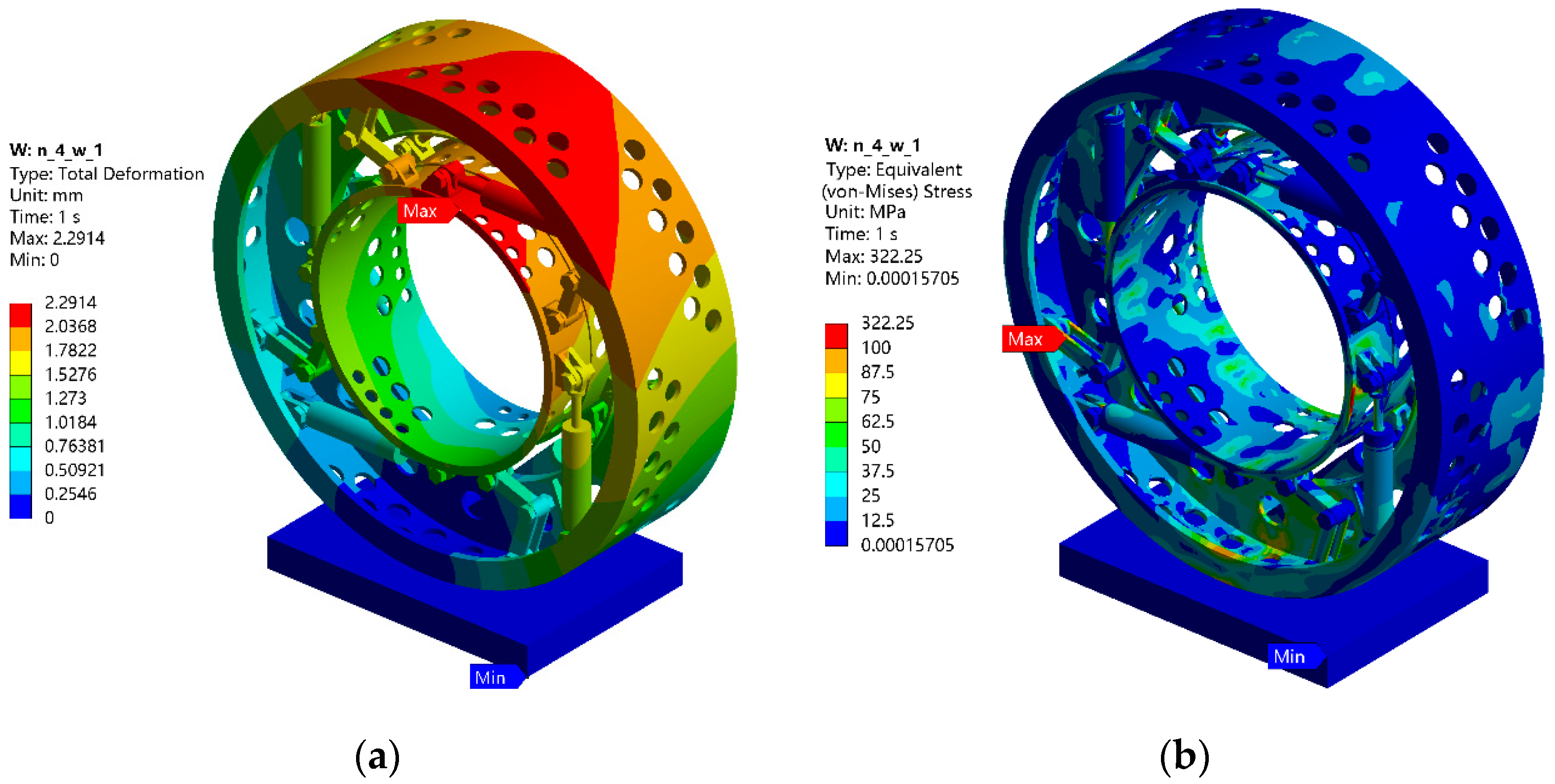
4.3. Whole Wheel
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gu, X.; Yang, K.; Wu, M.; Zhang, Y.; Zhu, J.; Zhang, W. Integrated optimization design of smart morphing wing for accurate shape control. Chin. J. Aeronaut. 2021, 34, 135–147. [Google Scholar] [CrossRef]
- De Gaspari, A. Multiobjective Optimization for the Aero-Structural Design of Adaptive Compliant Wing Devices. Appl. Sci. 2020, 10, 6380. [Google Scholar] [CrossRef]
- Baldzhiev, R.S.; Alekseyev, A.A.; Azarov, A.V. Topology optimization of the lattice payload adapter for carrier rocket. IOP Conf. Ser. Mater. Sci. Eng. 2019, 683, 012061. [Google Scholar] [CrossRef]
- Borda, F.; La Rosa, A.D.; Filice, L.; Gagliardi, F. Environmental impact of process constrained topology optimization design on automotive component’ life. Int. J. Mater. Form. 2023, 16, 48. [Google Scholar] [CrossRef]
- Tuncer, G.; Mansouri, D.; Şendur, P. The effect of spotwelds and structural adhesives on static and dynamic characteristics of vehicle body design. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2021, 235, 3207–3219. [Google Scholar] [CrossRef]
- Yu, Y.; Wei, M.; Cui, Y.; Sun, B.; Yu, Z.; Xu, Q.; Wu, Y. Reliability-based topology-topography optimization for ship bulkhead structures considering multi-failure modes. Ocean. Eng. 2024, 293, 116681. [Google Scholar] [CrossRef]
- Garbatov, Y.; Huang, Y.C. Multi-objective eliability-based design of ship structures subjected to fatigue damage and compressive collapse. J. Offshore Mech. Arct. Eng. 2020, 142, 051701. [Google Scholar] [CrossRef]
- Golecki, T.; Gomez, F.; Carrion, J.; Spencer, B.F., Jr. Topology optimization of high-speed rail bridges considering passenger comfort. Struct. Multidiscip. Optim. 2023, 66, 215. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. A New Strategy for Railway Bogie Frame Designing Combining Structural–Topological Optimization and Sensitivity Analysis. Vehicles 2024, 6, 651–665. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.J.; Jang, I.G. Integrated topology and shape optimization of the five-spoke steel wheel to improve the natural frequency. Struct. Multidiscip. Optim. 2022, 65, 78. [Google Scholar] [CrossRef]
- Zhang, Y.; Shan, Y.; Liu, X.; He, T. An integrated multi-objective topology optimization method for automobile wheels made of lightweight materials. Struct. Multidiscip. Optim. 2021, 64, 1585–1605. [Google Scholar] [CrossRef]
- Chu, D.; Bai, W.; He, Y.; Ye, M.; Li, J. Research on lightweight technology of new carbon fiber wheel hub structure. IOP Conf. Ser. Earth Environ. Sci. 2021, 632, 052071. [Google Scholar] [CrossRef]
- GB/T 5909-2009; Performance Requirements and Test Methods of Commercial Vehicles Wheels. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China: Beijing, China, 2009.
- Wang, D.; Zhang, S.; Xu, W. Multi-objective optimization design of wheel based on the performance of 13° and 90° impact tests. Int. J. Crashworthiness 2019, 24, 336–361. [Google Scholar] [CrossRef]
- Jang, I.G.; Sung, Y.H.; Yoo, E.J.; Kwak, B.M. Pattern design of a non-pneumatic tyre for stiffness using topology optimization. Eng. Optim. 2021, 24, 336–361. [Google Scholar] [CrossRef]
- Muller, P.; Mthembu, L. Topological Optimization of Mining Vehicle Tyre. Eng. Headw. 2024, 6706, 45–63. [Google Scholar] [CrossRef]
- Karthikeyan, K.; Kishore, R.; Jeeva, K.; Kumar, H.; Kannan, R.S. Topology optimization of an ATV wheel hub. J. Phys. Conf. Ser. 2021, 2027, 012022. [Google Scholar] [CrossRef]
- Zhang, S.; Lu, D.; Li, R.; Xu, L.; Jiang, H.; Cao, Y.; Xu, W. Fatigue life optimization and lightweight design of wheel based on entropy weight grey relation analysis and modified NSGA-II. Adv. Mech. Eng. 2023, 15, 16878132231189119. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Zhang, L.; Song, J.; Sun, W. Lightweight design of hub under three working conditions based on Topological optimization. J. Phys. Conf. Ser. 2022, 2338, 012074. [Google Scholar] [CrossRef]
- Jasoliya, D.; Shah, D.B.; Lakdawala, A.M. Topological optimization of wheel assembly components for all terrain vehicles. Mater. Today: Proc. 2022, 59 Pt 1, 878–883. [Google Scholar] [CrossRef]
- Kemeny, Z. Mine Material Processing Apparatus Including Gas Spring Wheel Assemblies and Related Methods. AU2022238788A1, 28 September 2023. [Google Scholar]
- Bendsoe, M.P.; Kikuchi, N. Generating optimal topologies instructural design using a homogenization method. Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Rozvany, N.I.G. A critical review of established methods of structural topology optimization. Struct. Multidisc. Optim. 2009, 37, 217–237. [Google Scholar] [CrossRef]
- Costa, G.; Montemurro, M.; Pailhès, J. Minimum length scale control in a NURBS-based SIMP method. Comput. Methods Appl. Mech. Eng. 2019, 354, 963–989. [Google Scholar] [CrossRef]
- Sethian, J.A.; Wiegmann, A. Structural boundary design vialevel set and immersed interface methods. J. Comput. Phys. 2000, 163, 489–528. [Google Scholar] [CrossRef]
- Wang, Y.M.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. A simple evolutionary procedure for structural optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elem. Anal. Des. 2007, 43, 1039–1049. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.; Zhong, W. Doing topology optimization explicitly and geometrically-a new moving morphable components based framework. J. Appl. Mech. 2014, 81, 081009. [Google Scholar] [CrossRef]
- Zhang, W.; Li, D.; Yuan, J.; Song, J.; Guo, X. A new three-dimensional topology optimization method based on moving morphable components (MMCs). Comput. Mech. 2017, 59, 647–665. [Google Scholar] [CrossRef]
- Zhang, W.; Li, D.; Kang, P.; Guo, X.; Youn, S.K. Explicit topology optimization using IGA-based moving morphable void (MMV) approach. Comput. Methods Appl. Mech. Eng. 2020, 360, 112685. [Google Scholar] [CrossRef]

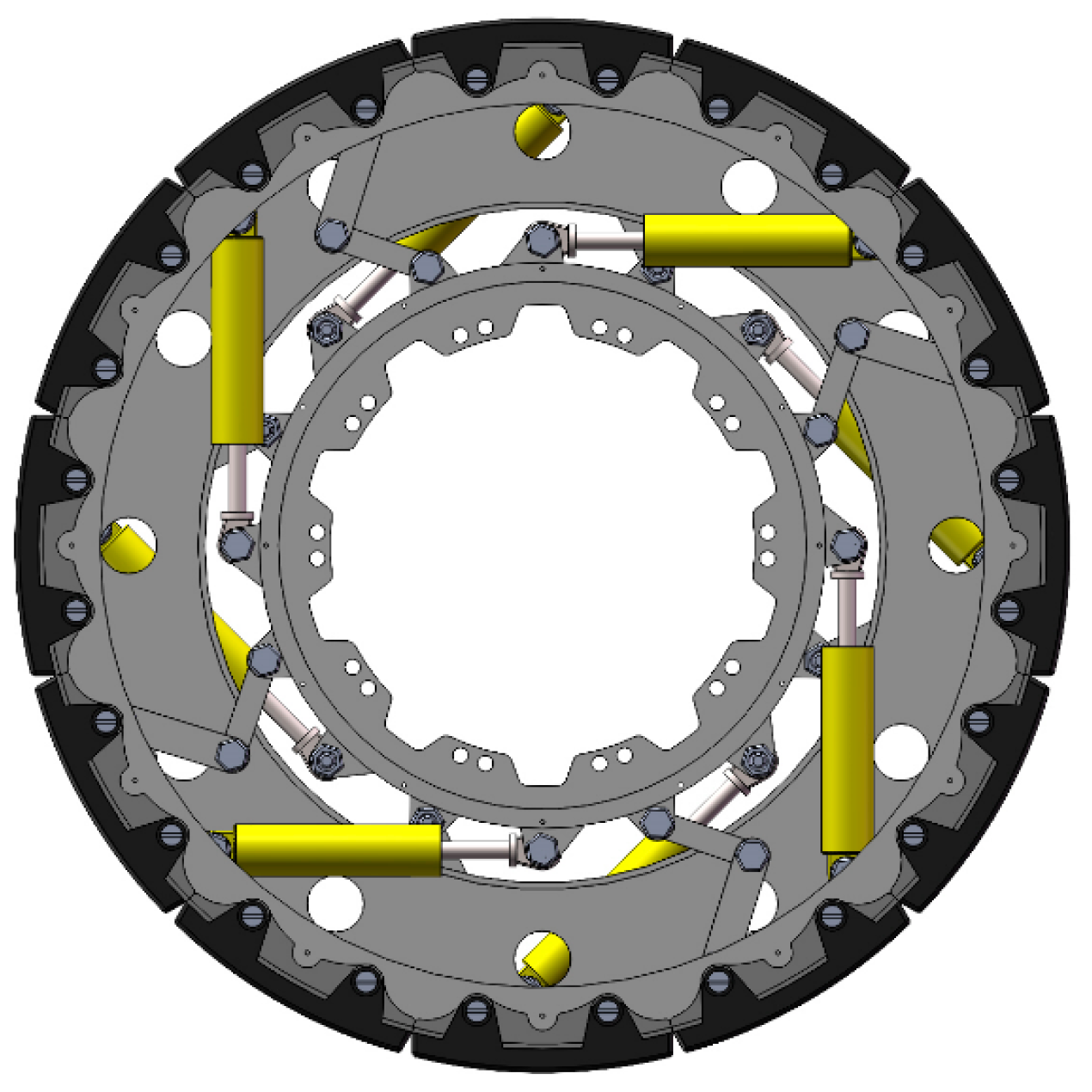

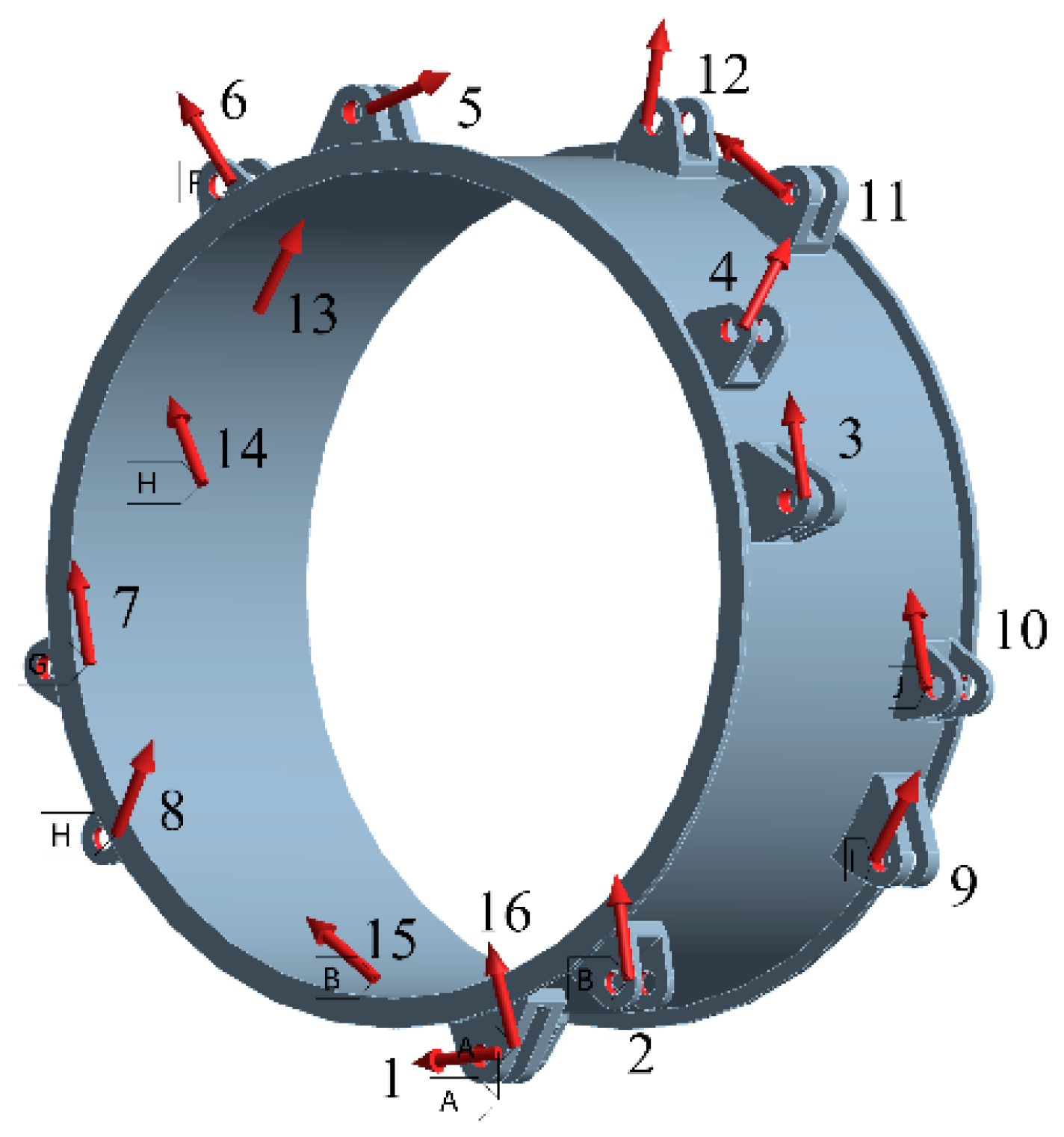
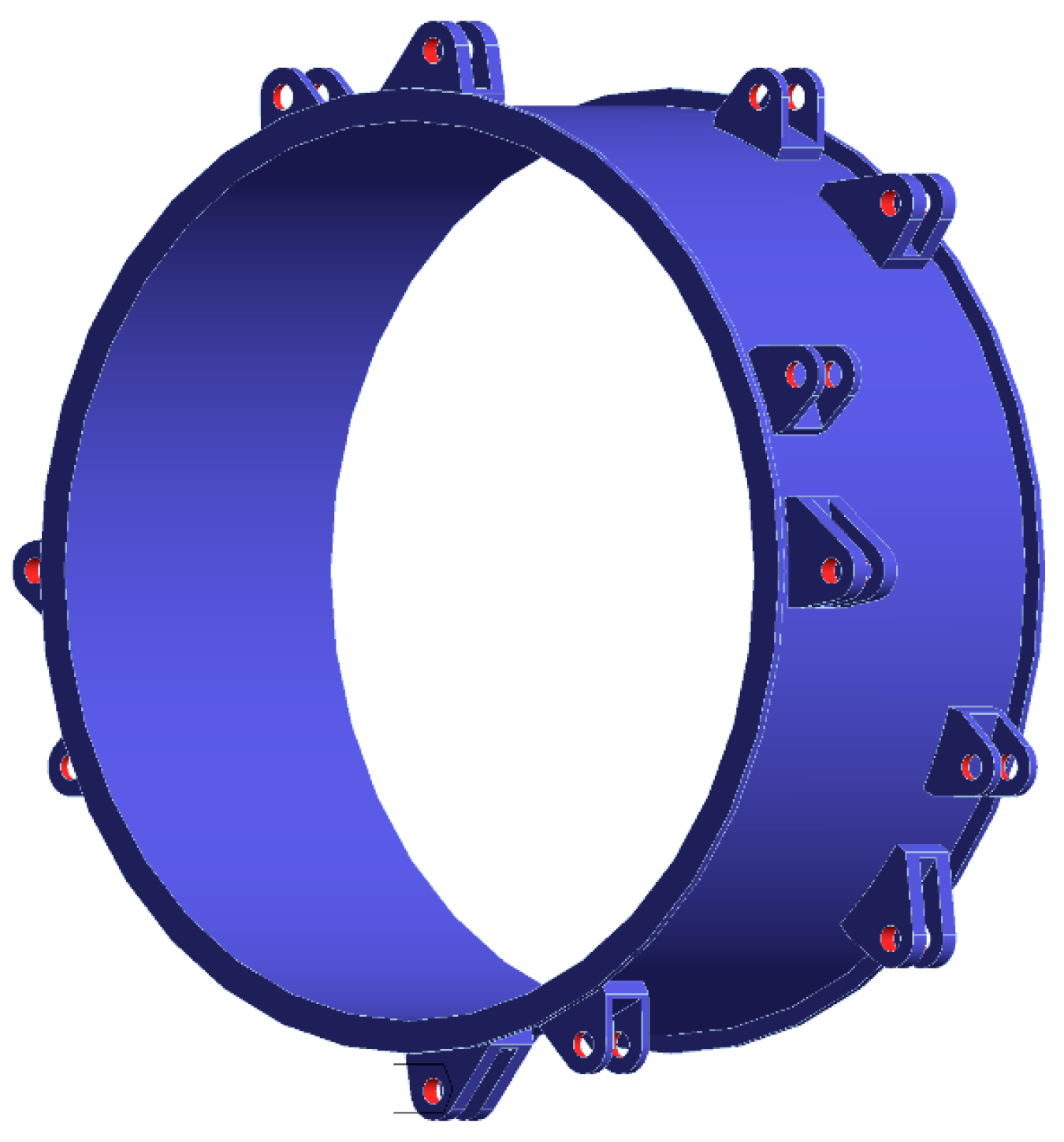
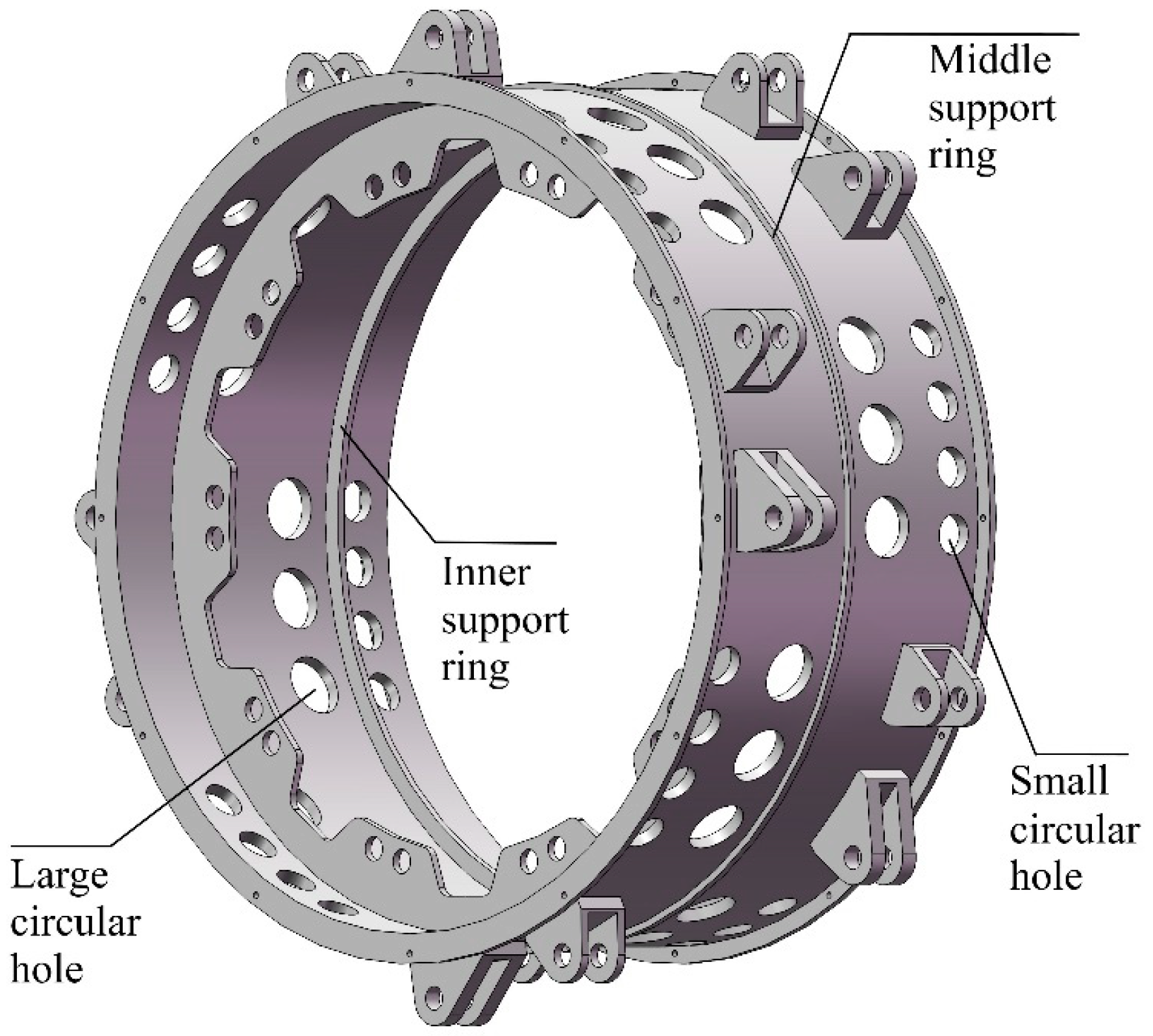



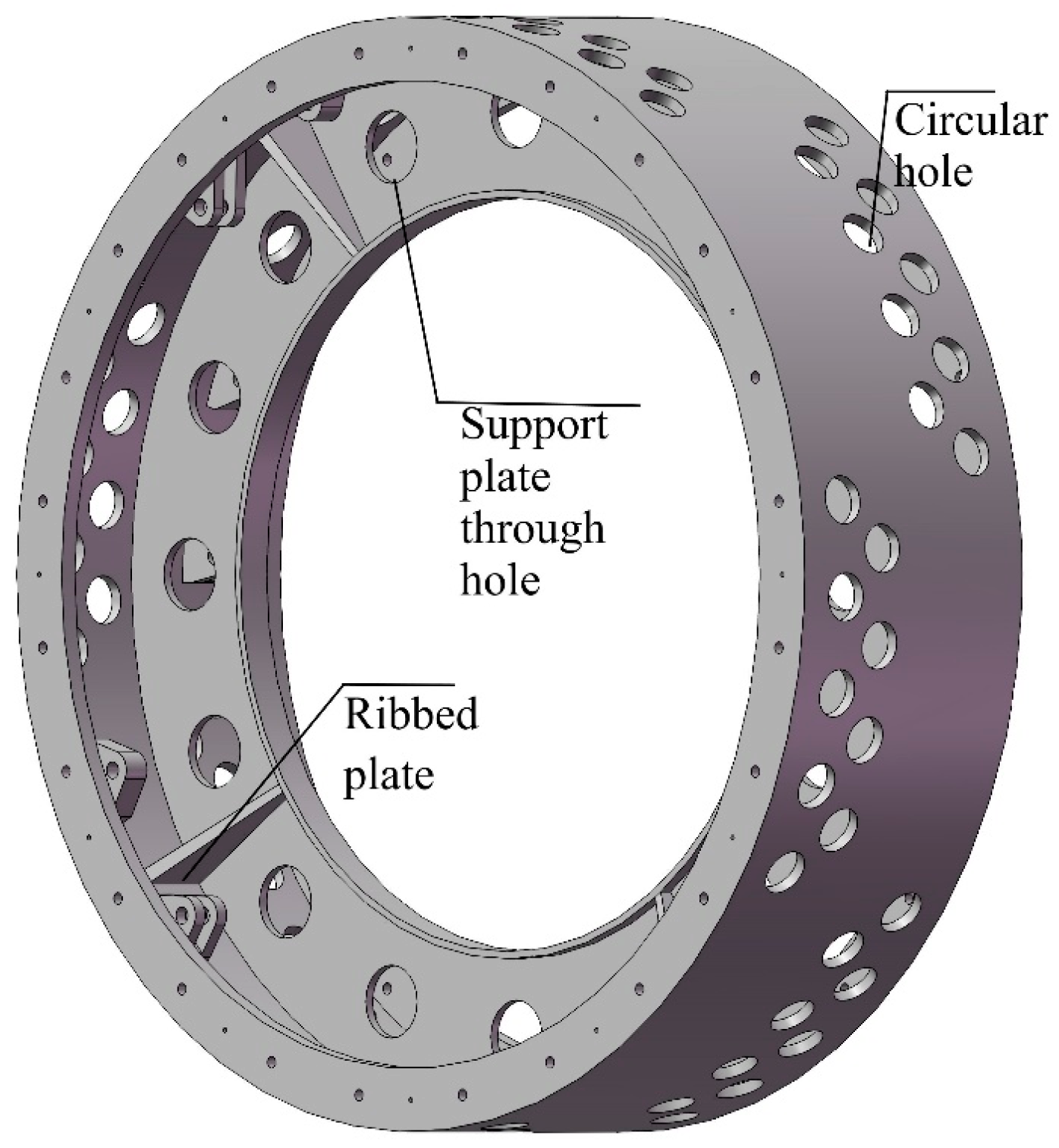


| Wheel Width (mm) | Wheel Outer Diameter (mm) | Outer Diameter of Outer Rim (mm) | Inner Diameter of Outer Rim (mm) | Inner Diameter of Support Plate (mm) | Outer Diameter of Inner Rim (mm) | Inner Diameter of Inner Rim (mm) |
|---|---|---|---|---|---|---|
| 712 | 2420 | 2290 | 2240 | 1550 | 1250 | 1212 |
| (a) | ||||||||
| Coordinate | 1 (N) | 2 (N) | 3 (N) | 4 (N) | 5 (N) | 6 (N) | 7 (N) | 8 (N) |
| X | −1820.1 | −11,844 | −88,780 | −4061.6 | −1622 | −16,348 | −75,930 | −10,919 |
| Y | −605.03 | 587.08 | −510.94 | 2578.8 | 210.28 | −2499 | 528.21 | −683.07 |
| Z | −24,413 | −236.28 | −1273.3 | 1487.8 | 9269.9 | −6646.2 | −2043.7 | 8482.4 |
| (b) | ||||||||
| Coordinate | 9 (N) | 10 (N) | 11 (N) | 12 (N) | 13 (N) | 14 (N) | 15 (N) | 16 (N) |
| X | −66,662 | −7296.5 | −35,062 | −15,686 | −38,439 | −3652.1 | −46,688 | −16,188 |
| Y | 569.51 | 1167.4 | 310.87 | 1335.9 | −321.1 | 753.75 | −573.58 | −2849.2 |
| Z | 60,605 | −1185.3 | −35,297 | 5016.4 | 34,637 | −1589.2 | −46,816 | 1.4433 |
| Method | Large Hole (mm) | Small Hole (mm) | Middle Support Ring (mm) | Inner Support Ring (mm) |
|---|---|---|---|---|
| 1 | 80 | 50 | 1300 | 1105 |
| 2 | 90 | 60 | 1300 | 1105 |
| 3 | 80 | 50 | 1270 | 1160 |
| 4 | 90 | 60 | 1270 | 1160 |
| (a) | ||||||||
| Coordinate | 1 (N) | 2 (N) | 3 (N) | 4 (N) | 5 (N) | 6 (N) | 7 (N) | 8 (N) |
| X | 88,780 | 11,844 | 1820.1 | 10,919 | 75,930 | 16,348 | 1622 | 4061.6 |
| Y | 510.94 | −587.08 | 605.03 | 683.07 | −528.21 | 2499 | −210.28 | −2578.8 |
| Z | 1273.3 | 236.28 | 24,413 | −8482.4 | 2043.7 | 6646.2 | −9269.9 | −1487.8 |
| (b) | ||||||||
| Coordinate | 9 (N) | 10 (N) | 11 (N) | 12 (N) | 13 (N) | 14 (N) | 15 (N) | 16 (N) |
| X | 66,662 | 16,188 | 46,688 | 3652.1 | 38,439 | 15,686 | 35,062 | 7296.5 |
| Y | −569.51 | 2849.2 | 573.58 | −753.75 | 321.1 | −1335.9 | −310.87 | −1167.4 |
| Z | −60,605 | −1.4434 | 46,816 | 1589.2 | −34,637 | −5016.4 | 35,297 | 1185.3 |
| Method | Support Plate Hole (mm) | Ribbed Plate (mm) | Circular Hole (mm) |
|---|---|---|---|
| 1 | 130 | 100 | 100 |
| 2 | 150 | 100 | 100 |
| 3 | 150 | 150 | 100 |
| 4 | 150 | 150 | 110 |
| 5 | 150 | 150 | 120 |
| 6 | 150 | 150 | 130 |
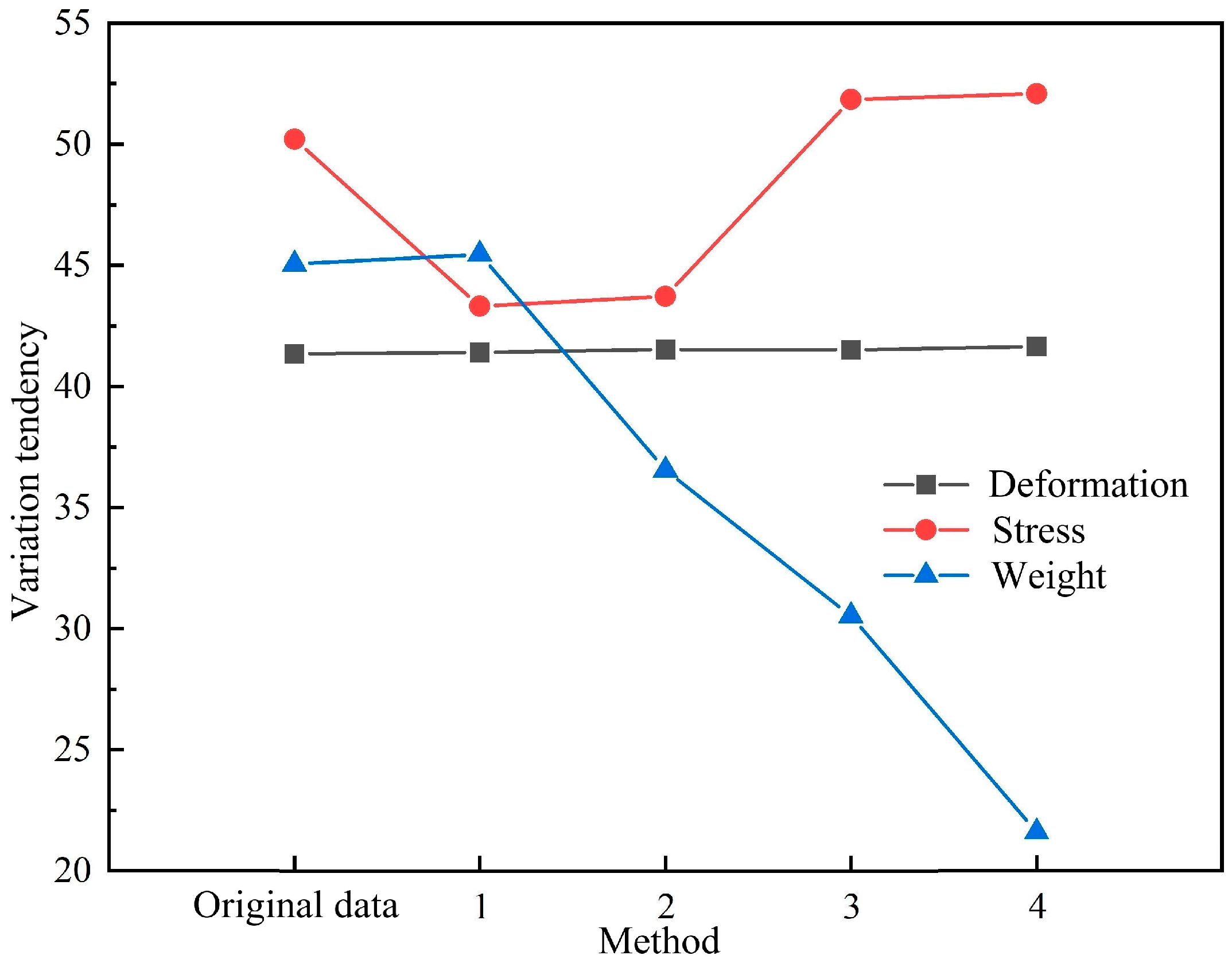
| Method | Deformation (mm) | Stress (MPa) | Weight (kg) |
|---|---|---|---|
| Original data | 2.0666 | 312.55 | 445.05 |
| 1 | 2.0702 | 310.83 | 445.45 |
| 2 | 2.0759 | 310.93 | 436.54 |
| 3 | 2.0757 | 312.96 | 430.53 |
| 4 | 2.0825 | 313.02 | 421.62 |
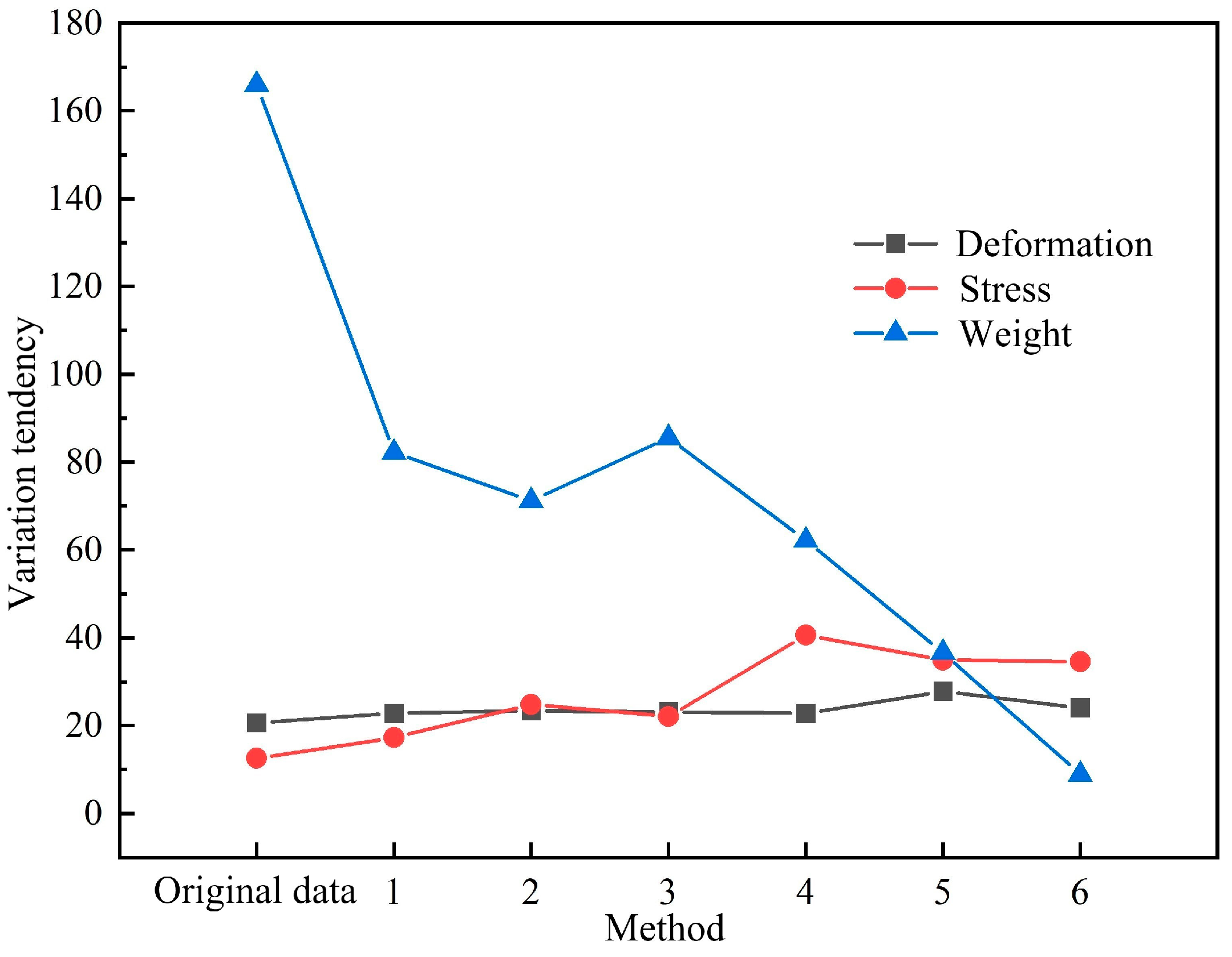
| Method | Deformation (mm) | Stress (MPa) | Weight (kg) |
|---|---|---|---|
| Original data | 2.0666 | 312.55 | 1746 |
| 1 | 2.2793 | 317.25 | 1662.2 |
| 2 | 2.3347 | 324.86 | 1651.2 |
| 3 | 2.3074 | 322.09 | 1665.5 |
| 4 | 2.2812 | 340.6 | 1642.2 |
| 5 | 2.7762 | 334.94 | 1616.6 |
| 6 | 2.4027 | 334.54 | 1588.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Feng, X.; Liu, P.; Sun, X. Topology Analysis and Structural Optimization of Air Suspension Mechanical-Vibration-Reduction Wheels. Machines 2024, 12, 488. https://doi.org/10.3390/machines12070488
Meng X, Feng X, Liu P, Sun X. Topology Analysis and Structural Optimization of Air Suspension Mechanical-Vibration-Reduction Wheels. Machines. 2024; 12(7):488. https://doi.org/10.3390/machines12070488
Chicago/Turabian StyleMeng, Xiao, Xianying Feng, Peihua Liu, and Xinhua Sun. 2024. "Topology Analysis and Structural Optimization of Air Suspension Mechanical-Vibration-Reduction Wheels" Machines 12, no. 7: 488. https://doi.org/10.3390/machines12070488
APA StyleMeng, X., Feng, X., Liu, P., & Sun, X. (2024). Topology Analysis and Structural Optimization of Air Suspension Mechanical-Vibration-Reduction Wheels. Machines, 12(7), 488. https://doi.org/10.3390/machines12070488





