A Method to Obtain Frequency Response Functions of Operating Mechanical Systems Based on Experimental Modal Analysis and Operational Modal Analysis
Abstract
:1. Introduction
2. Problem Description and the Main Assumption
3. The Proposed Method
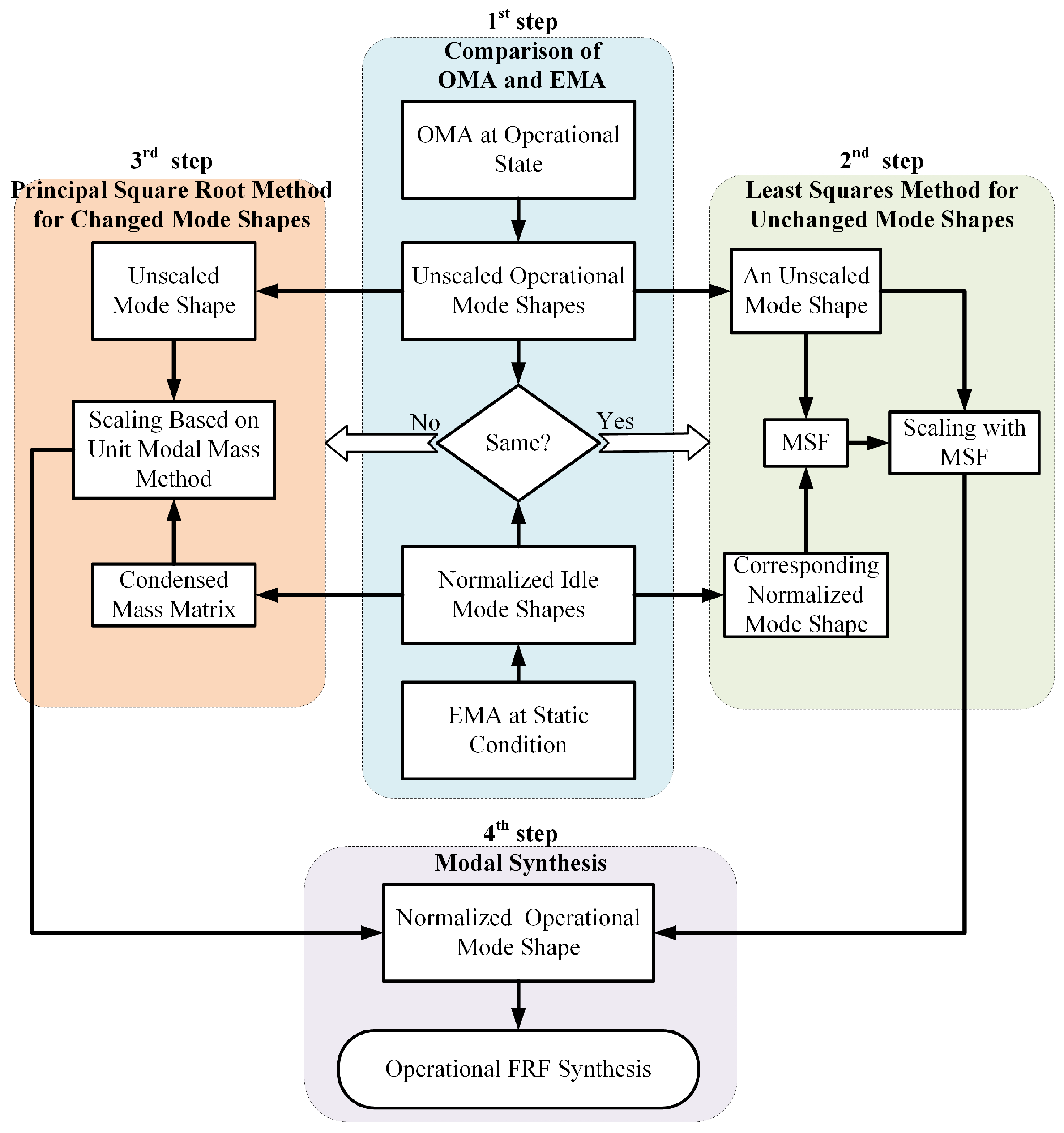
3.1. The Main Idea and Procedures
3.2. The Principal Square Root Method for the Third Step
3.3. The Stability of Condensed Mass and Countermeasures
3.4. Practical Implementation
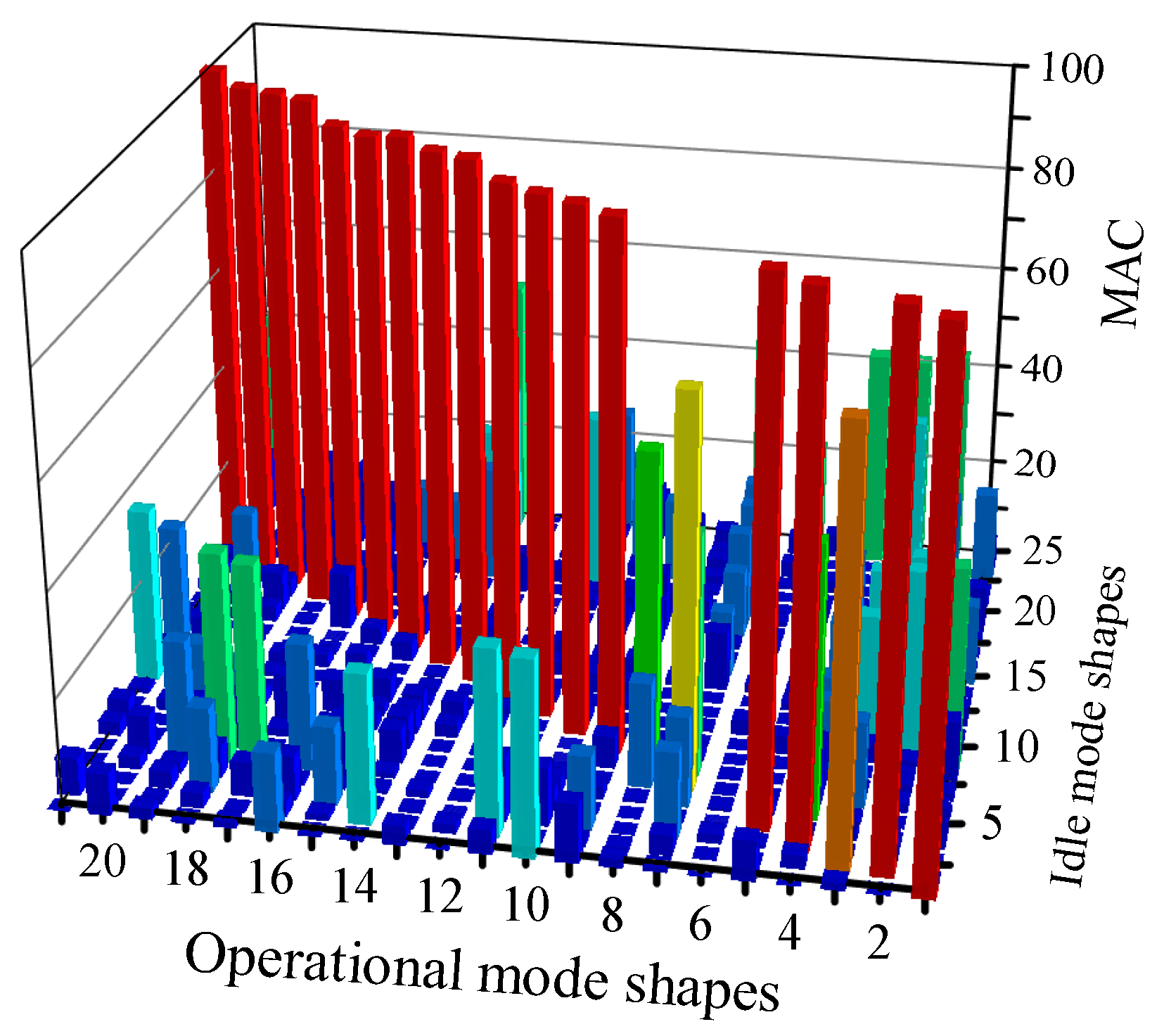
- The number of measured DOFs m should be sufficient to reduce the likelihood that MAC matrix for different idle mode shapes has large elements, which may result in a high . The exact number should be determined comprehensively considering test demands and the complexity of the structure.
- Modes beyond the frequency band of interest in OFRF are needed. They will supplement upper and low residues beyond frequency band and thus promote estimation accuracy of OFRFs.
- The proposed method is derived based on normal modes. For structures with high damping, the accuracy may decrease.
- All approaches that improve EMA precision can benefit the identification of OFRFs. For instance, selecting appropriate frequencies as boundaries during EMA, and checking for reciprocity. FRFs that significantly violate reciprocity would affect the estimation of modal shape and ultimately cause trouble in the normalization of operational modes.
4. Case Studies
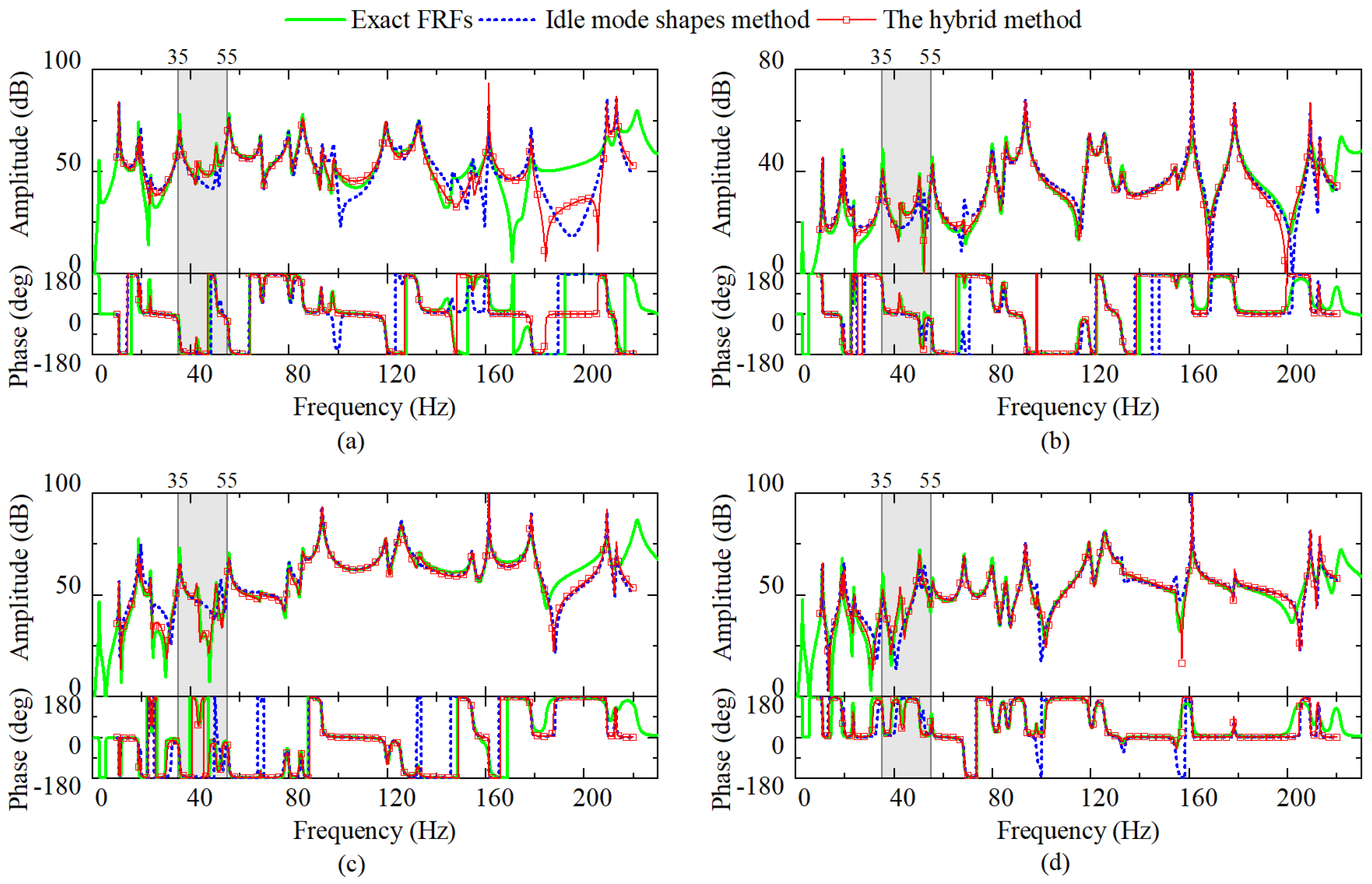
4.1. Simulation Example
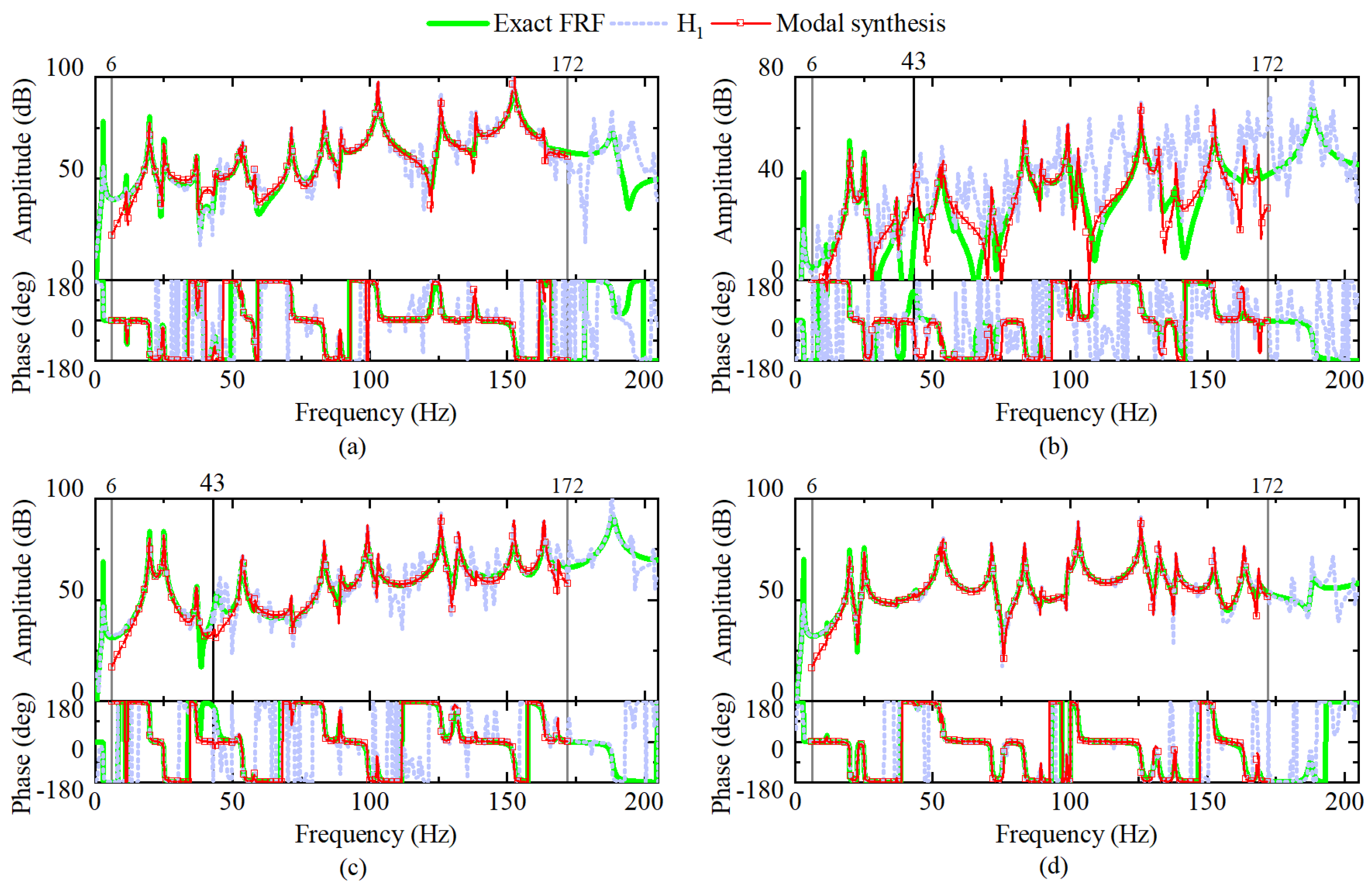
4.2. Experimental Example
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B

| Node | Coordinate | Node | Coordinate |
|---|---|---|---|
| 1001 | (1000.0, 0.0, 0.0) | 1011 | (0.0, 480.0, 0.0) |
| 1002 | (1000.0, 210.0, 0.0) | 1012 | (0.0, 180.0, 0.0) |
| 1003 | (1000.0, 490.0, 0.0) | 1013 | (0.0, 0.0, 0.0) |
| 1004 | (1000.0, 780.0, 0.0) | 1014 | (240.0, 0.0, 0.0) |
| 1005 | (1000.0, 1000.0, 0.0) | 1015 | (510.0, 0.0, 0.0) |
| 1006 | (760.0, 1000.0, 0.0) | 1016 | (790.0, 0.0, 0.0) |
| 1007 | (480.0, 1000.0, 0.0) | 1017 | (1000.0, 520.0, 0.0) |
| 1008 | (180.0, 1000.0, 0.0) | 1018 | (520.0, 1000.0, 0.0) |
| 1009 | (0.0, 1000.0, 0.0) | 1019 | (500.0, 1000.0, 0.0) |
| 1010 | (0.0, 790.0, 0.0) | 1020 | (0.0, 500.0, 0.0) |
Appendix C
| The Original Structure | The Targeted Structure |
|---|---|
| 11.3829 | 10.8636 |
| 19.7494 | 18.7843 |
| 25.0262 | 19.6450 |
| 36.8577 | 23.6460 |
| 43.3347 | 35.4094 |
| 52.3165 | 42.5321 |
| 53.6780 | 50.3279 |
| 57.9709 | 52.1611 |
| 71.4442 | 55.4953 |
| 83.3543 | 68.4422 |
| 89.5122 | 79.8620 |
| 99.1503 | 85.4602 |
| 102.9488 | 93.4075 |
| 125.8974 | 98.0684 |
| 132.2300 | 119.3317 |
| 138.6529 | 125.5628 |
| 152.4326 | 132.6460 |
| 163.3064 | 146.4351 |
| 168.6131 | 154.5092 |
| 188.2306 | 161.2042 |
| 218.2984 | 178.4255 |
| 223.2421 | 209.2524 |
| 229.6832 | 213.1208 |
| The Original Structure | The Targeted Structure |
|---|---|
| 11.3825 | 12.5928 |
| 19.7554 | 21.4307 |
| 25.0330 | 27.2876 |
| 36.8915 | 39.8742 |
| 43.6217 | 57.7508 |
| 52.6610 | 62.9120 |
| 53.7115 | 77.2842 |
| 57.9793 | 82.8056 |
| 71.4567 | 96.0678 |
| 83.3827 | 97.8849 |
| 89.4947 | 110.8344 |
| 99.1247 | 112.9849 |
| 102.9327 | 137.5893 |
| 125.8468 | 144.9645 |
| 132.2340 | 151.1522 |
| 138.5813 | 162.2044 |
| 152.3783 | 179.5252 |
| 163.3391 | 184.6468 |
| 168.6119 | 207.0478 |
| The Original Structure | The Targeted Structure |
|---|---|
| 56.2318 | 57.9509 |
| 64.9327 | 64.2205 |
| 109.6792 | 115.5228 |
| 154.3924 | 164.5742 |
| 201.9135 | 223.7241 |
| 232.8787 | 237.3319 |
| 260.2597 | 263.0481 |
| 284.6582 | 310.9808 |
| 319.4749 | 329.2040 |
| 333.7813 | 350.3971 |
| 372.3621 | 361.5300 |
| 405.0700 | 388.7280 |
| 420.2550 | 412.9673 |
| 443.1399 | 436.9488 |
References
- Pradhan, S.; Modak, S. A method for damping matrix identification using frequency response data. Mech. Syst. Signal Process. 2012, 33, 69–82. [Google Scholar] [CrossRef]
- Lin, R.; Zhu, J. Model updating of damped structures using FRF data. Mech. Syst. Signal Process. 2006, 20, 2200–2218. [Google Scholar] [CrossRef]
- Niu, Z. Frequency response-based structural damage detection using Gibbs sampler. J. Sound Vib. 2020, 470, 115160. [Google Scholar] [CrossRef]
- Zhang, Q.; Hou, J.; Duan, Z.; Jankowski, Ł.; Hu, X. Road Roughness Estimation Based on the Vehicle Frequency Response Function. Actuators 2021, 10, 89. [Google Scholar] [CrossRef]
- Song, J.H.; Lee, E.T.; Eun, H.C. Expansion of incomplete frequency response functions and prediction of unknown input forces. Arch. Appl. Mech. 2021, 91, 1055–1066. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, X.; Li, C.; Hou, H.; Wang, D.; Cao, Y. Electric Vehicle Interior Noise Contribution Analysis. In Proceedings of the SAE 2016 World Congress and Exhibition, Detroit, Michigan, 12–14 April 2016. [Google Scholar] [CrossRef]
- van der Seijs, M.V.; de Klerk, D.; Rixen, D.J. General framework for transfer path analysis: History, theory and classification of techniques. Mech. Syst. Signal Process. 2016, 68–69, 217–244. [Google Scholar] [CrossRef]
- Ocepek, D.; Vrtač, T.; Čepon, G.; Boltežar, M. Estimation of the frequency response functions for operational assemblies using independent source characterization. Mech. Syst. Signal Process. 2023, 182, 109542. [Google Scholar] [CrossRef]
- Carne, T.G.; James, G.H. The inception of OMA in the development of modal testing technology for wind turbines. Mech. Syst. Signal Process. 2010, 24, 1213–1226. [Google Scholar] [CrossRef]
- Li, B.; Luo, B.; Mao, X.; Cai, H.; Peng, F.; Liu, H. A new approach to identifying the dynamic behavior of CNC machine tools with respect to different worktable feed speeds. Int. J. Mach. Tools Manuf. 2013, 72, 73–84. [Google Scholar] [CrossRef]
- Özşahin, O.; Budak, E.; Özgüven, H. Identification of bearing dynamics under operational conditions for chatter stability prediction in high speed machining operations. Precis. Eng. 2015, 42, 53–65. [Google Scholar] [CrossRef]
- Grossi, N.; Sallese, L.; Montevecchi, F.; Scippa, A.; Campatelli, G. Speed-varying Machine Tool Dynamics Identification Through Chatter Detection and Receptance Coupling. In Proceedings of the 5th CIRP Global Web Conference—Research and Innovation for Future Production (CIRPe 2016), Patras, Greece, 4–6 October 2016; Volume 55, pp. 77–82. [Google Scholar] [CrossRef]
- Deng, K.; Gao, D.; Zhao, C.; Lu, Y. Prediction of in-process frequency response function and chatter stability considering pose and feedrate in robotic milling. Robot. Comput.-Integr. Manuf. 2023, 82, 102548. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Ahmadi, K. In-Process Frequency Response Function Measurement for Robotic Milling. Exp. Tech. 2023, 47, 797–816. [Google Scholar] [CrossRef]
- Karlsson, F.; Persson, A. Modelling Non-Linear Dynamics of Rubber Bushings-Parameter Identification and Validation. Master’s Thesis, Lund University, Lund, Sweden, 2003. [Google Scholar]
- Kindt, P.; Sas, P.; Desmet, W. Measurement and analysis of rolling tire vibrations. Opt. Lasers Eng. 2009, 47, 443–453. [Google Scholar] [CrossRef]
- Rocca, G.; Díaz, G.; Middelberg, J.; Kindt, P.; Peeters, B. Experimental Characterization of the Dynamic Behaviour of Tires in Static and Rolling Conditions. In Proceedings of the 18th International Congress on Sound & Vibration, Janeiro, Brazil, 10–14 July 2011. [Google Scholar]
- Gonzalez Diaz, C.; Kindt, P.; Middelberg, J.; Vercammen, S.; Thiry, C.; Close, R.; Leyssens, J. Dynamic behaviour of a rolling tyre: Experimental and numerical analyses. J. Sound Vib. 2016, 364, 147–164. [Google Scholar] [CrossRef]
- De Sitter, G.; Devriendt, C.; Guillaume, P.; Pruyt, E. Operational transfer path analysis. Mech. Syst. Signal Process. 2010, 24, 416–431. [Google Scholar] [CrossRef]
- Coppotelli, G. On the estimate of the FRFs from operational data. Mech. Syst. Signal Process. 2009, 23, 288–299. [Google Scholar] [CrossRef]
- Behnam, M.R.; Khatibi, M.M.; Malekjafarian, A. An accurate estimation of frequency response functions in output-only measurements. Arch. Appl. Mech. 2018, 88, 837–853. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. Stochastic system identification for operational modal analysis: A review. J. Dyn. Syst. Meas. Control Trans. Asme 2001, 123, 659–667. [Google Scholar] [CrossRef]
- Reynders, E. System Identification Methods for (Operational) Modal Analysis: Review and Comparison. Arch. Comput. Methods Eng. 2012, 19, 51–124. [Google Scholar] [CrossRef]
- Brincker, R.; Kirkegaard, P.H. Special issue on Operational Modal Analysis. Mech. Syst. Signal Process. 2010, 24, 1209–1212. [Google Scholar] [CrossRef]
- Parloo, E.; Verboven, P.; Guillaume, P.; Van Overmeire, M. Sensitivity-based operational mode shape normalisation. Mech. Syst. Signal Process. 2002, 16, 757–767. [Google Scholar] [CrossRef]
- López-Aenlle, M.; Fernández, P.; Brincker, R.; Fernández-Canteli, A. Scaling-factor estimation using an optimized mass-change strategy. Mech. Syst. Signal Process. 2010, 24, 1260–1273. [Google Scholar] [CrossRef]
- Khatibi, M.; Ashory, M.; Malekjafarian, A.; Brincker, R. Mass-stiffness change method for scaling of operational mode shapes. Mech. Syst. Signal Process. 2012, 26, 34–59. [Google Scholar] [CrossRef]
- Massa, F.; Tison, T.; Lallemand, B.; Cazier, O. Structural modal reanalysis methods using homotopy perturbation and projection techniques. Comput. Methods Appl. Mech. Eng. 2011, 200, 2971–2982. [Google Scholar] [CrossRef]
- Bernal, D. Modal Scaling from Known Mass Perturbations. J. Eng. Mech. 2004, 130, 1083–1088. [Google Scholar] [CrossRef]
- Bernal, D. A receptance based formulation for modal scaling using mass perturbations. Mech. Syst. Signal Process. 2011, 25, 621–629. [Google Scholar] [CrossRef]
- López-Aenlle, M.; Brincker, R.; Pelayo, F.; Canteli, A. On exact and approximated formulations for scaling-mode shapes in operational modal analysis by mass and stiffness change. J. Sound Vib. 2012, 331, 622–637. [Google Scholar] [CrossRef]
- Aenlle, M.; Brincker, R. Modal scaling in operational modal analysis using a finite element model. Int. J. Mech. Sci. 2013, 76, 86–101. [Google Scholar] [CrossRef]
- Brandt, A.; Berardengo, M.; Manzoni, S.; Vanali, M.; Cigada, A. Global scaling of operational modal analysis modes with the OMAH method. Mech. Syst. Signal Process. 2019, 117, 52–64. [Google Scholar] [CrossRef]
- Yi, T.Y.; Nikravesh, P.E. A method to identify vibration characteristics of modified structures for flexible vehicle dynamics. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2002, 216, 55–63. [Google Scholar] [CrossRef]
- Bartolozzi, G.; Danti, M.; Camia, A.; Vige, D. Enhancement of Full-Vehicle Road Noise Simulation Including Detailed Road Surface and Innovative Tire Modeling. SAE Int. J. Passeng. Cars-Mech. Syst. 2016, 9, 1091–1099. [Google Scholar] [CrossRef]
- Peng, Y.; Li, B.; Mao, X.; Liu, H.; Qin, C.; He, H. A method to obtain the in-process FRF of a machine tool based on operational modal analysis and experiment modal analysis. Int. J. Adv. Manuf. Technol. 2018, 95, 3599–3607. [Google Scholar] [CrossRef]
- O’Callahan, J.; Avitabile, P.; Riemer, R. System Equivalent reduction Expansion Process. In Proceedings of the 7th International Modal Analysis Conference, Kissimmee, FL, USA, 1–4 February 1988. [Google Scholar]
- Ibrahim, S.R. Computation of normal modes from identified complex modes. AIAA J. 1985, 23, 816a. [Google Scholar] [CrossRef]
- Alvin, K.; Park, K.; Peterson, L. Extraction of undamped normal modes and nondiagonal modal damping matrix from damped system realization parameters. In Proceedings of the 34th Structures, Structural Dynamics and Materials Conference, La Jolla, CA, USA, 19–22 April 1993. [Google Scholar] [CrossRef]
- Heylen, W.; Lammens, S.; Sas, P. Modal Analysis Theory and Testing, 2nd. ed.; Katholieke Universiteit Leuven: Leuven, Belgium, 1998. [Google Scholar]
- Higham, N. Functions of Matrices: Theory and Computation; Society for Industrial and Applied Mathematics: Pennsylvania, PA, USA, 2013. [Google Scholar]
- Friswell, M.; Mottershead, J. Finite Element Model Updating in Structural Dynamics; Springer Netherlands: Berlin/Heidelberg, Germany, 1995. [Google Scholar] [CrossRef]
- De Troyer, T.; Guillaume, P.; Pintelon, R.; Vanlanduit, S. Fast calculation of confidence intervals on parameter estimates of least-squares frequency-domain estimators. Mech. Syst. Signal Process. 2009, 23, 261–273. [Google Scholar] [CrossRef]






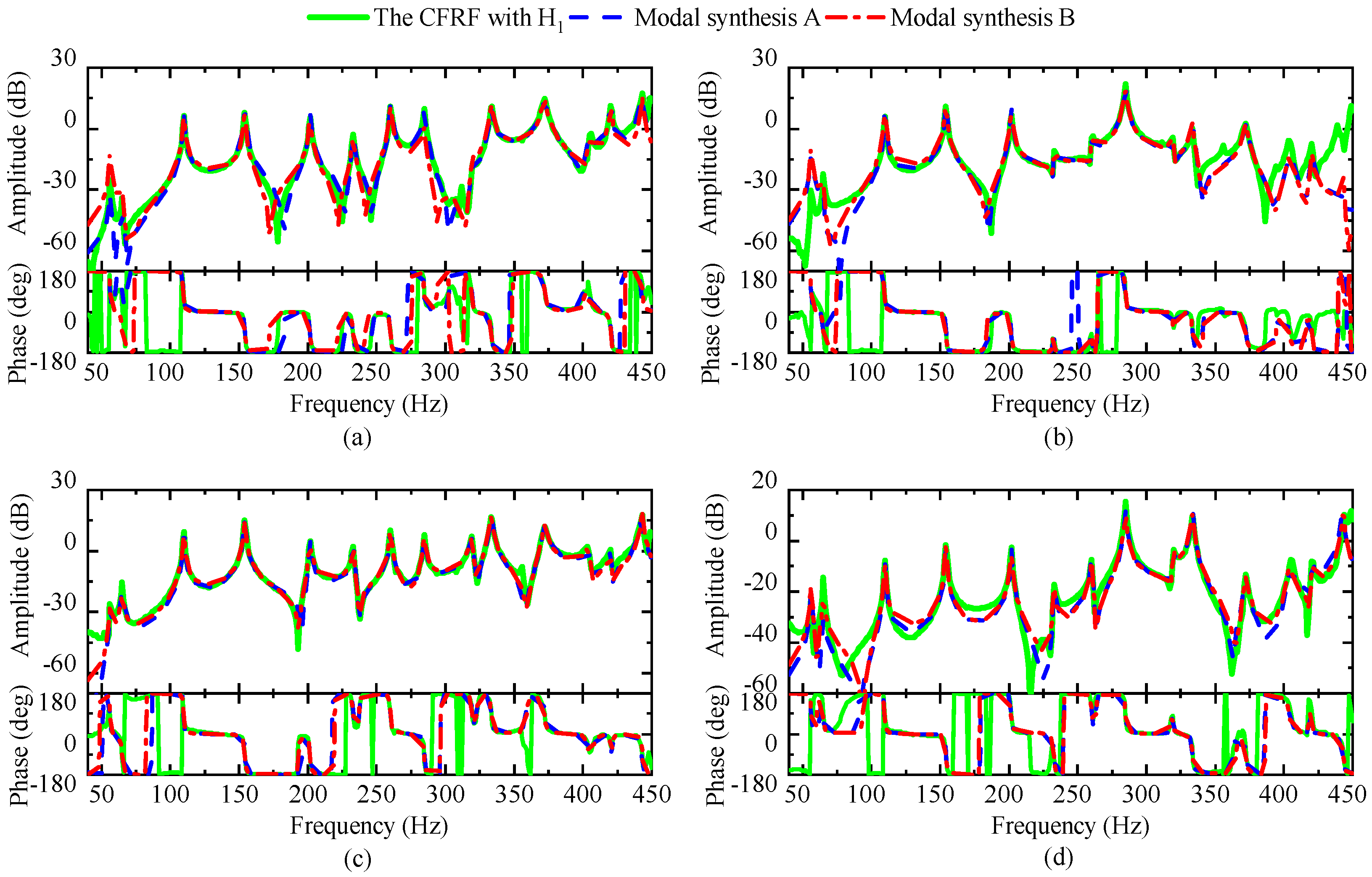
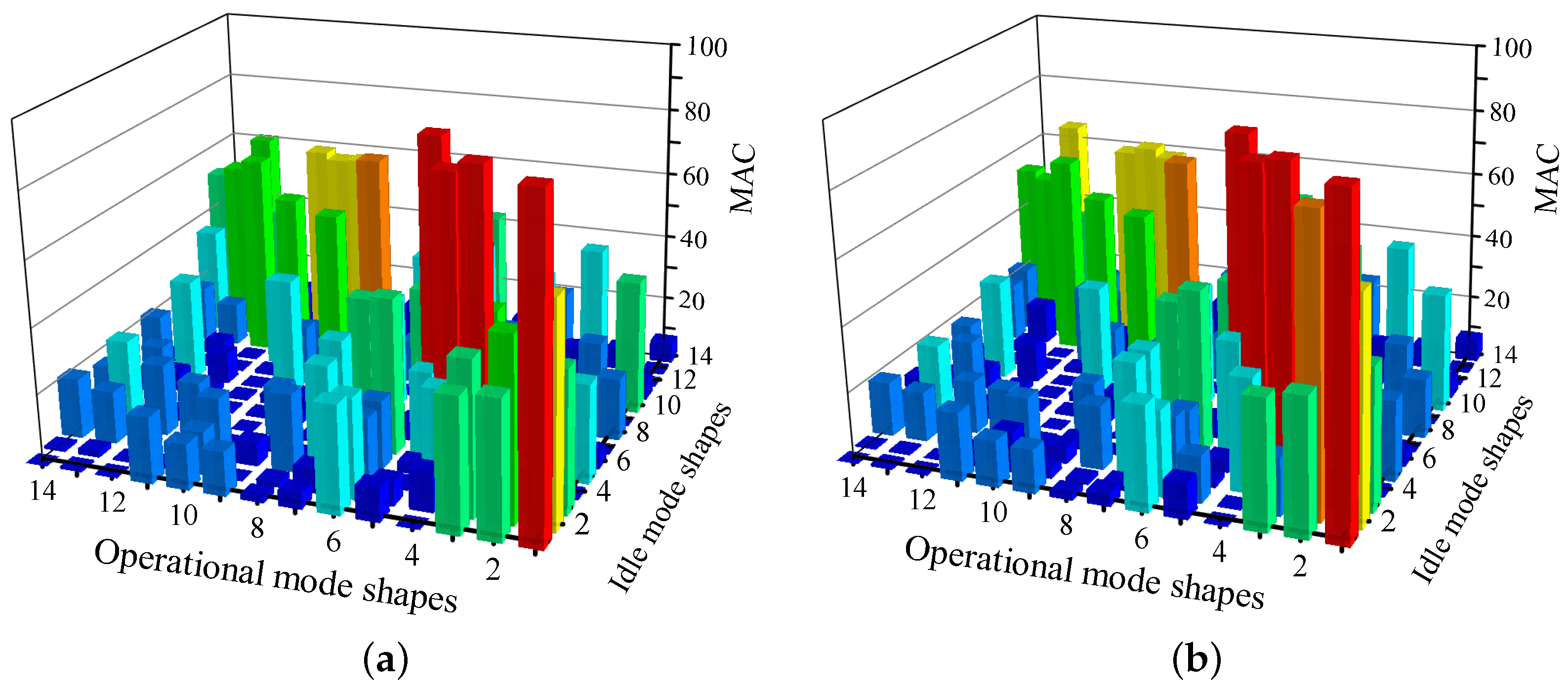
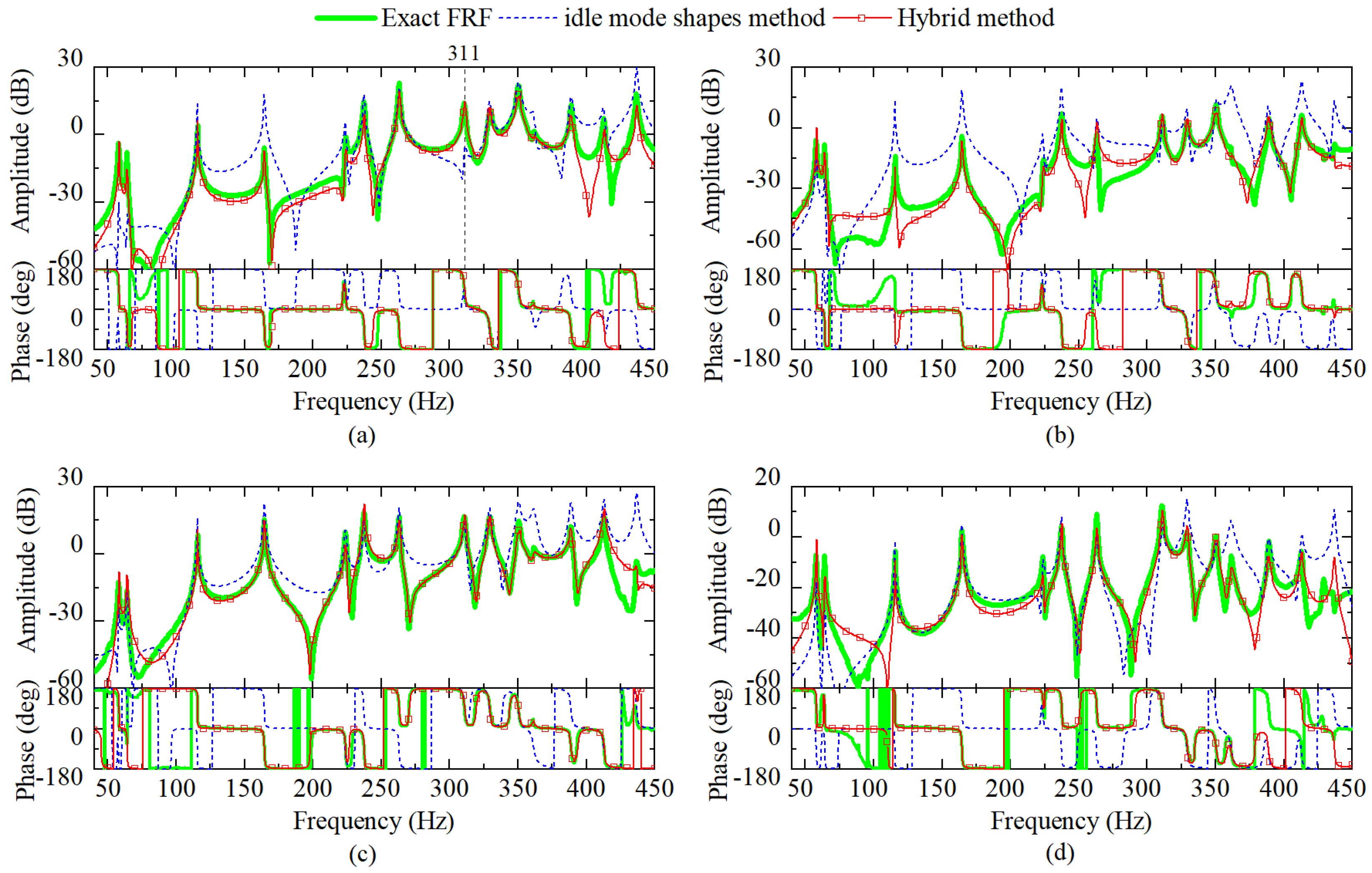
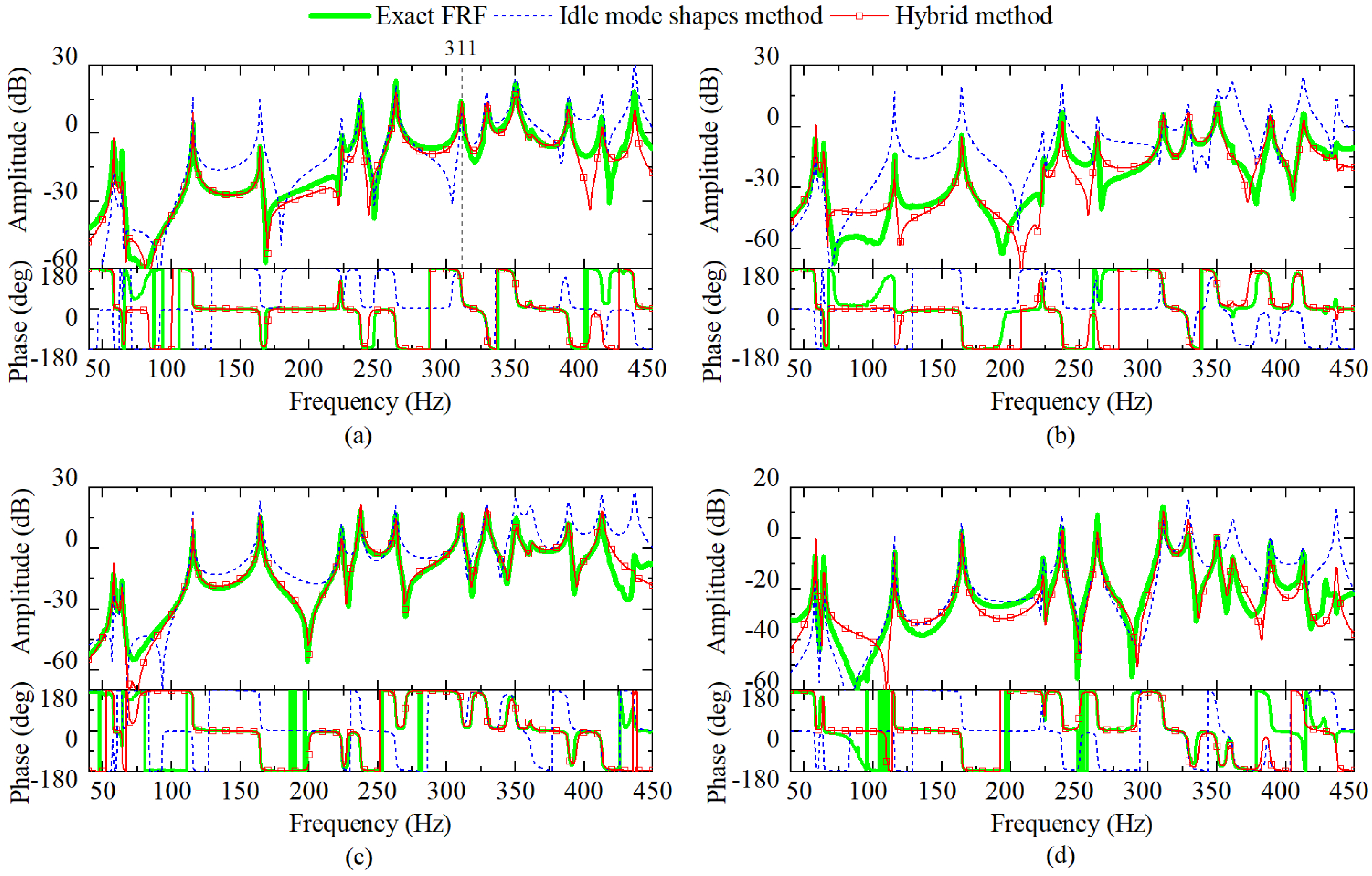
| Items | Original System | Unit |
|---|---|---|
| Coordinate of P | (300, 500, 300) | mm |
| Side length of plate | 1000 | mm |
| Thickness of plate | 5 | mm |
| Section diameter of beam | 6 | mm |
| Material density | kg/mm3 | |
| Elasticity modulus | 210 | GPa |
| Poisson’s ratio | 0.3 | — |
| Mass of mass point | 1 | kg |
| Stiffness of spring | 0.5, 100, 100 | N/mm |
| Damping of spring | 5, 100, 100 | N·s/mm |
| Shell element size | mm | |
| Number of elements per beam | 1 | — |
| DOF | The OMA Result | The Exact Mode Shape |
|---|---|---|
| A | 0.0525 − 0.1887i | −0.0623 |
| B | 0.1104 − 0.0493i | 0.0705 |
| C | −0.0585 + 0.0010i | −0.0590 |
| D | 1 | 1 |
| O | 0.4604 + 0.0466i | 0.4771 |
| The lumped mass | 0.1796 − 0.0151i | 0.1676 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, C.; Lu, C. A Method to Obtain Frequency Response Functions of Operating Mechanical Systems Based on Experimental Modal Analysis and Operational Modal Analysis. Machines 2024, 12, 516. https://doi.org/10.3390/machines12080516
Shen C, Lu C. A Method to Obtain Frequency Response Functions of Operating Mechanical Systems Based on Experimental Modal Analysis and Operational Modal Analysis. Machines. 2024; 12(8):516. https://doi.org/10.3390/machines12080516
Chicago/Turabian StyleShen, Cunrui, and Chihua Lu. 2024. "A Method to Obtain Frequency Response Functions of Operating Mechanical Systems Based on Experimental Modal Analysis and Operational Modal Analysis" Machines 12, no. 8: 516. https://doi.org/10.3390/machines12080516
APA StyleShen, C., & Lu, C. (2024). A Method to Obtain Frequency Response Functions of Operating Mechanical Systems Based on Experimental Modal Analysis and Operational Modal Analysis. Machines, 12(8), 516. https://doi.org/10.3390/machines12080516








