Numerical Study of Solid–Gas Two-Phase Flow and Erosion Distribution in Glass Fiber-Reinforced Polymer Ball Valves
Abstract
1. Introduction
2. Physical Model and Numerical Simulation Method
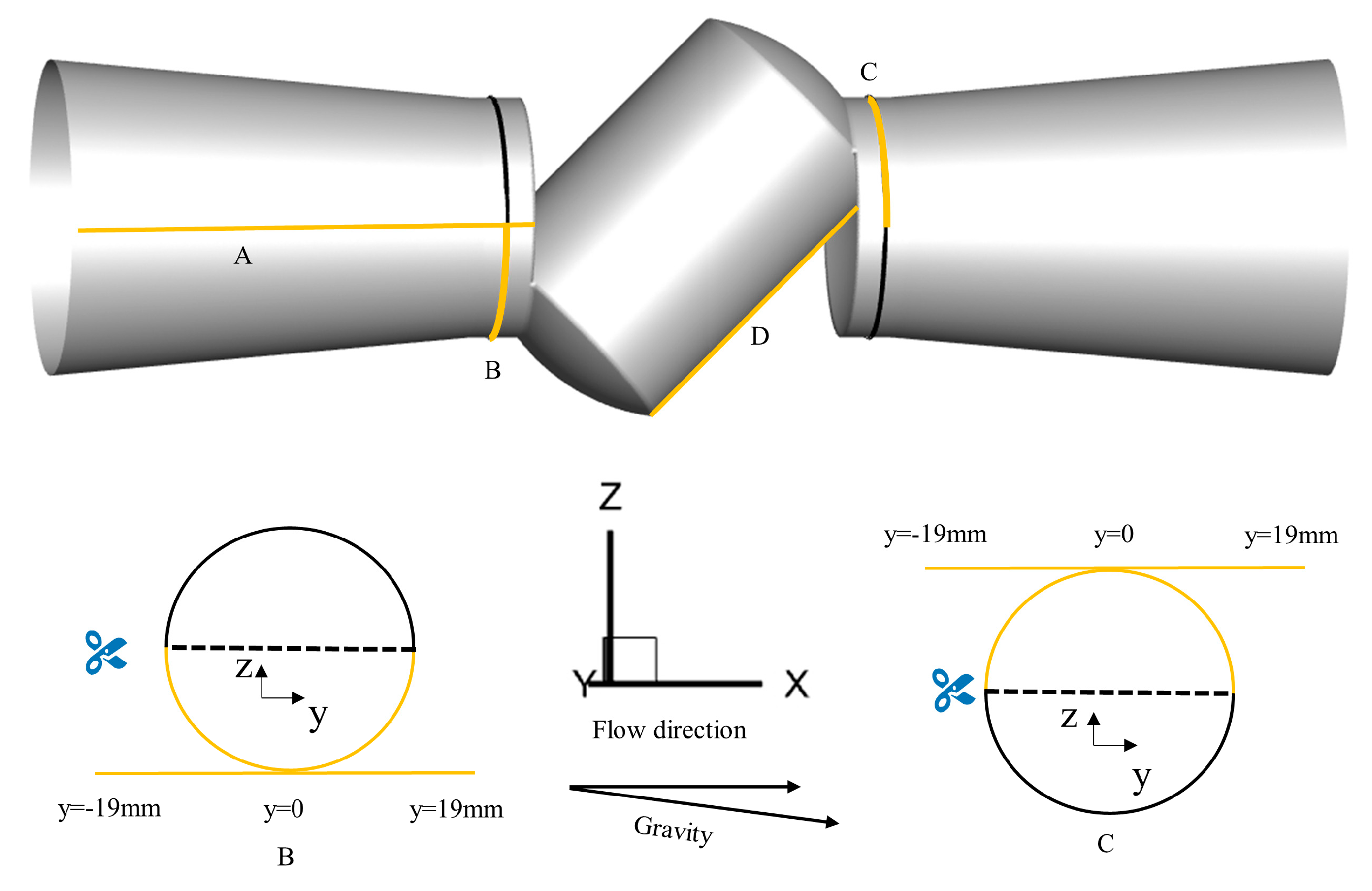
2.1. Problem Statement
2.2. Simulation Modeling
2.2.1. Gas Phase Model
2.2.2. Disperse Phase Model
2.2.3. Erosion Model
2.3. Simulation Modeling
2.3.1. Erosion Model
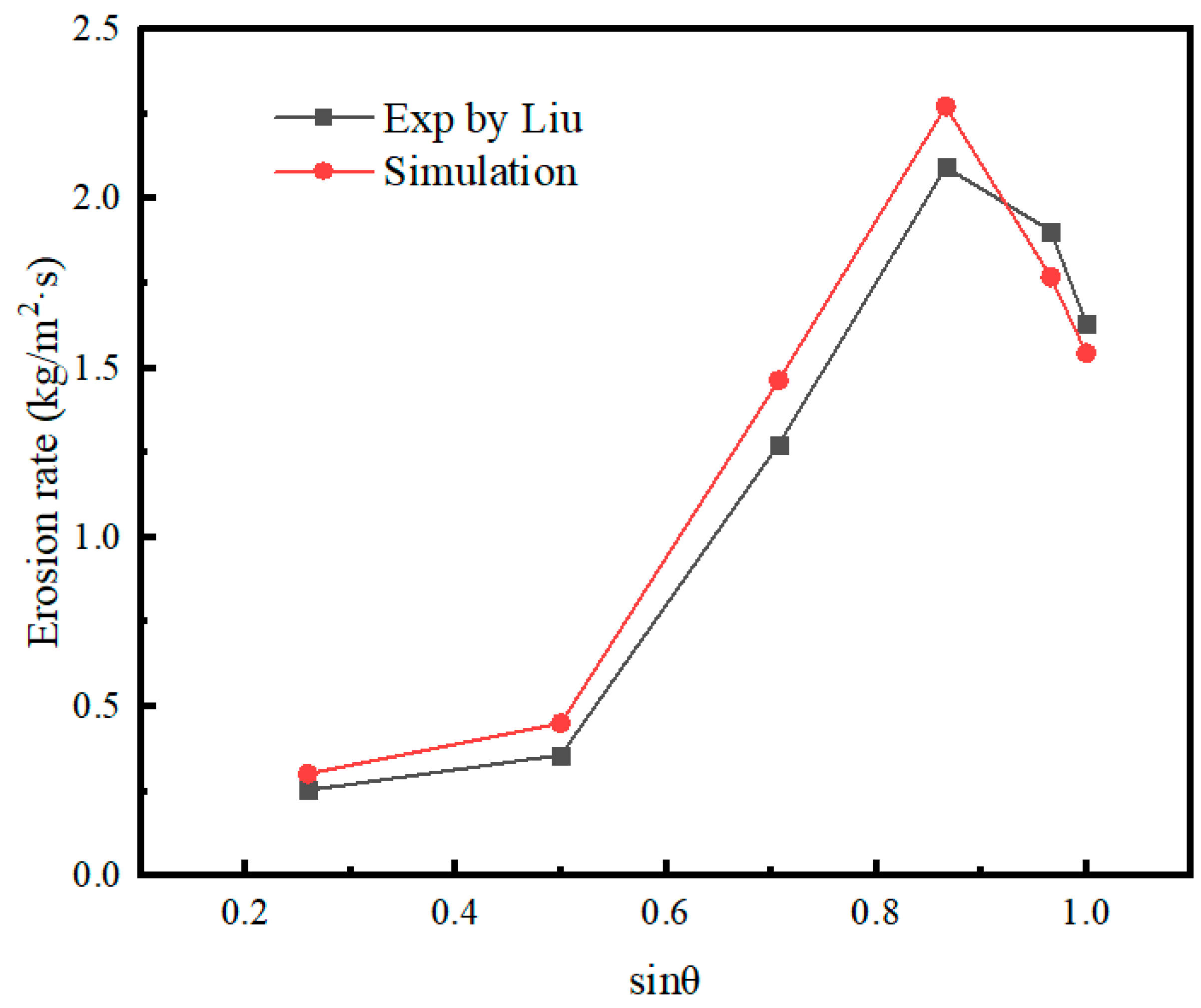
2.3.2. Grid Independence Test
3. Results and Discussion
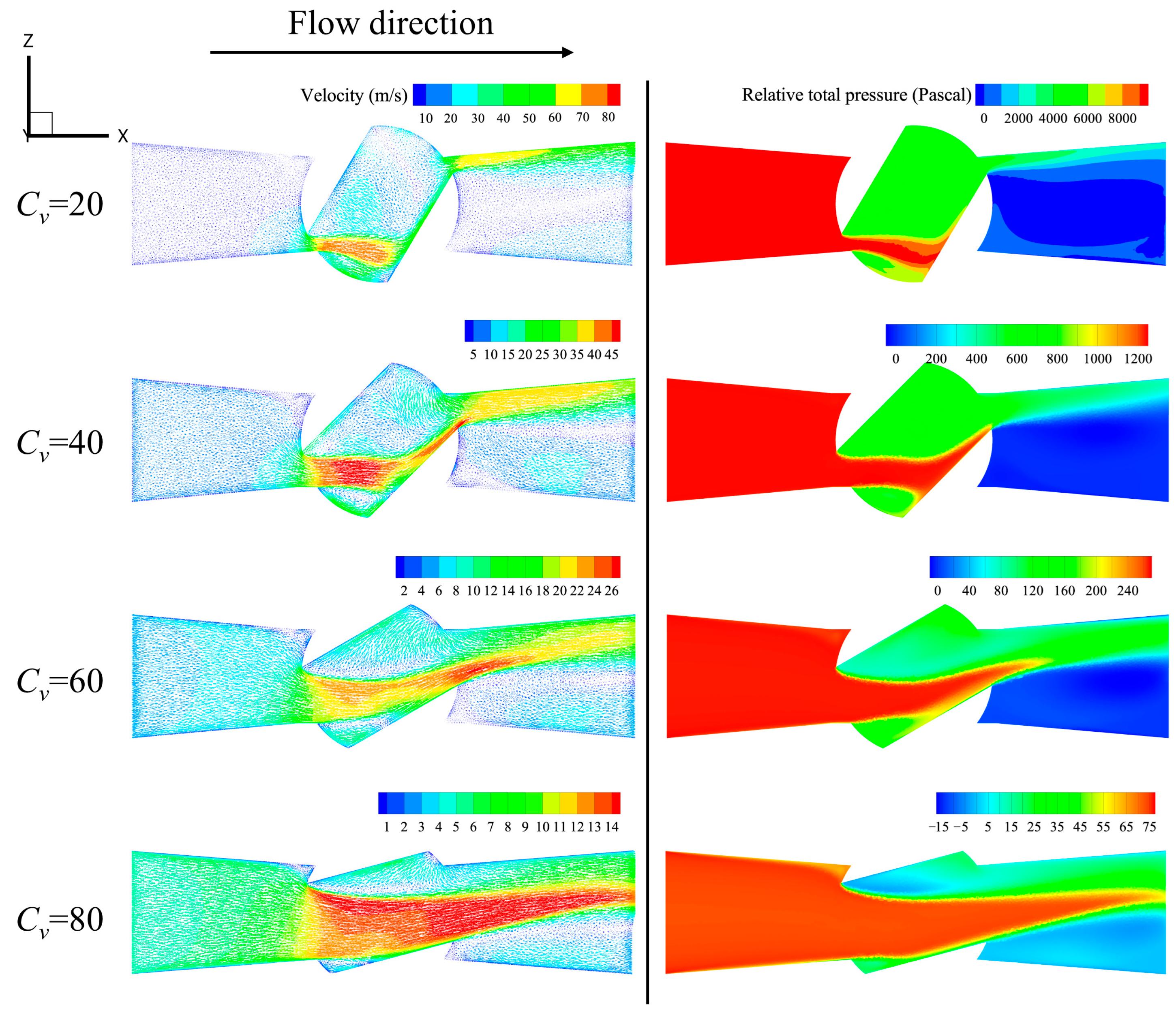
3.1. Effect of Relative Openness on Flow Field
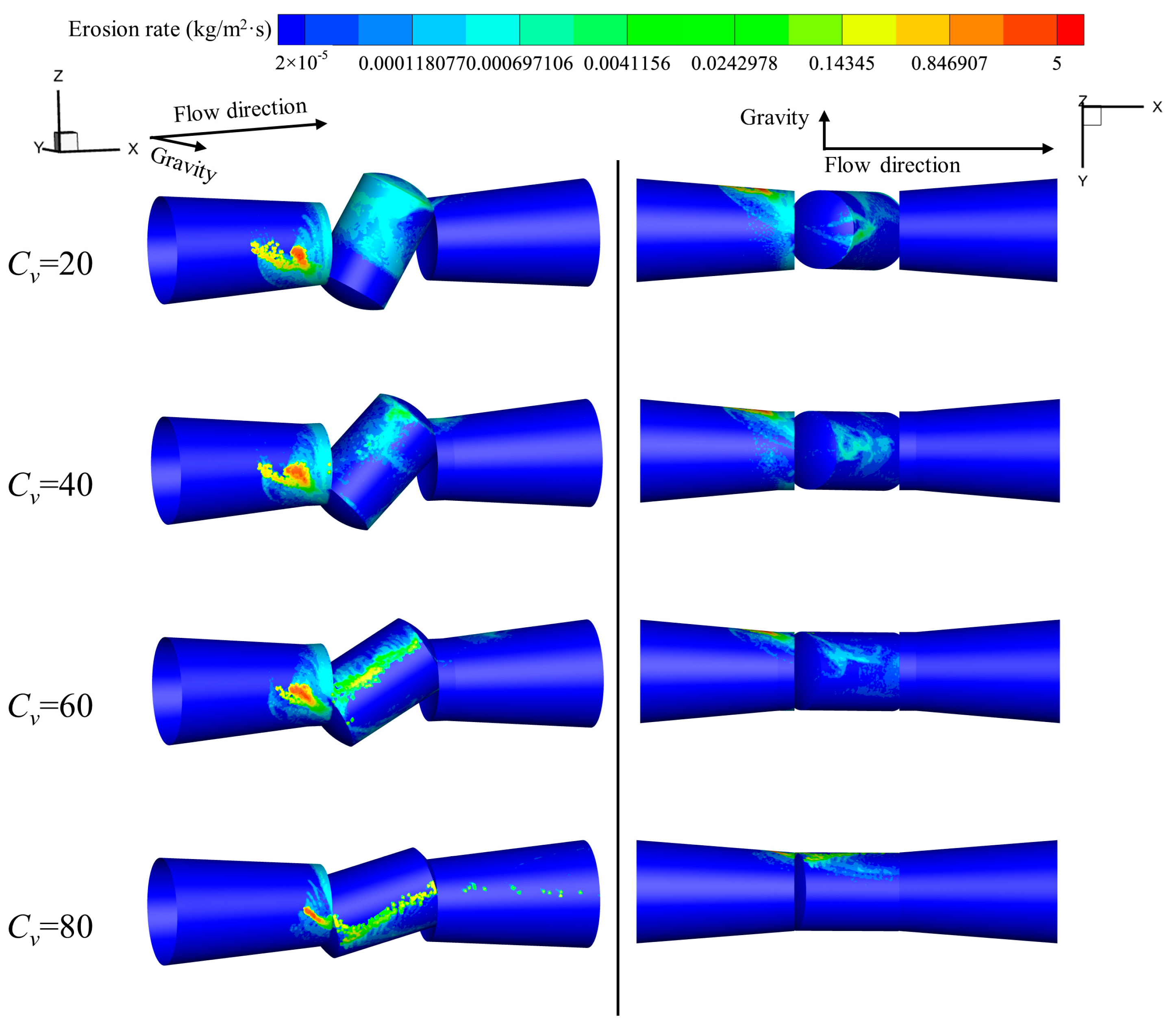
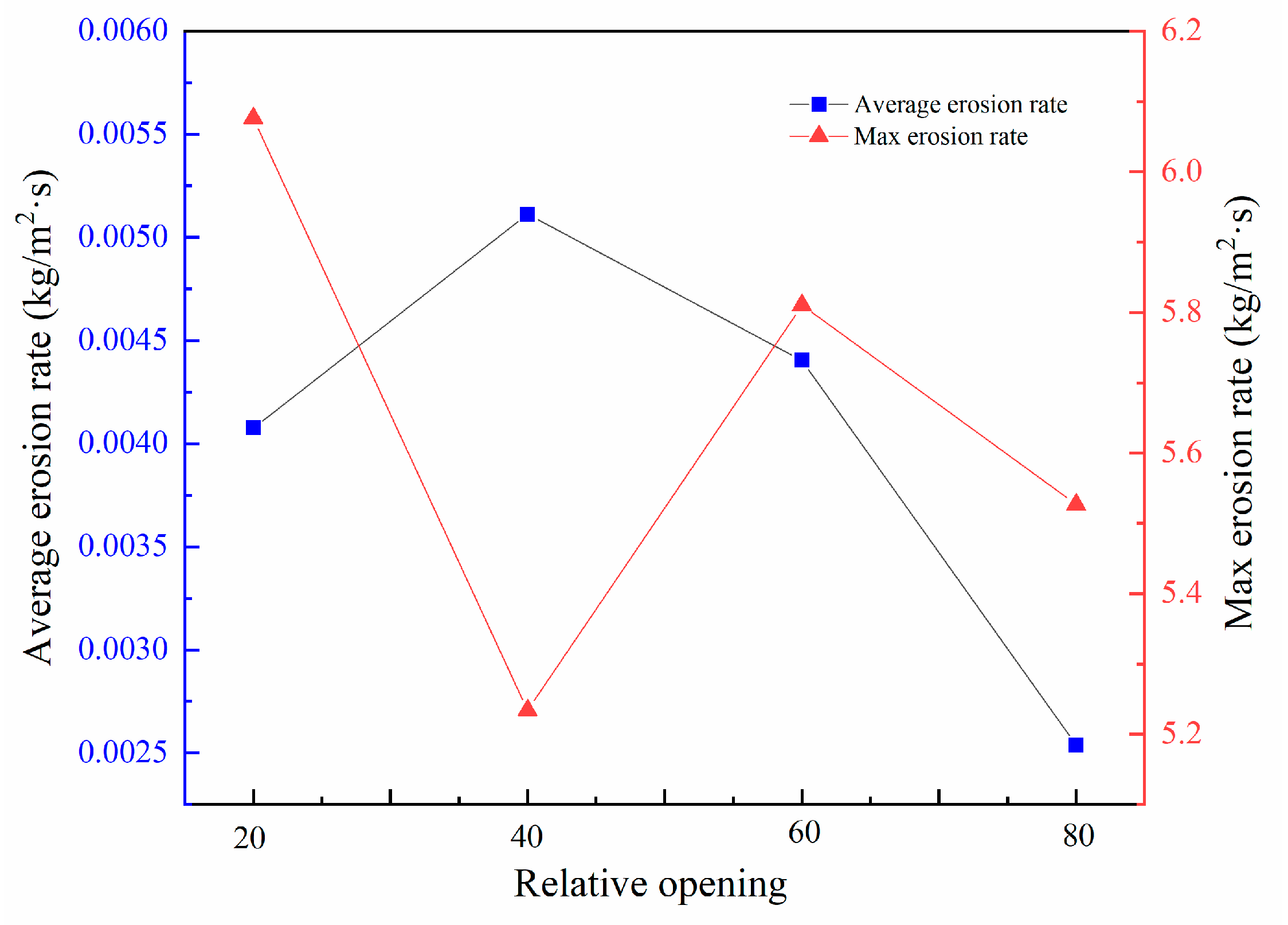
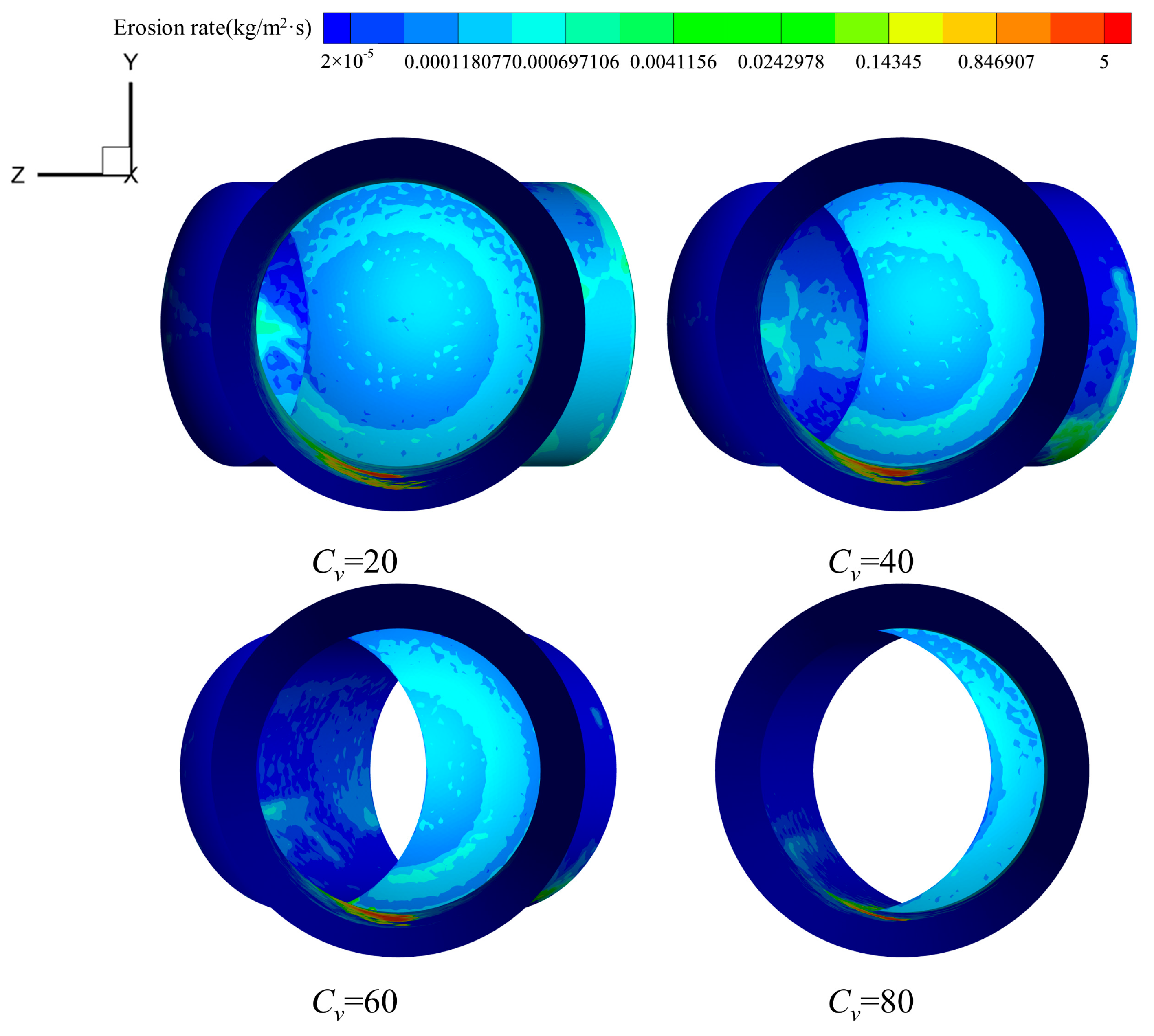
3.2. Effect of Relative Openness on Erosion Rate Distribution
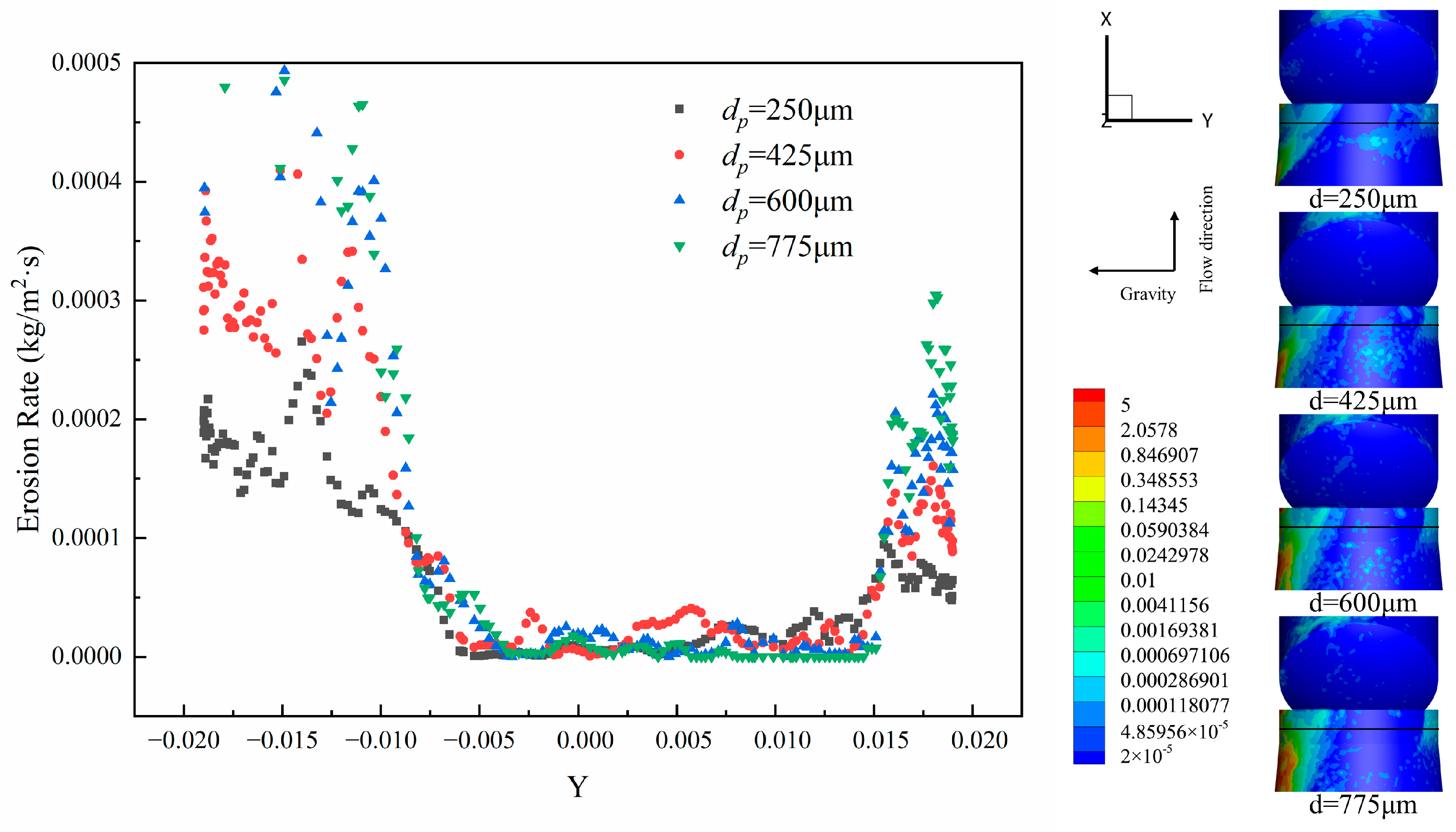
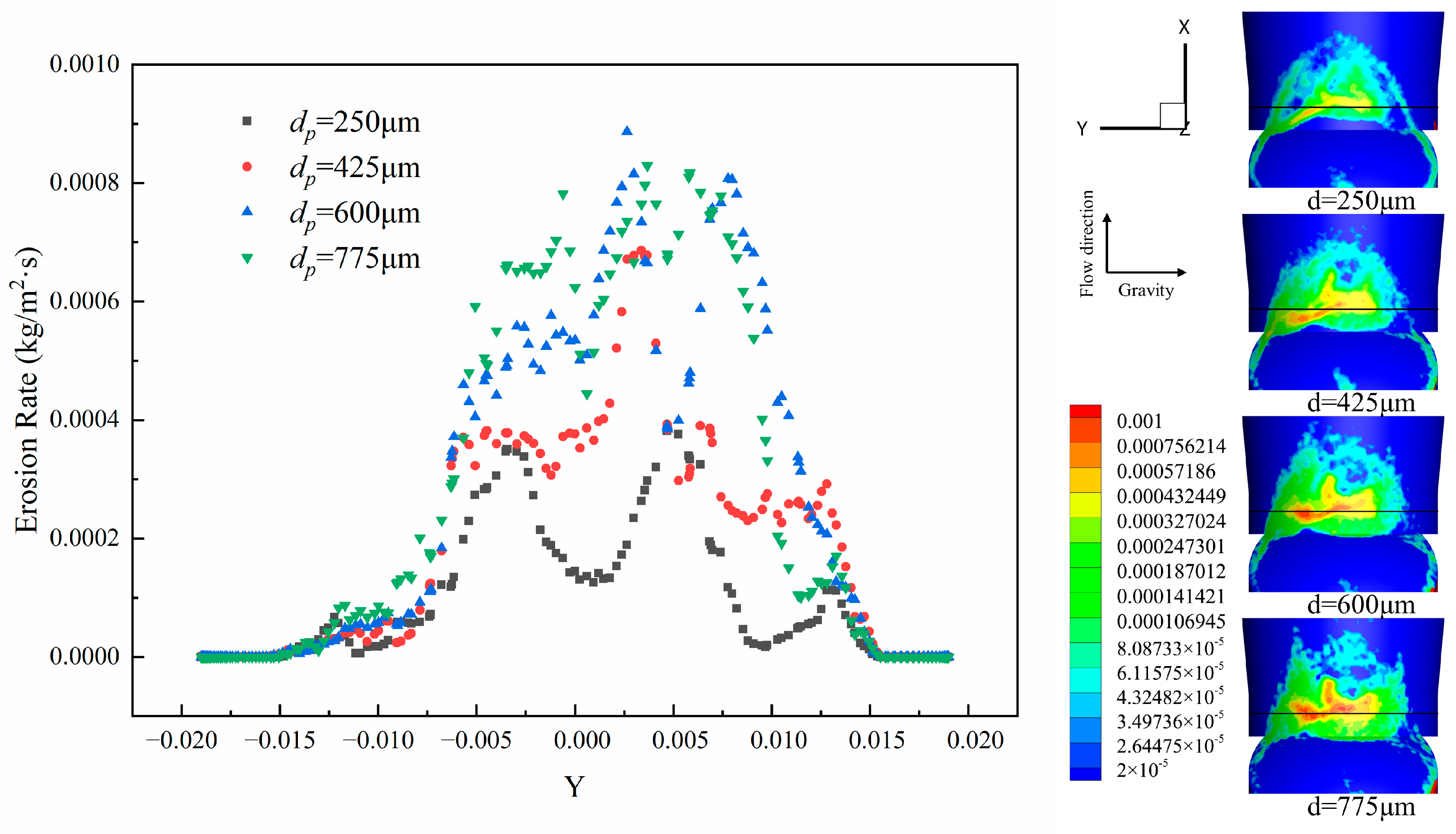
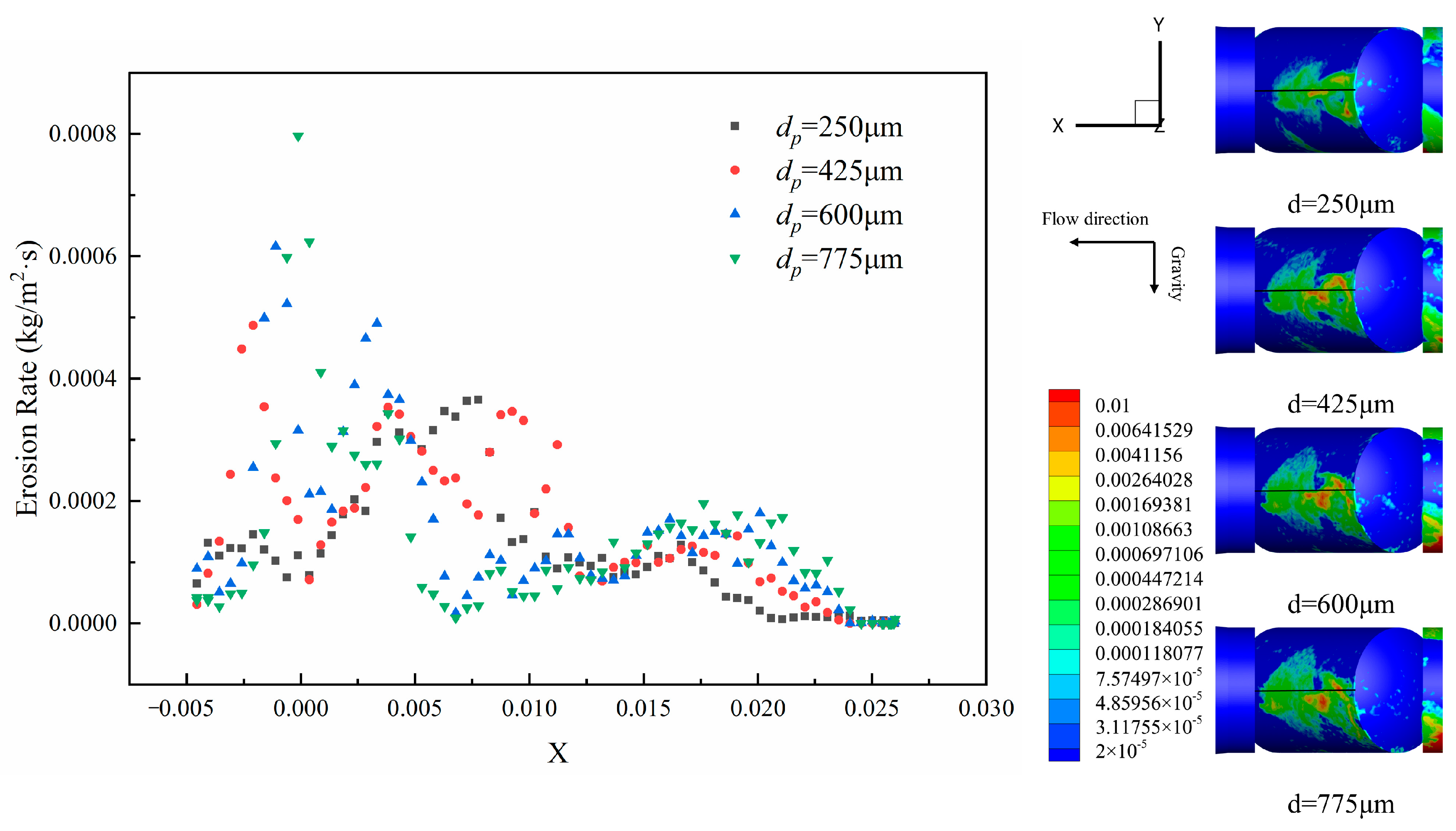
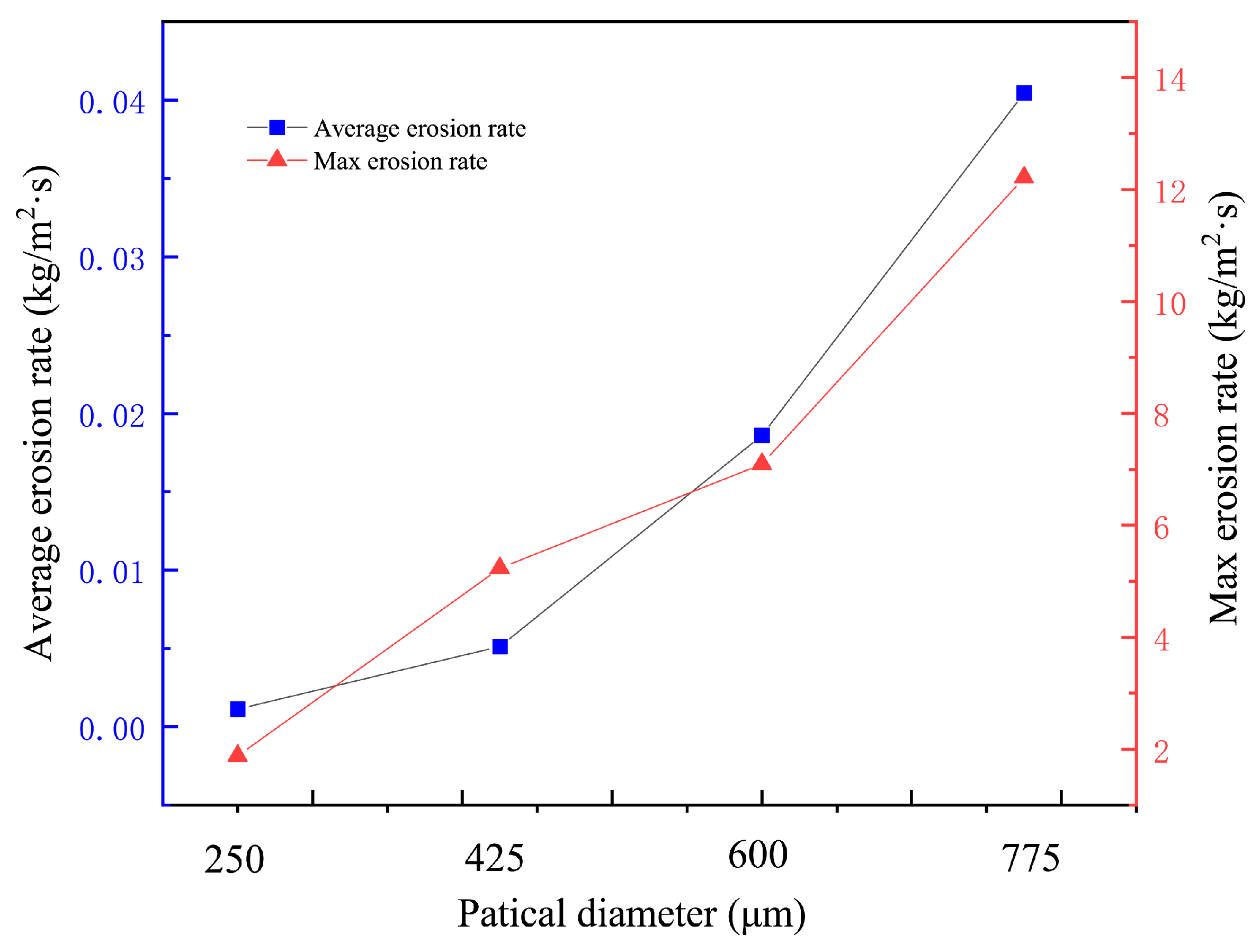
3.3. Effect of Particle Diameter on Erosion Rate Distribution
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sotoodeh, K. Optimized Valve Stem Design in Oil and Gas Industry to Minimize Major Failures. J. Fail. Anal. Prev. 2020, 20, 634–640. [Google Scholar] [CrossRef]
- Lin, Z.-H.; Li, J.-Y.; Jin, Z.-J.; Qian, J.-Y. Fluid dynamic analysis of liquefied natural gas flow through a cryogenic ball valve in liquefied natural gas receiving stations. Energy 2021, 226, 120376. [Google Scholar] [CrossRef]
- Han, Y.; Zhou, L.; Bai, L.; Xue, P.; Lv, W.; Shi, W.; Huang, G. Transient simulation and experiment validation on the opening and closing process of a ball valve. Nucl. Eng. Technol. 2022, 54, 1674–1685. [Google Scholar] [CrossRef]
- Gupta, P.K.; Kumar, N.; Krishna, R. Near-wall flow characteristics in pipe bend dense slurries: Optimizing the maximum sliding frictional power. Int. J. Sediment Res. 2024, 39, 435–463. [Google Scholar]
- Nikeghbali, P.; Benjankar, R.; Kheirkhahan, M. Erosion under drawdown flushing with the SPH method. Ocean. Eng. 2024, 310, 118743. [Google Scholar] [CrossRef]
- Zheng, S.; Luo, M.; Xu, K.; Li, X.; Bie, Q.; Liu, Y.; Yang, H.; Liu, Z. Case study: Erosion of an axial flow regulating valve in a solid-gas pipe flow. Wear 2019, 434–435, 202952. [Google Scholar] [CrossRef]
- Moses, D.; Haider, G.; Henshaw, J. An investigation of the failure of a 1/4 ball valve. Eng. Fail. Anal. 2019, 100, 393–405. [Google Scholar] [CrossRef]
- Ríos-Mercado, R.Z.; Borraz-Sánchez, C. Optimization problems in natural gas transportation systems: A state-of-the-art review. Appl. Energy 2015, 147, 536–555. [Google Scholar] [CrossRef]
- Shan, Y.; Jing, J.; Zhang, Z.; Sun, J.; Wang, N.; Zhuang, L.; Guo, Y. Investigation of erosion behavior of particle-fluid flow in offshore platform T-pipes. Int. J. Press. Vessel. Pip. 2024, 209, 105174. [Google Scholar] [CrossRef]
- Rajkumar, Y.; Shirazi, S.A.; Karimi, S. Effect of pipe size on erosion measurements and predictions in liquid-dominated multiphase flows for the elbows. Wear 2023, 523, 204797. [Google Scholar] [CrossRef]
- Wood, R.J.K. Erosion–corrosion interactions and their effect on marine and offshore materials. Wear 2006, 261, 1012–1023. [Google Scholar] [CrossRef]
- Rajahram, S.S.; Harvey, T.J.; Wood, R.J.K. Erosion–corrosion resistance of engineering materials in various test conditions. Wear 2009, 267, 244–254. [Google Scholar] [CrossRef]
- Al-Ghezi, M.K.; Al-Amiery, A.; Kadhum, A.; Al-Azawi, R.J.; Abass, R.H. Corrosion inhibitors. A review. Int. J. Corros. Scale Inhib. 2021, 10, 54–67. [Google Scholar] [CrossRef]
- Sotoodeh, K. A Review and Analysis of Industrial Valve Material Failures Due to Corrosion and Proposals for Prevention Measures Based on Industrial Experiences in the Offshore Sector of the Oil and Gas Industry. J. Fail. Anal. Prev. 2020, 21, 261–267. [Google Scholar] [CrossRef]
- Sotoodeh, K. Choosing the Right Coating System for Offshore Valves to Prevent External Corrosion. J. Bio- Tribo-Corros. 2023, 9, 55. [Google Scholar] [CrossRef]
- Sotoodeh, K. Optimized material selection for subsea valves to prevent failure and improve reliability. Life Cycle Reliab. Saf. Eng. 2020, 10, 173–182. [Google Scholar] [CrossRef]
- Sotoodeh, K. Case study of low-alloy steel material selection for the bodies of subsea valves: Failure prevention approaches. Prog. Addit. Manuf. 2022, 8, 77–85. [Google Scholar] [CrossRef]
- Sotoodeh, K. A Review of Valve Stem Sealing to Prevent Leakage from the Valve and Its Effect on Valve Operation. J. Fail. Anal. Prev. 2020, 21, 9–16. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Menezes, P.L.; Linul, E. Fiber-Reinforced Polymer Composites: Manufacturing, Properties, and Applications. Polymers 2019, 11, 1667. [Google Scholar] [CrossRef]
- Raja, T.; Mohanavel, V.; Ravichandran, M.; Kumar, S.S.; Albaqami, M.D.; Alotabi, R.G.; Murugesan, M.; Lu, W. Dynamic Mechanical Analysis of Banyan/Ramie Fibers Reinforced with Nanoparticle Hybrid Polymer Composite. Adv. Polym. Technol. 2022, 2022, 1560330. [Google Scholar] [CrossRef]
- Raja, T.; Devarajan, Y. Visco-elastic properties and thermal analysis of corchorus/elastane yarn–reinforced biocomposites. Biomass Convers. Biorefinery 2024, 14, 15363–15372. [Google Scholar] [CrossRef]
- Duo, Y.; Liu, X.; Liu, Y.; Tafsirojjaman, T.; Sabbrojjaman, M. Environmental impact on the durability of FRP reinforcing bars. J. Build. Eng. 2021, 43, 102909. [Google Scholar] [CrossRef]
- Tafsirojjaman, T.; Fawzia, S.; Thambiratnam, D.P.; Wirth, N. Performance of FRP strengthened full-scale simply-supported circular hollow steel members under monotonic and large-displacement cyclic loading. Eng. Struct. 2021, 242, 112522. [Google Scholar] [CrossRef]
- Tafsirojjaman, T.; Fawzia, S.; Thambiratnam, D.P.; Zhao, X.L. FRP strengthened SHS beam-column connection under monotonic and large-deformation cyclic loading. Thin-Walled Struct. 2021, 161, 161. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.-T.; Tafsirojjaman, T.; Ur Rahman Dogar, A.; AlAjarmeh, O.; Yue, Q.-R.; Manalo, A. A novel technique to improve the compressive strength and ductility of glass fiber reinforced polymer (GFRP) composite bars. Constr. Build. Mater. 2022, 326, 126782. [Google Scholar] [CrossRef]
- Tafsirojjaman, T.; Fawzia, S.; Thambiratnam, D.P.; Zhao, X.-L. Study on the cyclic bending behaviour of CFRP strengthened full-scale CHS members. Structures 2020, 28, 741–756. [Google Scholar] [CrossRef]
- Mlela, M.K.; Xu, H.; Sun, F.; Wang, H.; Madenge, G.D. Material Analysis and Molecular Dynamics Simulation for Cavitation Erosion and Corrosion Suppression in Water Hydraulic Valves. Materials 2020, 13, 453. [Google Scholar] [CrossRef]
- Lin, Z.; Sun, X.; Yu, T.; Zhang, Y.; Li, Y.; Zhu, Z. Gas–solid two-phase flow and erosion calculation of gate valve based on the CFD-DEM model. Powder Technol. 2020, 366, 395–407. [Google Scholar] [CrossRef]
- Hu, G.; Zhang, P.; Wang, G.; Zhu, H.; Li, Q.; Zhao, S.; Qiao, K.; Wang, T. Performance study of erosion resistance on throttle valve of managed pressure drilling. J. Pet. Sci. Eng. 2017, 156, 29–40. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, J.; Qian, J. Numerical analysis of cavitation erosion and particle erosion in butterfly valve. Eng. Fail. Anal. 2017, 80, 312–324. [Google Scholar] [CrossRef]
- Xu, B.; Lin, Z.; Zhu, Z.; Yu, T. Experimental and simulation study of the effect of gravity on the solid-liquid two-phase flow and erosion of ball valve. Adv. Powder Technol. 2022, 33, 103416. [Google Scholar] [CrossRef]
- Cui, B.; Lin, Z.; Zhu, Z.; Wang, H.; Ma, G. Influence of opening and closing process of ball valve on external performance and internal flow characteristics. Exp. Therm. Fluid Sci. 2017, 80, 193–202. [Google Scholar] [CrossRef]
- Cao, L.; Liu, S.; Hu, P.; Si, H. The influence of governing valve opening on the erosion characteristics of solid particle in steam turbine. Eng. Fail. Anal. 2020, 118, 104929. [Google Scholar] [CrossRef]
- Liu, X.; Ji, H.; Min, W.; Zheng, Z.; Wang, J. Erosion behavior and influence of solid particles in hydraulic spool valve without notches. Eng. Fail. Anal. 2020, 108, 104262. [Google Scholar] [CrossRef]
- Mao, Y.; Kong, Y.; Guan, M. GPU-accelerated SPH modeling of flow-driven sediment erosion with different rheological models and yield criteria. Powder Technol. 2022, 412, 118015. [Google Scholar] [CrossRef]
- Zhang, Y.; Reuterfors, E.P.; McLaury, B.S.; Shirazi, S.A.; Rybicki, E.F. Comparison of computed and measured particle velocities and erosion in water and air flows. Wear 2007, 263, 330–338. [Google Scholar] [CrossRef]
- Zhao, H. Improved Erosion Wear Model for Wind Turbine Blade Coatings. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2024. [Google Scholar]
- Niu, J.; Wang, S.; Li, J.; Tan, H. Experiment of particle rebound characteristics for impingement on resin coated /Al/alloysteel plate. J. Aerosp. Power 2018, 33, 928–935. [Google Scholar] [CrossRef]
- Liu, G. Study on the Erosion Wear of the GFRP Impacted by Air Flow Containing Sand. Master’s Thesis, Hefei Polytechnic University, Hefei, China, 2013. [Google Scholar]
- Liu, X.q.; Liu, F.; Ji, H.; Li, N.; Wang, C.; Lin, G. Particle erosion transient process visualization and influencing factors of the hydraulic servo spool valve orifice. Flow Meas. Instrum. 2023, 89, 102273. [Google Scholar] [CrossRef]





| n | l | k | R1 | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|---|---|
| 1.765 | 3.06288 | 1.26 × 10−8 | 3.087 | −8.027 | 8.477 | −3.909 | 0.672 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Xia, Y.; Yu, J.; Dai, Y.; Peng, K.; Zhang, T.; Liu, B. Numerical Study of Solid–Gas Two-Phase Flow and Erosion Distribution in Glass Fiber-Reinforced Polymer Ball Valves. Machines 2024, 12, 541. https://doi.org/10.3390/machines12080541
Chen Q, Xia Y, Yu J, Dai Y, Peng K, Zhang T, Liu B. Numerical Study of Solid–Gas Two-Phase Flow and Erosion Distribution in Glass Fiber-Reinforced Polymer Ball Valves. Machines. 2024; 12(8):541. https://doi.org/10.3390/machines12080541
Chicago/Turabian StyleChen, Qi, Yazhong Xia, Jiuyang Yu, Yaonan Dai, Kang Peng, Tianyi Zhang, and Bowen Liu. 2024. "Numerical Study of Solid–Gas Two-Phase Flow and Erosion Distribution in Glass Fiber-Reinforced Polymer Ball Valves" Machines 12, no. 8: 541. https://doi.org/10.3390/machines12080541
APA StyleChen, Q., Xia, Y., Yu, J., Dai, Y., Peng, K., Zhang, T., & Liu, B. (2024). Numerical Study of Solid–Gas Two-Phase Flow and Erosion Distribution in Glass Fiber-Reinforced Polymer Ball Valves. Machines, 12(8), 541. https://doi.org/10.3390/machines12080541





