Output Feedback-Based Neural Network Sliding Mode Control for Electro-Hydrostatic Systems with Unknown Uncertainties
Abstract
:1. Introduction
- Proposing a robust OF-NBSMC for uncertain EHPSs subject to unknown load disturbance, friction, matched uncertainty, and unstructured dynamical behavior.
- With only output available, an ESO is first employed to help observe other unmeasured states and suppress the influence of matched uncertainty.
- Conducting an RBFNN-based approximation integrated with a disturbance observer (DO)-based adaptive law to decouple the dynamical behavior of the mechanical part with the impact of load disturbance to satisfy specific working requirements.
- The system stability is theoretically proven and the feasibility of the proposed methodology is verified through comparative simulations.
2. Problem Formulation
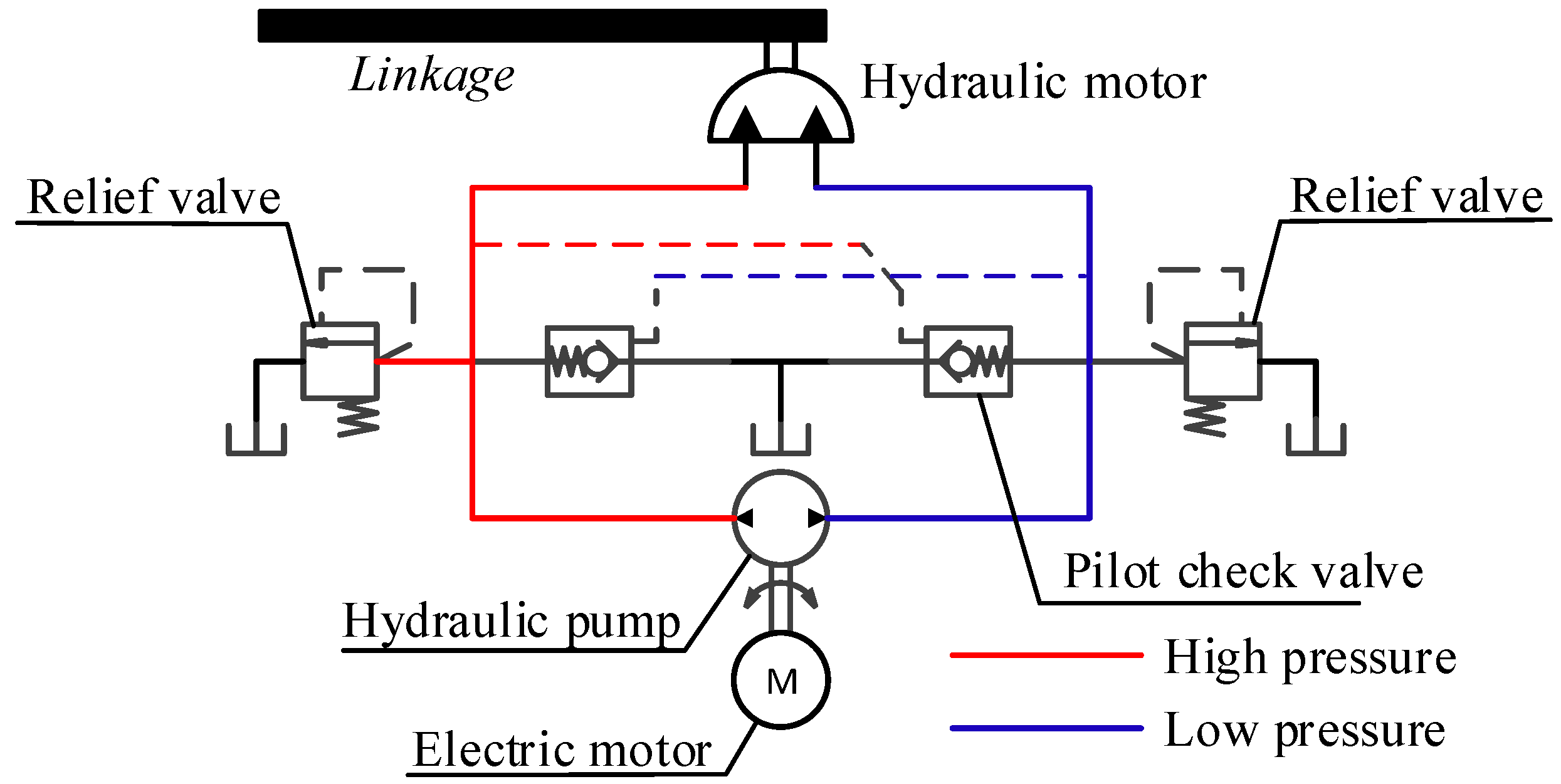
2.1. System Descriptions
2.2. Preliminaries
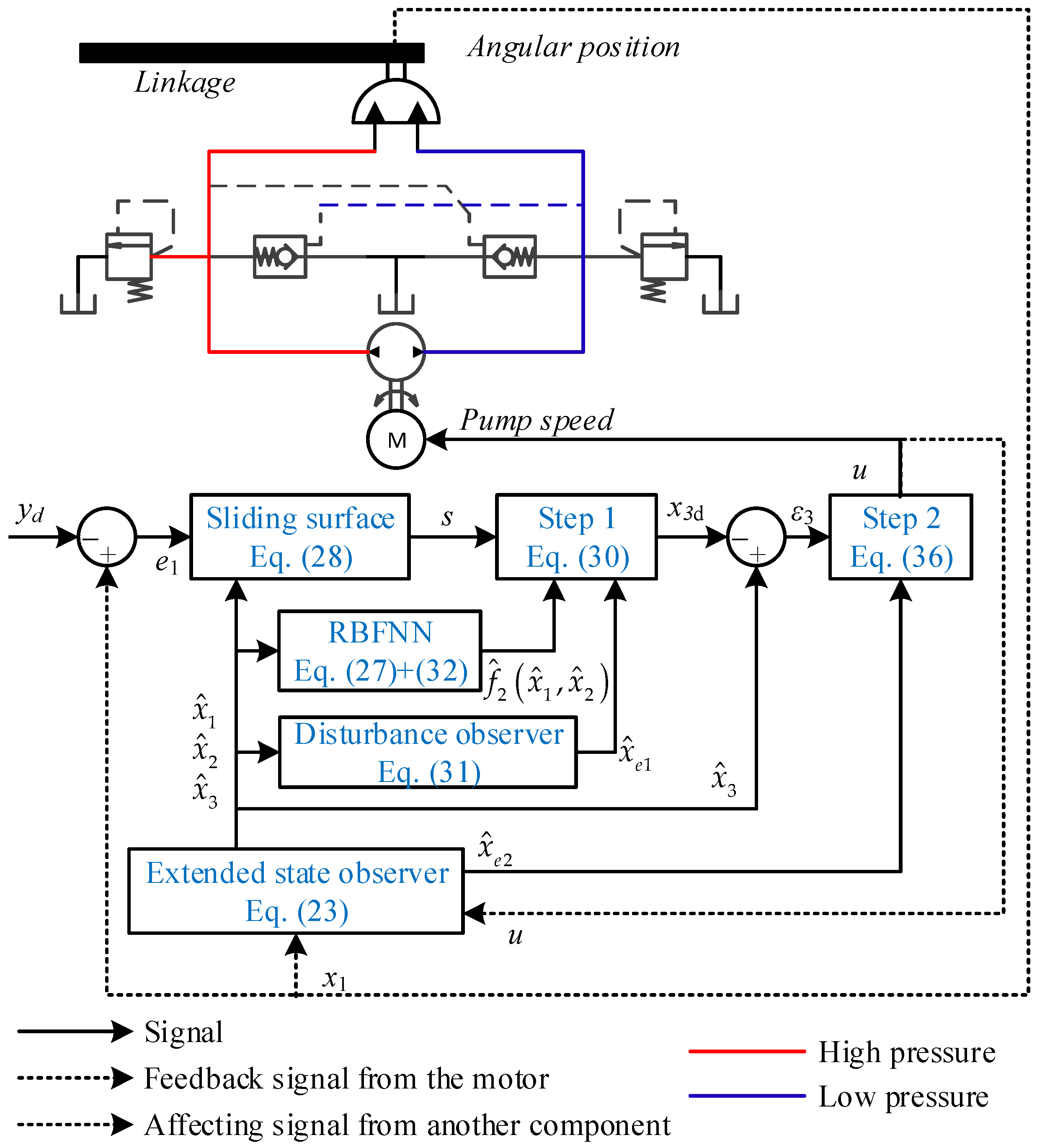
3. Observer and Approximation Mechanisms
3.1. Observer-Based Matched Uncertainty Suppression
3.2. Neural-Network-Based Approximation Engine
4. Estimator-Based Sliding Mode Control
4.1. Control Law Implementation
4.2. Closed-Loop System Stability
5. Numerical Simulation
5.1. Examined Scenario
- Scenario 1: No leakage and no disturbance, from the beginning to 6 s.
- Scenario 2: No disturbance and the leakage suddenly occurs at t = 6 s.
- Scenario 3: The load torque suddenly occurs at t = 12 s along with the leakage.
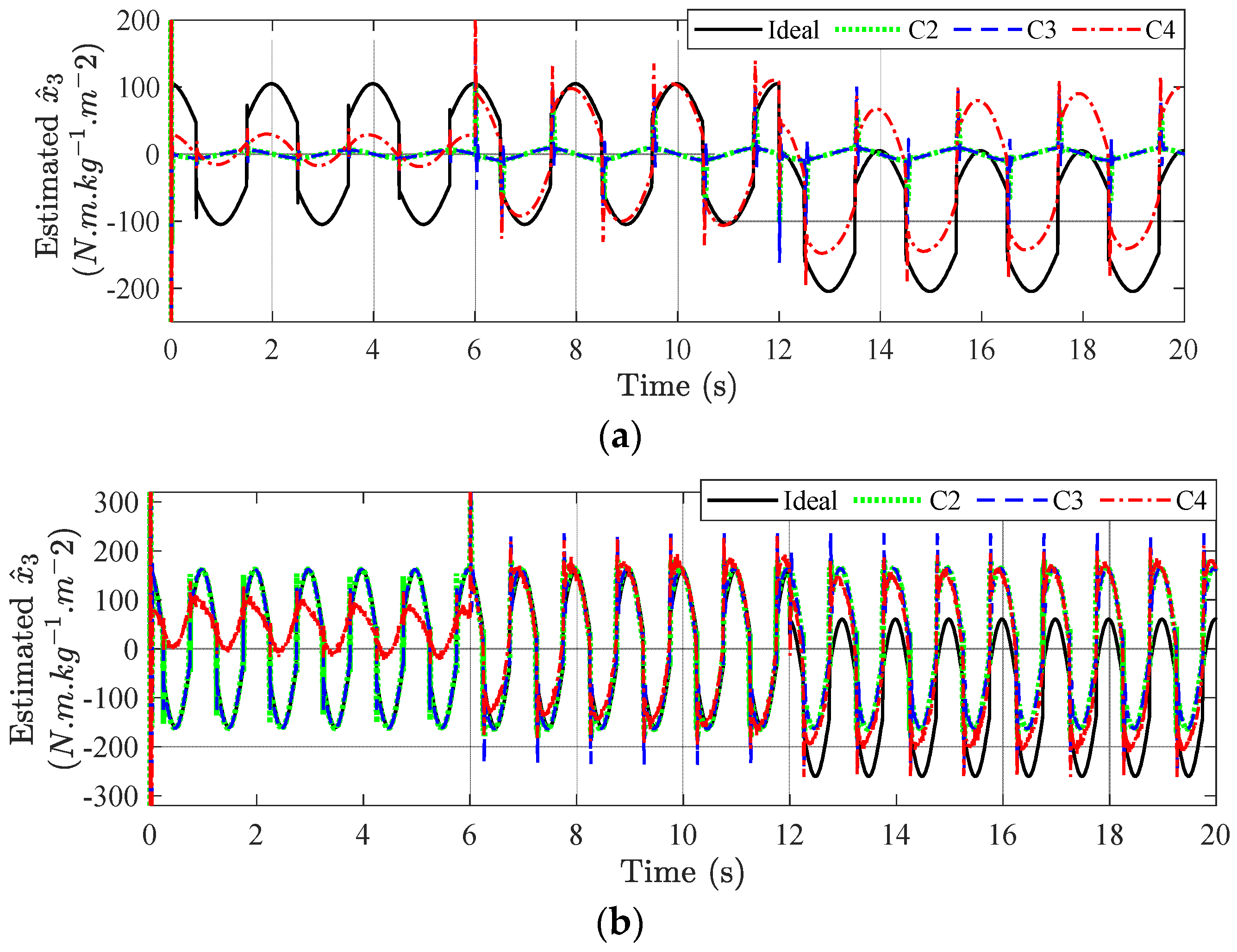
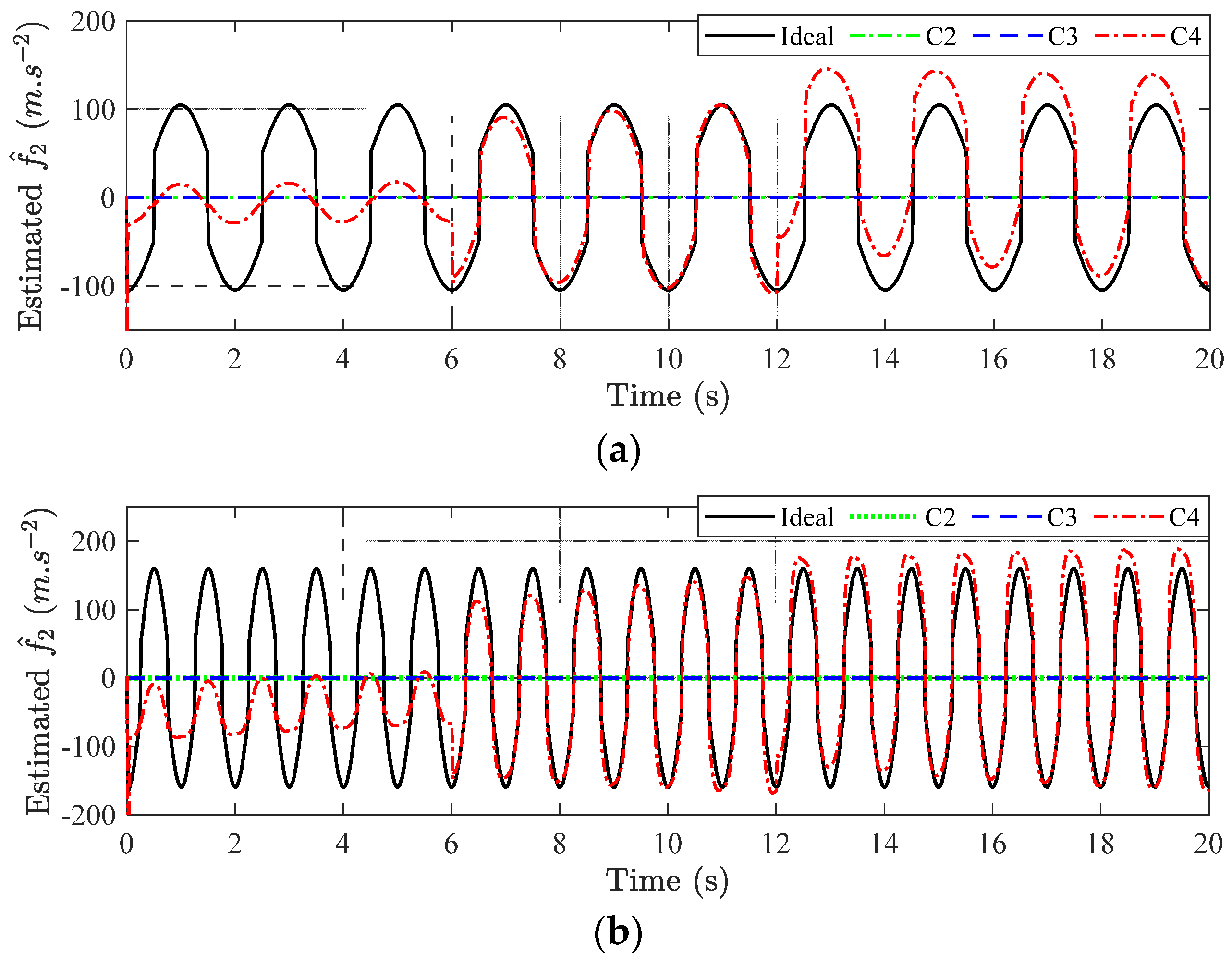
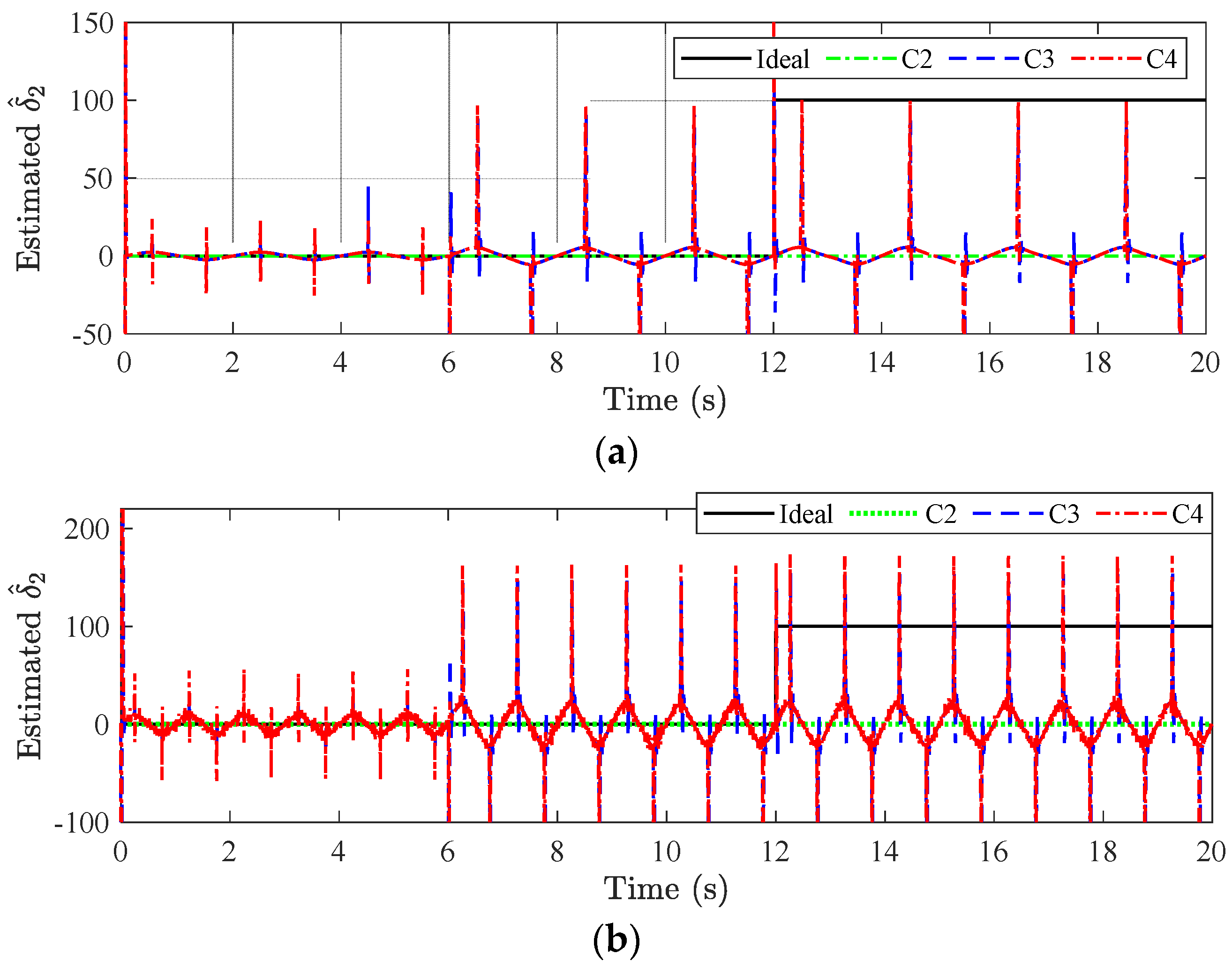
5.2. Main Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shang, Y.; Li, X.; Qian, H.; Wu, S.; Pan, Q.; Huang, L.; Jiao, Z. A Novel Hydrostatic Actuator System with Energy Recovery Module for More Electric Aircraft. IEEE Trans. Ind. Electron. 2020, 67, 2991–2999. [Google Scholar] [CrossRef]
- Du, S.; Zhou, J.; Zhao, H.P.; Ma, S. Research on the energy transfer and efficiency performance of an electro-hydrostatic actuator for wheel-legged robot joint. Energy 2024, 291, 130417. [Google Scholar] [CrossRef]
- Staman, K.; Veale, A.J.; Kooij, A. Design, Control and Evaluation of the Electro-Hydrostatic Actuator, PREHydrA, for Gait Restoration Exoskeleton Technology. IEEE Trans. Med. Robot. Bionics 2021, 3, 156–165. [Google Scholar] [CrossRef]
- Sun, M.; Ouyang, X.; Mattila, J.; Chen, Z.; Yang, H.; Liu, H. Lightweight Electrohydrostatic Actuator Drive Solution for Exoskeleton Robots. IEEE/ASME Trans. Mechatron. 2022, 27, 4631–4642. [Google Scholar] [CrossRef]
- Lee, W.; Kim, M.J.; Chung, W.K. Asymptotically stable disturbance observer-based compliance control of electrohydrostatic actuators. IEEE/ASME Trans. Mechatron. 2020, 25, 195–206. [Google Scholar] [CrossRef]
- Feng, H.; Yin, C.; Cao, D. Trajectory Tracking of an Electro-Hydraulic Servo System with an New Friction Model-Based Compensation. IEEE/ASME Trans. Mechatron. 2023, 28, 473–482. [Google Scholar] [CrossRef]
- Wang, Q.; Du, Z.; Chen, W.; Ai, C.; Kong, X.; Zhang, J.; Liu, K.; Chen, G. Maximum Power Point Tracking Control of Offshore Hydraulic Wind Turbine Based on Radial Basis Function Neural Network. Energies 2024, 17, 449. [Google Scholar] [CrossRef]
- Kumar, D.; Mahato, A.C. An accumulator-based hydro-mechanical power transmission technology for smoothing the power output from a wind turbine. Sādhanā 2023, 48, 241. [Google Scholar] [CrossRef]
- Nie, Y.; Lao, Z.; Liu, J.; Huang, Y.; Sun, X.; Tang, J.; Chen, Z. Disturbance Observer-Based Sliding Mode Controller for Underwater Electro-Hydrostatic Actuator Affected by Seawater Pressure. Machines 2022, 10, 1115. [Google Scholar] [CrossRef]
- Ahn, K.K.; Nam, D.N.C.; Jin, M.L. Adaptive Backstepping Control of an Electrohydraulic Actuator. IEEE/ASME Trans. Mechatron. 2014, 19, 987–995. [Google Scholar] [CrossRef]
- Huang, L.; Yu, T.; Jiao, Z.; Li, Y. Research on Power Matching and Energy Optimal Control of Active Load-Sensitive Electro-Hydrostatic Actuator. IEEE Access 2021, 9, 51121–51133. [Google Scholar] [CrossRef]
- Liu, J.; Hu, Y.; Zhu, Z.; Zhao, Z.; Gao, G.; Yao, J. Intelligent fault diagnosis for electro-hydrostatic actuator based on multisource information convolutional residual network. Meas. Sci. Technol. 2024, 35, 066114. [Google Scholar] [CrossRef]
- Liu, J.; Huang, Y.; Helian, B.; Nie, Y.; Chen, Z. Flow match and precision motion control of asymmetric electro-hydrostatic actuators with complex external force in four-quadrants. J. Frankl. Inst. 2024, 36, 1025–1039. [Google Scholar] [CrossRef]
- Truong, D.Q.; Ahn, K.K. Force control for hydraulic load simulator using self-tuning grey predictor—Fuzzy PID. Mechatronics 2009, 19, 233–246. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Li, G.; Liu, R.; Zhou, X. Design and Control of an Energy-Efficient Speed Regulating Method for Pump-Controlled Motor System under Negative Loads. Machines 2023, 11, 437. [Google Scholar] [CrossRef]
- Ma, W.; Ma, S.; Qiao, W.; Cao, D.; Yin, C. Research on PID Controller of Excavator Electro-Hydraulic System Based on Improved Differential Evolution. Machines 2023, 11, 143. [Google Scholar] [CrossRef]
- Cao, F. PID controller optimized by genetic algorithm for direct-drive servo system. Neural Comput. Appl. 2020, 32, 23–30. [Google Scholar] [CrossRef]
- To, X.D.; Tran, D.T.; Truong, H.V.A.; Ahn, K.K. Disturbance Observer Based Finite Time Trajectory Tracking Control for a 3 DOF Hydraulic Manipulator Including Actuator Dynamics. IEEE Access 2018, 6, 36798–36809. [Google Scholar]
- Chen, Y.; Zhang, Q.; Tian, Q.; Feng, X. Extended State Observer-Based Fuzzy Adaptive Backstepping Force Control of a Deep-Sea Hydraulic Manipulator with Long Transmission Pipelines. J. Mar. Sci. Eng. 2022, 10, 1467. [Google Scholar] [CrossRef]
- Mi, J.; Deng, W.; Yao, J.; Liang, X. Linear-Extended-State-Observer-Based Adaptive RISE Control for the Wrist Joints of Manipulators with Electro-Hydraulic Servo Systems. Electronics 2024, 13, 1060. [Google Scholar] [CrossRef]
- Dao, H.V.; Na, S.; Nguyen, D.G.; Ahn, K.K. High accuracy contouring control of an excavator for surface flattening tasks based on extended state observer and task coordinate frame approach. Autom. Constr. 2021, 130, 103845. [Google Scholar] [CrossRef]
- Ba, D.X.; Dinh, Q.T.; Bae, J.; Ahn, K.K. An Effective Disturbance-Observer-Based Nonlinear Controller for a Pump-Controlled Hydraulic System. IEEE/ASME Trans. Mechatron. 2020, 25, 32–43. [Google Scholar] [CrossRef]
- Trinh, H.A.; Truong, H.V.A.; Ahn, K.K. Fault Estimation and Fault-Tolerant Control for the Pump-Controlled Electrohydraulic System. Actuators 2020, 9, 132. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Dai, F. Integral Sliding Mode Backstepping Control of an Asymmetric Electro-Hydrostatic Actuator Based on Extended State Observer. Proceedings 2020, 64, 13. [Google Scholar] [CrossRef]
- Shen, W.; Zhao, H. Fault tolerant control of nonlinear hydraulic systems with prescribed performance constraint. ISA Trans. 2022, 131, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Lao, L.; Chen, P. Adaptive Sliding Mode Control of an Electro-Hydraulic Actuator with a Kalman Extended State Observer. IEEE Access 2024, 12, 8970–8982. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D. Extended-State-Observer-Based Output Feedback Nonlinear Robust Control of Hydraulic Systems with Backstepping. IEEE Trans. Ind. Electron. 2014, 61, 6285–6293. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J. Output feedback control of electro-hydraulic servo actuators with matched and mismatched disturbances rejection. J. Frankl. Inst. 2019, 356, 9152–9179. [Google Scholar] [CrossRef]
- Yang, X.; Yao, J.; Deng, W. Output feedback adaptive super-twisting sliding mode control of hydraulic systems with disturbance compensation. ISA Trans. 2021, 109, 175–185. [Google Scholar] [CrossRef]
- Tran, D.T.; Do, T.C.; Ahn, K.K. Extended High Gain Observer-Based Sliding Mode Control for an Electro-hydraulic System with a Variant Payload. Int. J. Precis. Eng. Manuf. 2019, 20, 2089–2100. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Ahn, K.K. Output Feedback Robust Tracking Control for a Variable-Speed Pump-Controlled Hydraulic System Subject to Mismatched Uncertainties. Mathematics 2023, 11, 1783. [Google Scholar] [CrossRef]
- Ye, N.; Song, J.; Ren, G. Model-Based Adaptive Command Filtering Control of an Electrohydraulic Actuator with Input Saturation and Friction. IEEE Access 2020, 8, 48252–48263. [Google Scholar] [CrossRef]
- Truong, H.V.A.; Nam, S.; Kim, S.; Kim, Y.; Chung, W.K. Backstepping-Sliding-Mode-Based Neural Network Control for Electro-Hydraulic Actuator Subject to Completely Unknown System Dynamics. IEEE Trans. Autom. Sci. Eng. 2023. Early access. [Google Scholar] [CrossRef]
- Truong, H.V.A.; Nguyen, M.H.; Tran, D.T.; Ahn, K.K. A novel adaptive neural network-based time-delayed estimation control for nonlinear systems subject to disturbances and unknown dynamics. ISA Trans. 2023, 142, 214–227. [Google Scholar] [CrossRef] [PubMed]
- Truong, H.V.A.; Phan, V.D.; Tran, D.T.; Ahn, K.K. A novel observer-based neural-network finite-time output control for high-order uncertain nonlinear systems. Appl. Math. Comput. 2024, 475, 128699. [Google Scholar] [CrossRef]
- Phan, V.D.; Vo, C.P.; Dao, H.V.; Ahn, K.K. Robust Fault-Tolerant Control of an Electro-Hydraulic Actuator with a Novel Nonlinear Unknown Input Observer. IEEE Access 2021, 9, 30750–30760. [Google Scholar] [CrossRef]
- Han, S.; Wang, H.; Tian, Y.; Christov, N. Time-delay estimation based computed orque control with robust adaptive RBF neural network compensator for a rehabilitation exoskeleton. ISA Trans. 2020, 97, 171–181. [Google Scholar] [CrossRef]
- Deng, W.; Yao, J. Extended-State-Observer-Based Adaptive Control of Electrohydraulic Servomechanisms without Velocity Measurement. IEEE/ASME Trans. Mechatron. 2020, 25, 1151–1161. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D.; Yan, L. High-Accuracy Tracking Control of Hydraulic Rotary Actuators with Modeling Uncertainties. IEEE/ASME Trans. Mechatron. 2014, 19, 633–641. [Google Scholar] [CrossRef]





| Parameter (Unit) | Symbol | Value | (SI Unit) |
|---|---|---|---|
| Bulk modulus | β | 1.5 × 109 | N/m2 |
| Pump displacement | Dp | 0.1544 × 10–7 | m3/rad |
| Pump coefficient | KPump | 10 | rad/s/vol |
| Initial volume of chamber 1 | V01 | 7.368 × 10–6 | m3 |
| Initial volume of chamber 2 | V02 | 7.368 × 10–6 | m3 |
| Gradient cross-section area | A | 5.8422 × 10–6 | m3/rad |
| Leakage coefficient | Ct | 4.267 × 10–12 |
| Parameter (Unit) | Symbol | Value | (SI Unit) |
|---|---|---|---|
| Actuator moment inertia | J | 0.2 | kg/m2 |
| Viscous friction coefficient | 10 | Nms/rad | |
| Coulomb friction coefficient | 10 | Nm | |
| Linkage mass | M | 0.1 | kg |
| Linkage length | L | 0.5 | m |
| External load | 20 | Nm |
| Controllers | Control Parameters |
|---|---|
| C1 | |
| C2 | Observer: Matched uncertainty estimation: α = 800 (ESO). |
| C3 | Observers: Matched uncertainty estimation: α = 800 (ESO-1); mismatched disturbance estimation: ω = 800 (ESO-2). |
| C4 | The estimators are structured as follows: with ones(21,1) being the column unit vector of 21 rows. Observers: Matched uncertainty estimation: α = 800 (ESO); mismatched disturbance estimation: ω = 50 (DO). |
| Controller | (Degree) | in Steady State (Degree) | in Steady State (Degree/s) | Scenario |
|---|---|---|---|---|
| C1 | 17.3649 | 2.368 | 12.147 | 1 |
| 8.048 | 45.35 | 2 | ||
| 12.07 | 45.281 | 3 | ||
| C2 | 1.3371 | 0.053 | 1.243 | 1 |
| 0.355 | 5.443 | 2 | ||
| 0.3623 | 5.5 | 3 | ||
| C3 | 0.8178 | 0.0263 | 1.96 | 1 |
| 0.1607 | 5.433 | 2 | ||
| 0.1608 | 5.482 | 3 | ||
| C4 | 0.4525 | 0.0225 | 0.367 | 1 |
| 0.1371 | 1.289 | 2 | ||
| 0.1371 | 1.324 | 3 |
| Controller | (Degree) | in Steady State (Degree) | in Steady State (deg/s) | Scenario |
|---|---|---|---|---|
| C1 | 48.2949 | 4.6491 | 38.4626 | 1 |
| 12.2459 | 98.5342 | 2 | ||
| 15.1787 | 98.895 | 3 | ||
| C2 | 3.0044 | 0.1436 | 1.2942 | 1 |
| 0.598 | 9.8975 | 2 | ||
| 0.6097 | 10.1341 | 3 | ||
| C3 | 1.9664 | 0.0576 | 1.771 | 1 |
| 0.2557 | 5.6202 | 2 | ||
| 0.2644 | 6.1146 | 3 | ||
| C4 | 1.1271 | 0.0574 | 0.8703 | 1 |
| 0.2178 | 1.9366 | 2 | ||
| 0.2237 | 2.5589 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, T.D.; Do, T.C.; Truong, H.V.A. Output Feedback-Based Neural Network Sliding Mode Control for Electro-Hydrostatic Systems with Unknown Uncertainties. Machines 2024, 12, 554. https://doi.org/10.3390/machines12080554
Dang TD, Do TC, Truong HVA. Output Feedback-Based Neural Network Sliding Mode Control for Electro-Hydrostatic Systems with Unknown Uncertainties. Machines. 2024; 12(8):554. https://doi.org/10.3390/machines12080554
Chicago/Turabian StyleDang, Tri Dung, Tri Cuong Do, and Hoai Vu Anh Truong. 2024. "Output Feedback-Based Neural Network Sliding Mode Control for Electro-Hydrostatic Systems with Unknown Uncertainties" Machines 12, no. 8: 554. https://doi.org/10.3390/machines12080554






