Assessment of the Uniform Wear Bending Strength of Large Modulus Rack and Pinion Pair: Theoretical vs. Experimental Results
Abstract
1. Introduction
2. Large Module Rack-and-Pinion Hoisting Mechanism Experimental Platform
2.1. Introduction of Lifting Structure
2.2. Introduction to Design Parameters
3. Theoretical Calculations of the Bending Strength
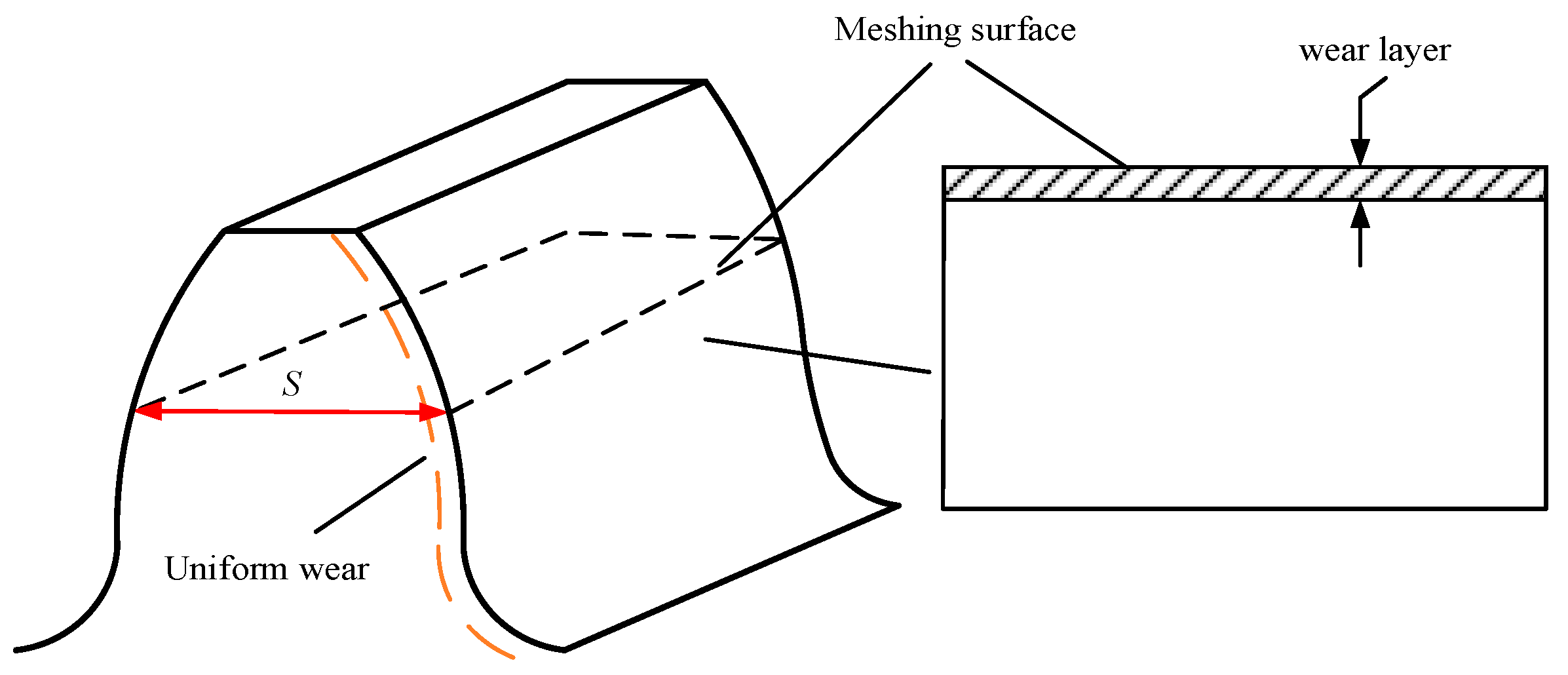
3.1. Introduction of the Gear Uniform Wear
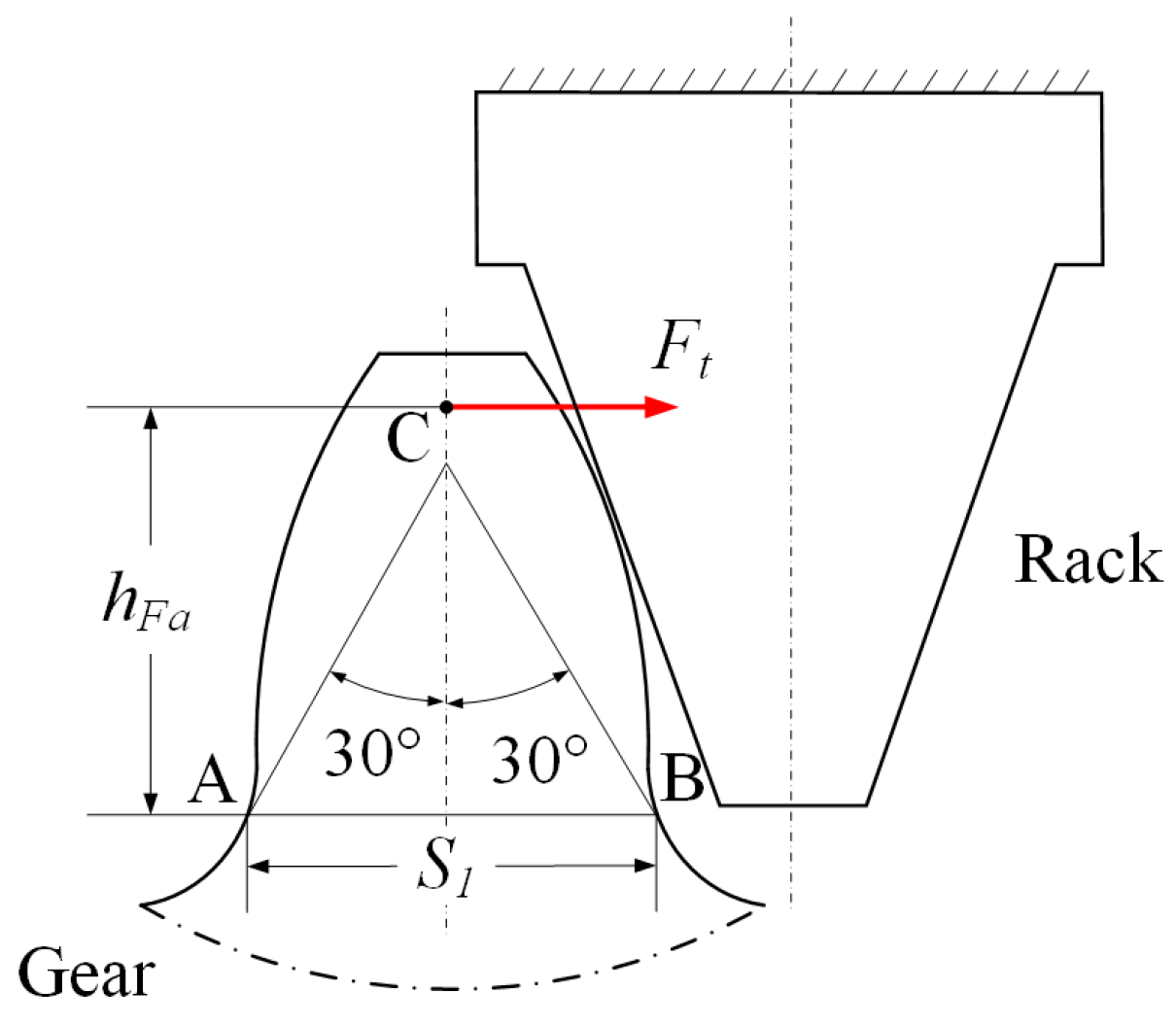
3.2. Calculation of the Bending Stress Parameters for Worn Gear
3.3. Bending Stress Calculation of Worn Gears
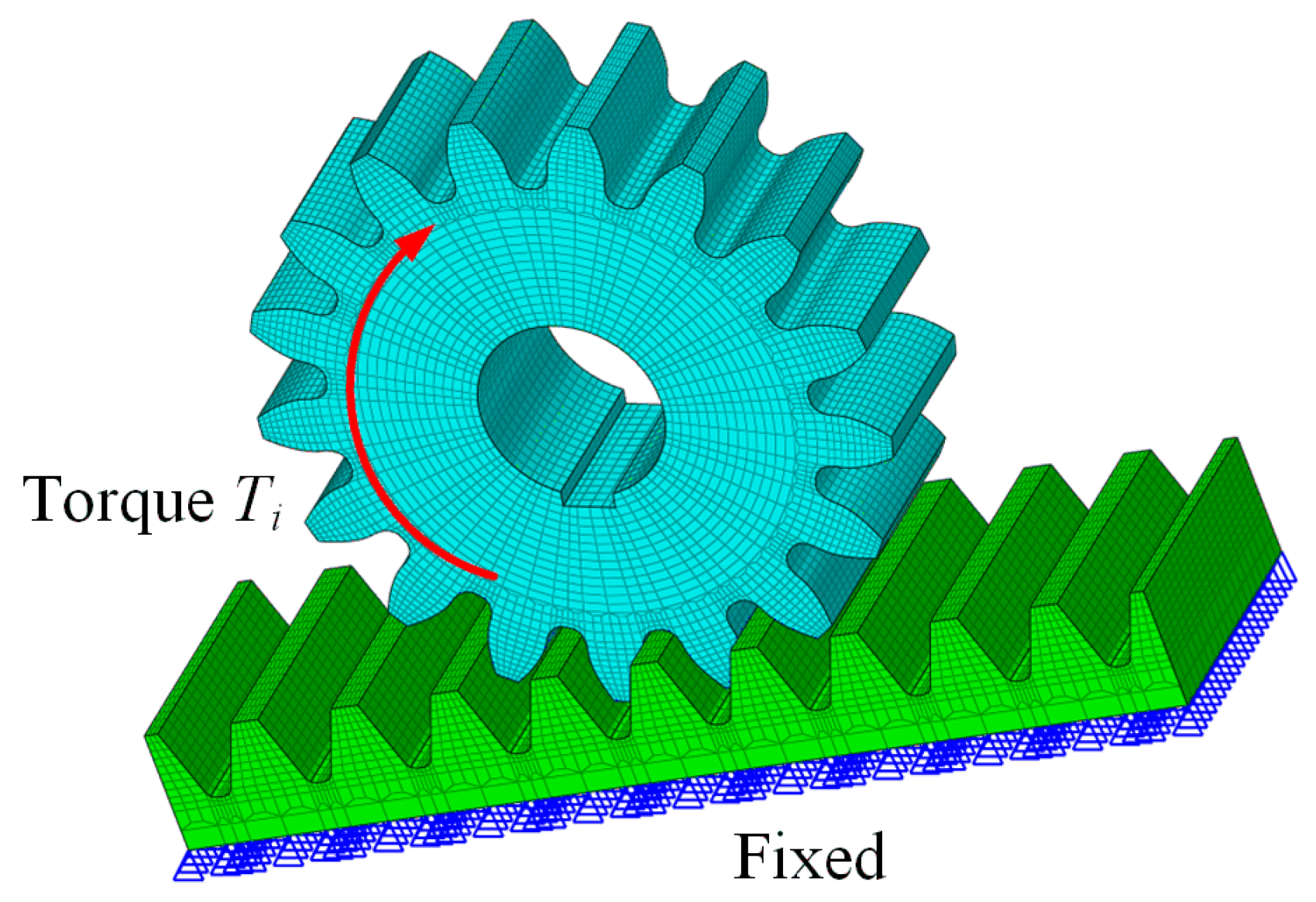
4. Finite Element Analysis
- Geometric assumptions: The FEM model assumed simplified geometric representations of the structures under analysis including the gear and rack. The teeth were completely intact and original, without any microcracks and dislocations.
- Mechanics of material assumptions: Material behavior was assumed to follow a linear elastic constitutive model, with properties described by 40Cr.
- Boundary condition assumptions: Imposing a fixed constraint on the bottom of the rack represents the displacement boundary condition while applying torque to the gear represents the only force boundary condition (see Figure 9).
- Mathematical assumptions: The model was based on assumptions of continuity, equilibrium, and numerical approximation associated with the FEM-based modeling.
5. Experimental Validation
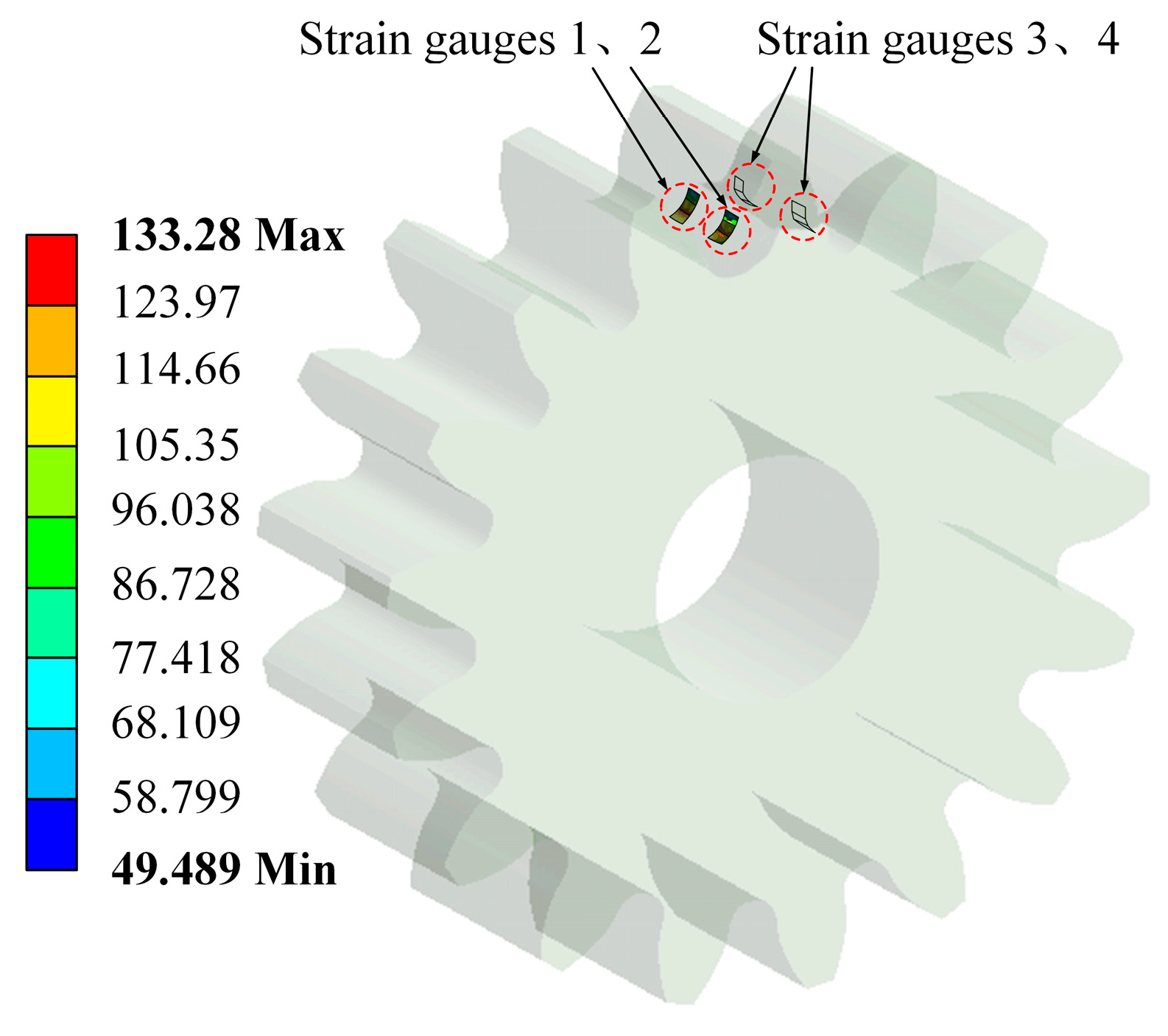
5.1. Data Collection
- The hydraulic cylinder oil pressure was controlled in the PLC, and the detailed data of the oil pressure under each working condition are listed in column 5 of Table 4;
- The hoisting mechanism was operated through the control cabinet, adjusting the meshing point of the rack-and-pinion according to the meshing radius of the gear;
- Data were collected and saved by the DHDAS.
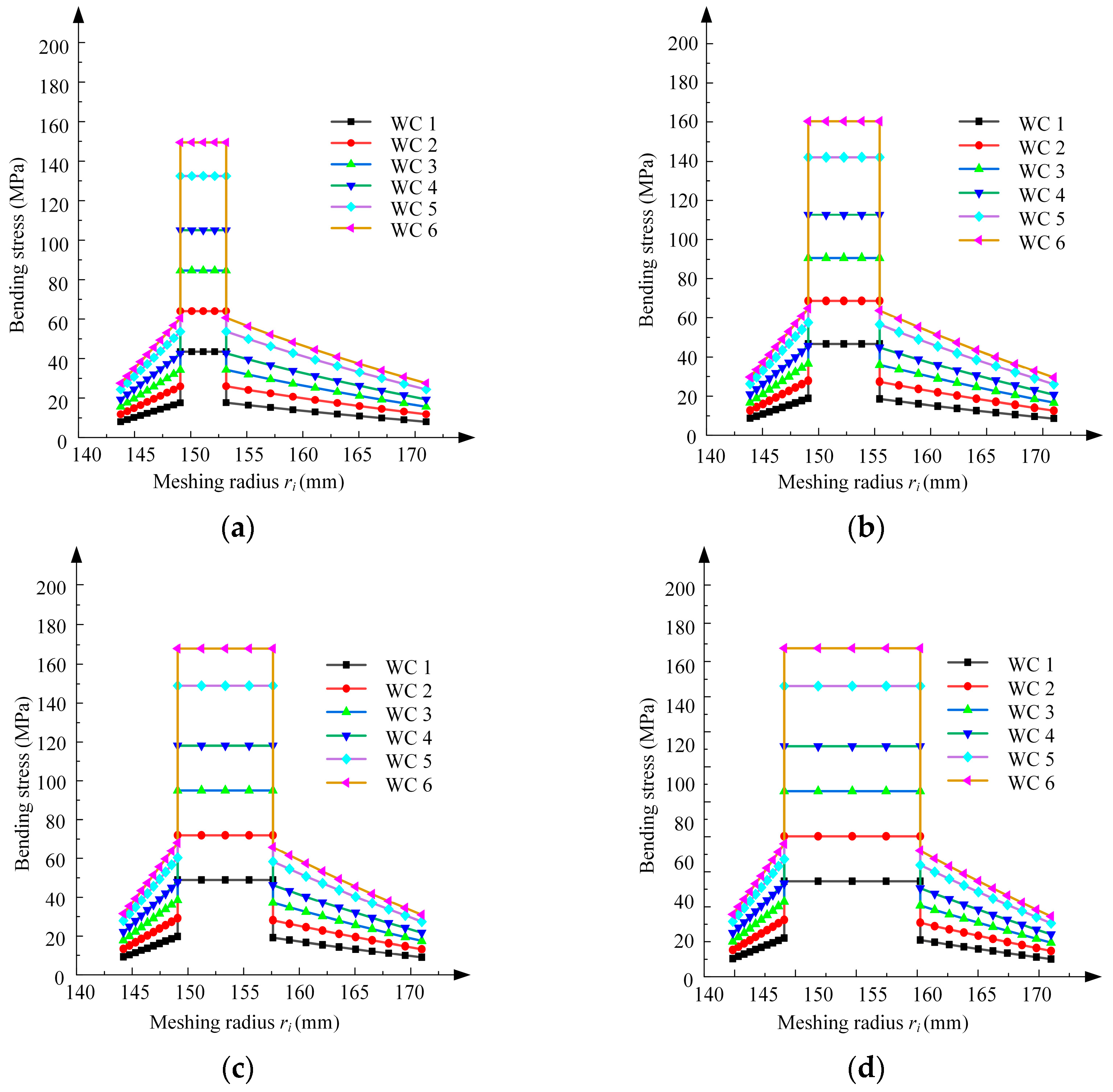
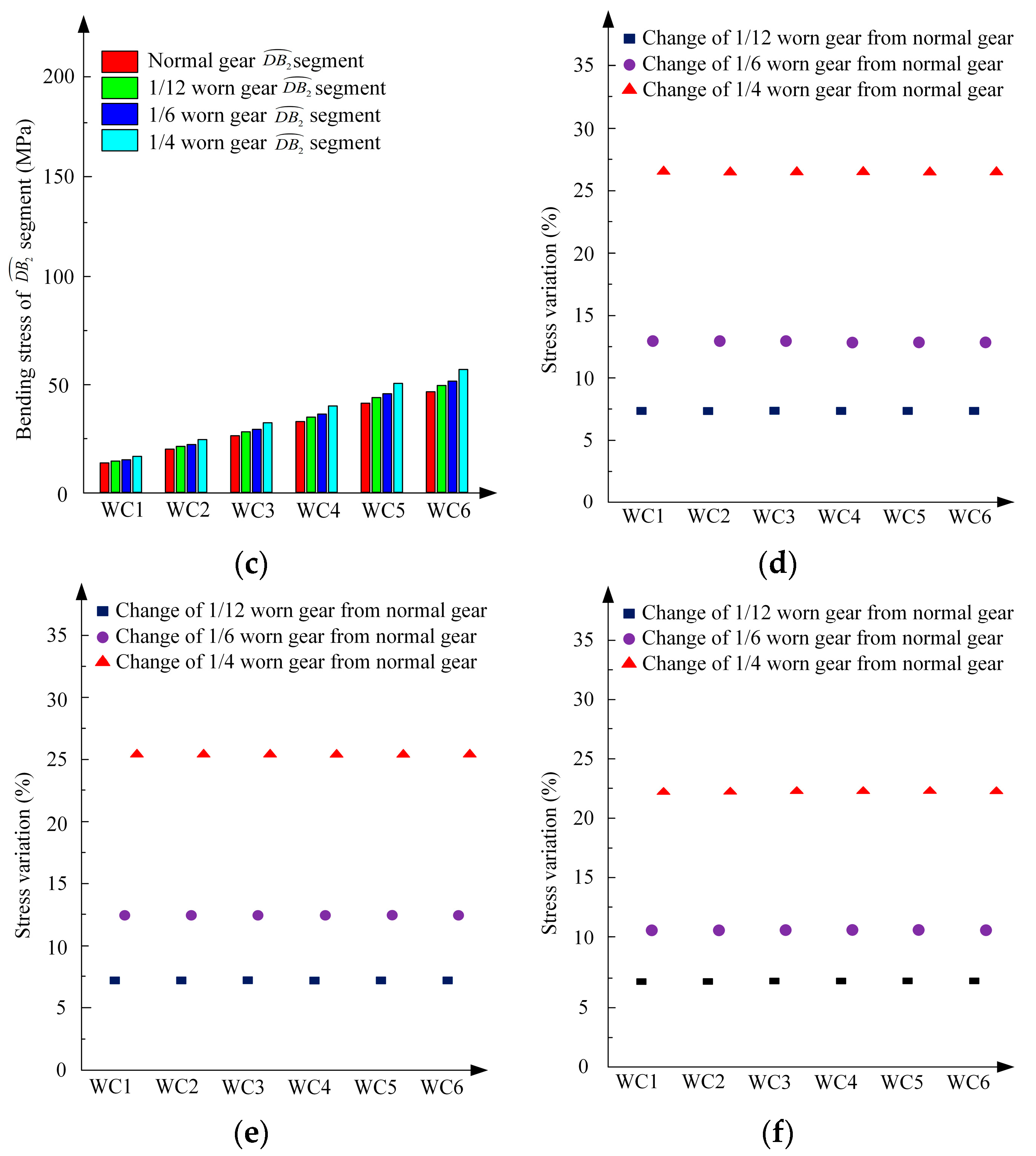
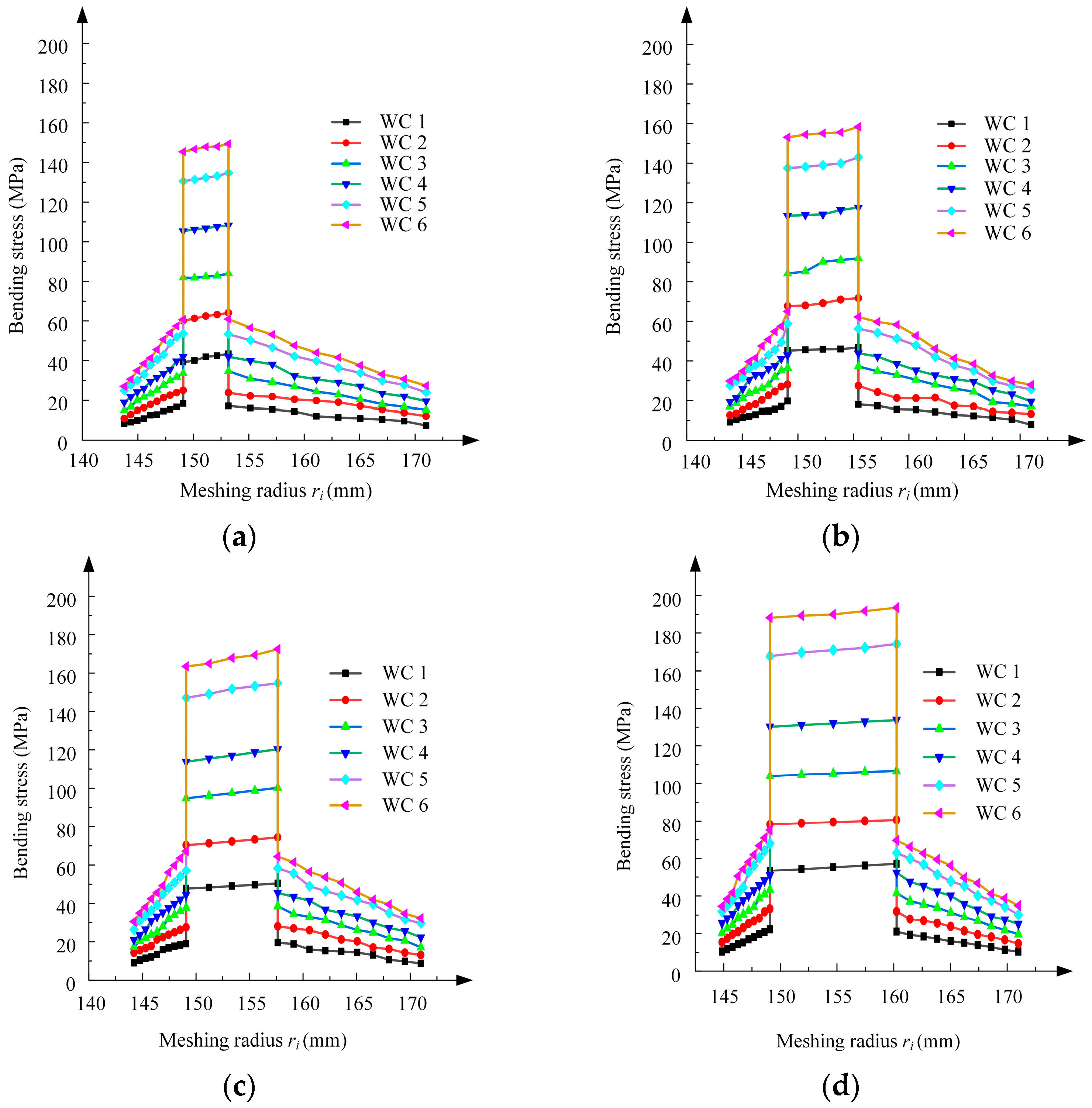
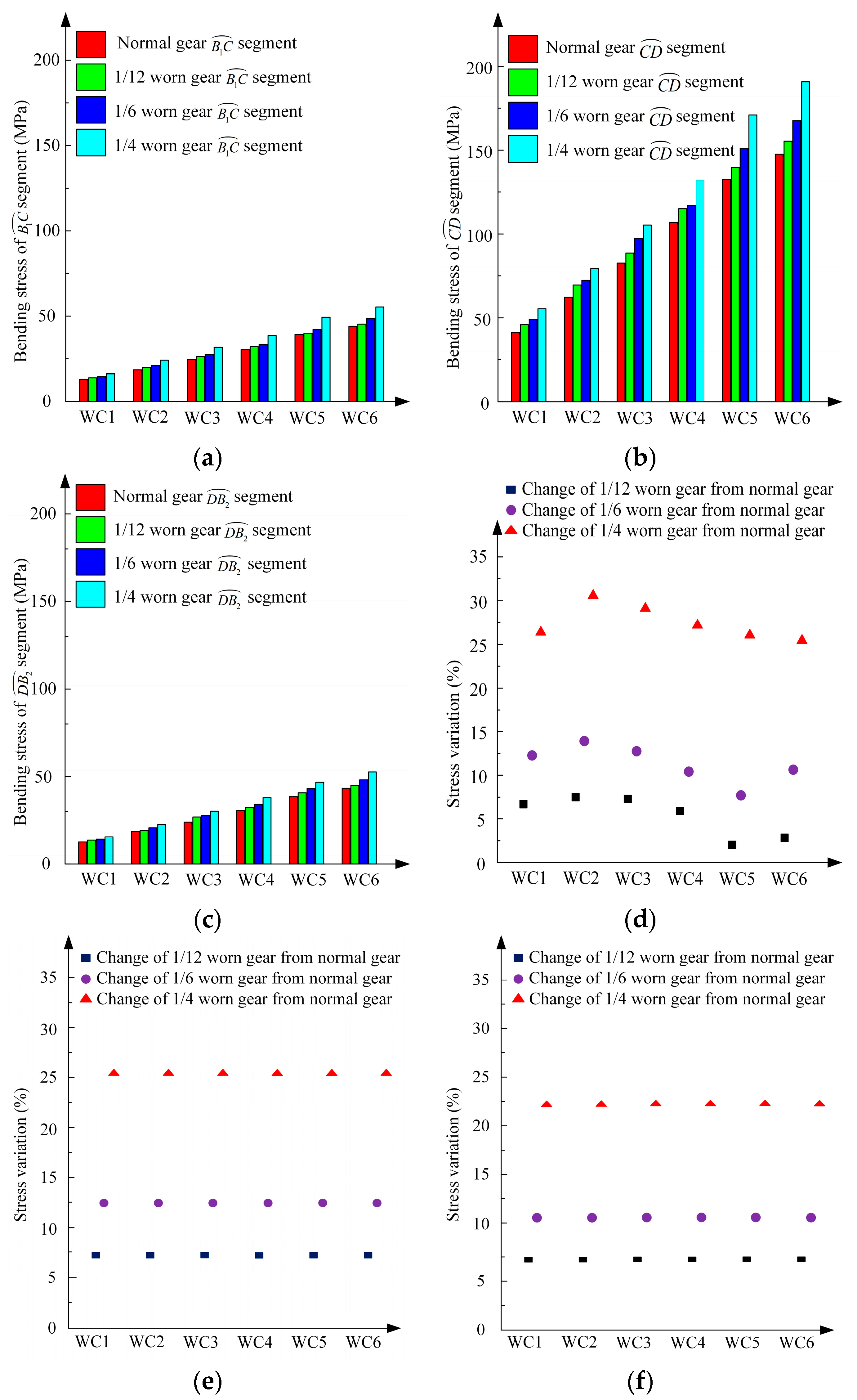
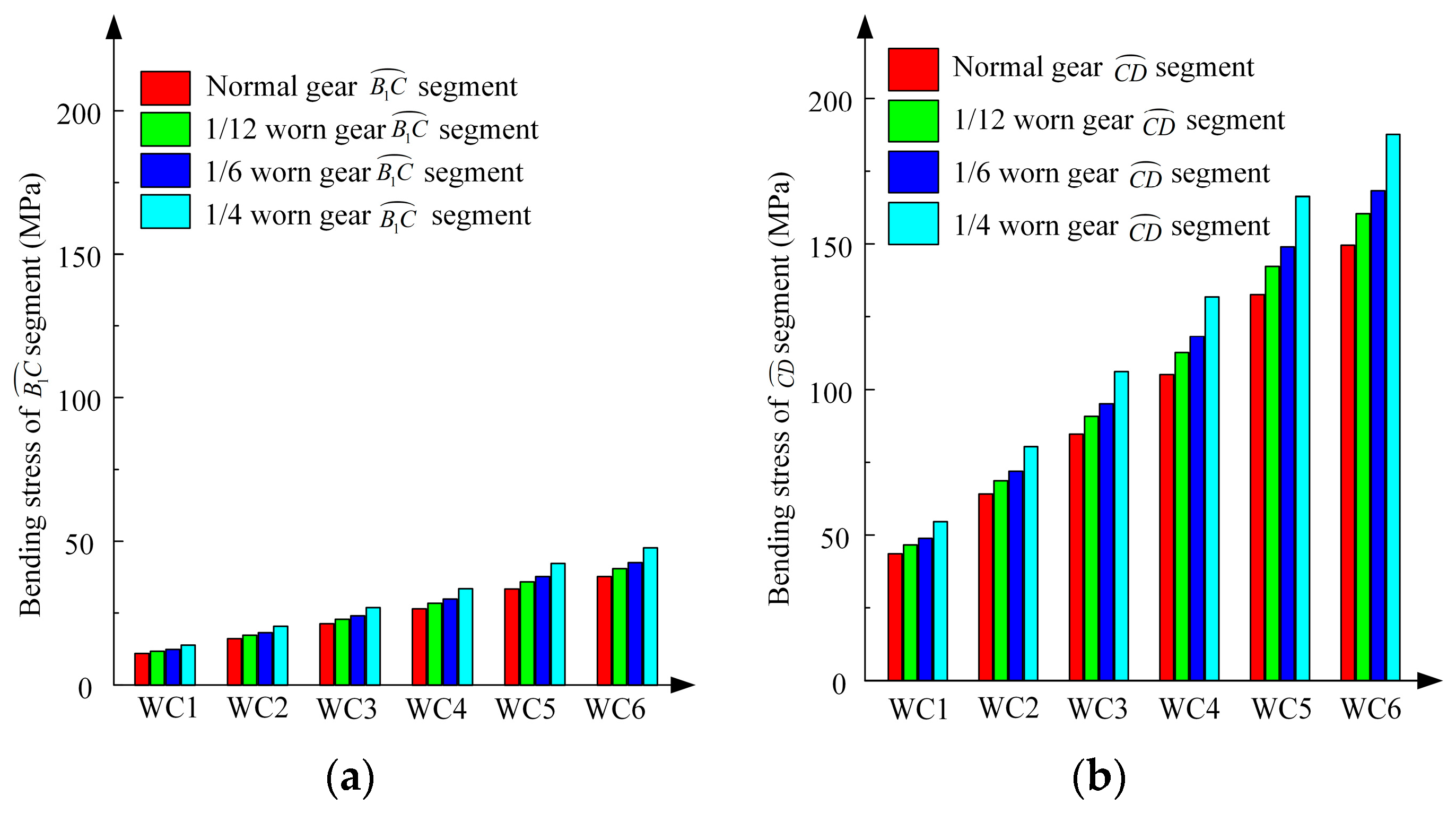
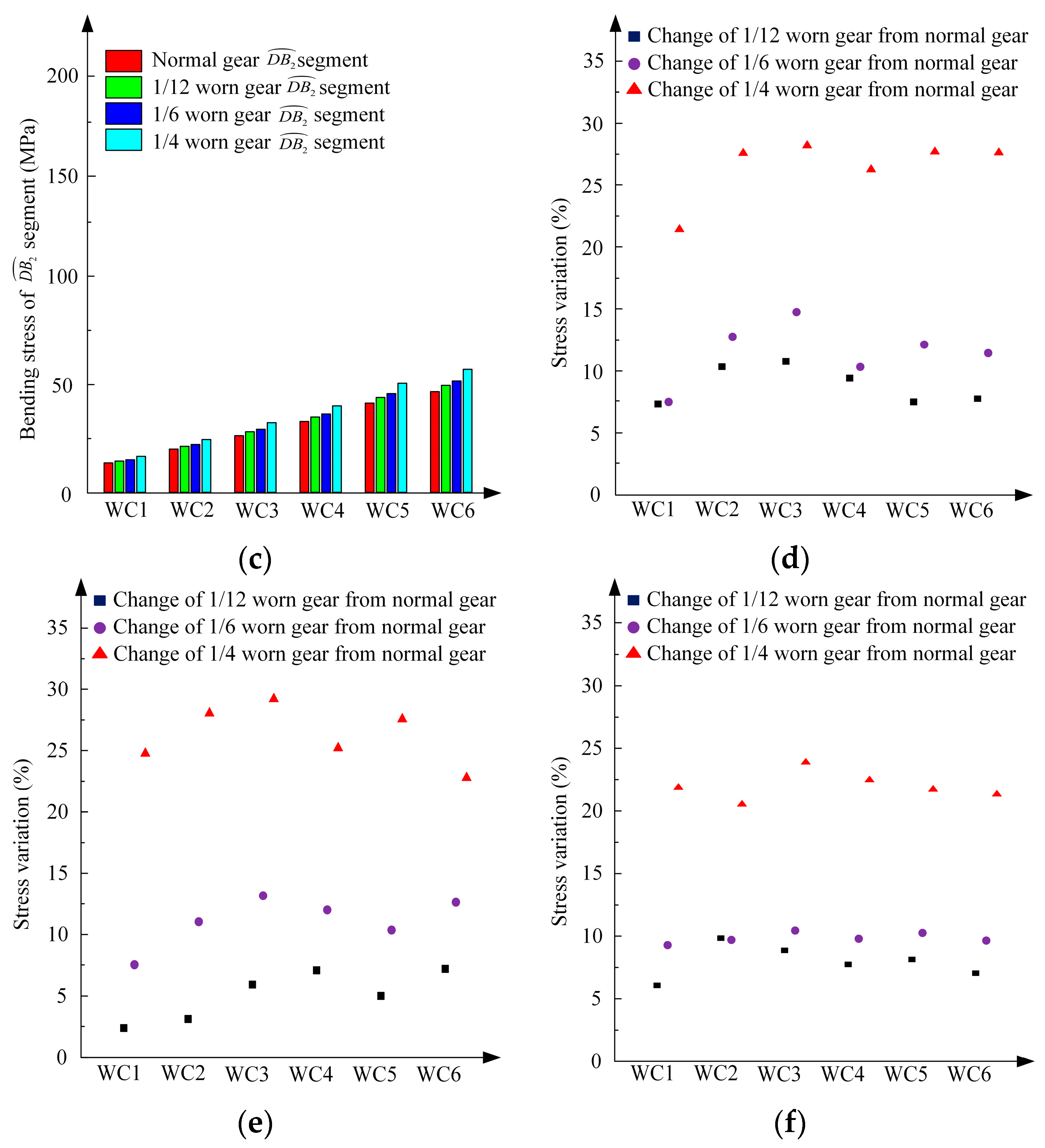
5.2. Analysis of the Experimental Results
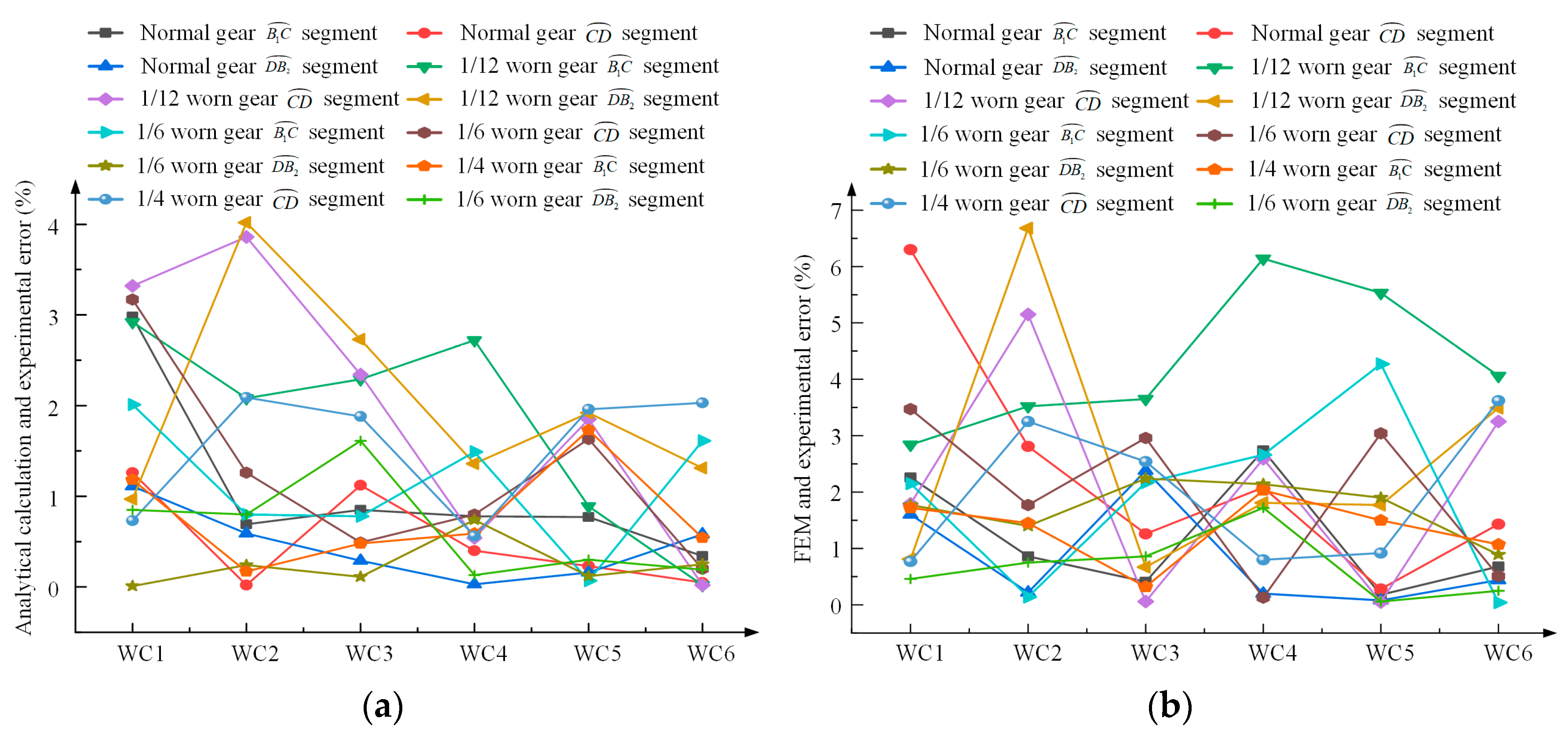
5.3. Comparative Analysis of Three Methods
- (1)
- Error of the analytical results through a comparison with the experimentally observed data
- (2)
- Error of the FEM results through a comparison with the experimentally observed data
6. Conclusions
- (1)
- In this paper, the rack-and-pinion transmission pair of the Three Gorges ship lift was considered as the research object to establish a simulation experimental platform for the working conditions of the vertical rack-and-pinion lifting mechanism. The changes in related parameters such as load along the tooth profile and the tooth thickness of the gear after uniform wear were methodically investigated by the modified gear method. Three methods, which were analytical calculation, FEM calculation, and experiment, were adopted to evaluate the bending stresses of the normal, 1/12, 1/6, and 1/4 uniform worn gears. The obtained results of the above three methodologies indicate that the bending stress in single-tooth meshing was substantially higher than that of double-tooth meshing to increase the degree of wear and loading. With increasing wear, the single-tooth meshing time increased, which revealed that gear wear deteriorated the working condition of the transmission system and accelerated the degradation process of the transmission system performance.
- (2)
- By analyzing the errors between the analytical and FEM results, analytical and experimental results, and FEM and experimental results, the obtained relative discrepancies among of the various results were all at a low level, and therefore, the three methods can confirm each other, which guarantees the accuracy of the analysis. As a result, this paper is able to provide theoretical support and an empirical basis for the kinematic analysis and dynamic analysis of large modulus rack-and-pinion transmission.
- (3)
- By examining the effect of different degrees of uniform wear on the tooth surface on the change in bending stress at the root of the large-module gear rack pair under the working condition of the Three Gorges ship lift, it is applicable to various application scenarios of the large-module gear rack pair. It plays a critical role in how to ensure the safe, reliable, and efficient performance status of a large-module gear rack pair lifting platform during service operations as well as monitoring and assessing the condition on-site or online. Similarly, studying the failure mechanism and dynamic response characteristics of rack-and-pinion transmission under complex working conditions and revealing the degradation of equipment service performance and the evolution of reliability is of great significance and practical engineering value.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Suo, L.; Niu, X.; Xie, H. 6.07-The Three Gorges Project in China, comprehensive renewable energy. Compr. Renew. Energy 2012, 6, 179–226. [Google Scholar] [CrossRef]
- Yuan, Y.; Ji, B.; Yuan, X.; Huang, Y. Lockage scheduling of Three Gorges-Gezhouba dams by hybrid of chaotic particle swarm optimization and heuristic-adjusted strategies. Appl. Math. Comput. 2015, 270, 74–89. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, Y.; Xiao, W.; Zhang, H. Method of calculation and experiment of bending stress for rough module racks. J. Mech. Eng. 2016, 52, 152–159. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Zhu, C.; Parker, R. Effects of lubrication on gear performance: A review. Mechan. Mach. Theory 2020, 145, 103701. [Google Scholar] [CrossRef]
- Li, G.; Geng, Z. Gear bending stress analysis of automatic transmissions with different fillet curves. Int. J. Automot. Sci. Technol. 2021, 5, 100–106. [Google Scholar] [CrossRef]
- Ko, K.E.; Lim, D.H.; Kim, P.Y.; Park, J. A study on the bending stress of the hollow sun gear in a planetary gear train. J. Mech. Sci. Technol. 2010, 24, 29–32. [Google Scholar] [CrossRef]
- Saribay, Z. Tooth geometry and bending stress analysis of conjugate meshing face-gear pairs. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 1302–1314. [Google Scholar] [CrossRef]
- Yu, Y.; Lin, C.; Hu, Y. Tooth bending stress analysis of high speed curve face gear of composite transmission. Mech. Ind. 2021, 22, 20. [Google Scholar] [CrossRef]
- Pedersen, N. Improving bending stress in spur gears using asymmetric gears and shape optimization. Mech. Mach. Theory 2010, 45, 1707–1720. [Google Scholar] [CrossRef]
- Cheng, X.; Shi, D.; Liu, C.; Xia, R.; Zhang, Y.; Zhou, J. Double cracks with single-inclusion fatigue propagation of surface-quenched large modulus rack. Adv. Mech. Eng. 2019, 11, 1687814019895745. [Google Scholar] [CrossRef]
- Cheng, X.; Shi, D.; Li, H.; Xia, R.; Zhang, Y.; Zhou, J. Stability and parameters influence study of fully balanced hoist vertical ship lift. Struct. Eng. Mech. 2018, 66, 583–594. [Google Scholar] [CrossRef]
- Yan, H.; Li, P.; Liu, H.; Wang, Z.; Wei, D. Research on the bending and fatigue damage degree of the climbing mechanism of the riprap leveling ship after wear. China Shipbuild. 2020, 61, 164–172. [Google Scholar]
- Zhou, C.; Dong, X.; Wang, H.; Liu, Z. Time-varying mesh stiffness model of a modified gear–rack drive with tooth friction and wear. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 213. [Google Scholar] [CrossRef]
- Tao, J.; Wen, A.; Liu, Z.; Yu, S. Lean lubrication of ultra large modulus open gear and rack pair: A case study of the gear-rack drive mechanism of the Chinese “Three Gorge Dam” ship lift. J. Clean. Prod. 2020, 282, 124450. [Google Scholar] [CrossRef]
- Zhao, T.; Shi, D.; Yao, Z.; Mao, H.; Cheng, S.; Peng, H. Crack spacing threshold of double cracks propagation for large-module rack. J. Cent. South Univ. 2015, 22, 2533–2539. [Google Scholar] [CrossRef]
- Shi, D.; Cai, D.; Wu, Z. Finite element analysis on nut post structure of Three Gorges Project ship lift. J. Cent. South Univ. Technol. 2009, 16, 614–620. [Google Scholar] [CrossRef]
- Zhao, X.; Lin, Q.; Yu, H. A co-scheduling problem of ship lift and ship lock at the three gorges dam. IEEE Access 2020, 8, 132893–132910. [Google Scholar] [CrossRef]
- Akkermann, J.; Wu, X. The ship lift at the Three-Gorges-Dam in China-construction of the world’s largest elevator. Bautechnik 2016, 93, 899–906. [Google Scholar] [CrossRef]
- Tang, X. Longyuan Zhenhua Three: The world’s largest wind power construction platform built by China’s power. Electr. Power Equip. Manag. 2018, 9, 96. [Google Scholar]
- Li, D.; Pang, X.; Fan, Y.-b.; Xue, L.; Wang, L.; Shi, Z. The jetting valve design of the leg shoe on the Shengli No. 5 workover platform. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2021; pp. 2696–2699. [Google Scholar]
- Dasgupta, K.; Kumar, N.; Kumar, R. Steady state performance analysis of hydrostatic transmission system using two motor summation drive. J. Inst. Eng. (India) Ser. C 2013, 94, 357–363. [Google Scholar] [CrossRef]
- Waragai, M.; Takayama, T. Development of a high-speed and low-torque loss two-way clutch. ROBOMECH J. 2022, 9, 21. [Google Scholar] [CrossRef]
- Liu, H. Tribological behavior of a novel magnetorheological fluid under adverse lubrication conditions. Tribol. Trans. 2019, 62, 834–841. [Google Scholar]
- Doerner, M.D. Effects of particle contamination on boundary lubricated wear. Wear 2020, 452–453, 203316. [Google Scholar] [CrossRef]
- Taylor, S. Influence of lubrication conditions on surface pitting and subsurface fatigue in rolling-sliding contacts. Tribol. Trans. 2016, 59, 437–448. [Google Scholar]
- Zhang, H. Effect of lubrication regimes on microstructure and fatigue behavior of high-strength steel. Wear 2017, 376–377, 1613–1622. [Google Scholar]
- Chen, X. Tribological performance and failure mechanism of gear surface under different lubrication conditions. J. Tribol. 2018, 140, 051501. [Google Scholar]
- Spitas, C.; Giannakopoulos, A.E. Influence of poor lubrication on the fatigue life of an engine camshaft. Int. J. Fatigue 2016, 91, 52–61. [Google Scholar]
- García-Rodríguez, A.; González-Morán, C.O. Influence of lubrication on the fatigue life of spur gears. Wear 2019, 426–427, 1652–1659. [Google Scholar]
- Yuan, H.; Lei, Z.; You, X.; Dong, Z.; Zhang, H.; Zhang, C.; Zhao, Y.; Liu, J. Fault diagnosis of driving gear in rack and pinion drives based on multi-scale local binary pattern extraction and sparse representation. Meas. Sci. Technol. 2023, 34, 055017. [Google Scholar] [CrossRef]
- Xi, C.; Yang, J.; Liang, X.; Ramli, R.B.; Tian, S.; Feng, G.; Zhen, D. An improved gated convolutional neural network for rolling bearing fault diagnosis with imbalanced data. Int. J. Hydromechatron. 2023, 6, 108–132. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, M.; Xu, X.; Zhang, N. Fault diagnosis of rolling bearings with noise signal based on modified kernel principal component analysis and DC-ResNet. CAAI Trans. Intell. Technol. 2023, 8, 1014–1028. [Google Scholar] [CrossRef]
- Zhen, D.; Li, D.; Feng, G.; Zhang, H.; Gu, F. Rolling bearing fault diagnosis based on VMD reconstruction and DCS demodulation. Int. J. Hydromechatron. 2022, 5, 205–225. [Google Scholar] [CrossRef]
- Jin, X.; Cheng, F.; Peng, Y.; Qiao, W.; Qu, L. Drivetrain gearbox fault diagnosis: Vibration-and current-based approaches. IEEE Ind. Appl. Mag. 2018, 24, 56–66. [Google Scholar] [CrossRef]
- Ehrmann, C.; Isabey, P.; Fleischer, J. Condition monitoring of rack and pinion drive systems: Necessity and challenges in production environments. Procedia CIRP 2016, 40, 197–201. [Google Scholar] [CrossRef]
- Feng, S.; Mao, J.; Xie, Y. Analysis and calculation of gear mesh stiffness with tooth wear. J. Mech. Eng. 2015, 51, 27–32. [Google Scholar] [CrossRef]
- Dong, P.; Zuo, S.; Du, S.; Tenberge, P.; Wang, S.; Xu, X.; Wang, X. Optimum design of the tooth root profile for improving bending capacity. Mechan Mach Theory 2020, 151, 103910. [Google Scholar] [CrossRef]
- Lin, C.; Wei, W.; Wang, S.; Xia, X.; Xin, Q. Bending stress analysis of eccentric straight and helical curve-face gear pair. Int. J. Mech. Mater. Des. 2020, 16, 401–414. [Google Scholar] [CrossRef]
- Shen, Z.; Qiao, B.; Yang, L.; Luo, W.; Chen, X. Evaluating the influence of tooth surface wear on TVMS of planetary gear set. Mech. Mach. Theory 2019, 136, 206–223. [Google Scholar] [CrossRef]
- Sekar, R. Determination of load dependent gear loss factor on asymmetric spur gear. Mech. Mach. Theory 2019, 135, 322–335. [Google Scholar] [CrossRef]
- Pedrero, J.; Pleguezuelos, M.; Artés, M.; Antona, J. Load distribution model along the line of contact for involute external gears. Mech. Mach. Theory 2010, 45, 780–794. [Google Scholar] [CrossRef]
- Sanchez, M.; Pleguezuelos, M.; Pedrero, J. Enhanced model of load distribution along the line of contact for non-standard involute external gears. Meccanica 2013, 48, 527–543. [Google Scholar] [CrossRef]
- Zheng, M.; Zhou, C.; Liu, Z. Transient thermal elastohydrodynamic lubrication for super-modulus modified gear-rack drive. J. Hunan Univ. (Nat. Sci.) 2021, 48, 11. [Google Scholar] [CrossRef]
- Park, C.; Jung, S.; Kim, J.; Kwak, S. Influence of gear surface lubrication on torque and friction in planetary gears. Tribol. Int. 2018, 126, 761–764. [Google Scholar]
- Zhang, L.; Zhang, W.; Liu, Y.; Ma, J. Effects of lubrication on tooth surface fatigue life and dynamic performance of spur gears. J. Tribol. 2019, 141, 051401. [Google Scholar]
- Belhocine, M.; Kahraman, A. Influence of lubrication on power loss and contact fatigue life of helical gears. J. Mech. Des. 2020, 142, 041401. [Google Scholar]
- Sekar, R.P.; Muthuveerappan, G. Estimation of tooth form factor for normal contact ratio asymmetric spur gear tooth. Mech. Mach. Theory 2015, 80, 187–218. [Google Scholar] [CrossRef]
- Wang, Z. Research of the Large Module Gear-Rack Bending Fatigue Strength. Master’s Thesis, Henan University of Technology, Zhengzhou, China, 2013. [Google Scholar]
- Smith, A.; Johnson, B. Influence of tooth load distribution factor and mesh radius on gear torque. Int. J. Mech. Eng. 2017, 6, 123–135. [Google Scholar]
- Wang, X.; Chen, Y.; Li, Z. Effects of tooth contact ratio and meshing radius on gear torque transmission. J. Tribol. 2018, 140, 041301. [Google Scholar]
- Brown, C.; Miller, D. Influence of gear tooth profile modification and mesh radius on torque distribution in spur gears. Tribol. Int. 2019, 131, 210–220. [Google Scholar]








| (MPa) | (kg/m3) | (MPa) | (MPa) | |
|---|---|---|---|---|
| 2.11 × 105 | 0.29 | 7850 | 382.5 | 355 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Module (mm) | 18 (62.667) | Tooth width of rack (mm) | 150 |
| Number of teeth | 17 (16) | Tooth height of rack (mm) | 80 |
| Pitch circle (mm) | 306 (1002.672) | Addendum coefficient | 1 |
| Pressure angle (°) | 20 | Clearance coefficient | 0.25 |
| Tooth width of gear (mm) | 100 (610) | Distance from gear center to rack reference line (mm) | 153 |
| Meshing Interval (mm) | Normal | 1/12 Wear | 1/6 Wear | 1/4 Wear | |
|---|---|---|---|---|---|
| Double-tooth | segment meshing radius | ||||
| segment meshing radius | |||||
| Single-tooth | segment meshing radius | ||||
| Working Condition | Working Conditions of the Three Gorges Ship Lift | (KN) | Test Bench under Pressure | Compression Size (t) | (KN) |
|---|---|---|---|---|---|
| WC1 | −10 cm misloaded water depth headwind to accelerate the rise | −583 | No-load + self-weight of the test bench | −(0 + 0.9) | 18.65 |
| WC2 | +10 cm misloaded water depth and descending at a constant speed against the wind | −770 | Oil cylinder + lift table dead weight | −(0.9 + 0.9) | −27.45 |
| WC3 | −5 cm misloaded water depth rising at a constant speed with the wind | 957 | Oil cylinder + lift table dead weight | (1.8 + 0.9) | −36.25 |
| WC4 | +5 cm misloaded water depth headwind accelerated descent | −1207 | Oil cylinder + lift table dead weight | (2.7 + 0.9) | 45.06 |
| WC5 | +5 cm misloaded water depth downwind to slow down and ascend | 1362 | Oil cylinder + lift table dead weight | (3.6 + 0.9) | −56.83 |
| WC6 | −5 cm misloaded water depth downwind to slow down and descend | 396 | Oil cylinder + lift table dead weight | −(4.5 + 0.9) | 64.13 |
| Parameters | Normal | 1/12 Wear | 1/6 Wear | 1/4 Wear |
|---|---|---|---|---|
| (mm) | 28.27 | 25.91 | 24.74 | 21.20 |
| 0 | −0.072 | −0.133 | −0.206 | |
| (°) | 20 | 20 | 20 | 20 |
| (°) | 32.780 | 32.092 | 31.492 | 30.749 |
| (mm) | 0 | 0 | 0 | 0 |
| 1.7478 | 1.63 | 1.53 | 1.41 | |
| 0.679 | 0.71 | 0.74 | 0.78 | |
| (mm) | 29.13 | 28.28 | 26.89 | 27.43 |
| (mm) | 33.75 | 32.77 | 31.91 | 31.14 |
| 2.47 | 2.56 | 2.58 | 2.79 | |
| 1.88 | 1.860 | 1.857 | 1.817 |
| Gear Condition | Normal | 1/12 Wear | 1/6 Wear | 1/4 Wear |
|---|---|---|---|---|
| Proportion of single-tooth meshing time (%) | 15.0 | 23.5 | 31.6 | 42.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Z.; Chen, B.; Cheng, X. Assessment of the Uniform Wear Bending Strength of Large Modulus Rack and Pinion Pair: Theoretical vs. Experimental Results. Machines 2024, 12, 570. https://doi.org/10.3390/machines12080570
Gong Z, Chen B, Cheng X. Assessment of the Uniform Wear Bending Strength of Large Modulus Rack and Pinion Pair: Theoretical vs. Experimental Results. Machines. 2024; 12(8):570. https://doi.org/10.3390/machines12080570
Chicago/Turabian StyleGong, Zongxing, Baojia Chen, and Xuan Cheng. 2024. "Assessment of the Uniform Wear Bending Strength of Large Modulus Rack and Pinion Pair: Theoretical vs. Experimental Results" Machines 12, no. 8: 570. https://doi.org/10.3390/machines12080570
APA StyleGong, Z., Chen, B., & Cheng, X. (2024). Assessment of the Uniform Wear Bending Strength of Large Modulus Rack and Pinion Pair: Theoretical vs. Experimental Results. Machines, 12(8), 570. https://doi.org/10.3390/machines12080570






