Numerical and Experimental-Based Framework for Fuel Cell System Fatigue Analysis in Frequency Domain
Abstract
:1. Introduction
2. Basic Theoretical Model
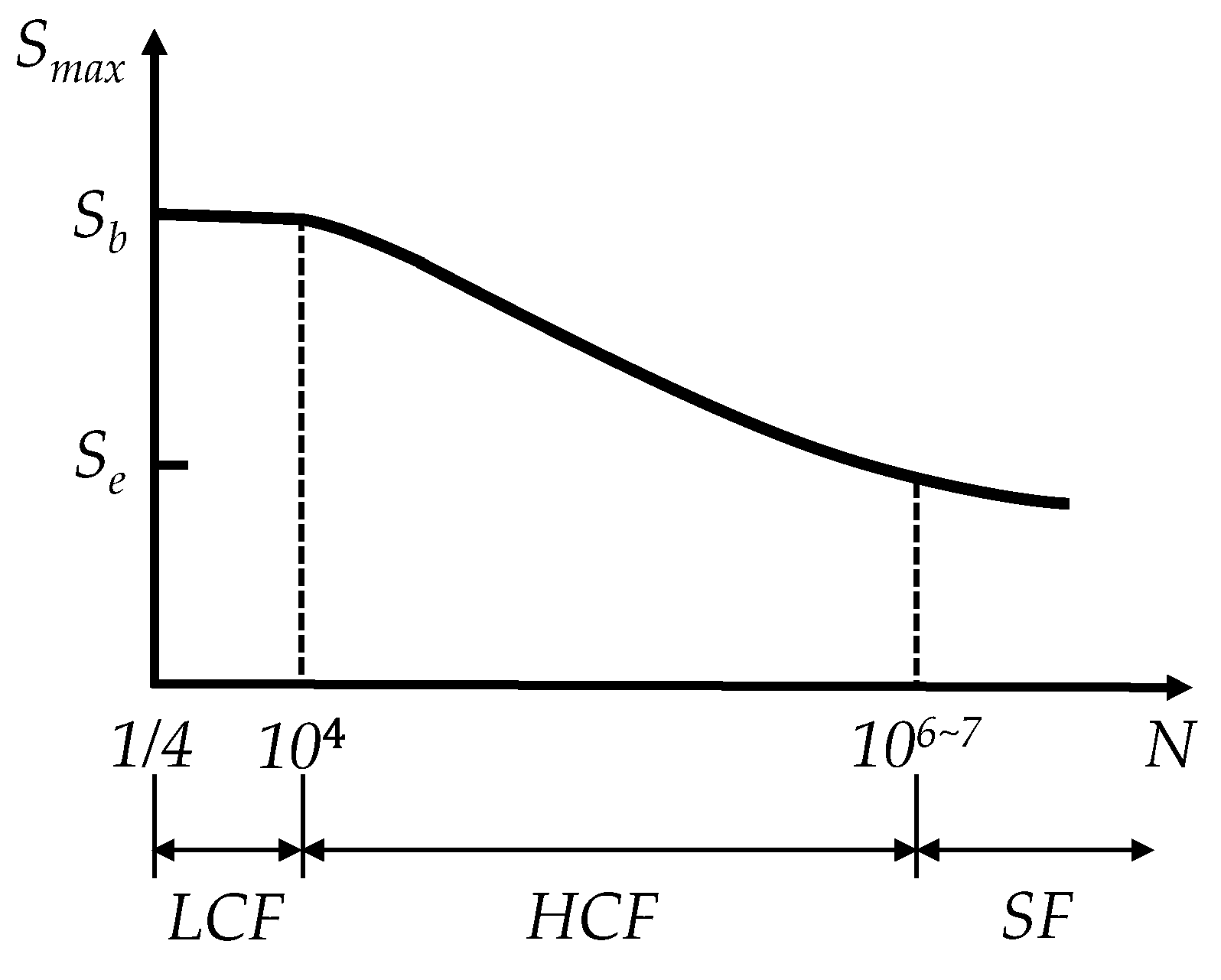
2.1. Miner Linear Damage Accumulation Theory
2.2. Power Spectral Density (PSD)
2.3. Stochastic Process Rain Flow Distribution Model
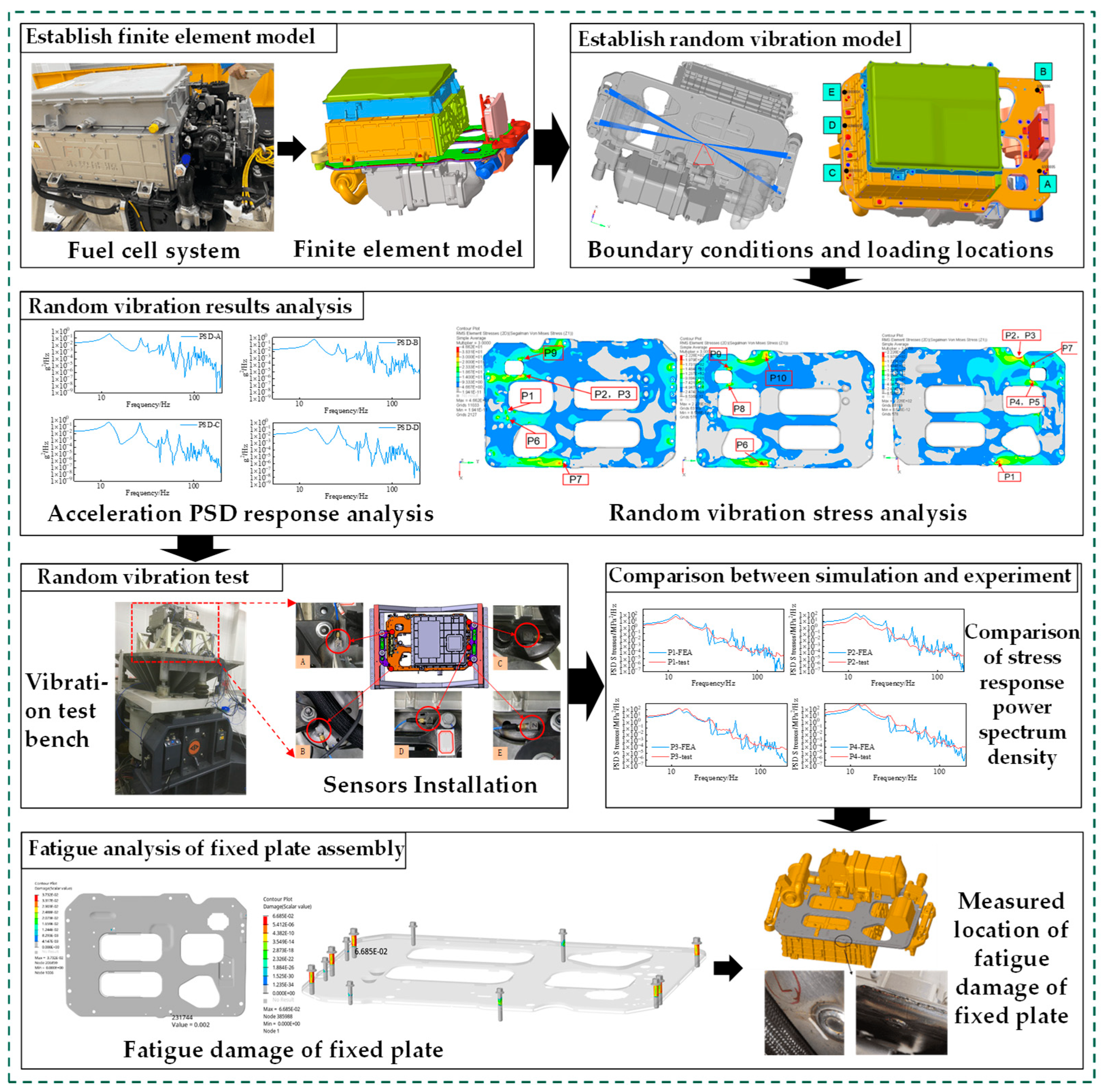
3. Analysis Process
4. Random Vibration Simulation Analysis
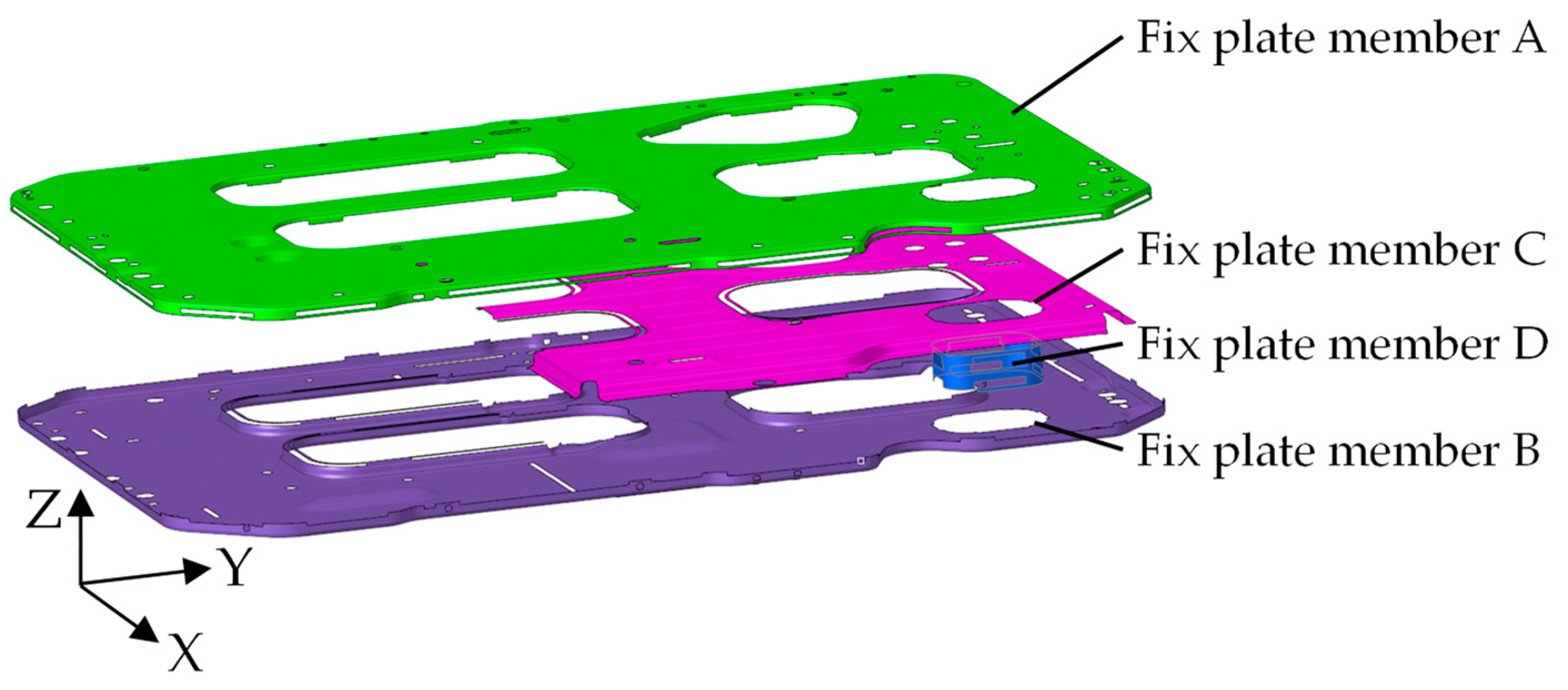
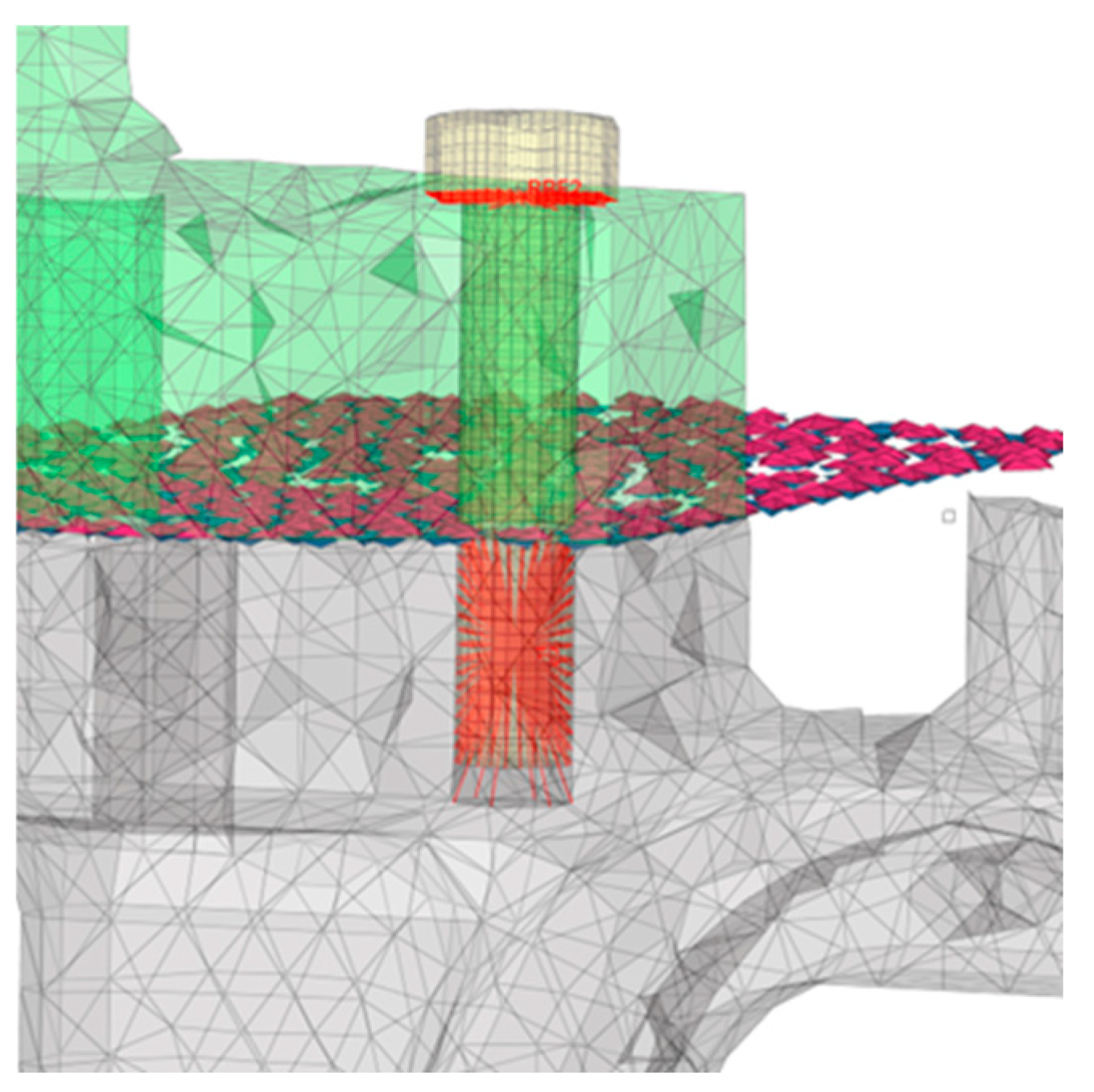
4.1. Establishment of Finite Element Model of Fuel Cell System
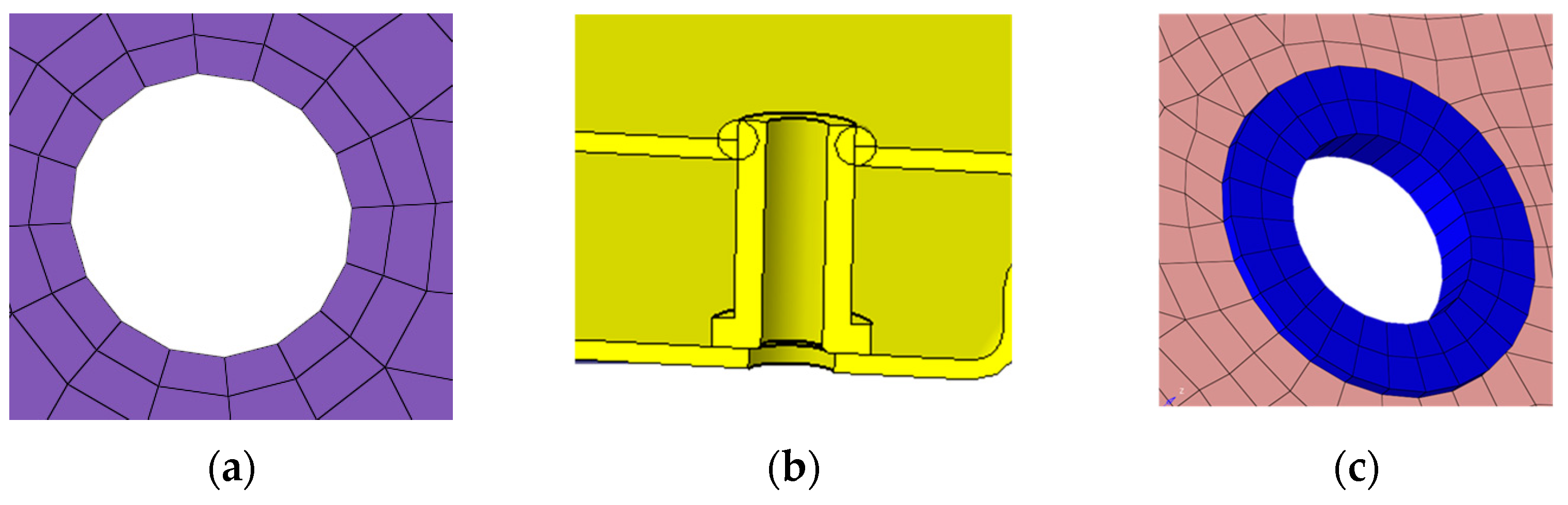
- (a)
- Holes with diameters smaller than 3 mm are excluded from the model to improve mesh quality.
- (b)
- For small flanges, a single row of elements is sufficient; however, when the flange size exceeds twice the size of the basic element, at least two rows of elements are required.
- (c)
- Chamfer features smaller than half the size of the basic element can be ignored unless stress concentration occurs at the chamfer, in which case the chamfer should be retained.
4.2. Establishment of Random Vibration Model
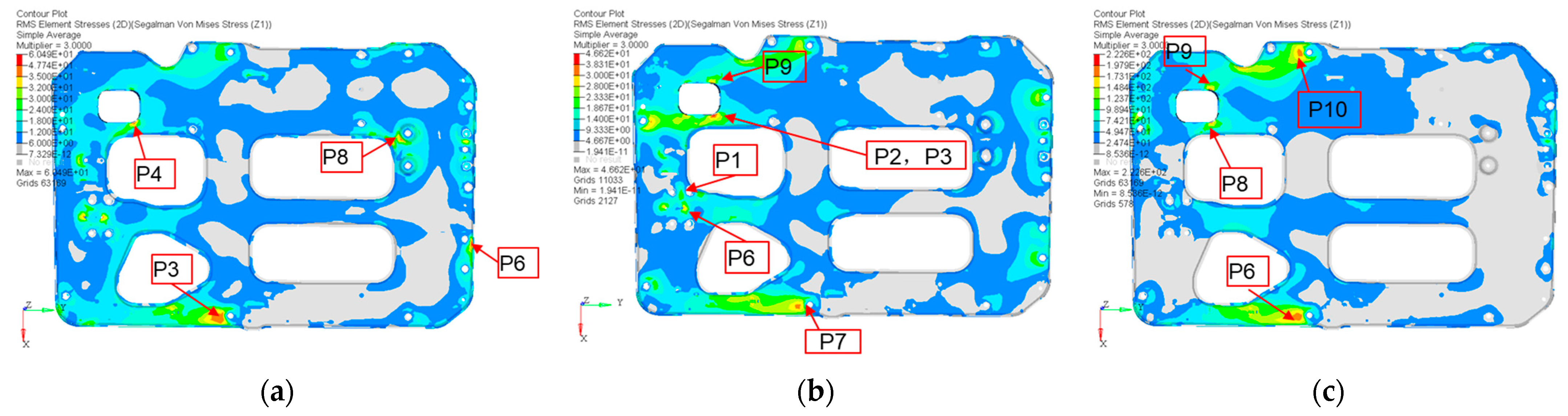
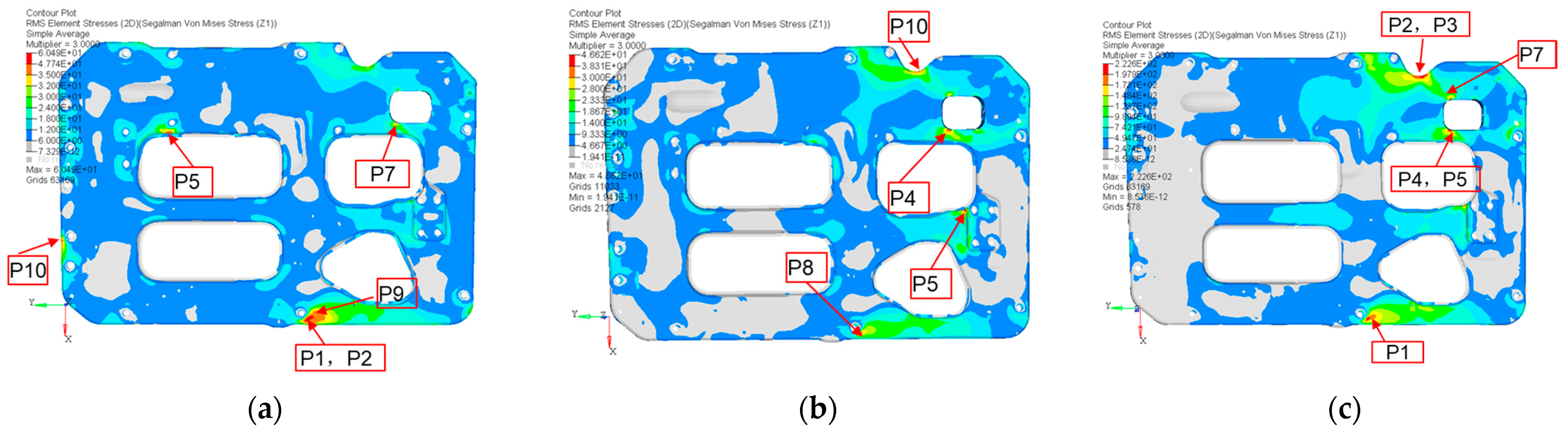
4.3. Random Vibration Stress Analysis of Fuel Cell System
5. Fuel Cell System Random Vibration Test
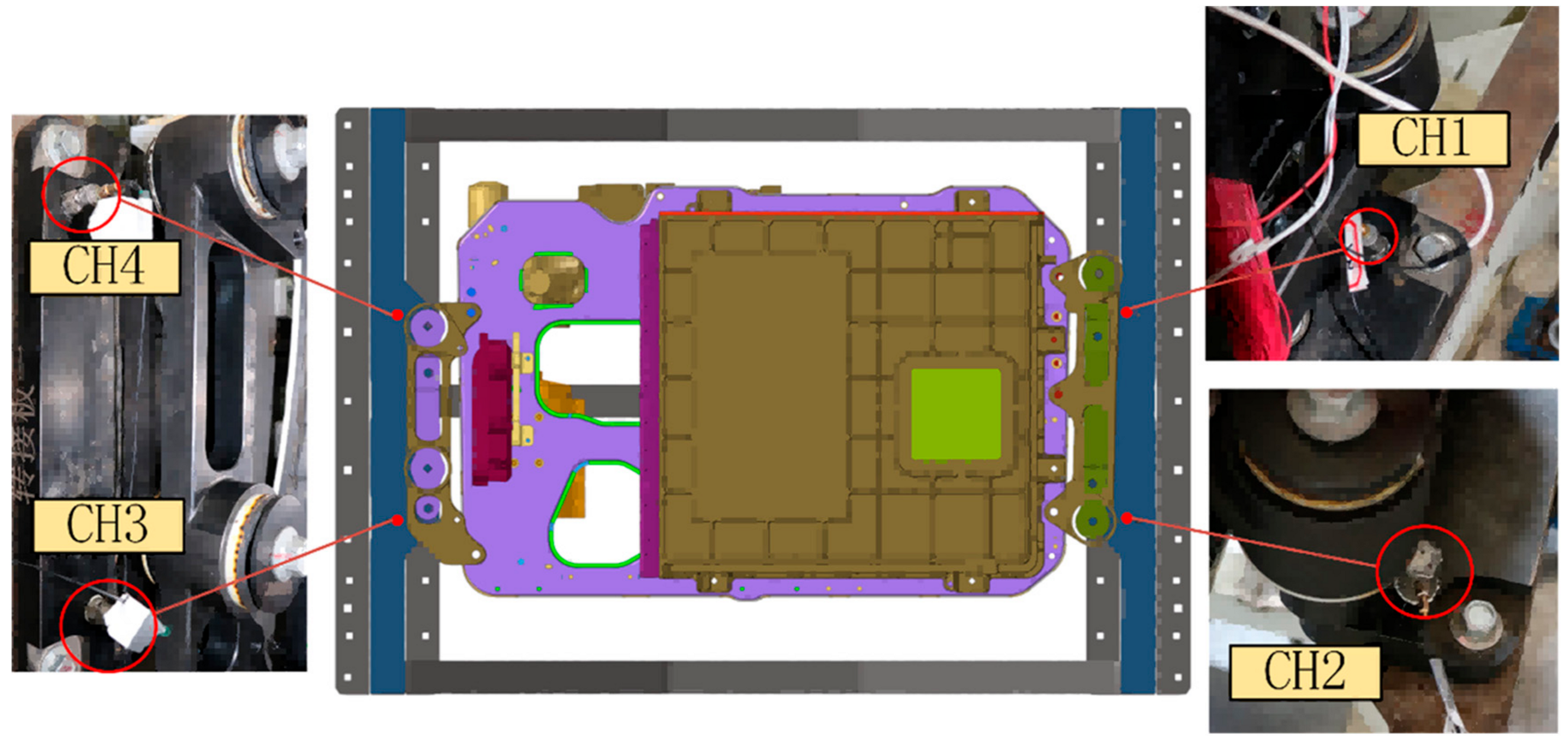
5.1. Test Environment Construction
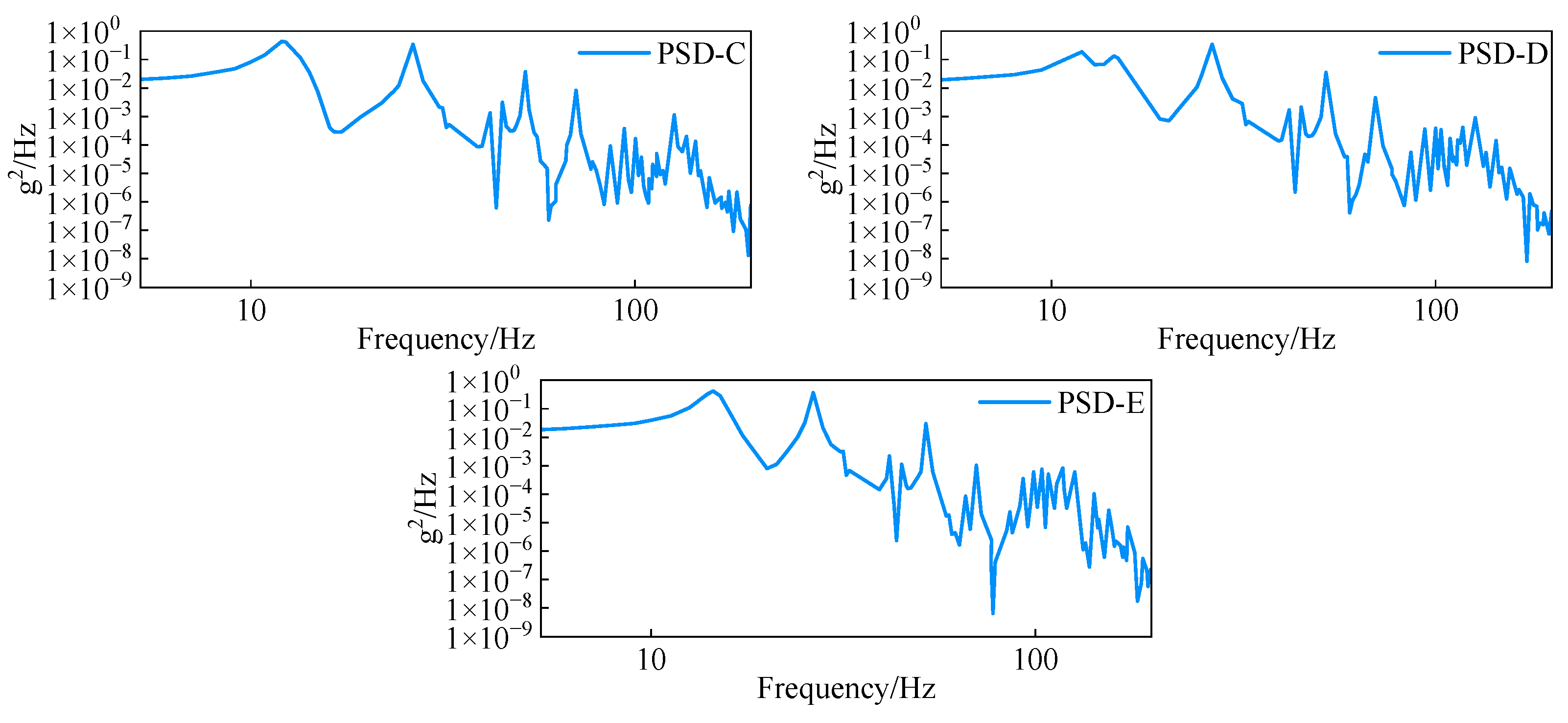
5.2. Random Vibration Stress Benchmark Test
6. Fatigue Life Analysis of the Fixed Plate Assembly of a Fuel Cell System
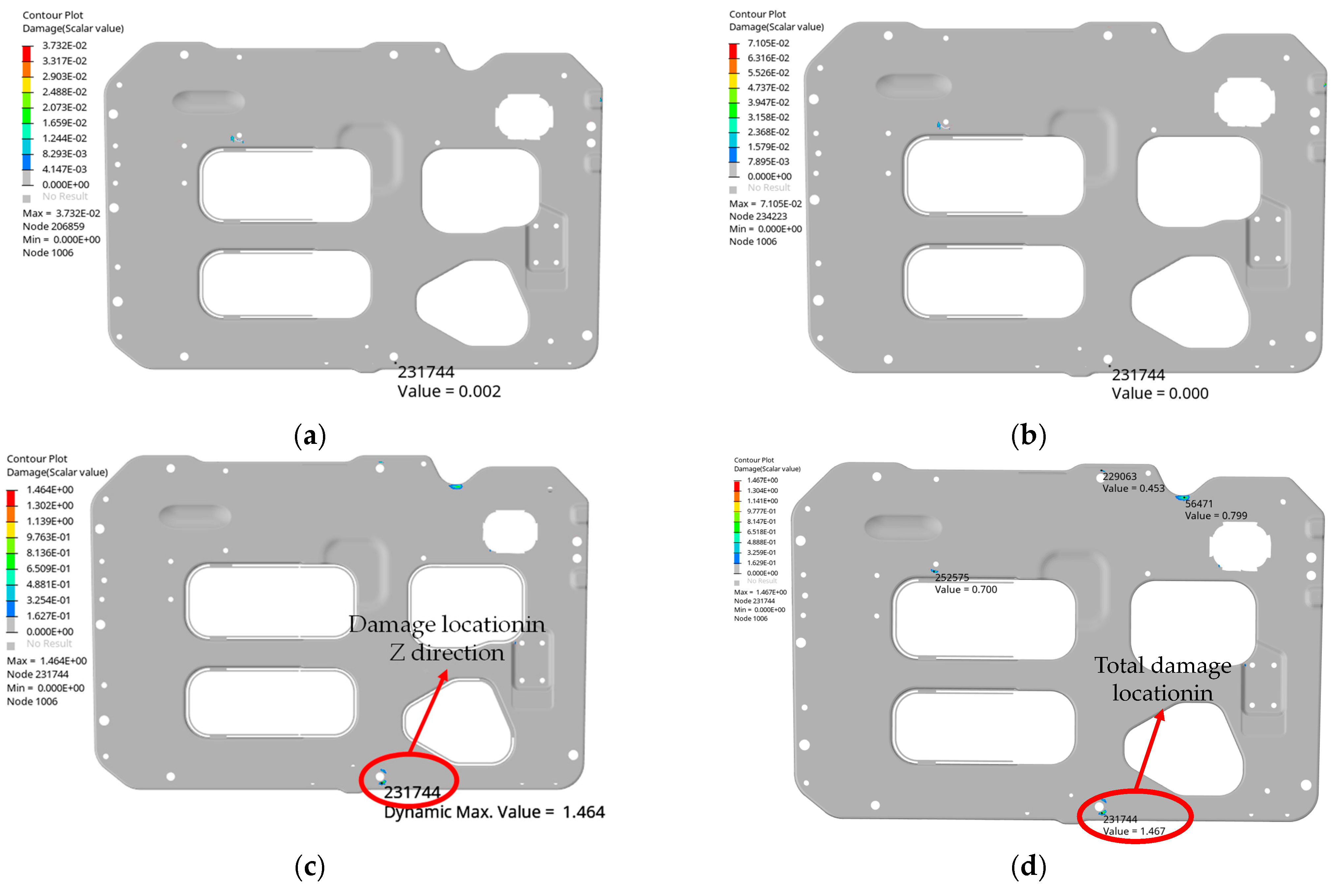
6.1. Frequency Domain Fatigue Analysis
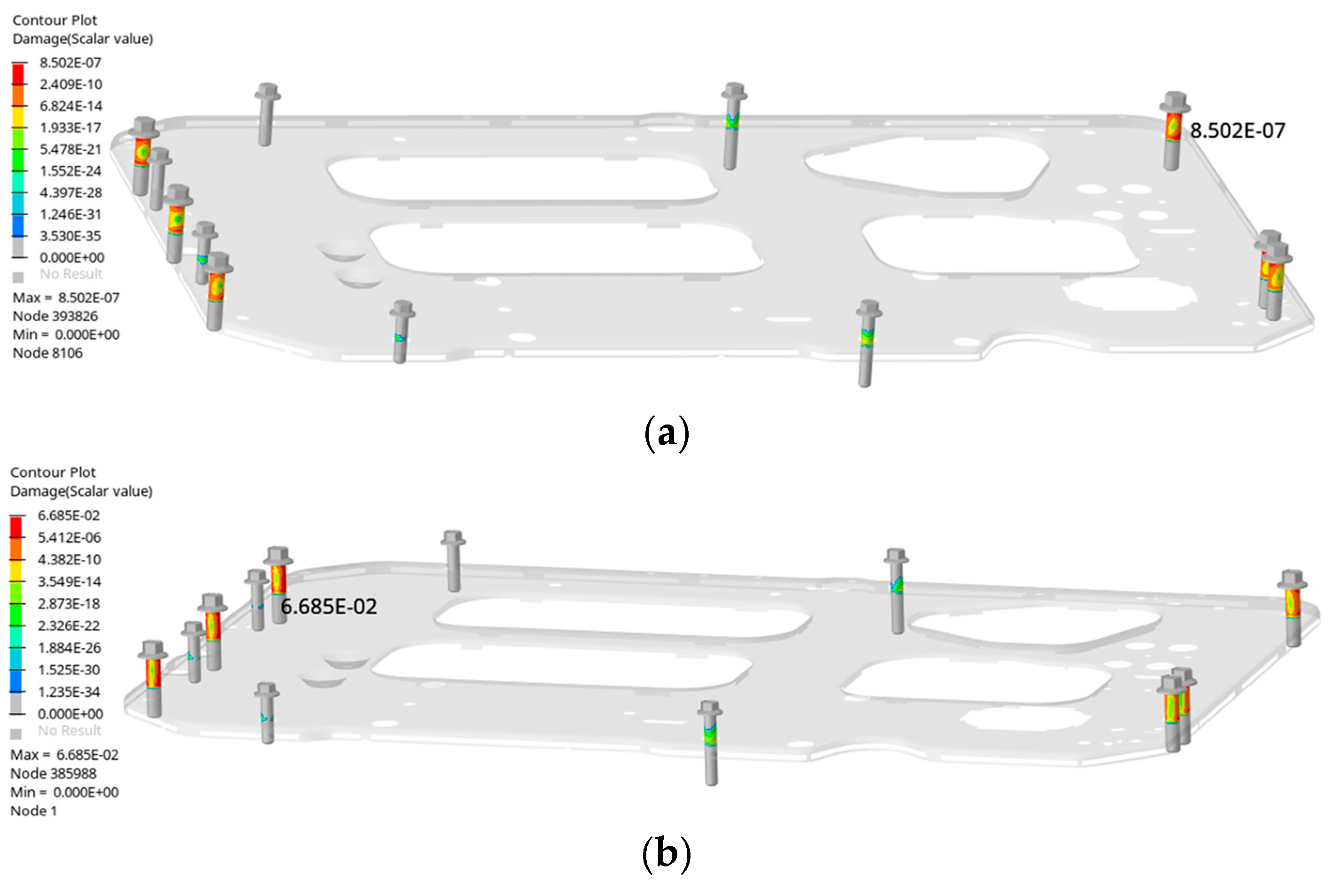
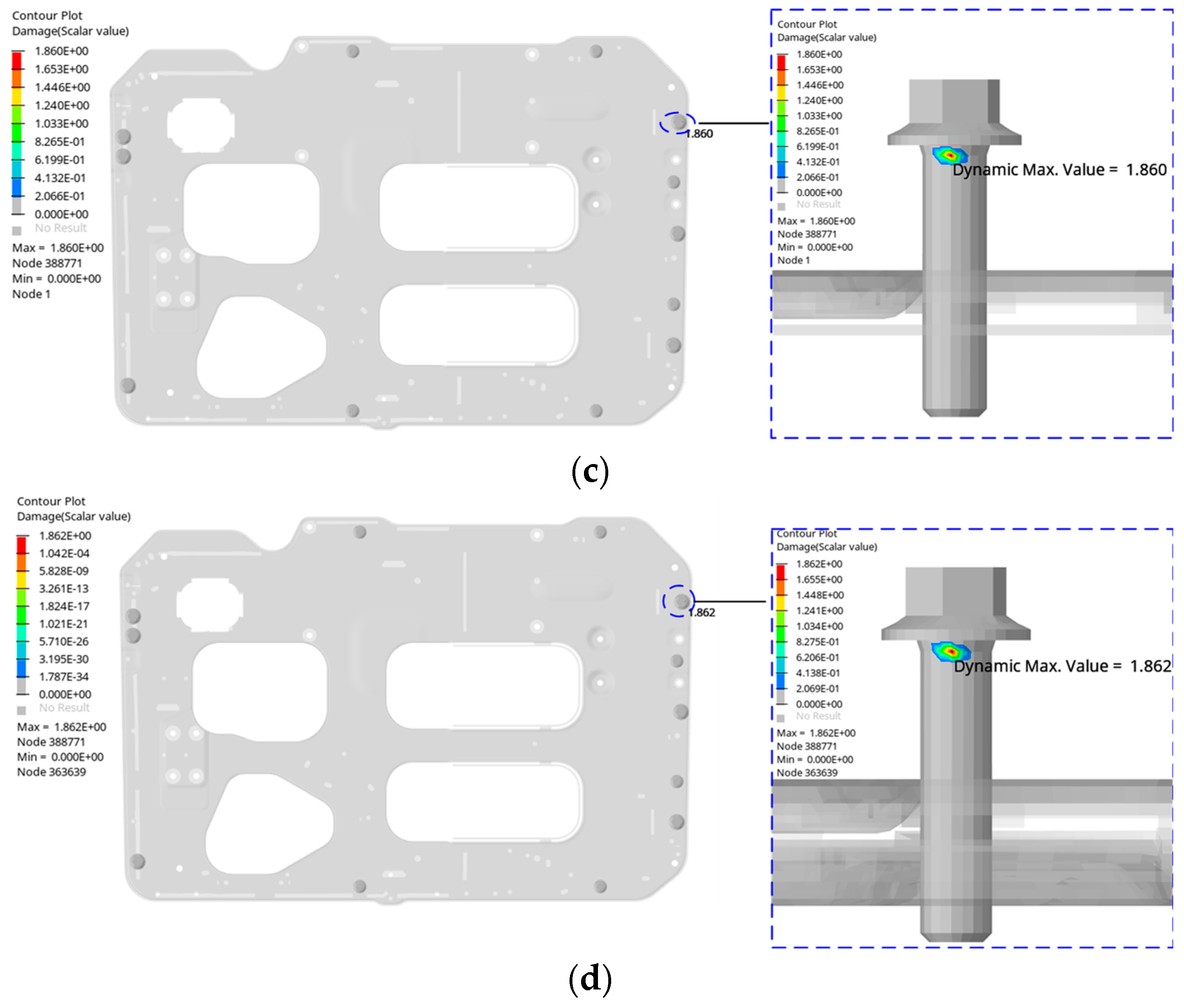
6.2. Bolt Fatigue Life Analysis
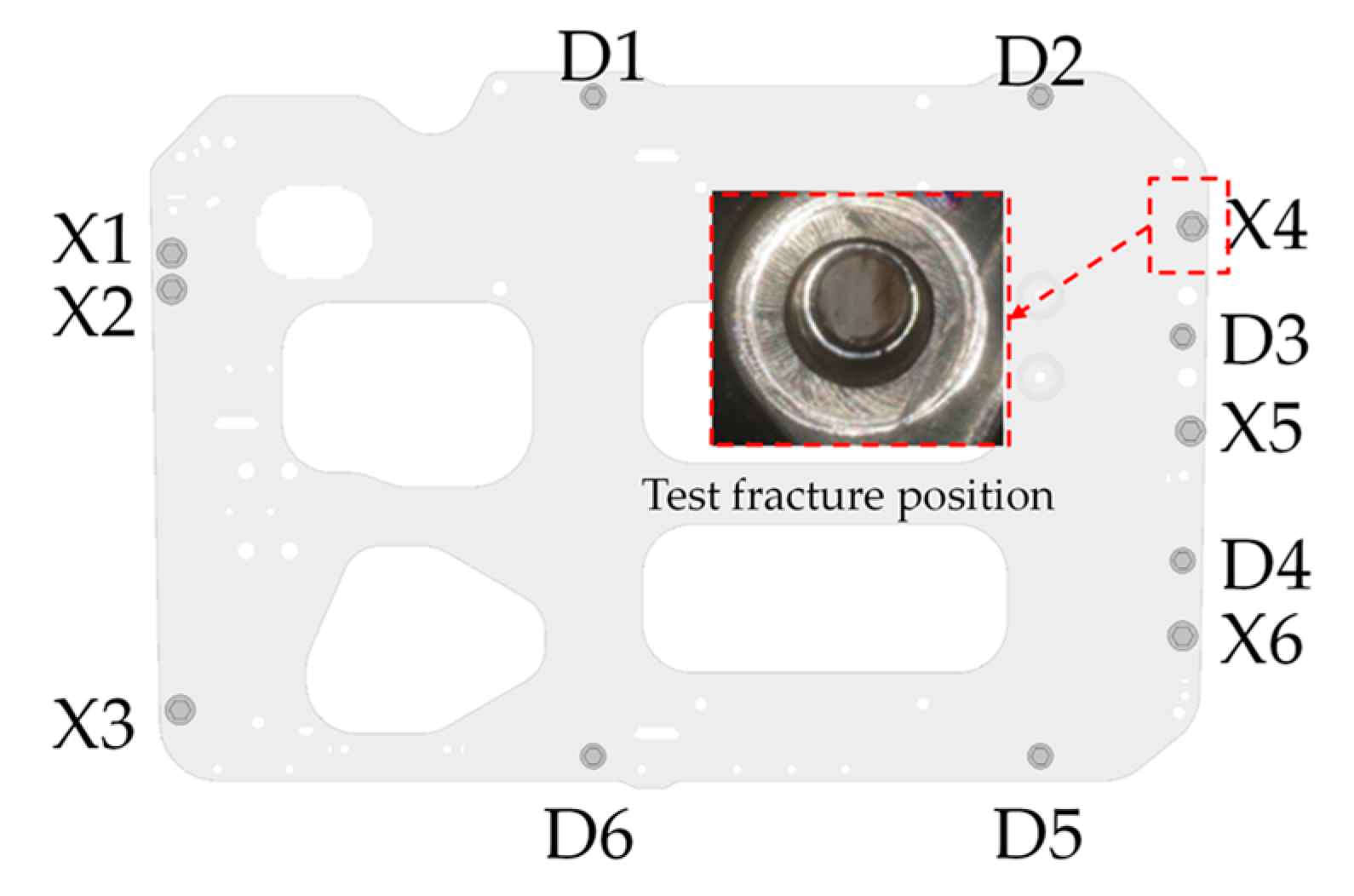
6.3. Comparison of Fatigue Simulation Results with Test Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hasan, M.; Chen, J.; Waldecker, J.R.; Santare, M.H. Predicting fatigue lifetimes of a reinforced membrane in polymer electrolyte membrane fuel cell using plastic energy. J. Power Sources 2022, 539, 231597. [Google Scholar] [CrossRef]
- Kim, H.G.; Kim, G.C.; Ji, W.; Lee, Y.S.; Jang, S.; Shin, C.M. Random vibration fatigue analysis of a multi-material battery pack structure for an electric vehicle. Funct. Compos. Struct. 2021, 3, 025006. [Google Scholar] [CrossRef]
- Chen, J.; Xuan, D.; Wang, B.; Jiang, R. Structure optimization of battery thermal management systems using sensitivity analysis and stud genetic algorithms. Appl. Sci. 2021, 11, 7440. [Google Scholar] [CrossRef]
- Shuai, W.; Li, E.; Wang, H.; Li, Y. Space mapping-assisted optimization of a thin-walled honeycomb structure for battery packaging. Struct. Multidiscip. Optim. 2020, 62, 937–955. [Google Scholar] [CrossRef]
- Shojayian, M.; Sebdani, M.M.; Kjeang, E. Simulation of fuel cell membrane durability under vehicle operation. J. Power Sources 2024, 613, 234855. [Google Scholar] [CrossRef]
- Salunkhe, A.; Kumar, N.G. New Generation Front Axle for EV and FCEV Buses; Technical Paper; SAE International: Warrendale, PA, USA, 2024. [Google Scholar]
- Kim, D.; Sim, K.; Park, J. Experimental study on vibration-induced clamping force reduction in fuel cell structures. Int. J. Hydrog. Energy 2022, 47, 37609–37616. [Google Scholar] [CrossRef]
- Yan, X.; Guo, D.; Wan, X.; Sun, J.; Quan, X.; Wang, Y. A Fatigue Damage Spectrum-Based Approach to Vibration Durability Test for Vehicle Batteries. SAE Int. J. Commer. Veh. 2024, 17, 20. [Google Scholar] [CrossRef]
- Xu, W.; Wang, D. Fatigue and impact analysis and multi-objective optimization design of Mg/Al assembled wheel considering riveting residual stress. Front. Mech. Eng. 2022, 17, 45. [Google Scholar] [CrossRef]
- Dong, S.; Lv, J.; Wang, K.; Li, W.; Tian, Y. Design and optimization for a new locomotive power battery box. Sustainability 2022, 14, 12810. [Google Scholar] [CrossRef]
- Zhu, G.; He, L.; Jia, X.; Tan, Z.; Qin, Q. Experimental Study on Vibration and Noise Reduction of Gear Transmission System Based on ISFD. Machines 2024, 12, 531. [Google Scholar] [CrossRef]
- Sahu, A.K.; Haddad, R.Z.; Al-Ani, D.; Bilgin, B. Thermomechanical Rotor Fatigue of an Interior Permanent Magnet Synchronous Motor. Machines 2024, 12, 158. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, G.; Wang, H.; Peng, C.; Liu, X.; Xiao, H.; Liang, X. Experimental Fatigue Evaluation of Bogie Frames on Metro Trains. Machines 2022, 10, 1003. [Google Scholar] [CrossRef]
- Pan, L.; Guan, X.; Luan, X.; Huang, Y.; Zhang, R.; Choi, J.-H.; Zhu, X. Fatigue Analysis of Dozer Push Arms under Tilt Bulldozing Conditions. Machines 2022, 10, 38. [Google Scholar] [CrossRef]
- Lu, H.; Wang, J.; Lian, Y.; Wen, Z.; Liu, T.; Yue, Z. Random vibration fatigue behavior of directionally solidified superalloy: Experiments and evaluation of life prediction methods. Int. J. Fatigue 2023, 175, 107746. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, B.; Zhang, G.; Liu, W.; Li, F.; Yin, Y. Improvement and lightweight design of power battery bracket based on random vibration fatigue analysis. Comput. Aided Eng. 2023, 32, 11–15. [Google Scholar]
- Wang, S.; Wu, C.; Sun, B.; Wang, H.; Ding, X.; Yu, H.; Ni, W.; Xiong, M.; Zhang, H. Data-based deep learning for random vibration fatigue life prediction of car seat frame. Nonlinear Dyn. 2024, 1–25. [Google Scholar] [CrossRef]
- Zhang, C.; Wan, R.; He, J.; Yu, J.; Zhao, Y. Non-stationary vibration fatigue life prediction of automotive components based on long short-term memory network. Int. J. Fatigue 2024, 187, 108459. [Google Scholar] [CrossRef]
- Zhang, X.; Xiong, Y.; Pan, Y.; Du, H.; Liu, B. Crushing stress and vibration fatigue-life optimization of a battery-pack system. Struct. Multidiscip. Optim. 2023, 66, 48. [Google Scholar] [CrossRef]
- Czerlunczakiewicz, E.; Majerczak, M.; Bonato, M. Fatigue Simulations for Automotive Components undergoing Vibration Loadings: Effect of nonlinear behavior. Procedia Struct. Integr. 2024, 57, 743–753. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar] [CrossRef]
- Osgood, C.C. Fatigue Design: International Series on the Strength and Fracture of Materials and Structures; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Parhi, K.K.; Ayinala, M. Low-Complexity Welch Power Spectral Density Computation. In IEEE Transactions on Circuits and Systems I: Regular Papers; IEEE: Piscataway, NJ, USA, 2014; Volume 61, pp. 172–182. [Google Scholar]
- Dirlik, T.; Benasciutti, D. Dirlik and Tovo-Benasciutti Spectral Methods in Vibration Fatigue: A Review with a Historical Perspective. Metals 2021, 11, 1333. [Google Scholar] [CrossRef]
- GB/T 2423.43-2008; Environmental Testing for Electric and Electronic Products-Part 2:Test Methods-Mounting of Specimens for Vibration, Impact and Similar Dynamic Tests. China Standards Press: Beijing, China, 2008.
- Tripathi, P.K.; Kumar, N. Fatigue damage spectrum-based assessment of vibration standards on battery pack for EV’s using stress as a response metric. In Proceedings of the 2019 IEEE Transportation Electrification Conference (ITEC-India), Bengaluru, India, 17–19 December 2019; pp. 1–6. [Google Scholar]
- Li, Y.; Lu, P.; Liu, C.; Ren, W.; Wen, J. Fatigue Life of a Comb Plate Expansion Joint. Machines 2023, 11, 494. [Google Scholar] [CrossRef]




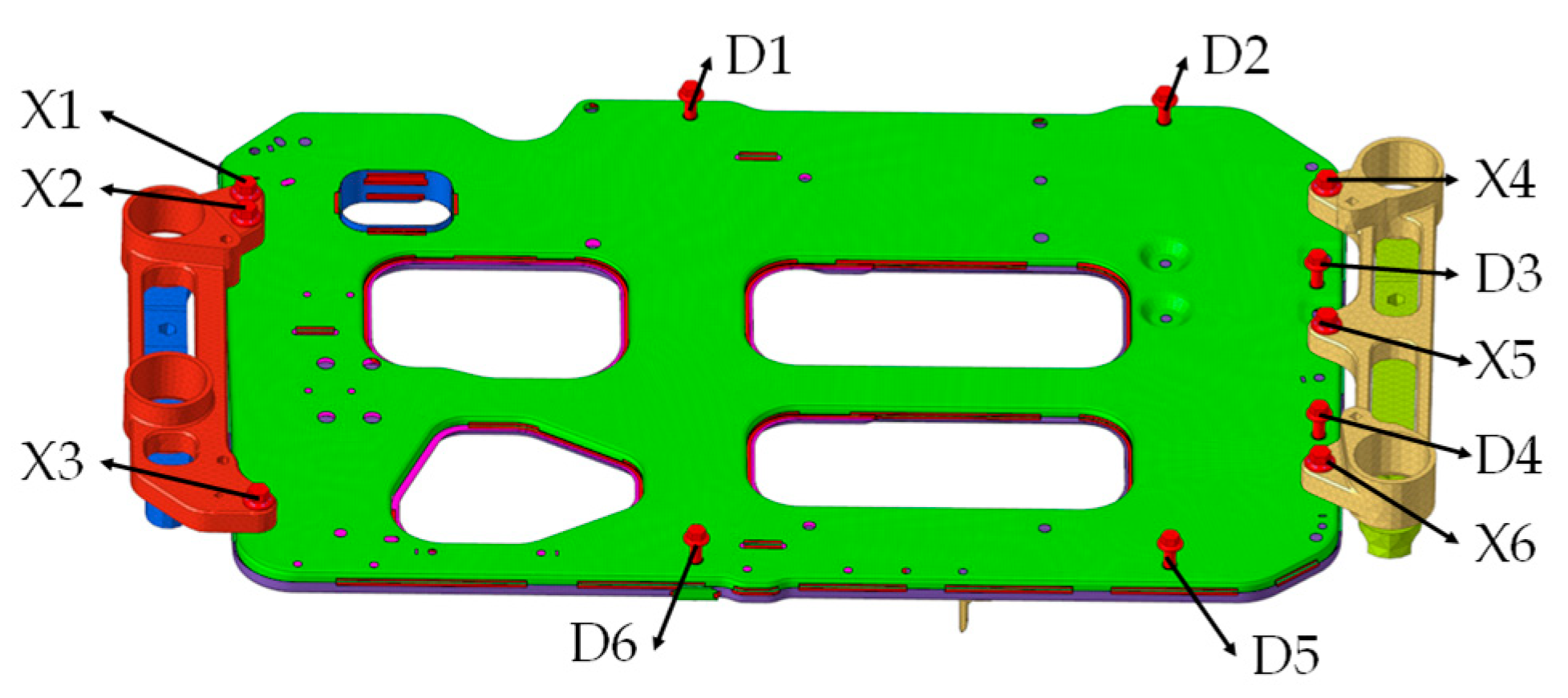
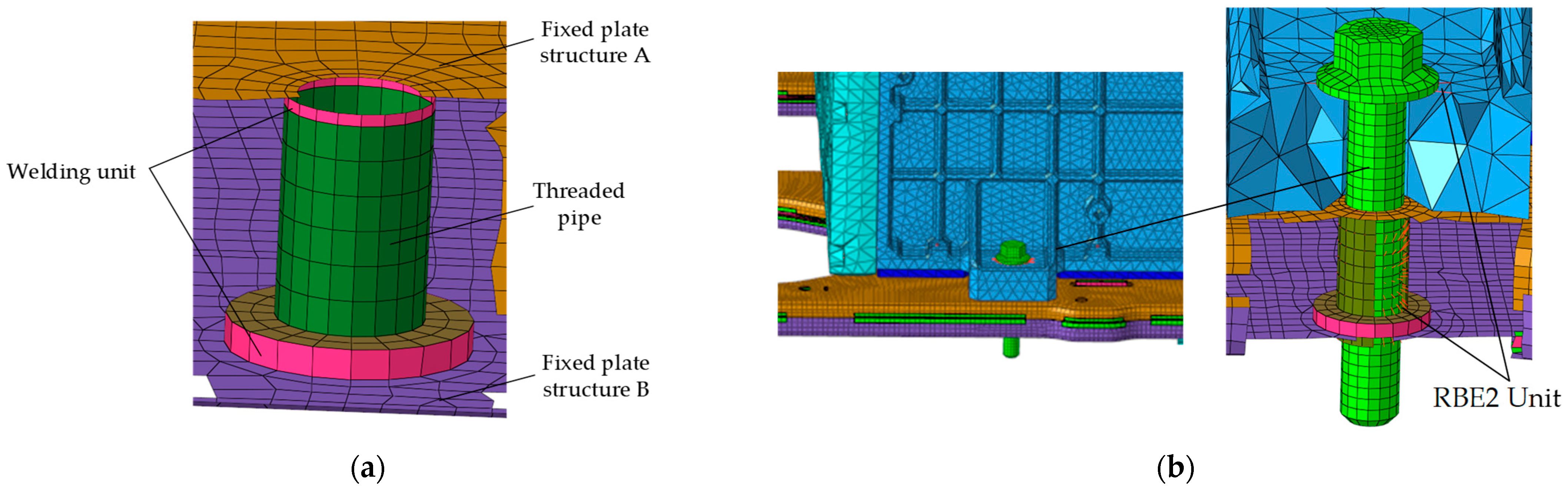
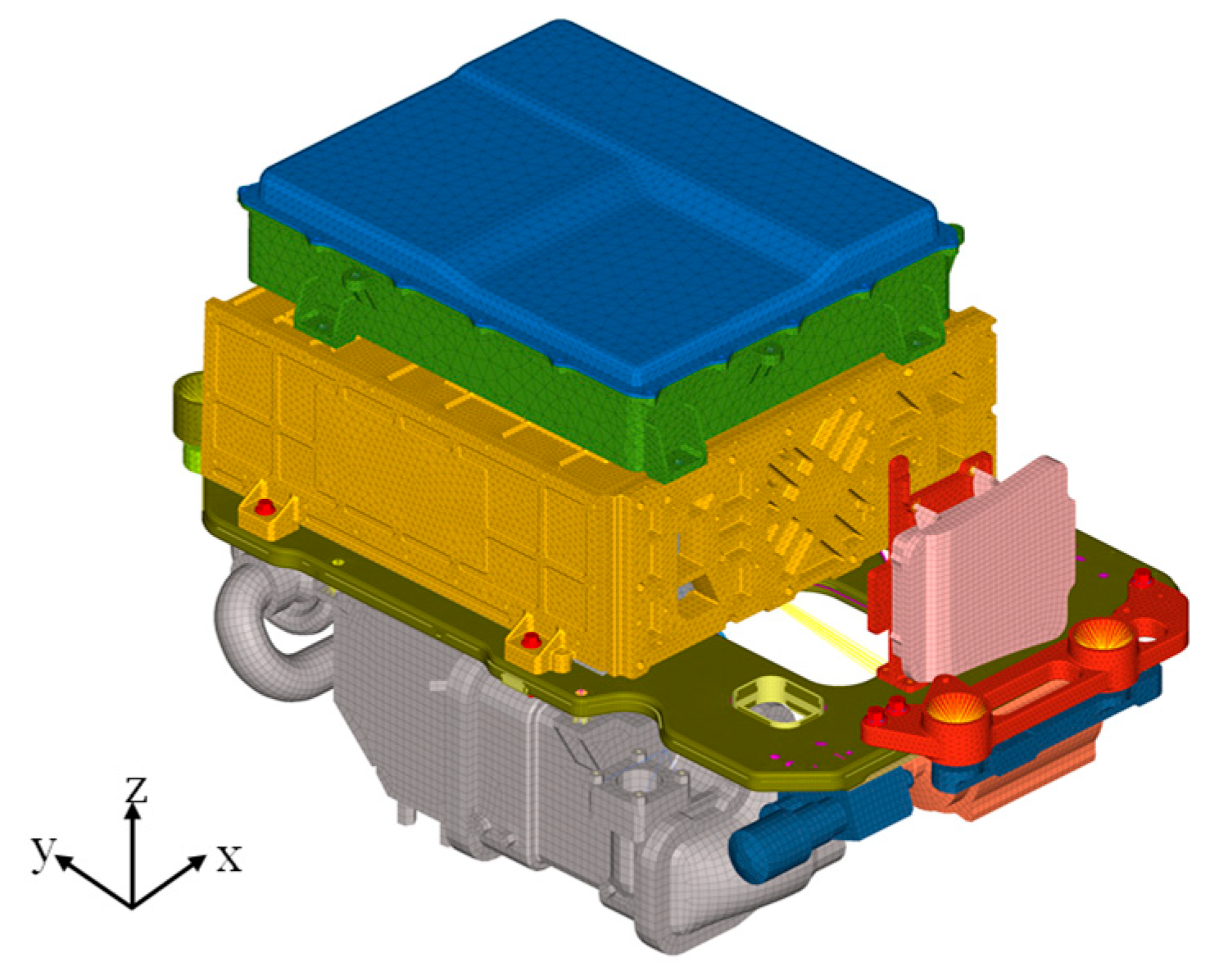
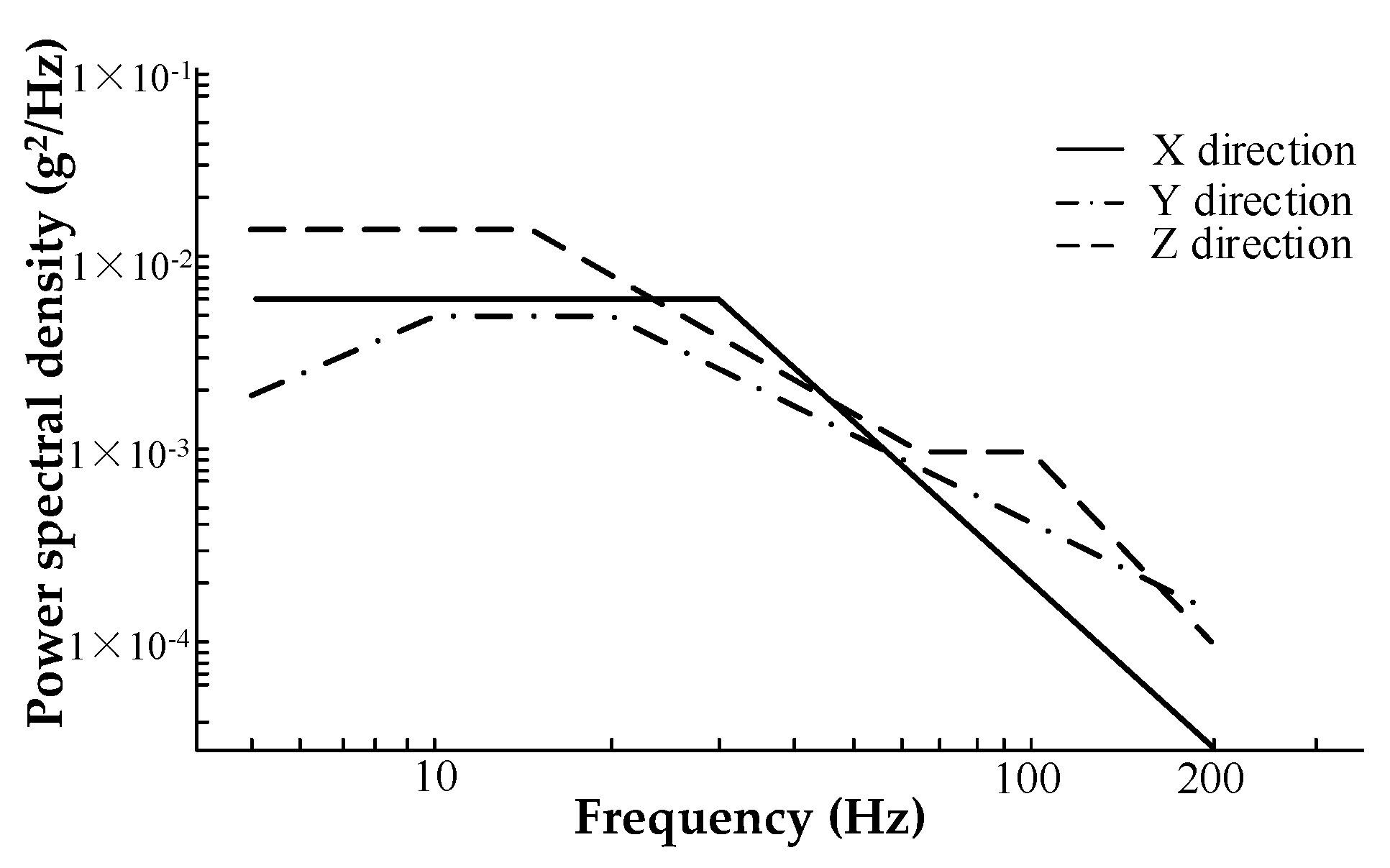








| Fuel Cell System | Number | Parts Name | Material | Mass (kg) |
|---|---|---|---|---|
| DC/DC converter assembly | 3 | DC Converter | Al | 25 |
| Battery stack assembly | 4 | Battery stack module assembly | 6061-T6 | 42.3 |
| Cooling module assembly | 1 | Heater | ADC12 | 2.7 |
| 2 | Heater bracket | 6061-T6 | 0.438 | |
| 14 | Water Pump | ADC12 | 25.6 | |
| System suspension assembly | 16 | Left suspension bracket | 45 steel | 5.06 |
| 6 | Right suspension bracket | 45 steel | 5.825 | |
| System fixing plate assembly | 5 | Support plate | 510L | 27 |
| Electrical module assembly | 15 | sensor | 6061-T6 | 0.5 |
| Air module assembly | 7 | Air compressor | ADC12 | 22 |
| 8 | Intercooler | 6061-T6 | 14.5 | |
| 9 | Diverter valve | 45 steel | 1.3 | |
| 10 | Air line | 6061-T6 | 0.343 | |
| 11 | Back pressure valve | 45 steel | 1.29 | |
| 12 | Humidifier | 6061-T6 | 15.43 | |
| 13 | Stop valve | 45 steel | 1.3 |
| Material | Young Modulus (MPa) | Density (kg/cm3) | Poisson Coefficient |
|---|---|---|---|
| Al | 70,000 | 2.7 × 10−3 | 0.3 |
| 6061-T6 | 72,000 | 2.7 × 10−3 | 0.3 |
| ADC12 | 70,000 | 2.7 × 10−3 | 0.3 |
| 45 steel | 210,000 | 7.1 × 10−3 | 0.3 |
| 510L | 210,000 | 7.85 × 10−3 | 0.3 |
| Seam | 210,000 | 7.85 × 10−3 | 0.3 |
| Order | 3 mm | 5 mm | 8 mm |
|---|---|---|---|
| 1 | 16.14 | 16.13 | 16.1 |
| 2 | 27.11 | 27.11 | 27.06 |
| 3 | 30.39 | 30.39 | 30.36 |
| 4 | 38.34 | 38.33 | 38.4 |
| 5 | 46.33 | 46.38 | 45.35 |
| 6 | 49.1 | 49.02 | 48.54 |
| Dimensional Parameters (mm) | x-Direction | y-Direction | z-Direction | Thickness |
|---|---|---|---|---|
| Value | 596 | 880 | 21 | 2 |
| Element Dimension | Element Type | Number of Element |
|---|---|---|
| 0D | RBE2 | 731 |
| COMN2 | 36,666 | |
| 1D | PBUSH | 4 |
| 2D | CQUAD | 160,714 |
| CTRIA | 4174 | |
| 3D | CHEXA | 22,096 |
| TETRA4 | 358,099 |
| Measuring Point | Stress Direction | Layer | Measured RMS Stress (MPa) | Simulation (MPa) | Error |
|---|---|---|---|---|---|
| P1 | Y | Board A | 17.9 | 19 | 6.13% |
| P2 | Y | Board A | 27.4 | 26.5 | −3.30% |
| P3 | Y | Board A | 27.9 | 25.8 | −7.53% |
| P4 | Y | Board B | 56.2 | 59.7 | 6.20% |
| P5 | Y | Board B | 26.7 | 26.5 | −0.70% |
| P6 | Y | Board B | 41.6 | 37.9 | −8.89% |
| P7 | Y | Board B | 39.4 | 37.5 | −4.87% |
| P8 | X | Board B | 4.1 | 3.9 | −4.90% |
| P9 | Y | Board B | 22.5 | 22.4 | −0.40% |
| Material Properties | Material | Young’s Modulus (GPa) | Tensile Strength (MPa) | Yield Strength (MPa) |
|---|---|---|---|---|
| Parameter | Alloy steel | 2.1 | 1050 | 625 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wang, M.; Guo, P.; Gao, D.; Gao, Y. Numerical and Experimental-Based Framework for Fuel Cell System Fatigue Analysis in Frequency Domain. Machines 2025, 13, 18. https://doi.org/10.3390/machines13010018
Liu Z, Wang M, Guo P, Gao D, Gao Y. Numerical and Experimental-Based Framework for Fuel Cell System Fatigue Analysis in Frequency Domain. Machines. 2025; 13(1):18. https://doi.org/10.3390/machines13010018
Chicago/Turabian StyleLiu, Zhe, Mingjie Wang, Pengbo Guo, Dawei Gao, and Yunkai Gao. 2025. "Numerical and Experimental-Based Framework for Fuel Cell System Fatigue Analysis in Frequency Domain" Machines 13, no. 1: 18. https://doi.org/10.3390/machines13010018
APA StyleLiu, Z., Wang, M., Guo, P., Gao, D., & Gao, Y. (2025). Numerical and Experimental-Based Framework for Fuel Cell System Fatigue Analysis in Frequency Domain. Machines, 13(1), 18. https://doi.org/10.3390/machines13010018





