Numerical Investigation and Experimental Verification of Vibration Behavior for a Beam with Cantilever-Hertzian Contact Boundary Conditions
Abstract
:1. Introduction
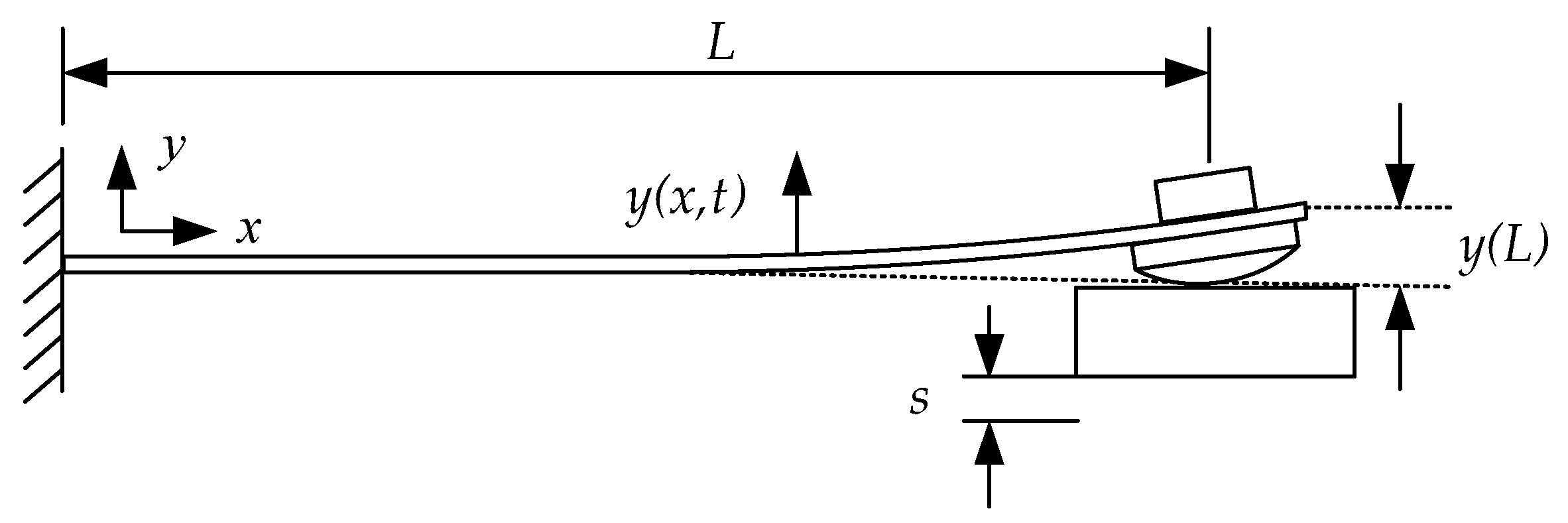
2. Theoretical Background
2.1. Governing Equations for Modal Analysis
2.2. Harmonic Response for Forced Vibration in Time Domain
2.3. Harmonic Response for Forced Vibration in Frequency Domain
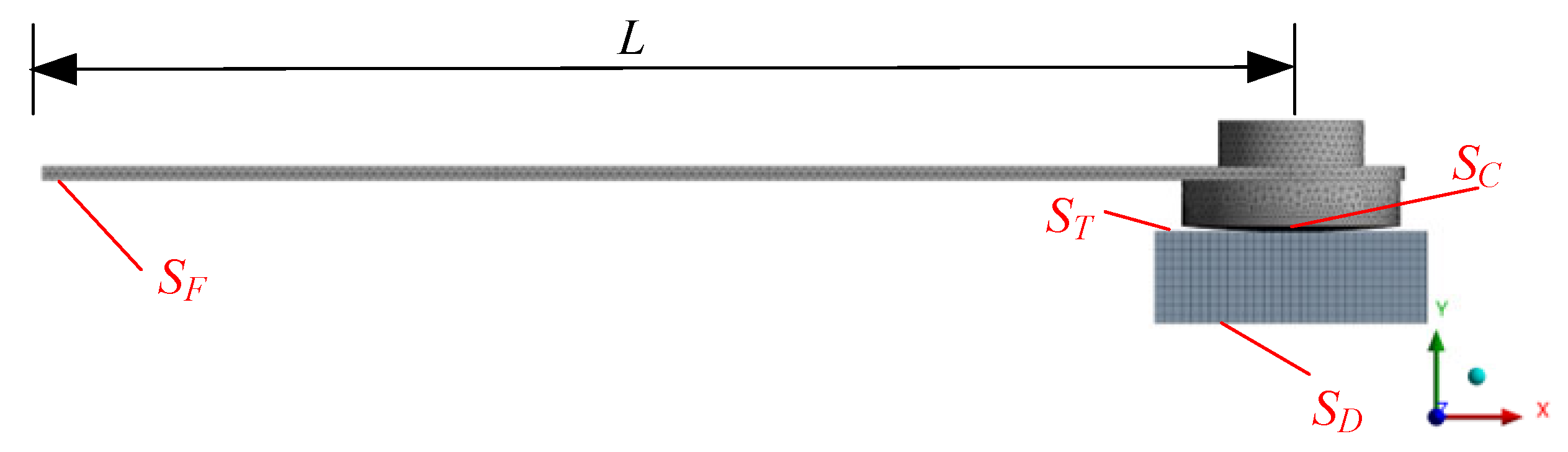
3. Finite Element Simulation Method
3.1. Modal Simulation with Prestressed Condition
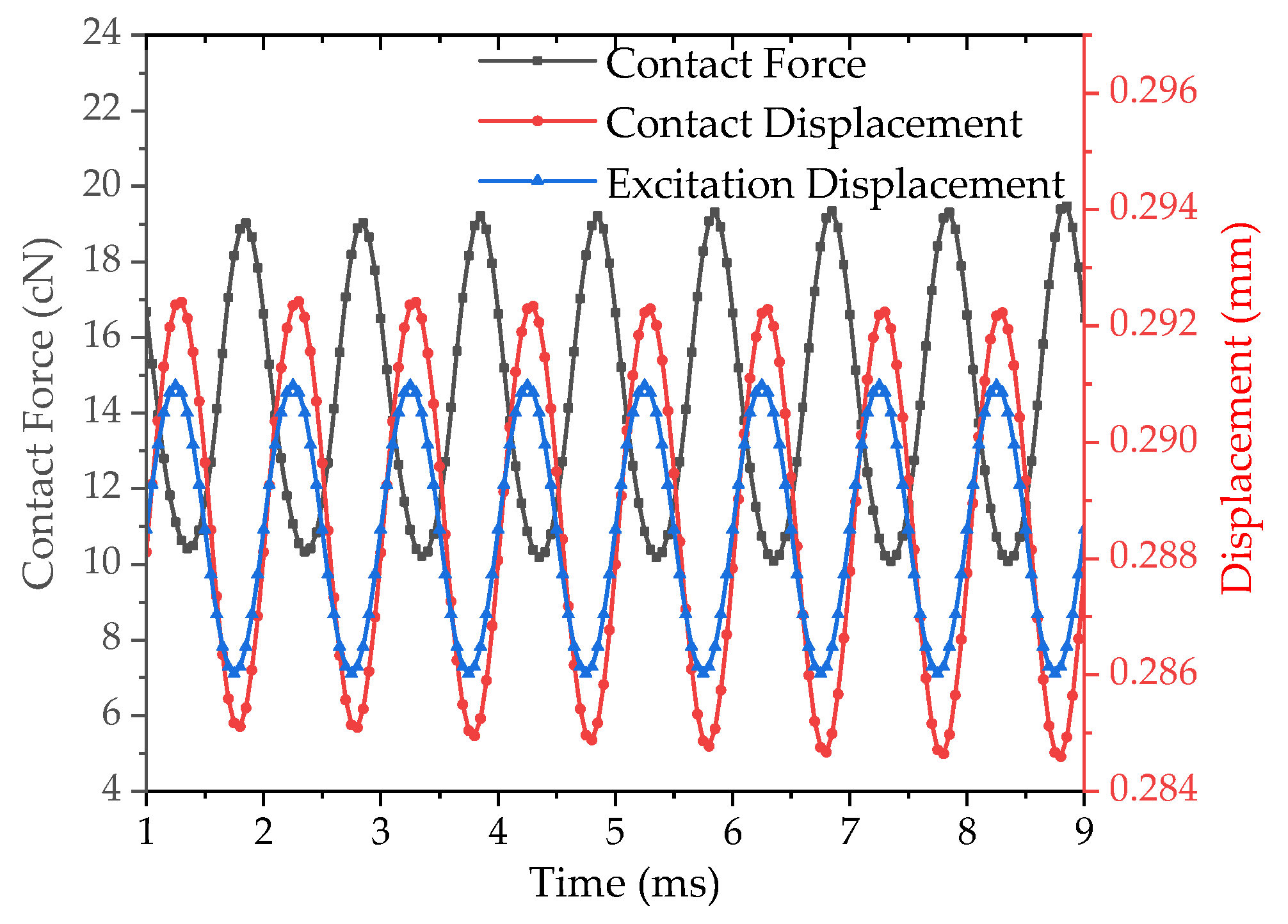
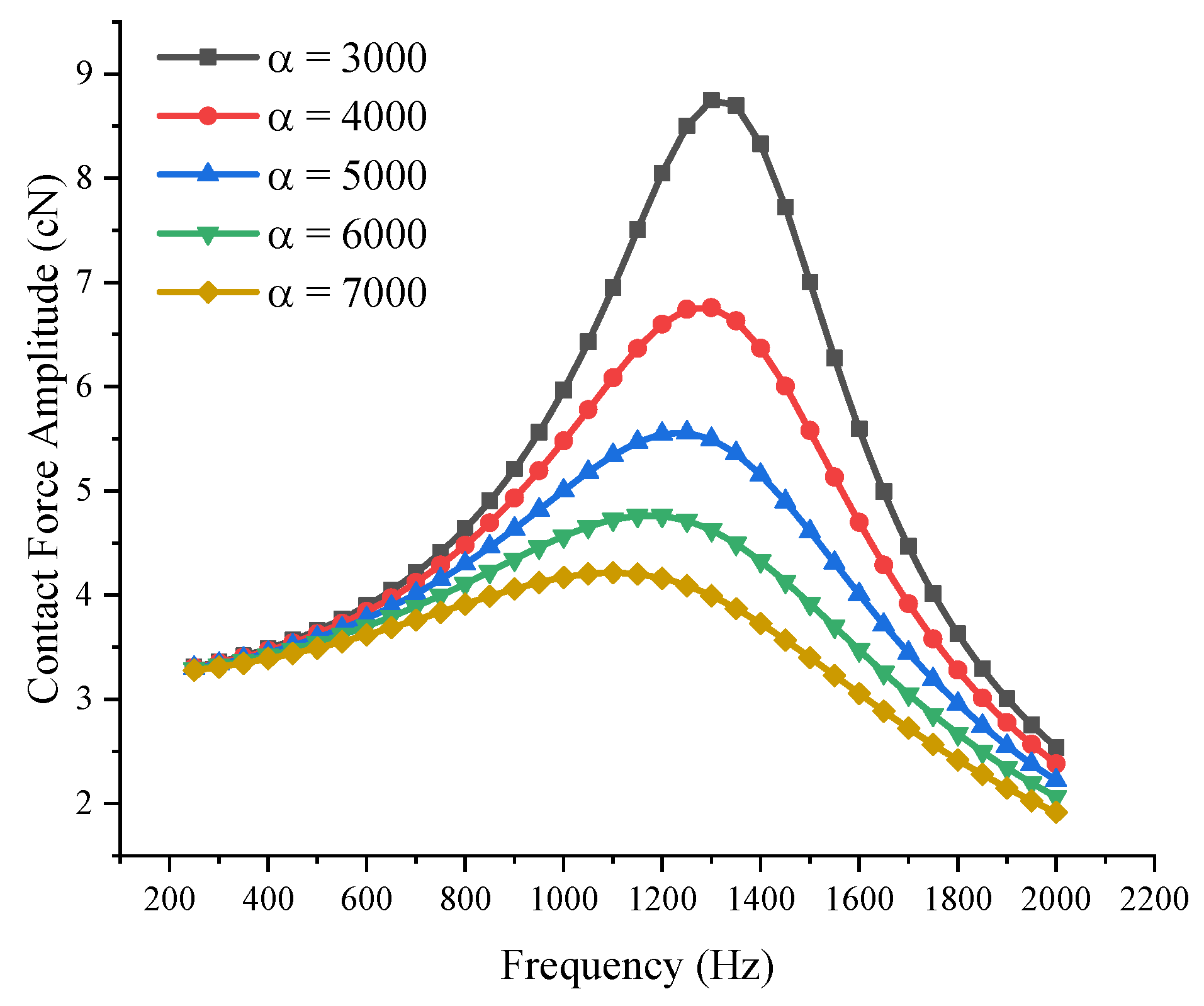
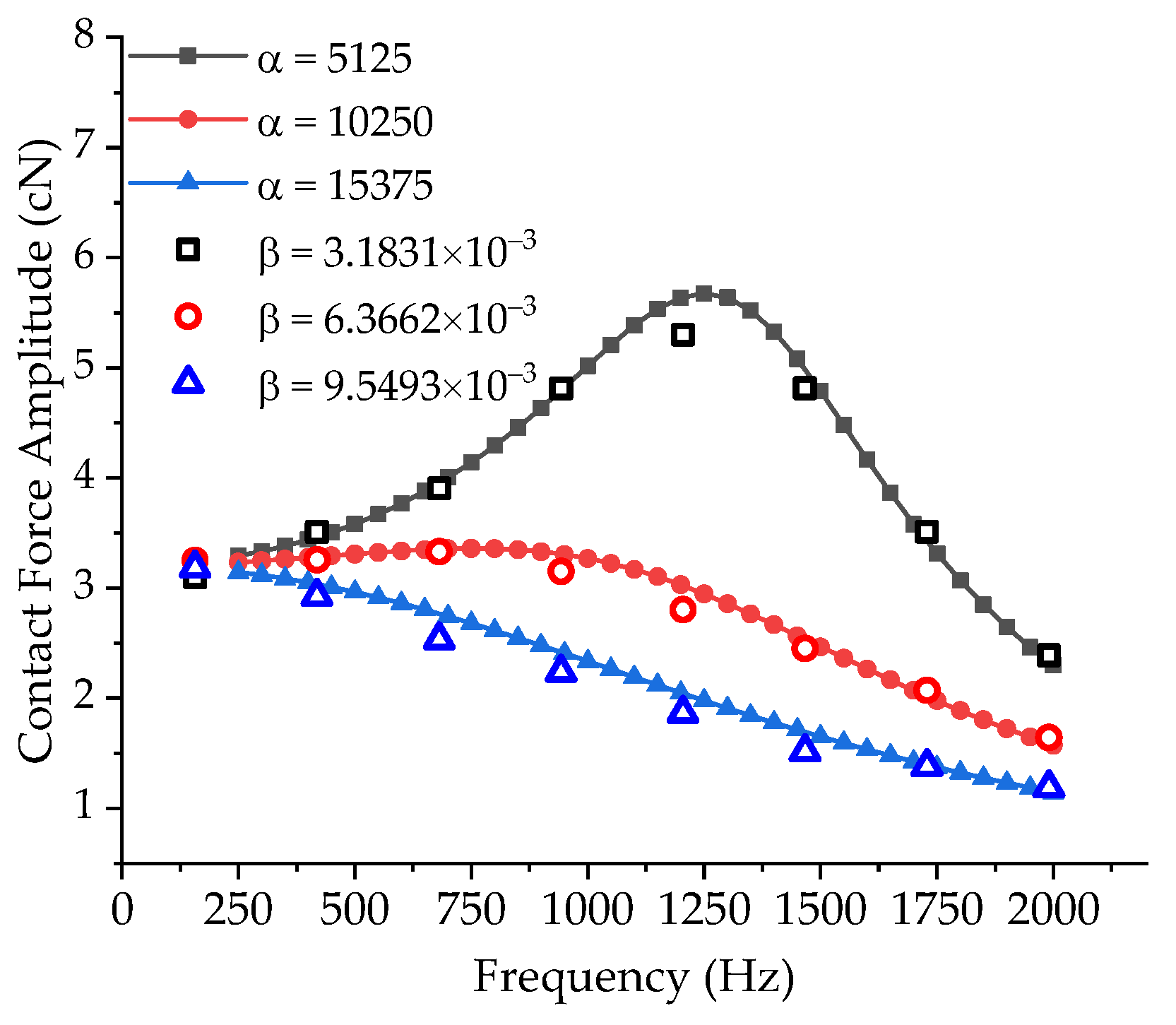
3.2. Harmonic Response Simulation
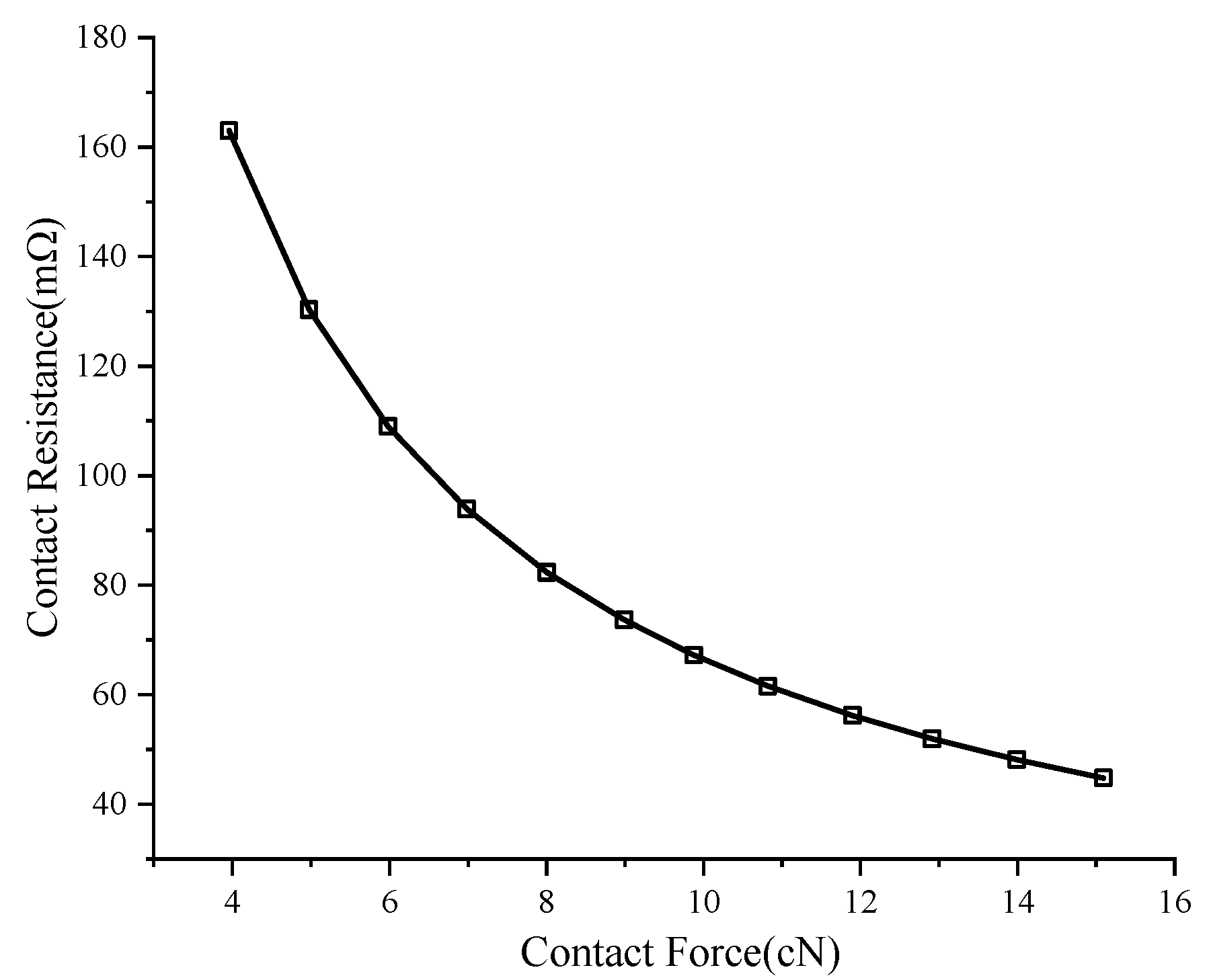
3.3. Contact Resistance Simulation
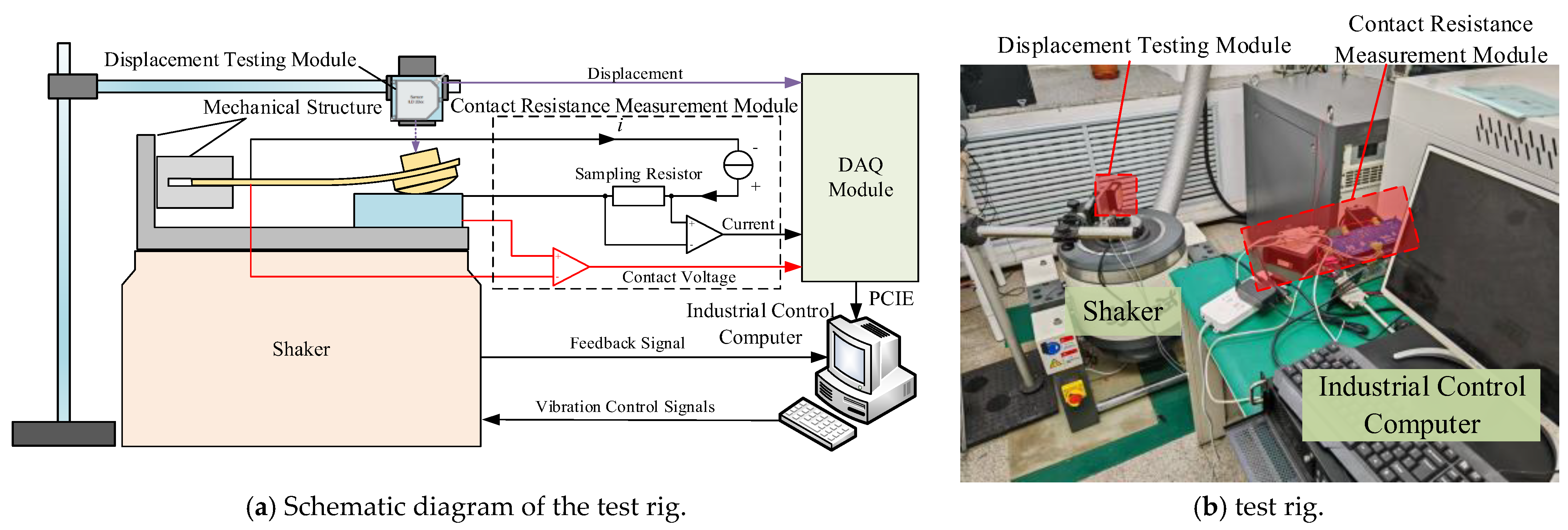
4. Experiments
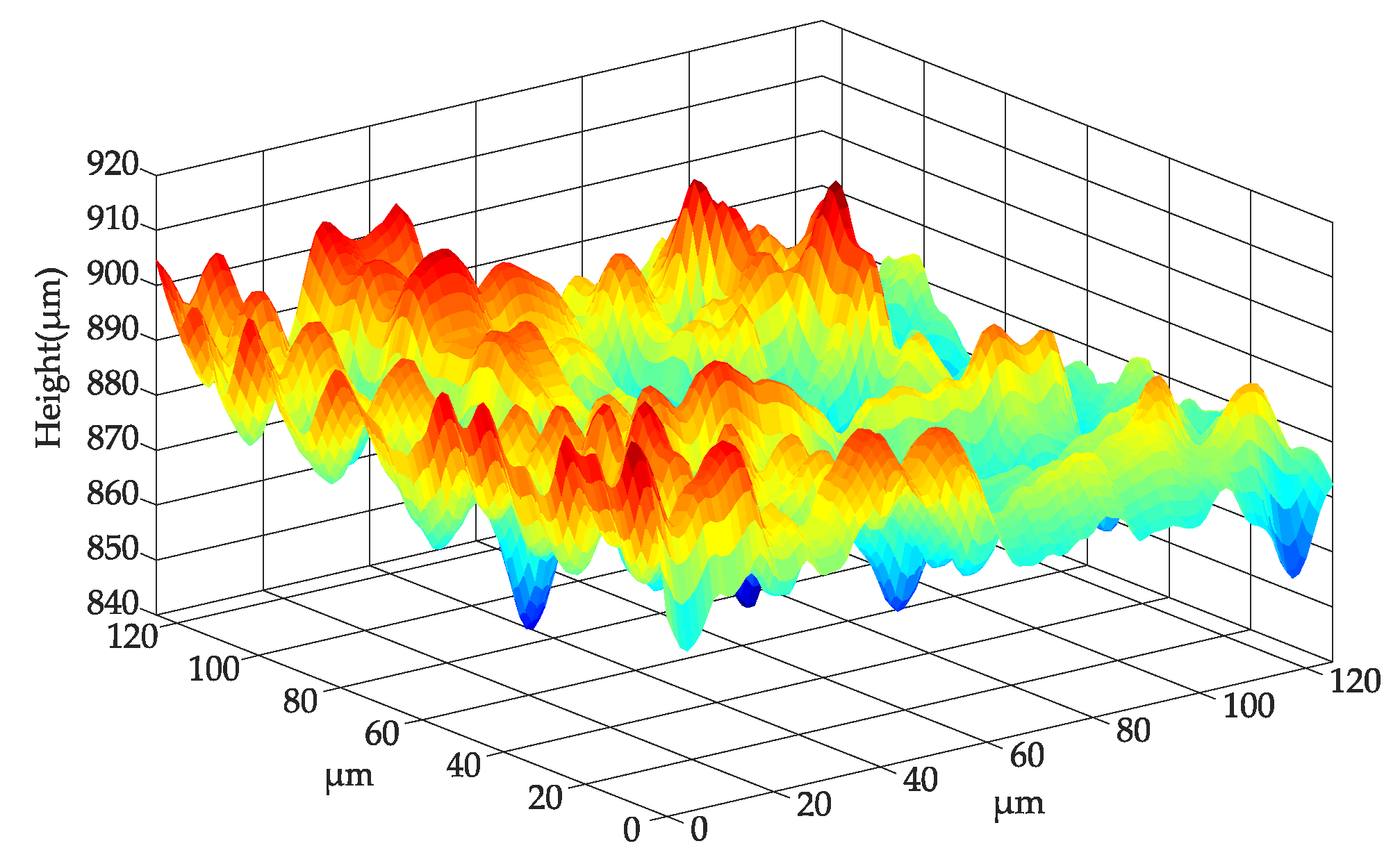
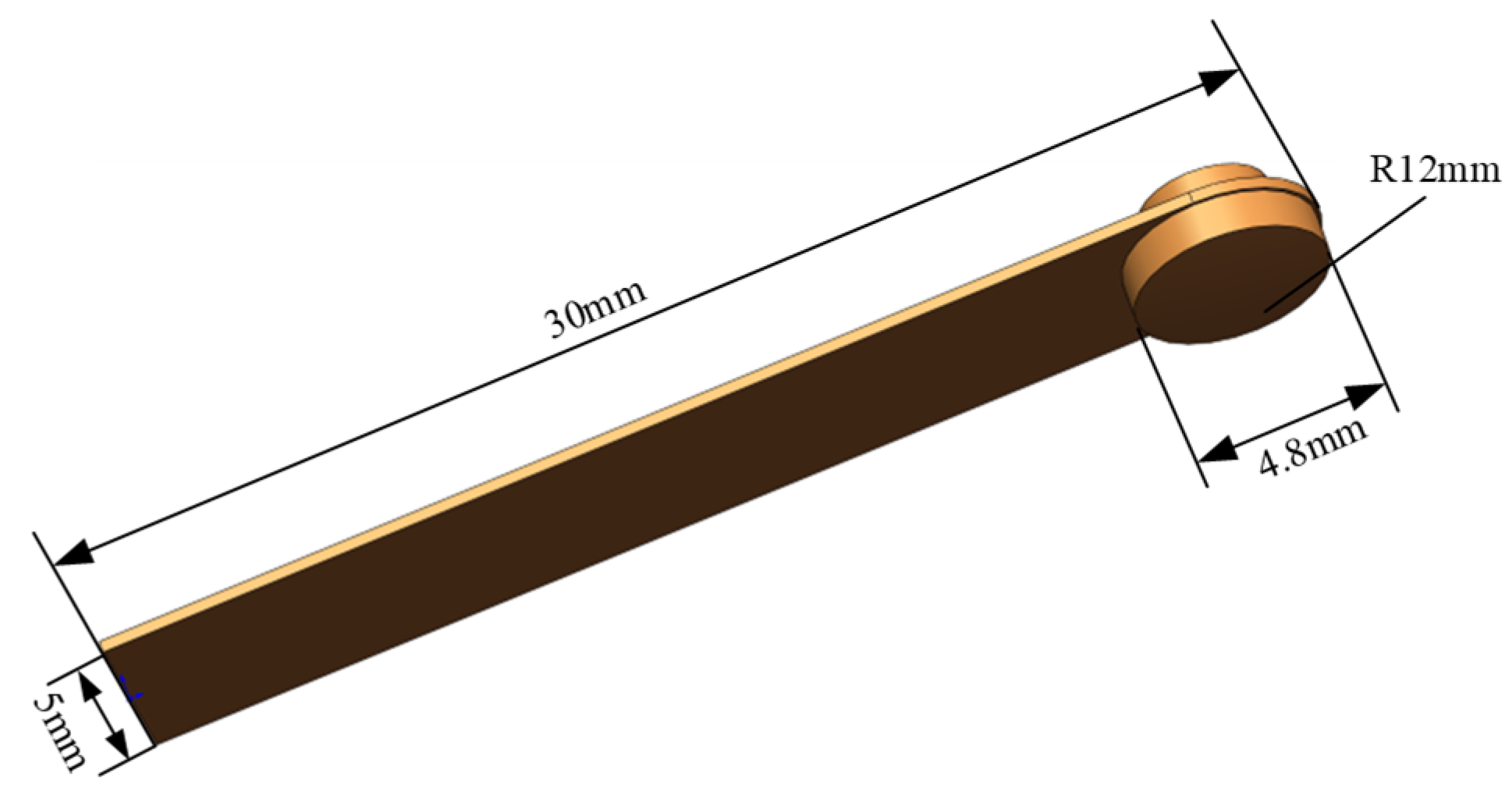
4.1. Experimental Details
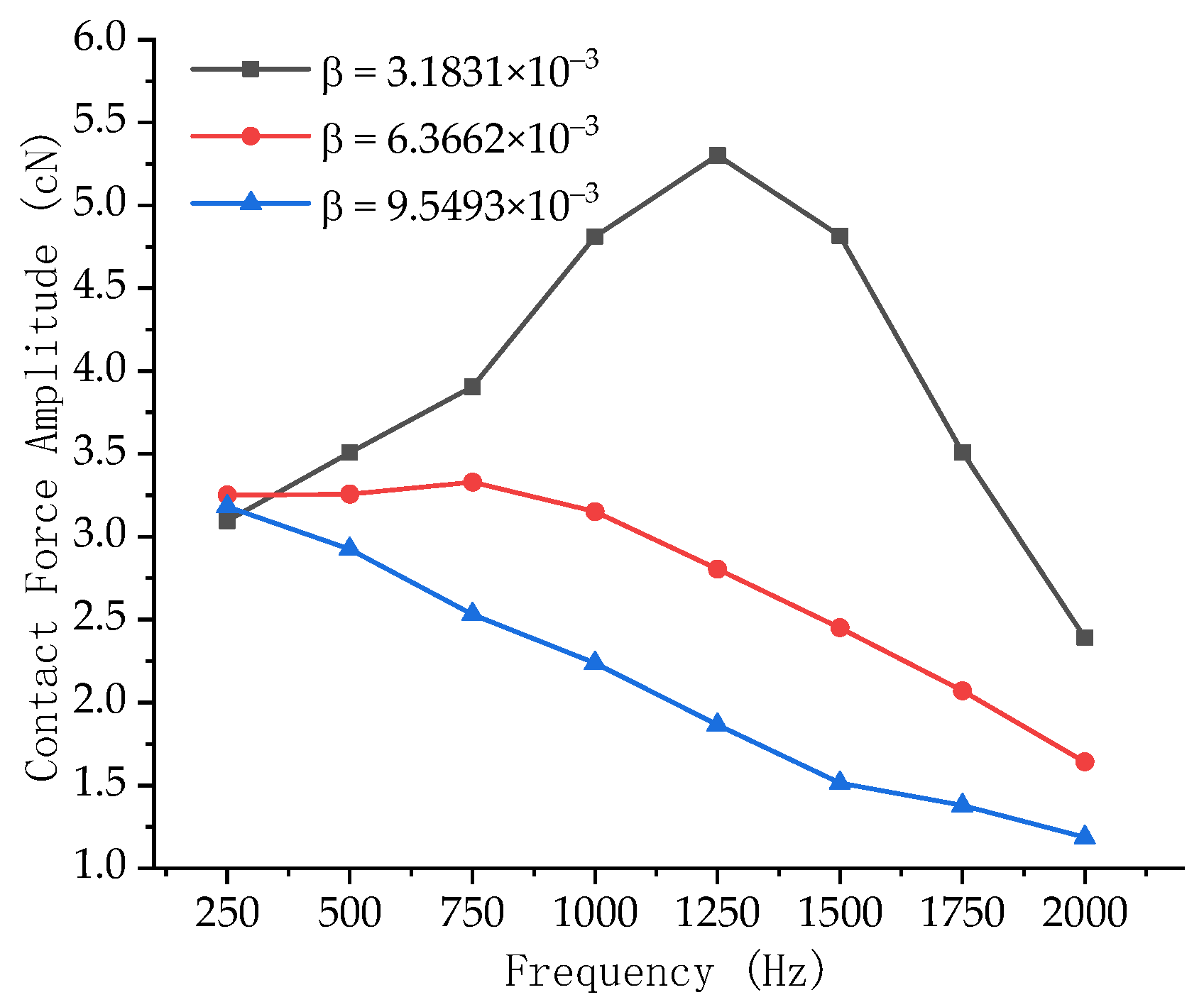
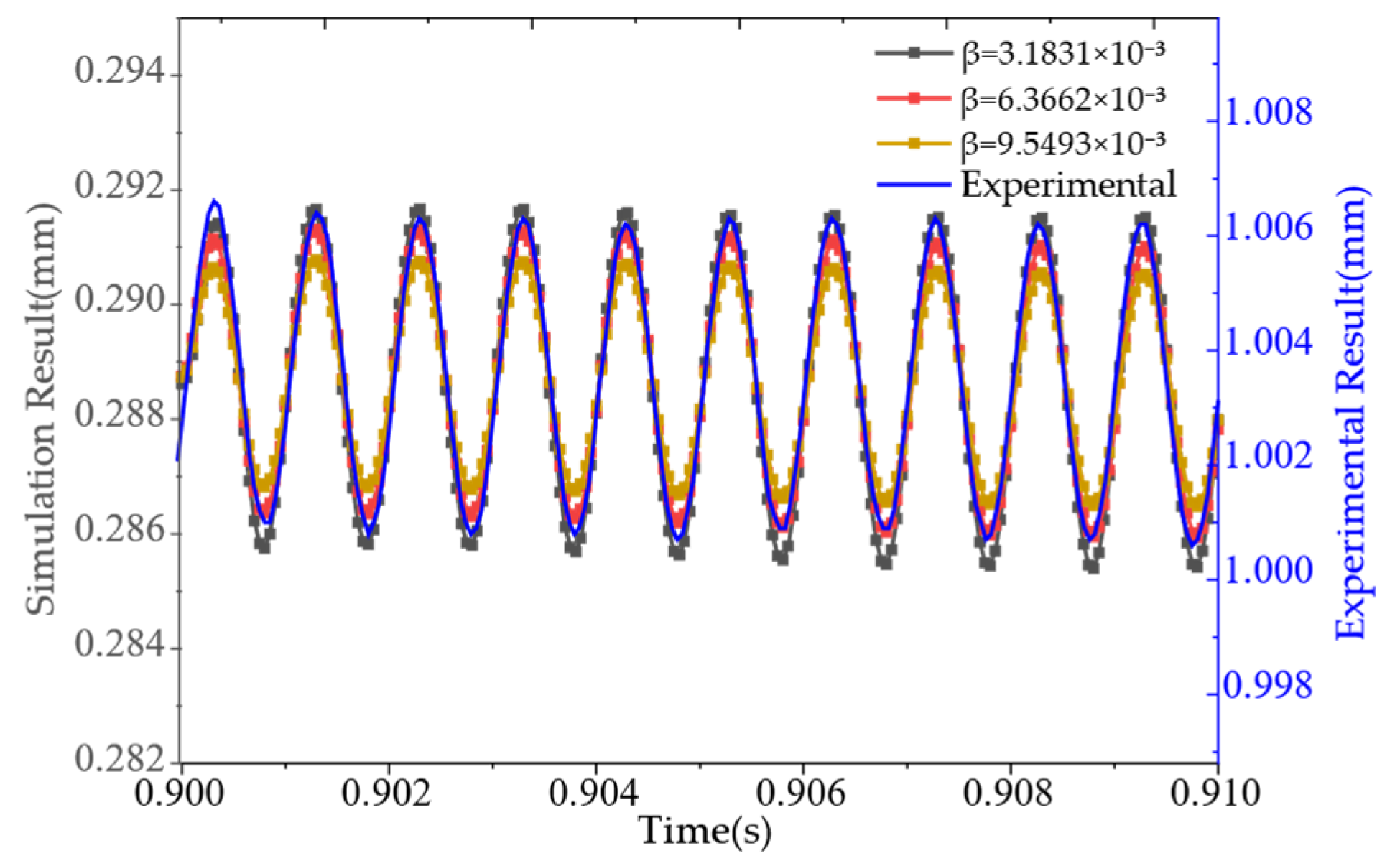
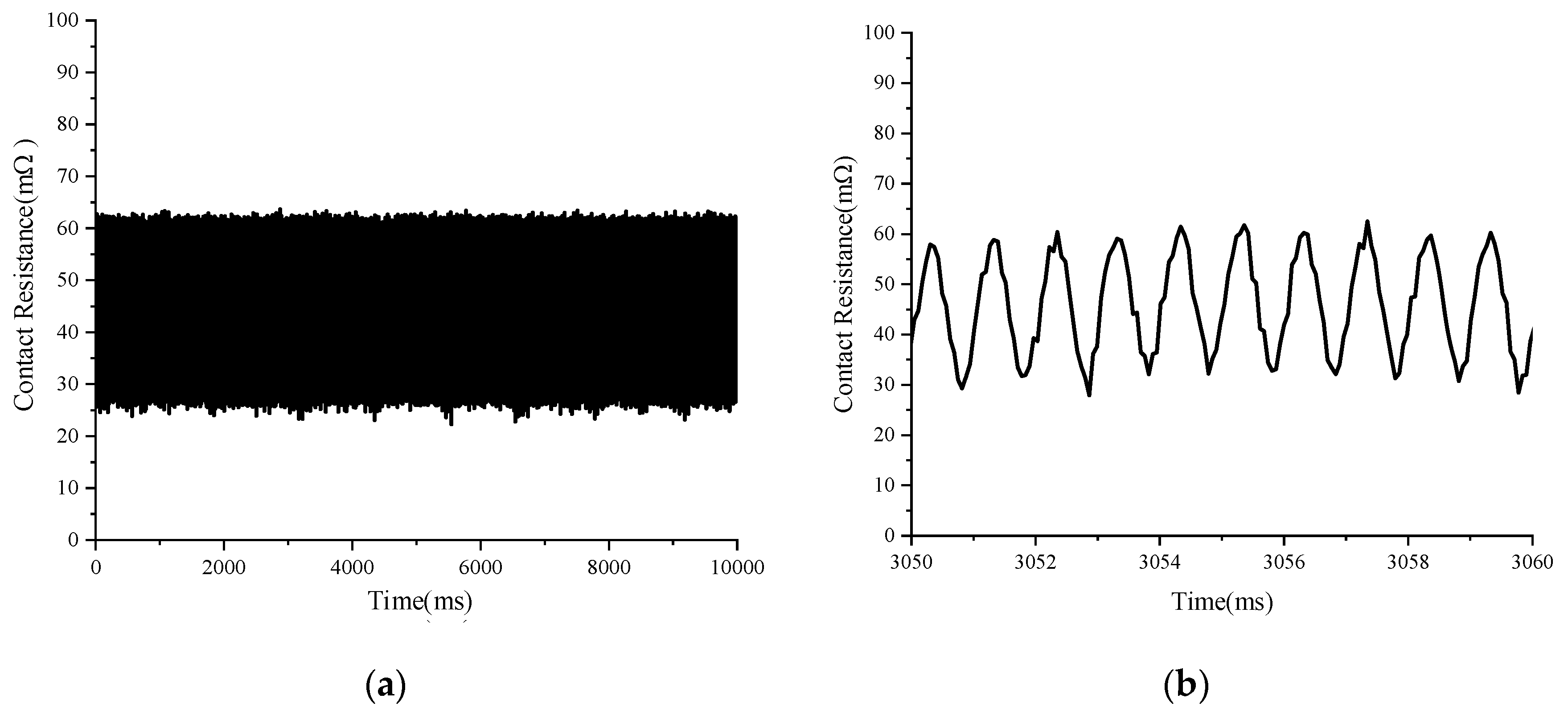
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Quantity | Unit | Description |
| s | m | Overtravel between model contact and support |
| y(L) | m | Deformation of the free end along the Y-axis |
| L | m | Length of free end |
| y(x,t) | m | Deformation of the beam |
| δ | m | Deformation of contact area |
| E | Pa | Beam Young’s modulus |
| I | m4 | Area moment of inertia |
| ρ | kg/m3 | Density of beam material |
| A | m2 | Cross-sectional area of the beam |
| N | N | Axial force |
| σ | / | Poisson’s ratio |
| kj | N/m | Stiffness of contact area |
| R | m | Surface curvature radius of contact |
| [M] | kg | Mass matrix |
| [C] | N∙s/m | Damping matrix |
| [K] | N/m | Stiffness matrix |
| [Φ] | / | Modal shape matrix |
| α | / | Mass coefficient |
| β | / | Stiffness coefficient |
| Rj | mΩ | Contact resistance |
| Fn | N | Contact force |
References
- Qiu, Z.-C.; Meng, F.-K.; Han, J.-D.; Liu, J.-G. Acceleration sensor-based first resonance vibration suppression of a double-clamped piezoelectric beam. Int. J. Acoust. Vib. 2016, 21, 11–23. [Google Scholar] [CrossRef]
- Shi, H.; Fan, S.; Zhang, Y.; Sun, J. Design and optimization based on uncertainty analysis in electro-thermal excited MEMS resonant sensor. Microsyst. Technol. 2015, 21, 757–771. [Google Scholar] [CrossRef]
- Gryzlov, A.A.; Grigor’ev, M.A. Improving the reliability of relay-protection and automatic systems of electric-power stations and substations. Russ. Electr. Eng. 2018, 89, 245–248. [Google Scholar] [CrossRef]
- Liu, Y.Q. Research on the electromagnetic relay selection and reliability. In Proceedings of the 2015 International Power, Electronics and Materials Engineering Conference, Dalian, China, 16–17 May 2015. [Google Scholar]
- Рoйзен. Miniature Sealed Electromagnetic Relay; Posts & Telecom Press: Beijing, China, 1979. [Google Scholar]
- Chambega, D. A qualitative analysis on the effect of external vibrations on the performance of relays. In Proceedings of the IEEE. AFRICON’96, Western Cape, South Africa, 25–27 September 1996. [Google Scholar]
- Ren, W.B.; Zhai, G.F.; Cui, L. Contact vibration characteristic of electromagnetic relay. IEICE Trans. Electron 2006, 89, 1177–1181. [Google Scholar] [CrossRef]
- Nayak, P.R. Contact vibrations. J. Sound Vib. 1972, 22, 297–322. [Google Scholar] [CrossRef]
- Szemplinska-Stupnicka, W. The Behavior of Nonlinear Vibrating Systems. Eng. Appl. Dyn. Chaos 1991, 1, 225–227. [Google Scholar]
- Turner, J.A. Non-linear vibrations of a beam with cantilever-Hertzian contact boundary conditions. J. Sound Vib. 2004, 275, 177–191. [Google Scholar] [CrossRef]
- Xie, F.; Flowers, G.T.; Chen, C.; Bozack, M.J.; Suhling, J.C.; Rickett, B.I.; Malucci, R.D.; Manlapaz, C. Analysis and prediction of vibration-induced fretting motion in a blade/receptacle connector pair. IEEE Trans. Compon. Packag. Technol. 2009, 32, 585–592. [Google Scholar] [CrossRef]
- Rezaei, I.; Sadeghi, A. Vibrational behavior of atomic force microscope beam via different polymers and immersion environments. Eur. Phys. J. Plus 2021, 137, 72. [Google Scholar] [CrossRef]
- Rezaei, I.; Sadeghi, A. Dynamic Behavior of Rectangular Atomic Force Microscope Cantilever by Supposing Diverse Polymeric Specimens and Immersion Media. J. Vib. Eng. Technol. 2022, 10, 2449–2479. [Google Scholar] [CrossRef]
- Angadi, S.V.; Jackson, R.L.; Pujar, V.; Tushar, M.R. A comprehensive review of the finite element modeling of electrical connectors including their contacts. IEEE Trans. Compon. Packag. Technol. 2020, 10, 836–844. [Google Scholar] [CrossRef]
- Echeverrigaray, F.G.; De Mello, S.R.S.; Leidens, L.M.; Boeira, C.D.; Michels, A.F.; Braceras, I.; Figueroa, C.A. Electrical contact resistance and tribological behaviors of self-lubricated dielectric coating under different conditions. Tribol. Int. 2020, 143, 106086. [Google Scholar] [CrossRef]
- Almeida, A.; Donadon, M.; de Faria, A.; de Almeida, S. The effect of piezoelectrically induced stress stiffening on the aeroelastic stability of curved composite panels. Compos. Struct. 2012, 94, 3601–3611. [Google Scholar] [CrossRef]
- Tchomeni, B.X.; Alugongo, A. Vibrations of misaligned rotor system with hysteretic friction arising from driveshaft–stator contact under dispersed viscous fluid influences. Appl. Sci. 2021, 11, 8089. [Google Scholar] [CrossRef]
- Tomović, R. A simplified mathematical model for the analysis of varying compliance vibrations of a rolling bearing. Appl. Sci. 2020, 10, 670. [Google Scholar] [CrossRef]
- Wnuk, M.; Iluk, A. Estimation of Resonance Frequency for Systems with Contact Using Linear Dynamics Methods. Appl. Sci. 2022, 12, 9344. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Ansys Inc. Ansys Help, Release 2021 R1; Ansys Inc.: Canonsburg, PA, USA, 2021; Available online: https://www.ansyshelp.ansys.com (accessed on 23 November 2024).
- MIL-STD-202-204; Test Method Standard for Electronic and Electrical Component Parts. U.S. Department of Defense: Washington, DC, USA, 1980.
- Holm, R. Electric Contacts: Theory and Application; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]





| Component | Material | Density (kg/m3) | Poisson’s Ratio | Young’s Modulus (GPa) |
|---|---|---|---|---|
| Spring | Beryllium bronze | 8300 | 0.35 | 124 |
| Support | Copper | 8200 | 0.34 | 81.92 |
| Contact | AgSnO2 | 9800 | 0.33 | 86 |
| Parameter | Range (mm) | Step Value (mm) |
|---|---|---|
| Free end length L | 7.5~15.5 | 4 |
| Overtravel s | 0.05~0.5 | 0.05 |
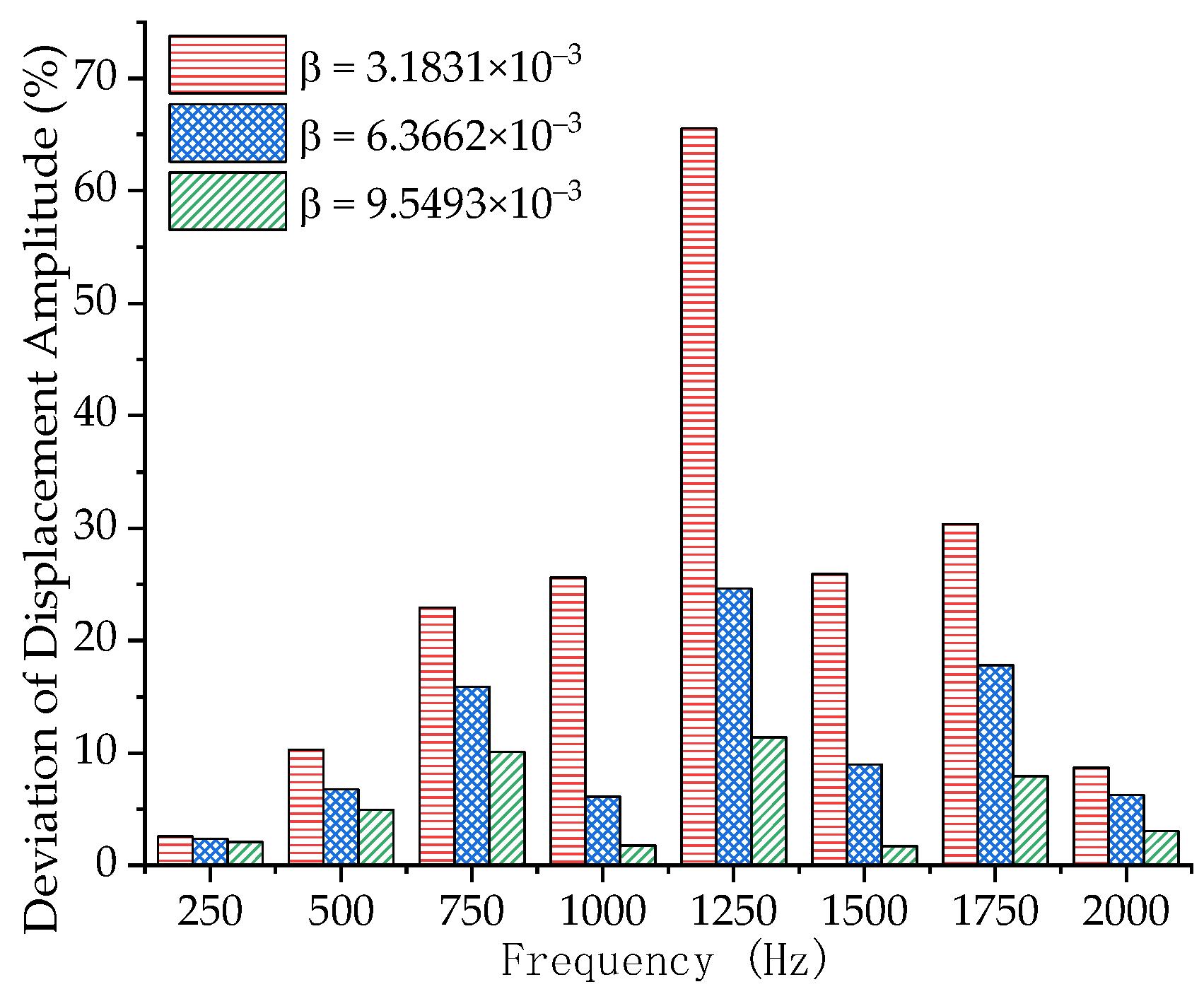
| Amplitude of Vibration Acceleration (m/s2) | Frequency (Hz) | Damping Ratios | Stiffness Coefficient β |
|---|---|---|---|
| 98 | 250 | 0.1 1 5 10 20 30 | 3.1831 × 10−5 3.1831 × 10−4 1.5916 × 10−3 3.1831 × 10−3 6.3662 × 10−3 9.5493 × 10−3 |
| 500 | |||
| 750 | |||
| 1000 | |||
| 1250 | |||
| 1500 | |||
| 1750 | |||
| 2000 |
| Frequency (Hz) | Damping Ratios | Simulate Displacement Amplitude (mm) |
|---|---|---|
| 1000 | 0.1 | 0.006485 |
| 1 | 0.004547 | |
| 5 | 0.003773 | |
| 10 | 0.003115 | |
| 20 | 0.002632 | |
| 30 | 0.002524 |
| Parameter | Value |
|---|---|
| Overtravel | 0.2 mm |
| Testing voltage/current | 6 V/100 mA |
| Sampling frequency | 15.625 KS/s |
| Temperature | 25 °C |
| Humidity | 55% ± 5% RH |
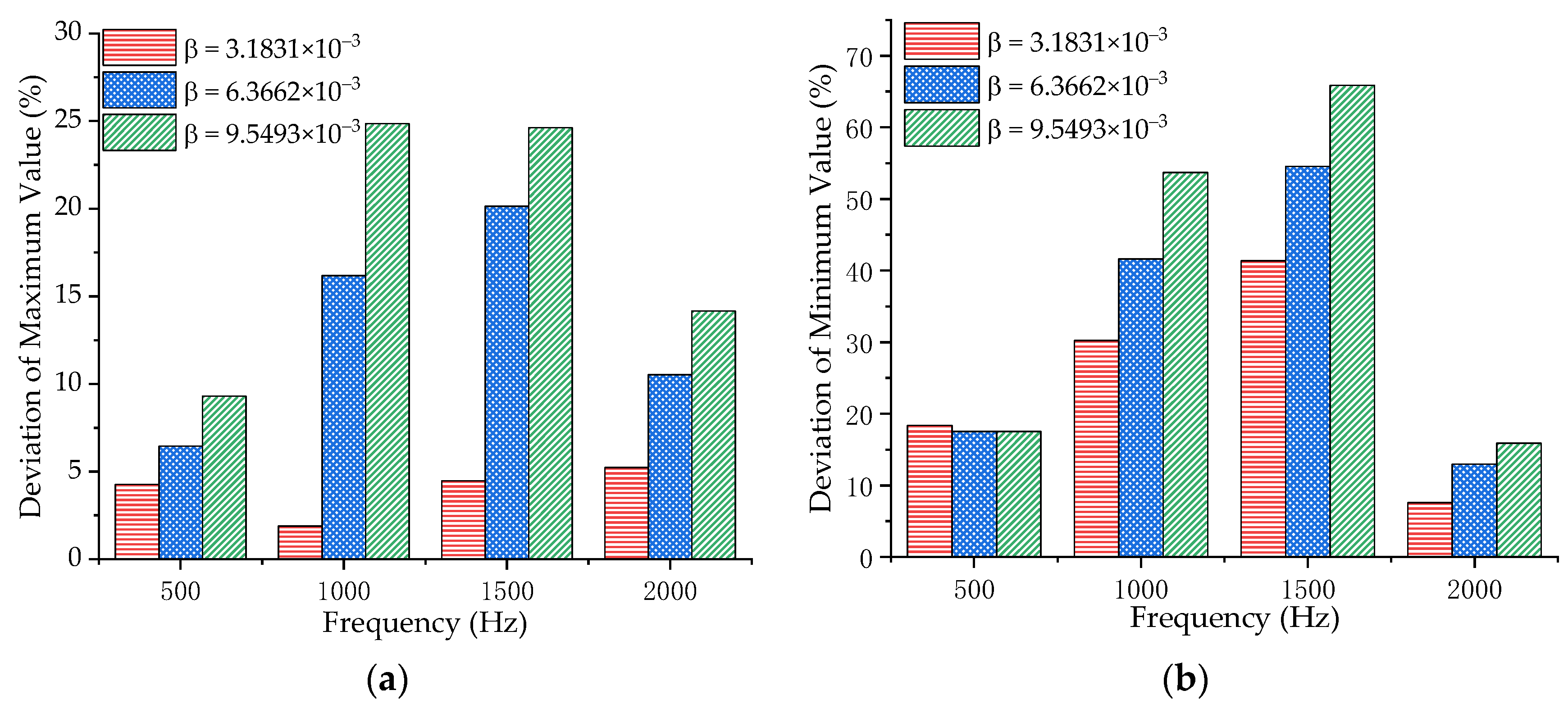
| Stiffness Coefficient β | Deviation of Minimum Contact Resistance Value (%) | Deviation of Maximum Contact Resistance Value (%) |
|---|---|---|
| 3.1831 × 10−3 | 30.23 | 1.89 |
| 6.3662 × 10−3 | 41.63 | 16.18 |
| 9.5493 × 10−3 | 53.69 | 24.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, C.; Meng, Y.; Ren, W. Numerical Investigation and Experimental Verification of Vibration Behavior for a Beam with Cantilever-Hertzian Contact Boundary Conditions. Machines 2025, 13, 52. https://doi.org/10.3390/machines13010052
Zhang Y, Zhang C, Meng Y, Ren W. Numerical Investigation and Experimental Verification of Vibration Behavior for a Beam with Cantilever-Hertzian Contact Boundary Conditions. Machines. 2025; 13(1):52. https://doi.org/10.3390/machines13010052
Chicago/Turabian StyleZhang, Yinnan, Chao Zhang, Yuan Meng, and Wanbin Ren. 2025. "Numerical Investigation and Experimental Verification of Vibration Behavior for a Beam with Cantilever-Hertzian Contact Boundary Conditions" Machines 13, no. 1: 52. https://doi.org/10.3390/machines13010052
APA StyleZhang, Y., Zhang, C., Meng, Y., & Ren, W. (2025). Numerical Investigation and Experimental Verification of Vibration Behavior for a Beam with Cantilever-Hertzian Contact Boundary Conditions. Machines, 13(1), 52. https://doi.org/10.3390/machines13010052






