Prior-Guided Residual Reinforcement Learning for Active Suspension Control
Abstract
1. Introduction
- (1)
- A residual reinforcement learning (RRL) control method based on policy learning is proposed to enhance the control performance of the suspension system. This method combines a LQR controller to provide the baseline actuator force and incorporates reinforcement learning to generate a corrective control input, thereby improving the system’s adaptability and disturbance-rejection capability.
- (2)
- An improved TD3 model integrating residual connections and LSTM layers is proposed to enhance training stability and better capture the dynamic and inertial characteristics of the suspension system.
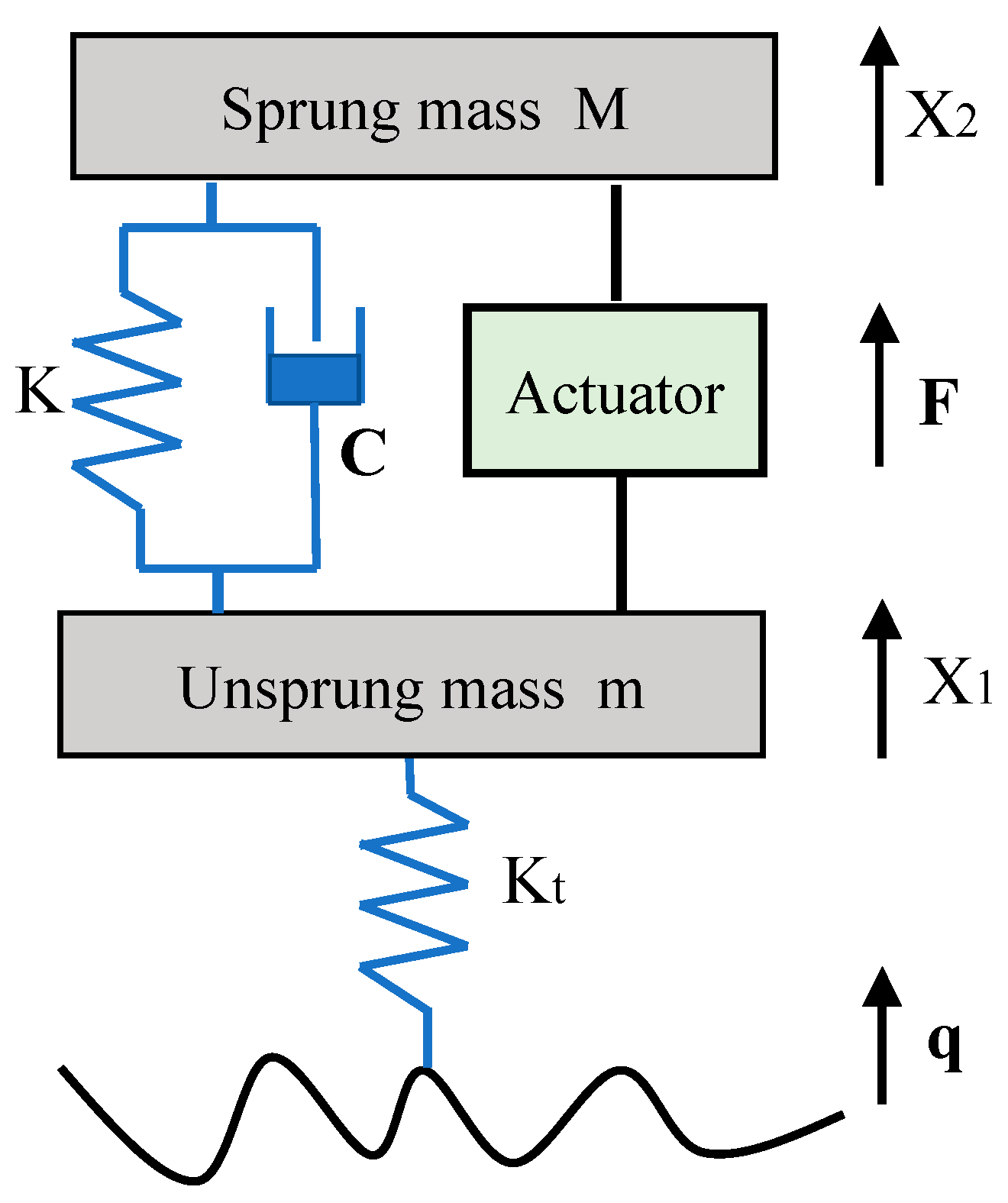
2. Active Suspension Model and Road Roughness Model
3. Methodology
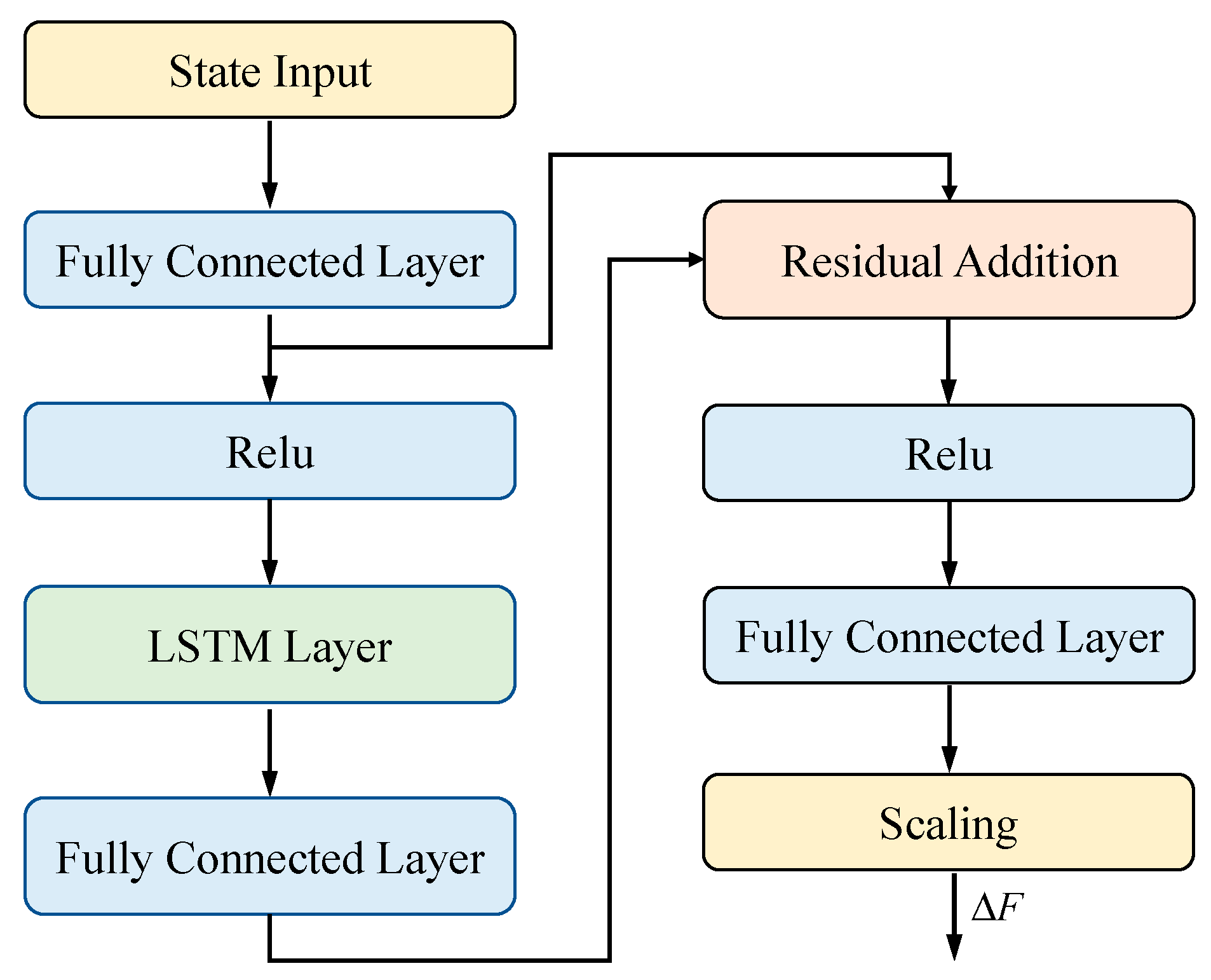
3.1. The Residual Policy Learning Control
3.2. The LQR Controller
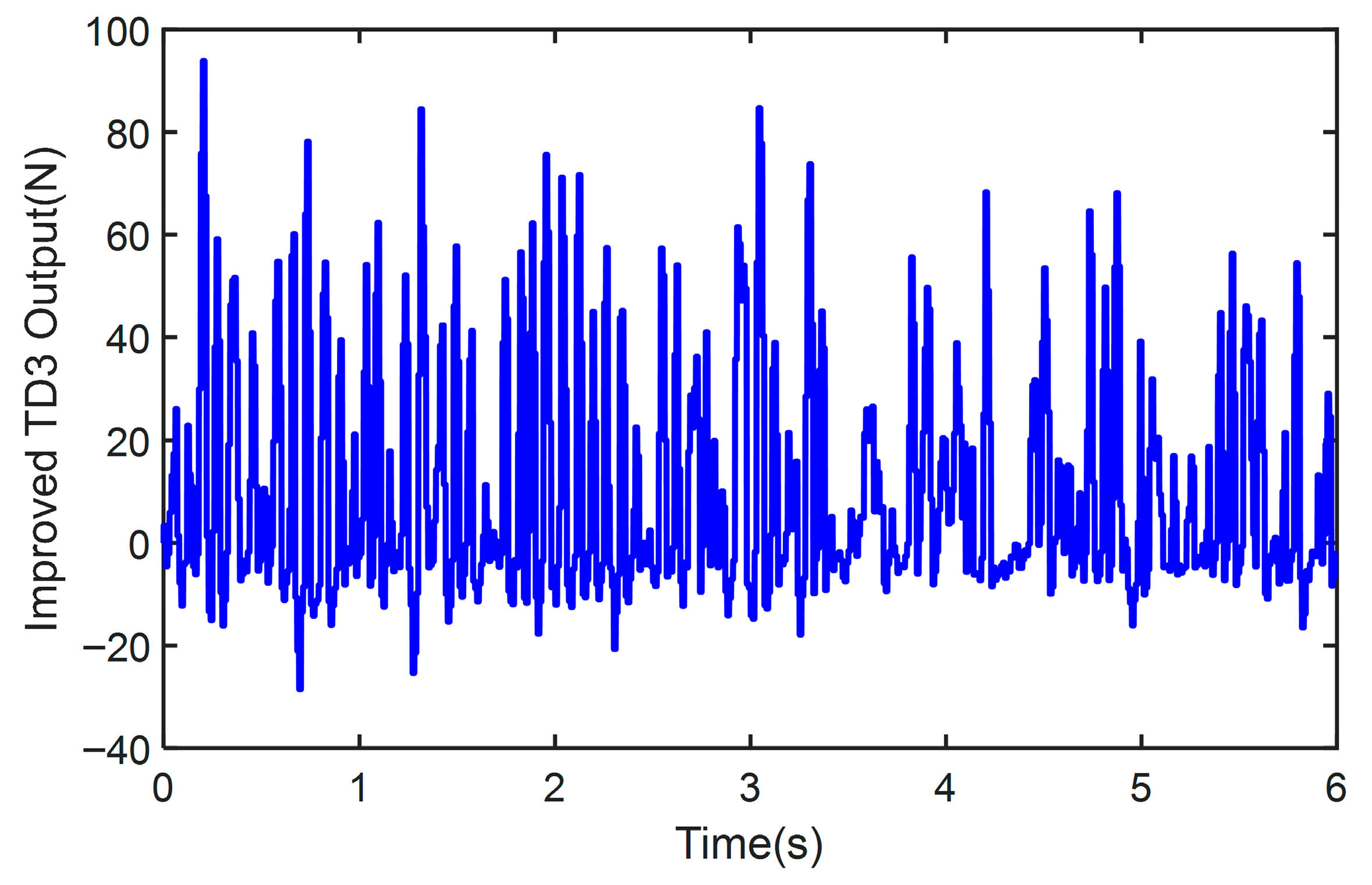
3.3. The Improved TD3
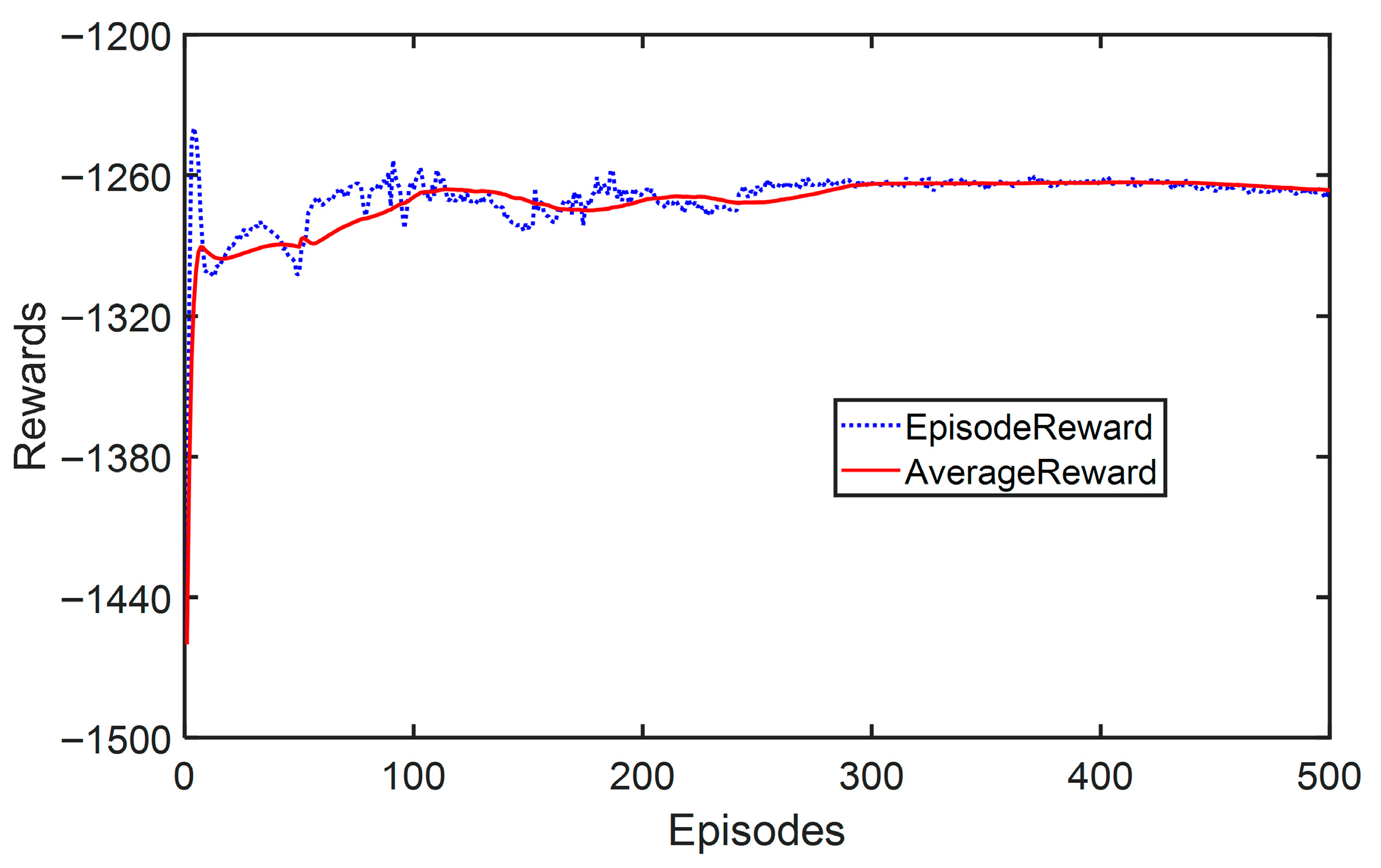
4. Results and Discussion
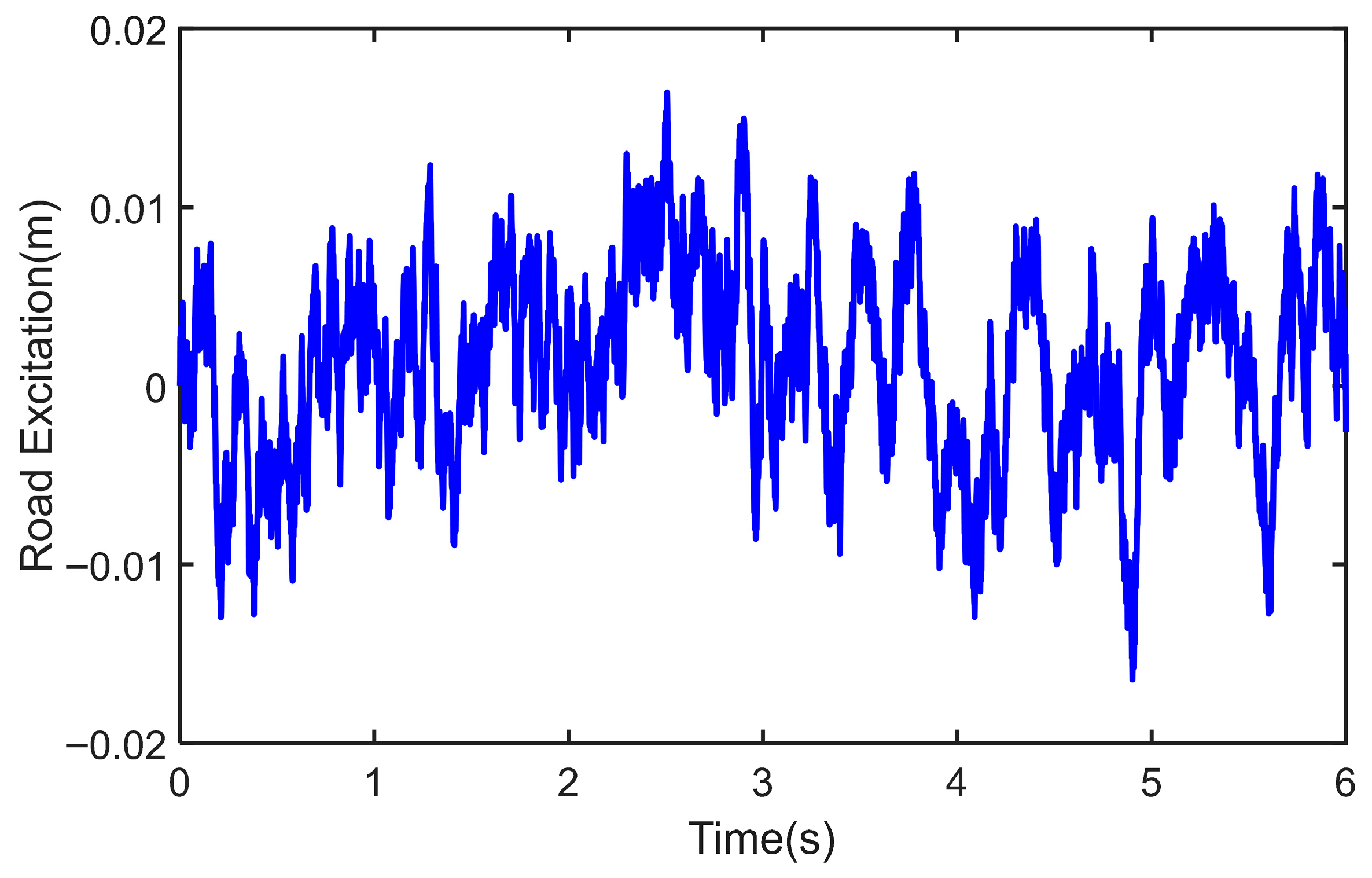
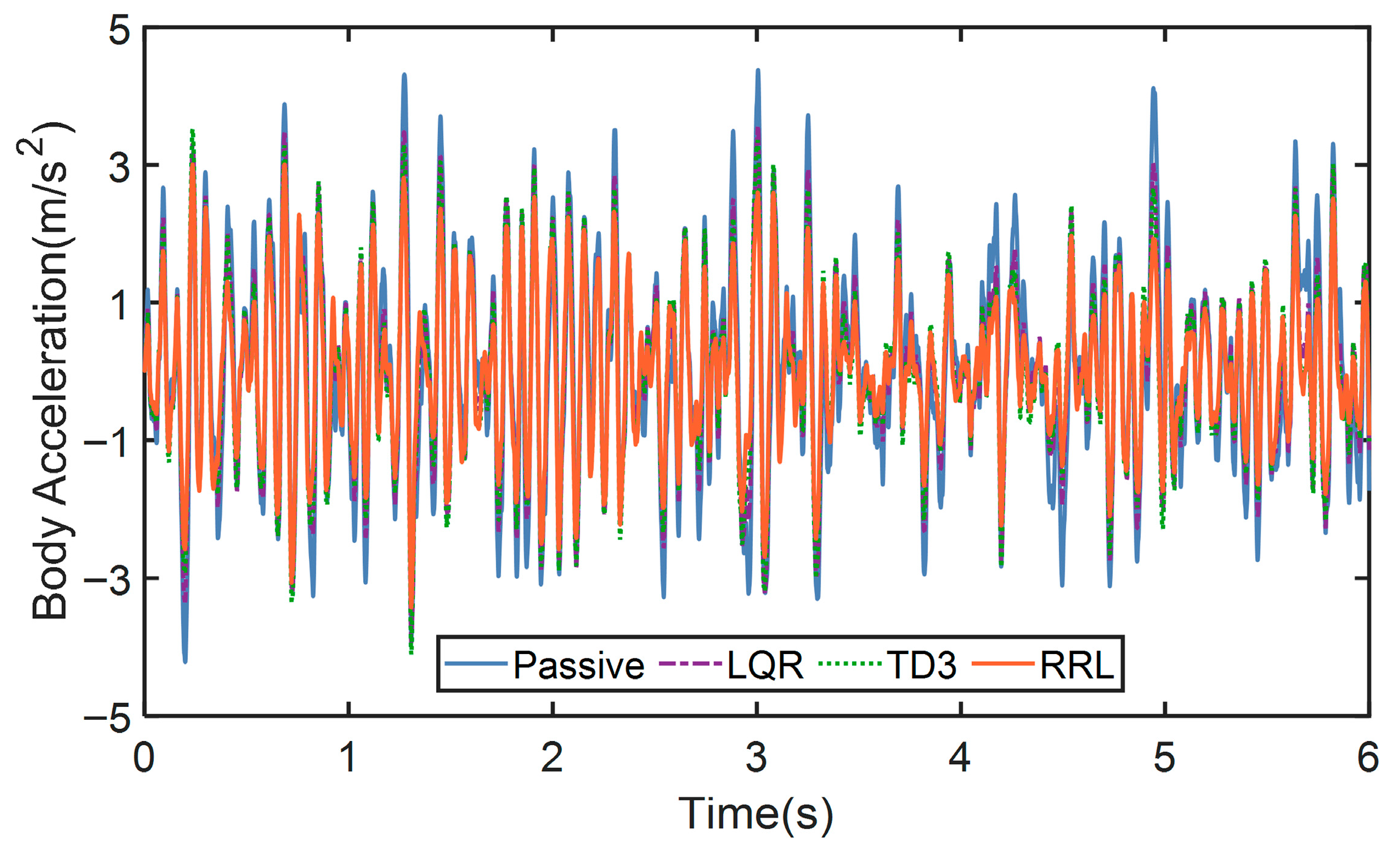
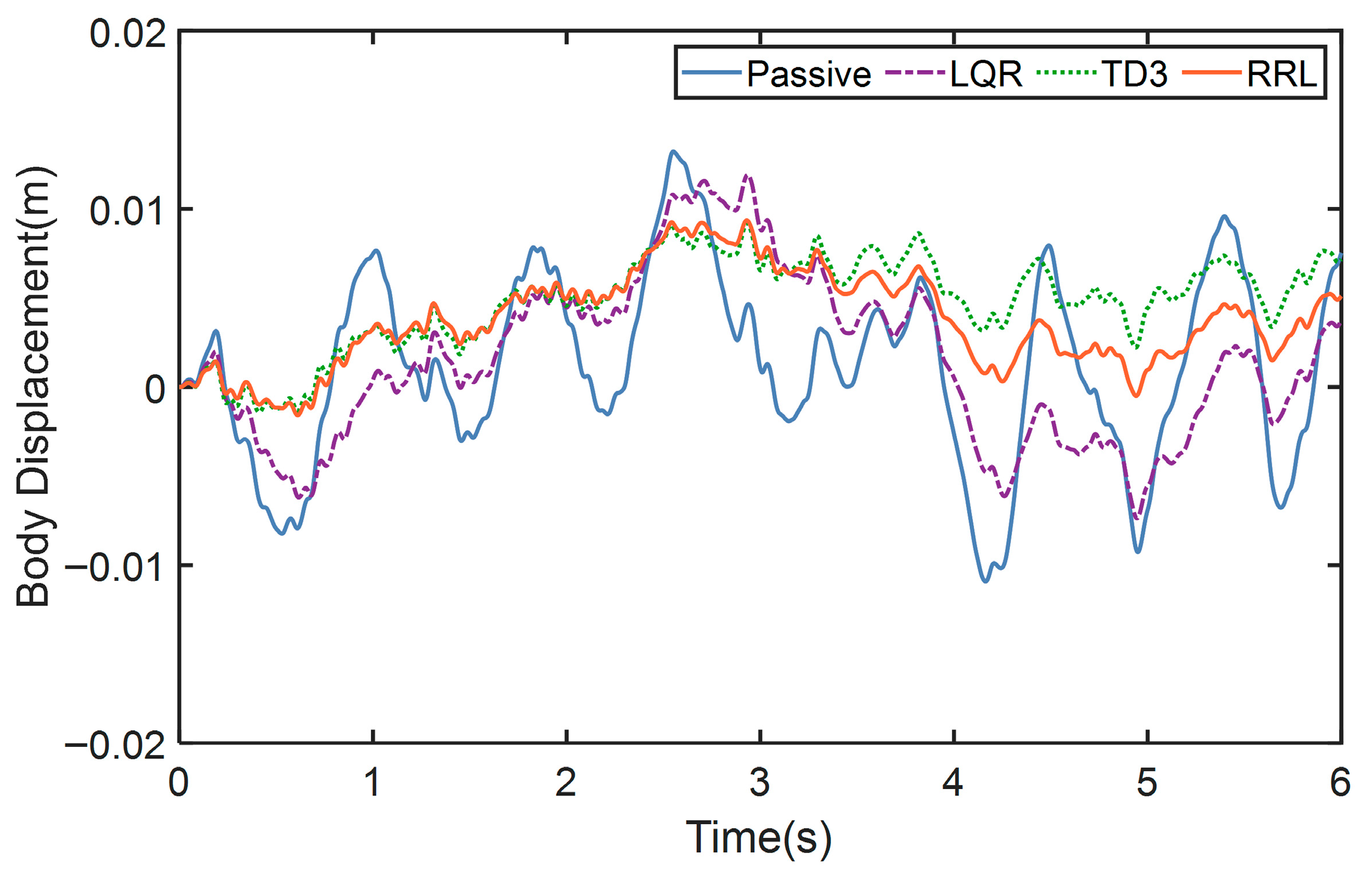
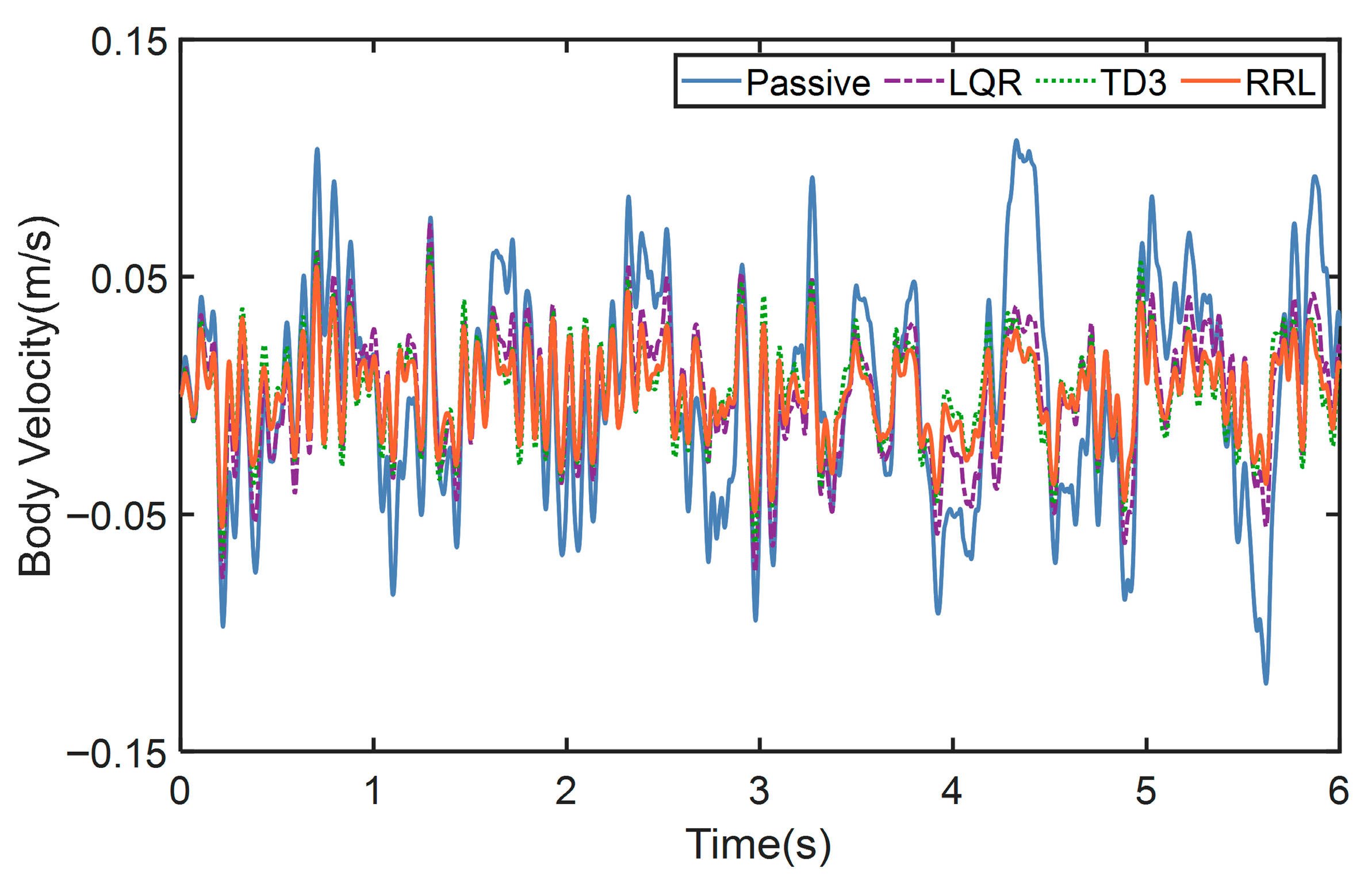
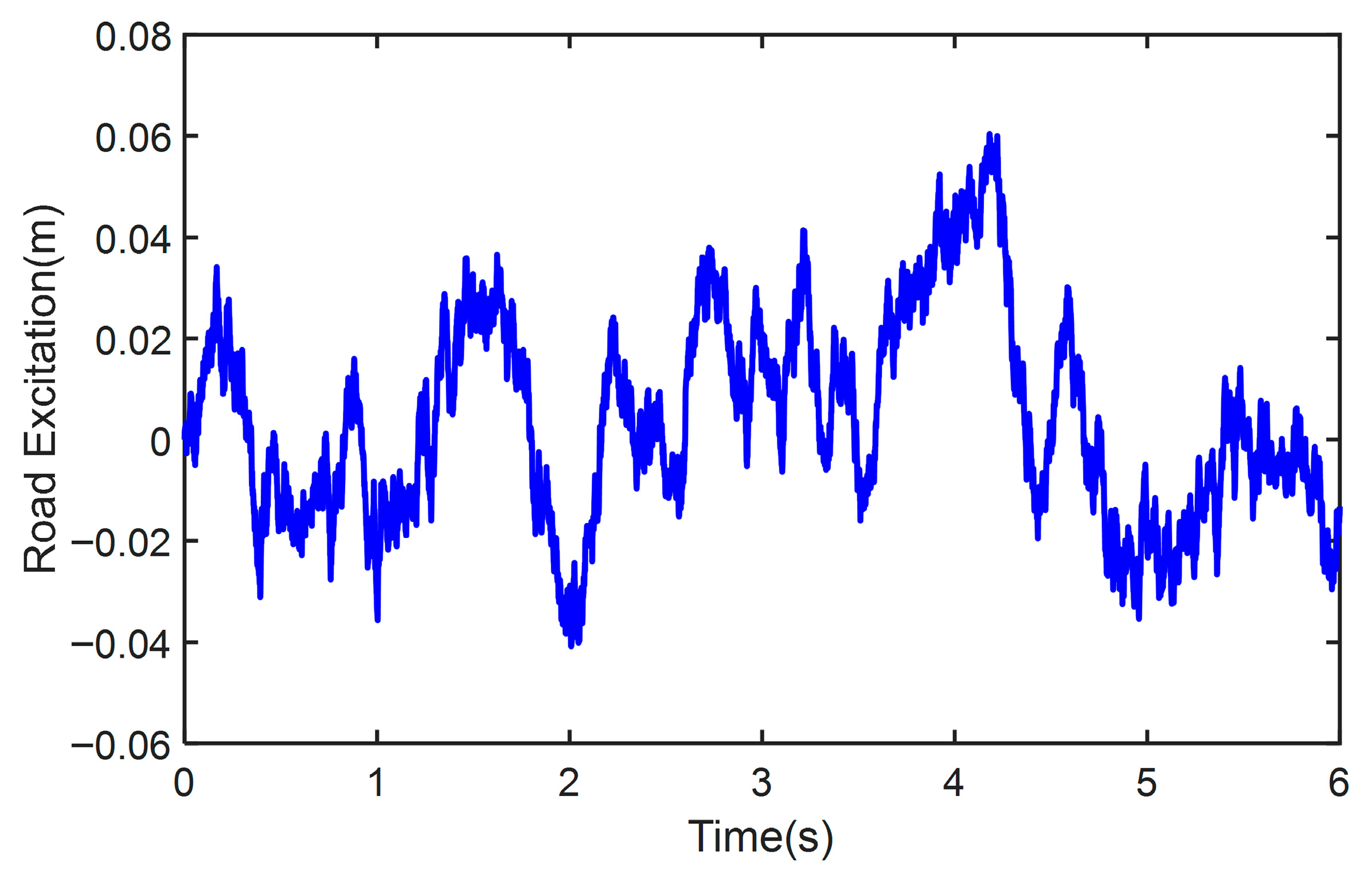
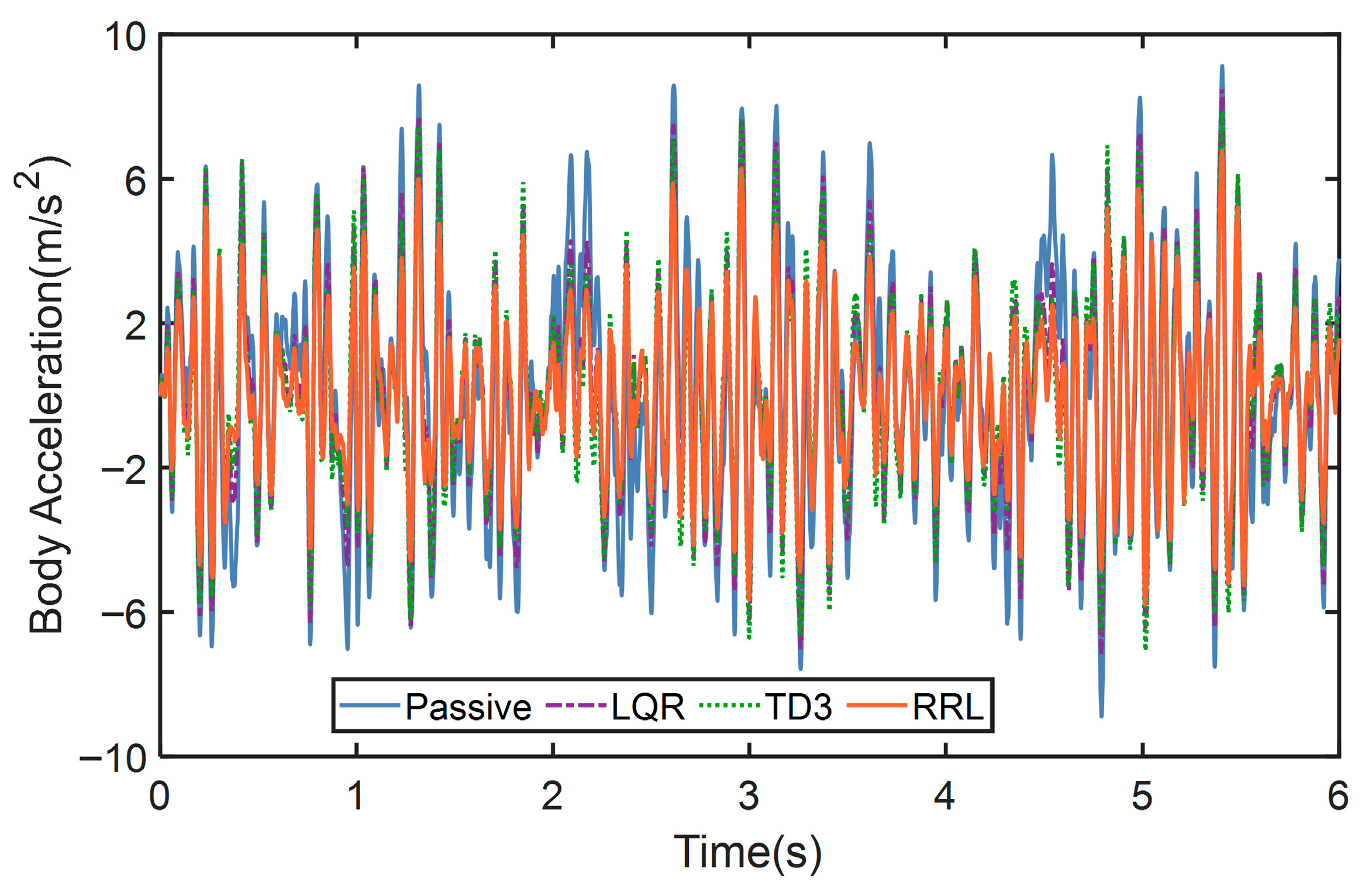
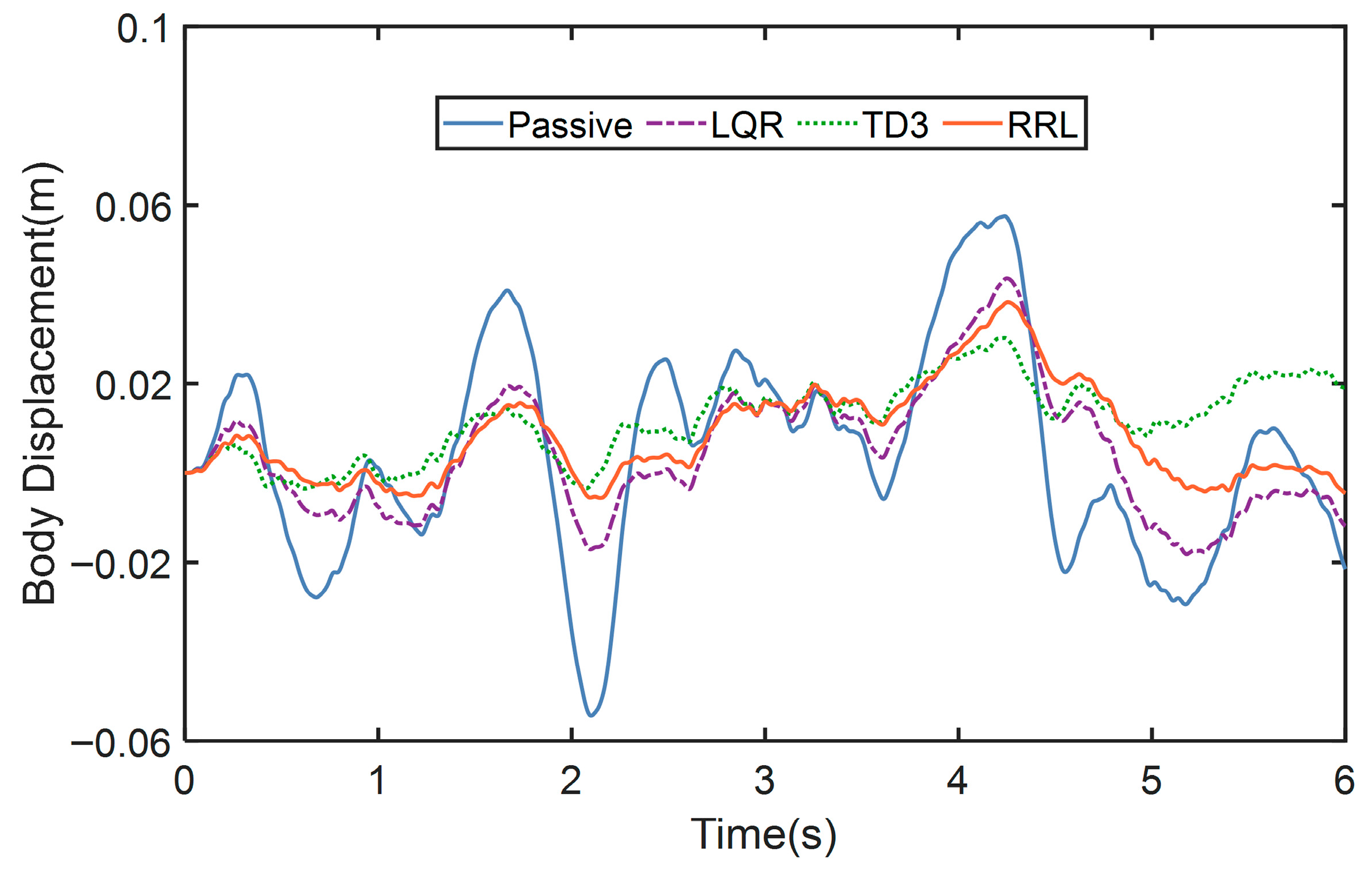
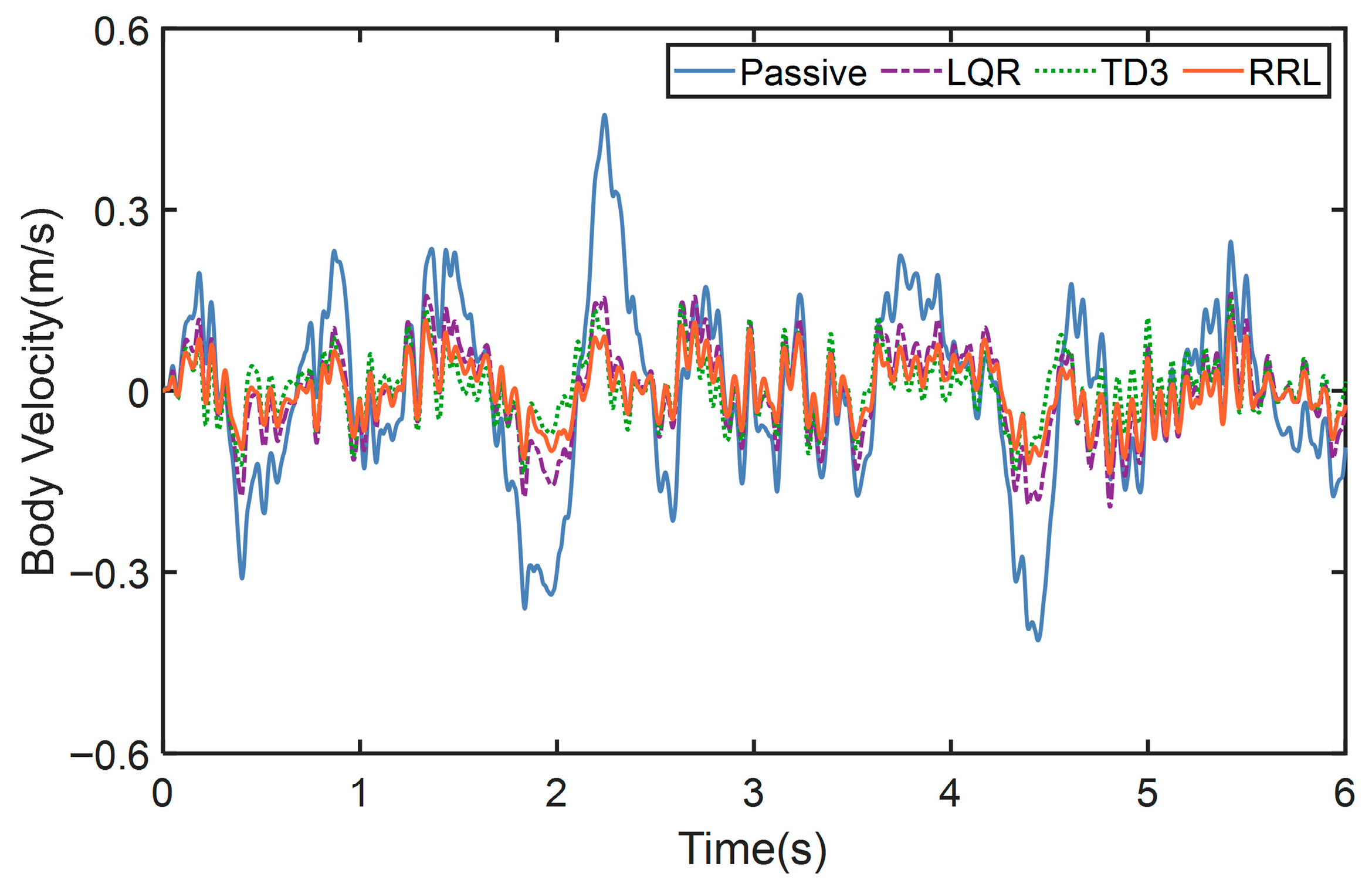
4.1. The Test on Class B Road
4.2. The Test on Class E Road
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, M.; Sun, W. Disturbance-resilient model predictive control for active suspension systems with perception errors in road preview information. J. Frankl. Inst. 2025, 362, 107957. [Google Scholar] [CrossRef]
- Pakštys, M.; Delfarah, K.; Galluzzi, R.; Tramacere, E.; Amati, N.; Tonoli, A. Damping allocation and comfort-oriented suspension control for electrodynamic maglev systems. J. Sound Vib. 2025, 618, 119311. [Google Scholar] [CrossRef]
- Lee, D.; Jin, S.; Lee, C. Deep reinforcement learning of semi-active suspension controller for vehicle ride comfort. IEEE Trans. Veh. Technol. 2023, 72, 327–339. [Google Scholar] [CrossRef]
- Rath, J.J.; Defoort, M.; Sentouh, C.; Karimi, H.R.; Veluvolu, K.C. Output-constrained robust sliding mode based nonlinear active suspension control. IEEE Trans. Ind. Electron. 2020, 67, 10652–10662. [Google Scholar] [CrossRef]
- Huang, Y.; Na, J.; Wu, X.; Gao, G. Approximation-free control for vehicle active suspensions with hydraulic actuator. IEEE Trans. Ind. Electron. 2018, 65, 7258–7267. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, X.; Wong, P.K.; Xie, Z.; Jia, J.; Li, W. Multi-objective frequency domain-constrained static output feedback control for delayed active suspension systems with wheelbase preview information. Nonlinear Dyn. 2021, 103, 1757–1774. [Google Scholar] [CrossRef]
- Moradi, M.; Fekih, A. Adaptive PID-Sliding-Mode fault-tolerant control approach for vehicle suspension systems subject to actuator faults. IEEE Trans. Veh. Technol. 2014, 63, 1041–1054. [Google Scholar] [CrossRef]
- Ding, X.; Li, R.; Cheng, Y.; Liu, Q.; Liu, J. Design of and research into a multiple-fuzzy PID suspension control system based on road recognition. Processes 2021, 9, 2190. [Google Scholar] [CrossRef]
- Çalışkan, K.; Henze, R.; Küçükay, F. Potential of road preview for suspension control under transient road inputs. IFAC-Pap. 2016, 49, 117–122. [Google Scholar] [CrossRef]
- Basargan, H.; Mihály, A.; Kisari, Á.; Gáspár, P.; Sename, O. Vehicle semi-active suspension control with cloud-based road information. Period. Polytech. Transp. Eng. 2021, 49, 242–249. [Google Scholar] [CrossRef]
- Shen, Y.; Li, J.; Huang, R.; Yang, X.; Chen, J.; Chen, L.; Li, M. Vibration control of vehicle ISD suspension based on the fractional-order SH-GH stragety. Mech. Syst. Signal Process. 2025, 234, 112880. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, F.; Wang, J.; Li, K. A Bayesian expectation maximization algorithm for state estimation of intelligent vehicles considering data loss and noise uncertainty. Sci. China Technol. Sci. 2025, 68, 1220801. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, G.; Hang, P.; Zhao, J.; Lin, Y.; Huang, C. Fundamental estimation for tire road friction coefficient: A model-based learning framework. IEEE Trans. Veh. Technol. 2025, 74, 481–493. [Google Scholar] [CrossRef]
- Shao, S.; Hu, G.; Gu, R.; Yang, C.; Tu, Y. Research on GA-LQR of automotive semi-active suspension based on MRD. Mod. Manuf. Eng. 2021, 11, 1–9. [Google Scholar]
- Li, G.; Gu, R.; Xu, R.X.; Hu, G.; Ouyang, N.; Xu, M. Study on fuzzy LQG control strategy for semi-active vehicle suspensions with magnetorheological dampers. Noise Vib. Control. 2021, 41, 129–136. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, F.; Geng, K.; Zhuang, W.; Dong, H.; Yin, G. Estimation of vehicle state using robust cubature Kalman filter. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), IEEE, Boston, MA, USA, 7–10 July 2020; pp. 1024–1029. [Google Scholar]
- Wang, Y.; Chen, H.; Yin, G.; Mo, Y.; de Boer, N.; Lv, C. Motion state estimation of preceding vehicles with packet loss and unknown model parameters. IEEE/ASME Trans. Mechatron. 2024, 29, 3461–3472. [Google Scholar] [CrossRef]
- Davila Delgado, J.M.; Oyedele, L. Robotics in construction: A critical review of the reinforcement learning and imitation learning paradigms. Adv. Eng. Inform. 2022, 54, 101787. [Google Scholar] [CrossRef]
- Zhou, B.; Li, X.; Liu, T.; Xu, K.; Liu, W.; Bao, J. Causal., KGPT: Industrial structure causal knowledge-enhanced large language model for cause analysis of quality problems in aerospace product manufacturing. Adv. Eng. Inform. 2024, 59, 102333. [Google Scholar] [CrossRef]
- Du, Y.; Chen, J.; Zhao, C.; Liao, F.; Zhu, M. A hierarchical framework for improving ride comfort of autonomous vehicles via deep reinforcement learning with external knowledge. Comput.-Aided Civ. Infrastruct. Eng. 2022, 38, 1059–1078. [Google Scholar] [CrossRef]
- Du, Y.; Chen, J.; Zhao, C.; Liu, C.; Liao, F.; Chan, C.-Y. Comfortable and energy-efficient speed control of autonomous vehicles on rough pavements using deep reinforcement learning. Transp. Res. Part C Emerg. Technol. 2022, 134, 103489. [Google Scholar] [CrossRef]
- Lin, Y.C.; Nguyen, H.L.T.; Yang, J.F.; Chiou, H.J. A reinforcement learning backstepping-based control design for a full vehicle active Macpherson suspension system. IET Control. Theory Appl. 2022, 16, 1417–1430. [Google Scholar] [CrossRef]
- Yong, H.; Seo, J.; Kim, J.; Kim, M.; Choi, J. Suspension control strategies using switched soft actor-critic models for real roads. IEEE Trans. Ind. Electron. 2023, 70, 824–832. [Google Scholar] [CrossRef]
- Han, S.-Y.; Liang, T. Reinforcement-learning-based vibration control for a vehicle semi-active suspension system via the PPO approach. Appl. Sci. 2022, 12, 3078. [Google Scholar] [CrossRef]
- Wang, C.; Cui, X.; Zhao, S.; Zhou, X.; Song, Y.; Wang, Y.; Guo, K. Enhancing vehicle ride comfort through deep reinforcement learning with expert-guided soft-hard constraints and system characteristic considerations. Adv. Eng. Inform. 2024, 59, 102328. [Google Scholar] [CrossRef]
- Li, Z.; Chu, T.; Kalabic, U. Dynamics-enabled safe deep reinforcement learning: Case study on active suspension control. In Proceedings of the 2019 IEEE Conference on Control Technology and Applications (CCTA), IEEE, Hong Kong, China, 19–21 August 2019; pp. 585–591. [Google Scholar]
- Deng, M.; Sun, D.; Zhan, L.; Xu, X.; Zou, J. Advancing active suspension control with TD3-PSC: Integrating physical safety constraints into deep reinforcement learning. IEEE Access 2024, 12, 115628–115641. [Google Scholar] [CrossRef]
- Goenaga, B.J.; Fuentes Pumarejo, L.G.; Mora Lerma, O.A. Evaluation of the methodologies used to generate random pavement profiles based on the power spectral density: An approach based on the International Roughness Index. Ing. Investig. 2017, 37, 49–57. [Google Scholar] [CrossRef]
- Lu, F.; Chen, S.Z. Modeling and simulation of road surface excitation on vehicle in time domain. Automot. Eng. 2015, 37, 549–553. [Google Scholar]


| Road Class | Lower Limit | Geometric Mean | Upper Limit |
|---|---|---|---|
| A | - | 16 × 10−6 | 32 × 10−6 |
| B | 32 × 10−6 | 64 × 10−6 | 128 × 10−6 |
| C | 128 × 10−6 | 256 × 10−6 | 512 × 10−6 |
| D | 512 × 10−6 | 1024 × 10−6 | 2048 × 10−6 |
| E | 2048 × 10−6 | 4096 × 10−6 | 8192 × 10−6 |
| Definition | Item | Values |
|---|---|---|
| Critic | LearnRate | 5 × 10−5 |
| GradientThreshold | 1 | |
| Actor | LearnRate | 1 × 10−4 |
| GradientThreshold | 1 | |
| Agent | SampleTime | 0.01 |
| TargetSmoothFactor | 1 × 10−3 | |
| DiscountFactor | 0.95 | |
| MiniBatchSize | 128 | |
| ExperienceBufferLength | 1 × 106 | |
| TargetUpdateFrequency | 10 | |
| MaxEpisodes | 500 | |
| LQR |
| Symbol | Values |
|---|---|
| Methods | Body Acceleration | Body Displacement | Body Velocity |
|---|---|---|---|
| Passive | 1.5339 | 0.0053 | 0.0453 |
| LQR | 1.3256 (13.5824%) | 0.0050 (5.6603%) | 0.0254 (43.914%) |
| TD3 | 1.2846 (16.2544%) | 0.0047 (11.3207%) | 0.0209 (53.9503%) |
| RRL | 1.0994 (28.3286%) | 0.0046 (13.1371%) | 0.0179 (60.4617%) |
| Methods | Body Acceleration | Body Displacement | Body Velocity |
|---|---|---|---|
| Passive | 3.2655 | 0.0239 | 0.1485 |
| LQR | 2.8384 (13.08%) | 0.0148 (37.9345%) | 0.0720 (51.5134%) |
| TD3 | 2.7677 (15.2438%) | 0.0147 (38.6219%) | 0.0507 (65.834%) |
| RRL | 2.2336 (31.5988%) | 0.0136 (43.2449%) | 0.0472 (68.1833%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Wang, S.; Bai, F.; Wei, M.; Sun, X.; Wang, Y. Prior-Guided Residual Reinforcement Learning for Active Suspension Control. Machines 2025, 13, 983. https://doi.org/10.3390/machines13110983
Yang J, Wang S, Bai F, Wei M, Sun X, Wang Y. Prior-Guided Residual Reinforcement Learning for Active Suspension Control. Machines. 2025; 13(11):983. https://doi.org/10.3390/machines13110983
Chicago/Turabian StyleYang, Jiansen, Shengkun Wang, Fan Bai, Min Wei, Xuan Sun, and Yan Wang. 2025. "Prior-Guided Residual Reinforcement Learning for Active Suspension Control" Machines 13, no. 11: 983. https://doi.org/10.3390/machines13110983
APA StyleYang, J., Wang, S., Bai, F., Wei, M., Sun, X., & Wang, Y. (2025). Prior-Guided Residual Reinforcement Learning for Active Suspension Control. Machines, 13(11), 983. https://doi.org/10.3390/machines13110983







