Economy Optimization by Multi-Strategy Improved Whale Optimization Algorithm Based on User Driving Cycle Construction for Hybrid Electric Vehicles
Abstract
1. Introduction
1.1. Literature Review of Driving Cycles
1.2. Literature Review on Economic Optimization of Hybrid Powertrains
1.3. Main Contributions and Structure of Article
- Select feature parameters oriented to average instantaneous fuel consumption characteristics. This research applies the stepwise regression method to complete the selection of characteristic parameters oriented to the average instantaneous fuel consumption characteristics, which addresses the problem of high randomness in the selection of eigenvalues and provides a guarantee for the clustering effect.
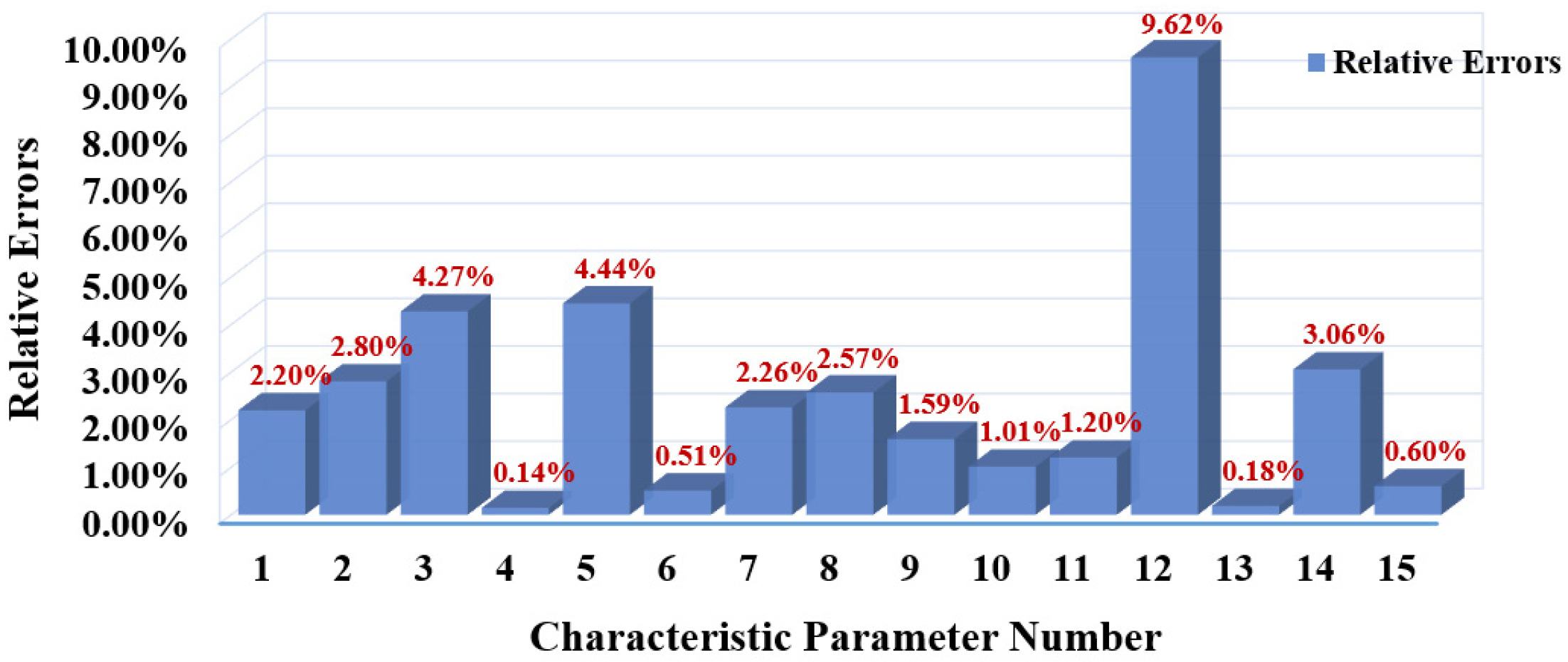
- The simulated annealing genetic algorithm fuzzy c-means clustering (SAGAFCM) methodology is employed to develop the user driving cycle. This method overcomes the problem that FCM is susceptible to the initial clustering center and converges to a local minimal point and thus improves the reliability of the clustering results. The average deviation of the 15 eigenvalues of the constructed conditions is 2.4313%, which is a high accuracy.
- This study proposes the MIWOA method to optimize the component parameters and control parameters of the hybrid powertrain under user driving cycles. The combination of Fuch and opposition-based learning (OBL) enhances the diversity of the initial population, which solves the problem of pseudo-randomness of the initial population generated by the random method of the original algorithm; the proposed variable spiral parameter enriches the search of whales and improves the ability of the algorithm to explore globally; and the adaptive weights are combined with t-distribution perturbation and random perturbation, respectively, to improve the likelihood of jumping out of the local optimum. Thus, the economic parameters of HEVs that are more in line with the user’s actual driving conditions are obtained, and the vehicle’s economy is enhanced.
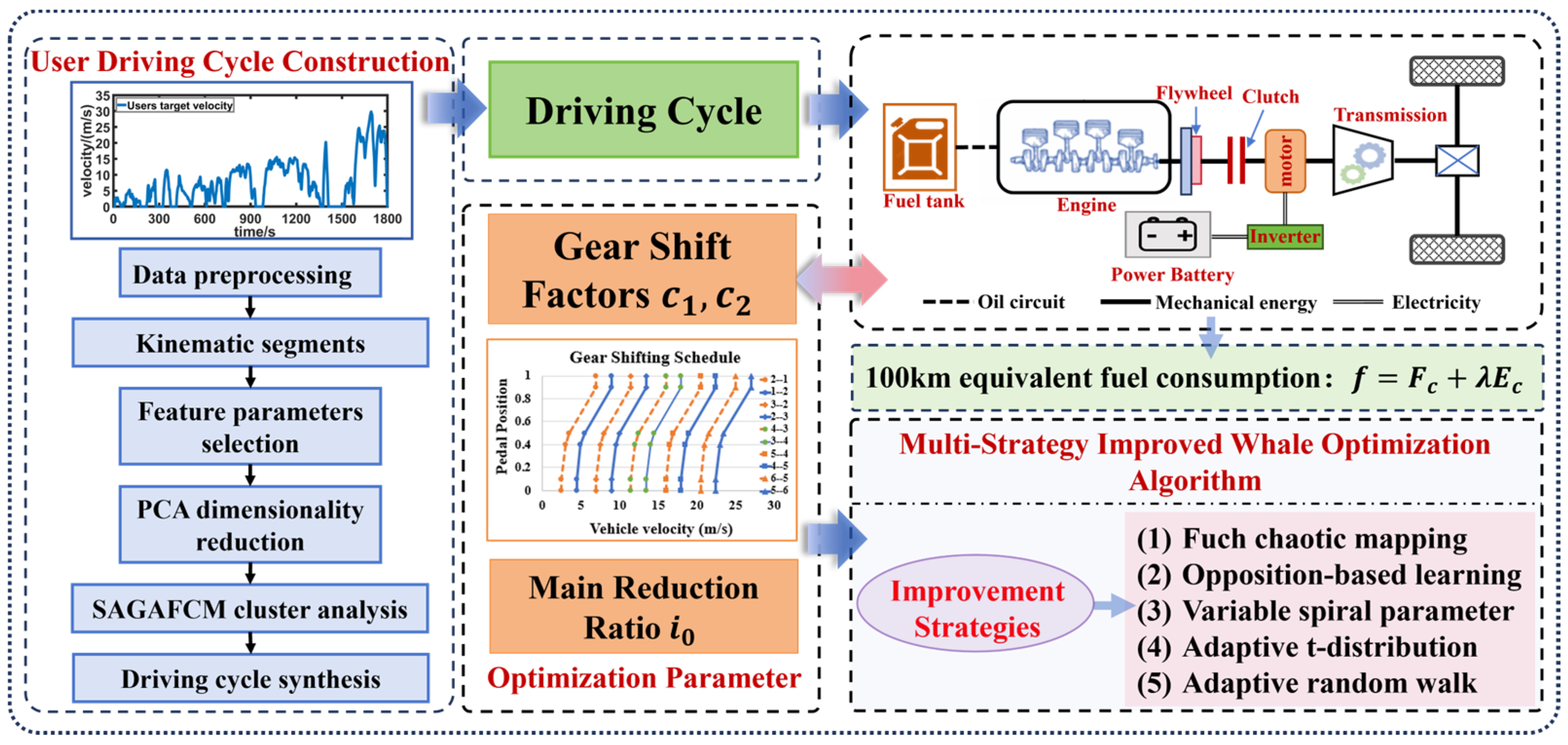
2. Model Framework Development and Driving Cycle Construction
2.1. Overview of Model Framework
- Driving cycle module: Based on the Vehicle Network Data, the kinematic segments are categorized using PCA and the SAGAFCM algorithm. Depending on the percentage of overall time accounted for by each type of kinematic segment, appropriate kinematic segments are selected from each category and together connected to synthesize user driving cycle that meets the features of the user database.
- Hybrid vehicle model: Under the user driving cycle, an HEV model of P2 configuration is built based on the rule-based strategy, which is required to fulfill power requirements of the user driving cycle and has good economy. Meanwhile, the model is verified under other standard driving cycles to ensure the rationality of the model. In fact, the vehicle needs to meet the driving requirements not only for the user driving cycle, but also for the standard driving cycles, so the model simulation verification is operated under the other three standard driving cycles to ensure the used model’s rationality.
- MIWOA optimization module: To comprehensively consider the economy of HEVs, the FC of the engine and the energy consumption of the battery are transformed into 100 km EFC. Based on the HEV model of user driving cycles, with 100 km EFC as the optimization objective function and the main reduction ratio and gear shift factors as the optimization variables, MIWOA is proposed to complete the economic optimization of the hybrid vehicle under the constraints, and then this paper compares the simulation results of the model before and after optimization. Meanwhile, the driving requirements of standard driving cycles should be considered, so the simulation results before and after optimization are compared under other standard driving cycles, which proves the effectiveness of the optimization method proposed in this paper.
2.2. Construction of User Driving Cycle
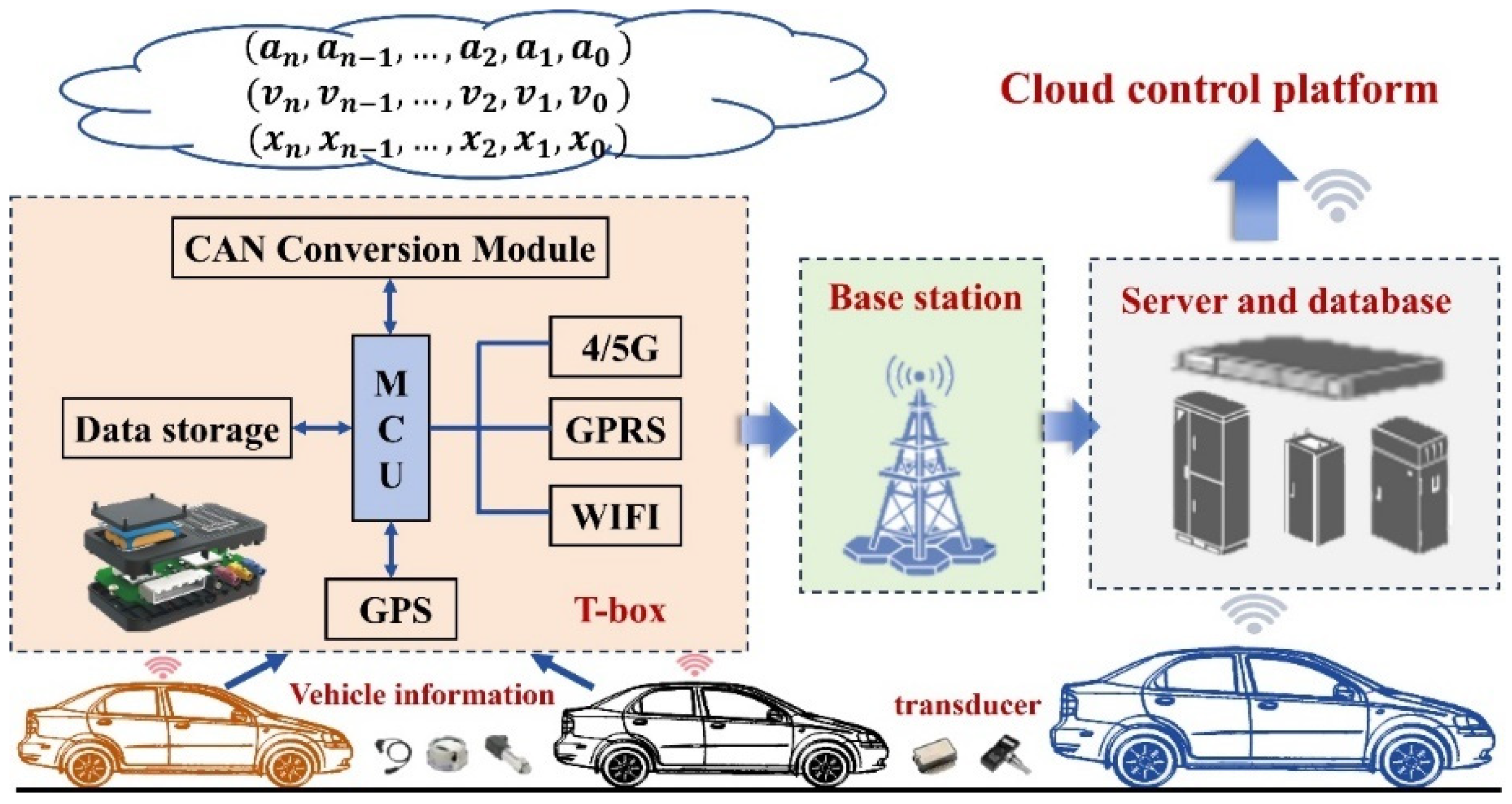
2.2.1. Data Sources
2.2.2. Data Pre-Processing and Establishment of Kinematic Fragment Library
2.2.3. Selection of Feature Parameters
- Dependent variable: First calculate the average instantaneous FC of each kinematic segment.
- Independent variable: Select and calculate the initial parameters of the kinematic segments, including 50 variables such as average velocity, average acceleration, standard deviation of velocity, average engine speed, etc.
- Establish a linear regression model of 50 feature parameters and average instantaneous FC.
2.2.4. Data Dimensionality Reduction
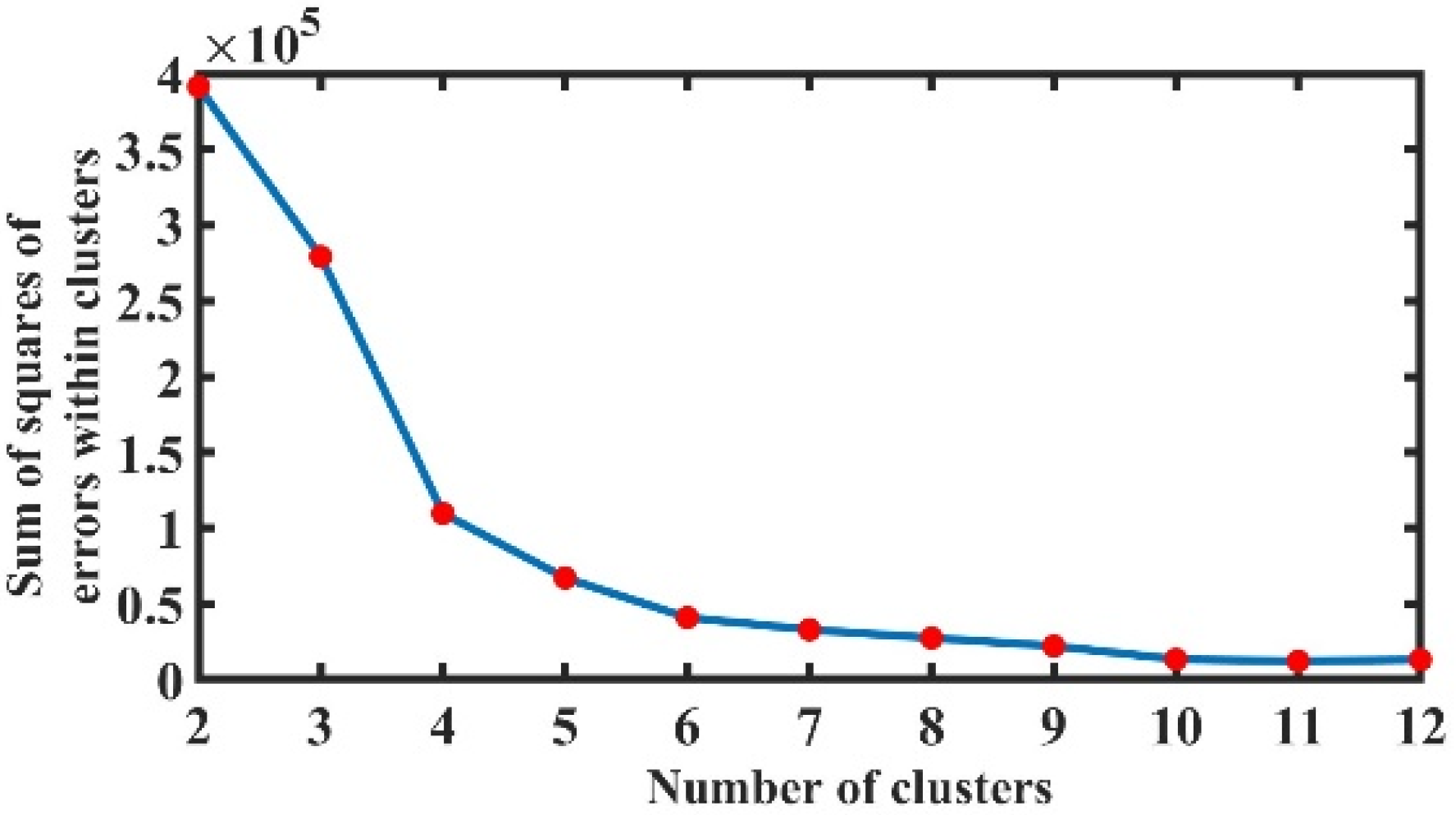
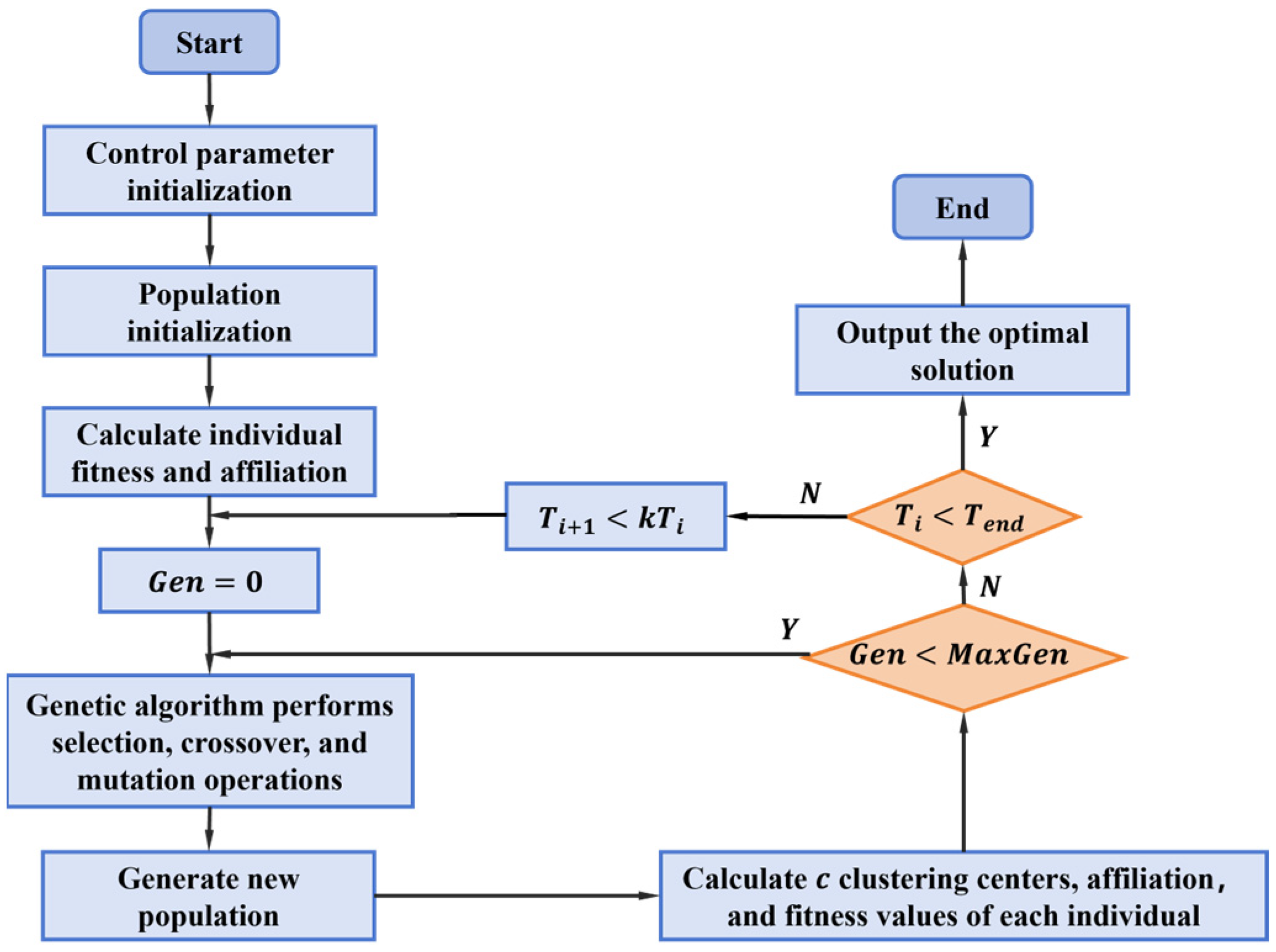
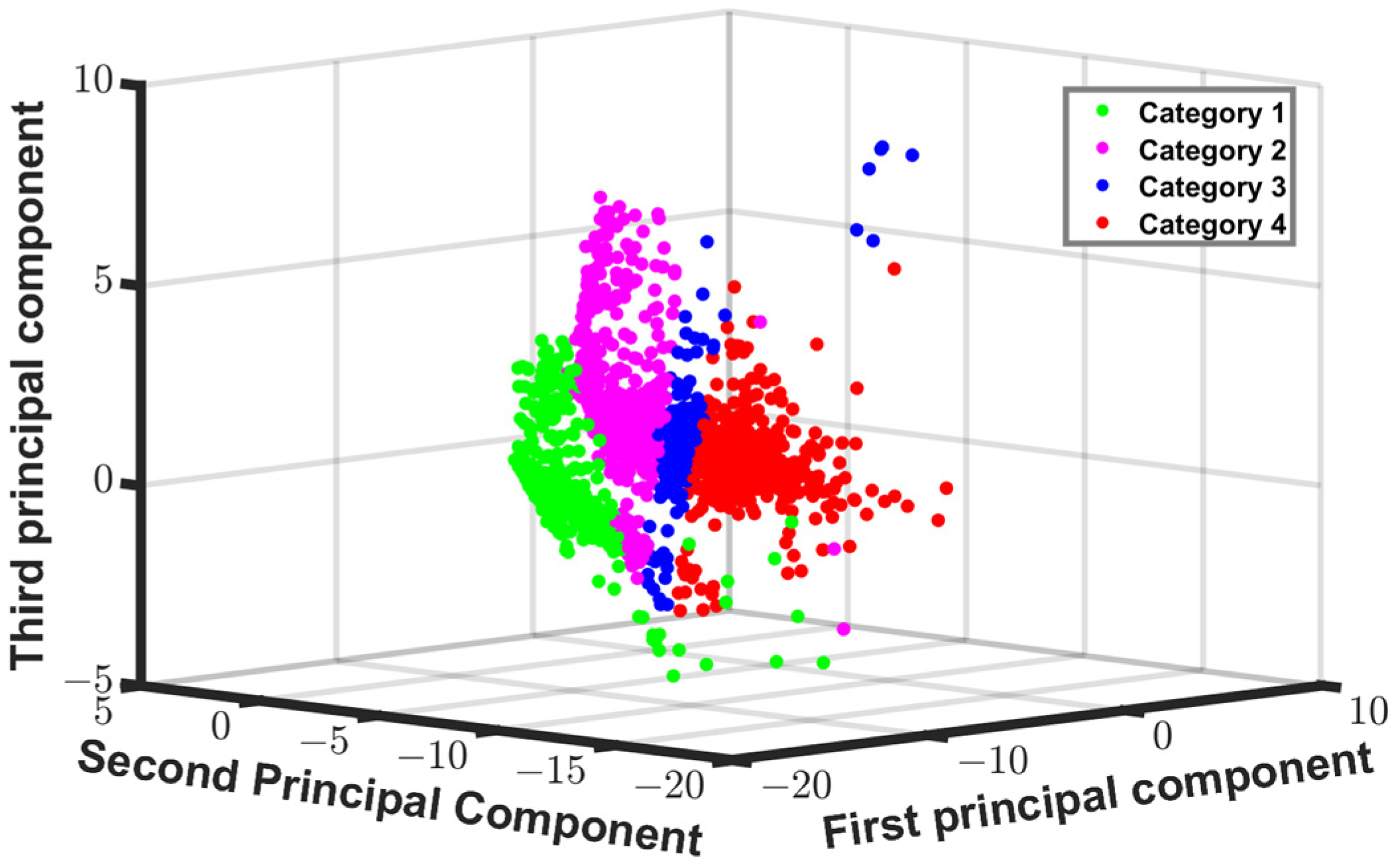
2.2.5. SAGAFCM Cluster Analysis
2.2.6. Synthesis of User Driving Cycles
3. Model and Simulation
3.1. Basic Information of Model
3.1.1. HEV Dynamics Model
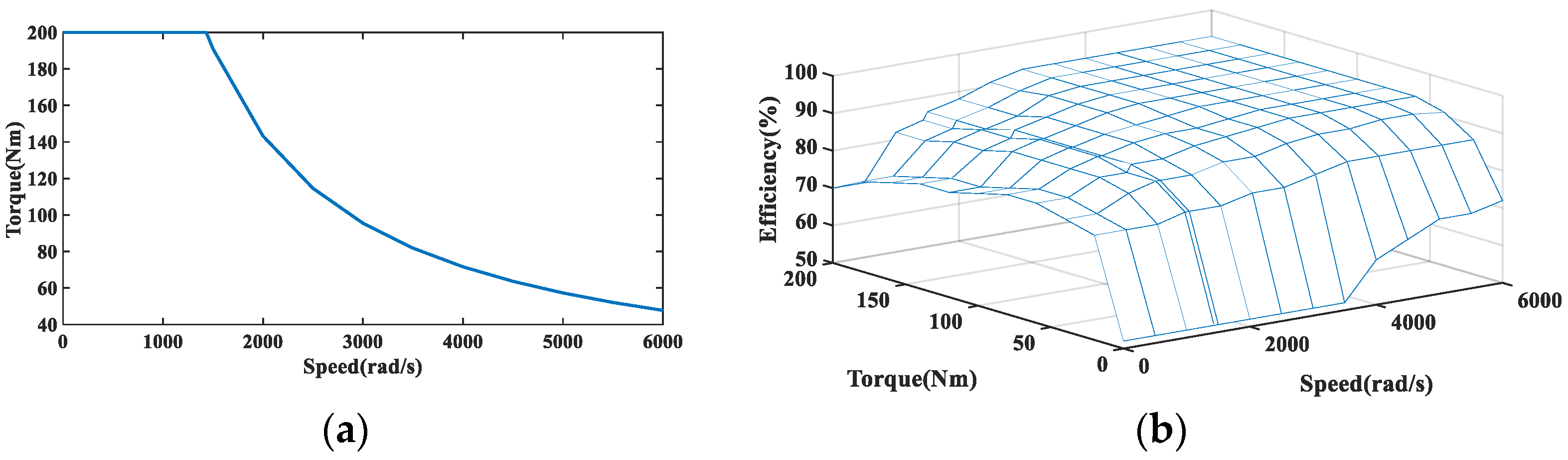
3.1.2. Motor Model
3.1.3. Power Battery Model
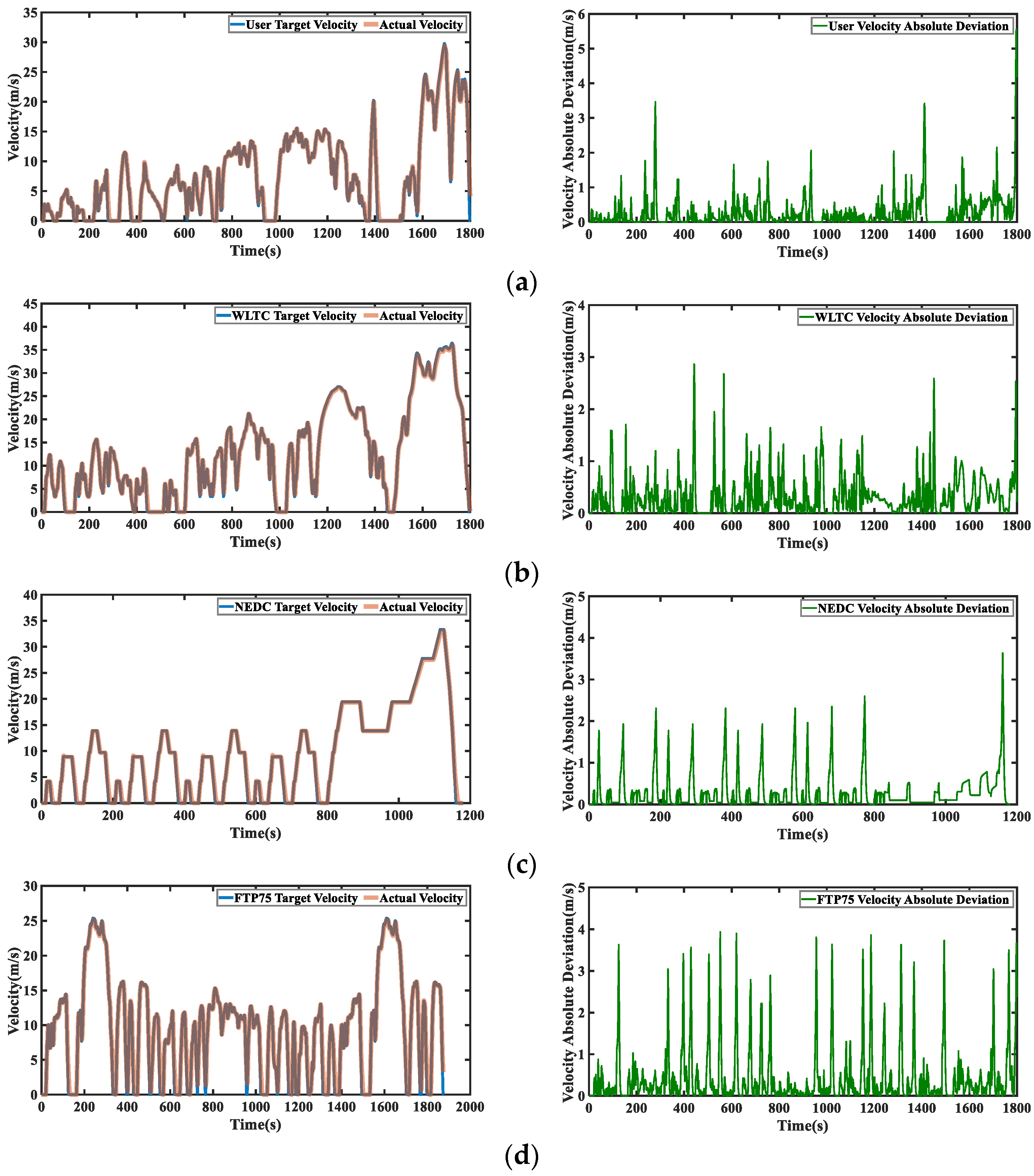
3.2. Model Simulation Results and Discussion
4. Optimization of Hybrid Powertrain Parameters
4.1. Establishment of Optimization Target
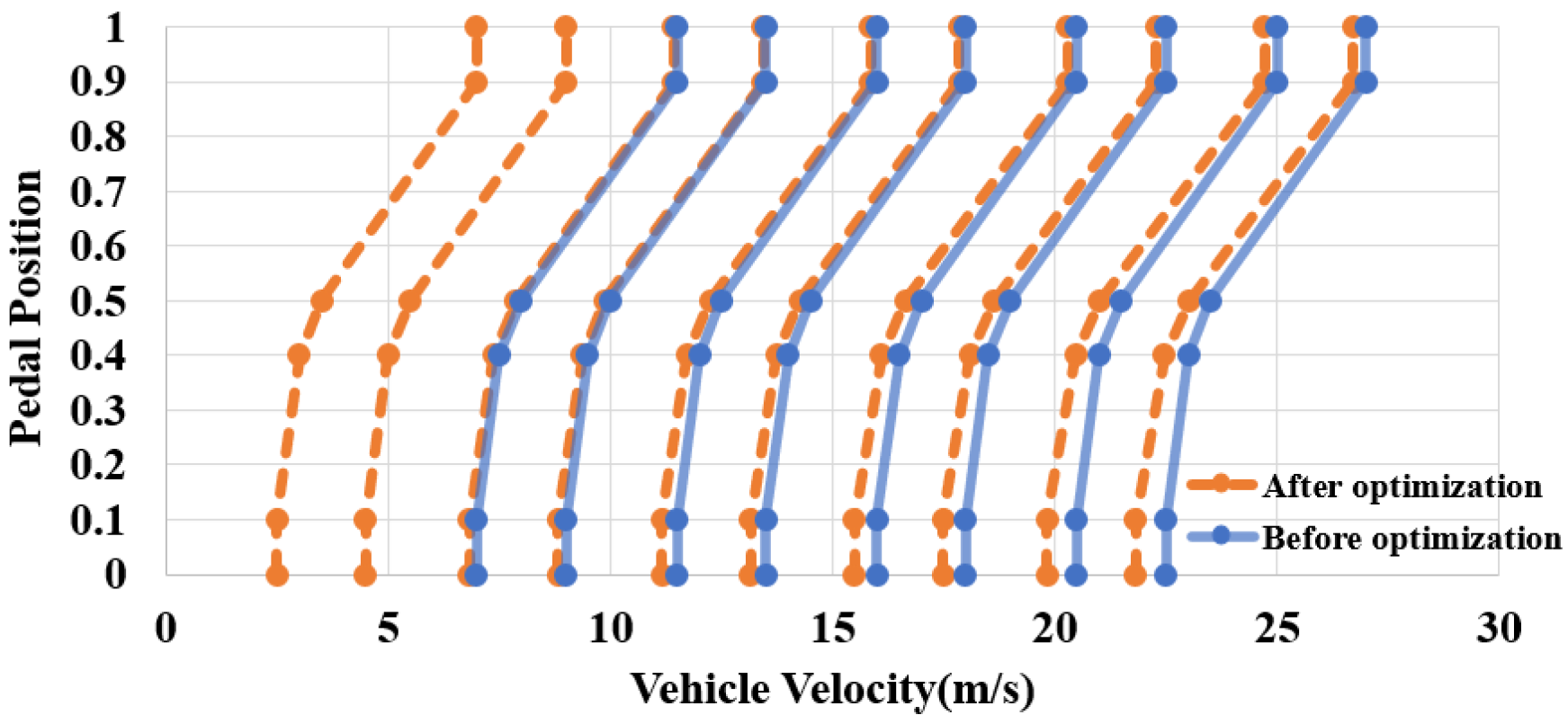
4.2. Selection of Optimization Variables
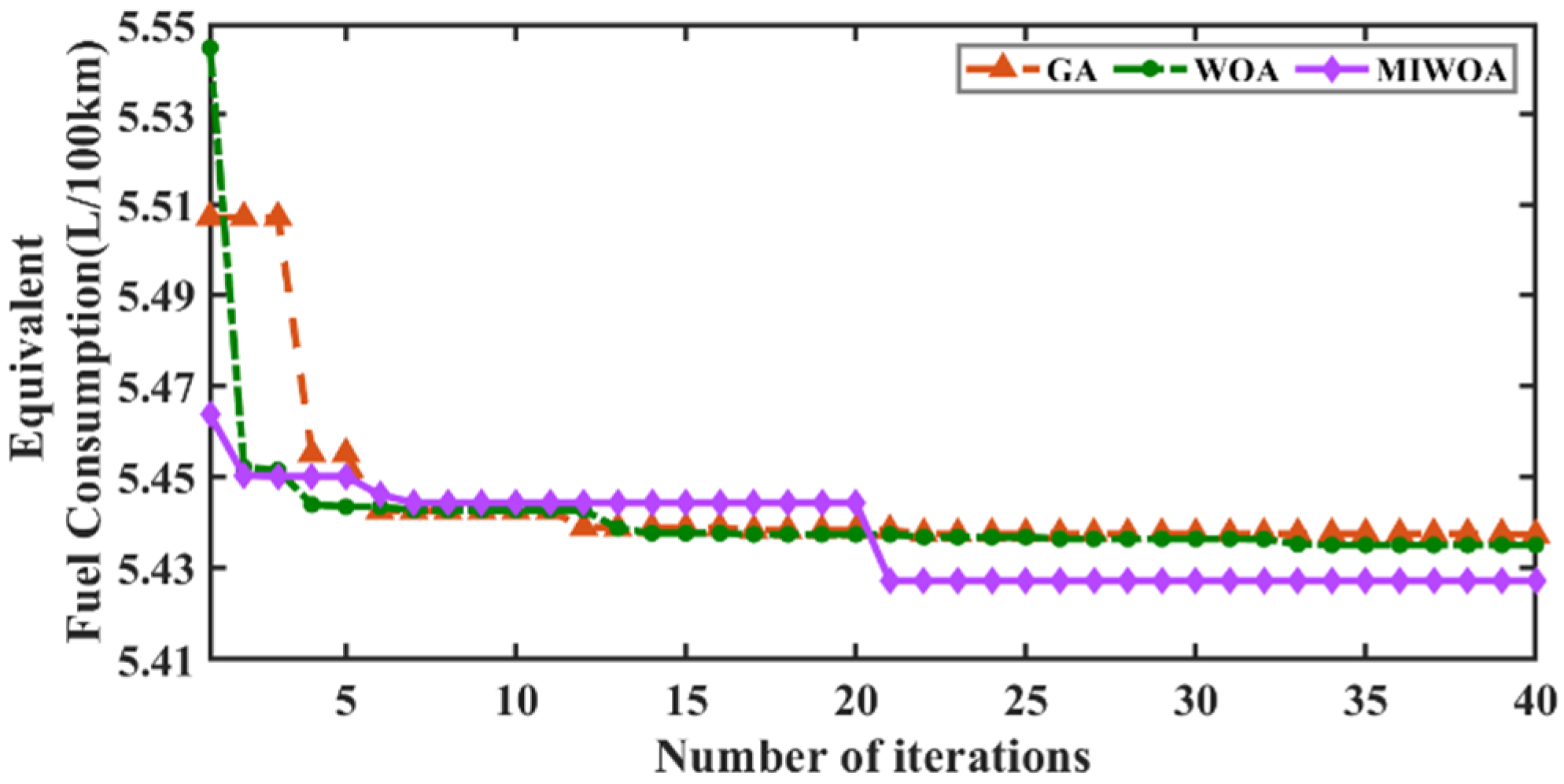
4.3. Optimization Method and Results
4.3.1. Fundamentals of WOA
- Encircle prey stage: After recognizing the prey, individual whales will transmit the prey’s location information to the group, and other whales will approach the prey location to encircle them. This behavior can be expressed by the following equation:
- 2.
- Bubble net attack: The whale first estimates the distance to its prey and then slowly approaches the prey’s position. The process of capturing the prey by forming a spiral of bubbles around the prey can be represented as follows:
- 3.
- Random search: When judging the parameters , the whale will choose its search agent to iteratively optimize toward a random individual position, perform a random search away from the present position, and search for the globally optimal solution. Its mathematical model is as follows:
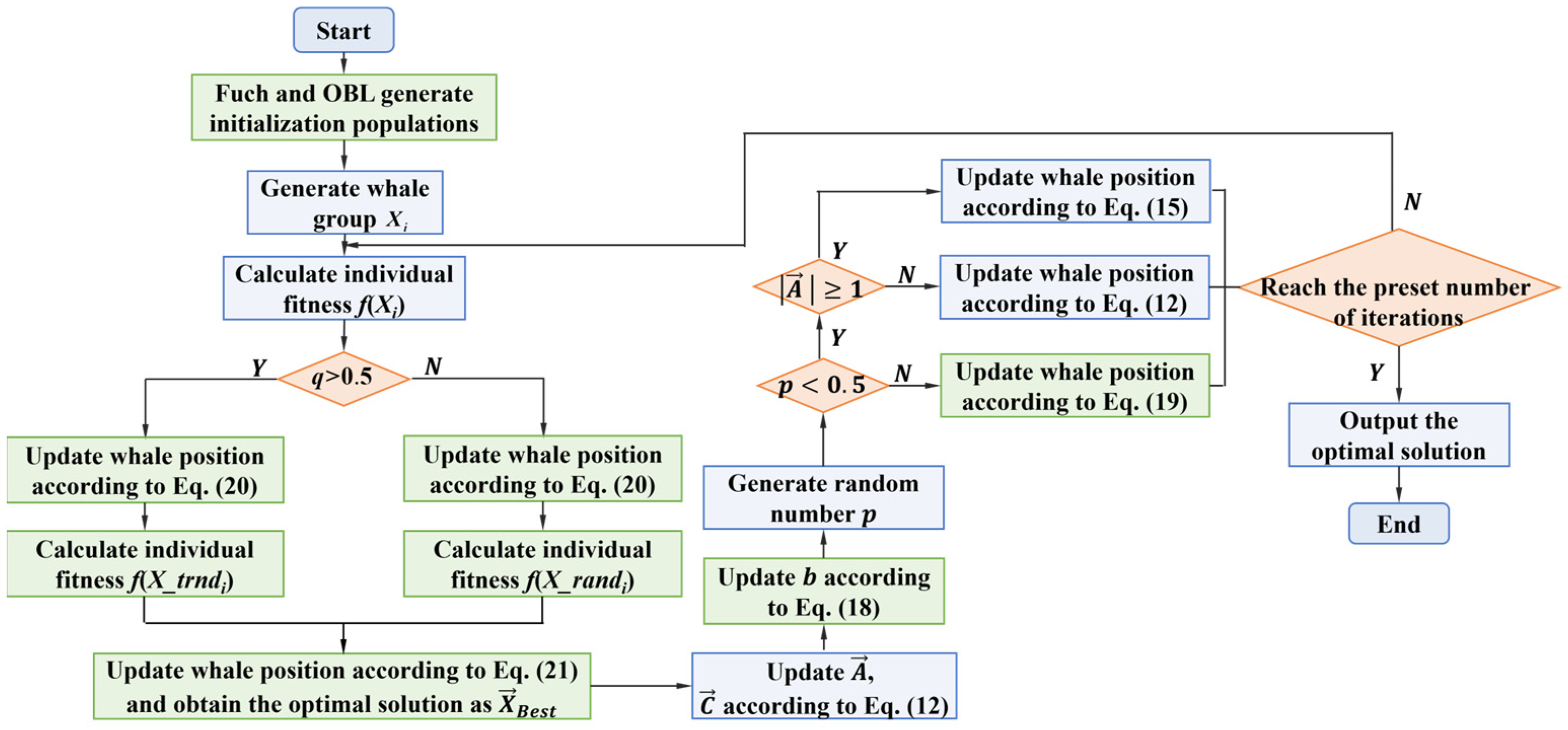
4.3.2. Fundamentals of MIWOA
- Fuch chaotic mapping is combined with OBL to generate more diverse initial populations.
- 2.
- Variable spiral parameter.
- 3.
- The adaptive weights are combined with t-distribution and random perturbation, respectively.
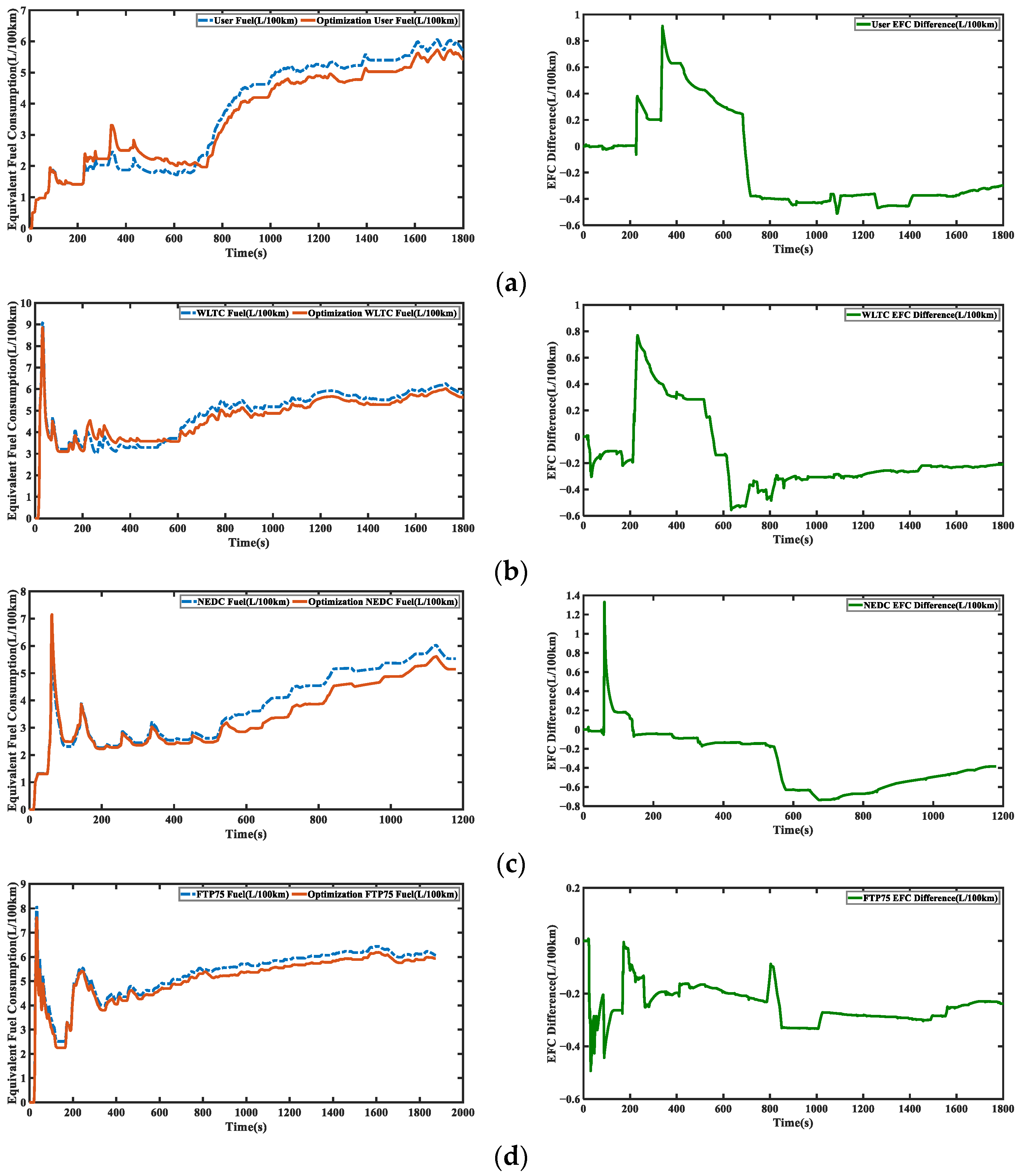
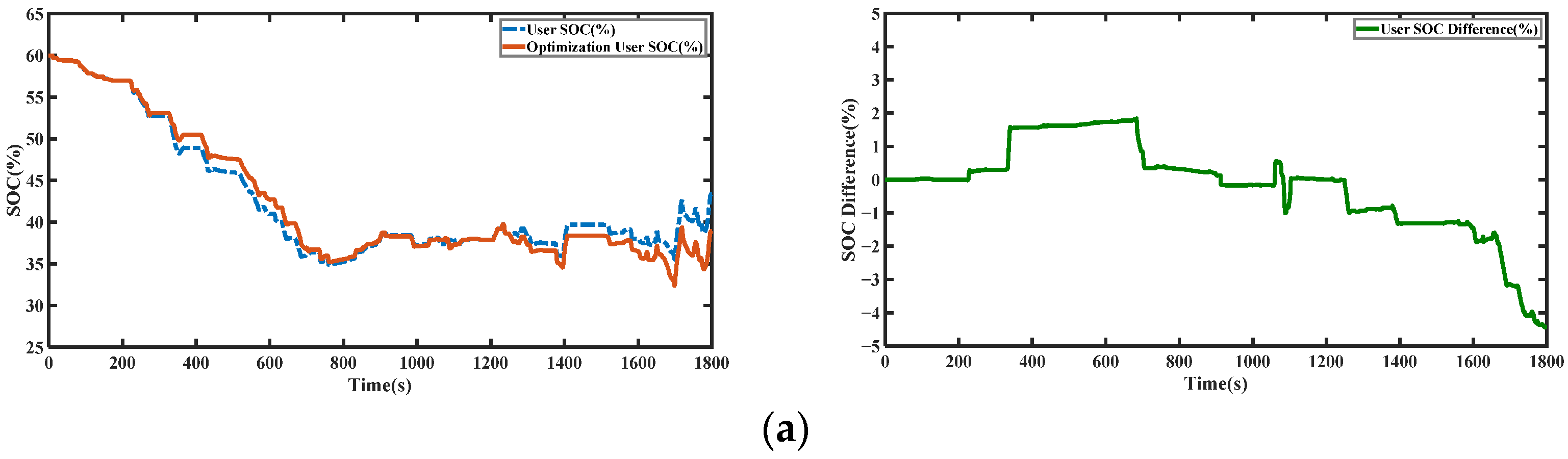
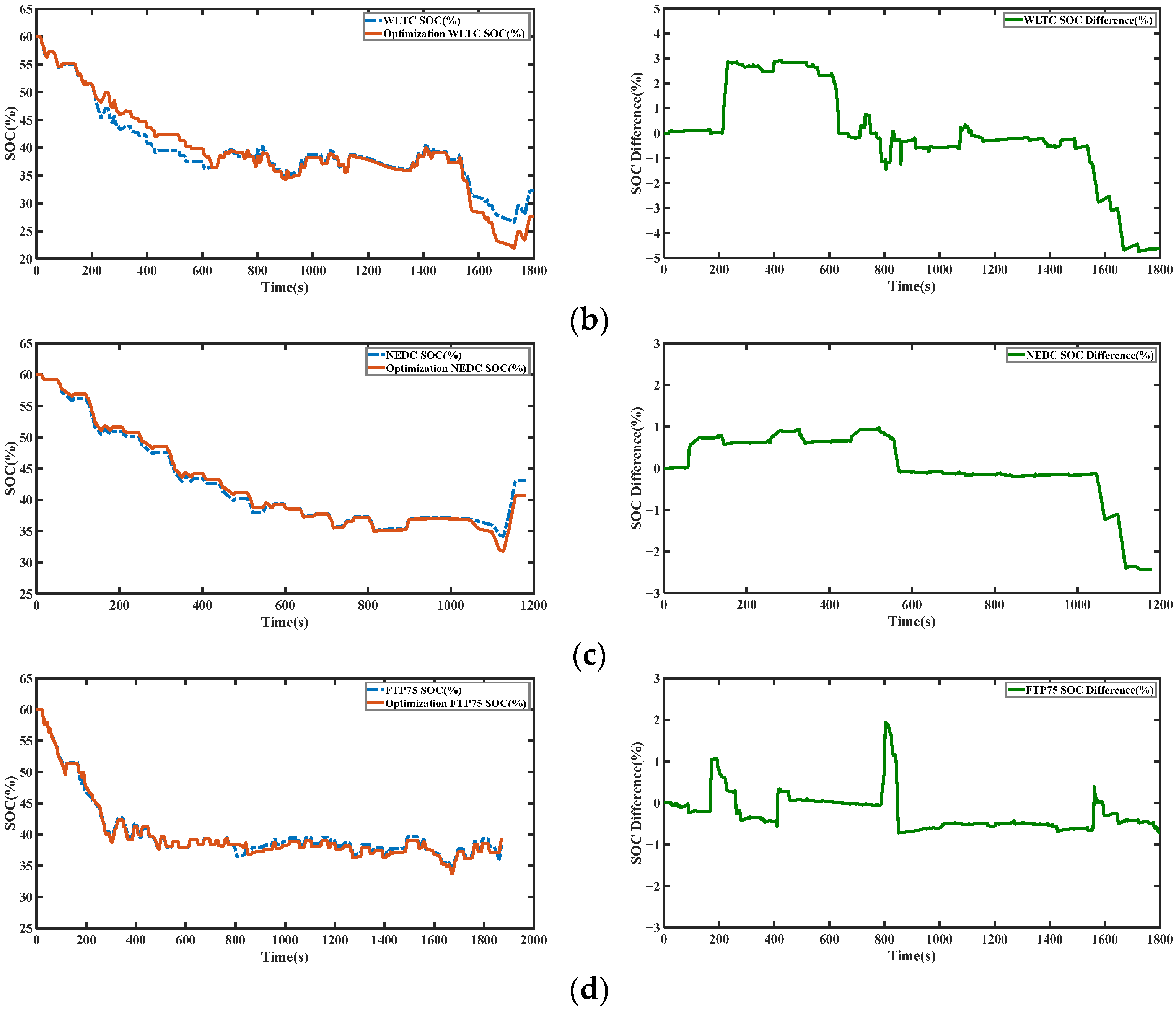
4.4. Optimization Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, L.; Hu, P.; Wei, H. Development of supercapacitor hybrid electric vehicle. J. Energy Storage 2023, 65, 107269. [Google Scholar] [CrossRef]
- Huang, R.; He, H.; Su, Q.; Härtl, M.; Jaensch, M. Enabling cross-type full-knowledge transferable energy management for hybrid electric vehicles via deep transfer reinforcement learning. Energy 2024, 305, 132394. [Google Scholar] [CrossRef]
- Shuai, Z.; Li, C.; Gai, J.; Han, Z.; Zeng, G.; Zhou, G. Coordinated motion and powertrain control of a series-parallel hybrid 8 × 8 vehicle with electric wheels. Mech. Syst. Signal Process. 2018, 120, 560–583. [Google Scholar] [CrossRef]
- Xue, J.; Jiao, X.; Yu, D.; Zhang, Y. Predictive hierarchical eco-driving control involving speed planning and energy management for connected plug-in hybrid electric vehicles. Energy 2023, 283, 129058. [Google Scholar] [CrossRef]
- Ruan, S.; Ma, Y.; Yang, N.; Yan, Q.; Xiang, C. Multiobjective optimization of longitudinal dynamics and energy management for HEVs based on nash bargaining game. Energy 2023, 262, 125422. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, X.; Tang, X.; Lin, X. Model predictive control of hybrid electric vehicles for fuel economy, emission reductions, and inter-vehicle safety in car-following scenarios. Energy 2020, 196, 117101. [Google Scholar] [CrossRef]
- Berzi, L.; Delogu, M.; Pierini, M. Development of driving cycles for electric vehicles in the context of the city of Florence. Transp. Res. Part D Transp. Environ. 2016, 47, 299–322. [Google Scholar] [CrossRef]
- Pacheco, F.; Cerrada, M.; Huertas, J.I. Threshold-guided multi-objective Generative Adversarial Networks for constructing artificial yet representative driving cycles. Eng. Appl. Artif. Intell. 2024, 129, 107665. [Google Scholar] [CrossRef]
- Brady, J.; O’mahony, M. Development of a driving cycle to evaluate the energy economy of electric vehicles in urban areas. Appl. Energy 2016, 177, 165–178. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Liu, P.; Zhang, Z.; Li, X.; Qu, C. Driving cycles construction for electric vehicles considering road environment: A case study in Beijing. Appl. Energy 2019, 253, 113514. [Google Scholar] [CrossRef]
- Lei, N.; Zhang, H.; Li, R.; Yu, J.; Wang, H.; Wang, Z. Physics-informed data-driven modeling approach for commuting-oriented hybrid powertrain optimization. Energy Convers. Manag. 2024, 299, 117814. [Google Scholar] [CrossRef]
- Wang, Y.; Li, K.; Zeng, X.; Gao, B.; Hong, J. Energy consumption characteristics based driving conditions construction and prediction for hybrid electric buses energy management. Energy 2022, 245, 123189. [Google Scholar] [CrossRef]
- Zhuang, W.; Eben, S.L.; Zhang, X.; Kum, D.; Song, Z.; Yin, G.; Ju, F. A survey of powertrain configuration studies on hybrid electric vehicles. Appl. Energy 2020, 262, 114553. [Google Scholar] [CrossRef]
- Qiu, H.; Cui, S.; Wang, S.; Wang, Y.; Feng, M. A Clustering-Based Optimization Method for the Driving Cycle Construction: A Case Study in Fuzhou and Putian, China. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18681–18694. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, H.; Ma, C.; He, H. Powertrain Parameters’ Optimization for a Series–Parallel Plug-In Hybrid Electric Bus by Using a Combinatorial Optimization Algorithm. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 32–43. [Google Scholar] [CrossRef]
- Lei, N.; Zhang, H.; Wang, H.; Wang, Z. An Improved Co-Optimization of Component Sizing and Energy Management for Hybrid Powertrains Interacting With High-fidelity Model. IEEE Trans. Veh. Technol. 2023, 72, 15585–15596. [Google Scholar] [CrossRef]
- Cui, Y.; Xu, H.; Zou, F.; Chen, Z.; Gong, K. Optimization based method to develop representative driving cycle for real-world fuel consumption estimation. Energy 2021, 235, 121434. [Google Scholar] [CrossRef]
- Tao, S.; Ding, K.; Li, Z.; Zhang, H. Development of a representative driving cycle for evaluating exhaust emission and fuel consumption for Chinese switcher locomotives. Appl. Energy 2022, 322, 119499. [Google Scholar] [CrossRef]
- Hull, C.; Collett, K.A.; McCulloch, M.D. Developing a representative driving cycle for paratransit that reflects measured data transients: Case study in Stellenbosch, South Africa. Transp. Res. Part A Policy Pr. 2024, 181, 103987. [Google Scholar] [CrossRef]
- Ma, R.; He, X.; Zheng, Y.; Zhou, B.; Lu, S.; Wu, Y. Real-world driving cycles and energy consumption informed by large-sized vehicle trajectory data. J. Clean. Prod. 2019, 223, 564–574. [Google Scholar] [CrossRef]
- Zhang, M.; Shi, S.; Lin, N.; Yue, B. High-Efficiency Driving Cycle Generation Using a Markov Chain Evolution Algorithm. IEEE Trans. Veh. Technol. 2019, 68, 1288–1301. [Google Scholar] [CrossRef]
- Nyberg, P.; Frisk, E.; Nielsen, L. Using Real-World Driving Databases to Generate Driving Cycles with Equivalence Properties. IEEE Trans. Veh. Technol. 2016, 65, 4095–4105. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, H.; Zhang, W.; Xuan, Y. Non-uniform state-based Markov chain model to improve the accuracy of transient contaminant transport prediction. Build. Environ. 2023, 245, 110977. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, X.; Yu, Q.; Ye, Y.; Yu, M. Development of a representative urban driving cycle construction methodology for electric vehicles: A case study in Xi’an. Transp. Res. D Transp. Environ. 2020, 81, 102279. [Google Scholar] [CrossRef]
- Yang, Y.; Li, T.; Zhang, T.; Yu, Q. Time dimension analysis: Comparison of Nanjing local driving cycles in 2009 and 2017. Sustain. Cities Soc. 2020, 53, 101949. [Google Scholar] [CrossRef]
- Huzayyin, O.A.; Salem, H.; Hassan, M.A. A representative urban driving cycle for passenger vehicles to estimate fuel consumption and emission rates under real-world driving conditions. Urban Clim. 2021, 36, 100810. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, L.; Kong, Z.; Yu, J.; Yan, C. Development of accelerated reliability test cycle for electric drive system based on vehicle operating data. Eng. Fail. Anal. 2022, 141, 106696. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, J.; Pi, D.; Lin, X.; Grzesiak, L.M.; Hu, X. Battery Health-Aware and Deep Reinforcement Learning-Based Energy Management for Naturalistic Data-Driven Driving Scenarios. IEEE Trans. Transp. Electrif. 2022, 8, 948–964. [Google Scholar] [CrossRef]
- Azad, S.; Alexander-Ramos, M.J. Robust Combined Design and Control Optimization of Hybrid-Electric Vehicles Using MDSDO. IEEE Trans. Veh. Technol. 2021, 70, 4139–4152. [Google Scholar] [CrossRef]
- Wang, Z.; Jiao, X. Optimization of the powertrain and energy management control parameters of a hybrid hydraulic vehicle based on improved multi-objective particle swarm optimization. Eng. Optim. 2021, 53, 1835–1854. [Google Scholar] [CrossRef]
- Eckert, J.J.; Silva, F.L.; da Silva, S.F.; Bueno, A.V.; de Oliveira, M.L.M.; Silva, L.C. Optimal design and power management control of hybrid biofuel–electric powertrain. Appl. Energy 2022, 325, 119903. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, W.; Cash, S.; Olatunbosun, O.; Xu, H.; Lu, G. Intelligent sizing of a series hybrid electric power-train system based on Chaos-enhanced accelerated particle swarm optimization. Appl. Energy 2017, 189, 588–601. [Google Scholar] [CrossRef]
- Jeoung, D.; Min, K.; Sunwoo, M. Automatic Transmission Shift Strategy Based on Greedy Algorithm Using Predicted Velocity. Int. J. Automot. Technol. 2020, 21, 159–168. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, X.; Sun, X.; Liang, J. Optimal Design of Shift Point Strategy for DCT Based on Particle Swarm Optimization. Machines 2021, 9, 196. [Google Scholar] [CrossRef]
- Eckert, J.J.; da Silva, S.F.; Santiciolli, F.M.; de Carvalho, Á.C.; Dedini, F.G. Multi-speed gearbox design and shifting control optimization to minimize fuel consumption, exhaust emissions and drivetrain mechanical losses. Mech. Mach. Theory 2022, 169, 104644. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, H.; Mi, S.; Zhao, W.; He, Z.; Qian, Y.; Lu, X. Comparative study of hybrid architectures integrated with dual-fuel intelligent charge compression ignition engine: A commercial powertrain solution towards carbon neutrality. Energy Convers. Manag. 2023, 292, 117423. [Google Scholar] [CrossRef]
- Jia, Q.; Zhang, C.; Zhang, H.; Zhang, Z.; Chen, H. Powertrain parameters and control strategy optimization of a novel master-slave electric-hydraulic hybrid vehicle. Energy Sources Part A Recover. Util. Environ. Eff. 2023, 45, 11752–11773. [Google Scholar] [CrossRef]
- Shen, P.; Zhao, Z.; Li, J.; Zhan, X. Development of a typical driving cycle for an intra-city hybrid electric bus with a fixed route. Transp. Res. Part D Transp. Environ. 2018, 59, 346–360. [Google Scholar] [CrossRef]
- Song, T.; Zhu, W.-X.; Su, S.-B.; Wang, W.-W. Distributed “End-Edge-Cloud” structural car-following control system for intelligent connected vehicle using sliding mode strategy. Commun. Nonlinear Sci. Numer. Simul. 2023, 126, 107468. [Google Scholar] [CrossRef]
- Yang, D.; Liu, T.; Zhang, X.; Zeng, X.; Song, D. Construction of high-precision driving cycle based on Metropolis-Hastings sampling and genetic algorithm. Transp. Res. Part D Transp. Environ. 2023, 118, 103715. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Chen, W. Data-driven fault diagnosis for PEMFC systems of hybrid tram based on deep learning. Int. J. Hydrogen Energy 2020, 45, 13483–13495. [Google Scholar] [CrossRef]
- Li, J. Research on Driving Condition Prediction and Adaptive Control Strategy of Plug-In Hybrid Electric Vehicle. Master’s Thesis, Jilin University, Changchun, China, 2020. [Google Scholar]
- Gao, H.; Zhang, X.; Zeng, X.; Yang, D.; Song, D.; Zhou, L. Predictive cruise control for hybrid electric vehicles based on hierarchical convex optimization. Energy Convers. Manag. 2024, 299, 117883. [Google Scholar] [CrossRef]
- Alpaslan, E.; Karaoğlan, M.U.; Colpan, C.O. Investigation of drive cycle simulation performance for electric, hybrid, and fuel cell powertrains of a small-sized vehicle. Int. J. Hydrogen Energy 2023, 48, 39497–39513. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H.; Varzaneh, Z.A.; Mirjalili, S. A Systematic Review of the Whale Optimization Algorithm: Theoretical Foundation, Improvements, and Hybridizations. Arch. Comput. Methods Eng. 2023, 30, 4113–4159. [Google Scholar] [CrossRef]
- Pham, Q.-V.; Mirjalili, S.; Kumar, N.; Alazab, M.; Hwang, W.-J. Whale Optimization Algorithm with Applications to Resource Allocation in Wireless Networks. IEEE Trans. Veh. Technol. 2020, 69, 4285–4297. [Google Scholar] [CrossRef]
- Che, Z.; Peng, C.; Yue, C. Optimizing LSTM with multi-strategy improved WOA for robust prediction of high-speed machine tests data. Chaos Solitons Fractals 2024, 178, 114394. [Google Scholar] [CrossRef]
- Yu, W.; Zhou, P.; Miao, Z.; Zhao, H.; Mou, J.; Zhou, W. Energy performance prediction of pump as turbine (PAT) based on PIWOA-BP neural network. Renew. Energy 2024, 222, 119873. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, Y.; Zhou, X.; Li, S.; Zhao, C.; Dou, C.; Shu, H. An aeration requirements calculating method based on BOD5 soft measurement model using deep learning and improved coati optimization algorithm. J. Water Process. Eng. 2024, 64, 105693. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; Volume 1, pp. 695–701. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, K.; Shi, D.; Li, M.; Yin, C. Research on economical shifting strategy for multi-gear and multi-mode parallel plug-in HEV based on DIRECT algorithm. Energy 2024, 286, 129574. [Google Scholar] [CrossRef]
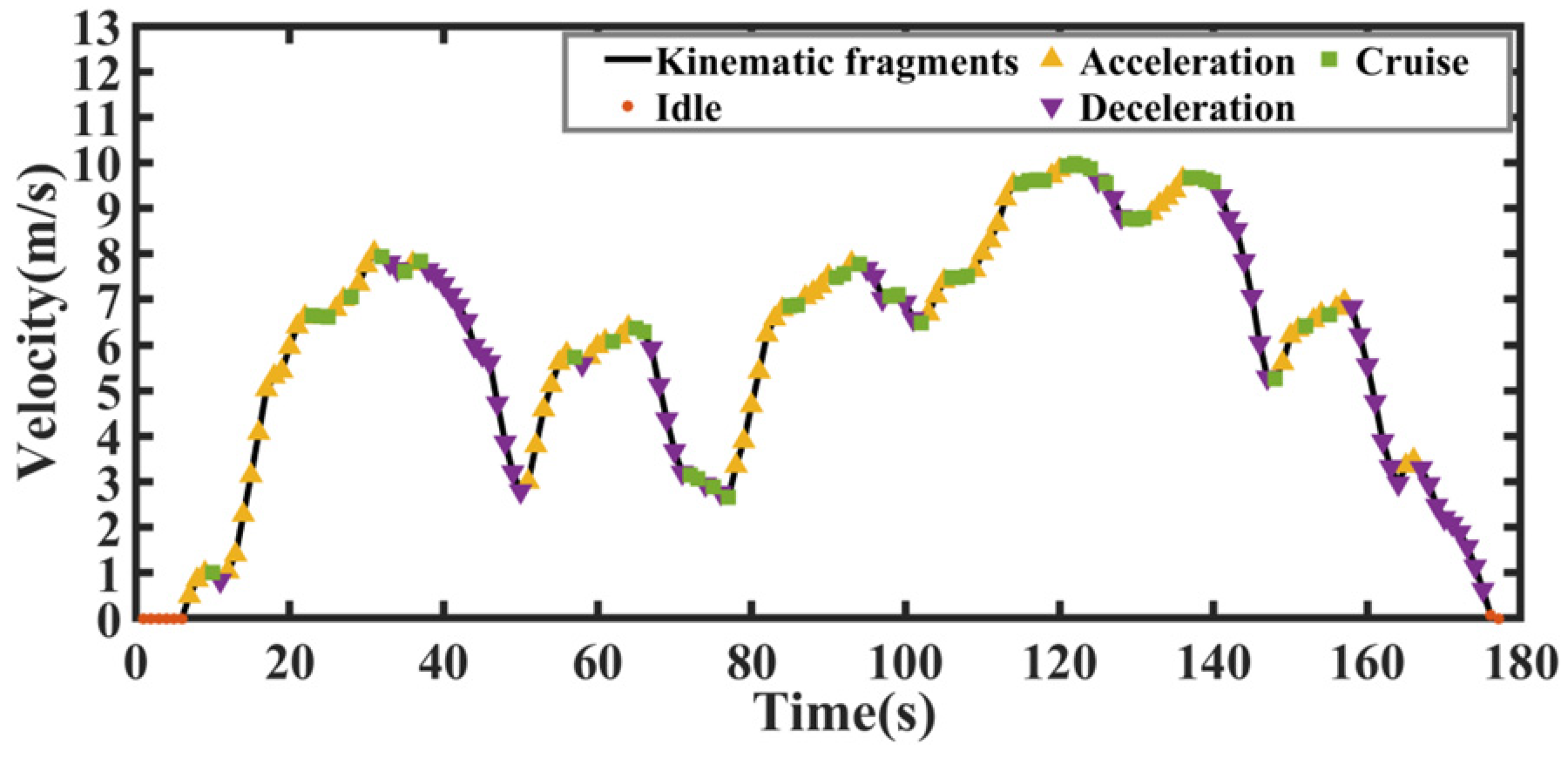



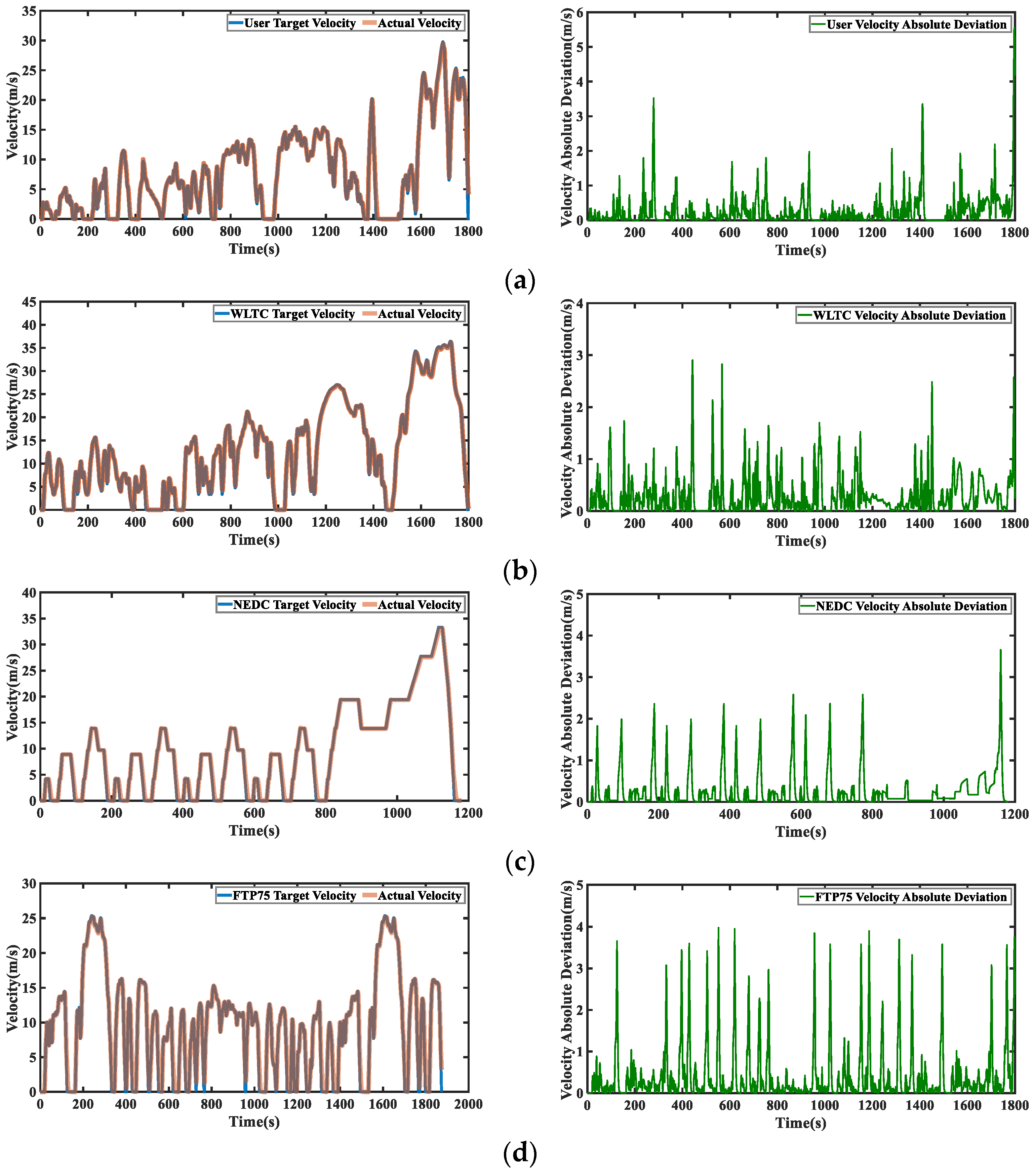
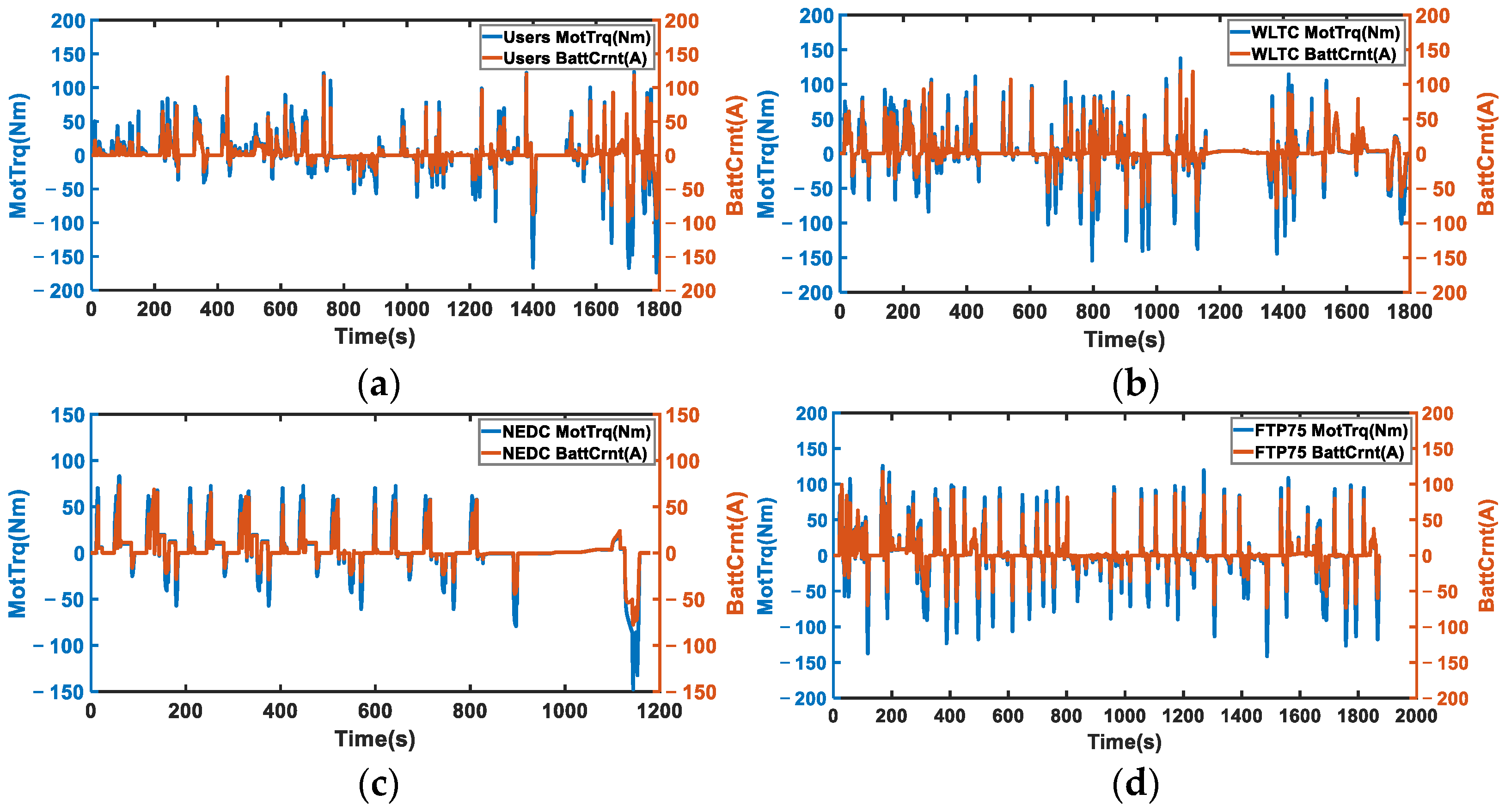


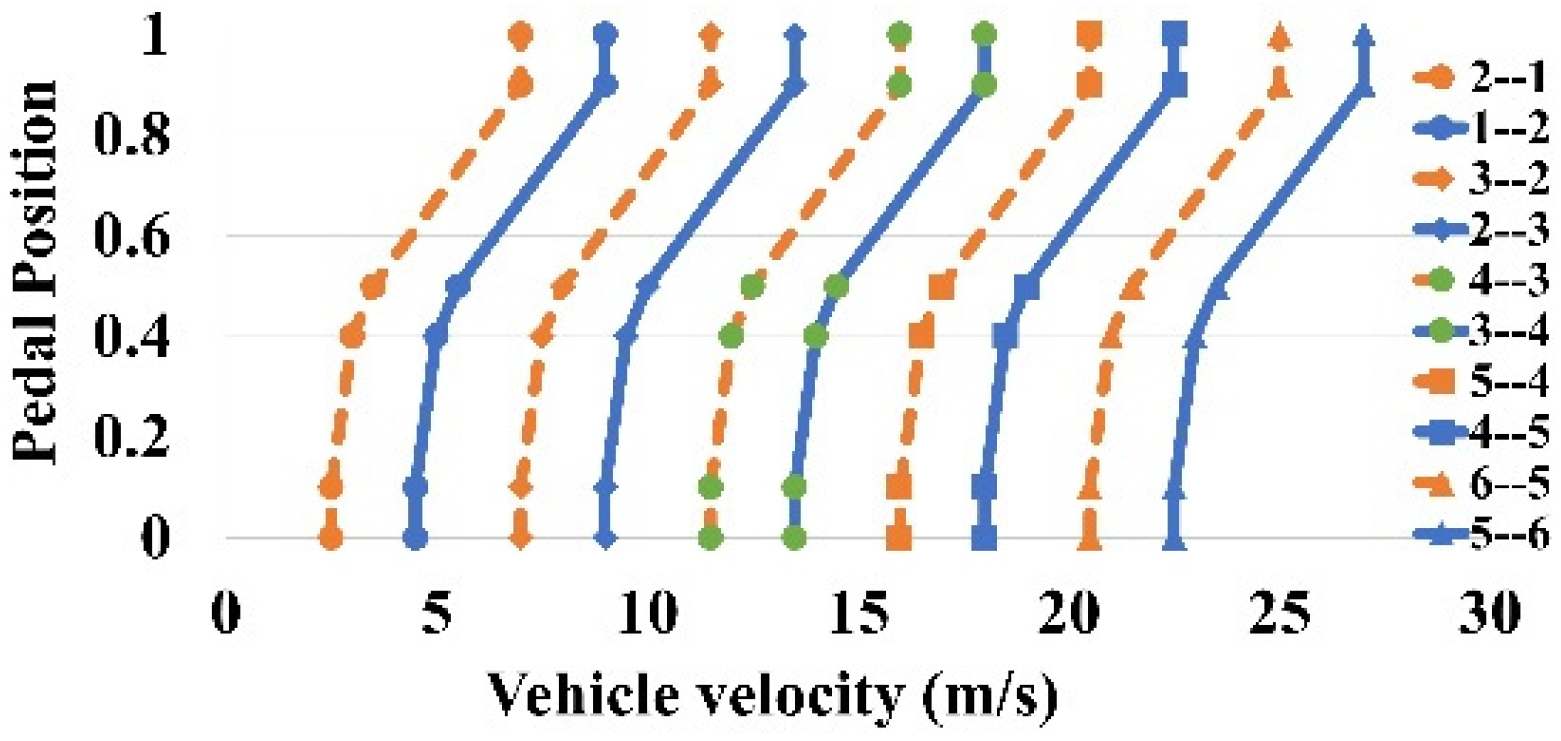

| Indicator | Idle | Acceleration | Deceleration | Cruise |
|---|---|---|---|---|
| Velocity (km/h) | <1 | ≥1 | ≥1 | ≥1 |
| Acceleration (m/s2) | - | >0.1 | <−0.1 | ≥−0.1 & ≤0.1 |
| No. | Feature Parameters | No. | Feature Parameters |
|---|---|---|---|
| 1 | ) | 15 | ) |
| 2 | ) | 16 | ) |
| 3 | ) | 17 | ) |
| 4 | ) | 18 | ) |
| 5 | ) | 19 | ) |
| 6 | ) | 20 | ) |
| 7 | Average pedal opening (%) | 21 | ) |
| 8 | ) | 22 | ) |
| 9 | ) | 23 | ) |
| 10 | time ratio | 24 | ) |
| 11 | time ratio | 25 | ) |
| 12 | time ratio | 26 | Maximum state of charge (SOC) (%) |
| 13 | time ratio | 27 | Average SOC (%) |
| 14 | time ratio |
| No. | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th |
|---|---|---|---|---|---|---|---|---|
| 1 | −15.17 | −17.79 | −0.423 | 0.39 | −1.69 | −2.00 | −1.17 | −0.09 |
| 2 | −18.04 | −15.30 | −2.72 | 0.60 | −0.63 | −0.60 | 0.06 | −0.05 |
| 3 | −14.76 | −18.18 | 0.50 | 0.59 | −0.83 | −2.65 | −1.07 | 0.37 |
| 4 | −17.43 | −16.05 | −0.05 | 0.77 | −0.83 | −1.55 | −0.69 | −0.38 |
| 5 | −18.14 | −15.22 | −2.50 | 0.17 | −0.92 | −0.32 | −0.13 | −0.002 |
| 6 | −13.62 | −19.03 | −0.18 | −0.62 | −1.64 | −3.02 | −0.86 | 0.42 |
| … | ||||||||
| 1841 | 2.47 | −1.57 | 2.59 | −0.56 | 0.25 | −1.68 | −0.32 | 0.20 |
| 1842 | 3.11 | −1.25 | −0.61 | −1.27 | −0.25 | −0.64 | −0.36 | 0.15 |
| No. | Characteristic Parameters | No. | Characteristic Parameters |
|---|---|---|---|
| 1 | Average velocity | 9 | Acceleration time ratio |
| 2 | Average traveling velocity | 10 | Deceleration time ratio |
| 3 | Standard deviation of velocity | 11 | Cruise time ratio |
| 4 | Average acceleration of acceleration section | 12 | Maximum velocity |
| 5 | Standard deviation of acceleration | 13 | Average engine speed |
| 6 | Average deceleration | 14 | Maximum voltage |
| 7 | Standard deviation of deceleration | 15 | Average voltage |
| 8 | Idle time ratio |
| Items | Parameters | Value |
|---|---|---|
| Vehicle | Mass | 1620 kg |
| Windward area | 2.46 m2 | |
| Engine | Displacement | 1.5 L |
| Maximum torque | 175 Nm | |
| Motor | Maximum power | 30 kW |
| Maximum torque | 200 Nm | |
| Battery | Capacity | 5.3 Ah |
| Transmission system | Transmission ratio | 0.772–4.212 |
| Main reduction ratio | 3.35 |
| Items | Before Optimization | After Optimization | Improvement |
|---|---|---|---|
| i0 | 3.35 | 3 | - |
| c1 | 4.5 | 4.2781 | |
| c2 | 0 | 0.3184 | |
| User EFC(L/100 km) | 5.7245 | 5.4271 | 5.20% |
| WLTC EFC (L/100 km) | 5.8325 | 5.6220 | 3.61% |
| NEDC EFC (L/100 km) | 5.5298 | 5.1435 | 6.99% |
| FTP-75 EFC (L/100 km) | 6.0717 | 5.9305 | 2.33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Pan, M.; Guan, W.; Zhang, Z.; Zhou, J.; Ye, N.; Qin, H.; Li, L.; Man, X. Economy Optimization by Multi-Strategy Improved Whale Optimization Algorithm Based on User Driving Cycle Construction for Hybrid Electric Vehicles. Machines 2025, 13, 158. https://doi.org/10.3390/machines13020158
Ma J, Pan M, Guan W, Zhang Z, Zhou J, Ye N, Qin H, Li L, Man X. Economy Optimization by Multi-Strategy Improved Whale Optimization Algorithm Based on User Driving Cycle Construction for Hybrid Electric Vehicles. Machines. 2025; 13(2):158. https://doi.org/10.3390/machines13020158
Chicago/Turabian StyleMa, Jie, Mingzhang Pan, Wei Guan, Zhiqing Zhang, Jingcheng Zhou, Nianye Ye, Haifeng Qin, Lulu Li, and Xingjia Man. 2025. "Economy Optimization by Multi-Strategy Improved Whale Optimization Algorithm Based on User Driving Cycle Construction for Hybrid Electric Vehicles" Machines 13, no. 2: 158. https://doi.org/10.3390/machines13020158
APA StyleMa, J., Pan, M., Guan, W., Zhang, Z., Zhou, J., Ye, N., Qin, H., Li, L., & Man, X. (2025). Economy Optimization by Multi-Strategy Improved Whale Optimization Algorithm Based on User Driving Cycle Construction for Hybrid Electric Vehicles. Machines, 13(2), 158. https://doi.org/10.3390/machines13020158







