Research and Mechanism Design Analysis of Leg Lifting Device Based on Human Body Stretching
Abstract
1. Introduction
2. Methods
2.1. Stages for Implementing the Leg Stretching Prototype
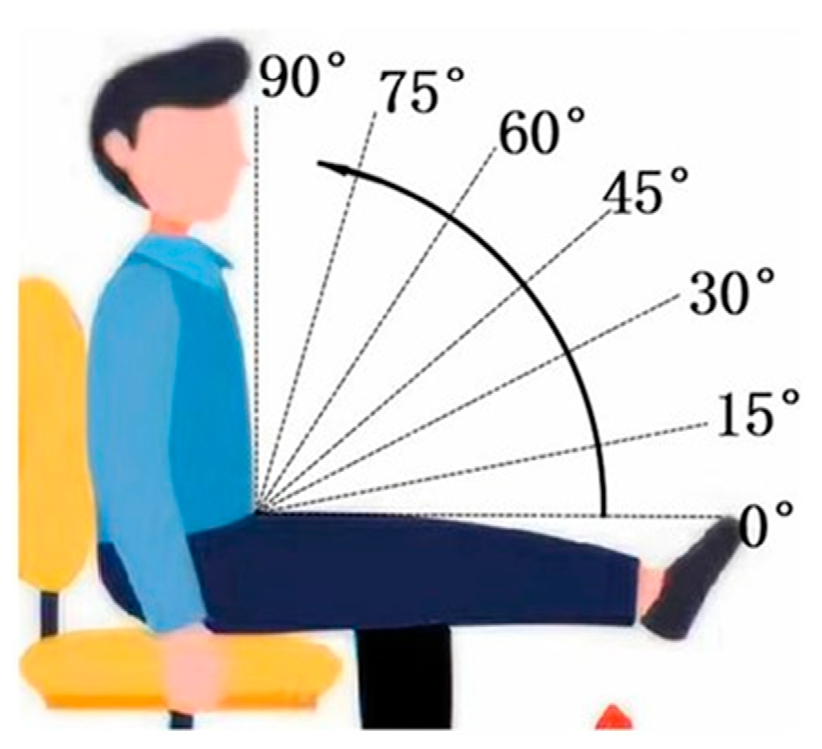
2.1.1. Stage 1: Requirements for Human Leg Lifting Action
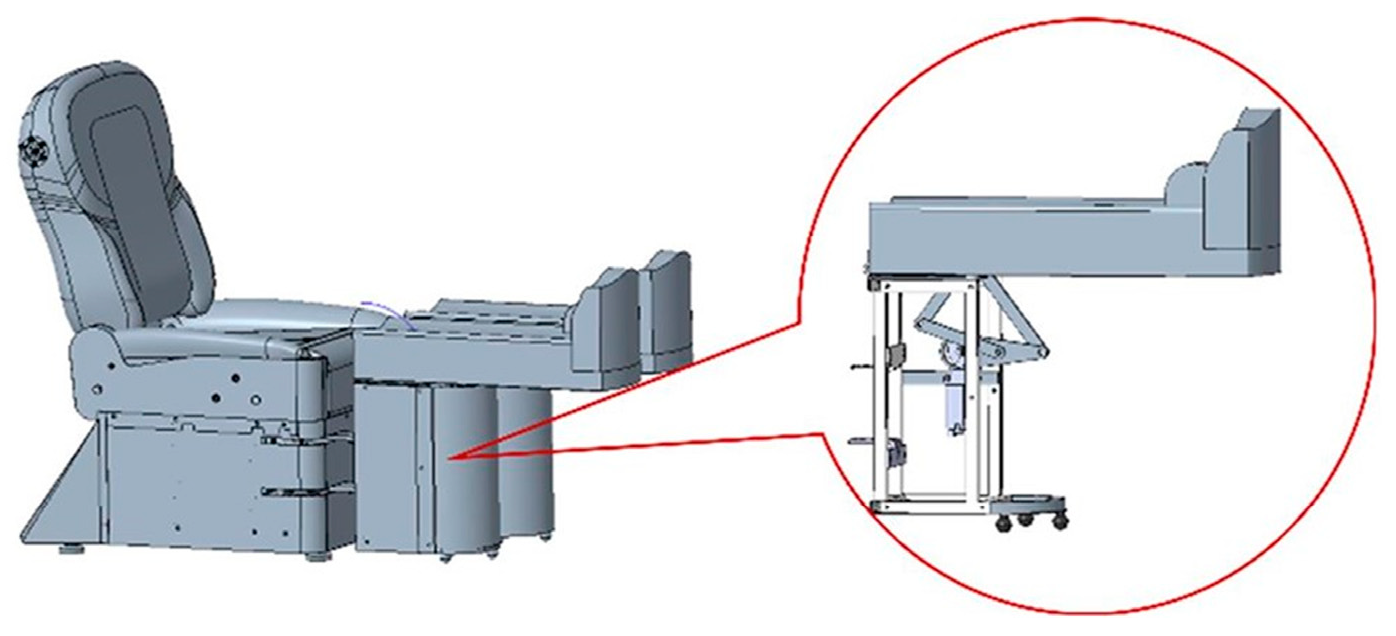
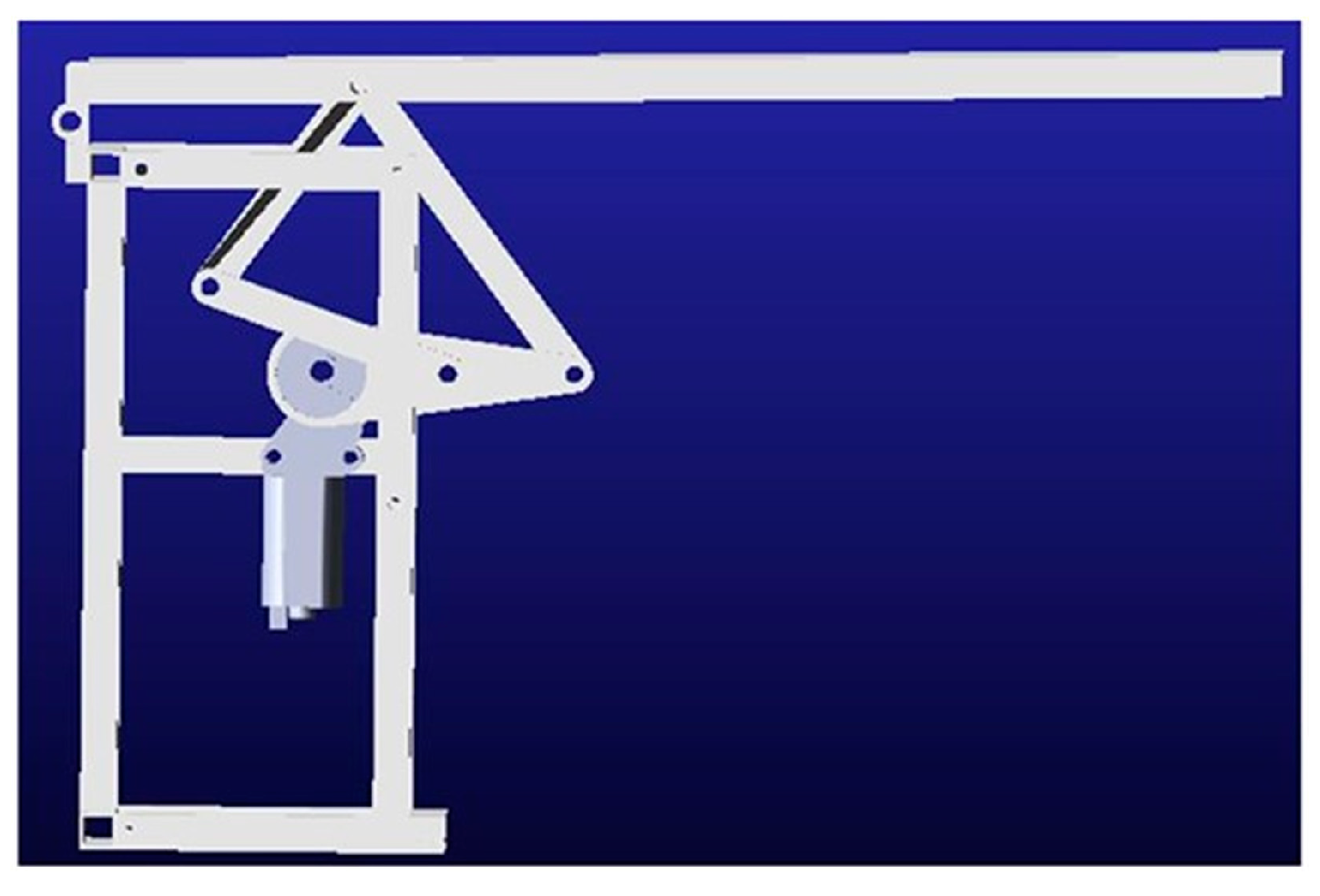
2.1.2. Stage 2: Design of Leg Lifting Action Mechanism
- (1)
- Location analysis
- (2)
- Speed analysis
- (3)
- Acceleration analysis
2.1.3. Stage 3: Motion Analysis of Leg Lifting Action Mechanism Based on ADAMS
2.1.4. Stage 4: Strength Analysis of Leg Lifting Action Mechanism Based on ABAQUS
2.2. Experiments
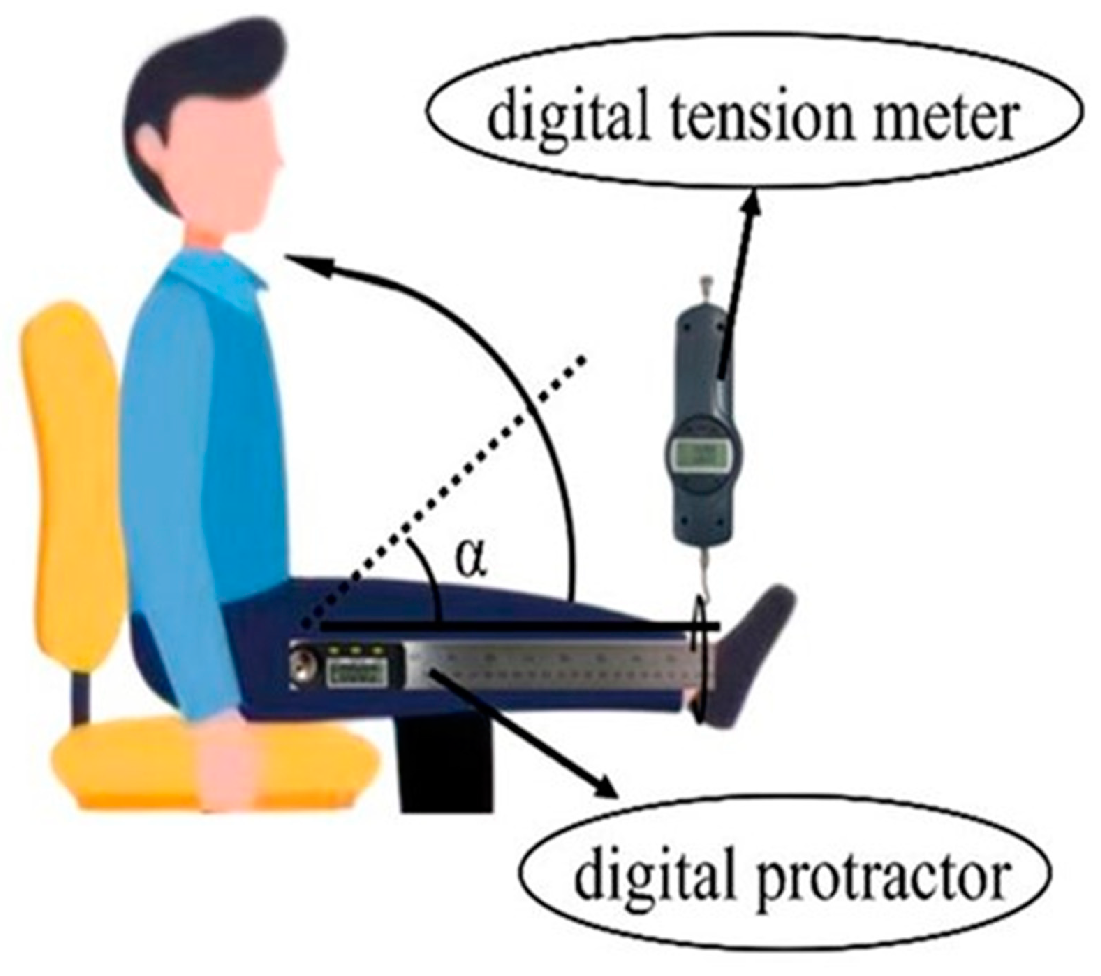
2.2.1. Experiments to Verify the Requirements for Human Leg Lifting Action
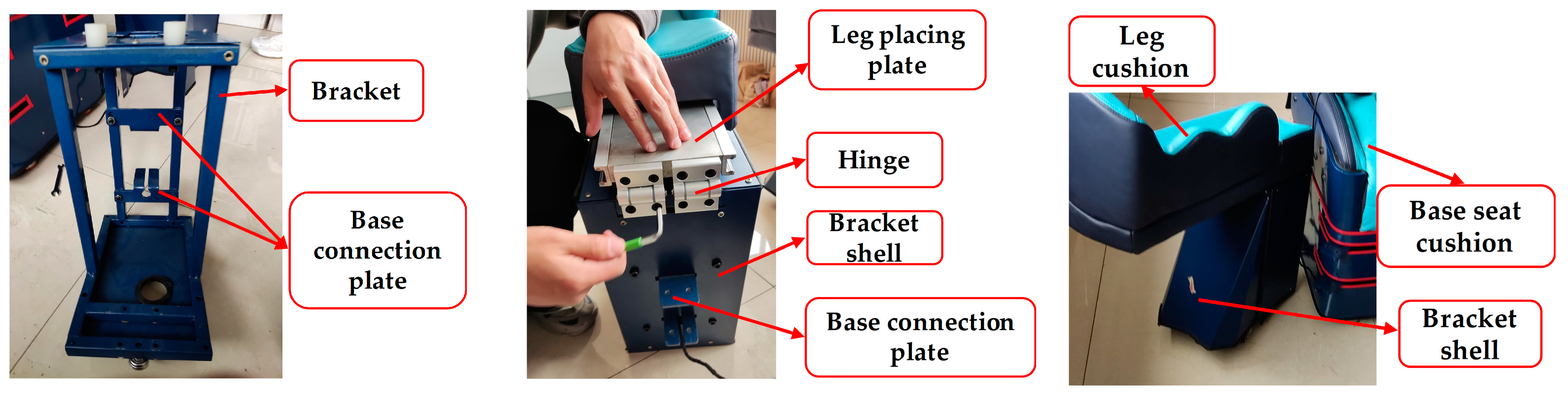
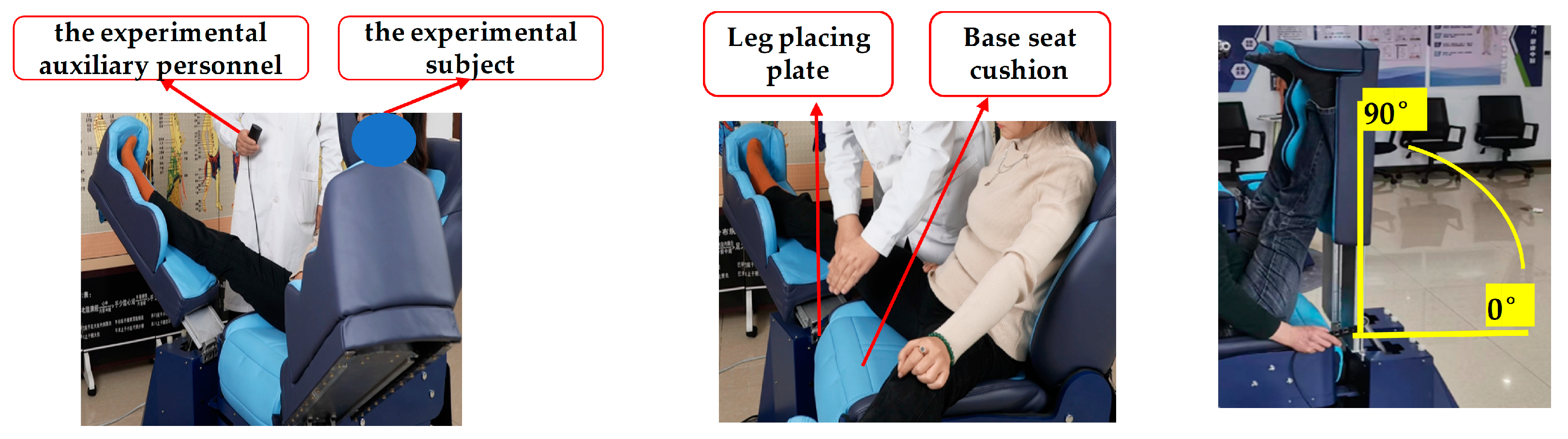
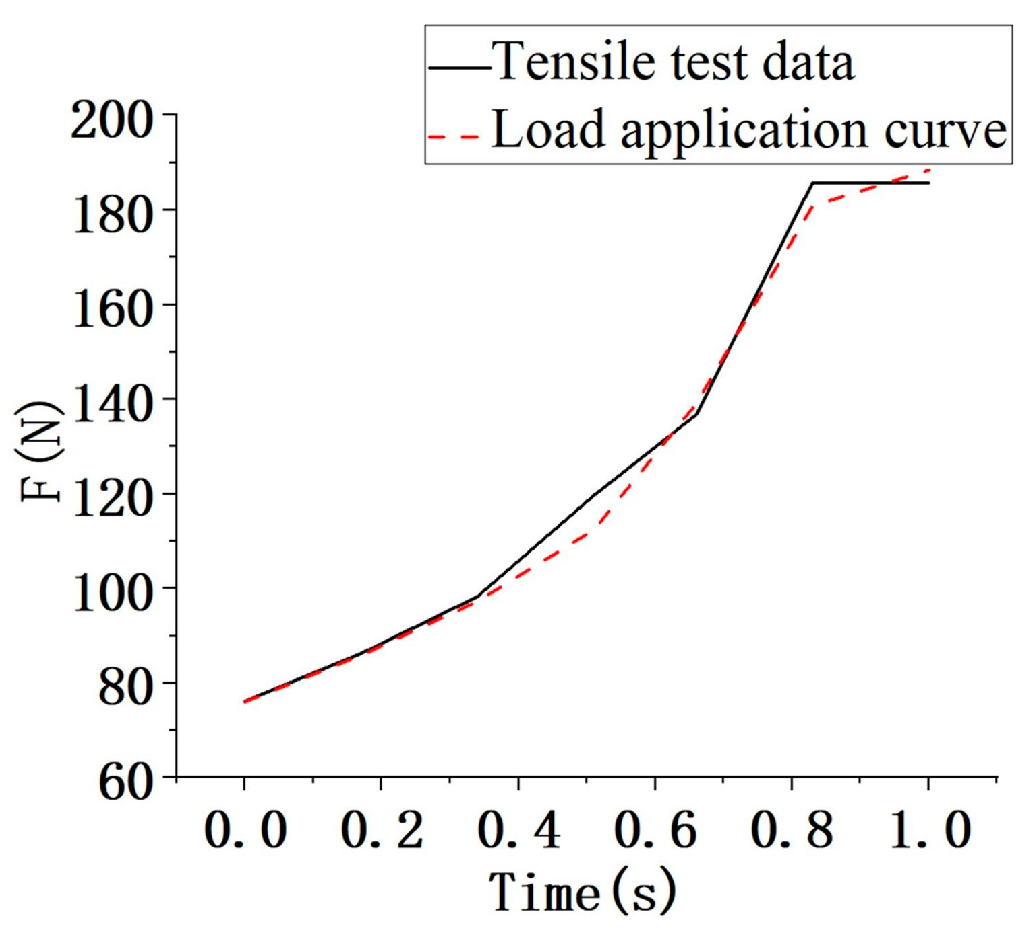
2.2.2. Experimental Verification of Device Prototype
3. Results and Discussion
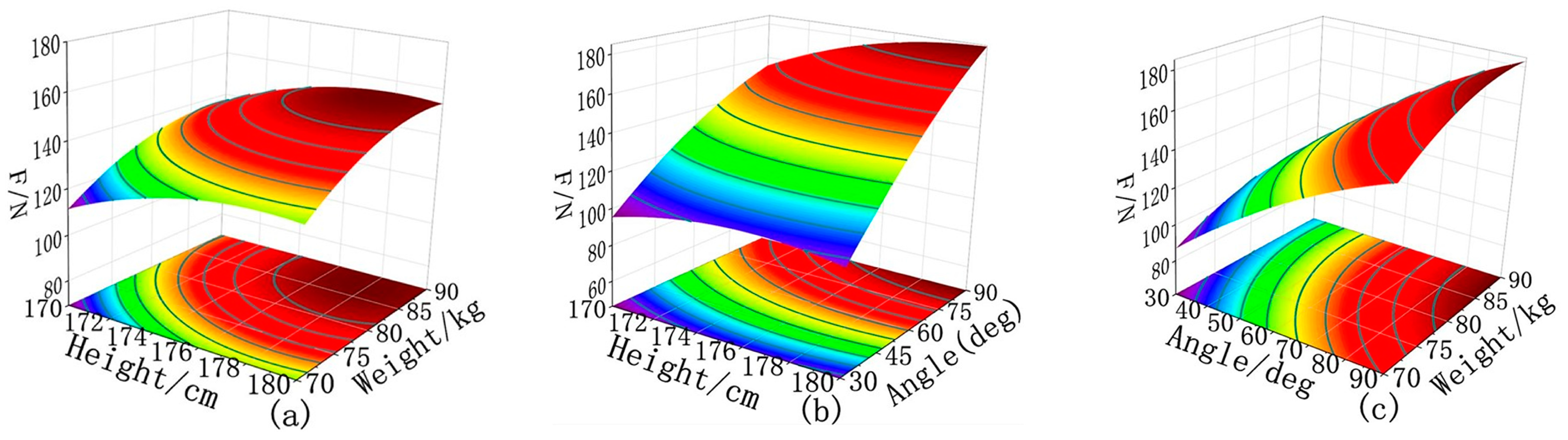
3.1. Results of the Requirements for Human Leg Lifting Action
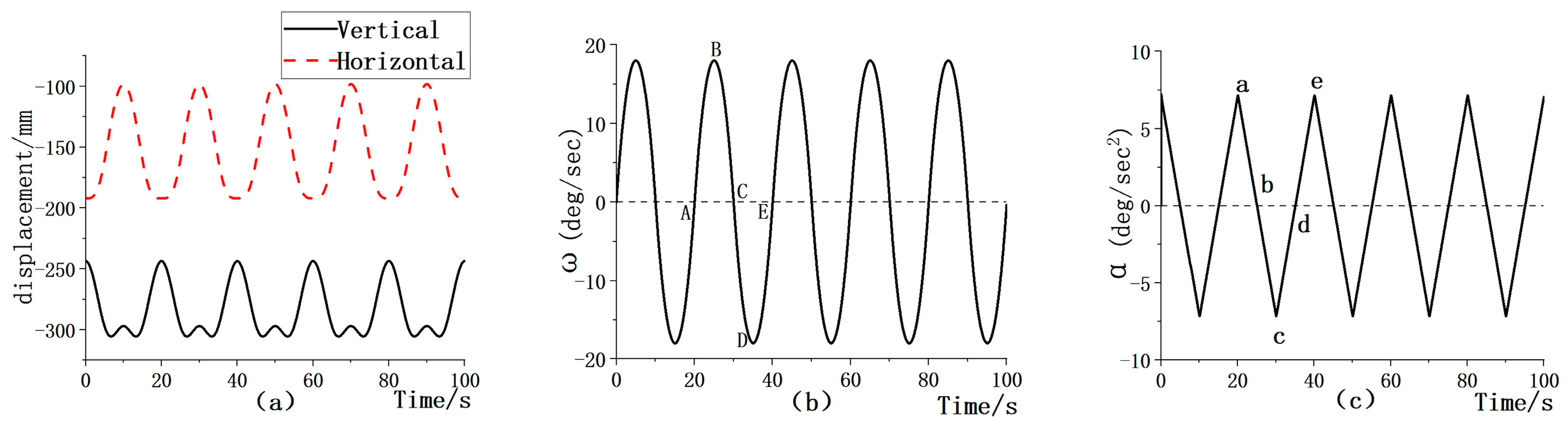
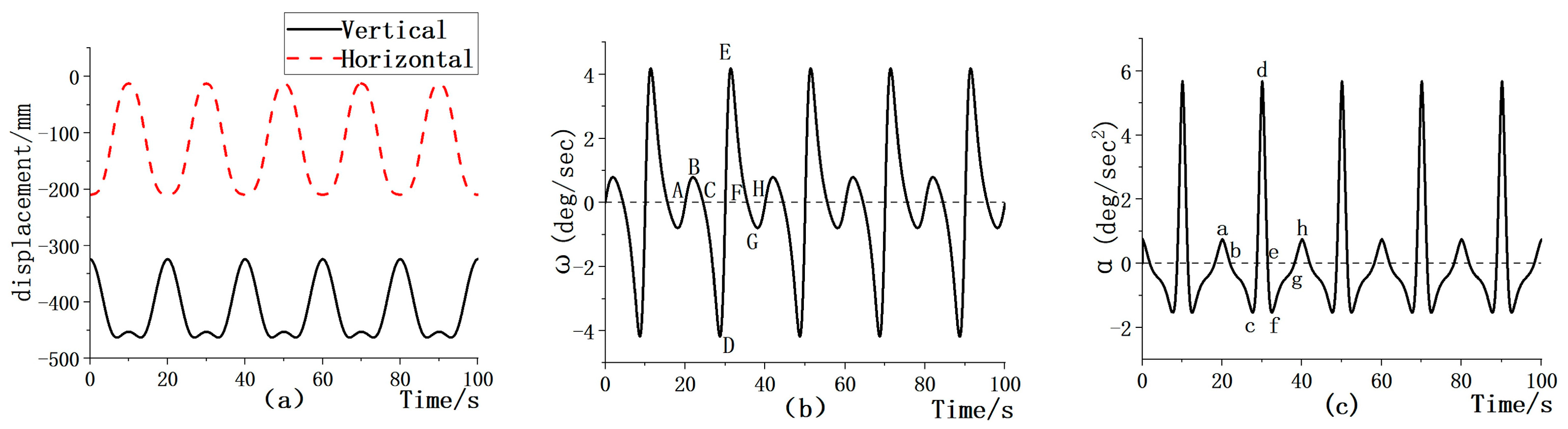
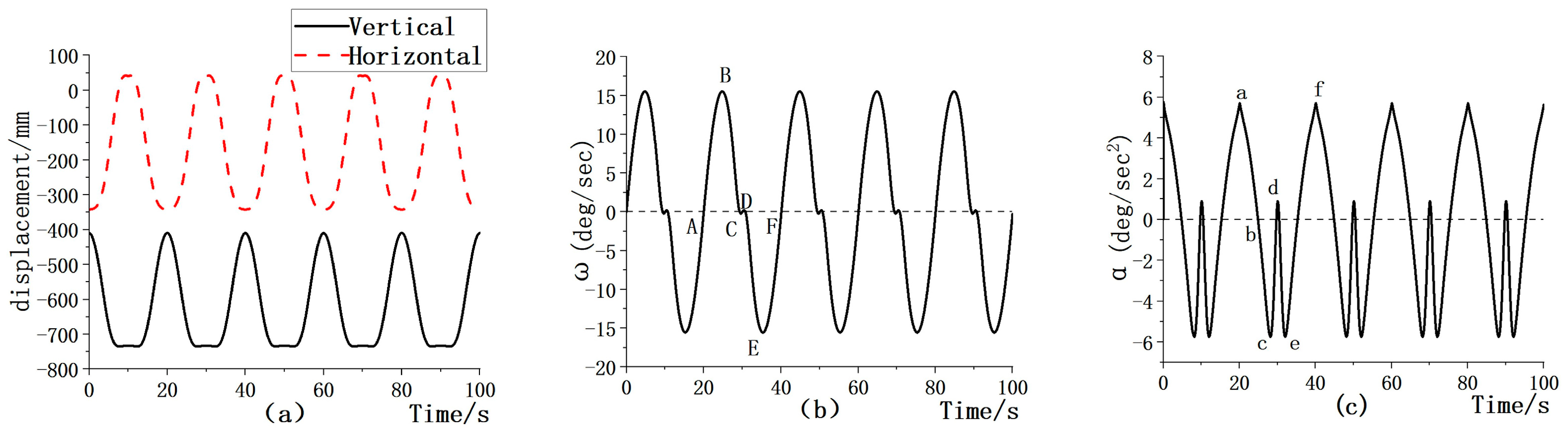
3.2. Results of Leg Lifting Action Mechanism Based on ADAMS
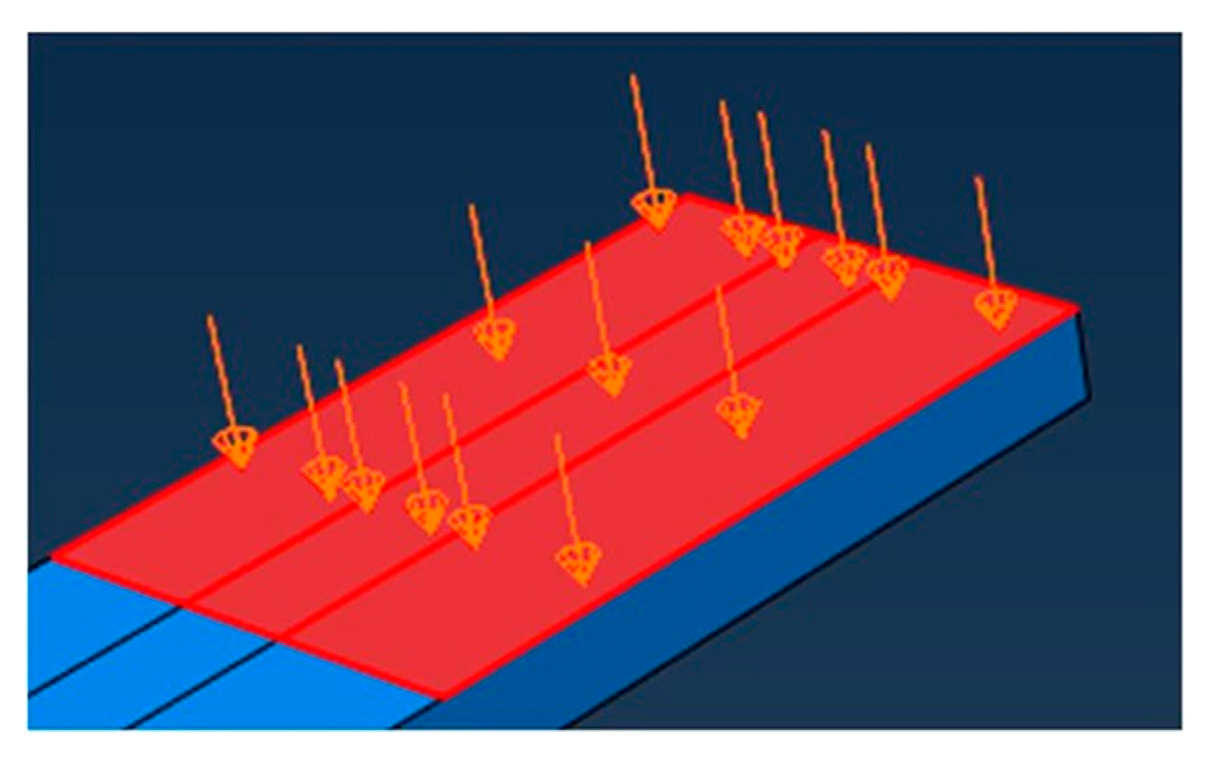
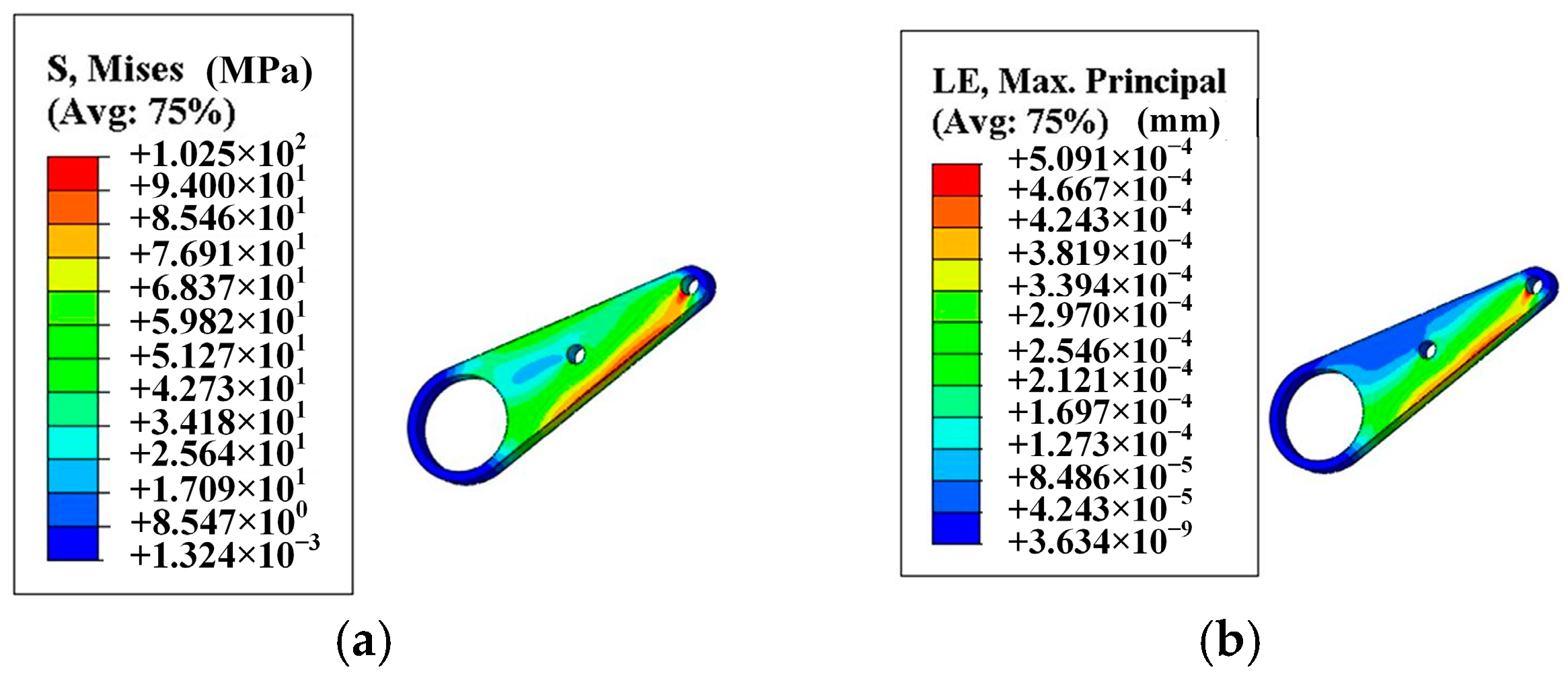
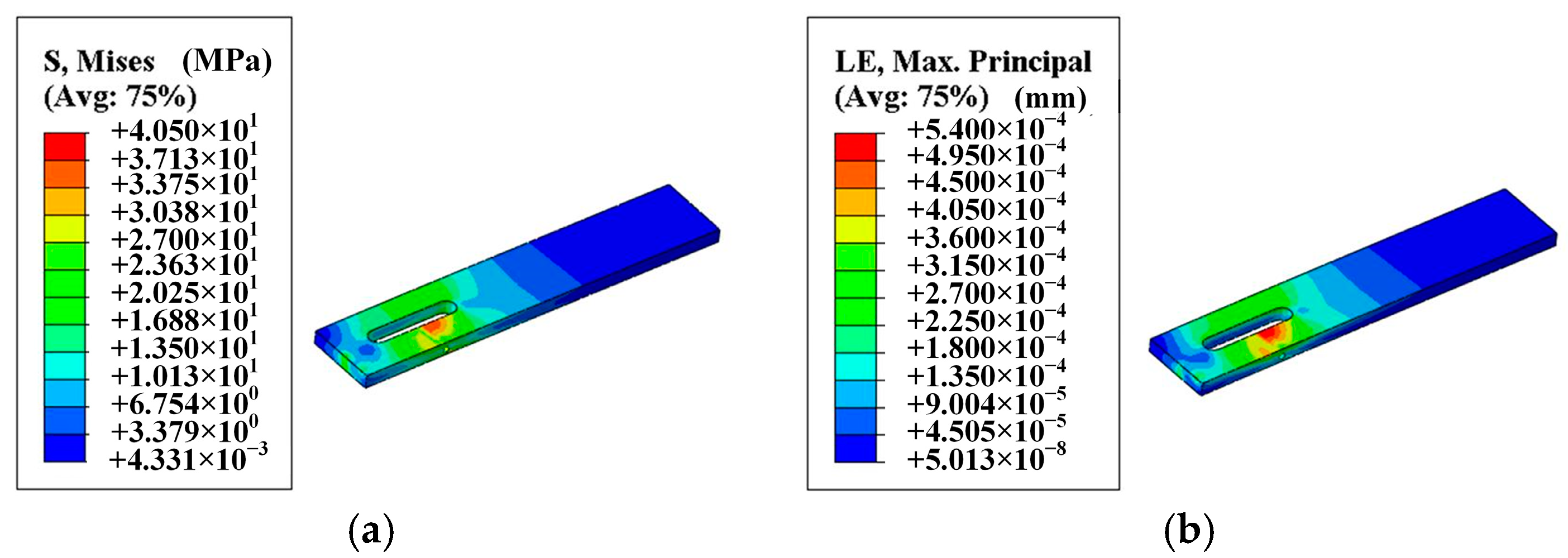
3.3. Results of Leg Lifting Action Mechanism Based on ABAQUS
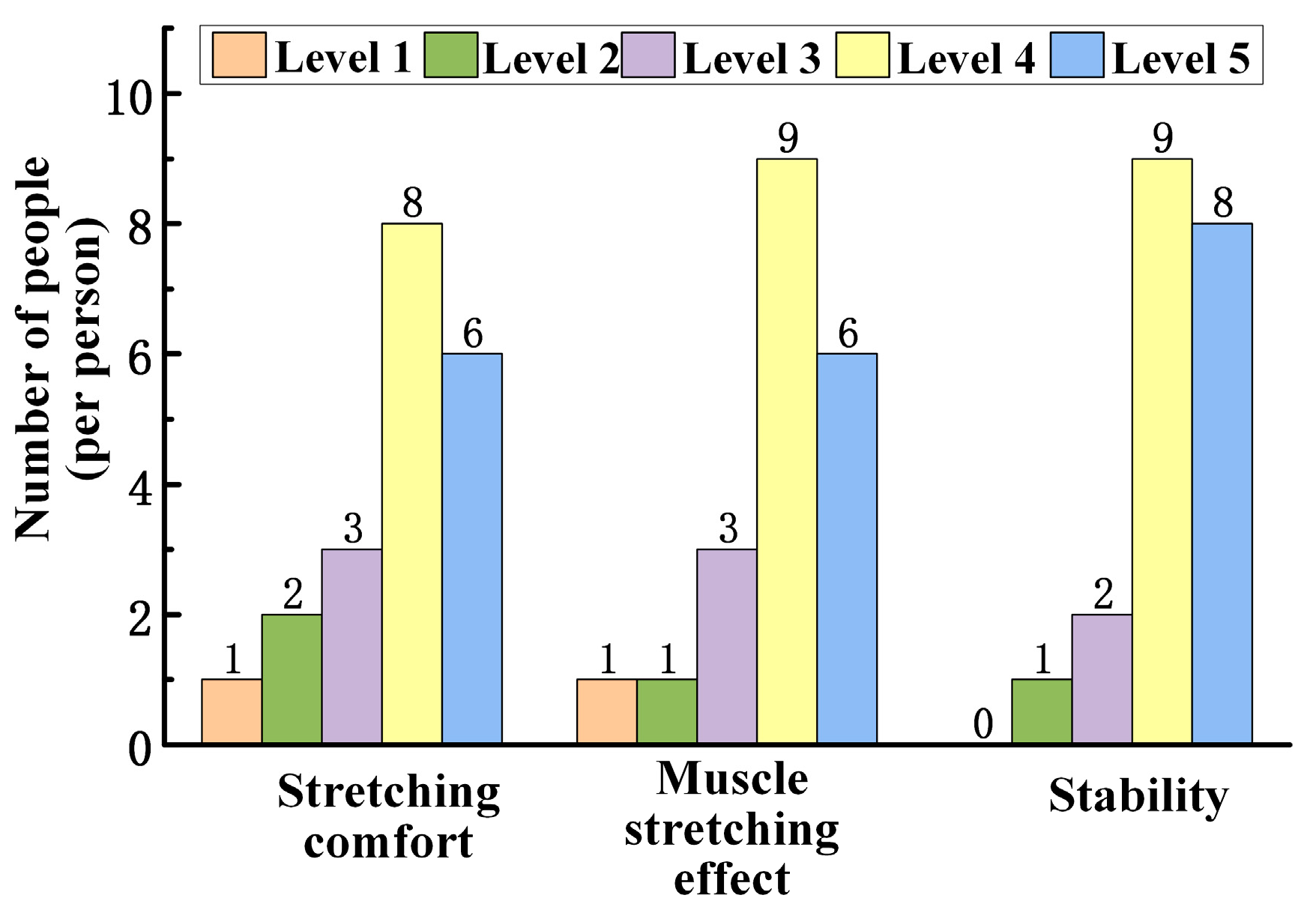
3.4. Results of the Device Prototype
4. Conclusions
- (1)
- Based on the BBD response surface method, the experimental results of the force change of the human leg during the lifting action show that the leg lifting angle has the most significant effect on the leg force. Under different height and weight conditions, the leg force is small when the leg lifting angle is 0–30°. As the lifting angle increases, the leg force also increases, and the maximum is at 90°, which guides the design of the leg lifting mechanism and the establishment of the model.
- (2)
- The human leg lifting mechanism was modeled using CREO, and the displacement equation, angular velocity equation, and angular acceleration equation of the mechanism were derived through a motion analysis and calculation of the mechanism. The simulation curves of the mechanism derived from ADAMS show that the motion process of the leg lifting mechanism is relatively smooth and the motion position meets the actual demand of leg extension.
- (3)
- Combined with the test results of the force changes during the leg lifting action, the strength of the key components during the movement of the mechanism was obtained through ABAQUS, and the results show that the maximum stress of the driving rod during the lifting process is 102.5 MPa, the maximum stress of the lifting rod is 88.12 MPa, and the maximum stress of the leg placing plate is 40.5 MPa, which are less than the material strength requirements, so the strength of the leg lifting mechanism meets the design requirements.
- (4)
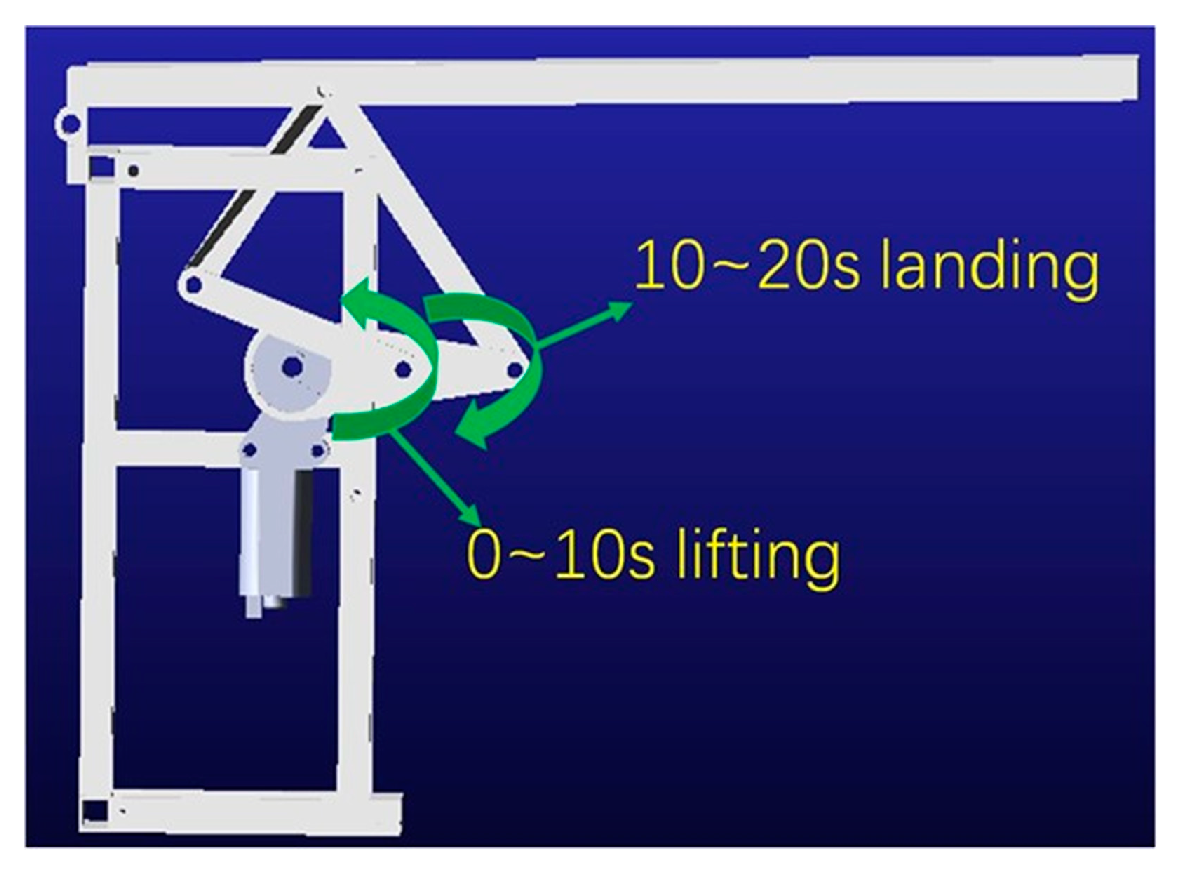
- A prototype of the device was made and experimentally validated with leg lifting. The experimental results show that the lifting angle of the leg lifting device ranges from 0° to 90°, which can meet the design requirements. In the process of stretching, the comfort and stability are good, and the muscle has an obvious stretching effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pega, F.; Náfrádi, B.; Momen, N.C.; Ujita, Y.; Streicher, K.N.; Prüss-Üstün, A.M.; Descatha, A.; Driscoll, T.; Fischer, F.M.; Godderis, L.; et al. Global, Regional, and National Burdens of Ischemic Heart Disease and Stroke Attributable to Exposure to Long Working Hours for 194 Countries, 2000–2016: A Systematic Analysis from the WHO/ILO Joint Estimates of the Work-Related Burden of Disease and Injury. Environ. Int. 2021, 154, 106595. [Google Scholar] [CrossRef] [PubMed]
- Qassim, H.M.; Wan Hasan, W.Z. A Review on Upper Limb Rehabilitation Robots. Appl. Sci. 2020, 10, 6976. [Google Scholar] [CrossRef]
- Ning, Y.; Wang, H.; Liu, Y.; Wang, Q.; Rong, Y.; Niu, J. Design and Analysis of a Compatible Exoskeleton Rehabilitation Robot System Based on Upper Limb Movement Mechanism. Med. Biol. Eng. Comput. 2024, 62, 883–899. [Google Scholar] [CrossRef]
- Kwakkel, G.; Kollen, B.J.; Krebs, H.I. Effects of Robot-Assisted Therapy on Upper Limb Recovery after Stroke: A Systematic Review. Neurorehabil. Neural Repair. 2008, 22, 111–121. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Z.; Wu, H.; Yang, W.; Chen, H. Effect of lower limb rehabilitation robot on lower limb motor function of hemiplegic patients after stroke. Chin. J. Contemp. Neurol. Neurosurg. 2017, 17, 334–339. [Google Scholar] [CrossRef]
- Talaty, M.; Esquenazi, A.; Briceno, J.E. Differentiating Ability in Users of the ReWalkTM Powered Exoskeleton: An Analysis of Walking Kinematics. In Proceedings of the 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 24–26 June 2013; pp. 1–5. [Google Scholar]
- Neuhaus, P.D.; Noorden, J.H.; Craig, T.J.; Torres, T.; Kirschbaum, J.; Pratt, J.E. Design and Evaluation of Mina: A Robotic Orthosis for Paraplegics. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–8. [Google Scholar]
- Li, Z.; Ren, Z.; Zhao, K.; Deng, C.; Feng, Y. Human-Cooperative Control Design of a Walking Exoskeleton for Body Weight Support. IEEE Trans. Ind. Inform. 2020, 16, 2985–2996. [Google Scholar] [CrossRef]
- Chen, Q. Design, Analysis and Experimental Study of a Cable-Driven Parallel Waist Rehabilitation Robot. J. Mech. Eng. 2018, 54, 126. [Google Scholar] [CrossRef]
- Zimmermann, Y.; Sommerhalder, M.; Wolf, P.; Riener, R.; Hutter, M. ANYexo 2.0: A Fully Actuated Upper-Limb Exoskeleton for Manipulation and Joint-Oriented Training in All Stages of Rehabilitation. IEEE Trans. Robot. 2023, 39, 2131–2150. [Google Scholar] [CrossRef]
- Pang, Z.; Wang, T.; Wang, Z.; Yu, J.; Sun, Z.; Liu, S. Design and Analysis of a Wearable Upper Limb Rehabilitation Robot with Characteristics of Tension Mechanism. Appl. Sci. 2020, 10, 2101. [Google Scholar] [CrossRef]
- Yan, H.; Wang, H.; Chen, P.; Niu, J.; Ning, Y.; Li, S.; Wang, X. Configuration Design of an Upper Limb Rehabilitation Robot with a Generalized Shoulder Joint. Appl. Sci. 2021, 11, 2080. [Google Scholar] [CrossRef]
- Fang, B.; Shen, L.; Li, Y.; Zhang, Y. Research of coordinated control for gait rehabilitation training robot. J. Mech. Electr. Eng. 2010, 27, 106–110. [Google Scholar] [CrossRef]
- Zou, Y.; Wang, N.; Wang, X.; Ma, H.; Liu, K. Design and Experimental Research of Movable Cable-Driven Lower Limb Rehabilitation Robot. IEEE Access 2019, 7, 2315–2326. [Google Scholar] [CrossRef]
- Kumar, S.; Wöhrle, H.; Trampler, M.; Simnofske, M.; Peters, H.; Mallwitz, M.; Kirchner, E.A.; Kirchner, F. Modular Design and Decentralized Control of the Recupera Exoskeleton for Stroke Rehabilitation. Appl. Sci. 2019, 9, 626. [Google Scholar] [CrossRef]
- Shi, X. Design & Analysis of the Mechanical System for a Spacial 4-DOF Series-Parallel Hybrid Lower Limb Rehabilitation Robot. J. Mech. Eng. 2017, 53, 48. [Google Scholar] [CrossRef]
- Ceccarelli, M.; Sanz, S.; Díaz, V.; Russo, M. Design and Construction of a Prototype of an Assisting Device for Arm Exercise. Machines 2024, 12, 145. [Google Scholar] [CrossRef]
- Jeon, K.-W.; Chung, H.-J.; Jung, E.-J.; Kang, J.-S.; Son, S.-E.; Yi, H. Development of Shoulder Muscle-Assistive Wearable Device for Work in Unstructured Postures. Machines 2023, 11, 258. [Google Scholar] [CrossRef]
- Russo, M.; Ceccarelli, M. Analysis of a Wearable Robotic System for Ankle Rehabilitation. Machines 2020, 8, 48. [Google Scholar] [CrossRef]
- Herrera-Valenzuela, D.; Díaz-Peña, L.; Redondo-Galán, C.; Arroyo, M.J.; Cascante-Gutiérrez, L.; Gil-Agudo, Á.; Moreno, J.C.; del-Ama, A.J. A Qualitative Study to Elicit User Requirements for Lower Limb Wearable Exoskeletons for Gait Rehabilitation in Spinal Cord Injury. J. NeuroEng. Rehabil. 2023, 20, 138. [Google Scholar] [CrossRef]
- Cho, D.Y.; Park, S.-W.; Lee, M.J.; Park, D.S.; Kim, E.J. Effects of Robot-Assisted Gait Training on the Balance and Gait of Chronic Stroke Patients: Focus on Dependent Ambulators. J. Phys. Ther. Sci. 2015, 27, 3053–3057. [Google Scholar] [CrossRef]
- Hassan, M.; Kadone, H.; Suzuki, K.; Sankai, Y. Wearable Gait Measurement System with an Instrumented Cane for Exoskeleton Control. Sensors 2014, 14, 1705–1722. [Google Scholar] [CrossRef]
- Zeng, D.; Jing, G.; Su, Y.; Wang, Y.; Hou, Y. A Novel Decoupled Parallel Mechanism with Two Translational and One Rotational Degree of Freedom and Its Performance Indices Analysis. Adv. Mech. Eng. 2016, 8, 1687814016646936. [Google Scholar] [CrossRef]
- Hu, J.; Sun, Y.; Cheng, Y. High Mechanical Advantage Design of Six-Bar Stephenson Mechanism for Servo Mechanical Presses. Adv. Mech. Eng. 2016, 8, 1687814016656108. [Google Scholar] [CrossRef]
- Menzemer, C.; Hilty, E.; Morrison, S.; Minor, R.; Srivatsan, T. Influence of Post Weld Heat Treatment on Strength of Three Aluminum Alloys Used in Light Poles. Metals 2016, 6, 52. [Google Scholar] [CrossRef]
- Jin, Y.; Gu, Q.; Liu, S.; Yang, C. Experimental Investigation and Modeling of Force-Induced Surface Errors for the Robot-Assisted Milling Process. Machines 2023, 11, 655. [Google Scholar] [CrossRef]
- Wen, S.; She, R.; Zhao, Z.; Gong, Y. Optimization of Motor Rotor Punch Wear Parameters Based on Response Surface Method. Machines 2024, 12, 671. [Google Scholar] [CrossRef]
- Lu, K.; Yin, C.; Qian, J.; Sun, Z.; Wang, L. Parameter Optimization Method for Centrifugal Feed Disc Discharging Based on Numerical Simulation and Response Surface. Machines 2024, 12, 799. [Google Scholar] [CrossRef]
- Essomba, T.; Phu, S.N. Kinematic Design of a Hybrid Planar-Tripod Mechanism for Bone Reduction Surgery. Mech. Ind. 2020, 21, 403. [Google Scholar] [CrossRef]
- GB/T 699-2015; Quality Carbon Structure Steels. SAC: Beijing, China, 2015.
- GB/T 3191-2019; Extrusion Rods and Bars of Aluminium and Aluminium Alloys. SAC: Beijing, China, 2019.






| Part Name | Model Drawing | Materials |
|---|---|---|
| Drive Rod |  | 45 Steel |
| Lift Rod |  | 45 Steel |
| Leg Placing Plate |  | Al6061 Alloy |
| Drive Auxiliary Rod |  | 45 Steel |
| Lift Auxiliary Rod |  | 45 Steel |
| Part Names | The Name of the Motion Pair | Number of Degrees of Freedom | Instructions |
|---|---|---|---|
| Motor | Fixed Pairs | 0 | Motor–Bracket |
| Drive Rod | Rotating Pairs | 1 | Drive Rod–Motor |
| Lift Rod | Rotating Pairs | 1 | Lift Rod–Drive Rod |
| Leg Placing Plate | Rotating Pairs | 1 | Leg Placing Plate–Lift Rod |
| Fixed Hinge | Fixed Pairs | 0 | Fixed Hinge–Bracket |
| Bracket | Fixed Pairs | 0 | Bracket–Earth |
| Moving Hinge | Rotating Pairs | 1 | Moving Hinge–Fixed Hinge |
| Drive Auxiliary Rod | Rotating Pairs | 1 | Drive Auxiliary Rod–Drive Rod |
| Lift Auxiliary Rod | Rotating Pairs | 1 | Lift Auxiliary Rod–Drive Auxiliary Rod |
| Lift Auxiliary Rod | Rotating Pairs | 1 | Lift Auxiliary Rod–Leg Placing Plate |
| Materials | Density (kg·cm−3) | Elastic Modulus/MPa | Poisson’s Ratio | Tensile Strength/MPa | Yield Strength/MPa |
|---|---|---|---|---|---|
| 45 Steel | 7.85 | 210,000 | 0.3 | 600 | 355 |
| Al6061 Alloy | 2.73 | 70,000 | 0.33 | 260 | 110 |
| Factors | Levels | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| Height/cm | 170 | 175 | 180 |
| Weight/kg | 70 | 80 | 90 |
| Angle/deg | 30 | 60 | 90 |
| Serial Number | Height/cm | Weight/kg | Angle/deg | F/N |
|---|---|---|---|---|
| 1 | 175~180 | 70~80 | 0~30 | 98.70 |
| 2 | 175~180 | 60~70 | 30~60 | 122.81 |
| 3 | 175~180 | 70~80 | 60~90 | 188.77 |
| 4 | 170~175 | 70~80 | 30~60 | 149.35 |
| 5 | 165~170 | 70~80 | 60~90 | 157.47 |
| 6 | 165~170 | 80~90 | 30~60 | 143.57 |
| 7 | 165~170 | 70~80 | 0~30 | 90.89 |
| 8 | 170~175 | 70~80 | 30~60 | 143.52 |
| 9 | 165~170 | 60~70 | 30~60 | 106.54 |
| 10 | 170~175 | 60~70 | 60~90 | 157.47 |
| 11 | 170~175 | 80~90 | 60~90 | 174.25 |
| 12 | 170~175 | 70~80 | 30~60 | 150.21 |
| 13 | 170~175 | 80~90 | 0~30 | 105.73 |
| 14 | 175~180 | 80~90 | 30~60 | 158.32 |
| 15 | 170~175 | 60~70 | 0~30 | 95.8 |
| Source | Sum of Squares | Mean Square | F-Value | p-Value | Distinctiveness |
|---|---|---|---|---|---|
| Model | 12,776.71 | 1419.63 | 18.45 | 0.0025 | Significant |
| A—Height | 614.78 | 614.78 | 7.99 | 0.0368 | |
| B—Weight | 1231.32 | 1231.32 | 16.00 | 0.0103 | |
| C—Angle | 10,284.65 | 10,284.65 | 133.66 | <0.0001 | |
| AB | 0.5776 | 0.5776 | 0.0075 | 0.9343 | |
| AC | 137.95 | 137.95 | 1.79 | 0.2382 | |
| BC | 11.73 | 11.73 | 0.1524 | 0.7123 | |
| A2 | 187.14 | 187.14 | 2.43 | 0.1796 | |
| B2 | 222.58 | 222.58 | 2.89 | 0.1497 | |
| C2 | 161.65 | 161.65 | 2.10 | 0.2069 | |
| Lack of Fit | 358.25 | 119.42 | 9.01 | 0.1015 | Not Significant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, R.; Gao, J.; Zhao, S.; Xing, H. Research and Mechanism Design Analysis of Leg Lifting Device Based on Human Body Stretching. Machines 2025, 13, 78. https://doi.org/10.3390/machines13020078
Gu R, Gao J, Zhao S, Xing H. Research and Mechanism Design Analysis of Leg Lifting Device Based on Human Body Stretching. Machines. 2025; 13(2):78. https://doi.org/10.3390/machines13020078
Chicago/Turabian StyleGu, Ruijie, Jiameng Gao, Shuaifeng Zhao, and Hao Xing. 2025. "Research and Mechanism Design Analysis of Leg Lifting Device Based on Human Body Stretching" Machines 13, no. 2: 78. https://doi.org/10.3390/machines13020078
APA StyleGu, R., Gao, J., Zhao, S., & Xing, H. (2025). Research and Mechanism Design Analysis of Leg Lifting Device Based on Human Body Stretching. Machines, 13(2), 78. https://doi.org/10.3390/machines13020078





