Non-Linear Hyperelastic Model Analysis and Numerical Validation of 3D Printed PLA+ Material Incorporating Various Infill Densities
Abstract
:1. Introduction
- Determine the strain energy behavior from the stress–strain curve obtained through experimental analysis.
- Identify the hyperelastic material constants for various hyperelastic models using curve fitting techniques.
- Perform numerical simulations in Ansys Mechanical to generate the stress–strain curve and convert it into a strain energy density vs. stretch curve.
- Compare the numerical strain energy density results with the experimental data to assess the model’s accuracy.
- Identify the most suitable hyperelastic model for PLA+ material, incorporating linear infill densities, based on the uniaxial tensile test results.
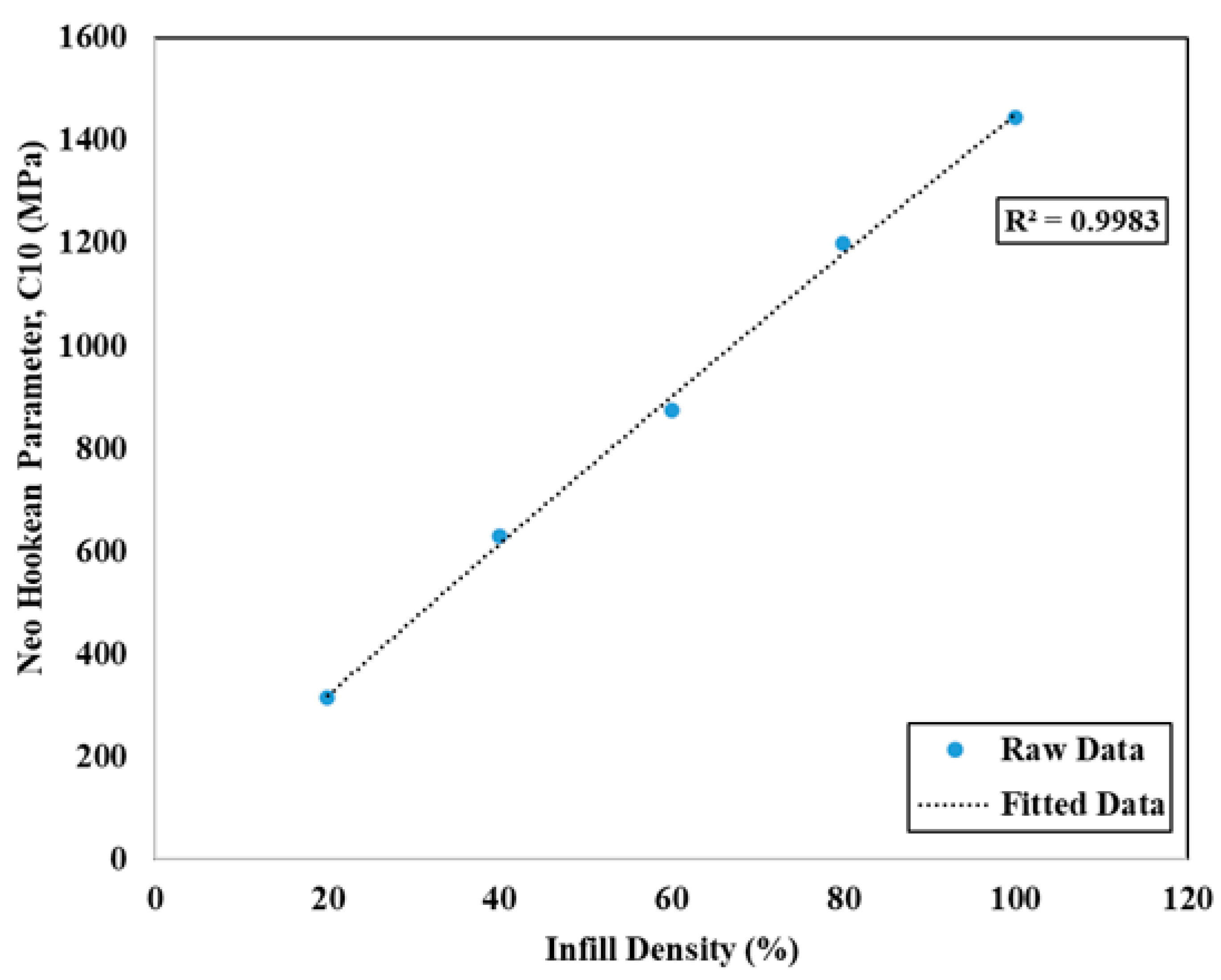
- Develop a new equation to determine material constants for the neo-Hookean model.
- Conclude with a discussion on the implications of the findings and provide recommendations for future research.
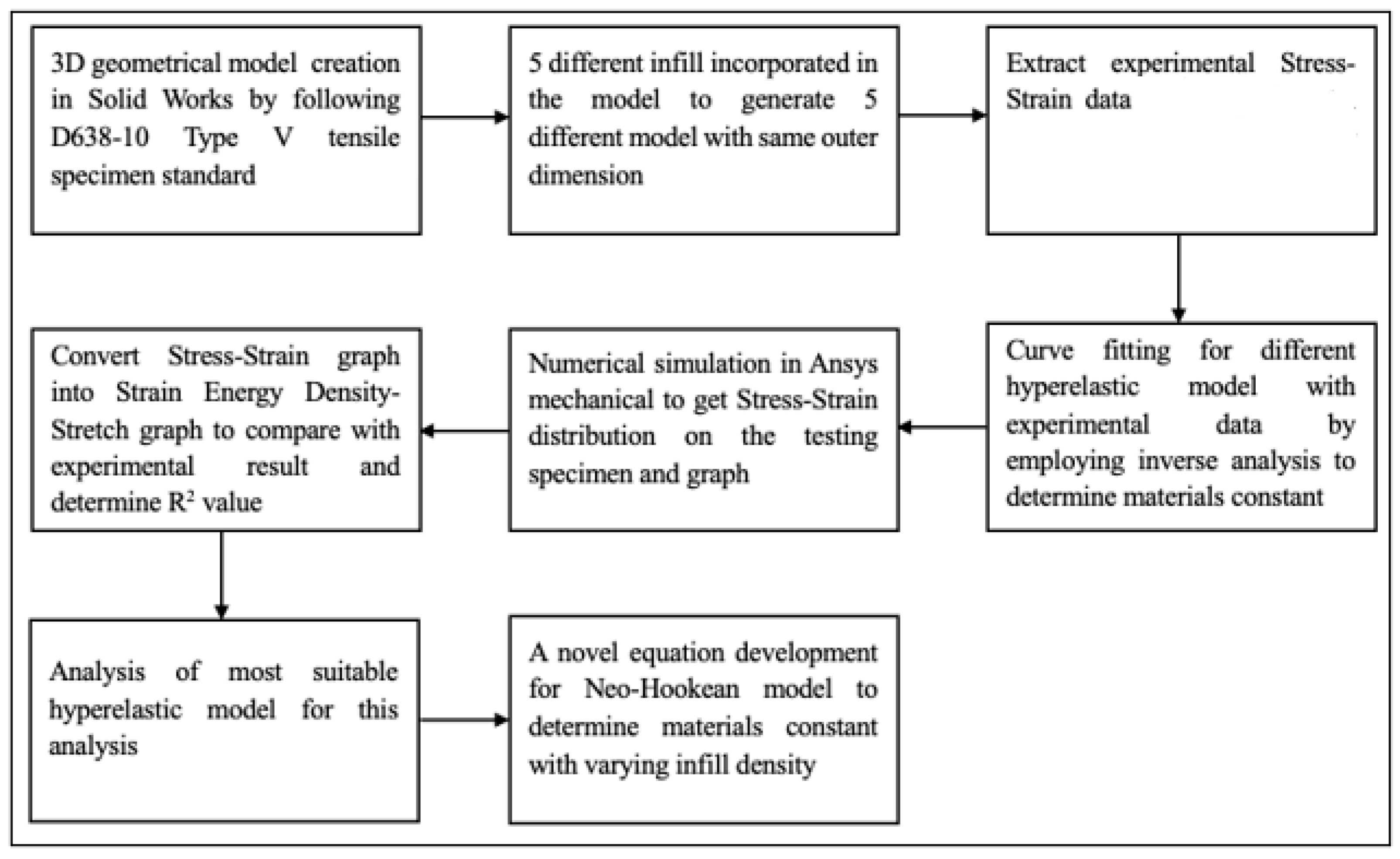
2. Model and Methodology
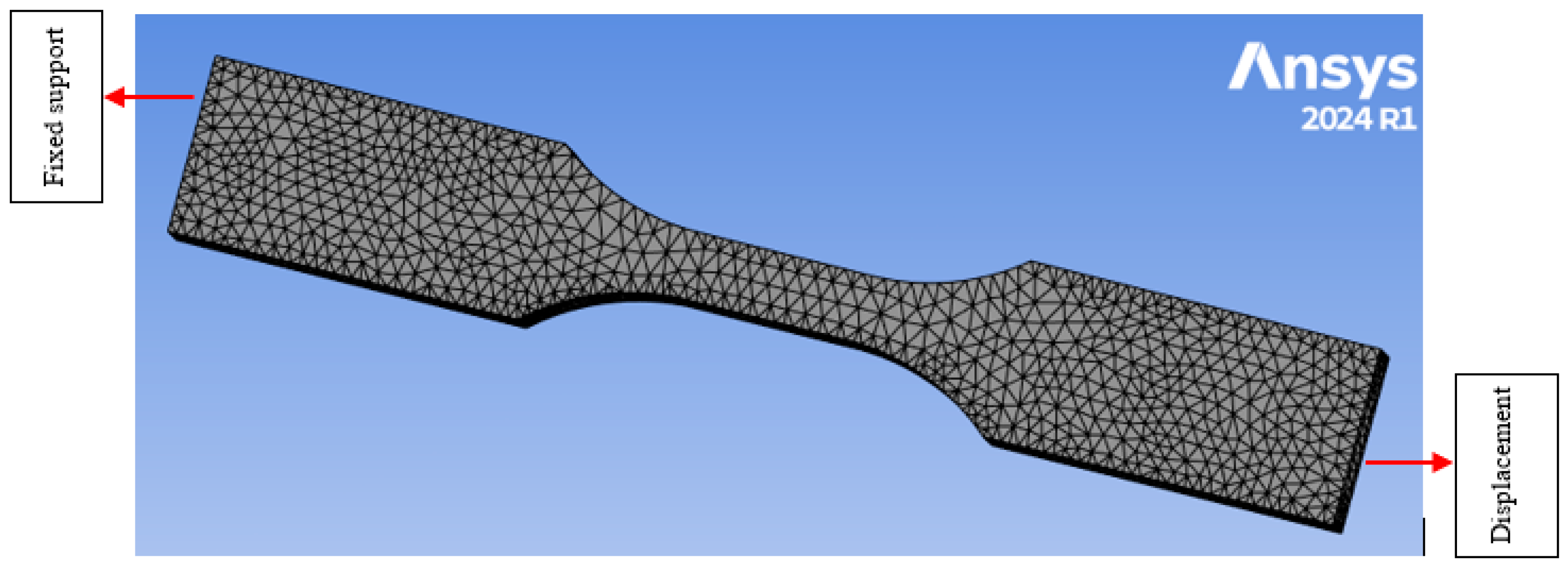
2.1. Three-Dimensional Geometrical Model
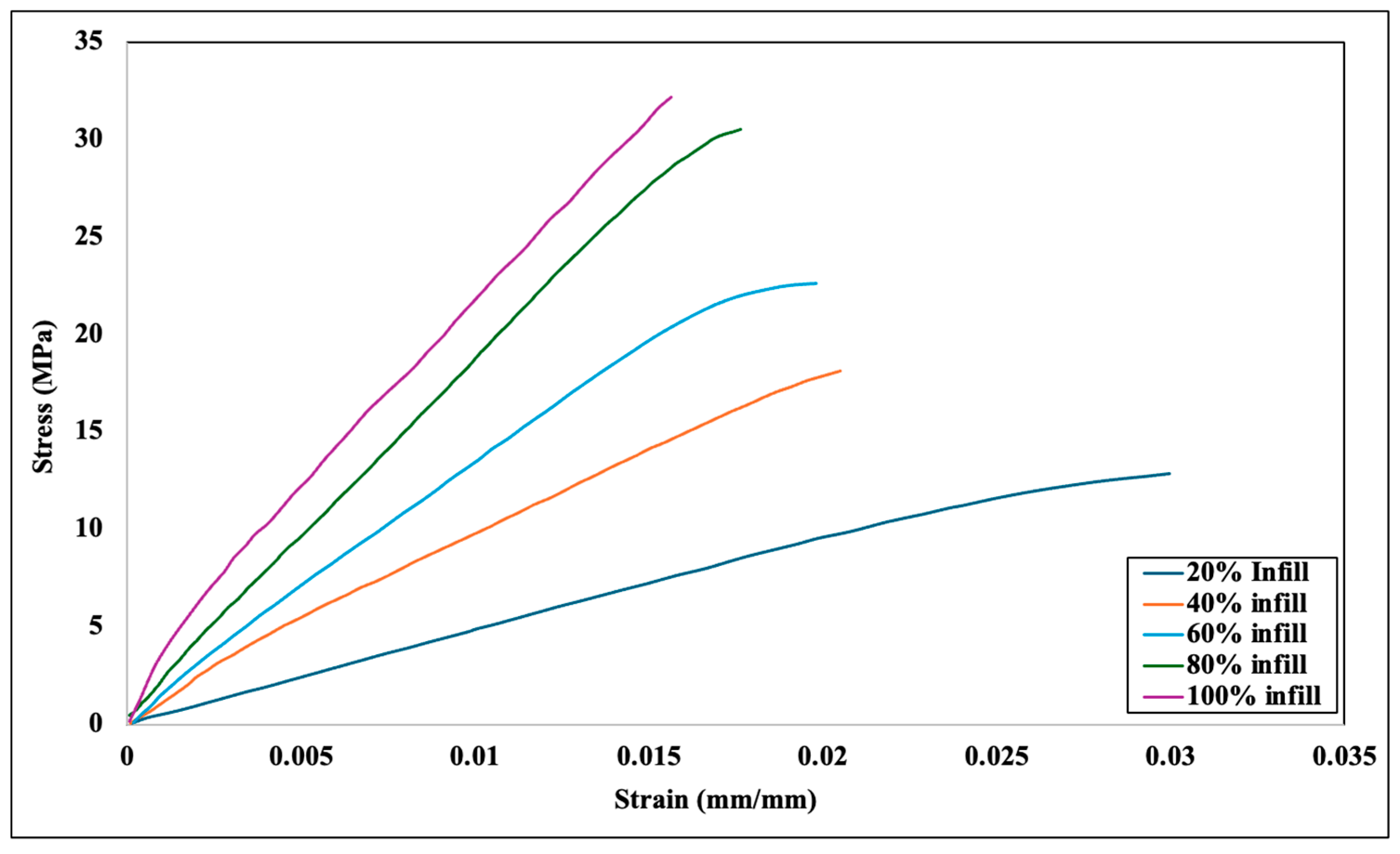
2.2. Experimental Data
2.3. Numerical Analysis Procedure
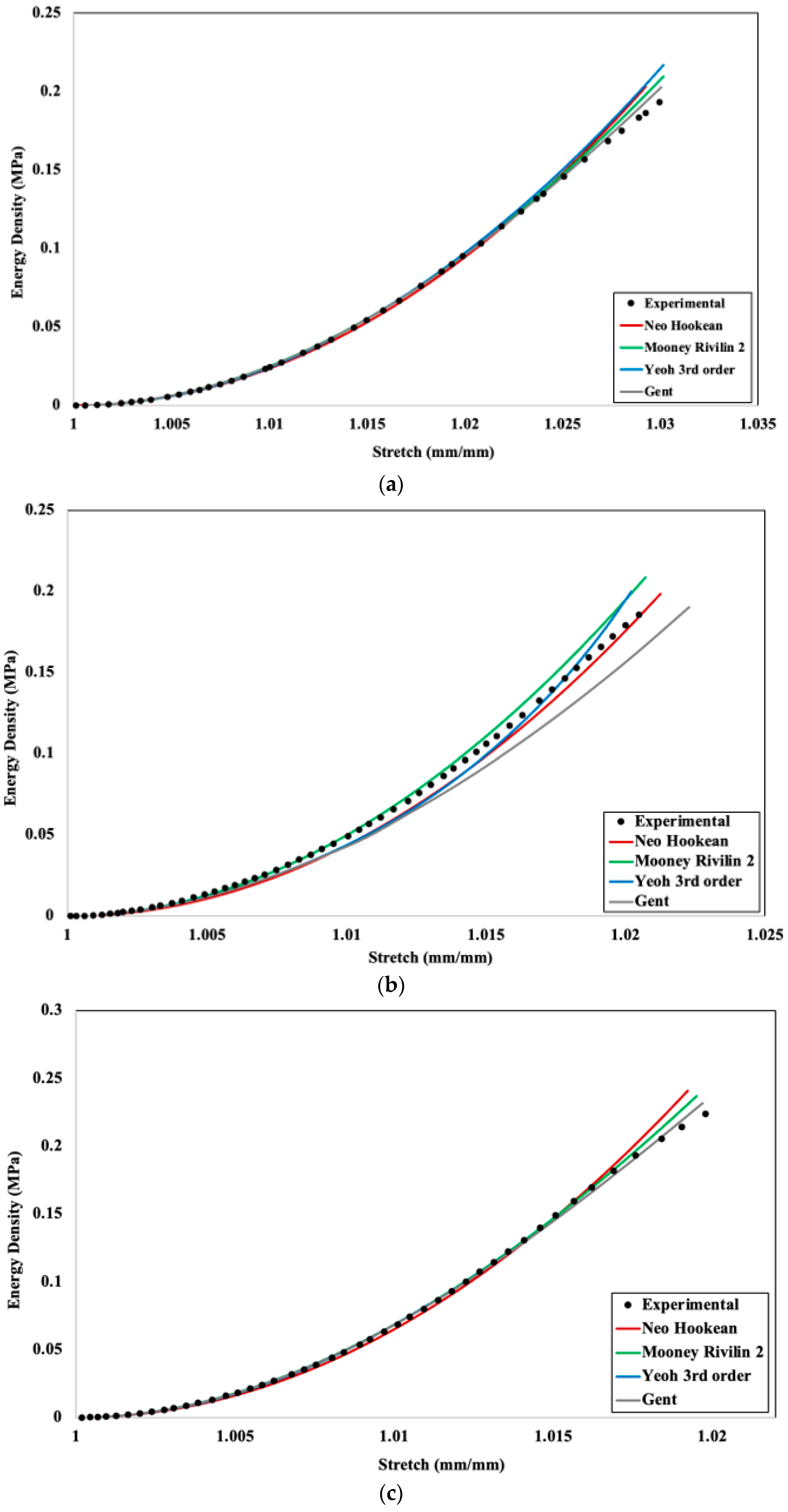
2.4. Strain Energy Density Calculation Methodology from Experimental Data
- Initial volume, V0;
- Initial length, L0;
- Stretch, and d;
- Cross-sectional area, A0.
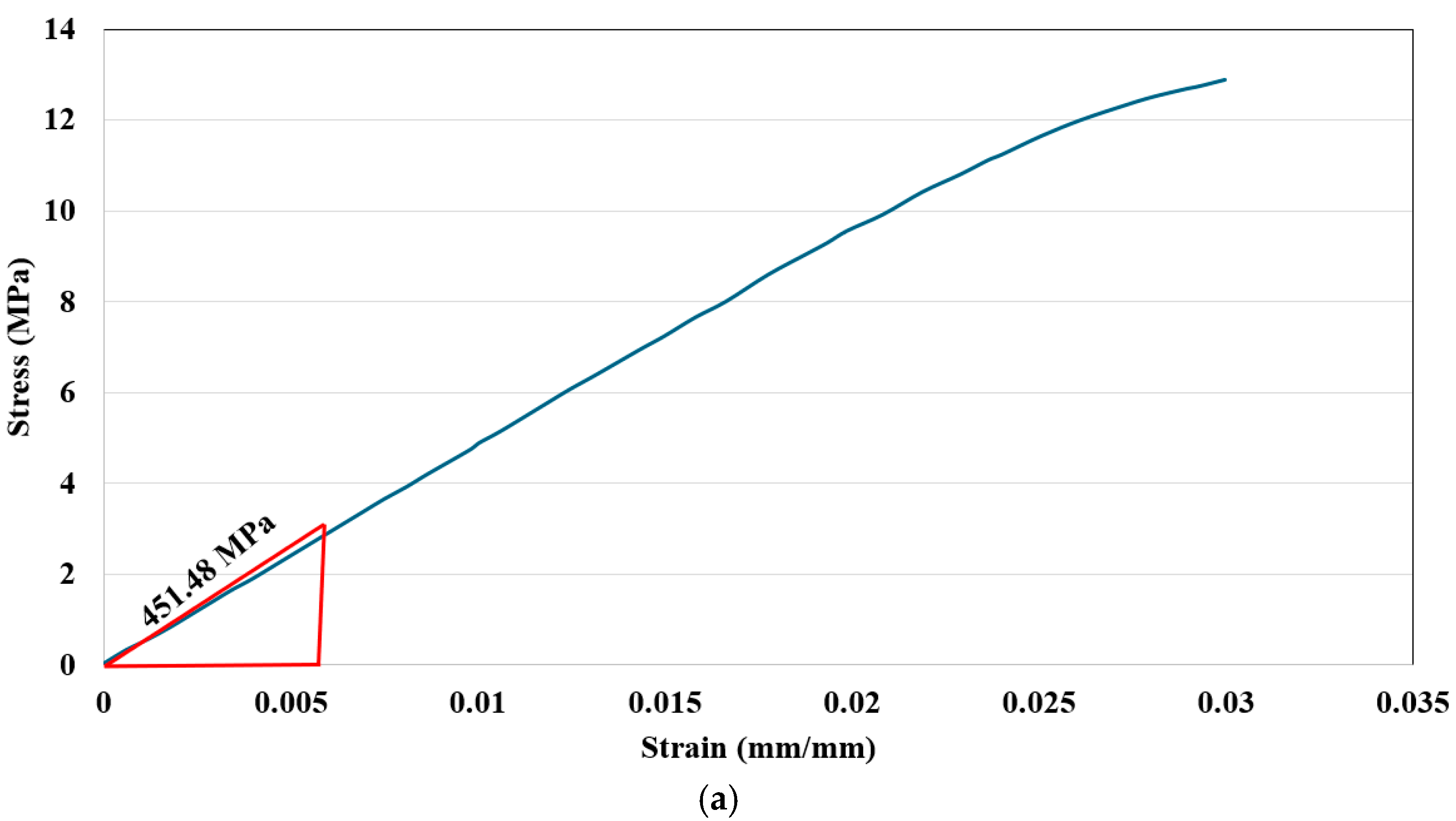

2.5. Hyperelastic Model
2.5.1. Neo-Hookean Model
2.5.2. Mooney–Rivlin Model
2.5.3. Yeoh (3rd-Order) Model
2.5.4. Gent Model
3. Parameter Determination in Hyperelastic Models
3.1. Inverse Analysis
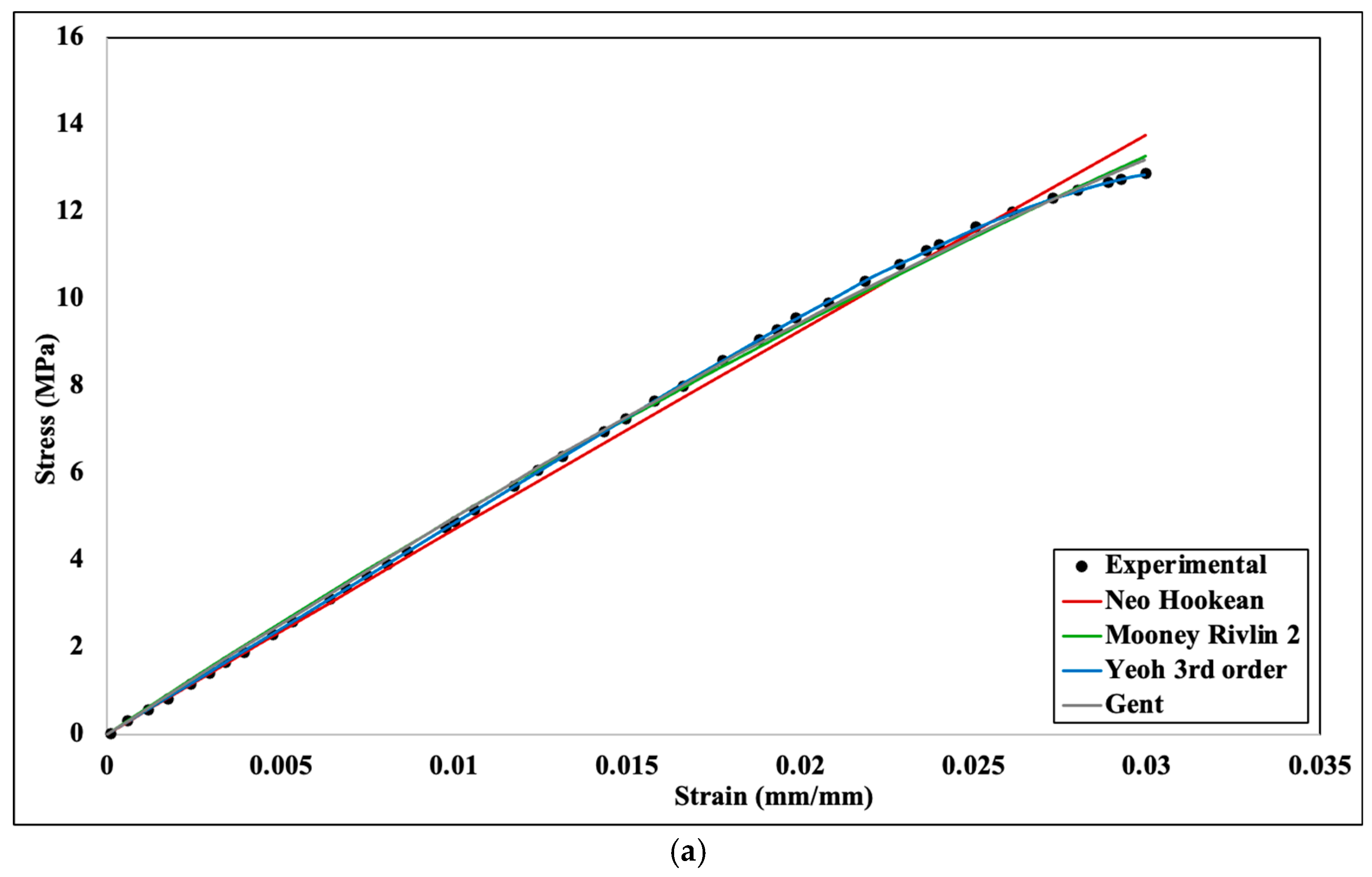


3.2. Curve Fitting for Hyperelastic Model
4. Results and Discussion
4.1. Finite Element Analysis (FEA)
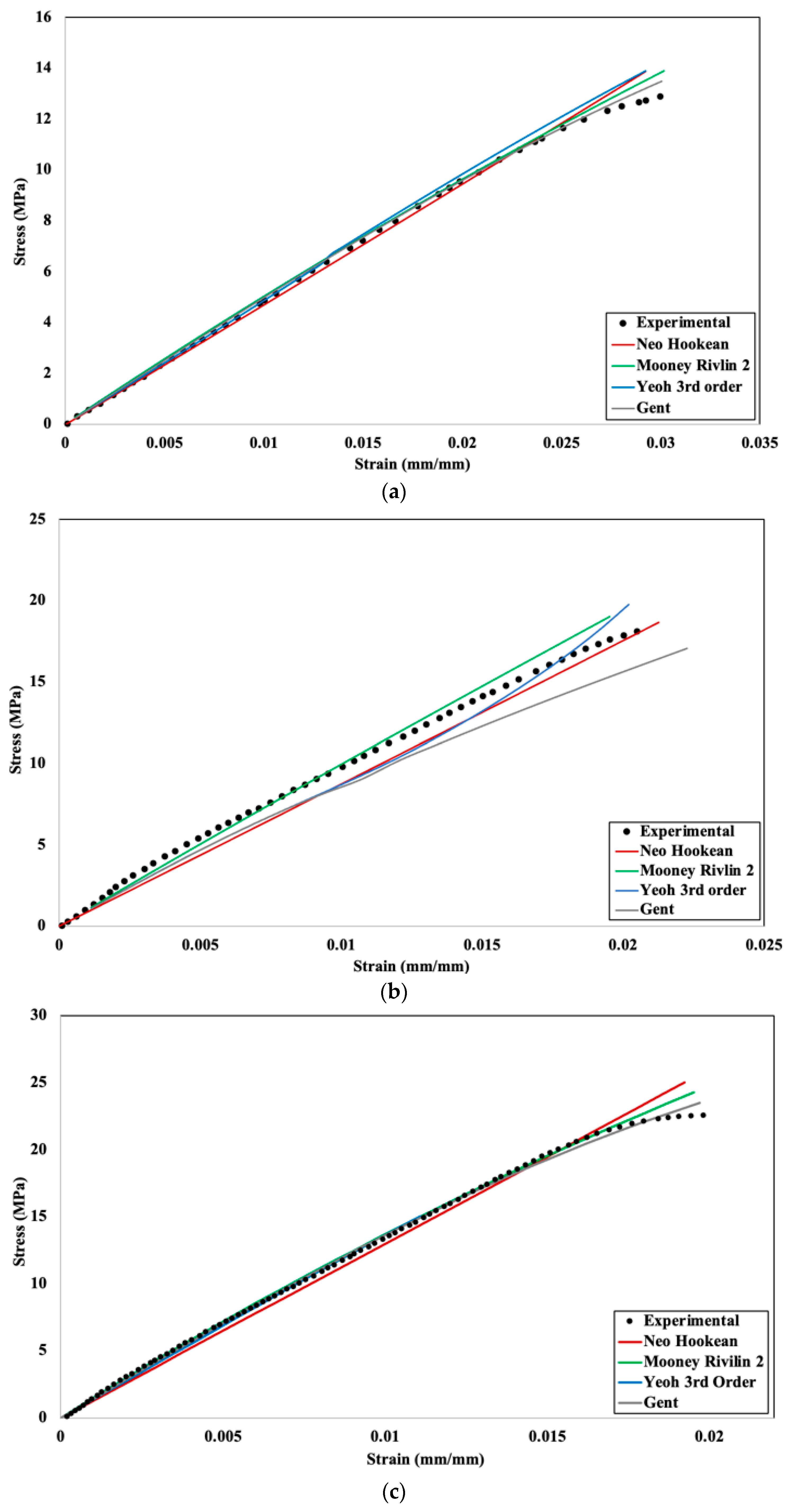
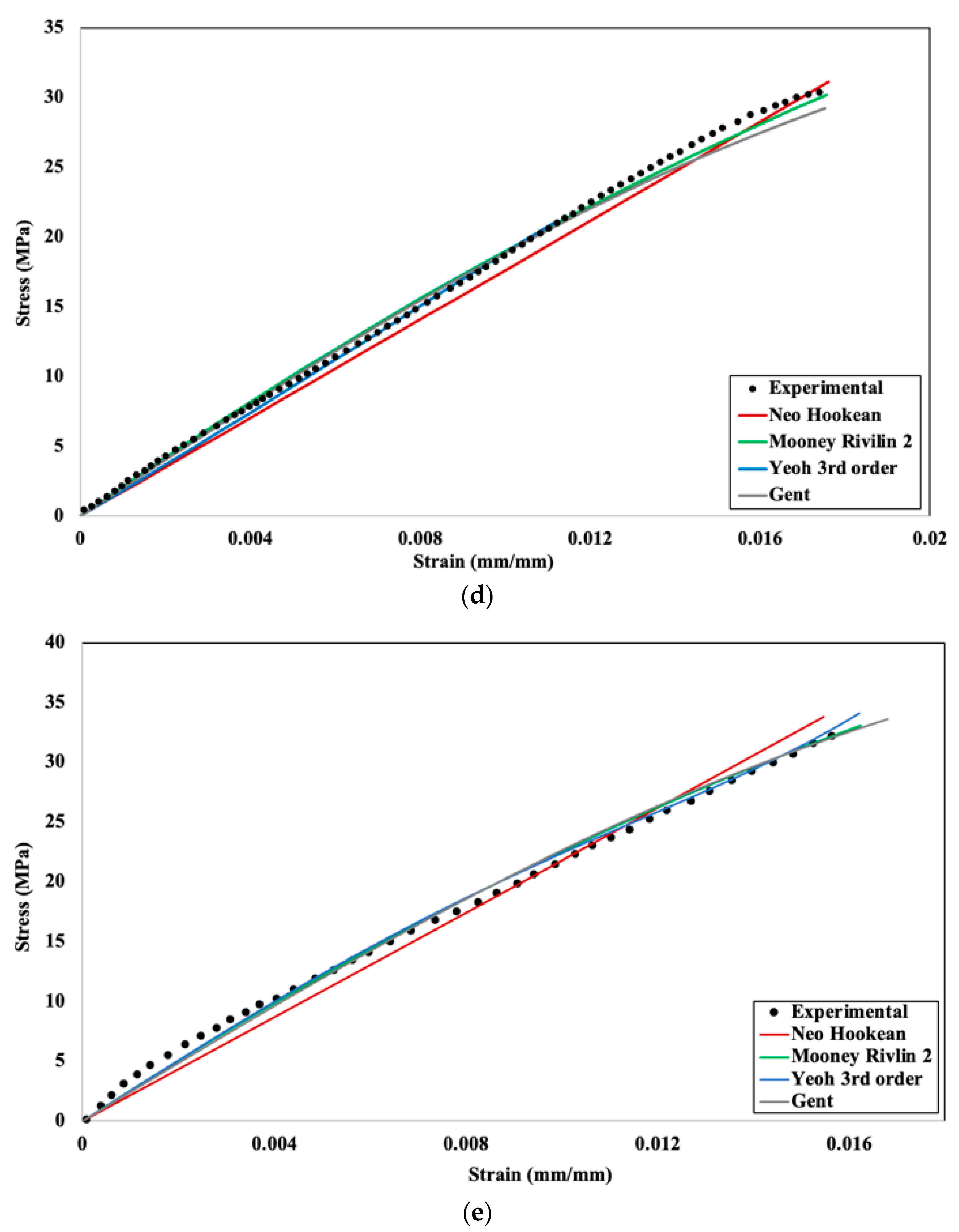
4.2. Numerical Validation with Stress–Strain Comparison
4.3. Numerical Validation with Strain Energy Density—Stretch Comparison
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Afshar, R.; Jeanne, S.; Abali, B.E. Nonlinear material modeling for mechanical characterization of 3-D printed PLA polymer with different infill densities. Appl. Compos. Mater. 2023, 30, 987–1001. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Ford, S.; Despeisse, M. Additive manufacturing and sustainability: An exploratory study of the advantages and challenges. J. Clean. Prod. 2016, 137, 1573–1587. [Google Scholar] [CrossRef]
- Mohammed, L.; Ansari, M.N.M.; Pua, G.; Jawaid, M.; Islam, M.S. A review on natural fiber reinforced polymer composite and its applications. Int. J. Polym. Sci. 2015, 2015, 243947. [Google Scholar] [CrossRef]
- Mohan, N.; Senthil, P.; Vinodh, S.; Jayanth, N. A review on composite materials and process parameters optimisation for the fused deposition modelling process. Virtual Phys. Prototyp. 2017, 12, 47–59. [Google Scholar] [CrossRef]
- Attaran, M. The rise of 3-D printing: The advantages of additive manufacturing over traditional manufacturing. Bus. Horiz. 2017, 60, 677–688. [Google Scholar] [CrossRef]
- Yang, H.; Ganzosch, G.; Giorgio, I.; Abali, B.E. Material characterization and computations of a polymeric metamaterial with a pantographic substructure. Z. Für Angew. Math. Und Phys. 2018, 69, 105. [Google Scholar] [CrossRef]
- McKeen, L.W. Introduction to plastics and polymers. In Film Properties of Plastics and Elastomers; Elsevier: Amsterdam, The Netherlands, 2012; pp. 1–18. [Google Scholar] [CrossRef]
- Lee, H.M.; Sung, J.; Ko, B.; Lee, H.; Park, S.; So, H.; Yoon, G.H. Modeling and application of anisotropic hyperelasticity of PDMS polymers with surface patterns obtained by additive manufacturing technology. J. Mech. Behav. Biomed. Mater. 2021, 118, 104412. [Google Scholar] [CrossRef]
- Alhazmi, M.W.; Backar, A. Influence of Infill density and Orientation on the Mechanical Response of PLA+ Specimens Produced using FDM 3D Printing. Int. J. Adv. Sci. Technol. 2020, 29, 3362–3371. [Google Scholar]
- Lee, H.; Chae, H.; Kim, Y.S.; Song, M.J.; Lim, S.; Prasad, K.; Krishnaswamy, H.; Jain, J.; An, K.; Lee, S.Y. Viscoplastic lattice strain during repeated relaxation of age-hardened Al alloy. Mech. Mater. 2021, 158, 103899. [Google Scholar] [CrossRef]
- Popescu, D.; Zapciu, A.; Amza, C.; Baciu, F.; Marinescu, R. FDM process parameters influence over the mechanical properties of polymer specimens: A review. Polym. Test. 2018, 69, 157–166. [Google Scholar] [CrossRef]
- Ziemian, C.W.; Ziemian, R.D. Steel benchmark frames for structural analysis and validation studies: Finite element models and numerical simulation data. Data Brief 2021, 39, 107564. [Google Scholar] [CrossRef]
- Arrieta, S.; Cicero, S.; Sánchez, M.; Castanon-Jano, L. Estimation of fracture loads in 3D printed PLA notched specimens using the ASED criterion. Procedia Struct. Integr. 2023, 47, 13–21. [Google Scholar] [CrossRef]
- Lin, P.-S.; De Bretagne, O.L.R.; Grasso, M.; Brighton, J.; StLeger-Harris, C.; Carless, O. Comparative analysis of various hyperelastic models and element types for finite element analysis. Designs 2023, 7, 135. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Ghayesh, M.H.; Chin, R.; Amabili, M. Hyperelastic structures: A review on the mechanics and biomechanics. Int. J. Non-Linear Mech. 2022, 148, 104275. [Google Scholar] [CrossRef]
- ASTME D638-10; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2015.
- Dal, H.; Açıkgöz, K.; Badienia, Y. On the Performance of Isotropic Hyperelastic Constitutive Models for Rubber-Like Materials: A State of the Art Review. Appl. Mech. Rev. 2021, 73, 020802. [Google Scholar] [CrossRef]
- Steinmann, H.H.; Dickeduisberg, M.; Theuvsen, L. Uses and benefits of glyphosate in German arable farming. Crop Prot. 2012, 42, 164–169. [Google Scholar] [CrossRef]
- Martins, P.A.L.S.; Jorge, R.M.N.; Ferreira, A.J.M. A comparative study of several material models for prediction of hyperelastic properties: Application to Silicone-Rubber and soft tissues. Strain 2006, 42, 135–147. [Google Scholar] [CrossRef]
- Yavari, A.; Goriely, A. Universal deformations in anisotropic nonlinear elastic solids. J. Mech. Phys. Solids 2021, 156, 104598. [Google Scholar] [CrossRef]
- Timbrell, C.; Wiehahn, M.; Cook, G.; Muhr, A.H. Simulation of Crack Propagation in Rubber. In Constitutive Models for Rubber III; Busfield, J., Muhr, A., Eds.; A A Balkema Publishers: Batsford, UK, 2003; pp. 11–20. [Google Scholar]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials IV. further developments of the general theory. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 241, 379–397. [Google Scholar] [CrossRef]
- Zheng, F.; Zhang, W.; Yuan, X.G.; Zhang, Y.F. Radial nonlinear vibrations of thin-walled hyperelastic cylindrical shell composed of Mooney–Rivlin materials under radial harmonic excitation. Nonlinear Dyn. 2023, 111, 19791–19815. [Google Scholar] [CrossRef]
- Barforooshi, S.D.; Mohammadi, A.K. Study Neo-Hookean and Yeoh Hyper-Elastic models in dielectric Elastomer-Based Micro-Beam resonators. Lat. Am. J. Solids Struct. 2016, 13, 1823–1837. [Google Scholar] [CrossRef]
- Renaud, C.; Cros, J.-M.; Feng, Z.-Q.; Yang, B. The Yeoh model applied to the modeling of large deformation contact/impact problems. Int. J. Impact Eng. 2008, 36, 659–666. [Google Scholar] [CrossRef]
- Fung, Y.-C. Biomechanics; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar] [CrossRef]
- Holzapfel, G.A. Nonlinear Solid Mechanics—A continuum approach for engineering. Meccanica 2002, 37, 489–490. [Google Scholar] [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover Publications: New York, NY, USA, 1997. [Google Scholar]
- Hamilton, W.R. Theory of conjugate functions, or algebraic couples.; with a preliminary and elementary essay on algebra as the science of pure time. Trans. R. Ir. Acad. 2000, 17, 293–422. [Google Scholar]
- Hudgins, R.G. Development of a constitutive relation for elastomers exhibiting self-reinforcement. Polym. Eng. Sci. 2006, 46, 919–929. [Google Scholar] [CrossRef]
- Madenci, E.; Guven, I. The Finite Element Method and Applications in Engineering Using ANSYS®; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]




| Material Model | Parameter | Infill Ratio | ||||
|---|---|---|---|---|---|---|
| 20% | 40% | 60% | 80% | 100% | ||
| Neo Hookean | Initial shear modulus, (mpa) | 157.96 | 314.32 | 437.28 | 599.67 | 722 |
| C10 (mpa) | 78.98 | 157.16 | 218.64 | 299.84 | 361 | |
| Mooney-Rivlin (2 parameters) | C10 (mpa) | −331.51 | −1597.57 | −2274.6 | −4079.4 | 5617.5 |
| C01 (mpa) | 419.69 | 258,599 | 2528.3 | 4443.1 | 6051.5 | |
| Yeoh (3rd order) | C10 (mpa) | 80.75 | 176.54 | 232.18 | 310.03 | 425.79 |
| C20 (mpa) | 1667.94 | −15,306.7 | −720.63 | 31,615 | −116,085 | |
| C30 (mpa) | 0.76 | 2.4 | −8.3 | −3.2 | 5.61 | |
| Gent | Initial shear modulus, (mpa) | 169.92 | 349.19 | 481.35 | 682.87 | 811.14 |
| Limiting value | −0.0208 | −0.00728 | −0.00618 | −0.00478 | −0.00376 | |
| Infill Density | Neo-Hookean | Mooney Rivlin 2 Parameter | Yeoh 3rd Order | Gent |
|---|---|---|---|---|
| 20% | 0.990 | 0.990 | 0.995 | 0.999 |
| 40% | 0.965 | 0.97 | 0.96 | 0.90 |
| 60% | 0.99 | 0.995 | 0.999 | 0.999 |
| 80% | 0.97 | 0.999 | 0.999 | 0.98 |
| 100% | 0.97 | 1 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhuiyan, M.Z.H.; Khanafer, K.; Rafi, E.I.; Shihab, M.S. Non-Linear Hyperelastic Model Analysis and Numerical Validation of 3D Printed PLA+ Material Incorporating Various Infill Densities. Machines 2025, 13, 91. https://doi.org/10.3390/machines13020091
Bhuiyan MZH, Khanafer K, Rafi EI, Shihab MS. Non-Linear Hyperelastic Model Analysis and Numerical Validation of 3D Printed PLA+ Material Incorporating Various Infill Densities. Machines. 2025; 13(2):91. https://doi.org/10.3390/machines13020091
Chicago/Turabian StyleBhuiyan, Md Zisanul Haque, Khalil Khanafer, Ehasanul Islam Rafi, and Md Shadman Shihab. 2025. "Non-Linear Hyperelastic Model Analysis and Numerical Validation of 3D Printed PLA+ Material Incorporating Various Infill Densities" Machines 13, no. 2: 91. https://doi.org/10.3390/machines13020091
APA StyleBhuiyan, M. Z. H., Khanafer, K., Rafi, E. I., & Shihab, M. S. (2025). Non-Linear Hyperelastic Model Analysis and Numerical Validation of 3D Printed PLA+ Material Incorporating Various Infill Densities. Machines, 13(2), 91. https://doi.org/10.3390/machines13020091







