The Application of Recurrence Plots to Identify Nonlinear Responses Using Magnetometer Data for Wind Turbine Design
Abstract
1. Introduction
2. Recurrence Plots
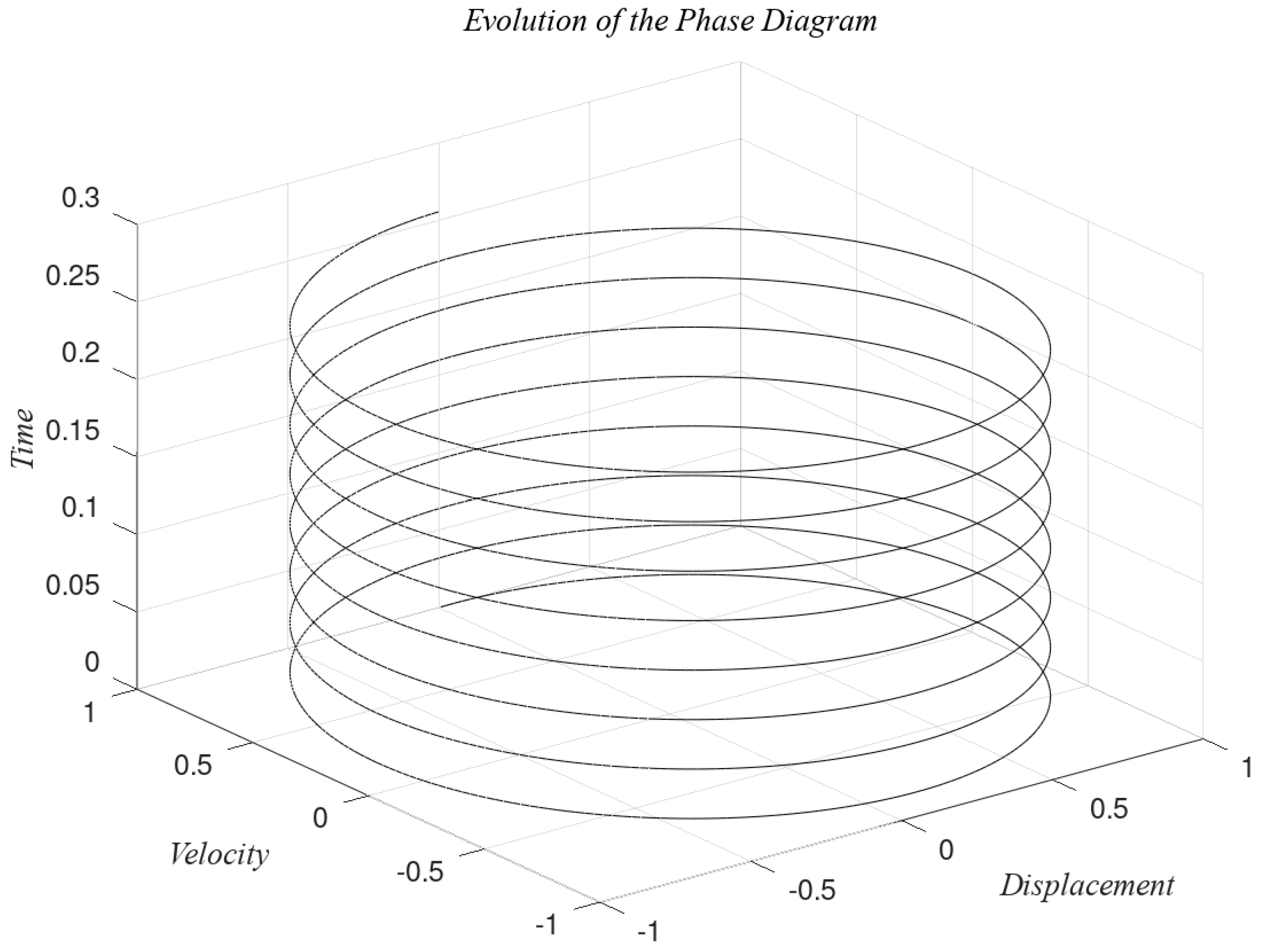
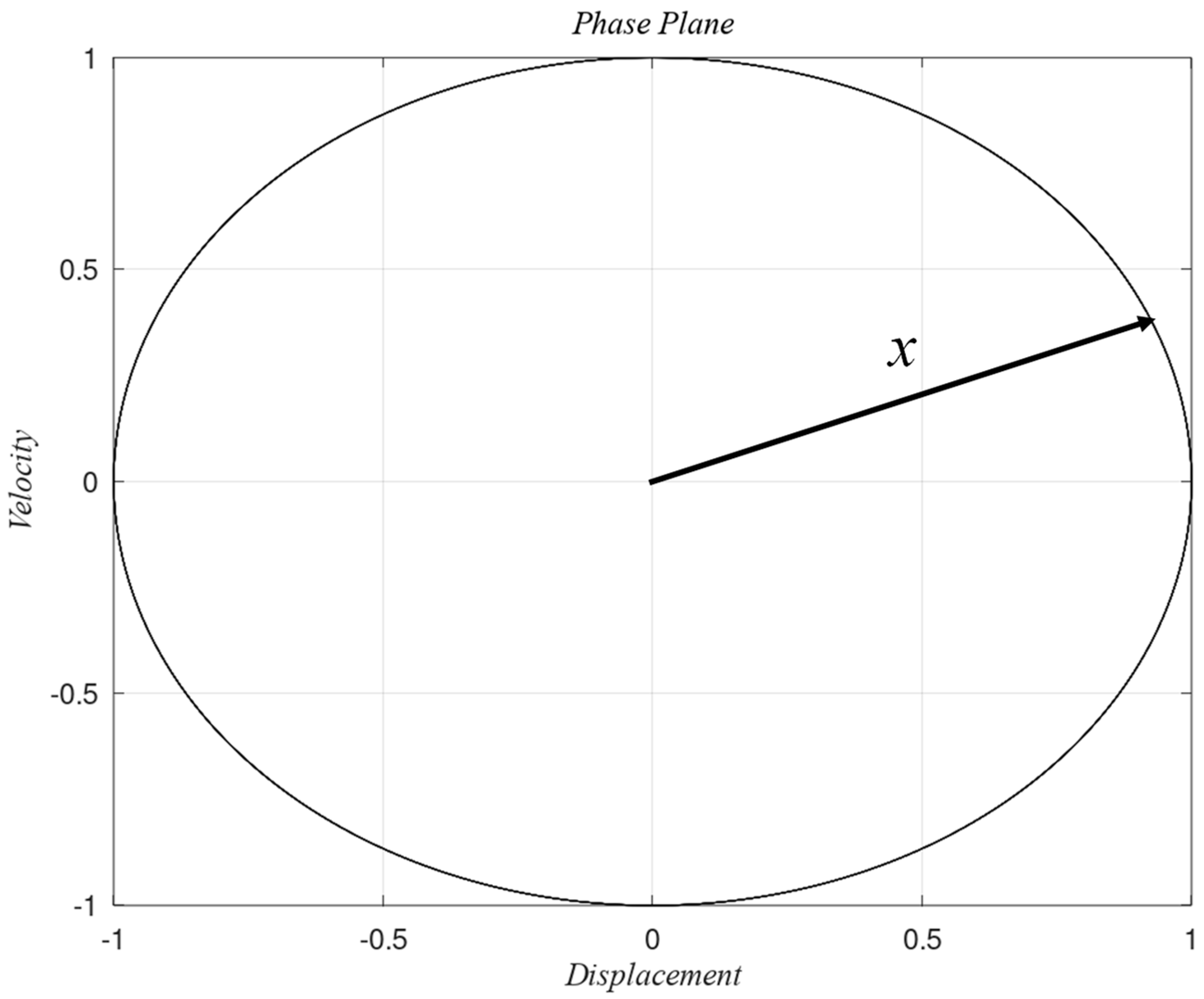
2.1. Phase Plane
2.2. Construction of the Phase Plane
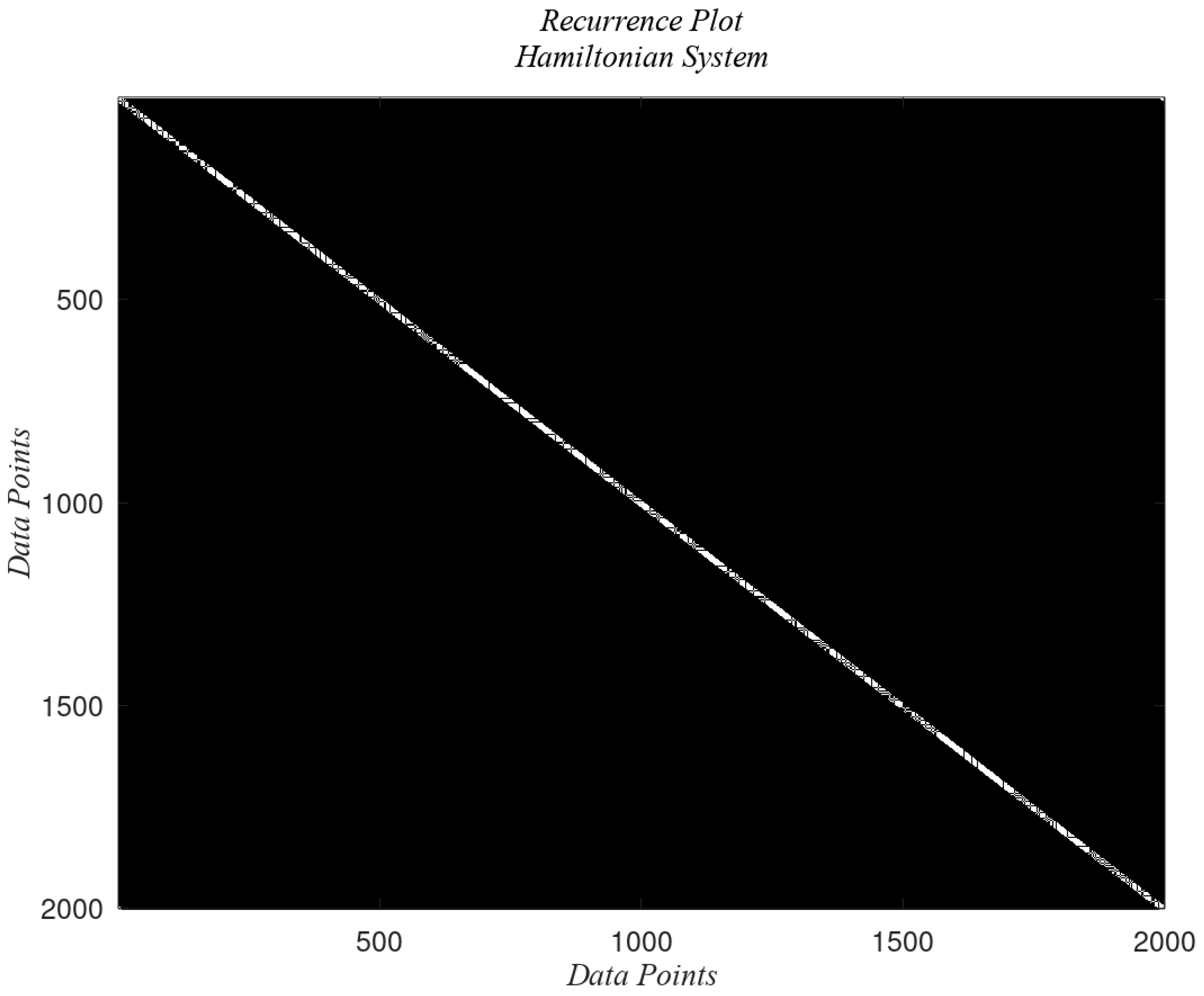
2.3. Recurrence Plot
2.4. Topology Analysis
- -
- Stationary systems show homogenous patterns (continuous diagonals);
- -
- Slow state changes display horizontal and vertical lines;
- -
- Non-stationary systems display drifts;
- -
- Constant variations of the states show single points;
- -
- Sudden changes in the system show clusters of white points;
- -
- Drifting systems produce black fringes.
3. Field Measurements
- -
- A three-axial MEMs magnetometer with a resolution of 0.58 mgaus/LSB (least significant bit) and a range of ±16 gauss;
- -
- A three-axial MEMs accelerometer with a resolution of 0.244 mg/LSB with a range of ±8 g;
- -
- An FPGA data processor;
- -
- A data acquisition system with a sampling rate of 1 kHz.
4. Results
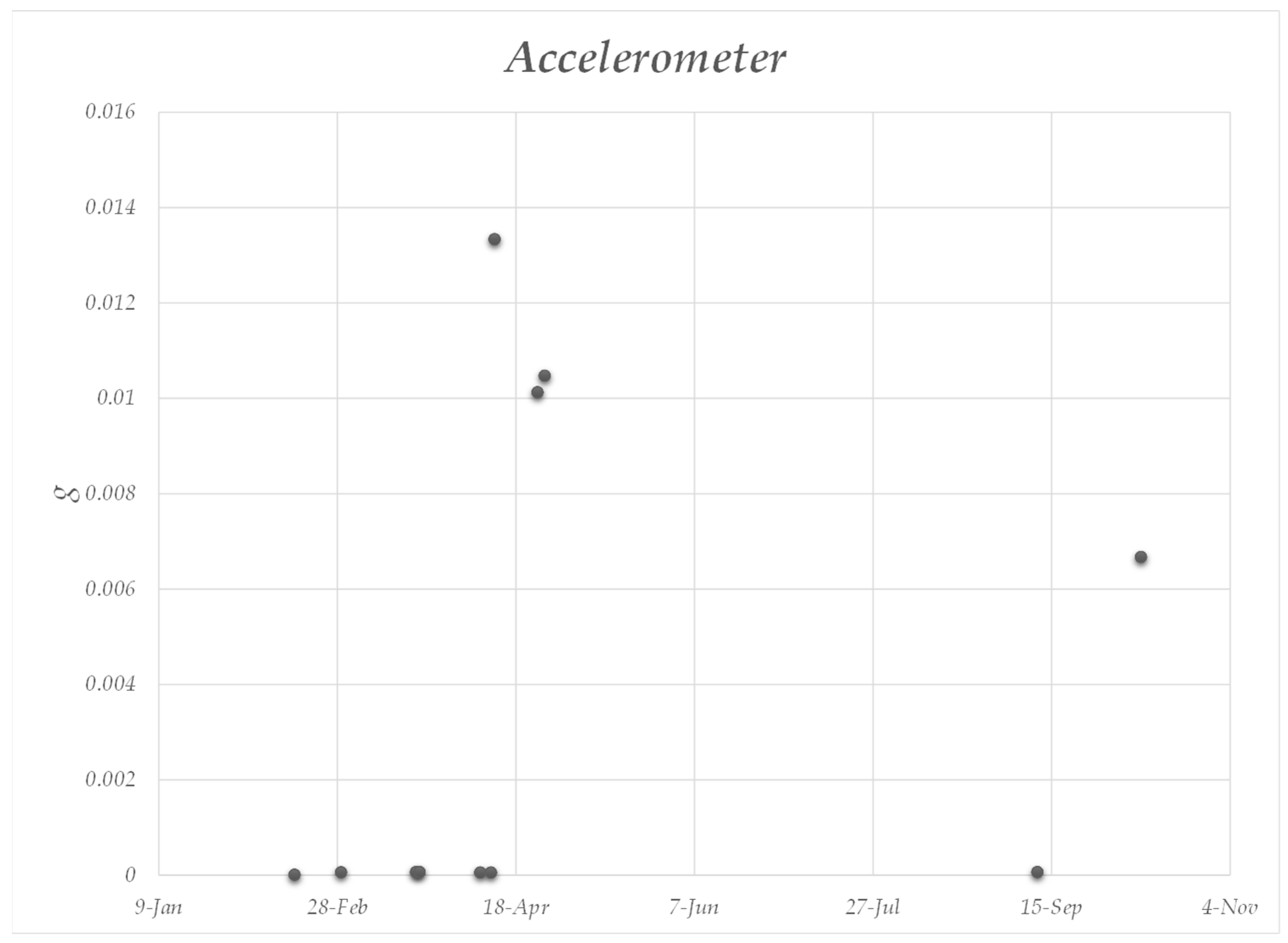
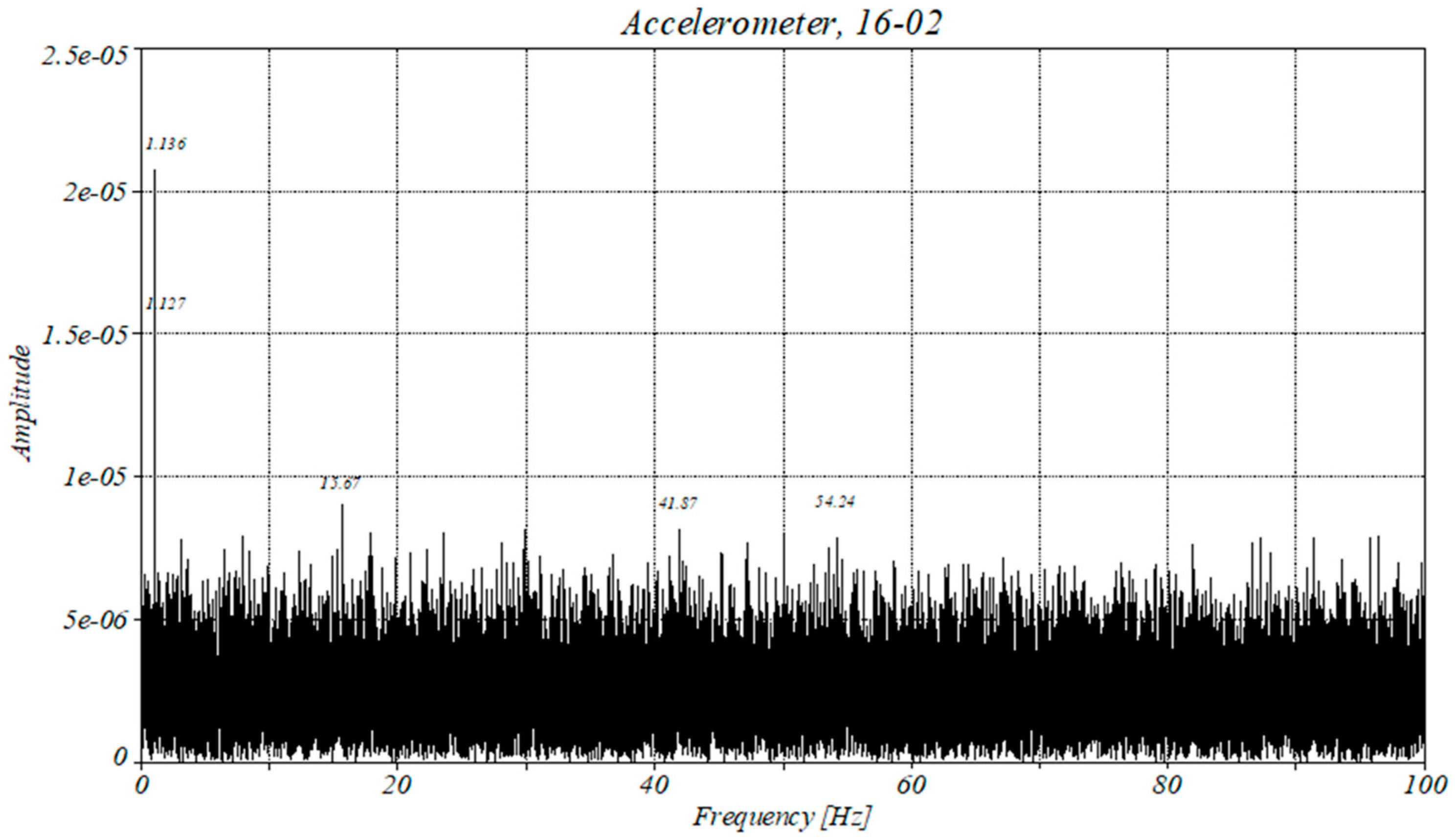
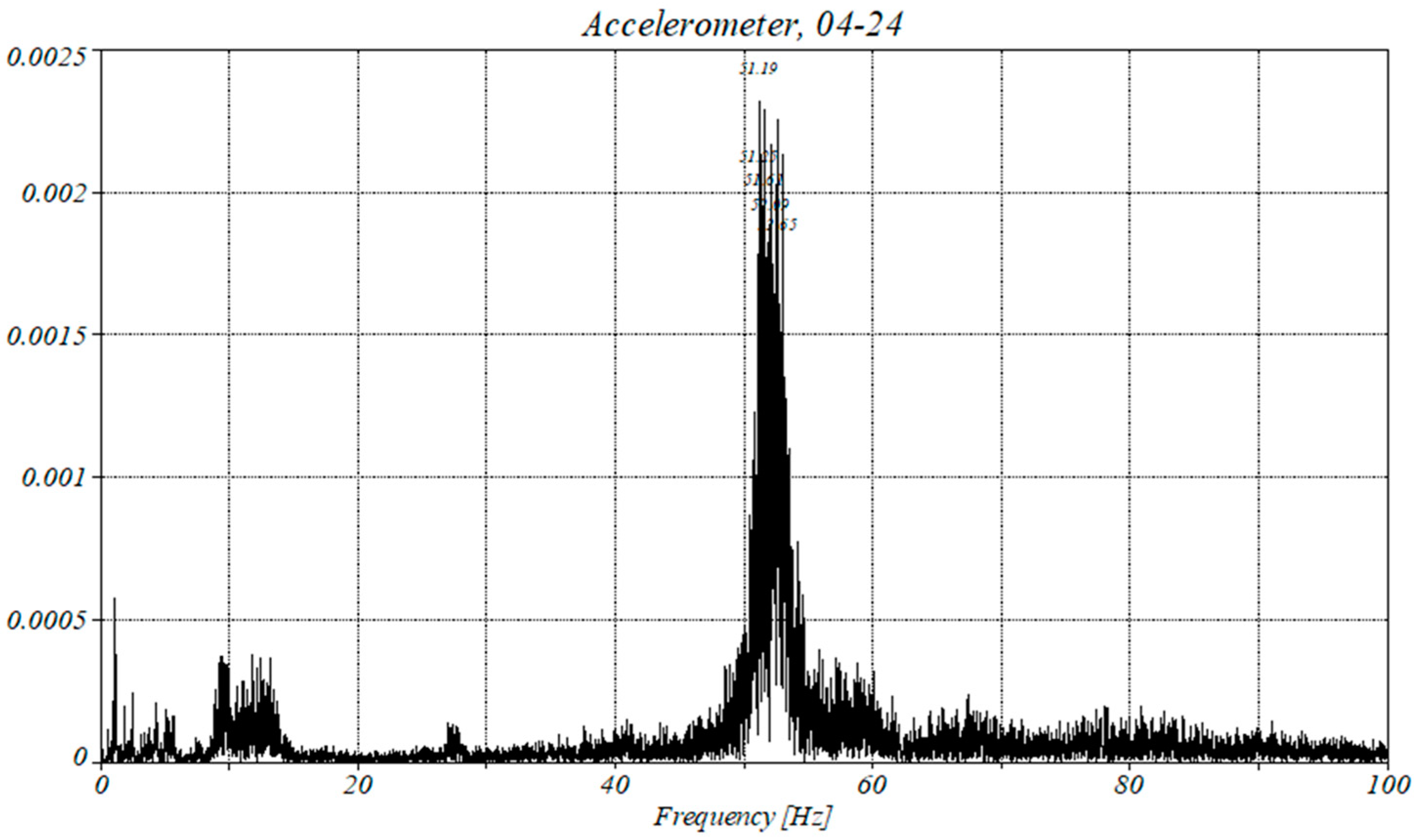
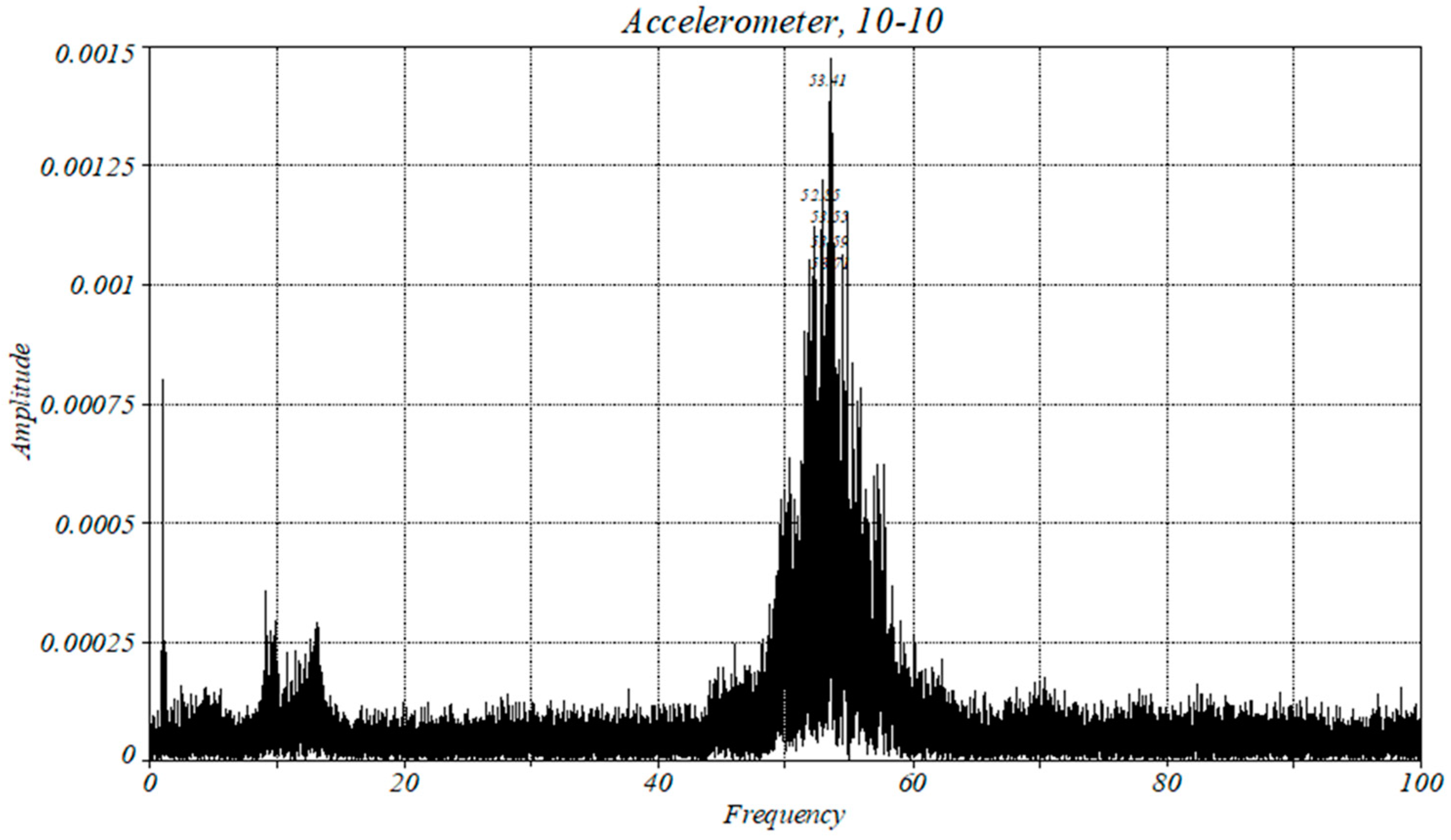
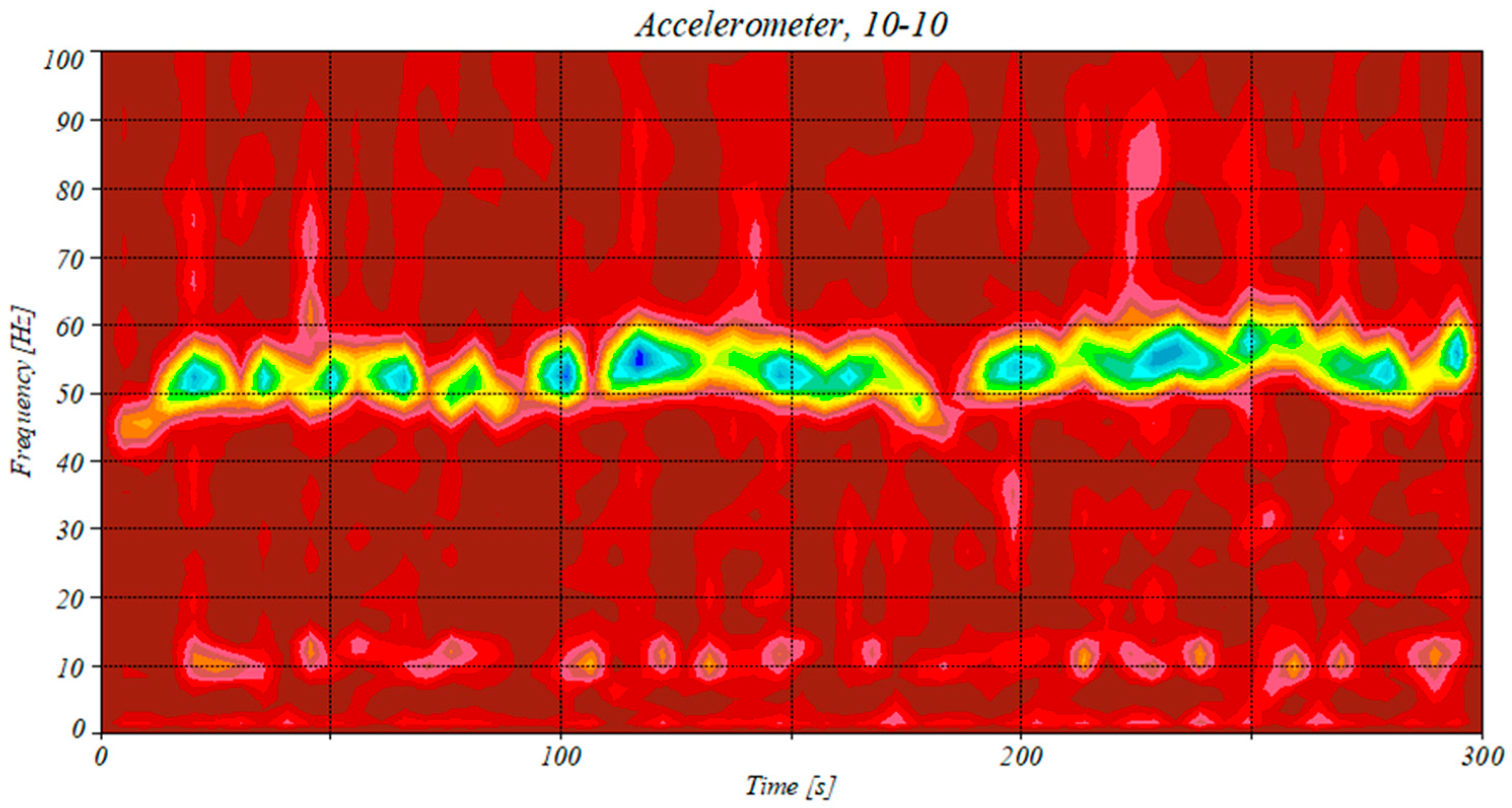
4.1. Analysis of the Accelerometer Data
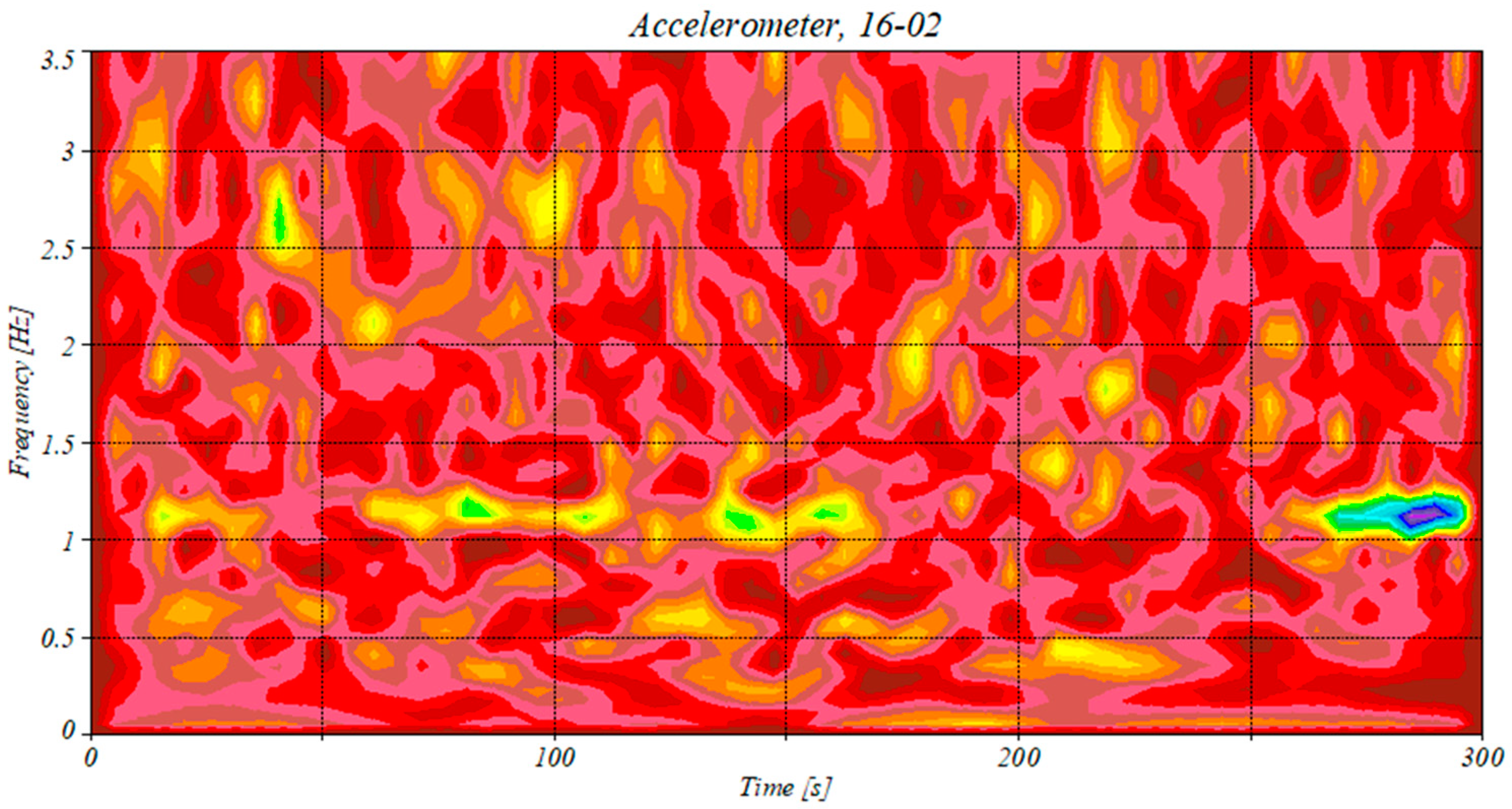
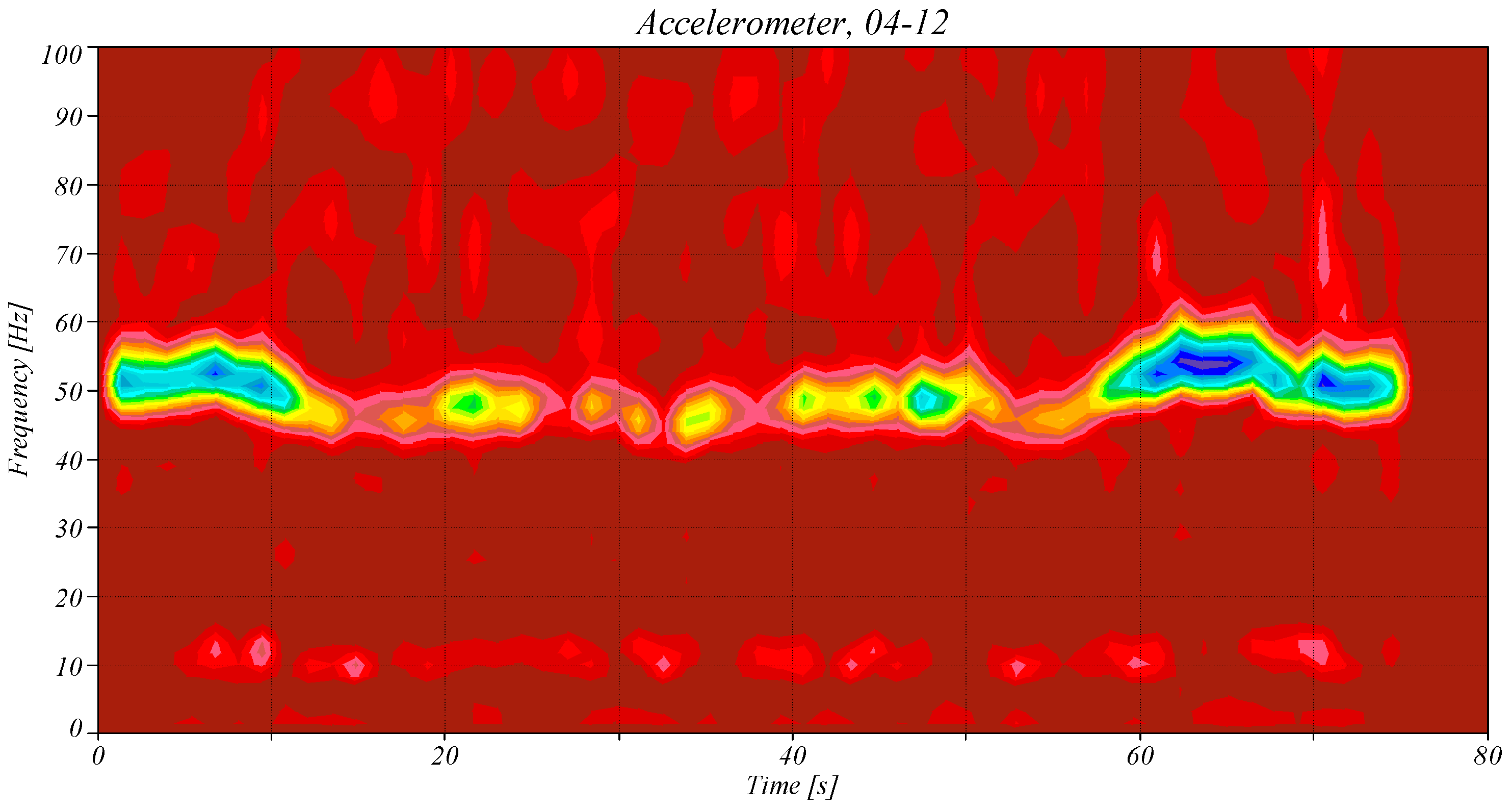
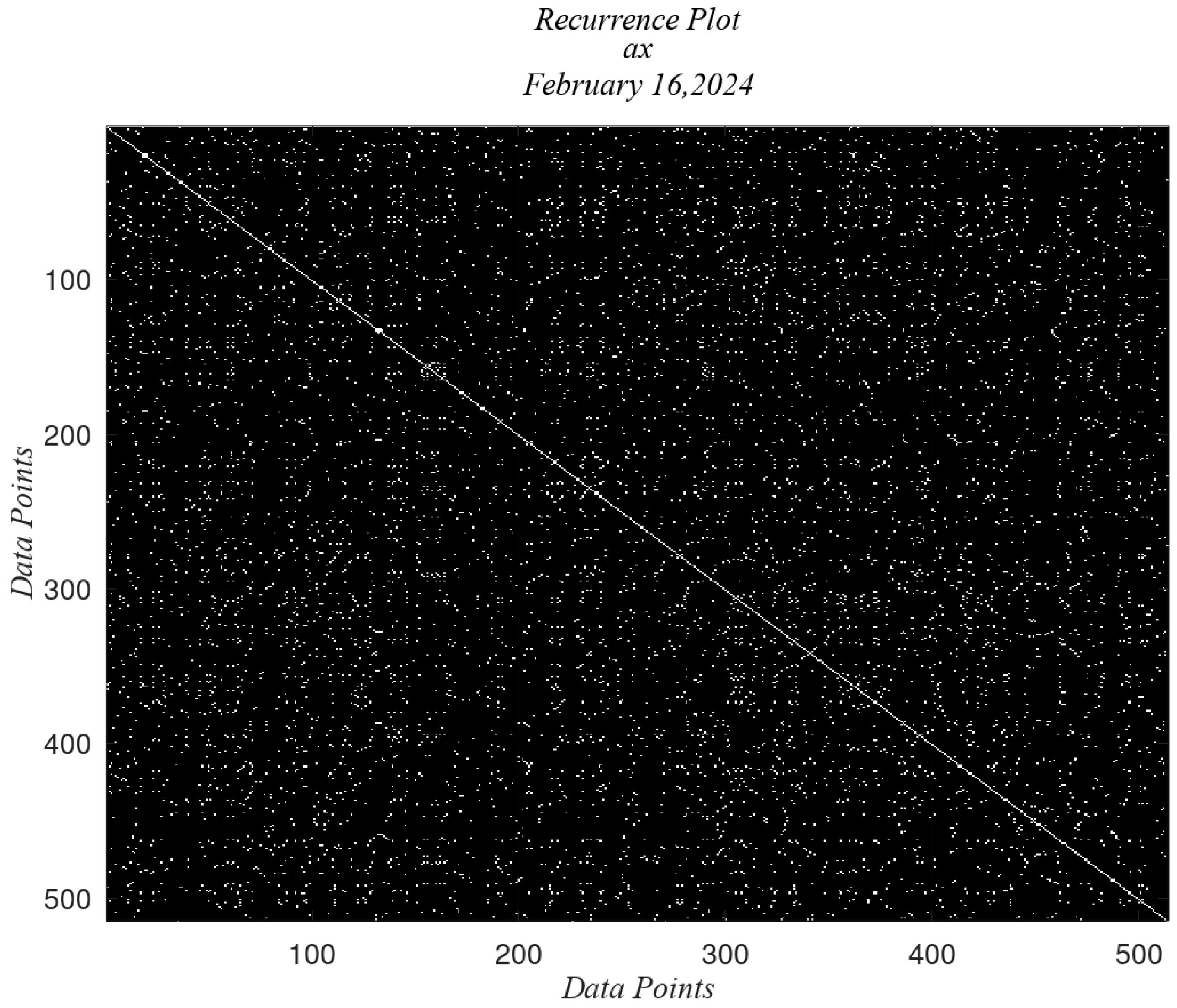
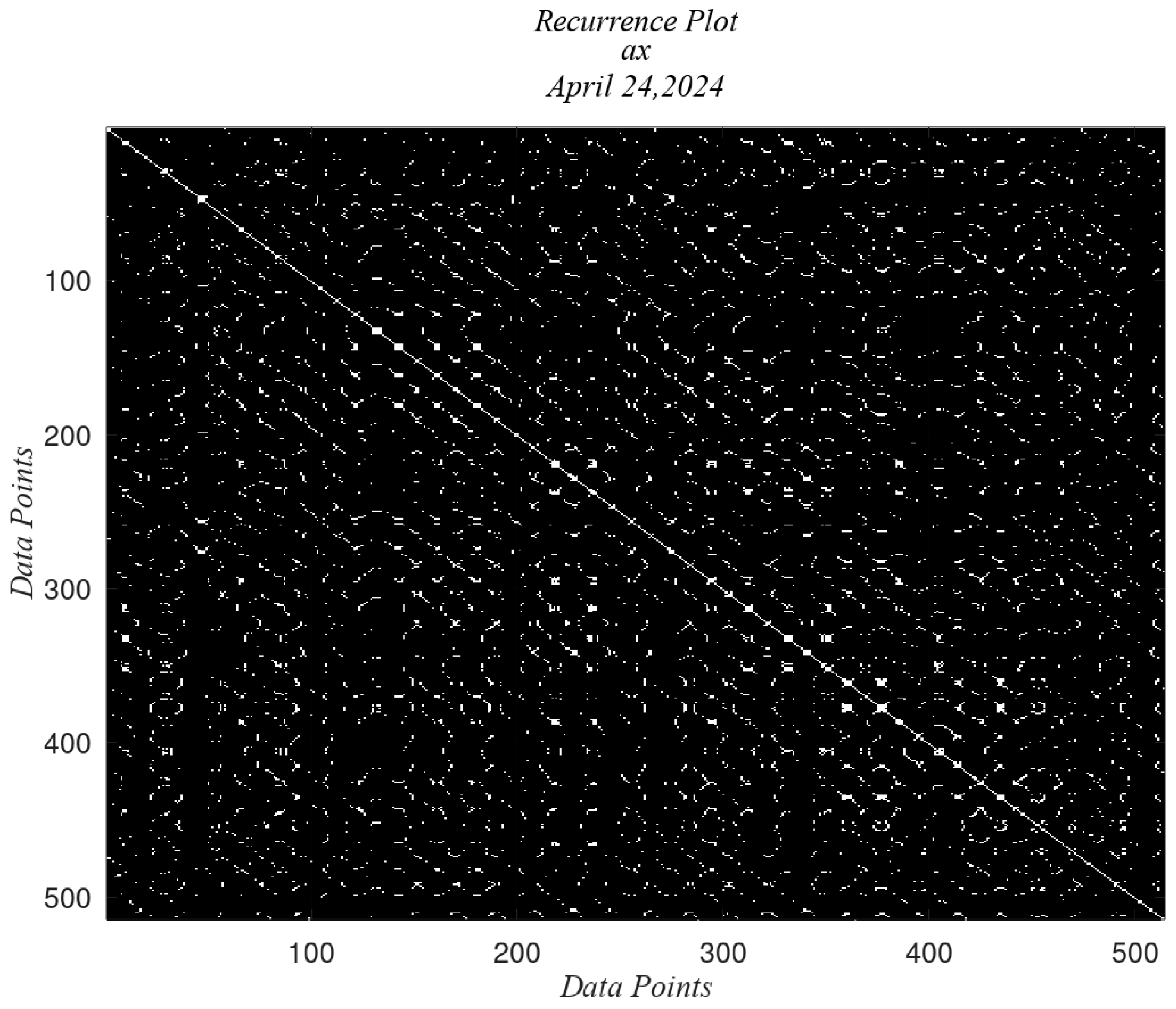
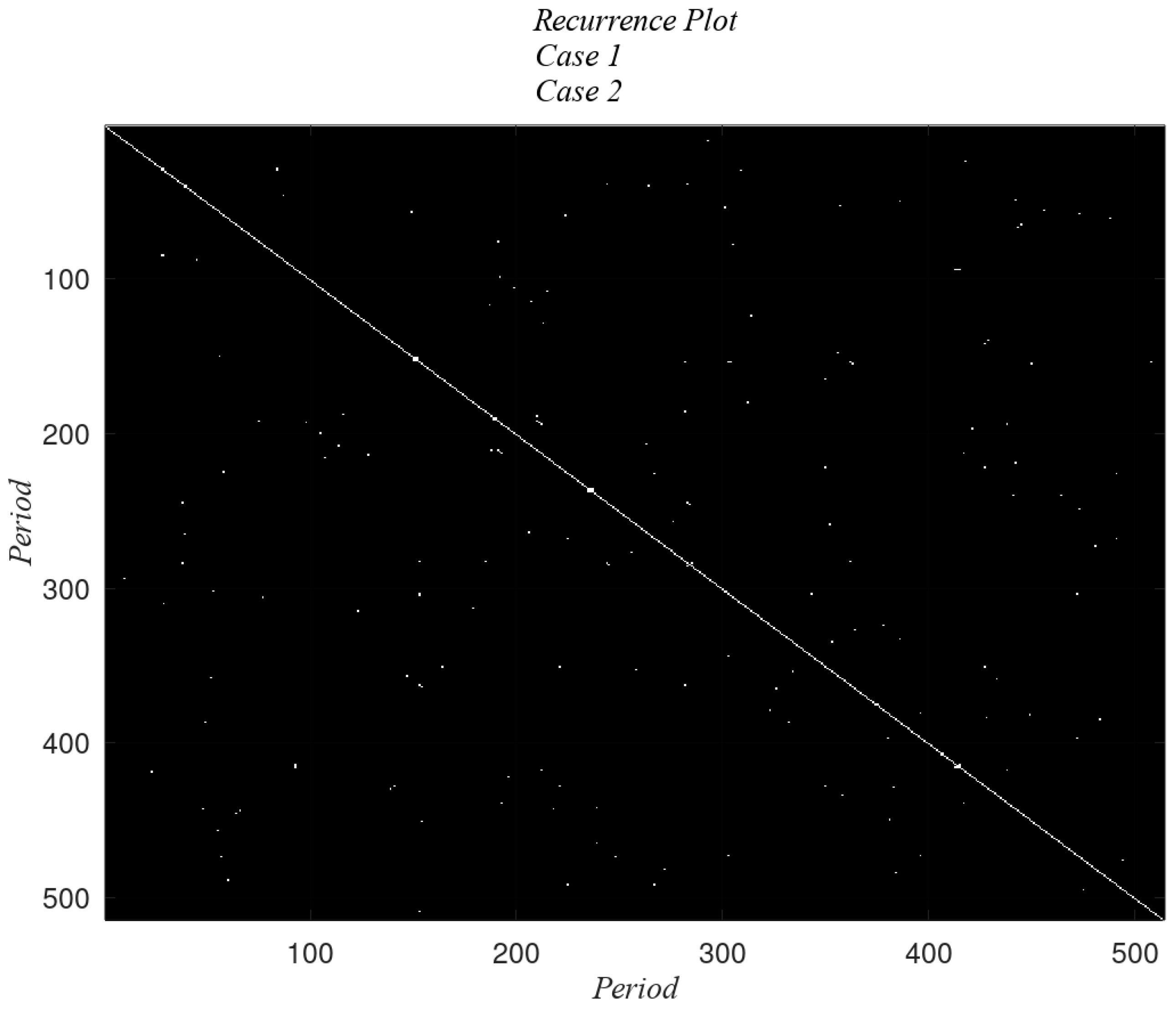
4.2. Application of the RPs to the Accelerometer Data
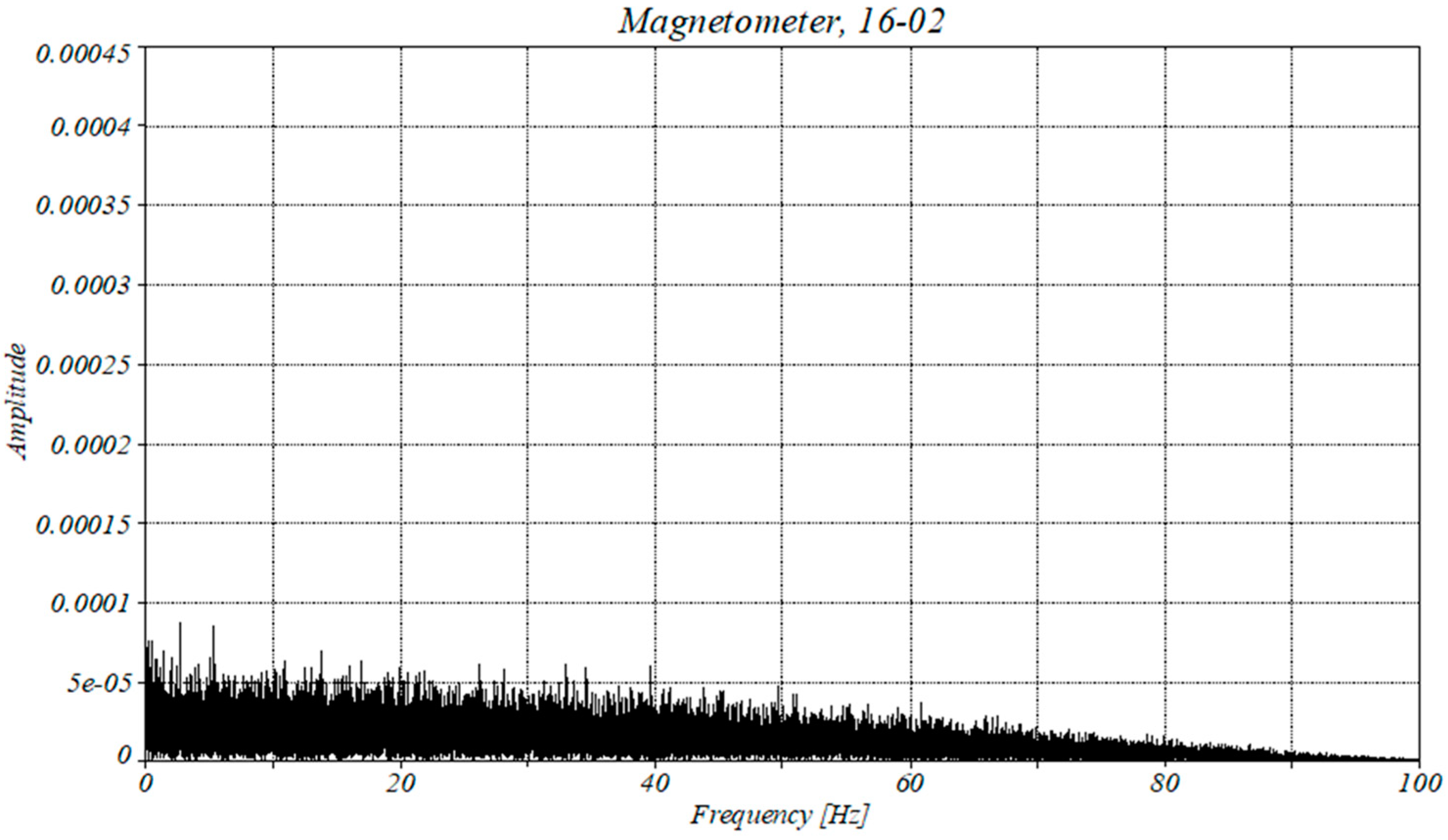
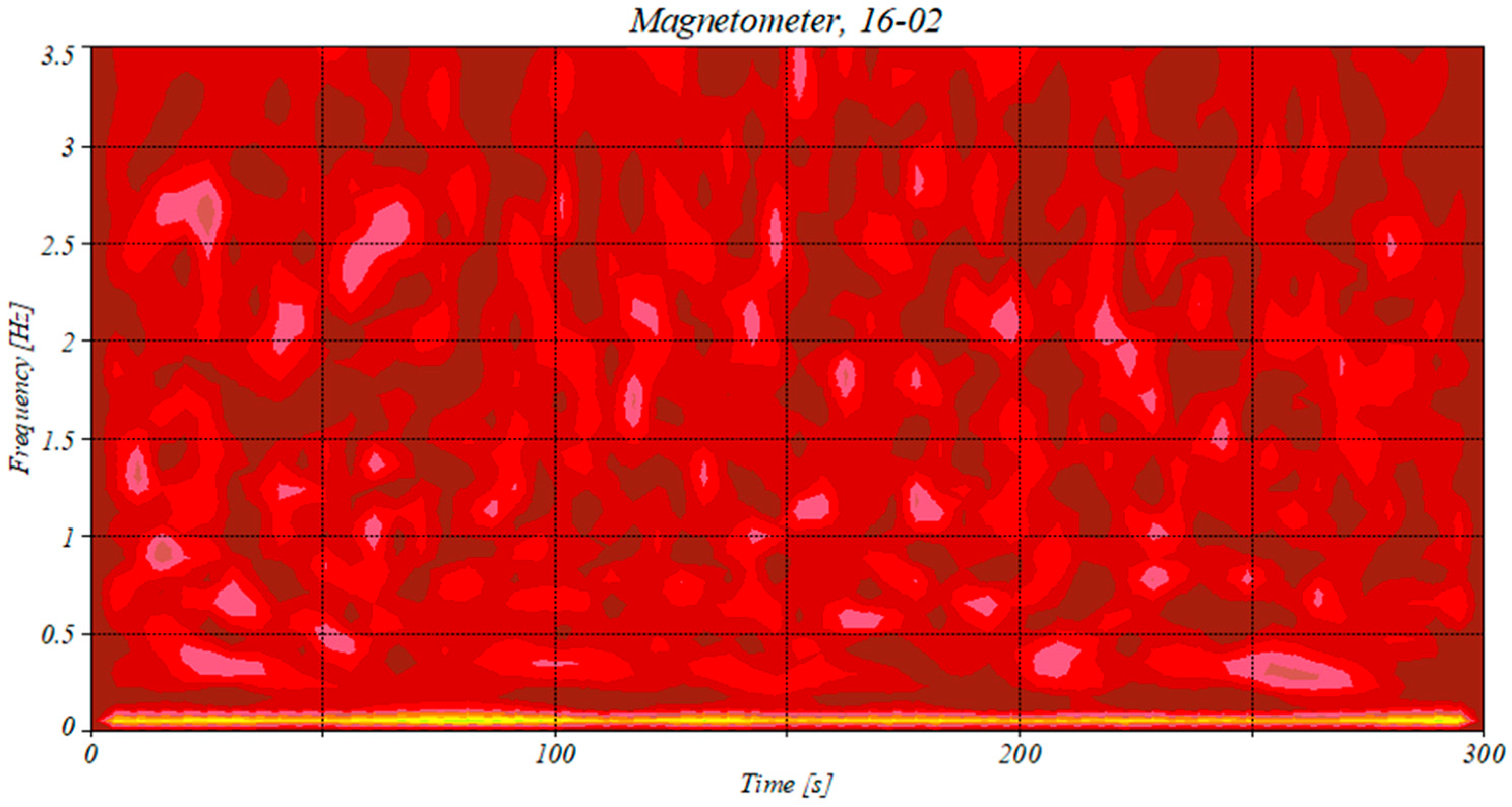
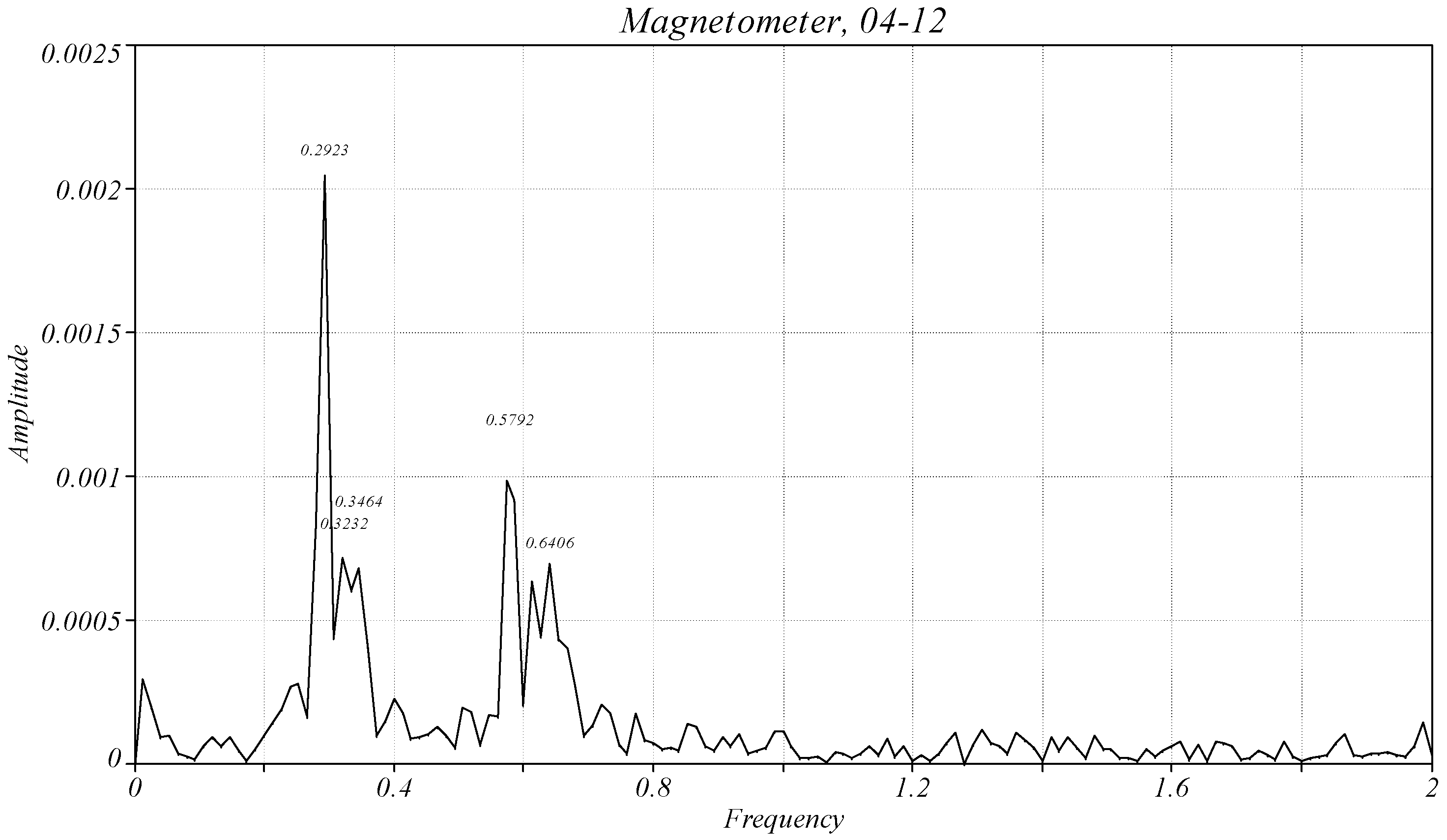
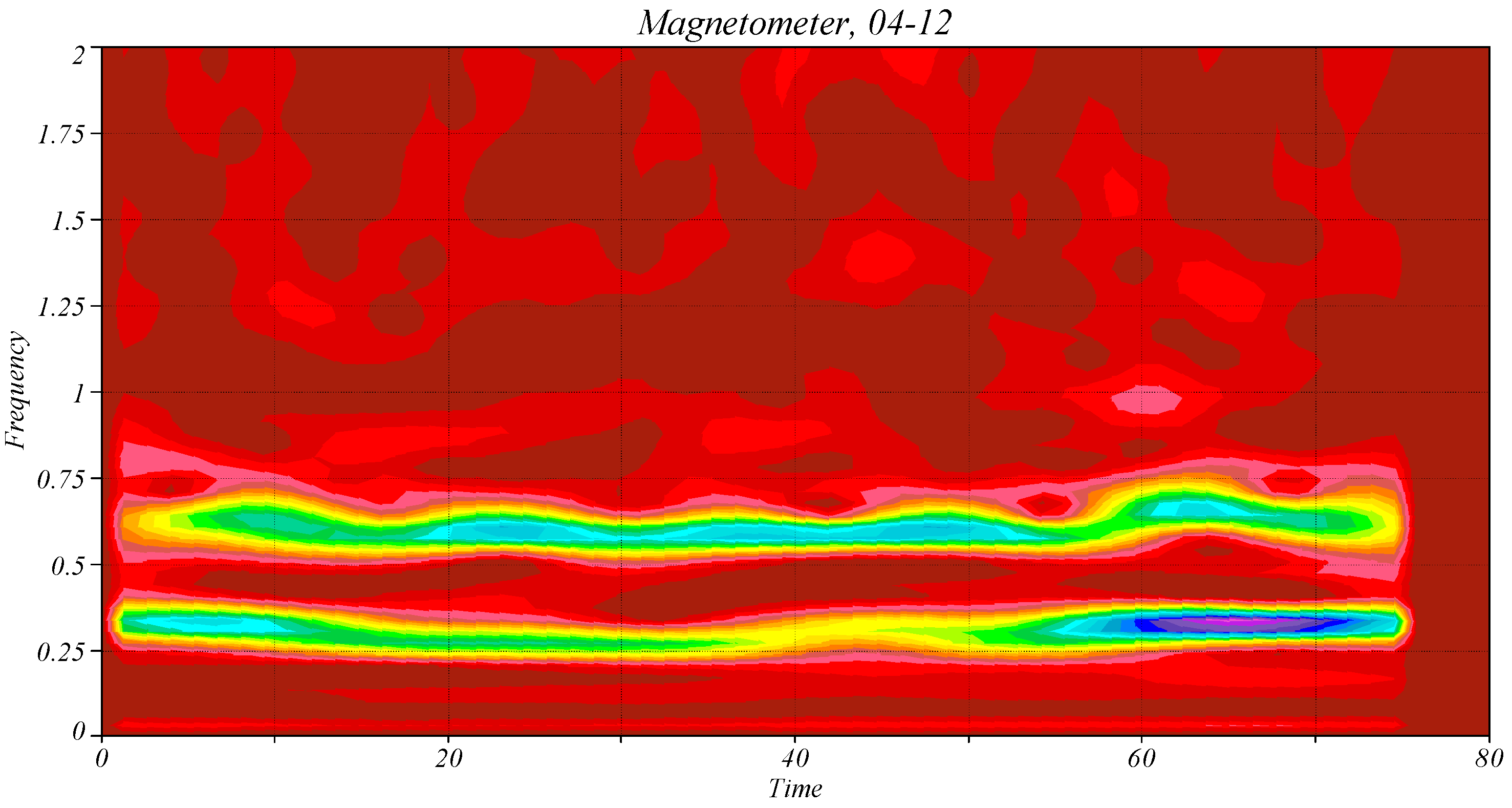
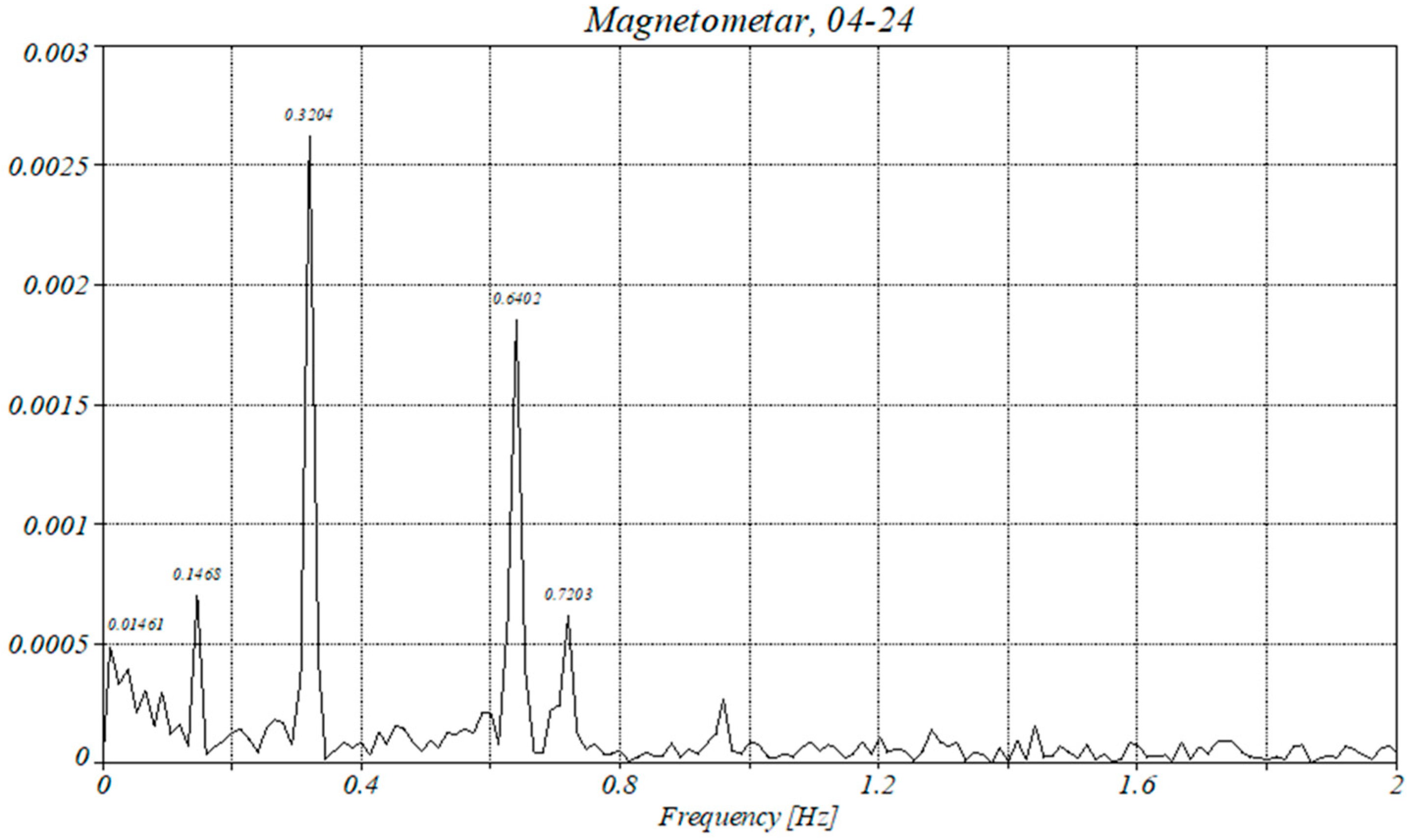
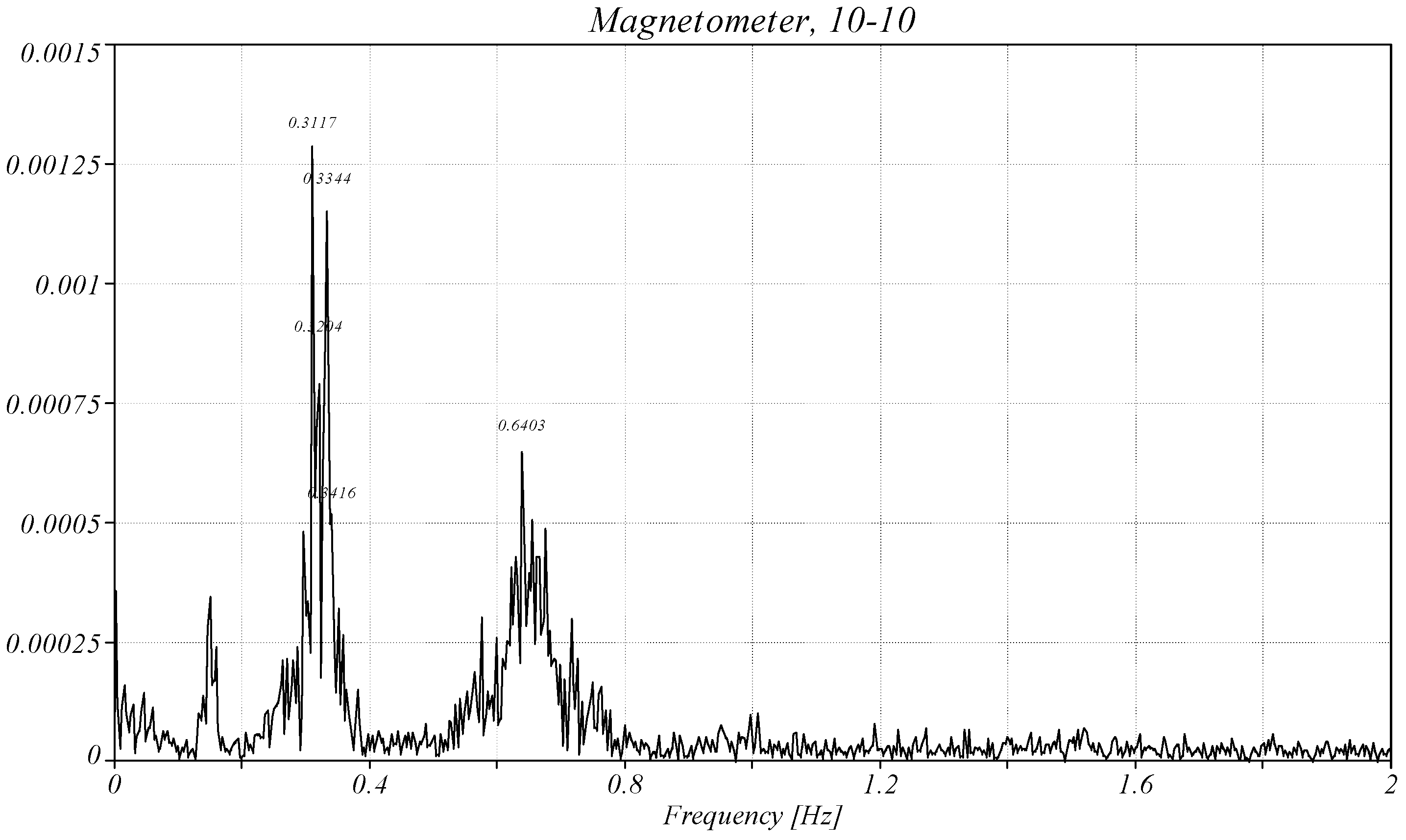
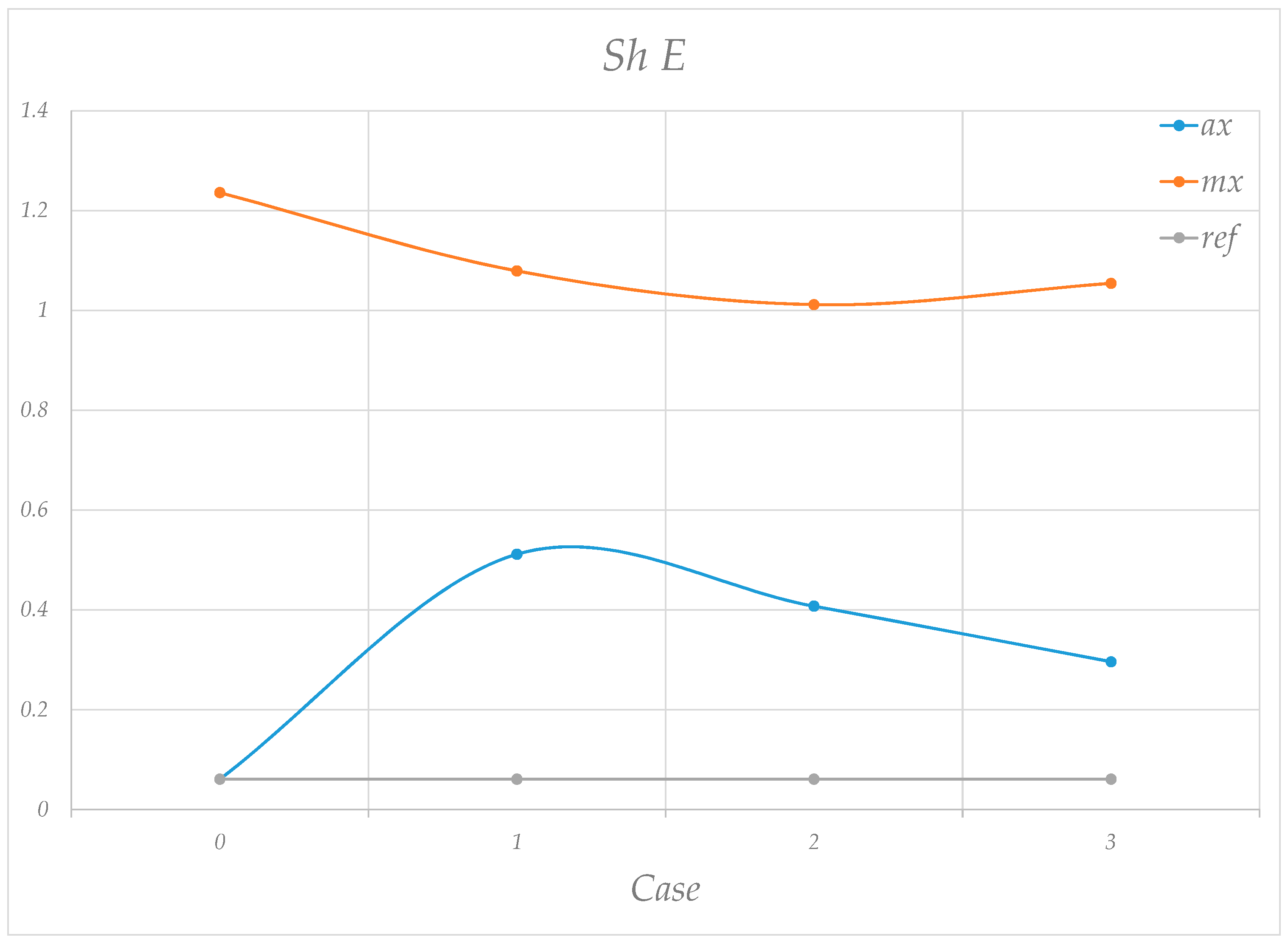
4.3. Analysis of the Magnetometer Data
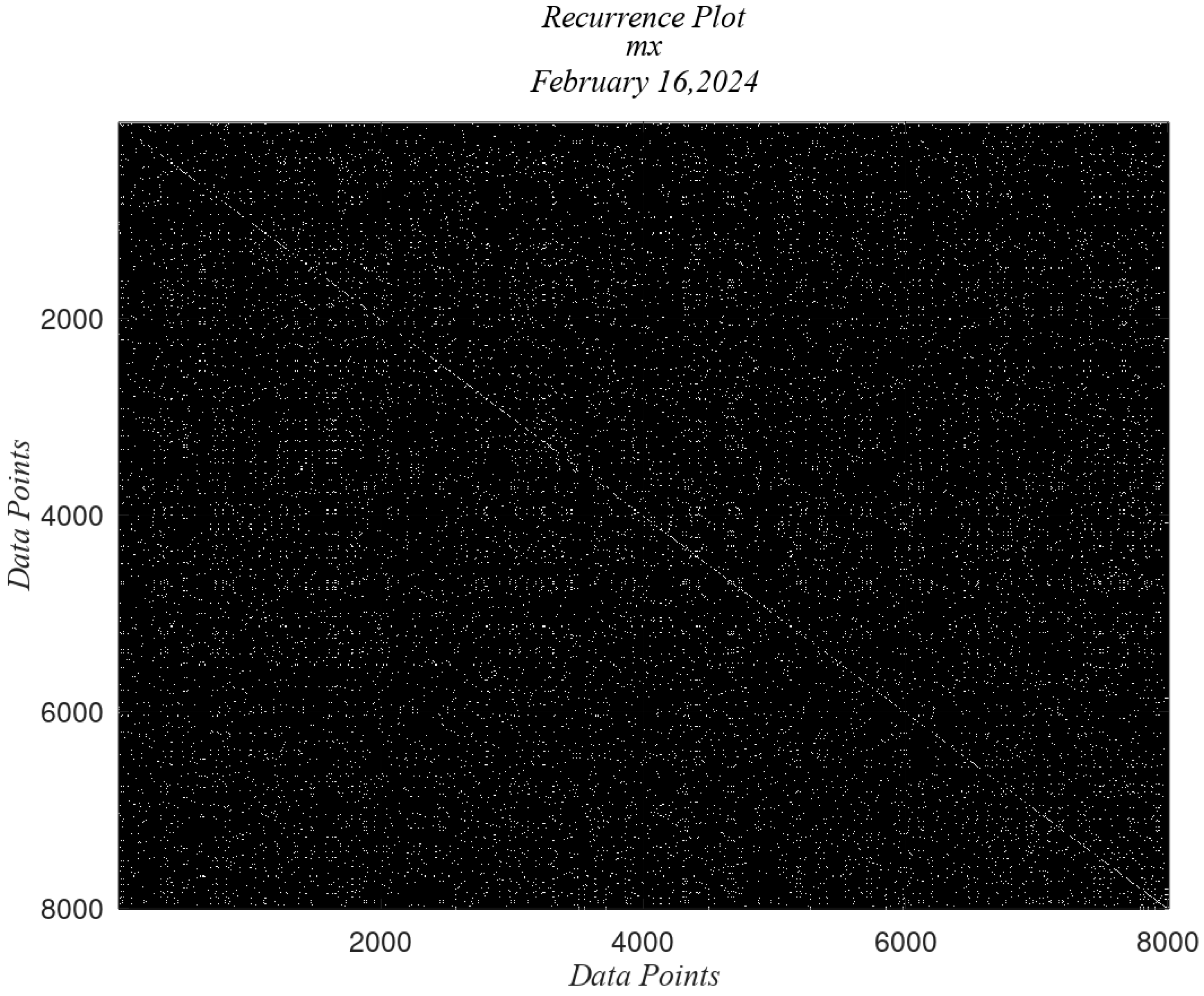
4.4. Application of the RPs to the Magnetometer Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jauregui-Correa, J.C.; Lozano-Guzmán, A. Mechanical Vibrations and Condition Monitoring, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2020; ISBN 978-0-12-819796-7. [Google Scholar]
- Eckmann, J.; Oliffson, S.; Ruelle, D. Recurrence Plots of Dynamical Systems. Eur. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef]
- Webber, C.L.; Ioana, C.; Marwan, N.; Symposium, I.; Plots, R. Recurrence Plots and Their Quantifications: Expanding Horizons; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 9783319299211. [Google Scholar]
- Marwan, N.; Webber, C.L. Mathematical and Computational Foundations of Recurrence Quantifications. In Recurrence Quantification Analysis; Marwan, N., Webber, C.L., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 3–43. ISBN 9783319071558. [Google Scholar]
- Thiel, M.; Romano, M.; Kurths, J. Spurious Structures in Recurrence Plots Induced by Embedding. Nonlinear Dyn. 2006, 44, 299–305. [Google Scholar] [CrossRef]
- Carrión, A.; Miralles, R. New Insights for Testing Linearity and Complexity with Surrogates: A Recurrence Plot Approach. In Recurrence Plots and Their Quantifications: Expanding Horizons; Webber, C.L., Ed.; Springer Proceedings in Physics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 91–112. ISBN 9783319299228. [Google Scholar]
- Kiss, Z.; Hudson, J.L. Synchronization Analysis of Coupled Noncoherent Oscillators. Nonlinear Dyn. 2006, 2, 135–149. [Google Scholar] [CrossRef]
- Kwuimy, C.; Samadani, M.; Nataraj, C. Bifurcation analysis of a nonlinear pendulum using recurrence and statistical methods: Applications to fault diagnostics. Nonlinear Dyn. 2014, 76, 1963–1975. [Google Scholar] [CrossRef]
- Girault, J.-M. Recurrence and symmetry of time series: Application to transition detection. Chaos, Solitons and Fractals 2015, 77, 11–28. [Google Scholar] [CrossRef]
- Belaire-Franch, J.; Contreras, D. Recurrence Plots in Nonlinear Time Series Analysis: Free Software. J. Stat. Softw. 2002, 7, 1–18. [Google Scholar] [CrossRef]
- Bot, O.L.; Mars, J.I.; Gervaise, C. Similarity matrix analysis and divergence measures for statistical detection of unknown deterministic signals hidden in additive noise. Phys. Lett. A 2015, 379, 2597–2609. [Google Scholar] [CrossRef]
- Feeny, B.F.; Lin, G. Fractional Derivatives Applied to Phase-Space Reconstructions. Nonlinear Dyn. 2004, 38, 85–99. [Google Scholar] [CrossRef]
- Lin, G.; Feeny, B.; Das, T. Fractional derivative reconstruction of forced oscillators. Nonlinear Dyn. 2009, 55, 239–250. [Google Scholar] [CrossRef][Green Version]
- Feeny, B.F.; Liang, J.W. Phase-Space Reconstructions and Stick-Slip. Nonlinear Dyn. 1997, 13, 39–57. [Google Scholar] [CrossRef]
- Kwuimy, C.A.K.; Kadji, H.G.E. Recurrence analysis and synchronization of oscillators with coexisting attractors. Phys. Lett. A 2014, 378, 2142–2150. [Google Scholar] [CrossRef]
- Kwuimy, C.A.K.; Nataraj, S.A.A.C. Characterization of the vibration transmitted in the human arm using selected recurrence quantification parameters. Nonlinear Dyn. 2017, 88, 2873–2887. [Google Scholar] [CrossRef]
- Kwuimy, C.A.K.; Nataraj, C. Recurrence and Joint Recurrence Analysis of Multiple Attractors Energy Harvesting System. In Structural Nonlinear Dynamics and Diagnosis: Selected Papers from CSNDD 2012 and CSNDD 2014; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Joelle, E.; Bialonski, S.; Marwan, N.; Kurths, J.; Geier, C.; Lehnertz, K. Evaluation of selected recurrence measures in discriminating pre-ictal and inter-ictal periods from epileptic EEG data. Phys. Lett. A 2016, 380, 1419–1425. [Google Scholar] [CrossRef]
- Puthanmadam, N.; Hyttinen, J. Characterization of dynamical systems under noise using recurrence networks: Application to simulated and EEG data. Phys. Lett. A 2014, 378, 3464–3474. [Google Scholar] [CrossRef]
- Yan, J.; Wang, Y.; Ouyang, G.; Yu, T.; Li, X. Using max entropy ratio of recurrence plot to measure electrocorticogram changes in epilepsy patients. Physica A 2016, 443, 109–116. [Google Scholar] [CrossRef]
- Leonardi, G. A Method for the computation of entropy in the Recurrence Quantification Analysis of categorical time series. Physica A 2018, 512, 824–836. [Google Scholar] [CrossRef]
- Viana, E.; Rubinger, R.; Albuquerque, H.; Dias, F.; Oliveira, A.; Ribeiro, G. Periodicity detection on the parameter-space of a forced Chua’ s circuit. Nonlinear Dyn. 2012, 67, 385–392. [Google Scholar] [CrossRef]
- Syta, A.; Bowen, C.R.; Kim, H.A.; Rysak, A.; Litak, G. Responses of bistable piezoelectric-composite energy harvester by means of recurrences. Mech. Syst. Signal Process. 2016, 76–77, 823–832. [Google Scholar] [CrossRef]
- Elias, J.; Namboothiri, V.N.N. Cross-recurrence plot quantification analysis of input and output signals for the detection of chatter in turning. Nonlinear Dyn. 2014, 76, 255–261. [Google Scholar] [CrossRef]
- Stender, M.; Tiedemann, M.; Hoffmann, N.; Oberst, S. Impact of an irregular friction formulation on dynamics of a minimal model for brake squeal q. Mech. Syst. Signal Process. 2018, 107, 439–451. [Google Scholar] [CrossRef]
- Chelidze, T.; Lursmanashvili, O.; Matcharashvili, N.; Zhukova, N.; Mepharidze, E. High-order synchronization of stick–slip process: Experiments on spring–slider system. Nonlinear Dyn. 2010, 59, 259–275. [Google Scholar] [CrossRef]
- Litak, G.; Górski, G.; Mosdorf, R.; Rysak, A. Study of dynamics of two-phase flow through a minichannel by means of recurrences. Mech. Syst. Signal Process. 2017, 89, 48–57. [Google Scholar] [CrossRef]
- Zhai, L.; Zong, Y.; Wang, H.; Yan, C.; Gao, Z. Characterization of flow pattern transitions for horizontal liquid–liquid pipe flows by using multi-scale distribution entropy in coupled 3D phase space. Physica A 2017, 469, 136–147. [Google Scholar] [CrossRef]
- Xiong, H.; Shang, P.; Bian, S. Detecting intrinsic dynamics of traffic flow with recurrence analysis and empirical mode decomposition. Physica A 2017, 474, 70–84. [Google Scholar] [CrossRef]
- Tang, J.; Wang, Y.; Wang, H.; Zhang, S.; Liu, F. Dynamic analysis of traffic time series at different temporal scales: A complex networks approach. Physica A 2014, 405, 303–315. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Karlaftis, M.G. Comparing traffic flow time-series under fine and adverse weather conditions using recurrence-based complexity measures. Nonlinear Dyn. 2012, 69, 1949–1963. [Google Scholar] [CrossRef]
- Ukherjee, S.; Ray, R.; Samanta, R.; Khondekar, M. Nonlinearity and chaos in wireless network traffic. Chaos Solitons Fractals Interd 2017, 96, 23–29. [Google Scholar] [CrossRef]
- Fontaine, S.; Dia, S.; Renner, M. Nonlinear friction dynamics on fibrous materials, application to the characterization of surface quality. Part I: Global characterization of phase spaces. Nonlinear Dyn. 2011, 66, 625–646. [Google Scholar] [CrossRef]
- Faure, P.; Lesne, A. Estimating kolmogorov entropy from recurrence plots. In Recurrence Quantification Analysis; Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 45–63. [Google Scholar] [CrossRef]
- Skowronek, K.; Barszcz, T.; Antoni, J.; Zimroz, R. Assessment of background noise properties in tima and time-frequency domains in the context of vibration-base local damage detection in real enviroment. Mech. Syst. Signal Process. 2023, 199, 110465. [Google Scholar] [CrossRef]
- Jauregui-Correa, J.C. Identification of nonlinearities in mechanical systems using recurrence plots. In Nonlinear Structural Dynamics and Damping; Springer International Publishing: Cham, Switzerland, 2019; Volume 69. [Google Scholar]
- Torres-Contreras, I.; Jauregui-Correa, J.C.; Lopez-Cajun, C.; Echeverria-Villagomes, S. Effects of Phase Shift Errors in Recurrence Plot for Rotating Machinery Fault Diagnosis. Appl. Sci. 2021, 11, 873. [Google Scholar] [CrossRef]
- Jauregui-Correa, J.C.; Torres-Contreras, I.; Villagomez, S.E.; Rangel, J.P.B. The Application of the Recurrence Plot to Analyze Rubbing in An Unbalance Rotating Disk. J. Vib. Eng. Technol. 2024, 12, 8993–9008. [Google Scholar] [CrossRef]





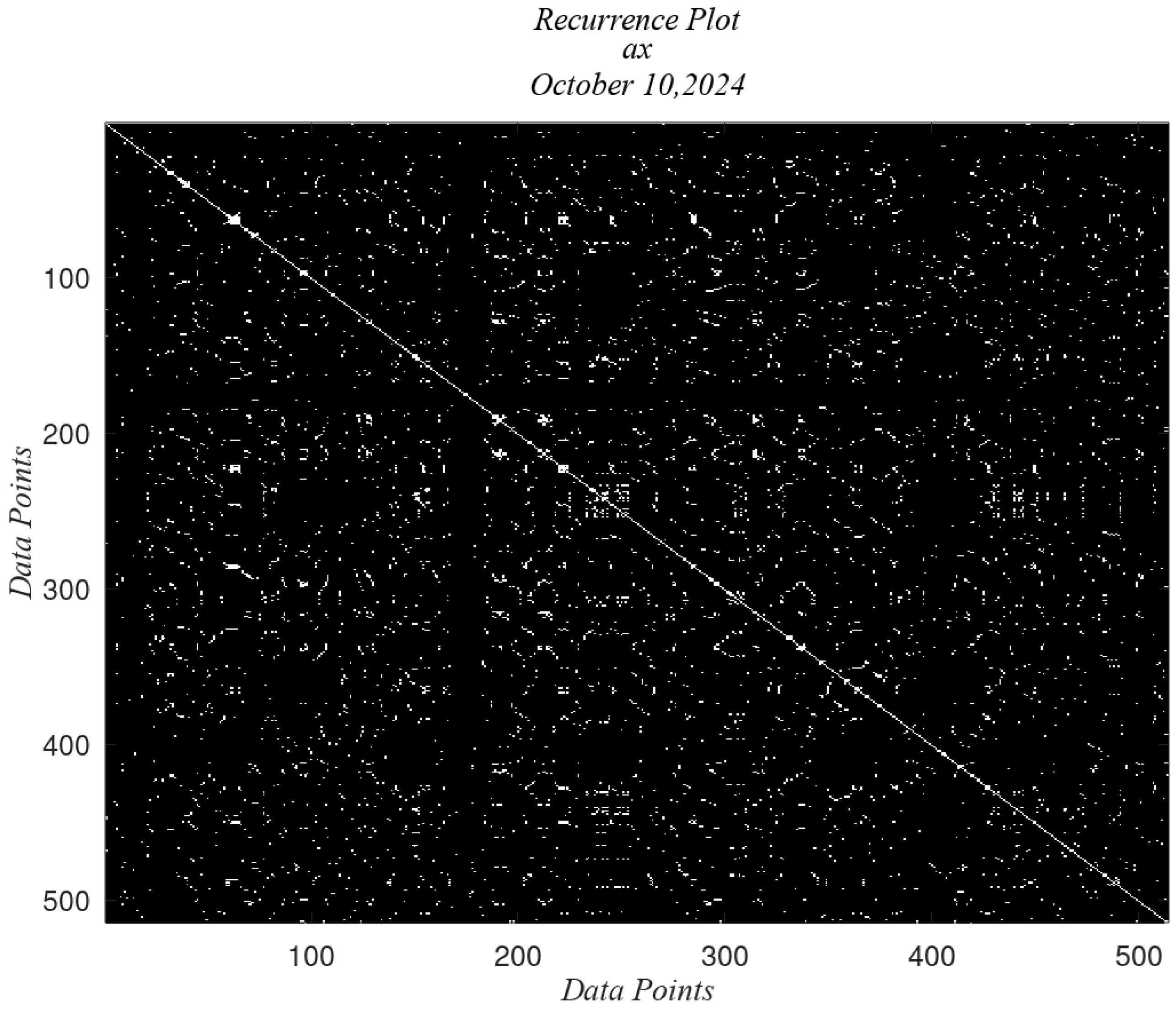






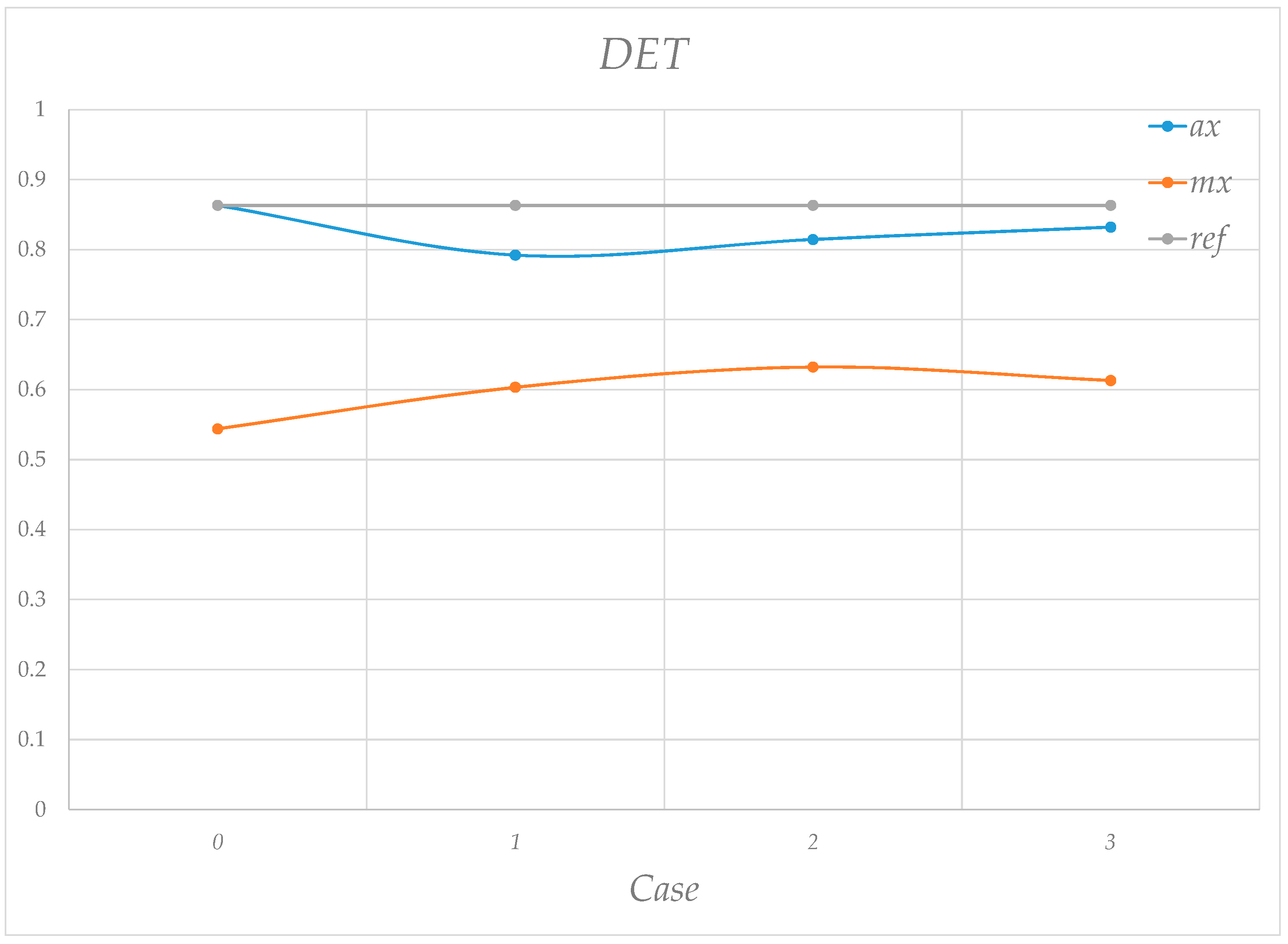
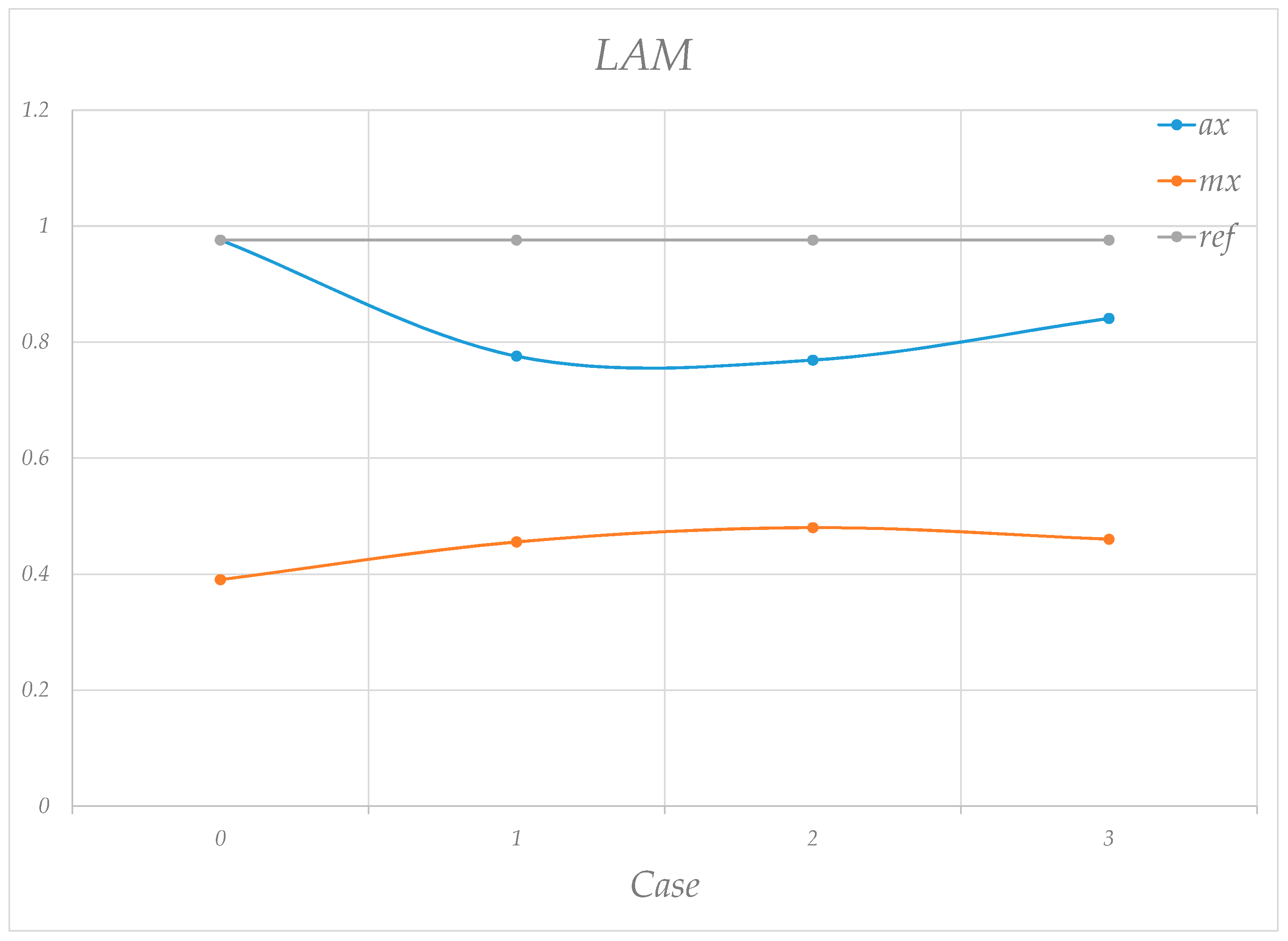
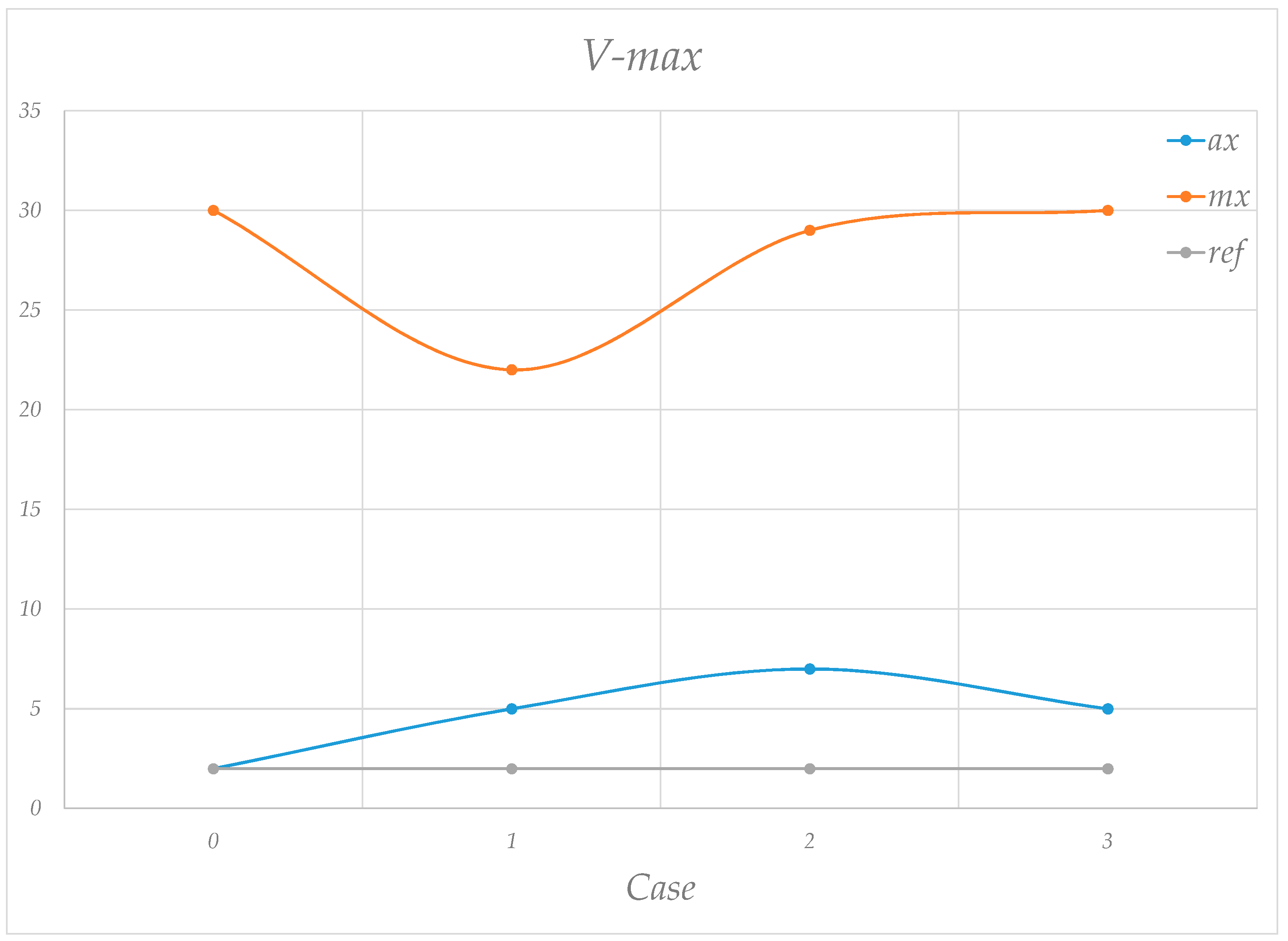
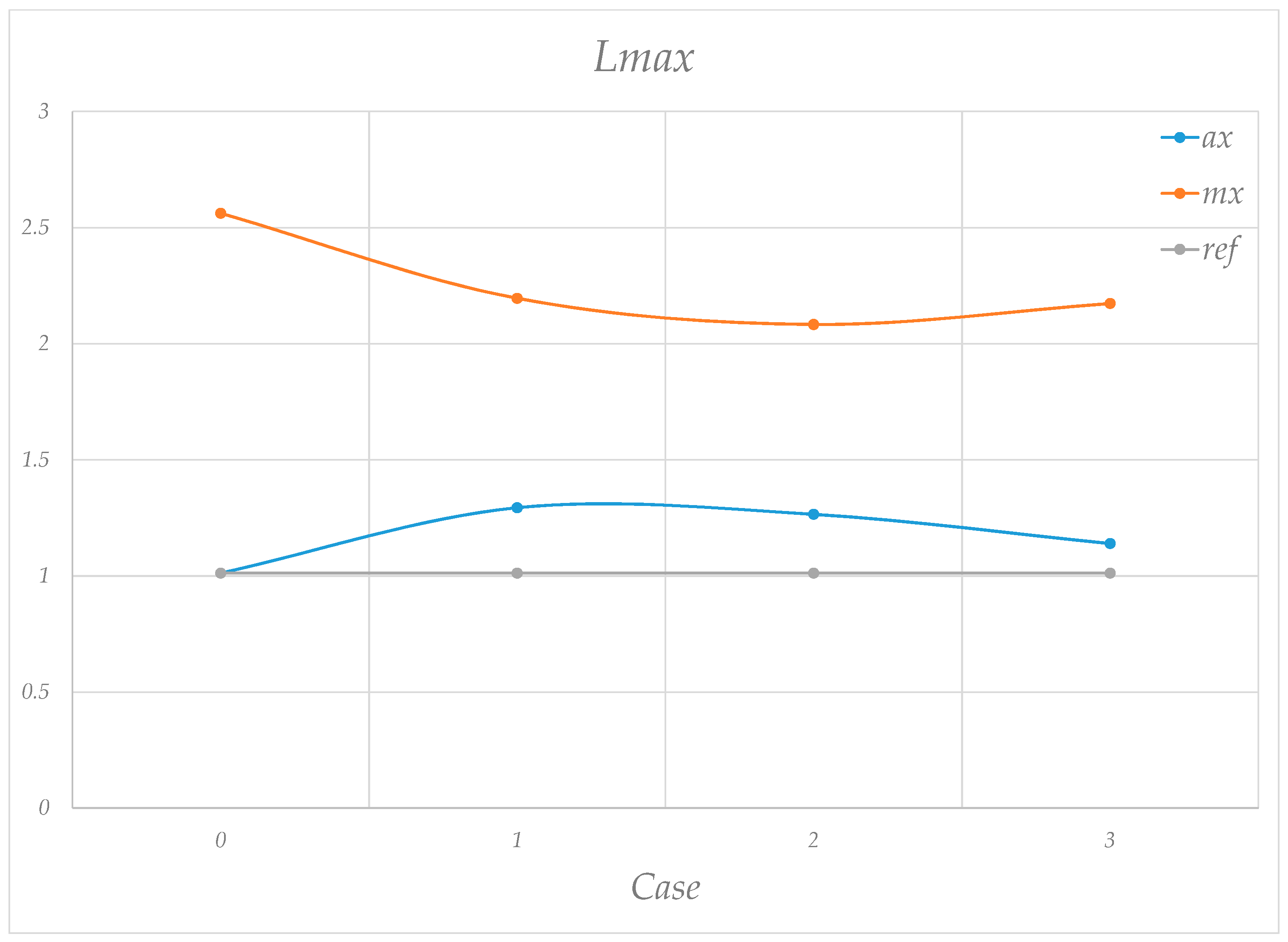

| RQA | Equation | Description |
|---|---|---|
| Recurrence Rate | Determines the average number of recurrence points. | |
| Determinism | Determines the percentage of points that are on a diagonal. is the index of each diagonal, and is the histogram of the diagonal. A chaotic system has short diagonals, and a periodic system forms regular diagonals, parallel to the main diagonal. | |
| Longest Diagonal | Measures the length (in points) of the longest diagonal. | |
| Average Vertical Length | Measures the percentage of recurrence points that lay on a vertical line. is the index corresponding to the vertical line, and is the histogram of the vertical line. | |
| Longest Vertical Line | Measures the length of the longest vertical line. | |
| Laminarity | Measures the percentage of recurrence points that create vertical lines. is the index of the corresponding vertical line, is the histogram of the vertical line. | |
| Shannon Entropy | Measures the disorder of the phase plane. For a linear and periodic system, the Shannon entropy is almost zero. For a non-deterministic and noisy system, the Shannon entropy will be almost infinite. is the relative frequency; it is calculated as the ratio of diagonal with non-recurrence points divided by the number of recurrent points. |
| 0.0005 | 0.0014985 | 1 | 2000 | 1 | 1 | 0.63651 |
| Case | Date | Wind Condition |
|---|---|---|
| 0 | 16 February | No |
| 1 | 12 April | Yes |
| 2 | 24 April | Yes |
| 3 | 10 October | Yes |
| Case | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Amplitude | 2 × 10−5 | 0.00125 | 0.0025 | 0.0015 |
| Case | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Amplitude | 0.00045 | 0.0021 | 0.0025 | 0.00125 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jauregui-Correa, J.C.; Morales-Velazquez, L. The Application of Recurrence Plots to Identify Nonlinear Responses Using Magnetometer Data for Wind Turbine Design. Machines 2025, 13, 233. https://doi.org/10.3390/machines13030233
Jauregui-Correa JC, Morales-Velazquez L. The Application of Recurrence Plots to Identify Nonlinear Responses Using Magnetometer Data for Wind Turbine Design. Machines. 2025; 13(3):233. https://doi.org/10.3390/machines13030233
Chicago/Turabian StyleJauregui-Correa, Juan Carlos, and Luis Morales-Velazquez. 2025. "The Application of Recurrence Plots to Identify Nonlinear Responses Using Magnetometer Data for Wind Turbine Design" Machines 13, no. 3: 233. https://doi.org/10.3390/machines13030233
APA StyleJauregui-Correa, J. C., & Morales-Velazquez, L. (2025). The Application of Recurrence Plots to Identify Nonlinear Responses Using Magnetometer Data for Wind Turbine Design. Machines, 13(3), 233. https://doi.org/10.3390/machines13030233






