The Optimized Design and Principal Analysis of a Toe-End Sliding Sleeve
Abstract
1. Introduction
2. Technical Analysis
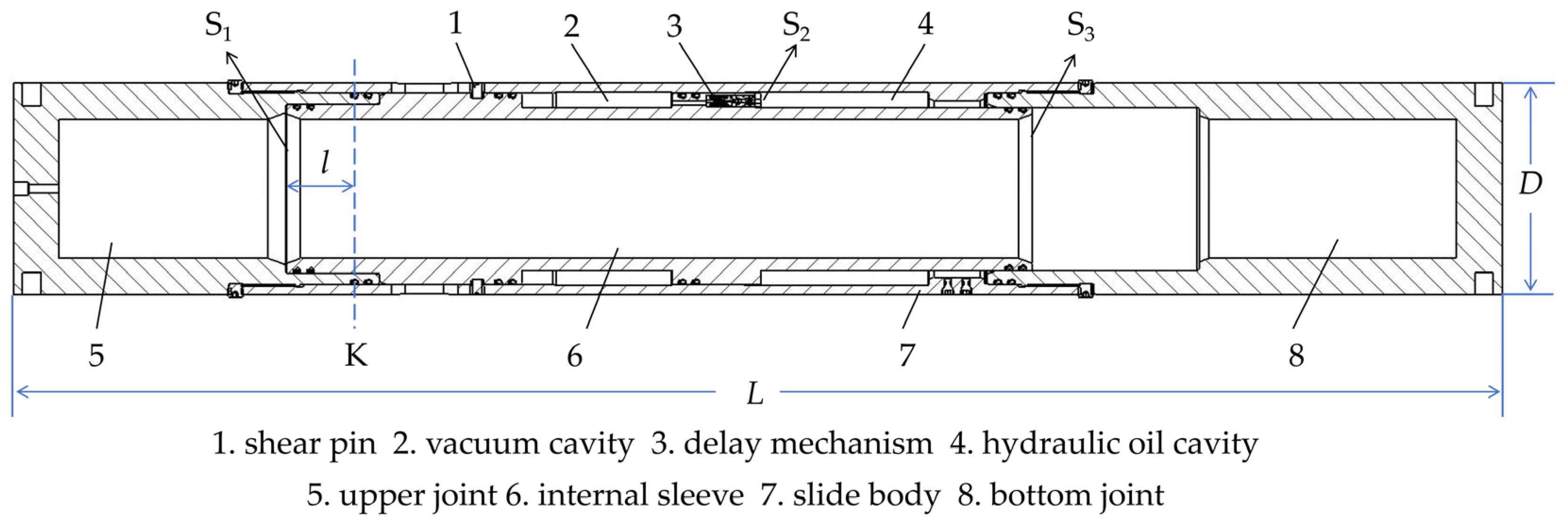
2.1. Structural Design
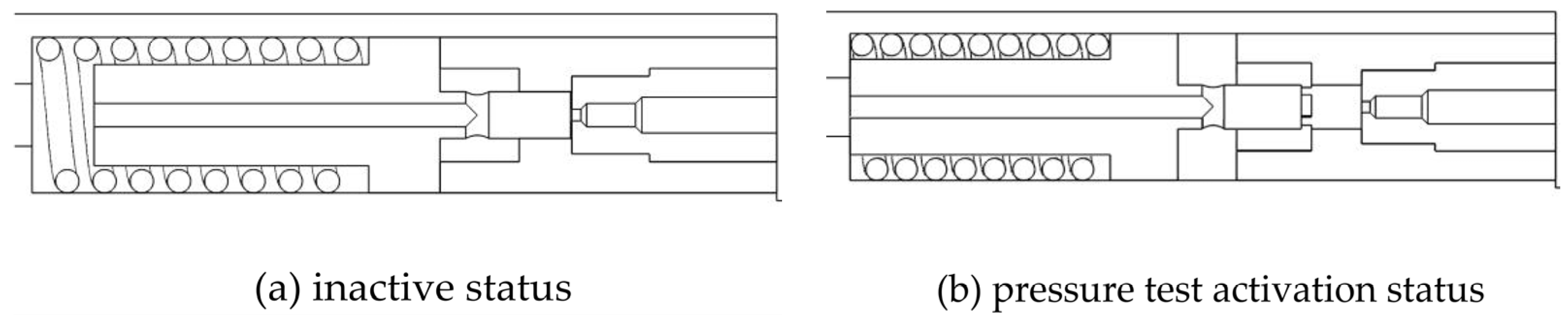
2.2. Working Principle
3. Numerical Simulation Methods
3.1. Numerical Simulation Equations
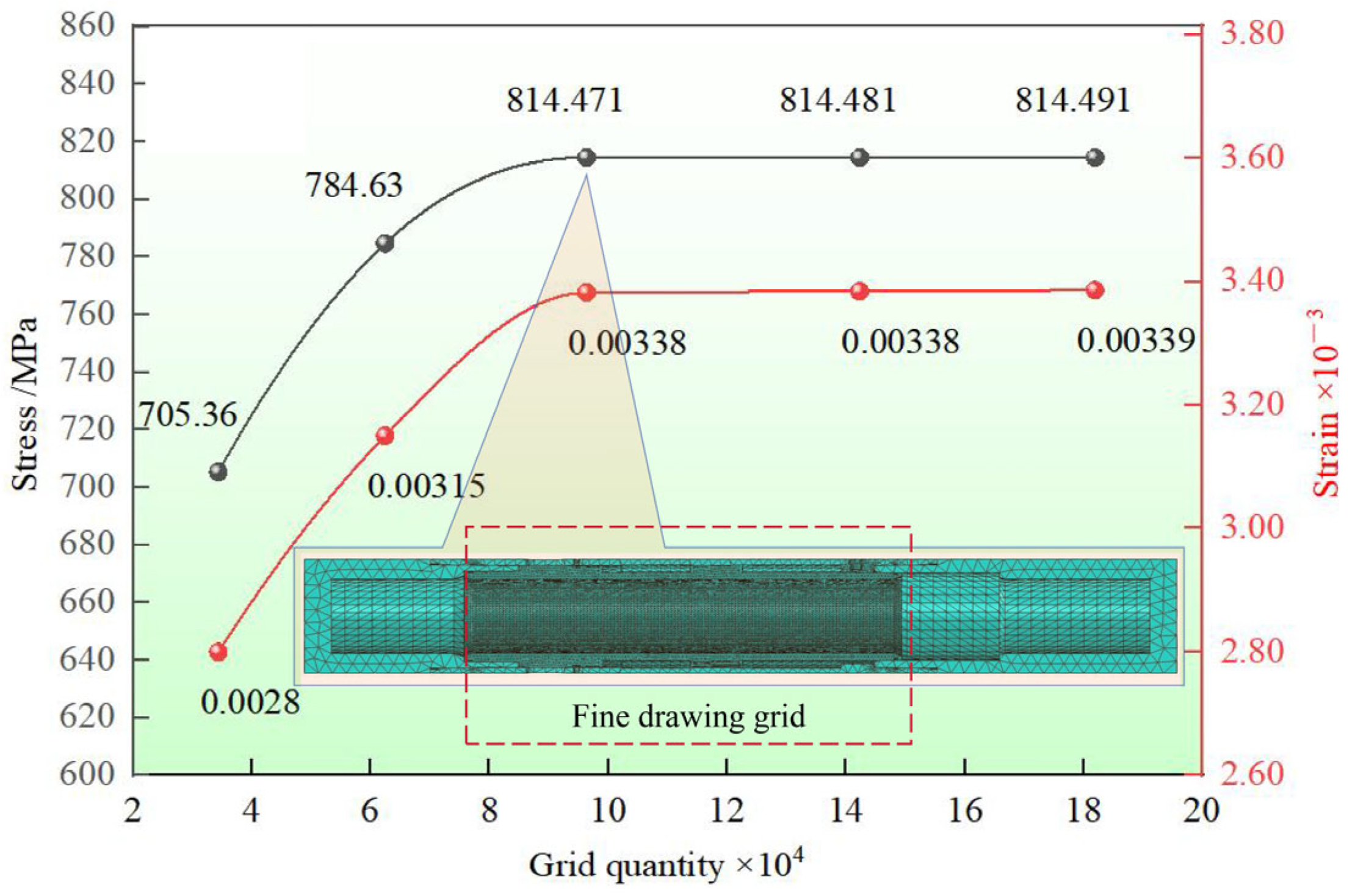
3.2. Meshing and Boundary Condition Setting
4. Results and Discussion
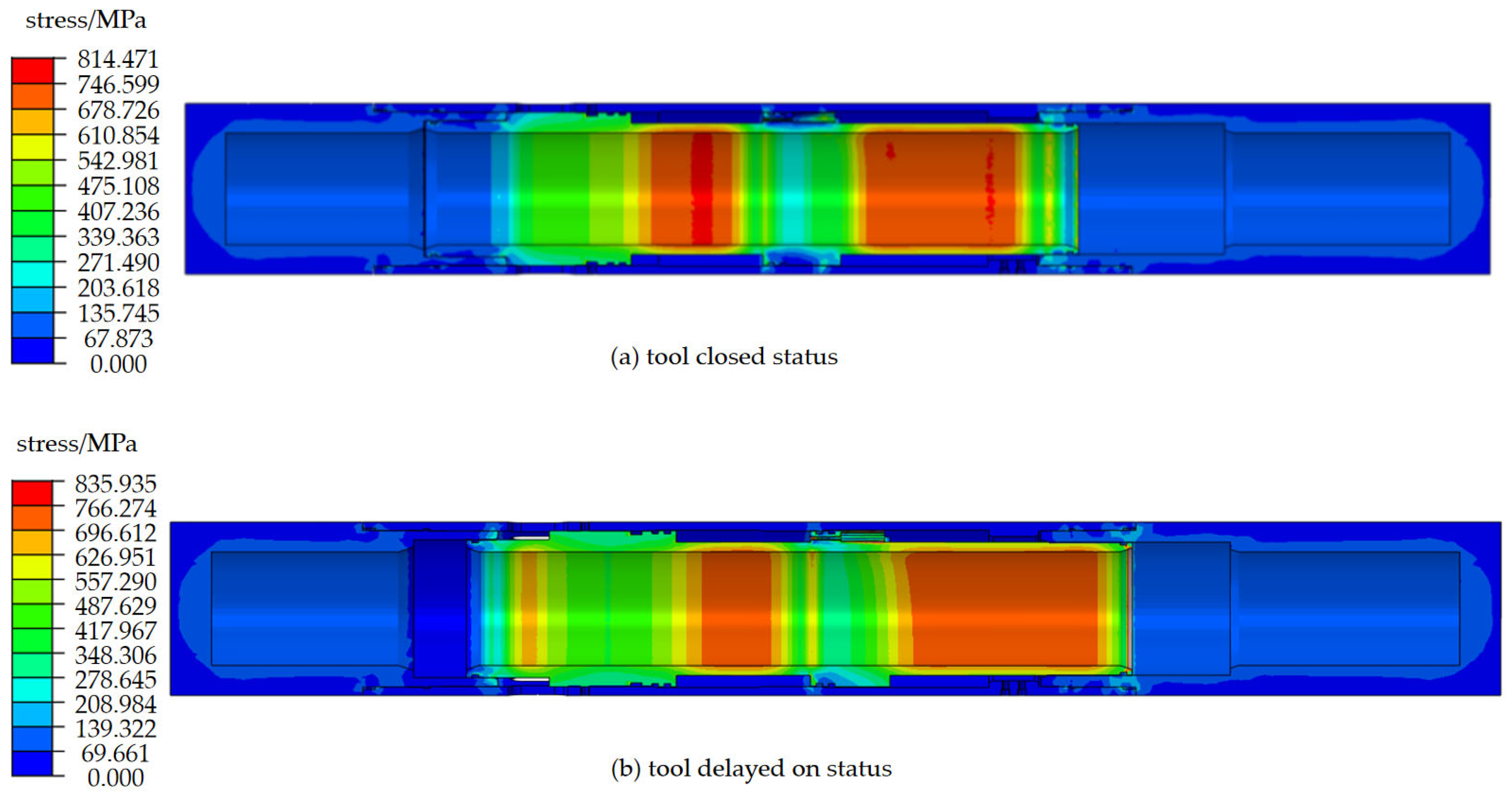
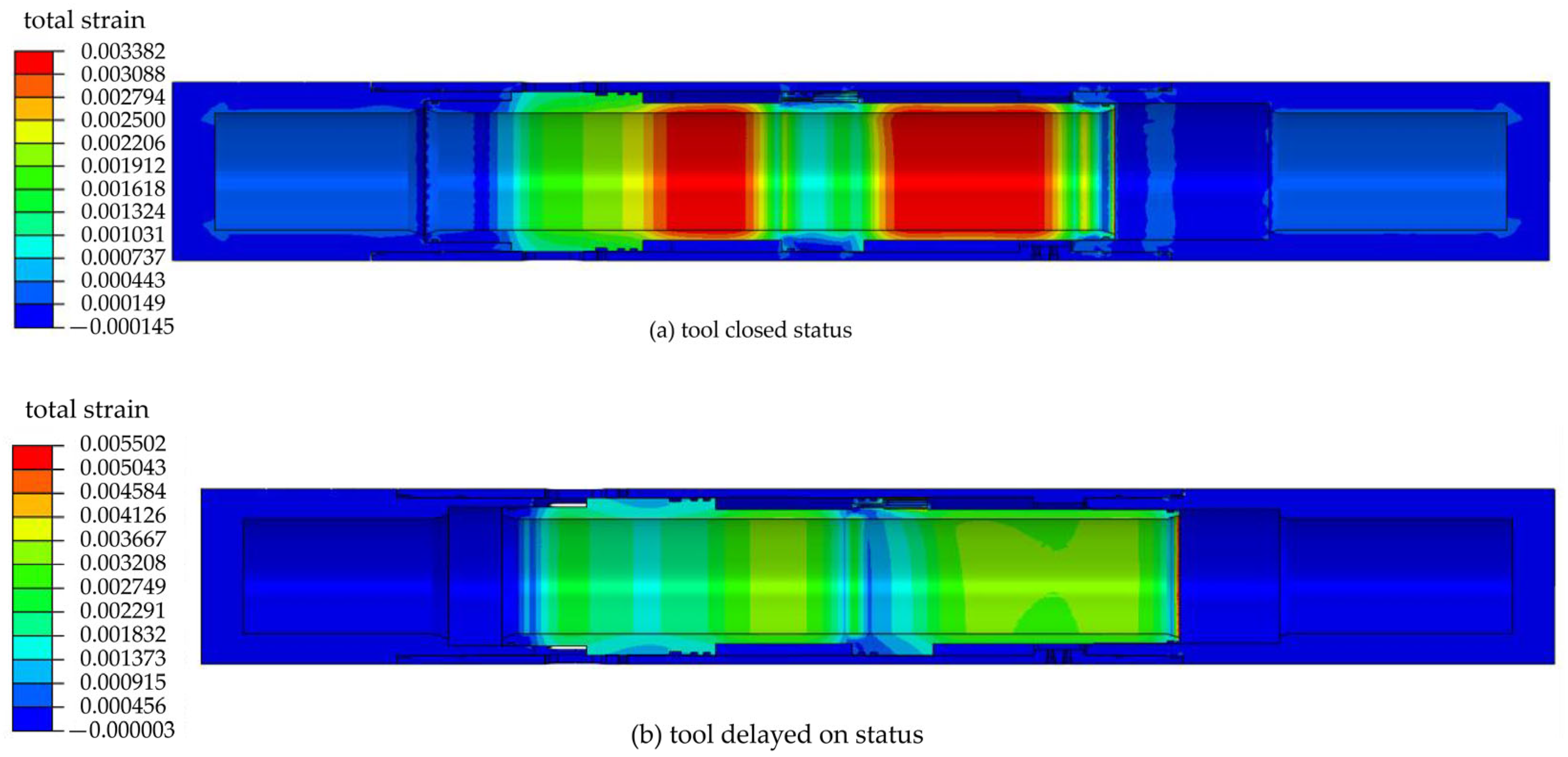
4.1. Tool Safety Performance Analysis
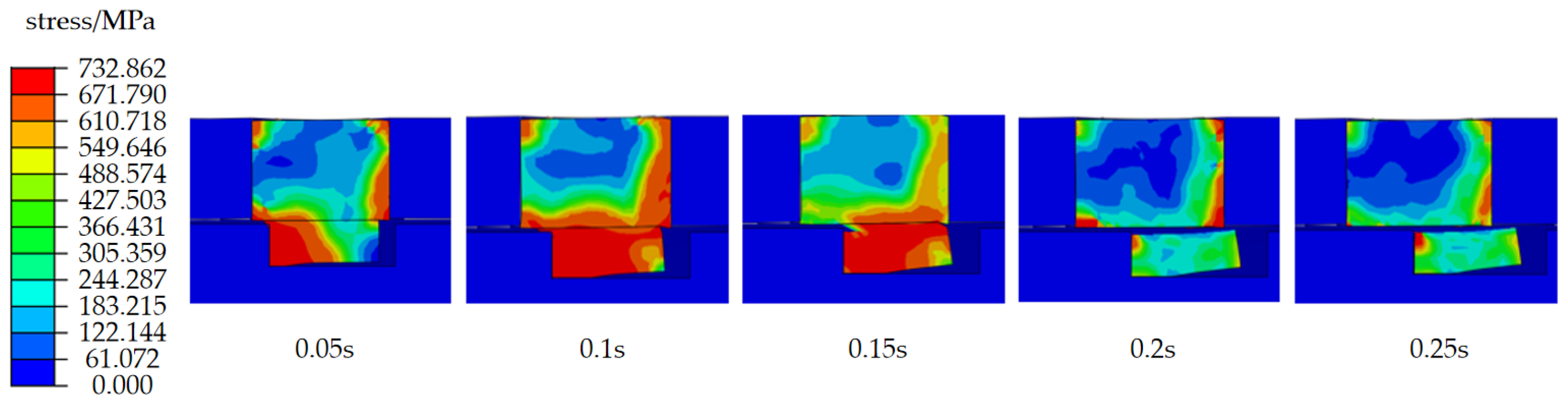
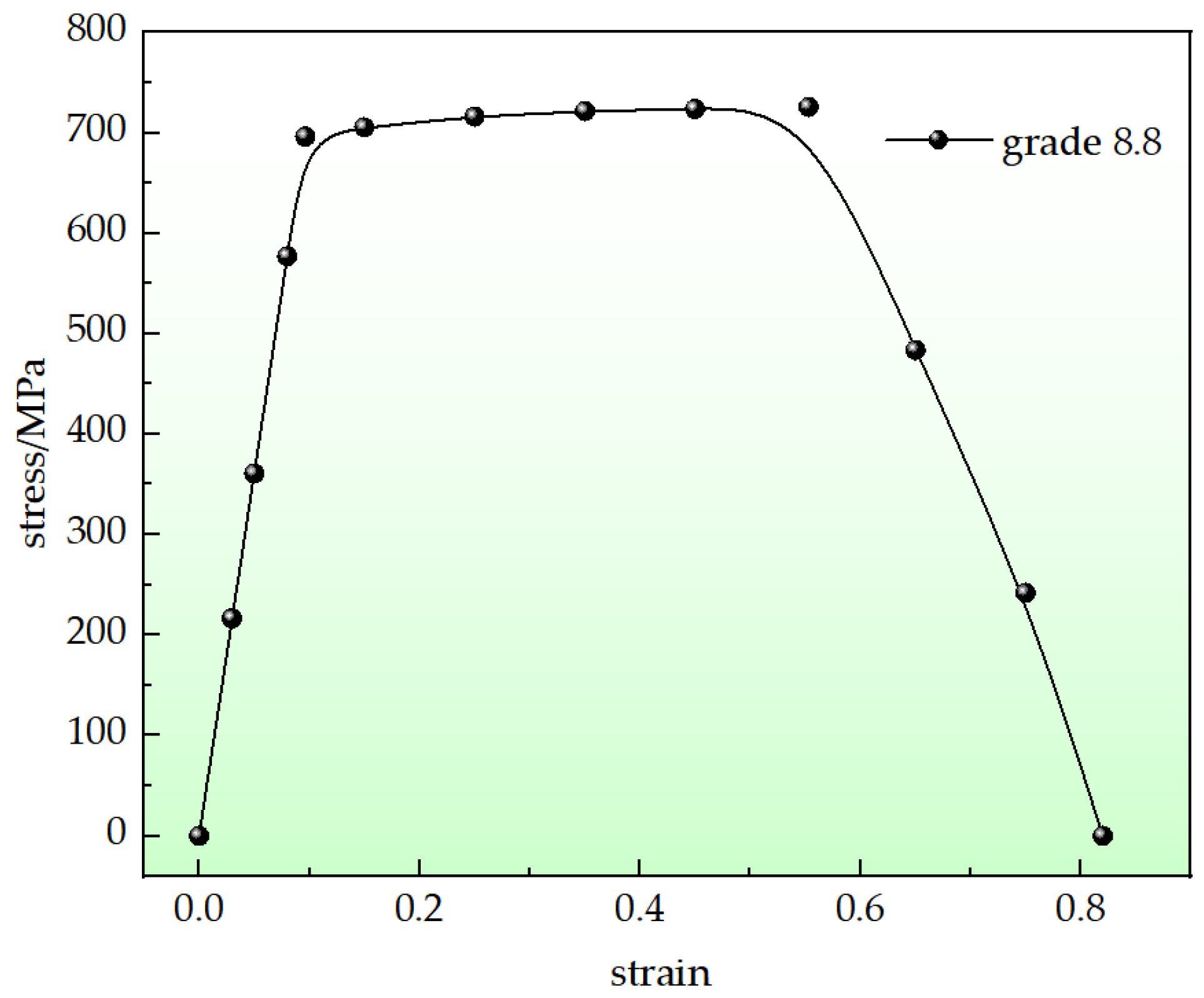
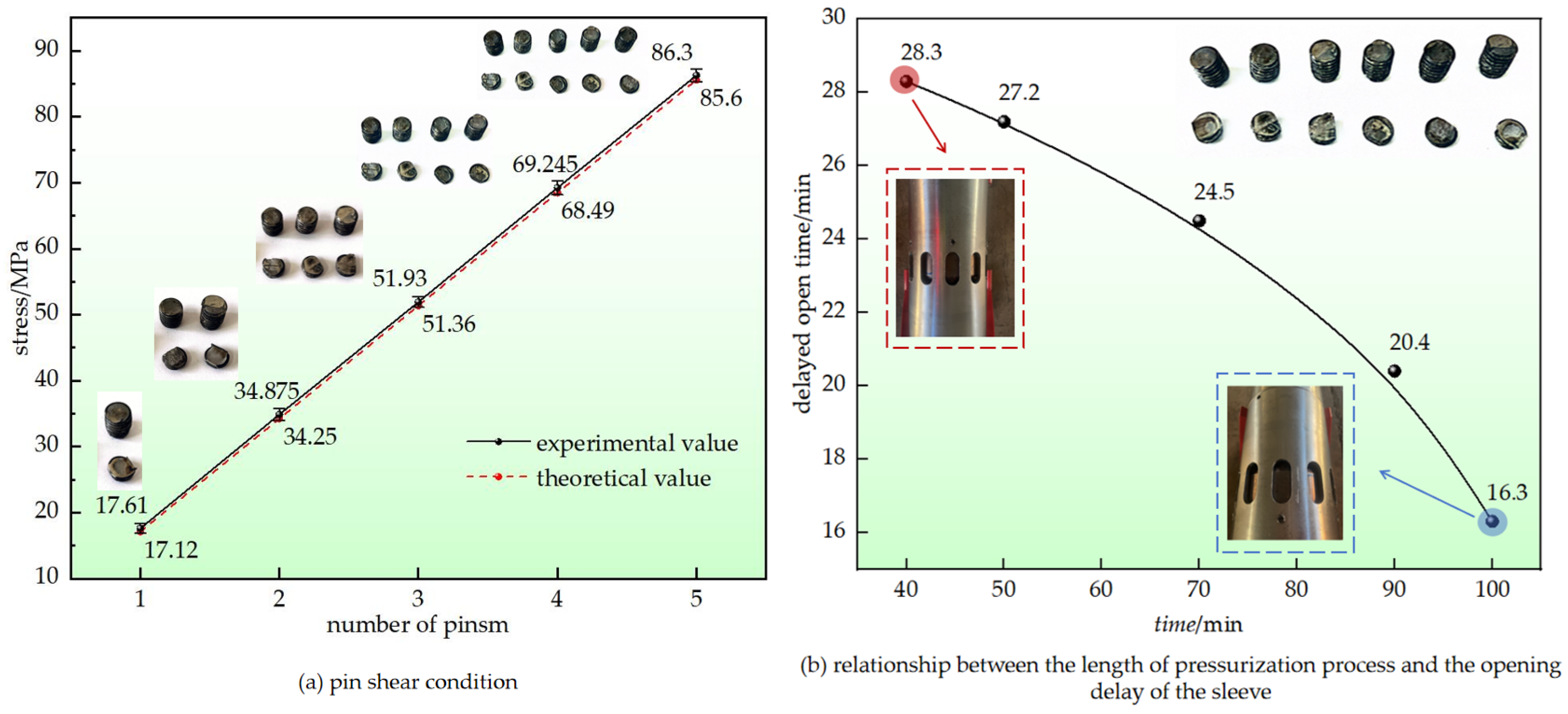
4.2. Shear Pin Failure Simulation Analysis
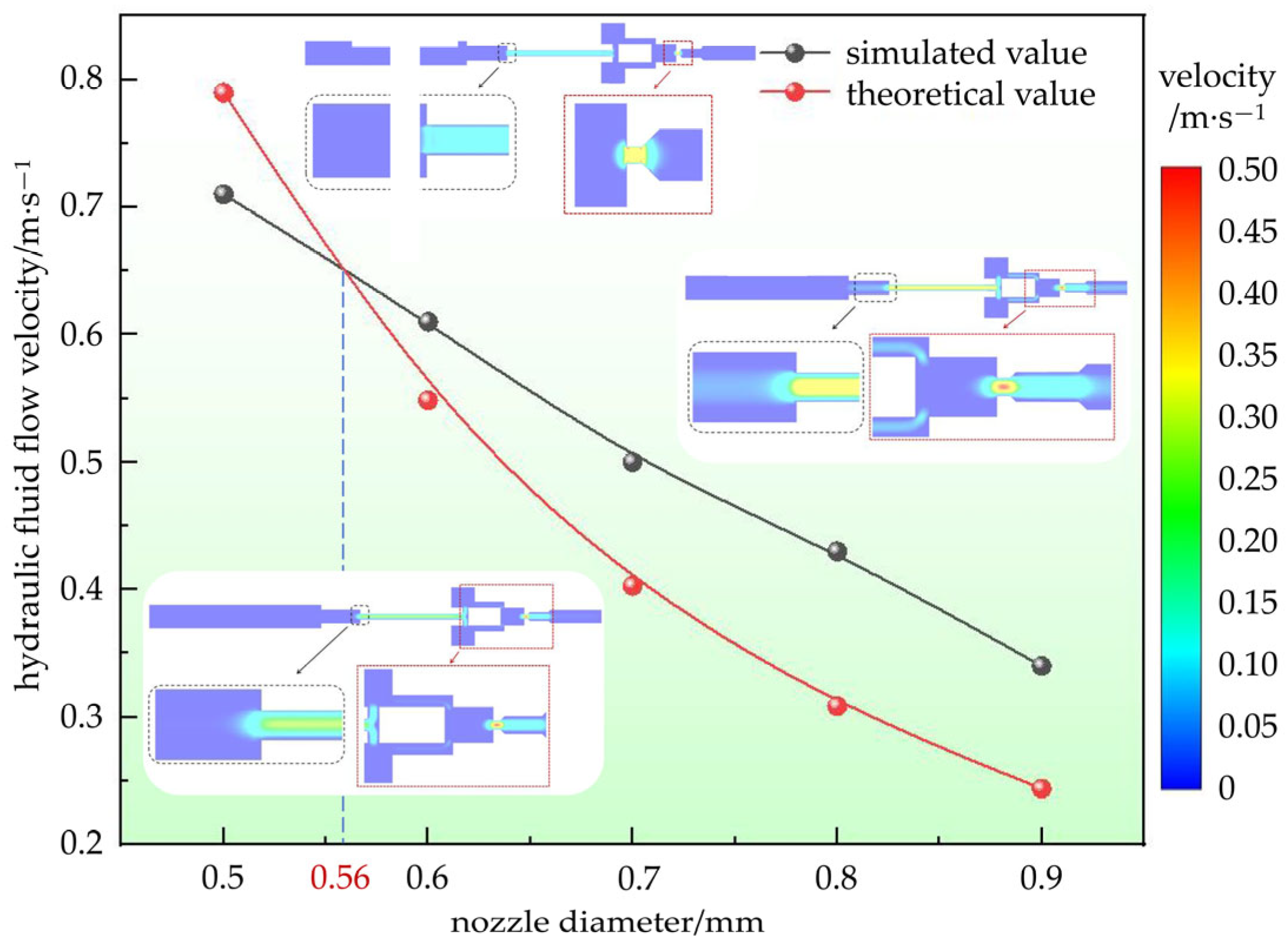
4.3. Optimization Analysis of the Nozzle of the Delay Mechanism
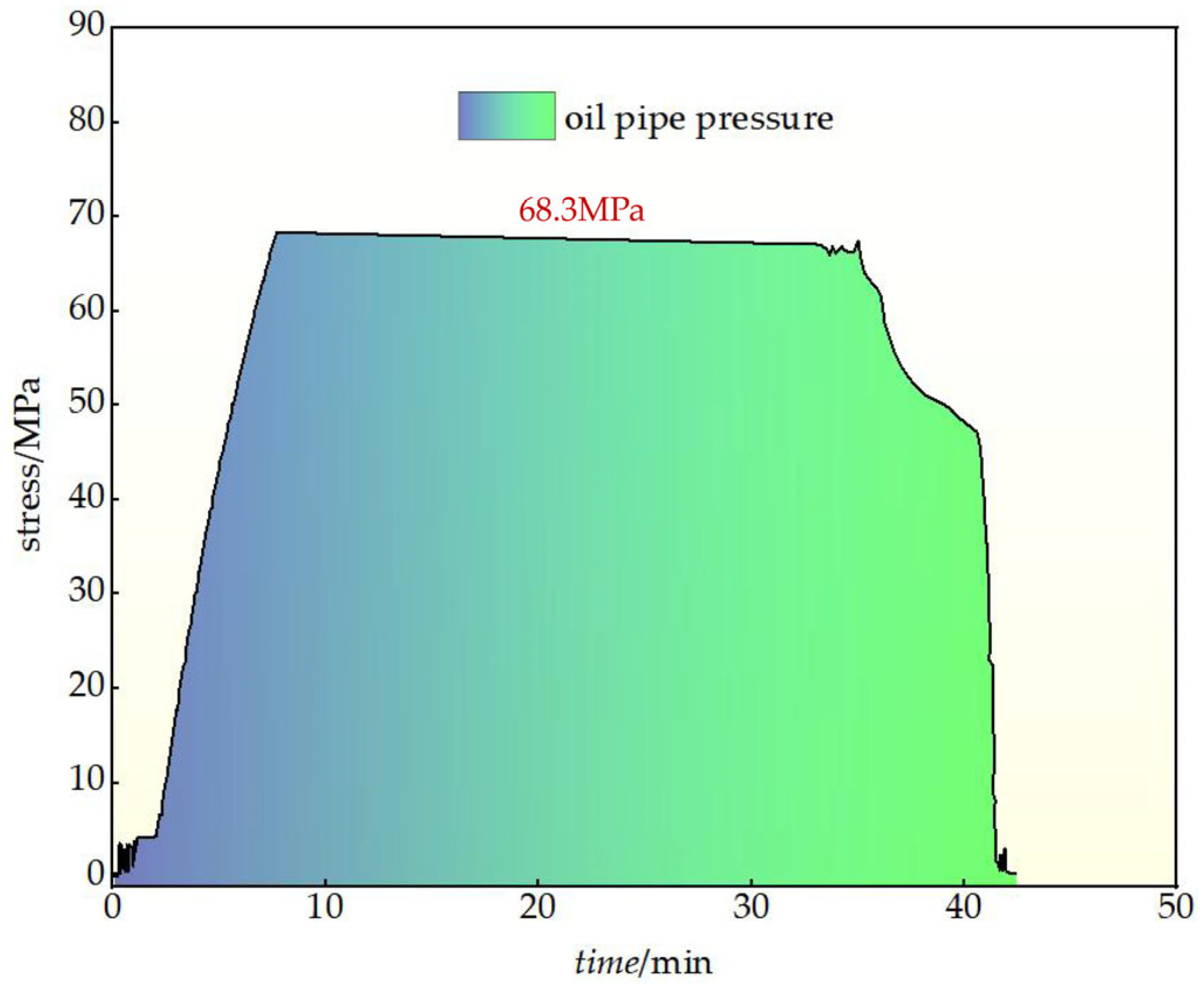
4.4. Indoor Test
4.4.1. Test Purpose and Process
4.4.2. Test Results Analysis
4.5. Field Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, H.M.; Huang, Y.Z.; Ren, S.; Liu, L.; Ci, J.F. Multi-stage fracturing technology and its application in horizontal well of tight gas reservoir. Drill. Prod. Technol. 2012, 35, 62–65. (In Chinese) [Google Scholar] [CrossRef]
- Wang, J.L.; Yi, W.K. Design of releasable staged fracturing string for cased hole. China Pet. Mach. 2017, 45, 107–110. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, M.; Wang, W.J.; Liu, H.B.; Wang, X.Q. Study on completion by coiled-tubing fracturing and cementing sliding sleeves in shale gas wells. Drill. Prod. Technol. 2017, 40, 59–62. (In Chinese) [Google Scholar] [CrossRef]
- Dusseault, M.; Mclennan, J.; Jiang, S. Massive malti-stage hydraulic fracturing for oil and gas recovery from low mobility reservoirs in china. Pet. Drill. Tech. 2011, 39, 6–16. (In Chinese) [Google Scholar] [CrossRef]
- Yang, T.Y.; Wei, L.; Feng, L.Y.; Ma, L.R.; Zhu, Y.J. Design and test of key tools in horizontal Well toe-end fracturing. Pet. Drill. Tech. 2018, 46, 54–58. (In Chinese) [Google Scholar] [CrossRef]
- Wang, J.Y.; Shuai, C.G.; Xu, W.N.; Yi, S.; Zhang, X.F. Analysis and inspirationof toe fracturing sliding sleeve technology. Drill. Prod. Technol. 2023, 46, 57–63. (In Chinese) [Google Scholar] [CrossRef]
- Guan, H.L.; Wang, Z.H.; Liu, B.H. The technical states of cementing sliding sleeve for staged fracturing. China Pet. Mach. 2021, 49, 84–92. (In Chinese) [Google Scholar] [CrossRef]
- Qin, J.L.; Chen, Z.; Yang, T.Y.; Dai, W.C.; Wu, C.F. Technology of staged fracturing with multi-stage sleeves for horizontal wells in the Ordos Basin. Pet. Drill. Tech. 2015, 43, 7–12. (In Chinese) [Google Scholar] [CrossRef]
- Qin, J.L.; Wu, J.H.; Cui, X.J.; Li, F.P.; Zuo, C.Y. Key technology on ball-activated sleeve for open hole staged fracturing. Pet. Drill. Technol. 2014, 42, 52–56. (In Chinese) [Google Scholar] [CrossRef]
- Wang, C.Q.; Shuai, C.G.; Wu, H.Q. Application of new cementing sliding sleeve technologies to Zi 203 well. Nat. Gas Explor. Dev. 2018, 41, 102–104. (In Chinese) [Google Scholar] [CrossRef]
- Zhu, Y.J.; Liu, X.P.; Wei, L. Research on key technology of time-delayed activation of toe sleeve in horizontal well. Drill. Prod. Technol. 2019, 42, 80–83. (In Chinese) [Google Scholar] [CrossRef]
- Shi, Z. Halliburton launches Elect voltage cracking sleeve. Pet. Drill. Tech. 2019, 47, 33. (In Chinese) [Google Scholar]
- NOV. i-Opener TD-Toe Sleeve. Available online: https://www.nov.com/-/media/nov/files/about/news/introducing-the-newest-additions-to-our-family-of-multistage-fracturing-toe-sleeves/iopener-td-technical-specifications.pdf (accessed on 19 March 2025).
- Packers Plus. Toe-XT Testable Hydraulic Sleeve Enables High Pressure Casing Test and Sleeve Opening below Formation Frac Pressure. Available online: https://www.packersplus.com/en/performances/toe-xt-testable-hydraulic-sleeve-enables-high-pressure-casing-test-and-sleeve-opening-below-formation-frac-pressure (accessed on 19 March 2025).
- Packers Plus. Toe-XT Hydraulic Sleeve Successfully Activated After 8 Months. Available online: https://www.packersplus.com/en/performances/toe-xt-hydraulic-sleeve-successfully-activated-after-8-months (accessed on 19 March 2025).
- Packers Plus. Packers Plus Toe-XT Hydraulic Sleeve Provides Flexibility for Casing Integrity Test. Available online: https://www.packersplus.com/en/performances/packers-plus-toe-xt-hydraulic-sleeve-provides-flexibility-for-casing-integrity-test (accessed on 19 March 2025).
- Guo, Z.H.; Wei, L.; Ma, L.R. Newtype stepless casing sliding sleeve and its application. China Pet. Mach. 2012, 40, 91–94, 99. (In Chinese) [Google Scholar] [CrossRef]
- Yuan, F.; Blanton, E.; Inglesfield, J. Single-size-ball interventionless multi-stage stimulation system improves stimulated reservoir volume and eliminates milling requirements: Case studies. In Proceedings of the SPE Russian Oil and Gas Exploration & Production Technical Conference and Exhibition, Moscow, Russia, 14–16 October 2014. [Google Scholar] [CrossRef]
- Algadi, O.; Filyukov, R.; Luna, D. Multistage hydraulic fracturing using coiled tubing-activated frac sleeves: Case study from the permian basin. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar] [CrossRef]
- Bybee, K. Multiple-layer completions for treatment of multilayer reservoirs. J. Pet. Technol. 2008, 60, 80–82. [Google Scholar]
- Stegent, N.; Howell, M. Continuous multistage fracture-stimulation completion process in a cemented wellbore. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 23–25 September 2009. [Google Scholar] [CrossRef]
- Baumgarten, D.; Bobrosky, D. Multi-stage acid stimulation improves production values in carbonate formations in western Canada. In Proceedings of the SPE Saudi Arabia Section Technical Symposium, Al-Khobar, Saudi Arabia, 9–11 May 2009. [Google Scholar] [CrossRef]
- Halliburton. RapidStage®. Multistage Frac Sleeve Systems. Available online: https://www.halliburton.com/en/products/halliburton-rapidstage-multistage-frac-sleeve-systems (accessed on 19 March 2025).
- Rytlewski, G.; Lima, J.; Dolan, B. Novel technology replaces perforating and improves efficiency during multiple layer fracturing operations. In Proceedings of the Rocky Mountain Oil & Gas Technology Symposium, Denver, CO, USA, 16–18 April 2007. [Google Scholar] [CrossRef]
- Rytlewski, G. Multiple-layer completions for efficient treatment of multilayer reservoirs. In Proceedings of the IADC/SPE Drilling Conference, Orlando, FL, USA, 4–6 March 2008. [Google Scholar] [CrossRef]
- Rytlewski, G.L.; Cook, J.M. A study of fracture initiation pressures in cemented cased-hole wells without perforations. In Proceedings of the SPE Gas Technology Symposium, Calgary, AB, Canada, 15–18 May 2006. [Google Scholar] [CrossRef]
- Liu, H.L.; Su, H.Y.; Ma, X.Z.; Guan, Z.Y.; Tang, H.; Guo, L.; Lu, W.T. Development and field test of toe end sliding sleeve for cementing. Drill. Prod. Technol. 2024, 47, 120–126. (In Chinese) [Google Scholar] [CrossRef]
- Zheng, R.Q. Technical analysis on the application of sliding sleeves at the oil toe of Daqing Gulong shale. Petro-Chem. Equip. 2024, 27, 142–145. (In Chinese) [Google Scholar]
- Liu, B. Development and experiment of electronic toe-end frac sliding sleeve. China Pet. Mach. 2024, 52, 103–108. (In Chinese) [Google Scholar] [CrossRef]
- Liu, T.; Hou, Z.M.; Hu, S.Q.; Zhao, W.; Pan, M. Development and application of unlimited-stages fracturing sliding sleeve on horizontal well. Oil Field Equip. 2016, 45, 75–77. (In Chinese) [Google Scholar] [CrossRef]
- Hu, Y.F.; Tian, Z.L.; Li, J.; Yang, H.L.; Zhang, H.; Ma, H. Optimization design and analysis of pressure differential sliding sleeve. China Pet. Mach. 2018, 46, 61–66. (In Chinese) [Google Scholar] [CrossRef]
- Yang, J. Analysis of key technology of test pressure-text toe-end sliding sleeve. J. Jianghan Pet. M Eng. Univ. 2020, 33, 54–56. (In Chinese) [Google Scholar] [CrossRef]
- Wei, L. Application analysis and structural improvement of toe-end sliding sleeve based on well conditions. Nat. Gas Ind. 2022, 42, 102–105. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, G.M.; Wang, Z.H.; Zhao, M.Q.; Bo, T.T.; An, Q.C.; Zhang, G.H.; Ren, Y. Application of integrated string for casing sliding sleeve fracturing and production. Drill. Prod. Technol. 2023, 46, 162–166. (In Chinese) [Google Scholar] [CrossRef]
- Wang, B.; Guo, Y.B.; Tian, X.Y.; Liu, B.; Wei, L.; Wang, D.G. Design of intelligent toe slide sleeve for horizontal well fracturing device. Oil Field Equip. 2021, 50, 52–59. (In Chinese) [Google Scholar] [CrossRef]
- Xu, C.Q. Analysis of anomalies and causes of pressure-test aelayed toe initiator valve (TIV) in fuling shale gas field. J. Jianghan Pet. Univ. Staff Work. 2024, 37, 33–35. (In Chinese) [Google Scholar] [CrossRef]
- Wang, J.J.; Wang, X.; Liu, J.C.; Wang, S.Q. Calculation and analysis on opening pressure of pressure sliding sleeve. Mech. Eng. 2022, 53–56. Available online: https://qikan.cqvip.com/Qikan/Article/Detail?id=7106970116&from=Qikan_Search_Index (accessed on 19 March 2025). (In Chinese).
- Zhao, X.Z.; Jin, F.M.; Chen, C.W.; Jiang, W.Y.; Han, W.Z.; Liu, X.W.; Tang, J.Z.; Xu, J.; Chai, G.Q.; Zhang, S.L.; et al. Technology and result evaluation of well cementing sliding sleeve single-cluster hole fracturing for continental shale oil reservoir. China Pet. Explor. 2024, 29, 136–147. (In Chinese) [Google Scholar] [CrossRef]
- Wang, X.X.; Li, W.W.; Xu, Y.T.; Qu, X.M.; Li, W. Research and analysis about application of NCS fracturing sleeve in large-scale fracturing on offshore. Shandong Chem. Ind. 2024, 53, 218–219. (In Chinese) [Google Scholar] [CrossRef]
- Liu, D.L.; Chen, Y.P.; Li, A.X.; Guo, L. A new first-stage fracturing process of horizontal well in unconventional oil and gas based on wetshoe cementing. Oil Drill. Prod. Technol. 2023, 45, 85–89. (In Chinese) [Google Scholar] [CrossRef]
- Liu, C.Y.; Xia, H.G.; Li, C.P.; Zhang, X. New progress and development suggestions on fracturing tools and technologies. Oil Field Equip. 2022, 51, 66–75. (In Chinese) [Google Scholar] [CrossRef]
- Xue, X.B.; Hua, Z.J.; Zhu, X.H.; Liu, H.J.; Zhang, C.C.; Qu, Y.; Shi, C.S.; Cheng, L.F. Sensitivity analysis and optimization of infinite cementing sliding sleeve sealing rubber cylinder parameters. Lubr. Eng. 2025, 50, 129–137. (In Chinese) [Google Scholar] [CrossRef]
- Chu, Y.J.; Wen, J.; Li, N.; Liu, S.; Bai, J.Y.; Xiong, L. Research on intelligent completion system of single tubing hydraulic control sliding sleeve. Petrochem. Ind. Technol. 2024, 31, 110–112. (In Chinese) [Google Scholar]
- Zhou, B.C. Analysis and measures of abnormal opening of unlimited-stage sliding sleeve in Nanchuan shale gas wells. Pet. Geol. Eng. 2024, 38, 94–99. (In Chinese) [Google Scholar]



| Company | Halliburton | NOV | Packers Plus | Schlumberger | —— |
|---|---|---|---|---|---|
| Tool name | Elect Sleeve | i-Opener | Toe-XT | TAP Fracturing Completion System | Delayed-opening toe-end sliding sleeve |
| Applications | Multi-productive zone fracturing completion | First-stage fracs | First-stage fracs | First-stage fracs | First-stage fracs |
| Features | Unlimited number of fracable areas | Cycle Open i-Open-er | Opens at a specific absolute pressure | Only applicable to wellbores above ϕ200 mm and casings of ϕ114.3 mm | Delayed opening |
| Activation method | Pitch | Hydraulic | Hydraulic | Insert rubber plug to activate | Hydraulic |
| Sliding sleeve type | Electronic fracturing sleeve | Mechanical sleeve | Mechanical sleeve | Mechanical sleeve | Mechanical Sleeve |
| Benefits | 1. Overcoming the number of fracturing stages 2. Optimizing reservoir channels 3. Coordination of software, hardware and mechanical tools | 1. Greater accuracy for activation pressure 2. Debris-tole-rant during activation 3. Compatible with industry-standard wiper plugs | 1. Saving time and cost in delivering an effective treatment of the first stage 2. Allows the casing string to be pressure tested a single time before opening | 1. The overall pressure resistance of the sliding sleeve reaches 70 MPa and the temperature resistance reaches 160 °C 2. After the fracturing is completed, the darts flow back to the lower part of the upper sliding sleeve ball seat and form a flow channel, which can effectively ensure that the subsequent drainage and production will not be blocked | 1. Simple structure, convenient installation, easy manufacturing, suitable for mass production 2. Able to work in harsh environments such as high temperatures and high pressures underground 3. No need to lower the first stage of coiled tubing perforation |
| Structural Parameters | Prototype Total Length L/mm | Prototype Diameter D/mm | Inner Sleeve Upper Section S1/mm2 | Circular Cross Section S2/mm2 | Inner Sleeve Lower Section S3/mm2 | Distance Between Section S1 and Section K l/mm |
|---|---|---|---|---|---|---|
| Numeric | 1298 | 185 | 22,201 | 5942 | 20,449 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Chen, F.; Cao, M.; Zhao, H.; Ning, W.; Ma, T.; Zhang, M. The Optimized Design and Principal Analysis of a Toe-End Sliding Sleeve. Machines 2025, 13, 253. https://doi.org/10.3390/machines13030253
Li W, Chen F, Cao M, Zhao H, Ning W, Ma T, Zhang M. The Optimized Design and Principal Analysis of a Toe-End Sliding Sleeve. Machines. 2025; 13(3):253. https://doi.org/10.3390/machines13030253
Chicago/Turabian StyleLi, Wei, Fulu Chen, Mengyu Cao, Huan Zhao, Wangluo Ning, Tianchi Ma, and Mingxiu Zhang. 2025. "The Optimized Design and Principal Analysis of a Toe-End Sliding Sleeve" Machines 13, no. 3: 253. https://doi.org/10.3390/machines13030253
APA StyleLi, W., Chen, F., Cao, M., Zhao, H., Ning, W., Ma, T., & Zhang, M. (2025). The Optimized Design and Principal Analysis of a Toe-End Sliding Sleeve. Machines, 13(3), 253. https://doi.org/10.3390/machines13030253






