Simplified Data-Driven Models for Gas Turbine Diagnostics
Abstract
1. Introduction
Gas Path Diagnostics
2. Typical Gas Turbine Models
2.1. Thermodynamic Model
2.2. Baseline Model
2.3. Linear Diagnostic Model
2.4. Linear Estimation of Fault Parameters
3. Methodological Considerations
- Engine type and application: three different engines;
- Model types: direct and inverse for each engine;
- Approximation functions: polynomials and MLP for each engine and model type;
- Fault classes: single and multiple for each engine;
- Number of fault classes: specific for each engine.
- The simplified models are obtained at the standard ambient conditions of engine operation. To extend the models to other ambient conditions, the known correction equations can be easily employed [40].
- As engine gas path models are studied, gas path faults are only presented in a diagnostic algorithm. Faults of control and measurement systems are not considered.
- All fault parameters have the same interval of variation.
- Only one well-known pattern recognition technique is used in Section 7 for the analysis of diagnostic reliability with different models employed. The problem of the best technique is not investigated.
4. Test-Case Engines
- Civil aircraft turbofan (Engine 1);
- Helicopter free-turbine engine (Engine 2);
- Industrial power plant (Engine 3).
5. Development of Simplified Direct Models
5.1. Polynomial and MLP Model Variations
5.2. Polynomial Models
5.2.1. Engine 1
5.2.2. Engine 2
5.2.3. Engine 3
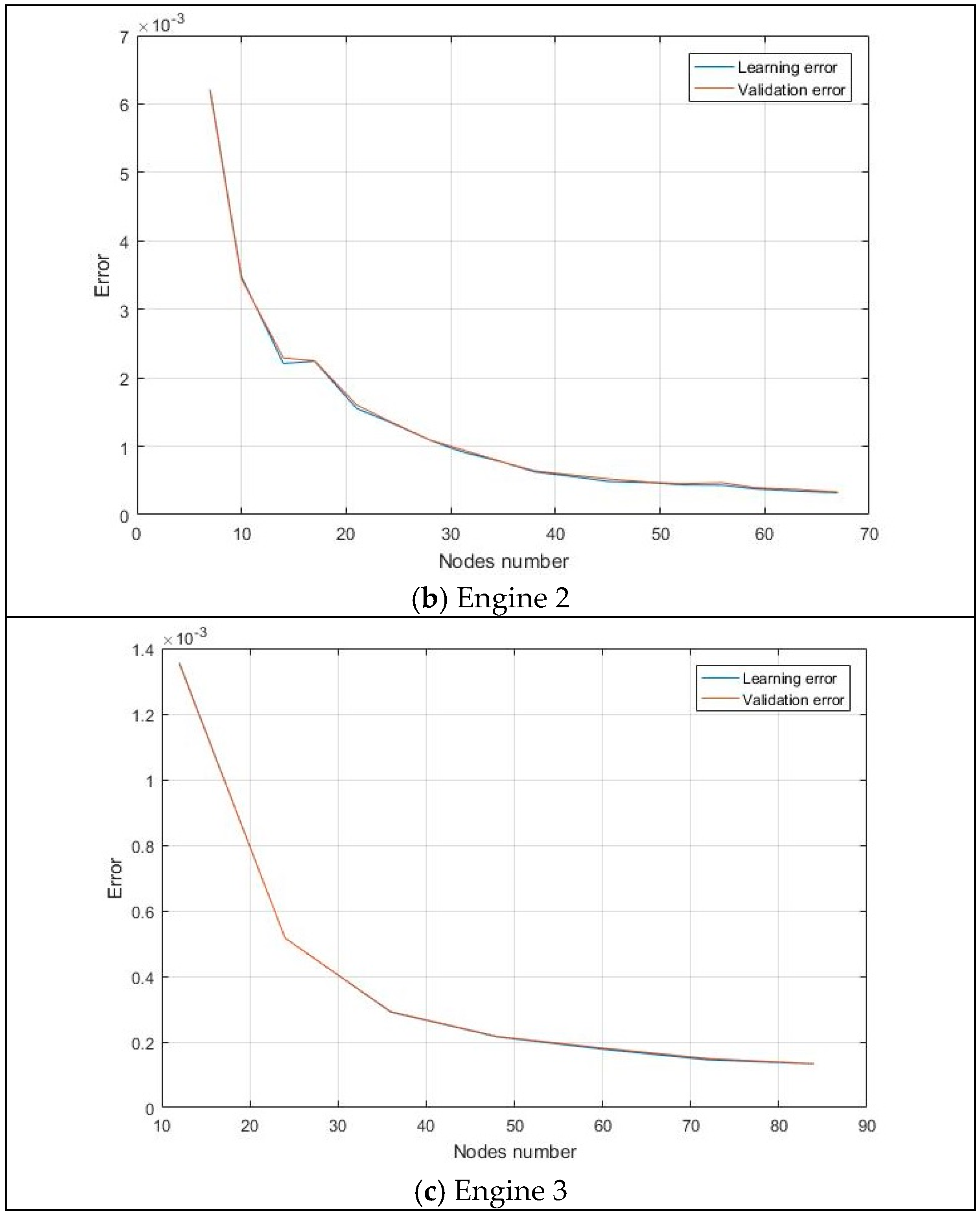
5.3. MLP-Based Models
5.3.1. Engine 1 MLP Model
- − The accuracy of the variables differs a lot. However, for all computational cases (learning and validation of both approximation techniques), the accuracy rank is conserved as the same from the most accurate compressor temperature TC to the least accurate thrust R.
- − The validation errors are larger, but very close to the learning errors for each case and variable. This is the confirmation of the correctness of a whole learning process. For all the cases and variables, MLP has a by-far-higher accuracy.
5.3.2. Engine 2 MLP Model
- The accuracy rank of variable Y is conserved as the same in the four computational cases presented.
- The closeness of the validation and learning errors confirms the correctness of a whole learning process.
- For all the cases and variables, MLP has a by-far-higher accuracy, and the mean errors are about 13-times smaller.
5.3.3. Engine 3 MLP Model
6. Inverse Models for the First Approach
6.1. Polynomial Models
6.1.1. Engine 1 Inverse Model
6.1.2. Engine 2 Inverse Model
6.1.3. Engine 3 Inverse Model
6.2. MLP-Based Models
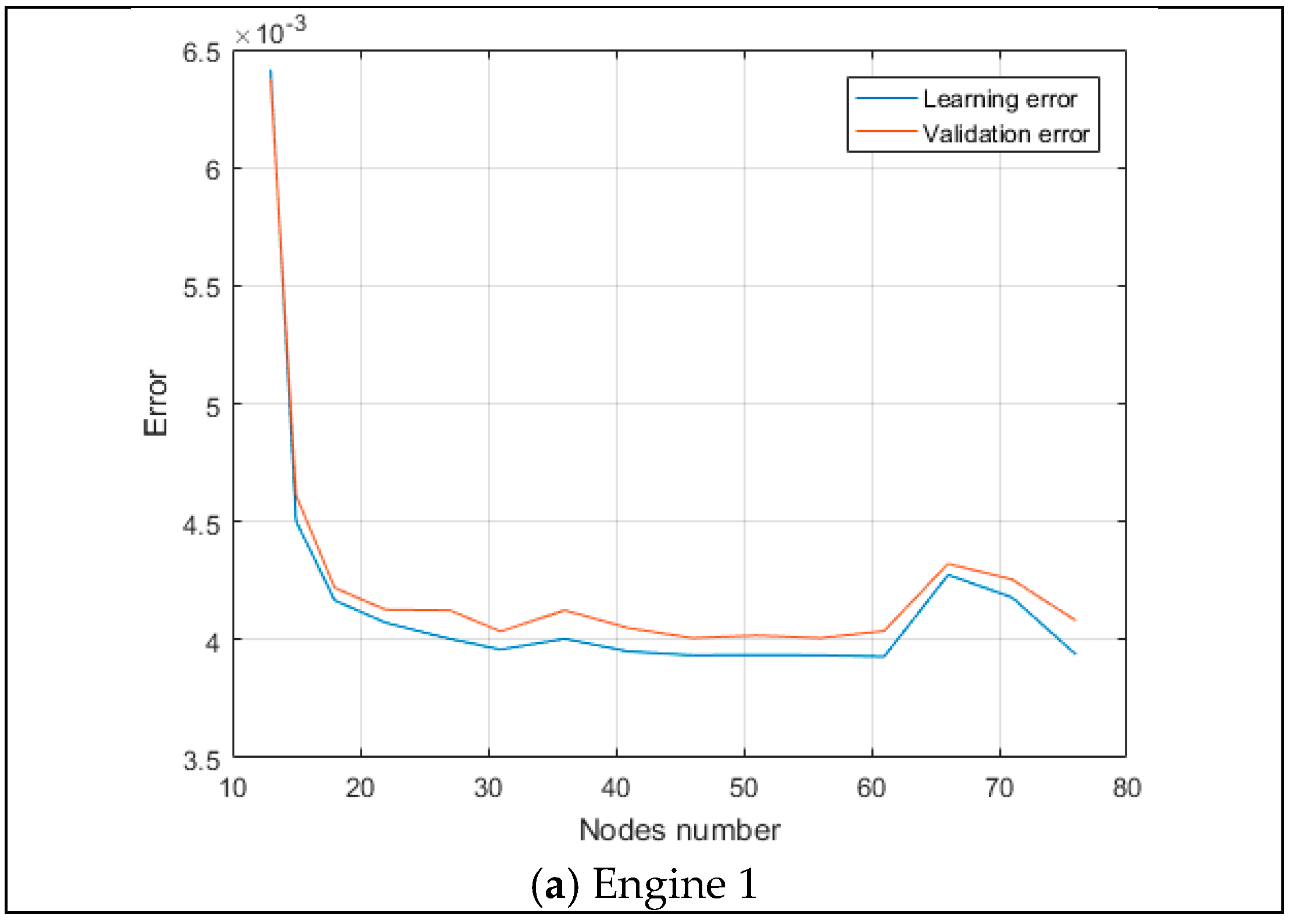
6.2.1. Engine 1 Inverse MLP Model
6.2.2. Engine 2 Inverse MLP Model
6.2.3. Engine 3 Inverse MLP Model
7. Diagnostic Reliability of the Second Approach with Simplified Models
8. Discussion
- The models of Engine 2 and Engine 3 are much more accurate than Engine 1 models and can be excellent surrogates to original thermodynamic models;
- Engine 3 models are generally the most accurate except in the case of inverse MLP-based models;
- In all comparison cases, the MLP-based models are superior to the corresponding polynomials models; thus, MLP is recommended for creating simplified data-driven models.
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Saravanamuttoo, H.I.H.; Rogers, G.F.C.; Cohen, H. Gas Turbine Theory, 5th ed.; Person Education Limited: London, UK, 2001. [Google Scholar]
- Boyce, M.P. Gas Turbine Engineering Handbook, 3rd ed.; Elsevier Inc.: Oxford, UK, 2006. [Google Scholar]
- Zhao, N.; Wen, X.; Li, S. A review on gas turbine anomaly detection for implementing health management. In Proceedings of the IGTI/ASME Turbo Expo 2016, Seoul, Republic of Korea, 13–17 June 2016. 14p; ASME Paper GT2016-58135. [Google Scholar]
- Tahan, M.; Tsoutsanis, E.; Muhammad, M.; Karim, Z.A. Performance based health monitoring, diagnostics and prognostics for condition based maintenance of gas turbines: A review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Baheta, A.T.; Gilani, S.I.; Kyprianidis, K.G. A review on gas turbine gas-path diagnostics: State of the art methods, Challenges and Opportunities. Aerospace 2019, 6, 83. [Google Scholar] [CrossRef]
- Li, Y.G. Performance-analysis-based gas turbine diagnostics: A review. Proc. Inst. Mech. Eng. Part A J. Power Energy 2002, 216, 363–377. [Google Scholar] [CrossRef]
- Volponi, A.J. Gas turbine engine health management past, present and future trends. ASME J. Eng. Gas Turbines Power. 2014, 136, 051201-1–051201-25. [Google Scholar] [CrossRef]
- Volponi, A.J. Gas Turbine Condition Monitoring and Fault Diagnostics I; Lecture Series 2003-01; Von Karman Institute for Fluid Dynamics: Rhode Saint Genèse, Belgium, 2003. [Google Scholar]
- Haykin, S. Neural Networks; Macmillan College Publishing Company: New York, NY, USA, 1994. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; Wiley-Interscience: New York, NY, USA, 2001. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Urban, L.A. Gas Path Analysis Applied to Turbine Engine Conditioning Monitoring; AIAA/SAE Paper 72–1082; AIAA/SAE: Washington, DC, USA, 1972. [Google Scholar]
- Volponi, A.J. Gas Turbine Condition Monitoring and Fault Diagnostics II; Lecture Series 2003-02; Von Karman Institute for Fluid Dynamics: Rhode Saint Genèse, Belgium, 2003. [Google Scholar]
- Doel, D.L. Interpretation of weighted-least-squares gas path analysis results. J. Eng. Gas Turbines Power. 2003, 125, 624–633. [Google Scholar] [CrossRef]
- Kamboukos, P.; Mathioudakis, K. Comparison of linear and non-linear gas turbine performance diagnostics. J. Eng. Gas Turbines Power. 2005, 127, 49–56. [Google Scholar] [CrossRef]
- Agrawal, R.K.; MacIsaac, B.D.; Saravanamuttoo, H.I.H. An analysis procedure for validation of on-site performance measurements of gas turbines. ASME J. Eng. Power 1979, 101, 405–414. [Google Scholar] [CrossRef]
- Saravanamuttoo, H.I.H.; MacIsaac, B.D. Thermodynamic models for pipeline gas turbine diagnostics. ASME J. Eng. Power 1983, 105, 875–884. [Google Scholar] [CrossRef]
- Stamatis, A.; Mathioudakis, K.; Papailiou, K.D. Adaptive simulation of gas turbine performance. J. Eng. Gas Turbines Power. 1990, 112, 168–175. [Google Scholar] [CrossRef]
- Gatto, E.L.; Li, Y.G.; Pilidis, P. Gas turbine off-design performance adaptation using a genetic algorithm. In Proceedings of the IGTI/ASME Turbo Expo 2006, Barcelona, Spain, 8–11 May 2006. 10p; ASME Paper GT2006-90299. [Google Scholar]
- Khustochka, O.; Yepifanov, S.; Zelenskyi, R.; Przysowa, R. Estimation of performance parameters of turbine engine components using experimental data in parametric uncertainty conditions. Aerospace 2020, 7, 6. [Google Scholar] [CrossRef]
- Stenfelt, M.; Zaccaria, V.; Kyprianidis, K.G. Automatic gas turbine matching scheme adaptation for robust GPA diagnostics. In Proceedings of the ASME Turbo Expo 2019, Phoenix, AZ, USA, 17–21 June 2019. 9p. [Google Scholar]
- Palme, T.; Fast, M.; Assadi, M.; Pike, A.; Breuhaus, P. Different condition monitoring models for gas turbines by means of artificial neural networks. In Proceedings of the IGTI/ASME Turbo Expo 2009, Orlando, FL, USA, 8–12 June 2009. 11p; ASME Paper GT2009-59364. [Google Scholar]
- Loboda, I.; Feldshteyn, Y. Polynomials and neural networks for gas turbine monitoring: A comparative study. Int. J. Turbo Jet Engines 2011, 28, 227–236. [Google Scholar] [CrossRef]
- Borguet, S.; Leonard, O.; Dewallet, P. Regression-based modelling of a fleet of gas turbine engines for performance trending. In Proceedings of the IGTI/ASME Turbo Expo 2015, Montreal, QC, Canada, 15–19 June 2015. 12p; ASME Paper GT2015-42330. [Google Scholar]
- Ogaji, S.O.T.; Li, Y.G.; Sampath, S.; Singh, R. Gas path fault diagnosis of a turbofan engine from transient data using artificial neural networks. In Proceedings of the IGTI/ASME Turbo Expo 2003, Atlanta, GA, USA, 16–19 June 2003. 10p; ASME Paper GT2003-38423. [Google Scholar]
- Butler, S.W.; Pattipati, K.R.; Volponi, A.; Hull, J.; Rajamani, R.; Siegel, J. An assessment methodology for data-driven and model based techniques for engine health monitoring. In Proceedings of the IGTI/ASME Turbo Expo 2006, Barcelona, Spain, 8–11 May 2006. 9p; ASME Paper GT2006-91096. [Google Scholar]
- Volponi, A.J.; DePold, H.; Ganguli, R. The Use of Kalman Filter and Neural Network Methodologies in Gas Turbine Performance Diagnostics: A Comparative Study. ASME J. Eng. Gas Turbines Power. 2003, 125, 917–924. [Google Scholar] [CrossRef]
- Loboda, I.; Olivares Robles, M.A. Gas turbine fault diagnosis using probabilistic neural networks. Int. J. Turbo Jet Engines 2014, 32, 175–192. [Google Scholar] [CrossRef]
- Ganguli, R. Gas Turbine Diagnostics; CRC Press: Boca Raton, FL, USA; Tailor & Francis Group: London, UK, 2013. [Google Scholar]
- Simon, D.L.; Volponi, A.; Bird, J.; Davison, C.; Iverson, R.E. Benchmarking gas path diagnostic methods: Public approach. In Proceedings of the IGTI/ASME Turbo Expo 2008, Berlin, Germany, 9–13 June 2008. 13p; ASME Paper GT2008-51360. [Google Scholar]
- Cruz-Manzo, S.; Panov, V.; Zhang, Y.; Latimer, A.; Agbonzikilo, F. A thermodynamic transient model for performance analysis of a twin shaft industrial gas turbine. In Proceedings of the IGTI/ASME Turbo Expo 2017, Charlotte, NC, USA, 26–30 June 2017. 8p; ASME Paper GT2017-64376. [Google Scholar]
- Zhang, X.; Avram, R.C.; Tang, L.; Roemer, M.J. A unified nonlinear approach to fault diagnosis of aircraft engines. In Proceedings of the IGTI/ASME Turbo Expo 2013, San Antonio, TX, USA, 3–7 June 2013. 10p; ASME Paper GT2013-95803. [Google Scholar]
- GasTurb GmbH. «GasTurb». Available online: http://www.gasturb.de/ (accessed on 12 April 2025).
- Gas Turbine Simulation Program (GSP). Available online: https://www.gspteam.com/ (accessed on 12 April 2025).
- Loboda, I. Gas Turbine Condition Monitoring and Diagnostics; Turbines, G., Injeti, G., Eds.; IntechOpen: London, UK, 2010; pp. 119–144. ISBN 978-953-307-146-6. Available online: https://www.intechopen.com/chapters/12088 (accessed on 12 April 2025).
- Fast, M.; Assadi, M.; De, S. Condition based maintenance of gas turbines using simulation data and artificial neural network: A demonstration of feasibility. In Proceedings of the IGTI/ASME Turbo Expo 2008, Berlin, Germany, 9–13 June 2008. 9p; ASME Paper GT2008-50768. [Google Scholar]
- Palme, T.; Liard, F.; Cameron, D. Hybris modeling of heavy duty gas turbines for on-line performance monitoring. In Proceedings of the IGTI/ASME Turbo Expo 2014, Dusseldorf, Germany, 16–20 June 2014. 10p; ASME Paper GT2014-26015. [Google Scholar]
- Loboda, I.; Castillo, I.G.; Yepifanov, S.; Zelenskyi, R. Nonlinear surrogate models for gas turbine diagnosis. In Proceedings of the ASME Turbo Expo 2022, Turbomachinery Technical Conference & Exposition, Rotterdam, The Netherlands, 13–17 June 2022. ASME Digital Collection: Paper GT2022-83550. [Google Scholar]
- Loboda, I.; Pérez-Ruiz, J.L.; Castillo, I.G.; Yepifanov, S. Applicability of simplified data-driven models in gas turbine diagnostics. In Proceedings of the ASME Turbo Expo 2023, Turbomachinery Technical Conference & Exposition, Boston, MA, USA, 26–30 June 2023. 10p; Paper GT2023-104176. [Google Scholar]
- Volponi, A.J. Gas turbine parameter corrections. In Proceedings of the International Gas Turbine & Aeroengine Congress & Exhibition, Stockholm, Sweden, 2–5 June 1998. 11p; ASME Paper 98-GT-347. [Google Scholar]
- Loboda, I.; Nakano Miyatake, M.; Goryachiy, A.; Gutiérrez Mojica, E.M.; González Aguilar, J.E. Gas turbine fault recognition by artificial neural networks. In Proceedings of the Memorias del 4to Congreso Internacional de Ingeniería Electromecánica y de Sistemas, ESIME, IPN, México, México, 14–18 November 2005; 6p. ISBN 970-36-0292-4. [Google Scholar]
- Castillo, I.G.; Loboda, I.; Ruiz, J.L.P. Data-driven models for gas turbine online diagnosis. Machines 2021, 9, 372. [Google Scholar] [CrossRef]



| No. | Name | Symbol | Engine 1 | Engine 2 | Engine 3 |
|---|---|---|---|---|---|
| 1 | Net thrust | R | x | - | - |
| 2 | Shaft power delivered | NLPT | - | x | - |
| 3 | Fuel consumption | GF | x | x | x |
| 4 | HPC pressure | PC | x | x | x |
| 5 | HPC temperature | TC | x | x | x |
| 6 | HPT pressure | PHPT | x | x | x |
| 7 | HPT temperature | THPT | - | x | x |
| 8 | LPT pressure | PLPT | x | x | - |
| 9 | LPT temperature | TLPT | x | x | x |
| 10 | LPT spool speed | nLPT | - | - | x |
| Total number of variables | m | 7 | 8 | 6–7 * |
| No. | Name | Symbol | Engine 1 | Engine 2 | Engine 3 |
|---|---|---|---|---|---|
| 1 | Fan capacity parameter | δGLPC | x | - | - |
| 2 | Fan efficiency parameter | δηLPC | x | - | - |
| 3 | HPC capacity parameter | δGHPC | x | x | x |
| 4 | HPC efficiency parameter | δηHPC | x | x | x |
| 5 | HPT capacity parameter | δAHPT | x | x | x |
| 6 | HPT efficiency parameter | δηHPT | x | x | x |
| 7 | LPT capacity parameter | δALPT | x | x | x |
| 8 | LPT efficiency parameter | δηLPT | x | x | x |
| 9 | Combustion chamber total pressure recovery coefficient | δσCC | - | - | (x) |
| 10 | Combustion chamber efficiency parameter | δηCC | - | - | (x) |
| Total number of parameters | r | 8 | 6 | 8–6 * |
| Engine 1 | ||
|---|---|---|
| Polynomial | Second order, k = 49 | Second order, k = 57 |
| Errors (without normalization) | 0.142018 | 0.027771 |
| Errors (with normalization) | 0.030626 | 0.011448 |
| Engine 2 | ||
| Polynomial | Second order, k = 38 | Third order, k = 100 |
| Errors | 0.004601 | 0.004406 |
| Engine 3 | ||
| Polynomial | Second order, k = 37 | Third order, k = 99 |
| Errors | 0.000817 | 0.000715 |
| Monitored Variables | Polynomials | MLP | ||
|---|---|---|---|---|
| Learning | Validation | Learning | Validation | |
| Engine 1 (polynomial: k = 57, MLP: k = 925) | ||||
| R | 0.04099 | 0.04287 | 0.00200 | 0.00244 |
| GF | 0.01148 | 0.01184 | 0.00098 | 0.00110 |
| PC | 0.00911 | 0.00929 | 0.00070 | 0.00077 |
| TC | 0.00121 | 0.00125 | 0.00019 | 0.00020 |
| PHPT | 0.01008 | 0.01033 | 0.00074 | 0.00084 |
| PLPT | 0.00539 | 0.00550 | 0.00035 | 0.00039 |
| TLPT | 0.00550 | 0.00556 | 0.00060 | 0.00069 |
| Mean | 0.011083 | 0.011448 | 0.000759 | 0.000874 |
| Engine 2 (polynomial: k = 100, MLP: k = 1080) | ||||
| NLPT1 | 0.01607 | 0.01631 | 0.00096 | 0.00096 |
| GF | 0.00536 | 0.00549 | 0.00046 | 0.00049 |
| PC | 0.00322 | 0.00334 | 0.00019 | 0.00020 |
| TC | 0.00051 | 0.00051 | 0.00009 | 0.00009 |
| PHPT | 0.00440 | 0.00452 | 0.00021 | 0.00022 |
| THPT | 0.00259 | 0.00263 | 0.00029 | 0.00031 |
| PLPT | 0.00044 | 0.00044 | 0.00003 | 0.00003 |
| TLPT | 0.00257 | 0.00259 | 0.00029 | 0.00029 |
| Mean | 0.004400 | 0.004482 | 0.000319 | 0.000329 |
| Engine 3 (polynomial: k = 99, MLP: k = 1267) | ||||
| GF | 0.00140 | 0.00140 | 0.00020 | 0.00022 |
| PC | 0.00029 | 0.00029 | 0.00010 | 0.00010 |
| TC | 0.00020 | 0.00020 | 0.00005 | 0.00005 |
| PHPT | 0.00085 | 0.00084 | 0.00013 | 0.00013 |
| THPT | 0.00060 | 0.00060 | 0.00013 | 0.00014 |
| TLPT | 0.00057 | 0.00058 | 0.00012 | 0.00012 |
| nLPT | 0.00027 | 0.00027 | 0.00008 | 0.00008 |
| Mean | 0.000713 | 0.000715 | 0.000132 | 0.000134 |
| Engine 1 | ||
|---|---|---|
| Polynomial | Second order, k = 57 | Third order, k = 169 |
| Learning Errors | 0.004306 | 0.003555 |
| Validation Errors | 0.004368 | 0.00377 |
| Engine 2 | ||
| Polynomial | Second order, k = 57 | Third order, k = 169 |
| Learning Errors | 0.001049 | 0.0002250 |
| Validation Errors | 0.001058 | 0.0002332 |
| Engine 3 | ||
| Polynomial | Second order, k = 46 | Third order, k = 136 |
| Learning Errors | 0.000272 | 0.000158 |
| Validation Errors | 0.000271 | 0.000159 |
| Fault Parameters | Third-Order Polynomials | MLP | ||
|---|---|---|---|---|
| Learning | Validation | Learning | Validation | |
| Engine 1 (polynomial: k = 169, MLP: k = 875) | ||||
| δGLPC | 0.01209 | 0.01274 | 0.01222 | 0.01254 |
| δηLPC | 0.00516 | 0.00555 | 0.00537 | 0.00548 |
| δGHPC | 0.00135 | 0.00149 | 0.00193 | 0.00198 |
| δηHPC | 0.00208 | 0.00289 | 0.00236 | 0.00239 |
| δAHPT | 0.00013 | 0.00015 | 0.00126 | 0.00129 |
| δηHPT | 0.00111 | 0.00122 | 0.00162 | 0.001644 |
| δALPT | 0.00376 | 0.00385 | 0.00387 | 0.00388 |
| δηLPT | 0.00274 | 0.00287 | 0.00284 | 0.00293 |
| Mean | 0.003554 | 0.003769 | 0.003936 | 0.004018 |
| Engine 2 (polynomial: k = 169, MLP: k = 1158) | ||||
| δGHPC | 0.000221 | 0.000227 | 0.000091 | 0.000095 |
| δηHPC | 0.000173 | 0.000177 | 0.000065 | 0.000068 |
| δAHPT | 0.000119 | 0.000123 | 0.000078 | 0.000081 |
| δηHPT | 0.000119 | 0.000121 | 0.000049 | 0.000051 |
| δALPT | 0.000261 | 0.000272 | 0.000094 | 0.000098 |
| δηLPT | 0.000457 | 0.000479 | 0.000097 | 0.000102 |
| Mean | 0.0002250 | 0.0002332 | 0.0000790 | 0.0000824 |
| Engine 3 (polynomial: k = 136, MLP: k = 1260) | ||||
| δGHPC | 0.000136 | 0.000137 | 0.000088 | 0.000090 |
| δηHPC | 0.000212 | 0.000213 | 0.000105 | 0.000106 |
| δAHPT | 0.000016 | 0.000016 | 0.000108 | 0.000127 |
| δηHPT | 0.000010 | 0.000010 | 0.000078 | 0.000076 |
| δALPT | 0.000236 | 0.000237 | 0.000107 | 0.000109 |
| δηLPT | 0.000175 | 0.000177 | 0.000098 | 0.000098 |
| Mean | 0.000158 | 0.000159 | 0.000098 | 0.000099 |
| Fault Type | Model | |
|---|---|---|
| Single | Thermodynamic | 0.82901 ± 0.0012 |
| Polynomial | 0.82910 ± 0.0012 | |
| Multiple | Thermodynamic | 0.87678 ± 0.0015 |
| Polynomial | 0.87826 ± 0.0015 |
| Fault Parameters | Direct Models | Inverse Models | ||
|---|---|---|---|---|
| Polynomials | MLP | Polynomials | MLP | |
| Engine 1 | 0.011448 | 0.000874 | 0.003769 | 0.004018 |
| Engine 2 | 0.004482 | 0.000329 | 0.0002332 | 0.000082 |
| Engine 3 | 0.000715 | 0.000134 | 0.000159 | 0.000099 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loboda, I.; Ruíz, J.L.P.; Castillo, I.G.; Arias, J.M.C.; Yepifanov, S. Simplified Data-Driven Models for Gas Turbine Diagnostics. Machines 2025, 13, 344. https://doi.org/10.3390/machines13050344
Loboda I, Ruíz JLP, Castillo IG, Arias JMC, Yepifanov S. Simplified Data-Driven Models for Gas Turbine Diagnostics. Machines. 2025; 13(5):344. https://doi.org/10.3390/machines13050344
Chicago/Turabian StyleLoboda, Igor, Juan Luis Pérez Ruíz, Iván González Castillo, Jonatán Mario Cuéllar Arias, and Sergiy Yepifanov. 2025. "Simplified Data-Driven Models for Gas Turbine Diagnostics" Machines 13, no. 5: 344. https://doi.org/10.3390/machines13050344
APA StyleLoboda, I., Ruíz, J. L. P., Castillo, I. G., Arias, J. M. C., & Yepifanov, S. (2025). Simplified Data-Driven Models for Gas Turbine Diagnostics. Machines, 13(5), 344. https://doi.org/10.3390/machines13050344





