Small Opening Flow Linearity Optimization of High-Pressure and Large-Flow Two-Way Proportional Throttle Valve
Abstract
:1. Introduction
2. Working Principle
3. Simulation and Optimization
3.1. Main Valve Spool Force Analysis
3.2. Modeling
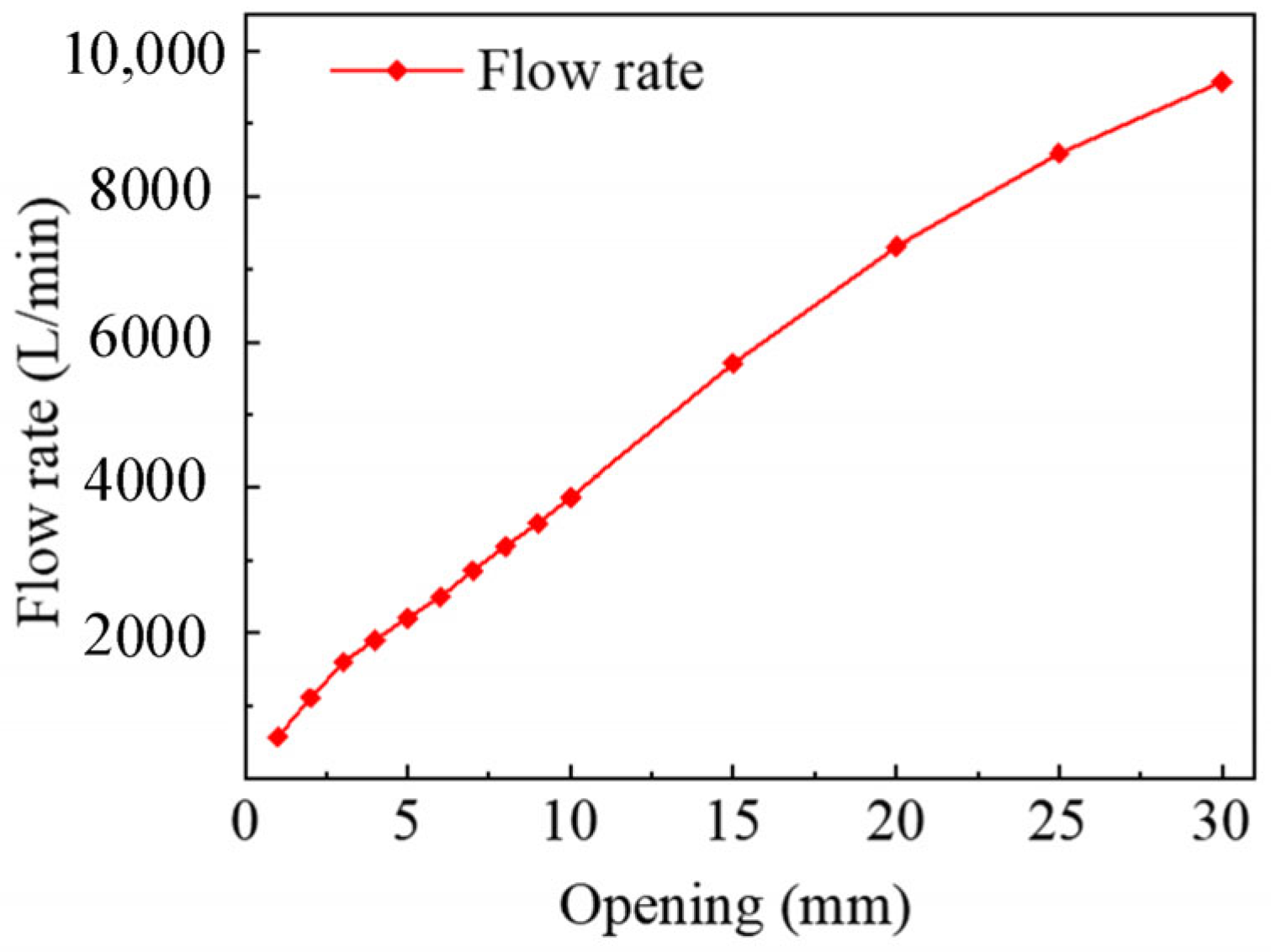
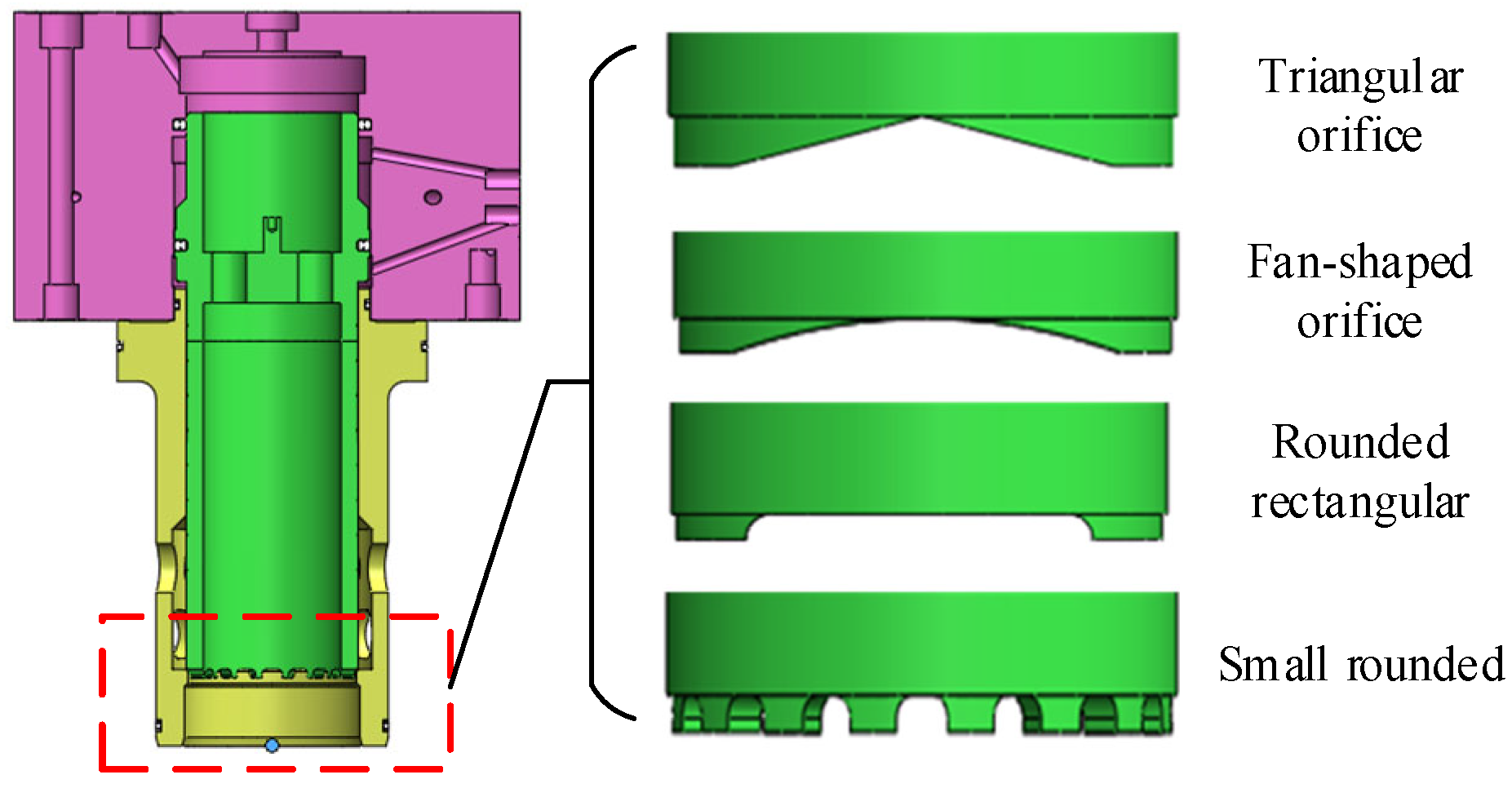
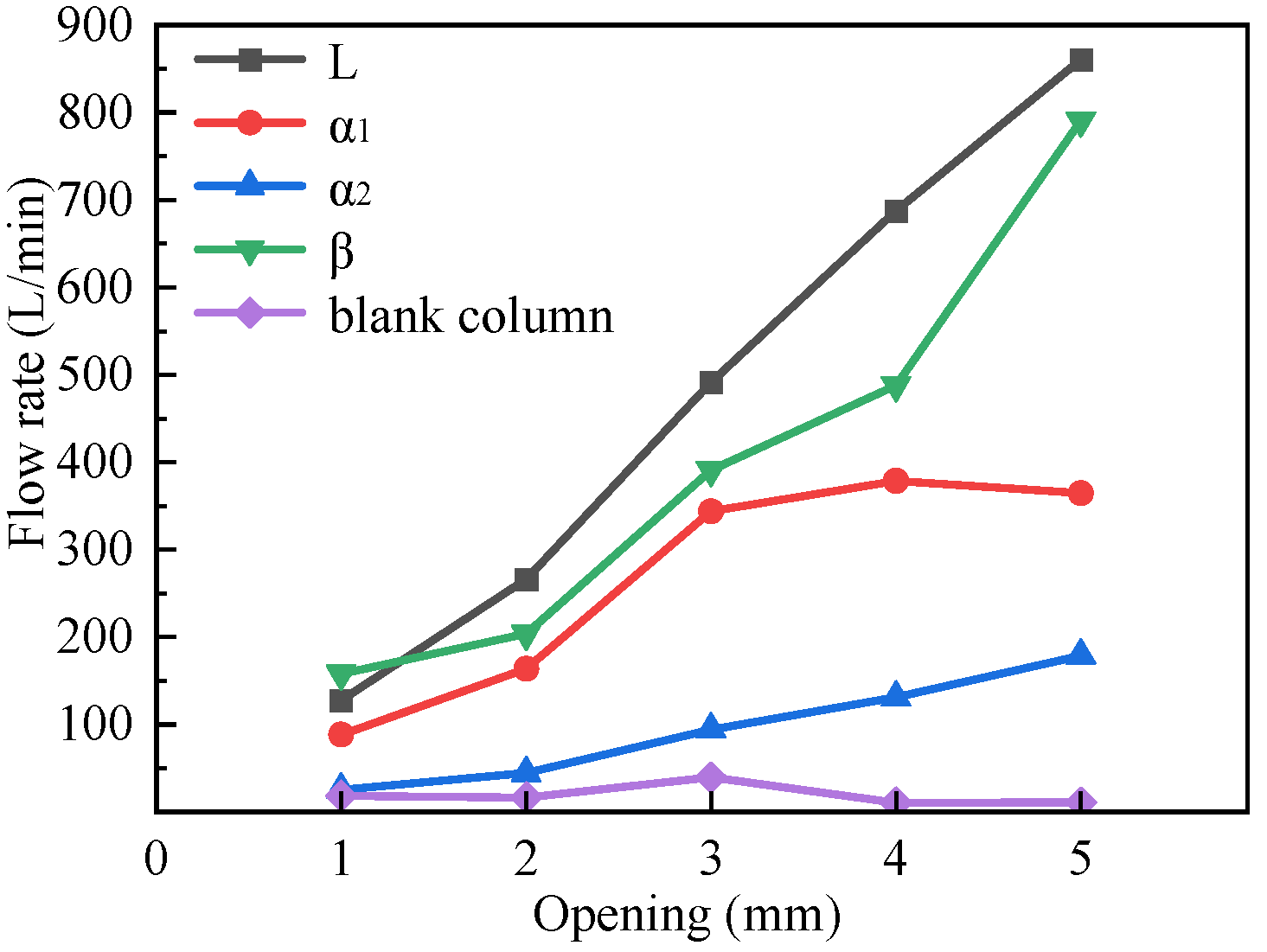
3.3. Flow Linearity Simulation of Four Different Structures
3.4. Optimization
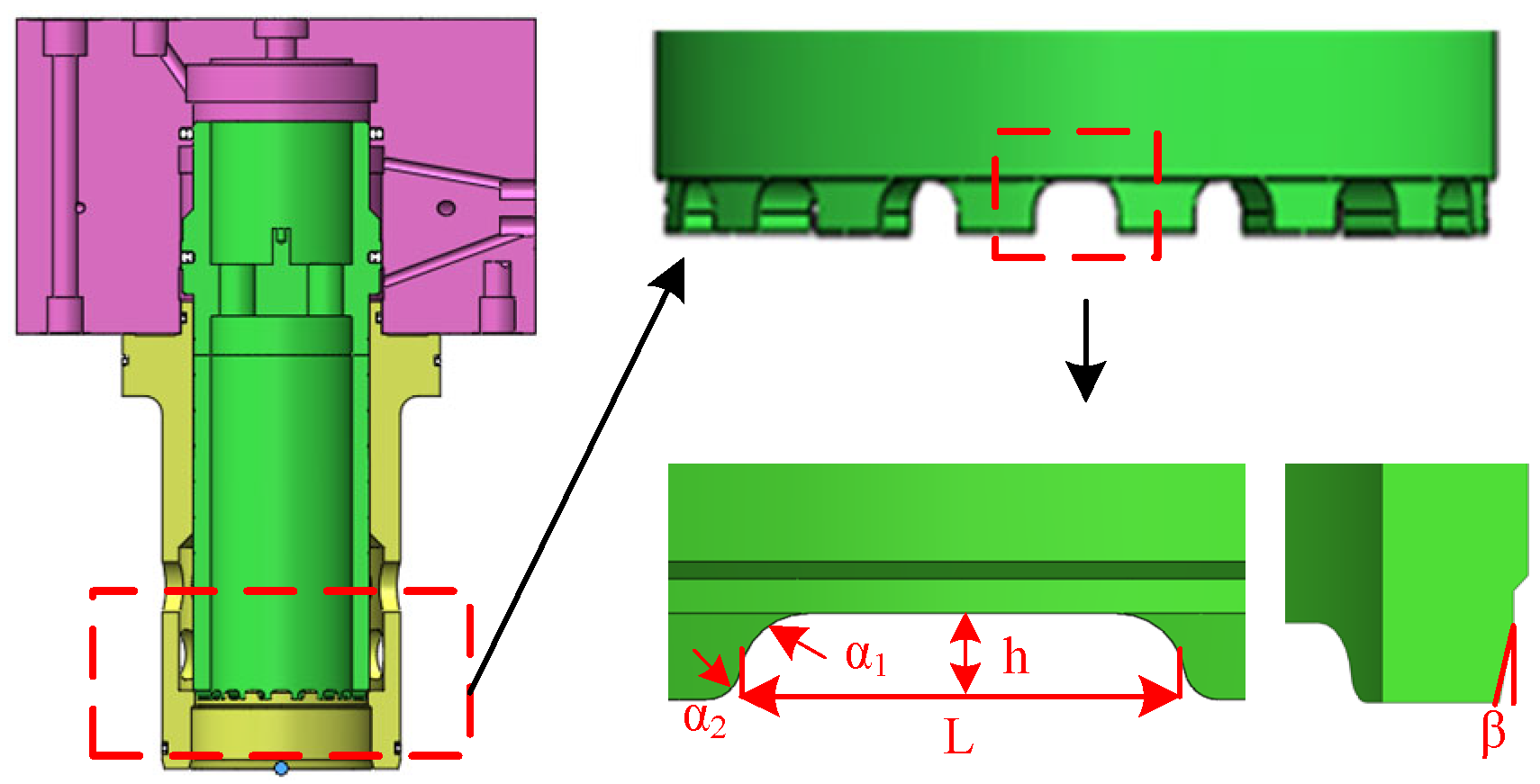
3.4.1. Orthogonal Test Program Design
- (1)
- Determination of test factors, levels, and indicators.
- (2)
- Orthogonal table composition.
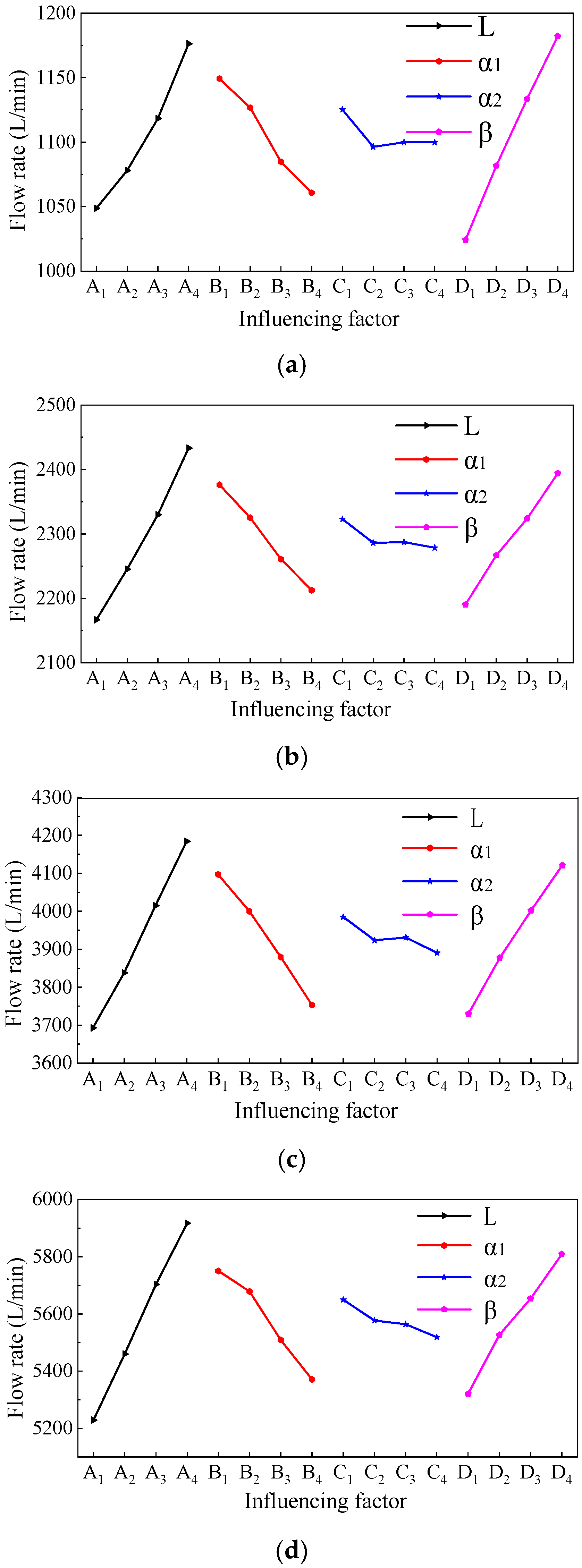
3.4.2. Orthogonal Test Results and Analysis
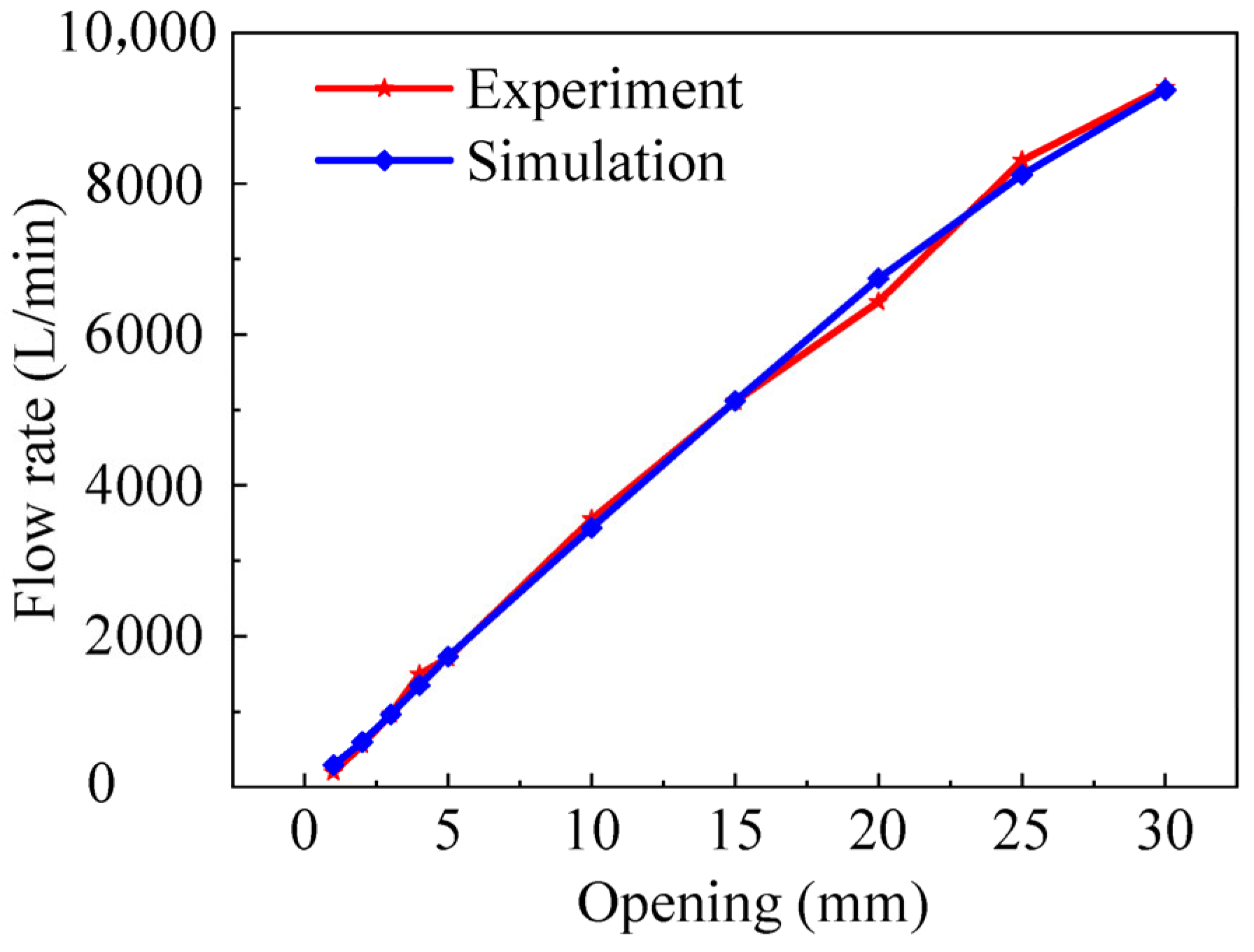
4. Experimental Platform and Results
5. Conclusions
- (1)
- The optimum flow linearity associated with the small rounded rectangle structure is obtained from the simulation analysis of four types of throttle orifices, namely triangle, sector, rounded rectangle, and small rounded rectangle.
- (2)
- By using orthogonal test and simulation analysis, it is found that the flow linearity of the proportional throttle valve with optimized structure is greatly improved by comparing it with the flow rate change curve of the spool in the form of no throttle port structure.
- (3)
- The simulation results and experimental test results show similar trends, verifying the accuracy of each other. Optimizing the parameters of the spool throttle port structure can effectively improve the flow linearity of the throttle valve.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tamburrano, P.; Plummer, A.R.; Distaso, E.; Amirante, R. A review of direct drive proportional electrohydraulic spool valves: Industrial state-of-the-art and research advancements. J. Dyn. Syst. Meas. Control 2019, 141, 020801. [Google Scholar] [CrossRef]
- Plummer, A. Electrohydraulic servovalves-past, present, and future. In Proceedings of the 10th International Fluid Power Conference, Dresden, Germany, 8–10 March 2016. [Google Scholar]
- Sciatti, F.; Tamburrano, P.; Distaso, E.; Amirante, R. Digital hydraulic valves: Advancements in research. Heliyon 2024, 10, e27264. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, R.; Yang, J.; Xu, J.; Yu, X. Recent advances in control strategies and algorithms for pilot-operated electro-hydraulic proportional directional valves. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2024, 09544089231223065. [Google Scholar] [CrossRef]
- Xie, S.; Song, Z.; Huang, J.; Zhao, J.; Ruan, J. Characterization of two-dimensional cartridge type bidirectional proportional throttle valve. Flow Meas. Instrum. 2023, 93, 102434. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, A.; Tang, J. Optimal design of multi-section proportional directional valve throttle grooves with artificial neural networks. MATEC Web Conf. EDP Sci. 2018, 237, 03003. [Google Scholar] [CrossRef]
- Ma, J.H. The Modeling and the Character Emulation of New Type Throttling Grooves on the Electromagnetic Proportion Throttle Valve. In Proceedings of the 2009 Second International Conference on Information and Computing Science, Manchester, UK, 21–22 May 2009; Volume 4, pp. 153–155. [Google Scholar]
- Wang, X.; Chang, J.; Wen, Y.; Zheng, J.; Sun, S. Analysis and emulation of steady-state characteristic for water hydraulic proportional throttle valve. In Proceedings of the 2009 IEEE 10th International Conference on Computer-Aided Industrial Design & Conceptual Design, Wenzhou, China, 26–29 November 2009. [Google Scholar]
- Liu, W.; Wei, H.J.; Hu, B. Analysis and Optimization of a Hydraulic-feedback Proportional Throttlecartridge Valve. Appl. Mech. Mater. 2014, 481, 162–170. [Google Scholar] [CrossRef]
- Xu, E.; Nie, C.; Jiang, X.; Miao, Z. Theoretical investigation on the throttle pressure reducing valve through CFD simulation and validating experiments. Korean J. Chem. Eng. 2021, 38, 400–405. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, L.; Wang, X.; Wang, D. Design for Improving the Linearised Flow Control Performance of Large Flow and High-pressure Proportional Valve. In Proceedings of the 20th International Conference of Fluid Power and Mechatronic Control Engineering, Jiaxing, China, 8–10 November 2019. [Google Scholar]
- Zhang, H.; Liao, Y.; Tao, Z.; Lian, Z.; Zhao, R. Modeling and Dynamic Characteristics of a Novel High-Pressure and Large-Flow Water Hydraulic Proportional Valve. Machines 2022, 10, 37. [Google Scholar] [CrossRef]
- Yao, J.; Yin, Y.; Dong, Z.; He, Y. Design of a 70 MPa Two-Way Proportional Cartridge Valve for Large-Size Hydraulic Forging Press. J. Beijing Inst. Technol. 2020, 29, 55–61. [Google Scholar]
- Liu, W.; Tian, J.; Wang, H.; Li, J.; Zhou, R.; Cao, Y. Investigation on the Dynamic Characteristics of a New High-Pressure Water Hydraulic Flow Control Valve. Machines 2024, 12, 640. [Google Scholar] [CrossRef]
- Gao, Q.; Zhu, Y.; Wu, C.; Jiang, Y. Development of a novel two-stage proportional valve with a pilot digital flow distribution. Front. Mech. Eng. 2021, 16, 420–434. [Google Scholar] [CrossRef]
- Han, M.; Liu, Y.; Wu, D.; Tan, H.; Li, C. Numerical Analysis and Optimisation of the Flow Forces in a Water Hydraulic Proportional Cartridge Valve for Injection System. IEEE Access 2018, 6, 10392–10401. [Google Scholar] [CrossRef]
- Avram, M.; Duminică, D.; Bucşan, C. Influence of the flow section geometry on the static characteristic curves of proportional hydraulic throttle valves. Appl. Mech. Mater. 2014, 555, 385–394. [Google Scholar] [CrossRef]
- Tan, L.; Xie, H.; Chen, H.; Yang, H. Structure optimization of conical spool and flow force compensation in a diverged flow cartridge proportional valve. Flow Meas. Instrum. 2019, 66, 170–181. [Google Scholar] [CrossRef]
- Meng, B.; Hao, X.; Jian, R.; Sheng, L. Theoretical and experimental investigation on novel 2d maglev servo proportional valve. J. Chin. Aviat. Engl. 2021, 34, 416–431. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, A.; Chen, Y.; Jiang, T. Optimization on the Topological Coupling-Throttling Structures for Directional Valves. IOP Conf. Ser. Earth Environ. Sci. 2020, 585, 012171. [Google Scholar]
- Xie, H.; Tan, L.; Liu, J.; Chen, H.; Yang, H. Numerical and experimental investigation on opening direction steady axial flow force compensation of converged flow cartridge proportional valve. Flow Meas. Instrum. 2018, 62, 123–134. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Retardation time | ≤10 ms |
| Step response test | ≤40 ms |
| Nominal flow rate (ΔP = 10 bar) | ≥10,500 L/min |
| Repeatability | <1% |
| Hysteresis | <3% |
| Work pressure | 350 bar |
| Number | Parameter Name | Unit | Value |
|---|---|---|---|
| 1 | Pressure inlet | bar | 350 |
| 2 | Pressure outlet | bar | 345 |
| 3 | Fluid density | kg/m3 | 880 |
| 4 | Fluid dynamic viscosity | Pa·s | 0.04 |
| Level | Influencing Factor | |||
|---|---|---|---|---|
| A: Length | B: Fillet 1 | C: Fillet 2 | D: Dip Angle | |
| 1 | 24 mm | 2 mm | 0.5 mm | 10° |
| 2 | 26 mm | 3 mm | 1 mm | 12° |
| 3 | 28 mm | 4 mm | 1.5 mm | 14° |
| 4 | 30 mm | 5 mm | 2 mm | 16° |
| Test Number | Experimental Factor | Test Target Flow (L/min) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | 1 mm | 2 mm | 3 mm | 4 mm | 5 mm | |
| 1 | 1 | 1 | 1 | 1 | 1 | 250.57 | 535.61 | 910.22 | 1285.86 | 1599.83 |
| 2 | 1 | 2 | 2 | 2 | 2 | 257.28 | 538.71 | 920.17 | 1321.26 | 1657.47 |
| 3 | 1 | 3 | 3 | 3 | 3 | 265.30 | 541.91 | 928.70 | 1308.22 | 1694.97 |
| 4 | 1 | 4 | 4 | 4 | 4 | 275.53 | 550.59 | 933.72 | 1313.29 | 1706.05 |
| 5 | 2 | 1 | 2 | 3 | 4 | 287.81 | 589.46 | 1021.74 | 1428.54 | 1821.14 |
| 6 | 2 | 2 | 1 | 4 | 3 | 294.30 | 595.13 | 1023.15 | 1447.17 | 1854.41 |
| 7 | 2 | 3 | 3 | 1 | 2 | 244.72 | 527.21 | 893.80 | 1283.53 | 1620.96 |
| 8 | 2 | 4 | 4 | 2 | 1 | 251.22 | 533.44 | 898.87 | 1300.44 | 1661.60 |
| 9 | 3 | 1 | 3 | 4 | 2 | 307.94 | 625.84 | 1089.00 | 1529.33 | 1944.38 |
| 10 | 3 | 2 | 1 | 3 | 1 | 293.22 | 599.24 | 1037.44 | 1467.09 | 1877.54 |
| 11 | 3 | 3 | 4 | 2 | 4 | 270.30 | 569.09 | 981.92 | 1398.35 | 1773.72 |
| 12 | 3 | 4 | 2 | 1 | 3 | 246.89 | 535.41 | 906.54 | 1308.30 | 1644.51 |
| 13 | 4 | 1 | 4 | 2 | 3 | 302.82 | 625.36 | 1076.03 | 1506.07 | 1883.91 |
| 14 | 4 | 2 | 3 | 1 | 4 | 281.92 | 592.06 | 1019.10 | 1442.61 | 1805.68 |
| 15 | 4 | 3 | 2 | 4 | 1 | 304.34 | 622.53 | 1074.99 | 1518.71 | 1956.88 |
| 16 | 4 | 4 | 1 | 3 | 2 | 287.15 | 593.01 | 1013.96 | 1449.08 | 1872.36 |
| Type | Equipment | Accuracy |
|---|---|---|
| Controller | AC801-0221-U0R0 (Inovance Technology, Shenzhen, China) | The response time is less than 10 ms |
| DC Stabilized Power Supply | DP310 (Inovance Technology, Shenzhen, China) | Accuracy ± 0.1% |
| Communication-interface Module | GL20-RTU-ETC (Inovance Technology, Shenzhen, China) | Accuracy ± 0.2% (full temperature range) |
| Analog Input Module | GL20-4AD (Inovance Technology, Shenzhen, China) | Accuracy ± 0.2% (full temperature range) |
| Analog Output Module | GL20-4DA (Inovance Technology, Shenzhen, China) | Accuracy ± 0.2% (full temperature range) |
| Displacement Transducer | LVDT TSDDCI300-360 (Hangzhou quanren electronic Technology, Hangzhou, China) | Stroke 0~36 mm, linear accuracy ≤ 0.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Yang, L.; Gao, T.; Meng, Q.; Xiao, S.; Ai, C. Small Opening Flow Linearity Optimization of High-Pressure and Large-Flow Two-Way Proportional Throttle Valve. Machines 2025, 13, 354. https://doi.org/10.3390/machines13050354
Wang B, Yang L, Gao T, Meng Q, Xiao S, Ai C. Small Opening Flow Linearity Optimization of High-Pressure and Large-Flow Two-Way Proportional Throttle Valve. Machines. 2025; 13(5):354. https://doi.org/10.3390/machines13050354
Chicago/Turabian StyleWang, Baosheng, Liu Yang, Tianxiong Gao, Qingxin Meng, Shouwen Xiao, and Chao Ai. 2025. "Small Opening Flow Linearity Optimization of High-Pressure and Large-Flow Two-Way Proportional Throttle Valve" Machines 13, no. 5: 354. https://doi.org/10.3390/machines13050354
APA StyleWang, B., Yang, L., Gao, T., Meng, Q., Xiao, S., & Ai, C. (2025). Small Opening Flow Linearity Optimization of High-Pressure and Large-Flow Two-Way Proportional Throttle Valve. Machines, 13(5), 354. https://doi.org/10.3390/machines13050354






