Simulated Centrifugal Fan Blade Fault Diagnosis Based on Modulational Depthwise Convolution–One-Dimensional Convolution Neural Network (MDC-1DCNN) Model

Abstract

Existing intelligent fault diagnosis methods have been widely developed and proven to be effective in monitoring the operating status of key mechanical components. However, centrifugal fans, as important equipment in energy and manufacturing industries, have been used for a long time in complex and harsh environments such as boiler plants and gas turbines. Therefore, the vibration signals they generate show complex and diverse characteristics, which brings great challenges to the monitoring of centrifugal fan operation status. To solve this problem, this paper proposes a centrifugal fan blade fault diagnosis method based on a modulational depthwise convolution (DWconv)–one-dimensional convolution neural network (MDC-1DCNN). Specifically, firstly, a convolutional modulation module (CMM) with strong local perception and global modeling capability is designed by drawing on the Transformer self-attention mechanism and global context modeling idea. Second, multiple DWconv layers of different sizes are introduced to capture high-frequency shocks and low-frequency fluctuation information of different frequencies and durations in the signal. Next, a DWconv layer of size 11 is embedded in the multilayer perceptron to enhance spatial information representation while saving computational resources. Finally, to verify the effectiveness of the method, this paper simulates and analyzes the actual working state of centrifugal fan blades, constructs a simulation dataset, and builds a centrifugal fan experimental bench to obtain a real dataset. The experimental results show that the MDC-1DCNN framework significantly outperforms the existing methods in both simulation and experimental bench datasets, fully proving its versatility and effectiveness in centrifugal fan blade fault diagnosis.

1. Introduction

Centrifugal fans, as a kind of driven fluid rotating machinery, are widely used in industrial ventilation and exhaust, energy and power, agricultural farming, and other fields [1,2]. However, centrifugal fans are highly prone to failures in harsh working environments, which can lead to significant economic losses and even pose life-threatening risks. Among them, the blade, as the core component of centrifugal fan, has a failure rate that accounts for more than 65% of overall failures and is the weakest link in the operation of a centrifugal fan [3]. Therefore, the development of efficient and accurate blade fault diagnosis methods is of great significance to ensure the stable operation of centrifugal fans and reduce the risk of failure.

Vibration signals carry a large amount of information reflecting the state of mechanical equipment, and the presence of faults can be effectively determined by extracting the features in the signals. These signals are primarily visualized and analyzed in both the time domain [4] and frequency domain [5]. Rao et al. [6] assessed the health of compressor blades in two operating plants by using the information of characteristic vibration signals to classify the cracked condition of the blades. Gubran et al. [7] investigated the differences between healthy and faulty blades by experimentally measuring the torsional vibration of the shaft. Although signal analysis methods are widely used in fault diagnosis of mechanical equipment, they are poorly adapted to deal with nonlinear systems. To address this issue, machine learning-based diagnostic methods, such as support vector machines [8], random forests [9], and K-nearest neighbors [10], have been shown to effectively address the challenges of fault diagnosis. Although machine learning methods perform well in many scenarios, they still have limitations in their reliance on manual feature extraction and expert experience.

Deep learning is capable of automatically extracting features, and intelligent diagnostic methods based on deep learning have been widely applied in the field of fault diagnosis. Su et al. [11] used a deep confidence network to diagnose faults in a gas turbine. Dao et al. [12] proposed a convolutional neural network–long short-term memory fault diagnostic model optimized based on Bayesian algorithms to diagnose faults in a hydraulic turbine.

Among many deep learning frameworks, convolution neural network (CNN)-based frameworks have been widely studied and well validated due to their outstanding performance [13]. Tang et al. [14] proposed a new fault diagnosis method to identify the fault types of hydraulic piston pumps by converting the vibration, pressure, and acoustic signals into time-frequency images and utilizing an improved CNN model. Zhang et al. [15] converted the signals into time-frequency grayscale images and constructed a four-channel CNN to extract features under different conditions for classification. Shao et al. [16] converted sensor signals into time-frequency distribution images and used a CNN for accurate fault identification of induction motors. Xie et al. [17] converted multi-signal data into three-channel RGB images through principal component analysis and utilized an improved residual network CNN model for fault identification of rotating machinery. Zhou et al. [18] enhanced defect feature representation by aggregating discriminative spatial features from non-classification feature maps. In addition, Zhang et al. [19] proposed a multi-modal fusion network that utilizes vibration signals and thermal images to comprehensively assess the health condition of gearboxes. Two-dimensional CNNs possess powerful feature extraction capabilities and images are rich in information, so 2D CNN-based diagnostic frameworks have been widely used and intensively developed in several fields. However, 2D images lose the original signal phase information, resulting in the rich failure information in vibration signals not being fully utilized.

One-dimensional CNNs have attracted much attention in the field of fault diagnosis due to their ability to directly capture local patterns and temporal dependencies in the original sequence, significantly reducing the complexity of data preprocessing and the possibility of information loss [20]. Yu et al. [21] proposed a one-dimensional residual convolutional autoencoder to extract features directly from vibration signals through unsupervised learning to achieve fault identification of gearboxes. Zhang et al. [22] proposed a supervised contrastive domain adaptation network that learns raw features from 1D signals and employs maximum mean discrepancy loss to achieve global alignment for solving rolling bearing fault diagnosis problems. Wang et al. [23] designed a feature mapping module based on a multi-attention one-dimensional convolutional neural network augmented with added channels and excitation attention. Dong et al. [24] proposed a new method combining an empirical wavelet transform and a one-dimensional improved self-attention augmented convolutional neural network for bearing fault recognition. However, since critical components can usually maintain normal operation for a long period of time, the frequency of faulty states is low, resulting in the number of faulty samples often being much less than that of normal samples [25]. Therefore, how to realize high-precision fault diagnosis under the condition of imbalanced data has become a focus of extensive attention.

In recent years, data-driven fault diagnosis has become an important research area which centers on the use of deep learning techniques to improve fault identification and classification [26]. Zhang et al. [27] proposed a novel method based on digital twins to address the issue of insufficient training data in rolling bearing fault diagnosis. Tao et al. [28] proposed a parameter optimization-based few-sample fault diagnosis method, and its feature metrics, for solving the problems of sparse fault samples and cross-domain discrepancies between datasets. Fan et al. [29] developed a digital twin-based approach to generate high-fidelity cage degradation signals and achieve accurate degradation assessment under data scarcity. Yin et al. [30] addressed the fault diagnosis problem of marine valve remote control hydraulic systems through simulation modeling, PCA dimensionality reduction, and multi-sensor information fusion. Hei et al. [31] proposed a domain-adaptive method with multiscale attention to generate high-fidelity labeled samples from unlabeled multi-condition data. Yu et al. [32] adopted different diagnosis methods for shared domain datasets and cross-domain datasets. In addition, Carrattieri [33] and Hammond [34] investigated fluid machinery using CFD, optimizing structural designs to obtain more accurate data. Based on the above studies, we found that the data-driven approach based on simulation analysis has significant advantages, including simplicity, feasibility, and high signal quality. However, there are still some challenges in this process. The traditional CNN structure extracts effective feature information from the image, but the image loses the original signal phase information, leading to the underutilization of the information. Furthermore, there is still limited research on the ability of 1D CNNs to perceive global feature information.

In order to solve the above problems, this study proposes a centrifugal fan blade fault diagnosis method based on a modulational depthwise convolution–one-dimensional convolution neural network (MDC-1DCNN). The specific contributions are as follows:

• A new convolutional neural network structure called a convolutional modulation module (CMM) is constructed. The CMM combines powerful local sensing capability and global modeling capability and is able to capture signal features more comprehensively.
• A fault diagnosis model called MDC-1DCNN is proposed. Multiple depthwise convolution (DWconv) convolutional layers of different sizes are introduced into Conv2Former to capture both high- and low-frequency information in the signal. In addition, embedding an 11 × 1 DWconv in the multilayer perceptron not only saves computational resources significantly but also enhances the representation of spatial information.
• Simulation and real datasets are constructed. We simulate and analyze the actual working state of centrifugal fan blades and construct a simulation dataset. At the same time, a rotating impeller experimental bench is built to obtain a dataset under real working conditions.

The sections of this paper are structured as follows. Section 2 introduces the specific details of the proposed method in detail. Section 3 introduces the data processing and experimental setting. In Section 4, the performance of the proposed method is verified using simulation and real datasets. Section 5 draws the conclusions.

2. Methodology

This section describes the details of the proposed method. The overall residual life prediction scheme is shown in Figure 1. The DWconv, CMM, and MDC-1DCNN are introduced. The CMM is the backbone of the MDC-1DCNN, and the DWconv layer enhances spatial information representation.

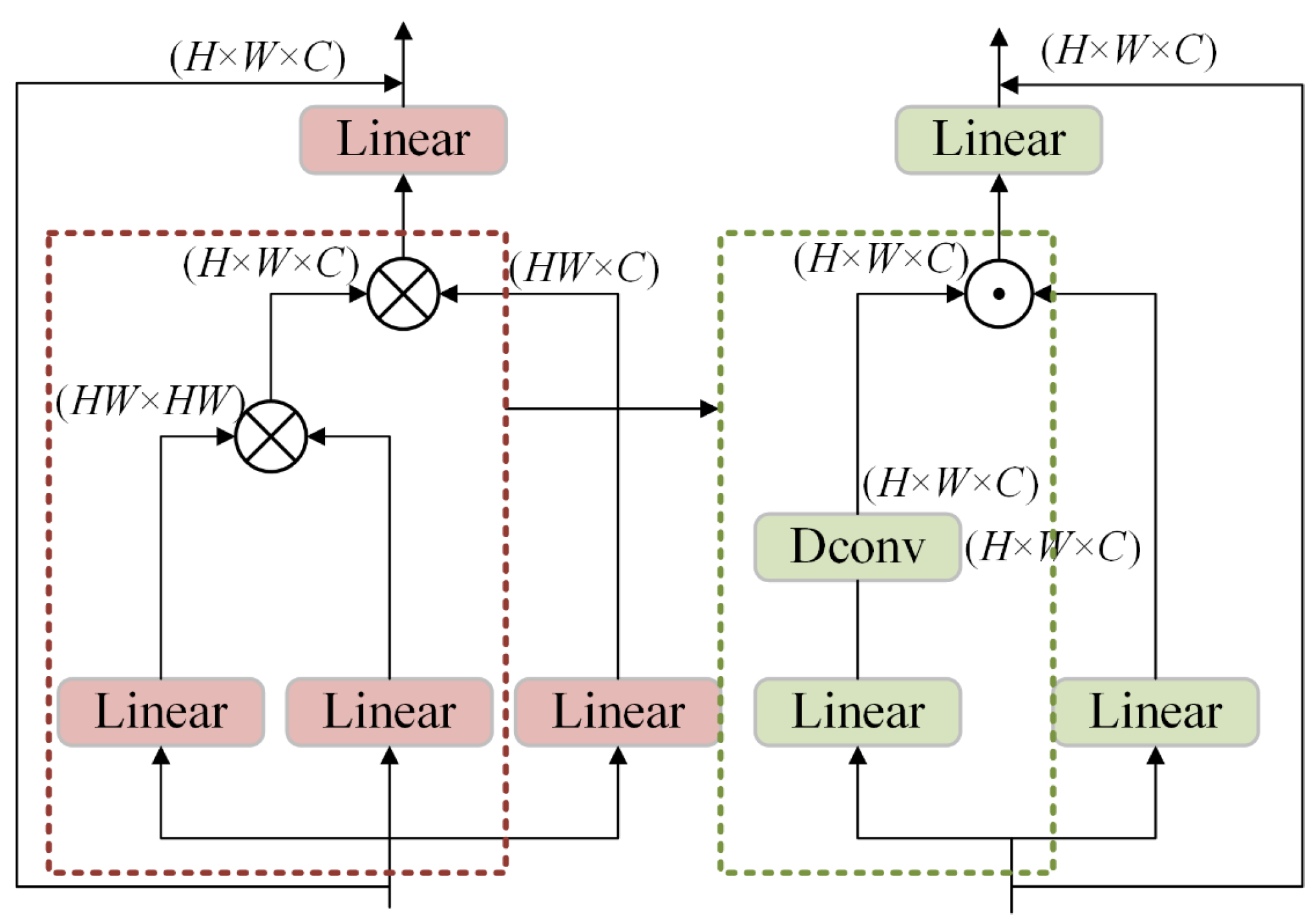
2.1. Details of DWconv

DWconv, as an improvement and optimization of standard convolution, was first proposed and applied to the MobileNet network architecture by Chollet [35] in 2017. The specific steps are illustrated in Figure 2. First, depthwise convolution is performed on each channel separately, and then the extracted feature information is blended using pointwise convolution.

The convolutional layer of DWconv performs feature dimensionality reduction on the input data, which prevents overfitting to a certain extent, but also significantly reduces the number of parameters and achieves the effect of ordinary convolution, enabling the neural network to have deeper layers. The convolution step is set to 1. The computational function for standard convolution is shown in Equation (1) and the computational function for DWconv is shown in Equation (2).

$$F_{\mathrm{out}}(x,y,co)={\displaystyle \sum _{i,j,ci}w(co,i,j,ci)\cdot }{F}_{in}(x+i,y+i,ci)$$

(1)

$${\hat{F}}_{\mathrm{out}}(x,y,ci)={\displaystyle \sum _{i,j,ci}\hat{W}(i,j,ci)\cdot }{F}_{in}(x+i,y+i,ci)$$

(2)

where F_out represents the location of the output feature map (x, y) and the number of channels (co). F_in represents the location of the input feature map (x + i, y + i) and the number of channels (ci).

It is assumed that the input image size of the standard convolutional feature map A is D_A × D_A × M, the output image size of the feature map B is D_B × D_B × N, and the size of the convolutional kernel is N × D_K × D_K × M, where D_A, D_B, and D_K denote the spatial heights and widths of the input feature maps, output feature maps, and convolution kernels, respectively, and M and N denote the number of channels for the input and output, respectively.

One standard convolutional operation is N × D_K × D_K × M × D_A × D_A. In contrast, the computational amount of depth-separable convolution is D_A × D_A × D_K × D_K × M + D_B × D_B × M × N. The ratio comparing the computational amount of DWconv with that of standard convolution is shown in Equation (3). When D_B and N are greater than 1, the ratio of the computational amount of DWconv to that of standard convolution is less than 1. This demonstrates that the computational amount of depth-separable convolution is much smaller compared to that of standard convolution.

$${\displaystyle \frac{D_A\times D_A\times D_K\times D_K\times M+D_B\times D_B\times M\times N}{N\times D_K\times D_K\times M\times D_A\times D_A}}={\displaystyle \frac{1}{N}}+{\displaystyle \frac{1}{D_B^2}}$$

(3)

2.2. Details of the CMM

The Transformer network was first proposed by Vaswani et al. [36] in 2017, and unlike traditional convolutional operations, the Transformer utilizes an attention mechanism to capture global dependencies between inputs and outputs. Additionally, it enables the parallel computation of sequential inputs.

Conv2Former is a novel CNN with a CMM which utilizes large-size DWconv layers to acquire spatial information and weight intermediate features. The CMM consists of two parts: a self-attention layer and a feed-forward neural network. The self-attention layer spatially encodes the inputs, while the feed-forward neural network fuses the multi-channel outputs, as illustrated in Figure 3. Instead of the self-attention layer in the CMM, a modulation layer with depth-separable convolution is used. The key value K, the query value Q, and the output value V are generated through linear operations in the self-attention layer, while at the same time the input X is also generated by a K × K deep convolution and a linear layer to generate the weight matrix (A). The weight matrix (A) and the values (V) are combined via the Hadamard product to generate the final output V, where A is the feature map obtained by transforming the input X by a K × K deep convolutional processing input through a linear layer, while the output V is the values obtained through another linear layer. Here, A can be viewed as a matrix similar to the attention weights which is obtained by spatial convolution. This design simplifies the model computation while maintaining efficient encoding of spatial features.

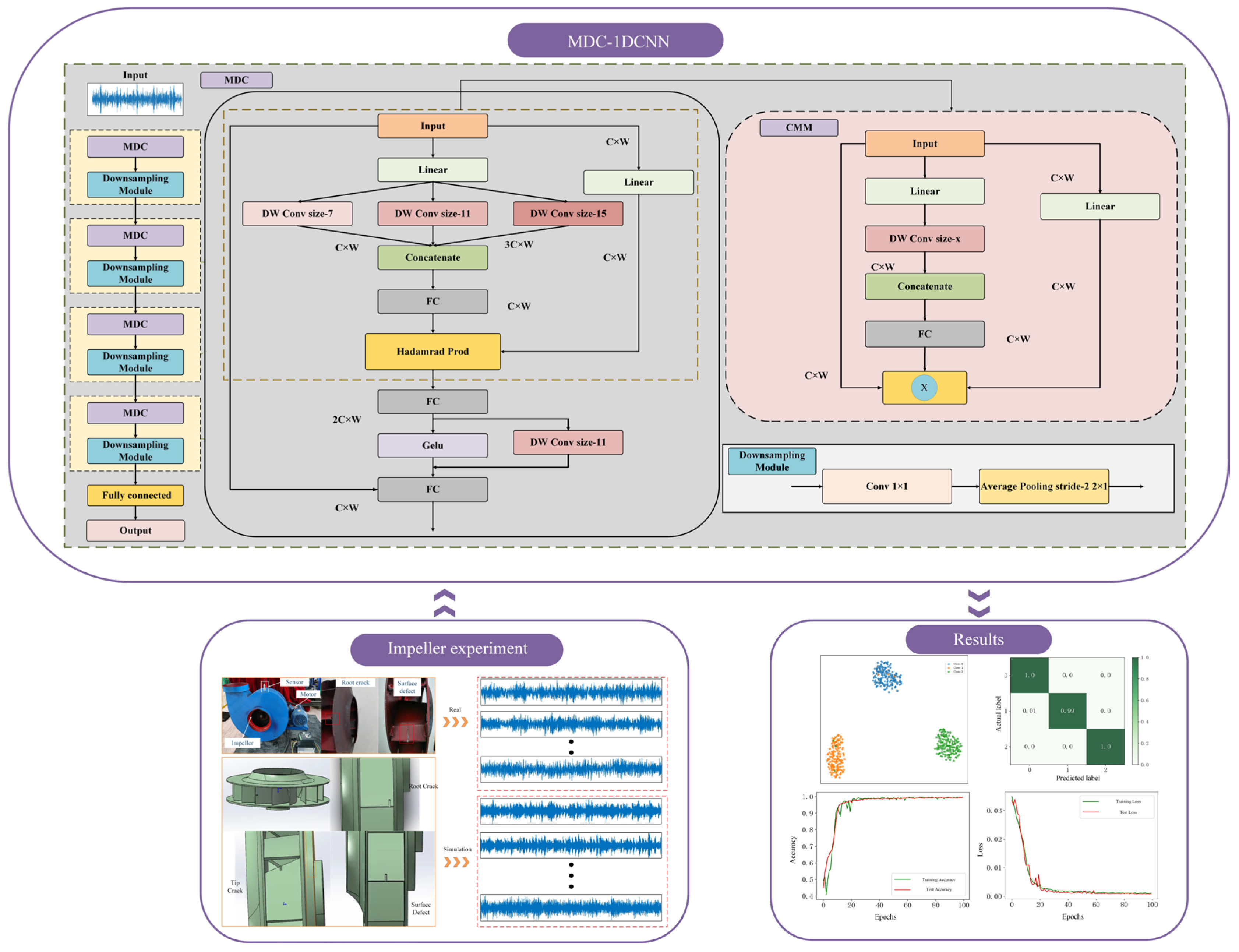
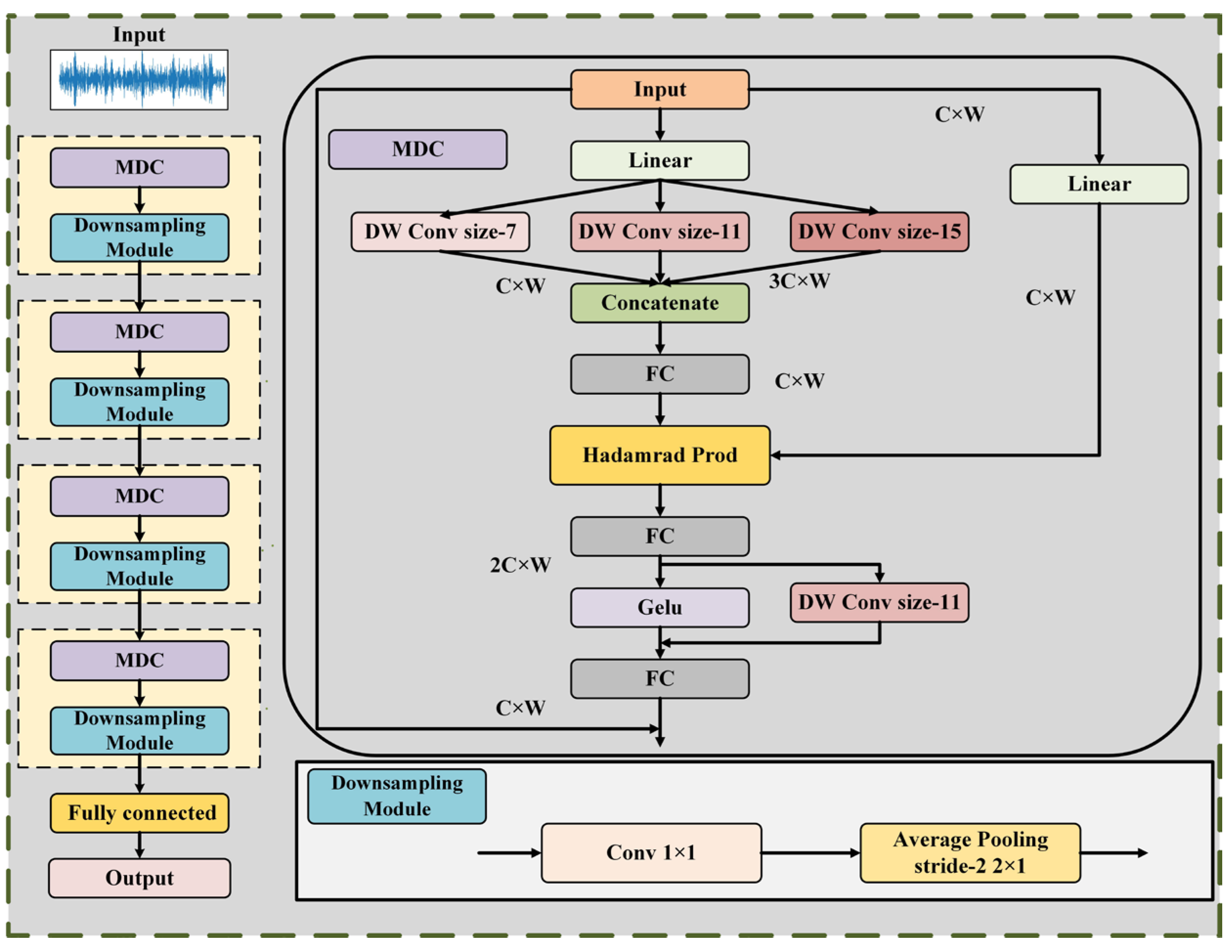
2.3. Details of the MDC-1DCNN

As shown in Figure 4, the MDC-1DCNN receives one-dimensional vibration signals as the input, and first extracts features at different scales adaptively by the MDC module. Subsequently, these features are downsampled by the downsampling module for dimensionality reduction, which reduces the amount of data while retaining key information. In the network structure, the MDC module and the downsampling module are stacked four times to gradually abstract and extract higher-level features. Finally, the fully connected layer transforms and integrates these higher-level features and outputs the final results.

The MDC module was inspired by the Conv2former and begins with three depth-separable convolutional layers of different sizes, with convolutional kernel sizes of 7 × 1, 11 × 1, and 15 × 1. Smaller convolutional kernels capture localized details, while larger kernels cover a wider area to obtain a broader range of contextual information. By fusing these features at different scales, the output dimension becomes 3C × W. The number of channels is then maintained to match the input dimension through a fully connected layer. Next, the features passing through the fully connected layer are multiplied via the Hadamard product with the features passing through the linear layer on the other branch, forming the convolutional modulation mechanism. This mechanism enables the model to perceive global dependencies between different locations in the input feature map. Further, the data are fed into another fully-connected layer to increase the number of output features to 2C × W. These features are then processed by a GELU nonlinear activation function to introduce nonlinear characteristics. At the same time, the data are also passed in parallel through a depth-separable convolutional layer of size 11 × 1 to enhance the model’s representation of the features. The downsampling module employs a convolutional kernel of size 1 × 1 and a convolutional kernel of size 2 × 1 with a stride size of 2 for average pooling.

3. Experimental Setting

This section describes the details for experimentation and data processing.

3.1. Details of Experiment

In order to obtain the time-domain signals of the rotating impeller in both the normal state and the fault state, a rotating impeller fault simulation experimental platform was built in this study. The platform is mainly composed of vibration sensors, a signal collector, a pulley driver, a drive motor, and other core components. For data acquisition, the Siemens LMS Scadas Mobile industrial hardware system was utilized, the high-precision performance of which provides a solid data foundation for the experiment. The hardware system adopts 24-bit delta-sigma analog-to-digital conversion technology, supports up to 16 channels, has a dynamic range of >110 dB, and delivers high-precision, highly reliable data acquisition. The vibration signals were acquired using a single-axis integrated electronic piezoelectric accelerometer with a sensitivity of 100 mV/g. The accelerometer has a measurement range of ±50 g, transverse sensitivity of <5%, and a frequency response range of 0.5 Hz to 10 kHz. Blade surface defects and blade root cracks, which are common types of faults in impellers, were modeled in this study as fault states for the experiment. The specific failure conditions are illustrated in Figure 5. During the preparation stage of the experiment, the healthy impeller was treated using welding and cutting techniques to simulate the impeller failure state. Acceleration sensors are usually mounted near the impeller housing to monitor its operational status. To ensure the stability of the sensor and the accuracy of the data, we fixed the sensor on the top of the housing, allowing for the collection of time-domain signals reflecting the vertical vibration of the impeller. The speed of the drive motor was maintained at a constant 1200 r/min.

3.2. Details of Simulation Experiment

In order to meet the demand for sufficient samples for centrifugal fan blade fault diagnosis, this study carries out simulation modeling of a Y6-41 boiler centrifugal fan. Its specific parameters are listed in

Table 1. Boiler centrifugal ventilator performance parameters.

Parameter	Value
Fan Total Pressure (pa)	1650
Air Volume (m3/h)	2322
Fan Speed (r/min)	2800
Motor Power (kw)	1.5

and

Table 2. Centrifugal fan impeller blade parameters.

Parameter	Value
Impeller Diameter (mm)	390.5
Length (mm)	110
Width (mm)	58
Thickness (mm)	2
Quantity	16

. In the model, crack widths are set to 1, 2, and 3 mm, while blade root and tip cracks with a length of 10 mm and a thickness of 2 mm, as well as blade surface defects with a length of 10 mm and a thickness of 1 mm, are established, as illustrated in Figure 6.

In the actual machining process, cracks are typically replaced by slits, which are primarily achieved through cutting processes. However, in this study, rectangular geometries are used for simulation [37]. To further improve the efficiency and accuracy of the model calculations, the following simplifications are applied to the three-dimensional model of the centrifugal fan.

(1) Tiny surfaces such as chamfers, keyways, bolt holes, etc. of the impeller disk are ignored [37];

(2) The ignored bolt holes are replaced by fixed contacts [37].

In the simulation study of the centrifugal fan, its operating speed was set to 1500 r/min and the inlet wind speed was adjusted to 5 m/s. The actual operating state was simulated by analyzing the blade using one-way fluid–solid coupling. The simulated vibration acceleration signal was collected, as shown in Figure 7.

3.3. Data Preparation

Preprocessing the centrifugal fan blade data collected by vibration sensors is a crucial step to ensure the accuracy of the subsequent analysis. To avoid the interference of errors introduced by rotational speed variation on network feature extraction and to optimize the training efficiency, the input signal x is normalized in this study. The normalization process is shown in Equation (4).

$$x*={\displaystyle \frac{x-\mu }{\sigma }}$$

(4)

where x_normalized represents the data value of the signal after the normalization process and x is the original data value that represents the signal at a particular moment in time, setting the statistical properties of the signal over time, the mean μ and the variance σ.

In this study, the training data samples and test data samples are divided in a 4:1 ratio and a total of 3000 samples are generated for the three states, with each sample having a length of 1024, as shown in

Table 3. The division of simulation experiment datasets.

Label	Fault Type	Training Set	Test Set
0	Normal	2000	500
1	Tip Crack (1 mm)
2	Tip Crack (2 mm)
3	Tip Crack (3 mm)
4	Root Crack (1 mm)
5	Root Crack (2 mm)
6	Root Crack (3 mm)
7	Surface Defects (1 mm)
8	Surface Defects (2 mm)
9	Surface Defects (3 mm)

. To strictly ensure the absolute independence of each sample, a random sampling method is adopted during the sample division process. We divided the simulation dataset by splitting the data into training set samples and test set samples in a ratio of 4:1. Specifically, each state contains 2500 samples, totaling 10 states, as shown in

Table 4. The division of experimental datasets.

Label	Fault Type	Training Set	Test Set
0	Normal	800	200
1	Root Crack
2	Surface Defects

. The length of each sample is fixed at 1024 data points to ensure the consistency and comparability of the data.

The experiment is implemented on Windows system with i7 12700H CPU and GTX 3060 GPU. The optimizer of the model training is Adam, the learning rate is 0.001, and the loss function is MSE. The epoch is set to 100.

4. Experimental Results and Discussion

4.1. Diagnostic Performance of the Proposed Method

In order to verify the effectiveness of the proposed MDC-1DCNN, we utilized the experimental dataset and simulation dataset respectively. By using the t-SNE technique to visualize the extracted features, as shown in Figure 8, we were able to intuitively reveal the distribution of different categories of blade vibration signal features, thus verifying the effectiveness of the model in feature extraction. From Figure 8a, we can see that the three state data features after the MDC-1DCNN model largely achieve accurate classification. This is mainly reflected in the fact that the features of each category form relatively independent clusters in the two-dimensional space, with the intra-class distances being significantly smaller than the inter-class distances. However, there is still a slight overlap between some categories. The orange feature 1 has a small overlap with the blue feature 0, and the green feature 2 has a similar distribution characteristic to the orange feature 1. In contrast, the feature distribution of the simulated dataset in Figure 8b demonstrates a more ideal classification performance. The features of different categories exhibit significant discriminability in the feature space, with each feature cluster showing a more compact distribution pattern and the decision boundaries between classes being clearer and more distinguishable. This discrepancy may stem from the fact that the simulation environment allows for precise control of variables, thereby generating more discriminative feature patterns. The MDC-1DCNN model demonstrates robust feature extraction capabilities across different types of datasets. It effectively captures the essential characteristics of blade vibration signals and maps high-dimensional features into a well-separable low-dimensional space. The above results demonstrate the effectiveness of the MDC-1DCNN.

In addition, we also plotted a confusion matrix to represent the specific classification situation. From the experimental dataset in Figure 9, it can be seen that the model is able to accurately classify in the vast majority of cases and only 2 samples belonging to class 1 are incorrectly classified into class 0, achieving an accuracy of 98.78%. The slight confusion between Class 0 and Class 1 may stem from the inherent similarity of their vibration patterns under certain operating conditions. In the simulation dataset, the performance of the MDC-1DCNN is even better, with the classification accuracy further improved to 99%. The confusion matrix exhibits a clean diagonal pattern with minimal off-diagonal elements. These results demonstrate that our MDC-1DCNN exhibits excellent generalization capability across different data types and outstanding discriminative power in feature extraction.

4.2. Comparison Experiments with Other Methods

In order to verify the performance of the proposed method, we designed a series of comparison experiments to compare the performance of the MDC-1DCNN with the current popular 1DCNN network models, including ResNet18 [38], ResNet50 [39], WDCNN [40], and MS-1DCNN [41]. The experimental results show that, as shown in

Table 5. Fault diagnosis accuracy of different models.

Model	Accuracy
ResNet18	96.15%
ResNet50	97.47%
WDCNN	86.50%
MS-1DCNN	97.12%
MDC-1DCNN	98.78%

, the MDC-1DCNN outperforms all other compared methods in terms of accuracy. The results validate the effectiveness of the multi-depth convolutional module design in the MDC-1DCNN and demonstrate the superiority of the hybrid dilated convolution strategy, which enhances classification accuracy while maintaining high computational efficiency. Particularly noteworthy is that compared to the more parameter-intensive ResNet50 model, the MDC-1DCNN achieves superior performance with a more compact network architecture. This comparative outcome especially highlights the breakthrough in lightweight model design achieved by the proposed method.

4.3. Ablation Study

In order to verify the superiority of the designed network techniques, we designed ablation experiments to investigate the network performance, and all the ablation experiments were conducted on the real experimental dataset of centrifugal fan blade failures. The specific ablation experiments conducted are as follows: using the original network model of the MDC-1DCNN, denoted as M0; using only a DWconv size of 7, denoted as M1; using only a DWconv size of 9, denoted as M2; using only a DWconv size of 11, denoted as M3; not using the self conv4 function, denoted as M4; and replacing the activation function GELU with the Tanh function, denoted as M5. Ten experiments were conducted for each scheme and the average was taken. The number of iterations was 100, the number of sampling points of the input data was 1024, the number of samples in each small batch was 30, and the initial learning rate was set to 0.001. The experimental results are shown in

Table 6. Ablation results.

Model	Accuracy
M0	98.78%
M1	97.50%
M2	96.89%
M3	97.43%
M4	94.63%
M5	98.33%
M1 + M5	97.85%
M2 + M5	97.68%
M3 + M5	98.18%
M4 + M5	95.82%
M1 + M4 + M5	95.62%
M2 + M4 + M5	95.79%
M3 + M4 + M5	95.49%

.

From the experimental results in Table 6, it can be seen that the models using only a single convolutional module (e.g., M1, M2, and M3) all have lower accuracy than the MDC-1DCNN model. Compared with either single-branch model, the accuracy of the MDC-1DCNN is improved by about 2–3%, which fully demonstrates the effectiveness of multi-channel models in feature extraction and fault diagnosis. In addition, when the self conv4 function in the MDC-1DCNN model is removed (M4), the accuracy decreases by 5.04% compared to the original model, which indicates that the self conv4 function plays a key role in the model performance. Similarly, after changing the activation function from GELU to Tanh (M5), the accuracy decreased by 1.34%, further highlighting the superiority of the GELU activation function. The results of the ablation experiments demonstrate the effectiveness of the MDC-1DCNN.

5. Conclusions

In this paper, the authors propose a fault diagnosis framework named the MDC-1DCNN which successfully addresses the issue of centrifugal fan blade fault diagnosis. Specifically, the MDC-1DCNN incorporates the self-attention mechanism of a Transformer and the concept of global context modeling to design a CMM that integrates both local perception and global modeling capabilities. Within the CMM, the authors introduce multiple DWconv layers of varying sizes to capture information related to high-frequency shocks and low-frequency fluctuations of different frequencies and durations in the signal. Additionally, a DWconv convolutional layer with a size of 11 × 1 is embedded within the multilayer perceptron to further enhance the representation of spatial information while conserving computational resources. Finally, the authors constructed a simulation dataset by simulating and analyzing centrifugal fan blades and validated the framework using the created impeller dataset. It can effectively solve the problem of blade data shortage in harsh environments. The experimental results demonstrate that the MDC-1DCNN effectively solves the centrifugal fan blade fault diagnosis problem, achieving an accuracy rate of 98.78% on the experimental dataset, thereby fully proving the model’s superiority and practicality.

Since we are introducing a CMM into a 1DCNN for the first time, we are to troubleshoot centrifugal fan blades and construct a dataset for blade simulation and analysis. Therefore, it is crucial to simulate a working environment that closely resembles real-world conditions. In our future research, we will focus on designing a network structure with fewer parameters to reduce computational resource consumption, thereby enabling the simulation of a more realistic blade operating environment.