A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing

Abstract

This paper presents an empirical study of feature extraction methods for the application of low-speed slew bearing condition monitoring. The aim of the study is to find the proper features that represent the degradation condition of slew bearing rotating at very low speed (≈1 r/min) with naturally defect. The literature study of existing research, related to feature extraction methods or algorithms in a wide range of applications such as vibration analysis, time series analysis and bio-medical signal processing, is discussed. Some features are applied in vibration slew bearing data acquired from laboratory tests. The selected features such as impulse factor, margin factor, approximate entropy and largest Lyapunov exponent (LLE) show obvious changes in bearing condition from normal condition to final failure.

1. Introduction

Slew bearings are large roller element bearings that are used in heavy industries such as mining and steel milling. They are particularly used in turntables, cranes, cranes, rotatable trolleys, excavators, reclaimers, stackers, swing shovels and ladle cars [1]. In this paper, the slew bearing being analyzed is the one typically used in BlueScope Steel Australia; specifically for the coal loading into the steel ladle turret, coal stacker and reclaimer. Slew bearing is different to typical rolling element bearing in terms of geometry, load and speed application. Slew bearings are usually operated at very low rotational speed, from 0.5 to 15 rpm in either continuous or reversible rotation and are designed with three axes to support high axial and radial loads. The bearings have large diameter (e.g., approximately from 200 mm to 5000 mm). Due to the high geometric and cost issue, industries purchase these bearings for replacement in a regular maintenance period. However, in some cases, these bearings may fail before the predicted time. To prevent catastrophic failure and to effectively schedule the bearing purchase for minimizing the replacement cost, a condition monitoring method for early failure detection is required.

Analyzing the vibration signatures of slew bearings that operate at a very low speed is more complex than that of typical rolling element bearings. Slew bearing signals have low energy. They are also non-stationary, non-linear, chaotic and practically hard to analyze. Due to their low energy, the signal is masked by a higher background noise level. Therefore, it is difficult to extract the pertinent bearing signal. It is necessary to have reliable condition monitoring parameters or features that could extract accurate information about the bearing condition from the signal.

The number of studies on slew bearing condition monitoring and early failure detection based on vibration analysis is lower than for rolling element bearing. Studies of slew bearing condition monitoring and life prediction utilizing vibration signal are presented in [2,3,4,5,6,7]. Žvokelj et al. [2] presents the condition monitoring method utilizing vibration signal based on ensemble empirical mode decomposition (EEMD) and principal component analysis (PCA). An extension work of [2] is presented in [3] which used combined EEMD with kernel PCA. Recent studies of the slew bearing fault detection and diagnosis is presented by Žvokelj et al. [4]. The paper presents combined EEMG and multiscale independent component analysis (ICA). Nevertheless, studies of slew bearing failure prediction and prognosis also increased recently [5,6,7]. Feng et al. [5] develops a reliability model for residual life prediction based on Weibull analysis. A method for degradation trend estimation of slew bearings was presented in [6]. The method employed PCA, particle swarm optimization (PSO) and least squares support vector machine (LSSVM). Another residual life prediction model study of slewing bearing can be found in [7]. The authors used PCA and support vector regression (SVR) to construct the model.

In order to monitor the condition of slew bearings, a feature that represents the trends related to degradation condition from normal to failure is necessary. Due to the unique vibration signal generated by the roller and raceway contact in slew bearing, a suitable and sensitive feature extraction method is mandatory in slew bearing fault diagnosis and prediction. There are numerous existing methods, which are divided into different categories. For instance, Henao et al. [8] presented diagnostic methods in a non-stationary condition. The methods are classified into four approaches: (1) frequency domain approach; (2) time domain analysis; (3) slip-frequency; (4) diagnosis in the time-frequency domain.

This paper particularly presents an empirical study of feature extraction methods for vibration signals acquired from naturally degraded slew bearings operating at very low rotational speed. In terms of feature extraction methods, six categories are reviewed, namely (i) time-domain features extraction; (ii) frequency-domain features extraction; (iii) time-frequency representation; (iv) phase-space dissimilarity measurement; (v) complexity measurement; and (vi) other features. Among the six categories, the time-domain features extraction method is found to be the most dominant method in typical rolling element bearings. In addition, the third and fourth methods are suitable for non-stationary, non-linear and chaotic signals.

2. Laboratory Slew Bearing Experiment

2.1. Slew Bearing Test-Rig and Sensor Location

The vibration data employed in this paper were acquired from a slew bearing test rig [1]. The test rig was designed to replicate real working conditions of a slew bearing in a steel company, such as a high-applied load and low rotational speed. The slew bearing used was a large thrust bearing with an inner and outer diameter of 260 mm and 385 mm, respectively. The rotational speed of the lab test rig can be operated from 1 to 12 r/min. A photo of the test rig and sensor location on the slew bearing is shown in Figure 1.

2.2. Data Acquisition Procedure

The vibration data for continuous rotation was collected from four accelerometers that were installed on the inner diameter surface at 90° to each other with 4880 Hz sampling rate. The accelerometers were IMI 608A11 ICP (IMI Sensors, PCB Piezotronics Division, New York, NY, USA) type sensors. The accelerometers were connected to a high-speed PicoScope DAQ (PS3424) (Pico Technology, St Neots, UK). The bearing was subjected to an axial load of 15 tons. The bearing began running in 2006 with rotational speed of 1 r/min. However, to provide continuous monitoring and produce run-to-failure bearing data, the bearing data was collected on a daily basis from February to August 2007 with total number of 139 days. To accelerate the bearing service life, coal dust was injected into the bearing in mid-April 2007 (58 days from the beginning). In practice, especially in steel-making companies, the slew bearing is located in open air where the bearing is exposed to a dusty environment and for this reason the coal dust was inserted in mid-April to simulate the real working conditions. The schematic of the vibration data acquisition from slew bearing test-rig is presented in Figure 2.

3. Features Extraction Methods and Its Application on Slew Bearing Vibration Signal

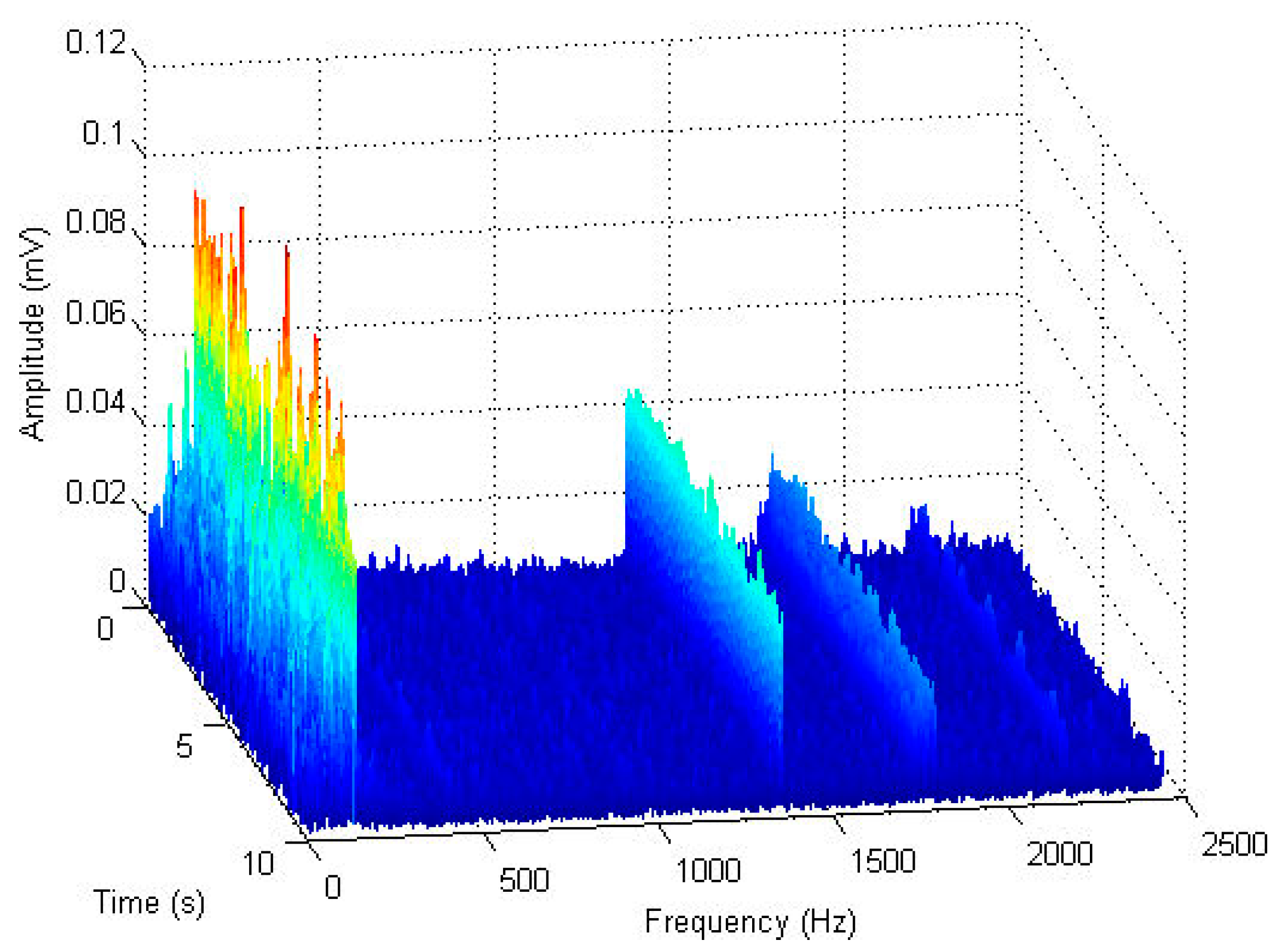
3.1. Category 1: Time-Domain Features Extraction

3.1.1. Statistical Time-Domain Features

Statistical time-domain features such as mean, root mean square (RMS), standard deviation and variance were usually used in past studies to identify the differences between one vibration signal and another. More advanced statistical-based features such as skewness and kurtosis can be applied to the signal which is not purely stationary. These features examine the probability density function (PDF) of the signal. It is a well-known fact that if the condition of the bearing changes, the PDF also changes, thus the skewness and kurtosis might also be affected. In particular, skewness is used to measure whether the signal is negatively or positively skewed, while kurtosis measures the peak value of the PDF and indicates if the signal is impulse in nature. For a signal with a normal distribution i.e., normal bearing signal has a skewness value of zero.

In addition, kurtosis is obtained from the peak of the PDF of the vibration signal, while skewness is obtained from the mean value of the PDF of the vibration signal. It is well known that the kurtosis value of vibration signal from normal bearing is approximately three [9] and the skewness value of approximately zero. Then, when the PDF of vibration signal changes due to faults, the kurtosis value will increase to greater than three and the skewness value will shift to either negative or positive. Other features which can be calculated from PDF of the vibration signal includes: entropy, which calculates the histogram of the PDF and measures the degree of randomness of the vibration signal; lower bound and upper bound histogram, which measure the lower and upper values of the PDF respectively.

Aside from the statistical time-domain features mentioned above, there are other non-dimensional features such as shape factor (defines as RMS divided by mean) and crest factor (defines as standard deviation divided by RMS). Both features will change as the mean, RMS and standard deviation change. The summary of the statistical time-domain features is presented in

Table 1. Brief review of statistical time-domain features extraction applied in condition monitoring of typical rolling element bearings [10].

Feature Name	Description
	Brief Definition	Formula
RMS	The RMS value increase gradually as fault developed. However, RMS is unable to provide the information of incipient fault stage while it increases with the fault development [11].	$\mathrm{RMS}=\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{x}_i^2}}$
Variance	Variance measures the dispersion of a signal around their reference mean value.	$\mathrm{Var}=\frac{{\displaystyle {\sum }_{i=1}^N{\left(x_i-m\right)}^2}}{\left(N-1\right){\sigma }^2}$
Skewness	Skewness quantifies the asymmetry behavior of vibration signal through its probability density function (PDF).	$\mathrm{Sk}=\frac{{\displaystyle {\sum }_{i=1}^N{\left(x_i-m\right)}^3}}{\left(N-1\right){\sigma }^3}$
Kurtosis	Kurtosis quantifies the peak value of the PDF. The kurtosis value for normal rolling element bearing is well-recognized as 3.	$\mathrm{Ku}=\frac{{\displaystyle {\sum }_{i=1}^N{\left(x_i-m\right)}^4}}{\left(N-1\right){\sigma }^4}$
Shape factor	Shape factor is a value that is affected by an object’s shape but is independent of its dimensions [12].	$\mathrm{SF}=\frac{\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{x}_i^2}}}{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\left|x_i\right|}}$
Crest factor	Crest factor (CF) calculates how much impact occur during the rolling element and raceway contact. CF is appropriate for “spiky signals” [12].	$\mathrm{CF}=\frac{\max \left|x_i\right|}{\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{x}_i^2}}}$
Entropy	Entropy, $e(p)$, is a calculation of the uncertainty and randomness of a sampled vibration data. Given a set of probabilities, $(p_1,p_2,\dots ,p_n)$, the entropy can be calculated using the formulas as shown in the right column.	$e(p)=-{\displaystyle \sum _{i=1}^{n}p(z_i){\log }_{2}p(z_i)}$

.

3.1.2. Upper and Lower Bound of Histogram

The application of the histograms or a discrete PDF for time-domain feature extraction is presented in [13]. Let $d$ be the number of division that group the ranges, and $h_i$ with $0\le i<d$ be the columns of the histogram for the time $x_i$

$$h_i={\displaystyle \sum _{j=0}^n\frac{1}{n}{r}_i(x_i),\forall i,0\le i<d}$$

(1)

$$r_i=\{\begin{array}{ll}1,& if\frac{i(\max (x_i)-\min (x_i))}{d}\le x<\frac{(i+1)(\max (x_i)-\min (x_i))}{d}\\ 0,& otherwise\end{array}$$

(2)

The upper bound $h_U$ and lower bound $h_L$ of histogram are defined as

$$h_U=\max (x_i)+\Delta /2$$

(3)

$$h_L=\max (x_i)-\Delta /2$$

(4)

where $\Delta =(\max (x_i)-\min (x_i))/(n-1)$.

According to the features extraction results presented in Figure 3, some features, such as RMS, kurtosis, histogram upper bound and histogram lower bound, show the fluctuation in the last measurement day, approximately from the 90th day to the 139th day. These indicate that some features are sensitive to the slew bearing condition while others are less. The incipient damage occurred in day 90th that is clearly indicated by RMS, kurtosis, histogram upper bound and histogram lower bound feature, where the fluctuation is associated with roller and outer race defects. However, more appropriate and reliable features are necessary for the condition monitoring of slew bearing to detect an impending damage and to estimate the degradation index.

3.1.3. Autoregressive (AR) Coefficients

In other studies [13], autoregressive (AR) coefficients of the vibration signal are calculated as bearing vibration features. It is known that a faulty vibration signal of typical rolling element bearing produces different autoregressive coefficients compared to that of normal vibration signal. The following is a common univariate time series model to calculate the AR coefficients:

$$y_t=a_1{y}_{t-1}+a_2{y}_{t-2}+\dots +a_n{y}_{t-n}+{\epsilon }_t={\displaystyle \sum _{i=1}^n{a}_i{y}_{t-1}+{\epsilon }_t}$$

(5)

where $a_1$ to $a_n$ are the autoregressive coefficients, $y_t$ is the digitized vibration signal, $n$ is the order of the AR model ($n=8$) and $\epsilon$ is the residual (Gaussian white noise).

The RMS, skewness, kurtosis, entropy and AR coefficients have been applied in vibration datasets from induction motor [14] and rolling element bearing [15]. These papers have made great contributions to the research areas on the bearing condition monitoring and fault diagnosis. However, the features were applied for artificially bearing damage. In practice, the damage is typically developed naturally rather than artificially.

The AR coefficients results are presented in Figure 4. It is shown that most of the features are less relevant to represent the slew bearing condition except for AR coefficient 4 which is shown fluctuating in the last measurement.

Other time domain features such as impulse factor (IF) and margin factor (MF) have been recently used [12,16,17]. Similar to CF, IF is used to measure how much impact is generated from the bearing defect. The CF measures the impact by dividing the maximum absolute value of vibration signal and RMS value, while IF divides the maximum absolute value by the mean of absolute value. The formula is presented as follows:

$$\mathrm{IF}=\frac{\max \left|x_i\right|}{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\left|x_i\right|}}$$

(6)

Margin factor (MF) measures the level of impact between rolling element and raceway. The MF is calculated by dividing the maximum absolute value of vibration signal to the RMS of absolute value of vibration signal (7):

$$\mathrm{MF}=\frac{\max \left|x_i\right|}{{\left(\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\sqrt{\left|x_i\right|}}\right)}^2}$$

(7)

The progression of slew bearing deterioration of IF and MF features are more apparent compared to RMS, kurtosis and histogram lower features as presented in Figure 5.

3.1.4. Hjorts’ Parameters

In addition to the time-domain features mentioned in previous subsections, Hjorts’ parameters also falls into this category [18]. These features are calculated based on the first and the second derivatives of the vibration signal. In the time series context, the numerical values for the derivatives are obtained as the differences between the current value and the prior value. The first Hjorth’s parameter is called ‘activity’. The activity of vibration signal can be computed by simply calculating the variance of the vibration signal amplitude ${\sigma }_x^2$, where ${\sigma }_x$ is the standard deviation of the sampled vibration signal $x=(x_1,x_2,x_3,\dots ,x_N)$.

The ‘mobility’ parameter of vibration signal is calculated as the square root of the ratio of the activity of the first derivative and the activity of the vibration signal.

$$\mathrm{mobility}=\frac{{\sigma }_{x^{\prime }}}{{\sigma }_x}$$

(8)

where ${\sigma }_{x^{\prime }}$ is the standard deviation of the first derivative of the vibration signal. The numerical values for the derivatives can be obtained as the differences between samples as follows.

$$x^{\prime }=x_{(i+1)}-x_{i}i=1,\dots ,N-1$$

(9)

The last parameter called ‘complexity’ which is calculated as the ratio of mobility of the first derivative and the mobility of the vibration signal.

$$\mathrm{complexity}=\frac{{\sigma }_{x^{″}}/{\sigma }_{x^{\prime }}}{{\sigma }_{x^{\prime }}/{\sigma }_x}$$

(10)

These parameters have been used in electroencephalography (EEG) signals to detect the epileptic seizures [19]. They have never been used in vibration bearing signal except for activity feature, which is similar to the variance feature in the statistical time-domain features extraction. It can be seen from Figure 6 that the progression of bearing condition is difficult to track using mobility and complexity feature. In contrast, the activity or variance feature shows one highest peak at approximately the 90th day and continue fluctuation on the last measurement days.

3.1.5. Mathematical Morphology (MM) Operators

In image processing, mathematical morphology (MM) was introduced as a non-linear method to analyze two dimensional (2D) image data including binary images and grey-level images based on set theory [20]. The fundamental principle of the MM method is to modify the shape of the original signal by transforming it through its intersection with another object called the ‘structuring element’ (SE). Four operators including erosion, dilation, closing and opening are used to achieve the transformation.

After having been applied successfully in 2D image processing, the MM method has been used in biomedical research field to analyze one dimensional (1D) EEG signals [21,22,23] and electrocardiography (ECG) signals [24]. The first known study of MM in 1D vibration signals was presented by Nikolaou and Antoniadis [25]. The authors used the MM method for vibration data with inner race and outer race faults. The effects of four MM operators on the enveloping impulse-type signals were examined. The result shows that the ‘closing’ operator is more suitable for extracting the impulse signal corresponding to the bearing fault type. The SE value was empirically investigated within the range of 0.2 T to 1.2 T. The optimum SE for a signal with additive noise was selected as 0.6 T (0.6 times the pulse repetition period). In addition, T is the period of each bearing component frequency such as BPFO, BPFI and BSF.

The original discrete one dimensional (1D) signal and structuring element (SE) must be first determined to use the four basic operators in the MM method. Suppose the discrete 1D vibration signal $x=\{x(1),x(2),\dots ,x(N)\}$, which functions over a domain $x\left(n\right)=(1,2,\dots ,N)$. Let $S=\{S(1),S(2),\dots ,S(M)\}$ be the SE, which is the discrete function over a domain $S(m)=(1,2,\dots ,M)$, where $N$ and $M$ are integers and $N\ge M$. Then, the four morphology operators for the discrete 1D vibration signal can be defined as follows:

• Erosion: also refer to as min filter.

  $$(x\Theta S)(n)=\min \left(x(n+m)-S(m)\right)$$

  (11)
• Dilation: also refer to as max filter.

  $$(x\oplus S)(n)=\max \left(x(n-m)+S(m)\right)$$

  (12)
• Closing: Dilates 1D signal and then erodes the dilated signal using the similar structuring element for both operations.

  $$(x•S)(n)=\left((x\oplus S)\Theta S\right)(n)$$

  (13)
• Opening: Erodes 1D signal and then dilates the eroded signal using the similar structuring element for both operations.

  $$(x\circ S)(n)=\left((x\Theta S)\oplus S\right)(n)$$

  (14)

where $n\in (1,2,\dots ,N)$ and $m\in (1,2,\dots ,M)$, the notations $\Theta ,\oplus ,•,\circ$ denote the erosion operator or Minkowski subtraction, dilation operator or Minkowski addition, closing operator and opening operator in the MM method, respectively.

The original simulated 1D signal is shown in the first row of Figure 7. The various effects of the basic MM operators application in the simulated 1D vibration signal are presented in the second to fifth row of Figure 7. The second row of Figure 7 to the fifth row of Figure 7 illustrate the effect of erosion, dilation, closing and opening, respectively. Please note that the solid blue line represents the original signal and the dashed red line is the signal after being processed or transformed by the MM operators. The simulated signal has zero mean value, which is typical to 1D vibration signals. The work principle of the basic MM operators can be summarized as follows: erosion of $x(n)$ by the structuring element $A(m)$ reduces the positive part and enlarges the negative part of $x(n)$, while dilation of $x(n)$ by the structuring element $A(m)$ reduces the negative part and enlarges the positive part of $x(n)$. In addition, closing of $x(n)$ smoothens the signal $x(n)$ by cutting down any impulses in the negative part and opening $x(n)$ smoothens the signal $x(n)$ by cutting down its impulses in the positive part.

In rolling element bearing, the MM method has been studied. The multi-scale morphological analysis was developed by Zhang et al. [26]. The method shows independency of empirical rules in terms of SE selection, but the technique is rather complex. Wang et al. [27] proposed an improved morphological filter as features of periodic impulse signals. An average weighted combination of open-closing and close-opening morphological operators was employed to eliminate the statistical deflection of amplitude and to extract the impulse component from the original signal. To optimize the SE, they used a new criterion called impulse attenuation (IMA). Dong et al. [28] presented the fault diagnosis of rolling element bearings using the modified morphological method. The morphological operator used in their method was the average weight combination of the closing and opening operator. They proposed a new criterion called SNR criterion to optimize the length of SE. Another recently published research on MM method was presented by Raj and Murali [29]. The authors combined the MM operators with fuzzy inference to classify the artificial bearing defects. The vibration data used in [29] were similar to the data used in Zhang et al. [26].

The application of the MM method in detecting the bearing fault frequencies from among impulsive-type signals have been demonstrated [26,27,28,29]. These signals are generated from known bearing conditions such as inner and/or outer race faults. It is acknowledged that the signals from artificial faults are easier to be identified than those from natural bearing faults. Besides, typically, the impulse-type signals are easily identified visually without any additional tool or processing step [28]. The application of MM method to the naturally damaged slew bearing is presented in Figure 8, Figure 9 and Figure 10.

The MM method has been used effectively for the damage detection of high speed rolling bearing. It is because when the damage occurred, the contact between the damage spot and rolling element generates detectable impulse due to the contact between the defect spot and race way or roller. In the case of naturally degraded low-speed slew bearing, the multiple damage e.g., outer race, inner race and roller are typically occurred at close sequence time and the magnitude of impulse is very low. Thus, it is difficult to identify the origin of impulse from outer race, inner race or roller damage. Therefore, the feature extraction result of MM for the three conditions: BPFO, BPFI and BSF present an identical figure.

3.2. Category 2: Frequency-Domain Features Extraction

To apply frequency-domain features, the time-domain vibration signals must initially be transformed into frequency-domain signals using fast Fourier transform (FFT). FFT is a common method in vibration analysis for bearing fault detection. FFT measures the dominant frequency of the repetitive impulse period of certain faults due to the contact between rolling elements and defective spot. Therefore, the type of bearing defects such as outer race, inner race or ball defect can be detected. FFT performed effectively in stationary periodic signals; however, it is less effective for non-stationary signals that arise from time-dependent events [30].

3.2.1. Statistical Frequency-Domain Features

Other frequency-domain features such as frequency centre (FC), root mean square frequency (RMSF) and root variance frequency (RVF) have been studied in [13]. When fault exists, the frequency element changes, and the values of the FC, RMSF and RVF also change. The FC and RMSF indicate the position changes of main frequencies, while the RVF shows the convergence of the power spectrum. Another feature called median frequency is sometimes used. The median frequency is measures by dividing the area of the amplitude spectrum into two equal part. In addition, the mean frequency (FC) can be defined as the first-order moment of the Fourier spectrum, RVF as the second-order moment, SS as the third-order moment and SK as the fourth-order moment of the Fourier spectrum [18]. These features can be calculated as follows:

$$\mathrm{FC}=\frac{{\displaystyle {\sum }_{i=2}^N{x}_i^{\prime }{x}_i}}{2\pi {\displaystyle {\sum }_{i=1}^N{x}_i^2}}$$

(15)

$$\mathrm{MSF}=\frac{{\displaystyle {\sum }_{i=2}^N{(x_i^{\prime })}^2}}{4{\pi }^2{\displaystyle {\sum }_{i=1}^N{x}_i^2}}$$

(16)

$$\mathrm{RMSF}=\sqrt{\mathrm{MSF}}$$

(17)

$$\mathrm{RVF}=\sqrt{\mathrm{MSF}-{\mathrm{FC}}^2}$$

(18)

The result of FC, RMSF and RVF feature extraction is presented in Figure 11.

3.2.2. Spectral Skewness, Spectral Kurtosis, Spectral Entropy and Shannon Entropy Feature

Recently, new methods such as spectral skewness, spectral kurtosis, spectral entropy and Shannon entropy have been developed. Spectral skewness (SS) and spectral kurtosis (SK) are the advanced statistical measures applied to the magnitude spectrum. The SS measures the symmetry of the distribution of the spectral magnitude values around its mean [31]. It is defined by

$$\mathrm{SS}(n)=\frac{2{\displaystyle \sum _{k=0}^{{\mathrm{{\rm B}}}_L/2-1}{(|X(k,n)|-{\mu }_{\left|X\right|})}^3}}{{\mathrm{{\rm B}}}_L\cdot {\sigma }_{\left|X\right|}^3}$$

(19)

The SK measures the distribution of the spectral magnitude values and compare to a Gaussian distribution. It is defined by

$$\mathrm{SK}(n)=\frac{2{\displaystyle \sum _{k=0}^{{\mathrm{{\rm B}}}_L/2-1}{(|X(k,n)|-{\mu }_{\left|X\right|})}^4}}{{\mathrm{{\rm B}}}_L\cdot {\sigma }_{\left|X\right|}^4}-3$$

(20)

Antoni and Randall [32] presents the development of classical kurtosis analysis called spectral kurtosis (SK) to deal with the transient behaviour in a signal. SK can be used to detect incipient faults even in the presence of resilient masking noise. The concept of spectral statistic is adopted in this method to supplement the classical power spectral density (PSD). PSD ideally gives zeros values at those frequencies when the signal has stationary Gaussian noise, and it gives high positive values at those frequencies during the occurrence of the transients. When the noise-to-signal ratio is high, the transient signal will be buried in the background noise, thus the incipient fault cannot be clearly detected. SK can overcome this problem by analyzing the entire frequency band and to select the sensitive frequency band that correspond to the bearing condition.

3.3. Category 3: Time-Frequency Representation

Time-frequency domain representation methods such as short-time Fourier transform (STFT), wavelet transform and Wigner-Ville distribution (WVD) are commonly used for non-stationary or transient signal. These methods implement a mapping of one-dimensional time-domain signals to a two-dimensional function of time and frequency. The objective is to provide a true time-frequency representation of a signal. A review of time-frequency analysis methods for machinery fault diagnosis has been presented by Feng et al. [33].

3.3.1. Short-Time Fourier Transform (STFT)

Due to its low computational complexity and definite physical meaning, STFT is often used as an initial pre-processing tool to analyze non-stationary vibration signals. The STFT maps the vibration signal into a two-dimensional (2D) function of time and frequency [34]. STFT divides a non-stationary signal into small windows of equal time frame. The Fourier transformation is then applied to the time segment. Unlike FFT where the frequency transformation includes the whole original signal, in STFT original signal is decomposed using FFT at pre-defined time intervals. By doing this, the defect signal frequency can be identified in a particular window of time. The key to this method is the selection of the time interval. The STFT can be expressed as follows [35]:

$$\mathrm{STFT}(f,t)={\displaystyle \underset{t-T/2}{\overset{t+T/2}{\int }}w(t-\tau )x(\tau )e^{j2\pi f\tau }d\tau }$$

(21)

where $\mathrm{STFT}(f,t)$ is short-term frequency spectrum, $t$ is the time, $f$ is frequency, $w(t-\tau )$ is the shifted window, $x(\tau )$ denotes the input vibration signal, $\exp (j2\pi f\tau )$ is the complex exponential, $T$ is the window interval and $w(\tau )$ is the windowing function which satisfies $w(\tau )=0$ for $\left|\tau \right|=>T/2$.

By taking the square magnitude of the STFT in (21), an energy density using the spectrogram $\mathrm{S}(t,f)$ method can be obtained

$$\mathrm{S}(t,f)={\left|\mathrm{STFT}(t,f)\right|}^2$$

(22)

Equation (22) represents the energy density of the vibration signal $x(\tau )$ windowed by $w(\tau )$.

The visualization of window length and hop size is presented in Figure 12. The vibration signal with the sample index $i$ is split into overlapping blocks of length ${\mathrm{{\rm B}}}_L$ and block index $n$. While, the hop size ${\mathrm{{\rm H}}}_s$ is the distance from the start of one particular block and its subsequent block. The STFT result of one day slew bearing signal measurement is shown in Figure 13 for 10 s vibration signal with window length of 2048, hop size of 256 and number of FFT points of 16,384. It can be seen that during 10 s sampled signal, the amplitudes at lower frequencies were higher than the amplitude at high frequencies (approximately at 1300 Hz and 1750 Hz). This indicates that slew bearing frequencies were dominated by low frequency contents.

3.3.2. Wavelet Transform and Wavelet Decomposition

Wavelet transform is well-known as an appropriate method to analyze non-stationary and transient signal [14,36]. Wavelet transformation employs wavelet function instead of sinusoidal function as the basis function. It enhances a scale variable in addition to the time variable in the inner product transformation [33]. For any limited energy signal $x(t)\in L^2(R)$, the wavelet function is defined as [26]

$${\mathrm{WT}}_x(t,a)=\frac{1}{\sqrt{a}}{\displaystyle {\int }_{-\infty }^{+\infty }x(\tau )\psi \left(\frac{\tau -t}{a}\right)}d\tau$$

(23)

where wavelet $\psi [(\tau -t)/a]$ is derived by dilating and translating the wavelet basis $\psi (t)$, $a$ is the scale parameter $(a>0)$, $t$ is the time shift and $1/\sqrt{a}$ is a normalization factor to maintain energy preservation.

A review of the wavelet transform applications in machine condition monitoring and fault diagnostics is presented by Peng et al. [37]. As a non-stationary signal analysis method, wavelet transform can be applied in machine fault diagnostics as a feature extraction method [37]. Since the wavelet transformations can provide an excellent energy concentration properties due to the uses of the wavelet basis function; the wavelet transform can represent the signal with a certain number of coefficients. The process is usually called wavelet decomposition.

Wavelet decomposition technique decomposes a non-stationary vibration signal into linear form of time-scale units. It decomposes and organizes original signal into several signal components according to the translation of the wavelet function. This changes the scale and shows the transition of each frequency component [38]. Through this decomposition, a selected coefficient can be used directly as the fault features. In wavelet decomposition, the input signal is basically decomposed into two coefficients. The input signal that is passed through the low-pass filter becomes the ‘approximation coefficient’. The input signal which is passed through the high-pass filter becomes the ‘detail coefficient.’ Since the low-frequency component is the most sensitive part to extract the useful information related to the bearing condition, the ‘approximate coefficient’ is passed to the next wavelet decomposition loop in multilevel wavelet decomposition process. Figure 14 shows three level wavelet decomposition structures. The structure illustrates the decomposition of slew bearing vibration signal into approximate coefficient (A) and detailed coefficient (D) at each level. For further processing, features such as mean, variance, skewness and kurtosis are calculated from the detailed coefficients of level 3 (D3) [39]. The features extraction results are presented in Figure 15, it can be seen that kurtosis can predict the damage compared to mean, variance and skewness calculated from signal D3 of the wavelet decomposition due to the significant changes after day 90 of the bearing life time.

The application of wavelet decomposition to the transient stator current signal acquired from induction motor is presented by Niu et al. [40]. Statistical features have also been used to reveal the fault information from the selected coefficients. Another study that uses the wavelet coefficients as the fault features for ball bearing is presented by Liu et al. [41].

3.3.3. Empirical Mode Decomposition-Based Hilbert Huang Transform

Empirical mode decomposition (EMD) [42] has been used in some applications that involve non-stationary signals (see, e.g., Braun and Feldman [43]). A review of EMD applications in fault diagnosis of rotating machinery is discussed in [44]. The review gives a detailed introduction to EMD application in various areas such as bearings, gears and rotors etc.

The EMD decomposes the vibration signal into several signals from high to low frequencies content, namely intrinsic mode functions (IMFs) based on the enveloping technique, i.e., Hilbert-Huang transform (HHT). From the specific frequencies content information, the bearing fault frequency can be identified. In some preliminary studies on condition monitoring [39,45], the original EMD [46] is used for non-stationary slew bearing data. A bearing fault such as outer race, inner race or rolling element fault has occurred when one of the IMF frequencies is identical to one of the bearing fault frequencies (as shown in

Table 2. Fault frequencies of slew bearing test-rig (run at 1 r/min).

Defect Mode	Fault Frequencies (Hz) (Calculation is Given in Appendix A)
	Axial	Radial
Outer raceway (BPFO)	1.32	0.55
Inner raceway (BPFI)	1.37	0.55
Rolling element (BSF)	0.43	0.54

) [45]. The EMD results for slew bearing data are presented in

Table 3. Decomposition result of EMD method for the slew bearing data.

Vibration Data		IMFs of EMD (Hz)
	IMF2	IMF3	IMF4	…	IMF11	IMF12	IMF13	IMF14	IMF15
24 February	641.81	694.52	390.35	…	2.47	1.44	0.69	0.33	1.99
3 May	702.88	684.34	346.23	…	2.04	1.23	0.64	0.43	0.19
30 August	651.72	679.86	245.92	…	1.37	0.68	0.33	0.10

. A detail EMD result is presented in [39,45].

According to Table 3, the frequencies that correspond to the bearing fault condition did not appear on 24 February. In contrast, the fault frequency of rolling element (BSF axial) is identified on 3 May at 0.43 Hz. This frequency is associated to the roller defects as shown in Figure 16a. Interesting result was obtained from data on 30 August, where the BSF axial is hidden by BPFI axial of 1.37 Hz. The reason could be that the amplitude of signal 0.43 Hz is too weak and is covered by the background noise. The photo of the outer raceway damage is shown in Figure 16b. The roller and outer race damage photo was taken after final failure during the bearing dismantle on 2 September. The detailed vibration data used from the slew bearing test rig is presented in [39]. Statistical features from the decomposition results of EMD method is shown in Figure 17. The mean, variance, skewness and kurtosis features are calculated from the summation of the low IMF frequencies (from IMF 9 to the lowest IMF) of the EMD results. The selection of these IMFs is based on the characteristic of slew bearing signal being dominated by low frequency components as presented previously in STFT result.

3.3.4. Wigner-Ville Distribution (WVD)

The Wigner distribution (WD) is derived from the relationship between the power spectrum and the autocorrelation function for time-variant and non-stationary processes [47]. The correlation function is a product of the function at a posterior time with the function at a subsequent time [48]. The original WD for real signal $x(t)$ is defined as [49]

$$W_x(t,f)={\displaystyle {\int }_{-\infty }^{+\infty }{x}^{\ast }\left(t-\frac{\tau }{2}\right)x\left(t+\frac{\tau }{2}\right)}{e}^{-j2\pi f\tau }d\tau$$

(24)

The symbol ($\ast$) in Equation (24) denotes the complex conjugate.

When the WD is applied for the analytical signal $x_A(t)$, it is called the Wigner-Ville distribution (WVD). The analytical signal is defined as

$$x_A(t)=x(t)+j{x}_h(t)$$

(25)

where $x_h(t)$ is the Hilbert transform of $x(t)$:

$$\mathrm{H}[x(t)]=x_h(t)=\frac{1}{\pi }{\displaystyle {\int }_{-\infty }^{+\infty }x(\tau )\frac{1}{t-\tau }d\tau }$$

(26)

The WVD has been used for gear fault detection [47,48] and it is recently used for rolling element bearing to represent the time-frequency features of vibration signals [50].

3.4. Category 4: Phase-Space Dissimilarity Measurement

Phase-space dissimilarity measurements, such as fractal dimension, correlation dimension approximate entropy and largest Lyapunov exponent (LLE), are developed based on the chaos theory. These methods have been applied in biomedical engineering studies [19,51] and vibration signals [52,53]. Present studies have conducted investigations into these methods in the slew bearing condition monitoring for features extraction. The motivation is that multiple defects occur more frequently than single defects in slew bearings, therefore the phase-space dissimilarity measurements can be used to analyze the irregular or chaotic vibration signals. The phase-space can be computed as follows:

$$X=\left[\begin{array}{ccccc}{y}_1\hfill & y_{1+J}\hfill & y_{1+2J}\hfill & \dots \hfill & y_{1+(m-1)J}\\ y_2\hfill & y_{2+J}\hfill & y_{2+2J}\hfill & \dots \hfill & y_{2+(m-1)J}\hfill \\ y_3\hfill & y_{3+J}\hfill & y_{3+2J}\hfill & \dots \hfill & y_{3+(m-1)J}\hfill \\ ⋮& ⋮& ⋮& & ⋮\\ y_M& y_{M+J}& y_{M+2J}& \dots & y_{M+(m-1)J}\end{array}\right]$$

(27)

where $J$ is reconstruction delay that can be calculated by time lag/$\Delta t$, $m$ is the embedding dimension and $M$ is the number of reconstructed vectors. The relation between $N$, $J$, $m$ and $M$ can be defined as: $N=M+(m-1)J$ or $M=N-(m-1)J$. Thus, the dimension of phase-space is a $M\times m$ matrix.

3.4.1. Fractal Dimension

Fractal dimension is a method to quantify the signal complexity by characterizing fractal patterns. The complexity can be quantified by examining the dynamical behaviours of phase-space matrix. The frequently used algorithm of fractal dimension was proposed by Higuchi [54]. The field is rapidly growing as estimated fractal dimensions for statistically self-similar phenomena. This method has been applied in many fields including image analysis [55], neuroscience [56,57], medicine [58], physics [59] and acoustics [60]. The application of fractal dimension in vibration signal of rolling element bearing has been presented in [10,61]. The algorithm of fractal dimension is shown in (28) [10]. Once the phase-space matrix, $X$ is obtained (27), the mean absolute length between $J^{th}$ and ($J^{th}-1$) element of $X$ is defined as follows:

$$\begin{array}{l}fora=1:J\\ forb=2:m\\ L_1(a,b-1)=\left|X(a,b)-X(a,(b-1))\right|\\ L_m(a,b-1)=mean(L_1)\\ end\\ end\end{array}$$

(28)

where $J$ and $m$ is reconstruction delay and embedding dimension, respectively. The fractal dimension $D$ can be calculated using standard least-square fitting method of the logarithmic natural of $(1/m)$ and $L_m$.

3.4.2. Correlation Dimension

Correlation dimension can be used to quantify the self-similarity of vibration signal. A large value of correlation dimension corresponds to less-similarity of vibration signal. An example application of correlation dimension in vibration signal for bearing fault diagnosis was proposed by Logan and Mathew [52]. The correlation dimension was applied for vibration signals acquired from four different conditions: (1) normal (new bearing); (2) outer race fault; (3) inner race fault; and (4) roller fault. The damages were artificially introduced to the bearing parts. The method is able to identify four different bearing conditions.

The commonly used procedure to calculate the correlation dimension was introduced by Grassberger and Procaccia [62]. Similar to fractal dimension, the phase-space matrix (27) is fed to the correlation dimension algorithm as an input matrix. The formula for correlation dimensionis given by:

$$\mathrm{C}(l)=\underset{x\to \infty }{\lim }\left[\frac{2}{M^2}{\displaystyle \sum _{i=1}^{M-k}}{\displaystyle \sum _{j=i+k}^M\Theta \left(l\left|X_i-X_j\right|\right)}\right]$$

(29)

where $X_i$ and $X_j$ are the position vectors on attractor, $l$ is the distance under consideration, $\Theta (x)$ is the Heaviside step function, $\Theta (x)=0$ if $X\le 0$, $\Theta (x)=1$ if $X>0$, $k$ is the summation offset, $M$ is the number of reconstructed vectors from the original vibration signal and $\mathrm{C}(l)$ is the correlation dimension.

3.4.3. Approximate Entropy

The approximate entropy quantifies the degree of regularity in the vibration signal. The smaller the value of the approximate entropy, the more the regularity of the behavior of the signal is. An application example of approximate entropy in vibration signal was proposed by Yan et al. [63] for high speed rolling element bearing. Moreover, Yan et al. [63] mentioned that the deterioration of bearing condition corresponds to the increase of number of frequency components. In addition, when the bearing starts to deteriorate the regularity will decrease and the corresponding approximate entropy value will increase. Similar to fractal dimension and correlation dimension, approximate entropy also uses phase-space matrix, $X$ in (27) as an input. The initial step analysis of the approximate entropy algorithm is to measure the distance between two vectors $X(i)$ and $X(j)$ which can be defined as the maximum difference in their respective corresponding elements [63]:

$$d(X(i),X(j))=\underset{k=1,2,\dots ,m}{\max }(|x(i+k-1)-x(j+k-1)|)$$

(30)

where $i=1,2,\dots ,N-m+1$, $j=1,2,\dots ,N-m+1$ and $N$ is the number of data points in the vibration signal. A calculation that describes the similarity between the vector $X(i)$ and all other vectors $X(j)$, where $j\ne i$ can be constructed as

$$C_i^m(r)=\frac{1}{N-(m-1)}{\displaystyle {\sum }_{j\ne 1}\Theta \left\{r-d\left[X(i),X(j)\right]\right\}}$$

(31)

the Heaviside step function, $\Theta (x)$ is similar to the symbol in correlation dimension where $\Theta (x)=0$ if $X\le 0$ and $\Theta (x)=1$ if $X>0$.

The symbol $r$ in (31) denotes a predetermined tolerance value, defined as

$$r=k.std(Y)$$

(32)

where $std(Y)$ refers to the standard deviation of vibration signal, $Y$ and $k$ is a constant $(k>0)$. By defining

$${\phi }^m(r)=\frac{1}{N-m+1}{\displaystyle {\sum }_i\ln \left[C_i^m(r)\right]},i=1,2,\dots ,N-m+1$$

(33)

the approximate entropy value of time series can be computed as

$$\mathrm{ApEn}(m,r)=\underset{N\to \infty }{\lim }[{\phi }^m(r)-{\phi }^{m+1}(r)]$$

(34)

3.4.4. Largest Lyapunov Exponent

The largest Lyapunov exponent (LLE) algorithm is an established method and has been used in some areas such as biomedical signal processing analysis especially for electroencephalography (EEG) signal [19]. The LLE algorithm calculates the exponential divergence (either positive or negative exponential) of two initial neighboring trajectories in a phase-space matrix. In other words, the LLE algorithm quantifies the degree of chaos of vibration signal in certain time. The degree of chaos corresponds to any local instability vibration signal due to the dynamic contact between rolling elements and defect spots during the data acquisition. The detailed discussion and the application of LLE in slew bearing vibration data is presented in [64].

The features extraction result for correlation dimension, fractal dimension and approximate entropy from slew bearing vibration data is presented in Figure 18. It can be seen that the approximate entropy shows better result in presenting the degradation condition of the slew bearing than the correlation dimension and fractal dimension. A fluctuation in the approximate entropy in the last measurement (after the 90th day) indicates that the slew bearing condition has changed.

3.5. Category 5: Complexity Measurement

3.5.1. Kolmogorov-Smirnov Test

The Kolmogorov-Smirnov (KS) test is a nonparametric test that can be used to compare or to measure the similarity of two cumulative distribution functions (CDFs), $\mathrm{T}(x)$ and $\mathrm{R}(x)$ [65]. $\mathrm{T}(x)$ is a target CDF and $\mathrm{R}(x)$ is a reference CDF. Because the signature of bearing condition can be identified by its CDF, therefore the KS test can be applied in bearing condition monitoring to distinguish bearing health signal from faulty signal. In order to distinguish the two CDFs, $\mathrm{T}(x)$ and $\mathrm{R}(x)$, a statistical distance $\mathrm{D}$ is calculated. The distance $\mathrm{D}$ can be defined as the maximum absolute distance between $\mathrm{T}(x)$ and $\mathrm{R}(x)$. This is defined as follows

$$\mathrm{D}=\underset{-\infty <x<\infty }{\max }\left|\mathrm{T}(x)-\mathrm{R}(x)\right|$$

(35)

The KS feature of slew bearing vibration data is presented in Figure 19. The ‘0’ represents normal condition and ‘1’ represent abnormal condition. It can be seen that at the beginning of the measurement, the condition of bearing was still normal. Then it changed to abnormal condition when bearing had run for a couple of days. This result needs further investigation as the abnormal detection happened too early.

3.5.2. Sample Entropy

The sample entropy has been proposed by Richman and Moorman [66] to improve the approximate entropy. Chen et al. [67] presents an application of sample entropy for features extraction of gearbox vibration signals. However, the application of the sample entropy for bearing vibration signal is still limited [68]. The sample entropy feature for slew bearing vibration data is presented in Figure 20. It can be observed from Figure 20 that the sample entropy feature is not effective for slew bearing damage detection.

3.6. Category 6: Other Features

3.6.1. Singular Value Decomposition (SVD)

The singular value decomposition (SVD) is usually applied to quantify the periodicity of the time series data [69]. A comparison study [70] has been shown that SVD performs the Fourier decomposition in terms of information content and robustness. Formula of SVD can be found in [71].

3.6.2. Piecewise Aggregate Approximation (PAA) and Adaptive Piecewise Constant Approximation (APCA)

In online bearing condition monitoring cases, the changes of bearing condition can be effectively identified by measuring the similarity between two vibration signals (i.e., normal or reference and monitored signal) using Euclidean distance. However, the size of the measured data is a problem in Euclidean distance method. The similarity search methods are techniques that perform dimensionality data reduction methods such as piecewise aggregate approximation (PAA) [72,73] and adaptive piecewise constant approximation (APCA) [72]. The APCA [74], is another approach of PAA that allows arbitrary length segments. Either PAA or APCA have particular advantages; for example, PAA has twice as many approximating segments, and APCA is able to separate a single segment in an area of low activity and many segments in areas of high activity [74]. The PAA has been applied in previous study [39] for data pre-processing stage of circular domain features extraction. The detailed discussion and the application of PAA in slew bearing vibration data is presented in [39].

4. Conclusions

Features extraction methods in wide range application such as mechanical engineering (i.e., for bearing vibration signals), biomedical engineering area (i.e., for EEG and ECG signals) and finance area (i.e., for time series signals) have been presented. According to the certain characteristic of existing feature extraction methods, the methods in this paper were classified into six categories: (1) time-domain features extraction; (2) frequency-domain features extraction; (3) time frequency representation; (4) phase-space dissimilarity measure; (5) complexity measure; and (6) other features. Some of features extraction methods in each category have been empirically tested using actual normal to failure slew bearing vibration signal. It was shown that some features do not show bearing degradation trend clearly and the others are shown to be potential slew bearing condition parameters. The potential features are: impulse factor, margin factor, mathematical morphology operators, wavelet decomposition-kurtosis, approximate entropy and largest Lyapunov exponent.

Since slew bearing operating at very low speed with highly applied load, the vibration signals exhibit non-linear, non-stationary and chaotic behaviour. The methods such as impulse factor and margin factor measured the statistical properties of vibration signal and therefore could revealed the information related to the impulse level. Other potential methods based on the phase-space dissimilarity measurement such as approximate entropy and LLE algorithm can be used to extract pertinent bearing signal corresponding to the bearing damage progression. This is because the methods analyzed the vibration signal in certain time-frame to extract the useful information from the non-linear and non-stationary behaviour.