Review of Multiaxial Testing for Very High Cycle Fatigue: From ‘Conventional’ to Ultrasonic Machines
Abstract
:1. Introduction
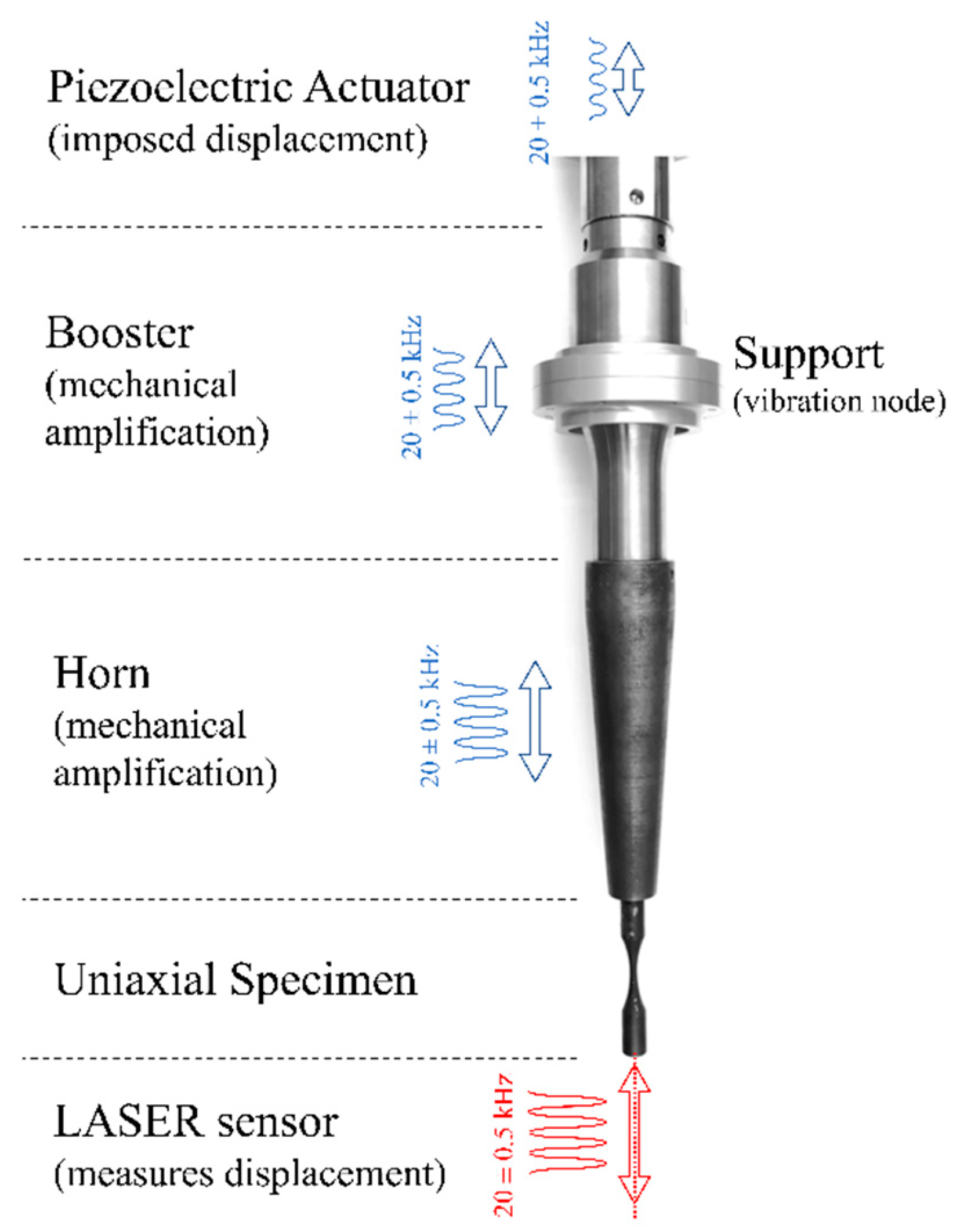
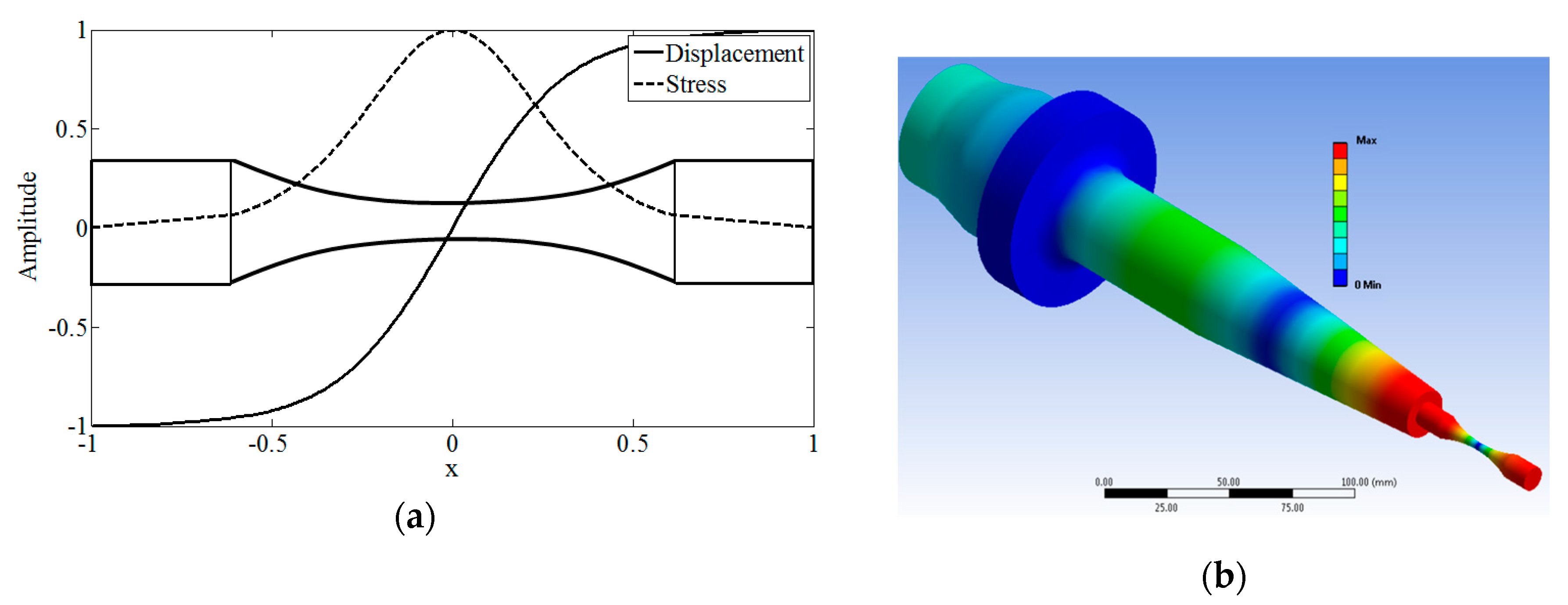
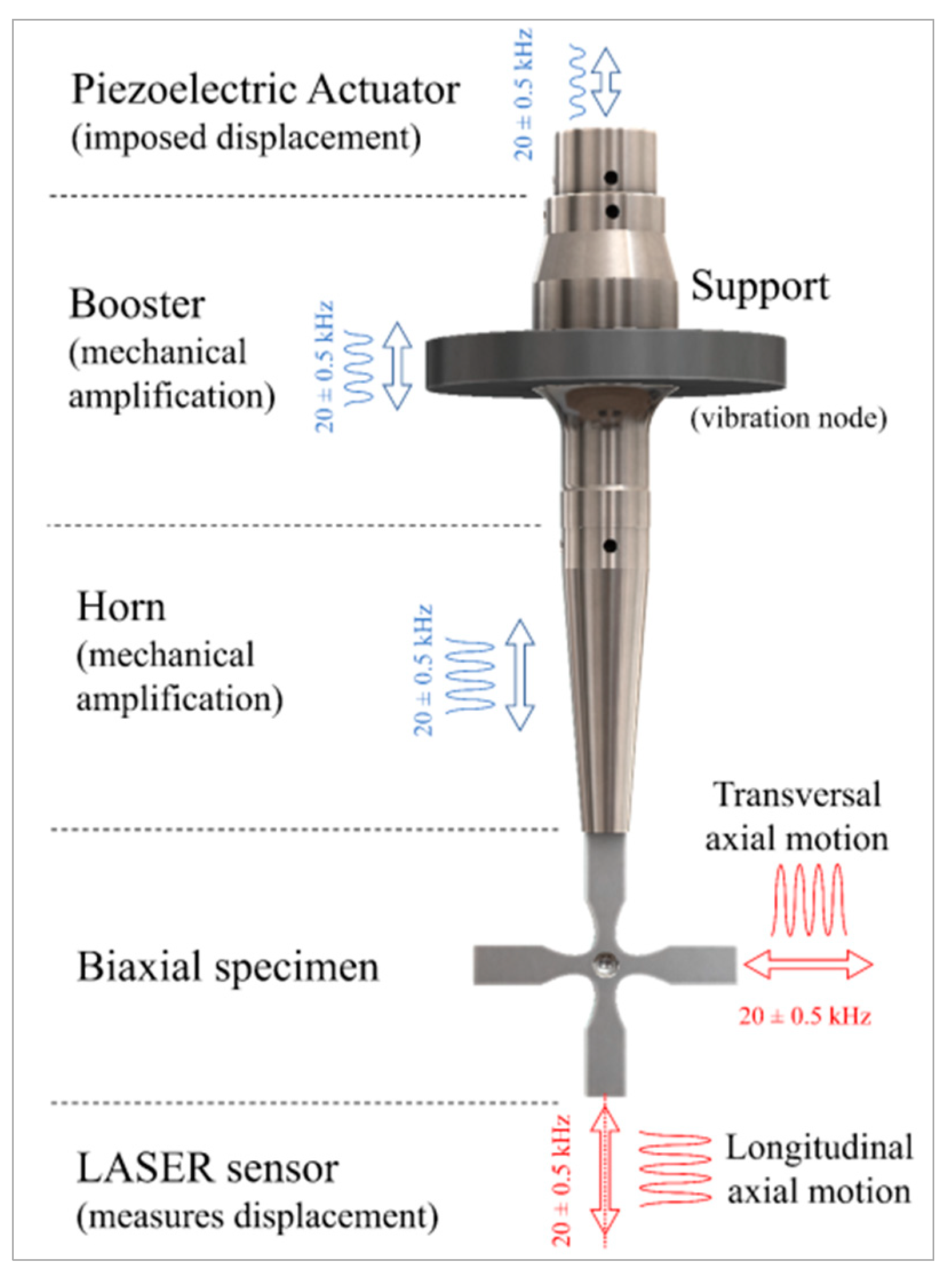
2. Ultrasonic Fatigue Testing at Very High Number of Cycles
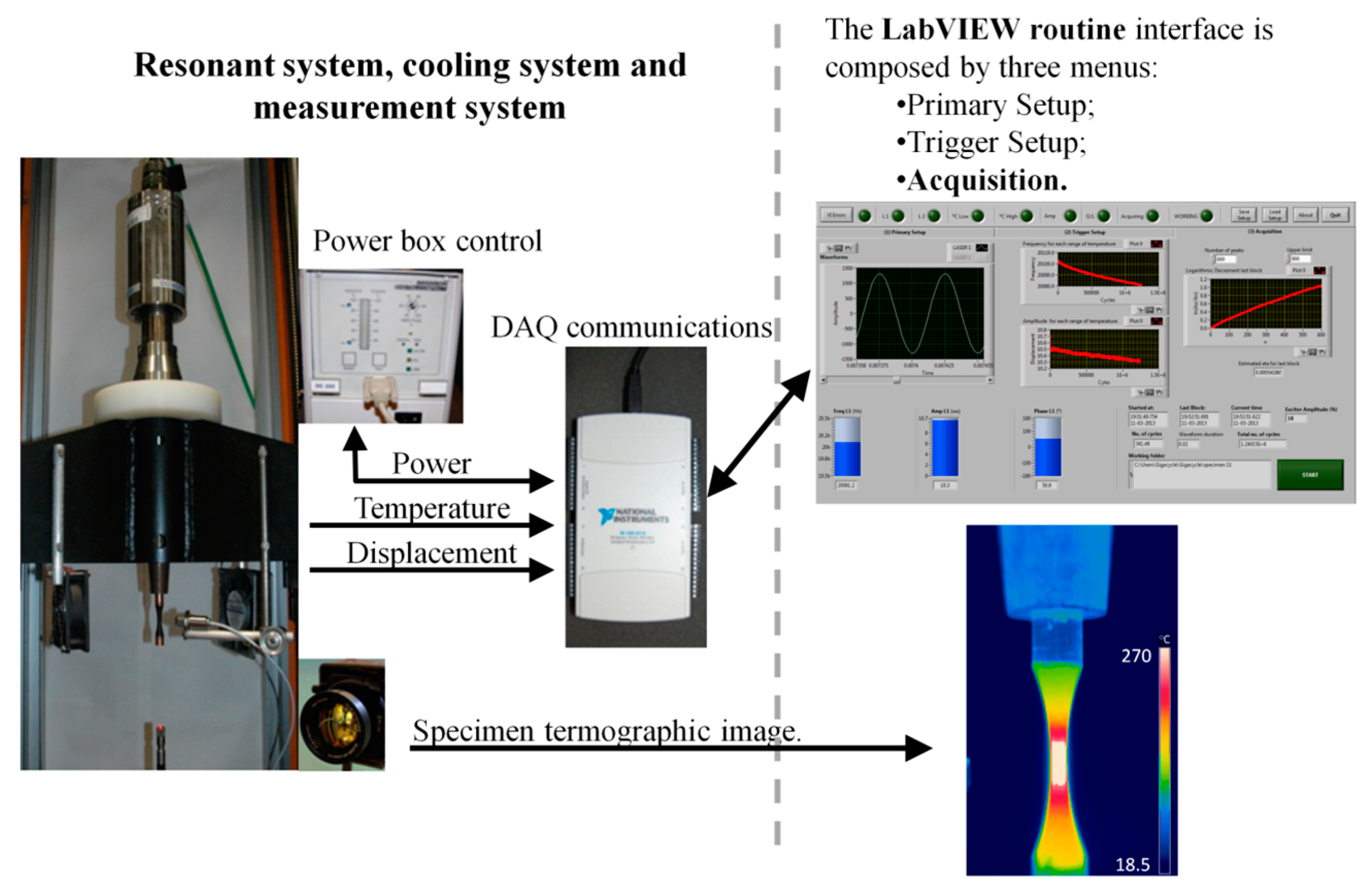
- A measurement or data acquisition system which can be made of various instrumentation devices from strain gauges, laser doppler vibrometers, thermocouples, infrared cameras, and other data-gathering transducers. Here, different configurations can be found due to resources’ limitations (usually budget related) or the objectives of the experiments being conducted;
- A control or safeguarding system which monitors and maintains suitable conditions for the experiment through the implementation of a feedback control loop system, for example. This system is usually responsible for avoiding the overheating of the test specimen, which has is one of the greatest problems in UFT.
3. Multiaxial Fatigue Testing
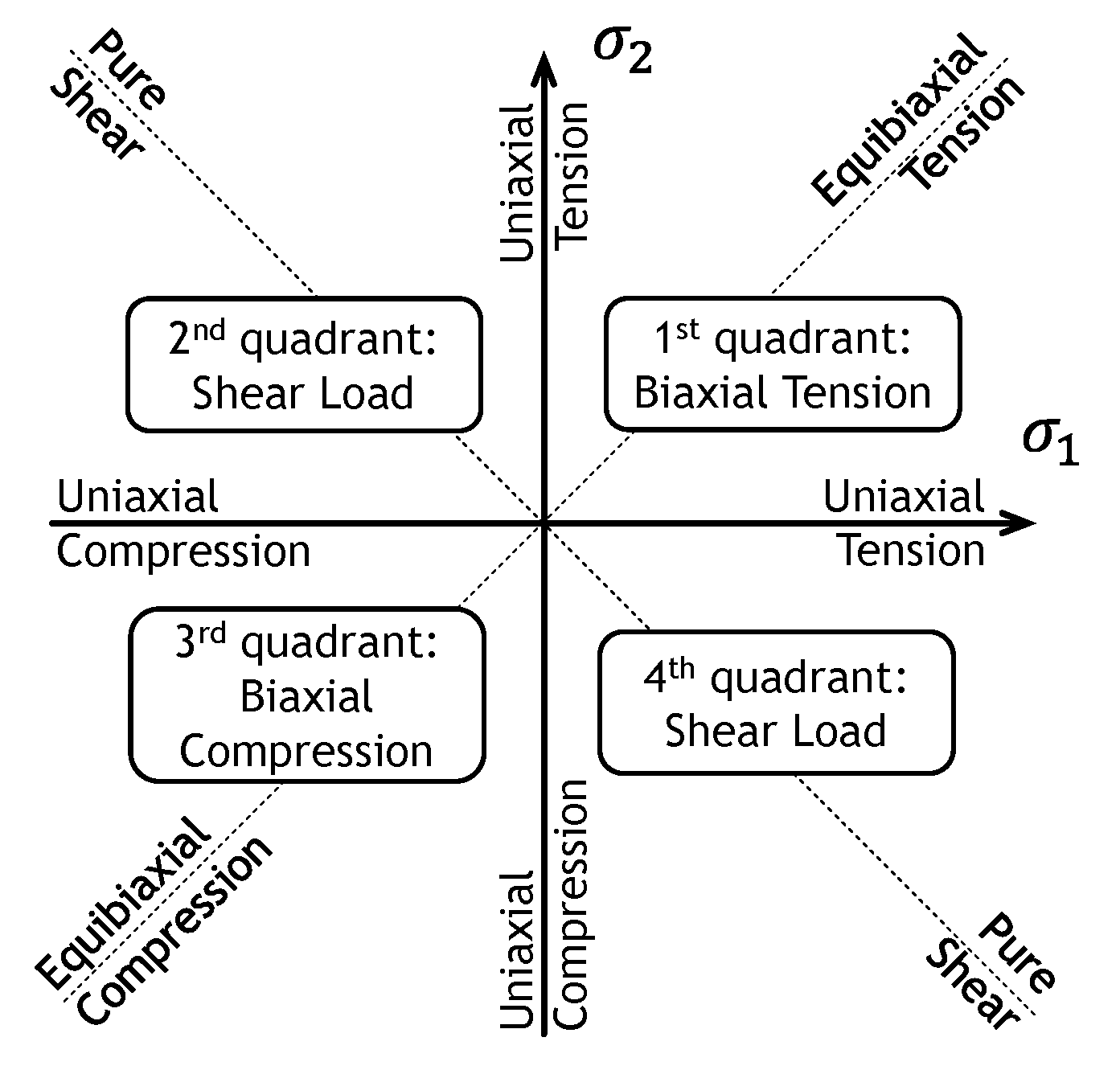
3.1. Multiaxial Stress States
3.2. General Testing Procedures and Machines
- A machine suitable for applying multiaxial loads and with reliable instrumentation capable of handling complex experimental conditions (temperature, vibrations, etc.);
- A specimen capable of producing the desired level of biaxiality required across the area of interest which will be the origin of the fatigue failure. This aspect is far from straightforward mainly due to the various spots of stress concentrations encountered with biaxial specimens. Besides, the gauge area is usually fairly limited which can make achieving a good homogenous biaxial stress state a rather thorny task;
- A test configuration or measuring system which allows for the recording of the necessary data (displacement, stresses, temperature, etc.). Therefore, there needs to be a free or easy access to the surface of the specimen for acquiring data.
3.3. Specimens for ‘Conventional’ Multiaxial Fatigue Testing
3.3.1. Cylindrical Solid and Tubular Biaxial Fatigue Specimens
3.3.2. Flat Square Biaxial Specimen or Flat Coupons
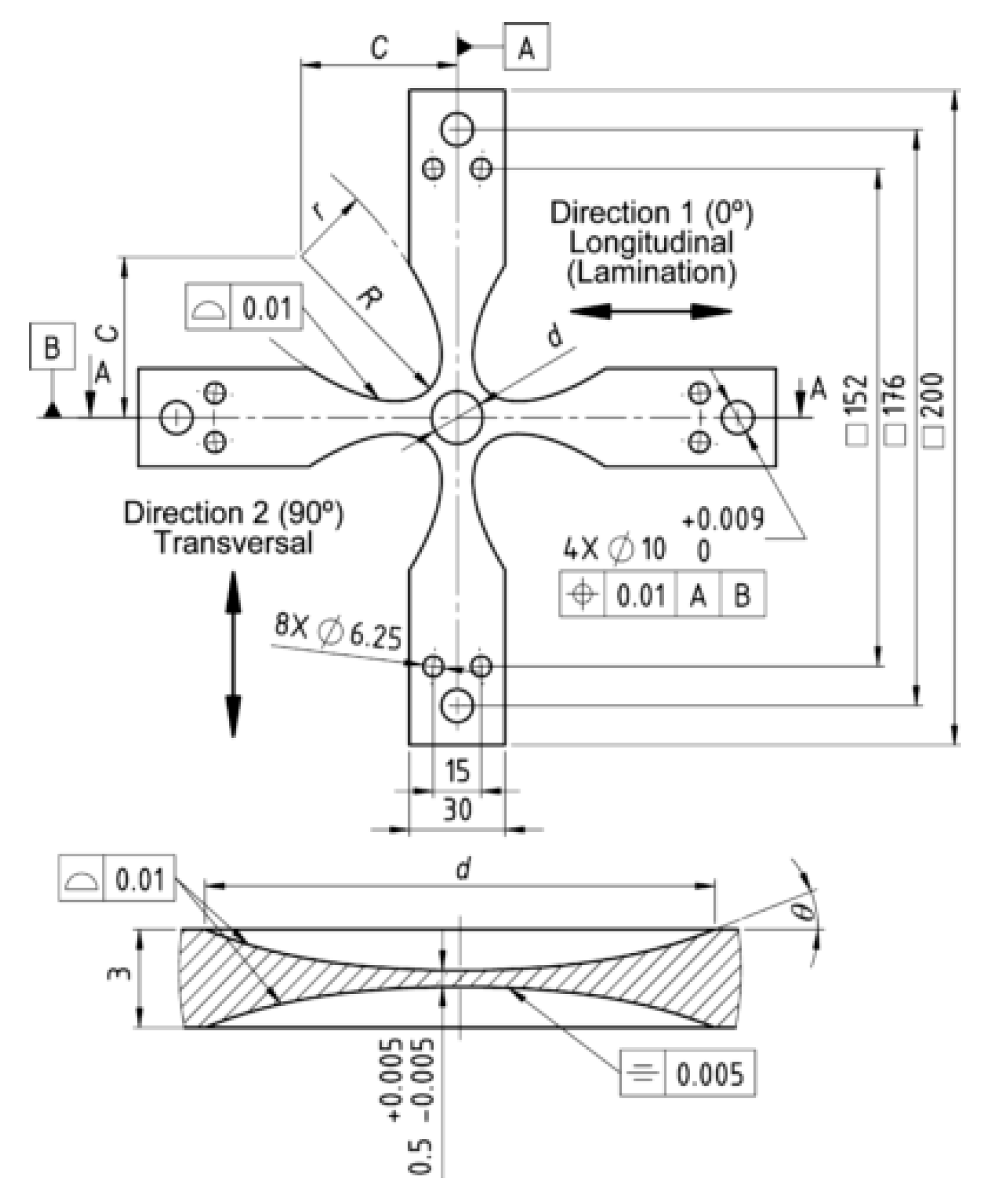
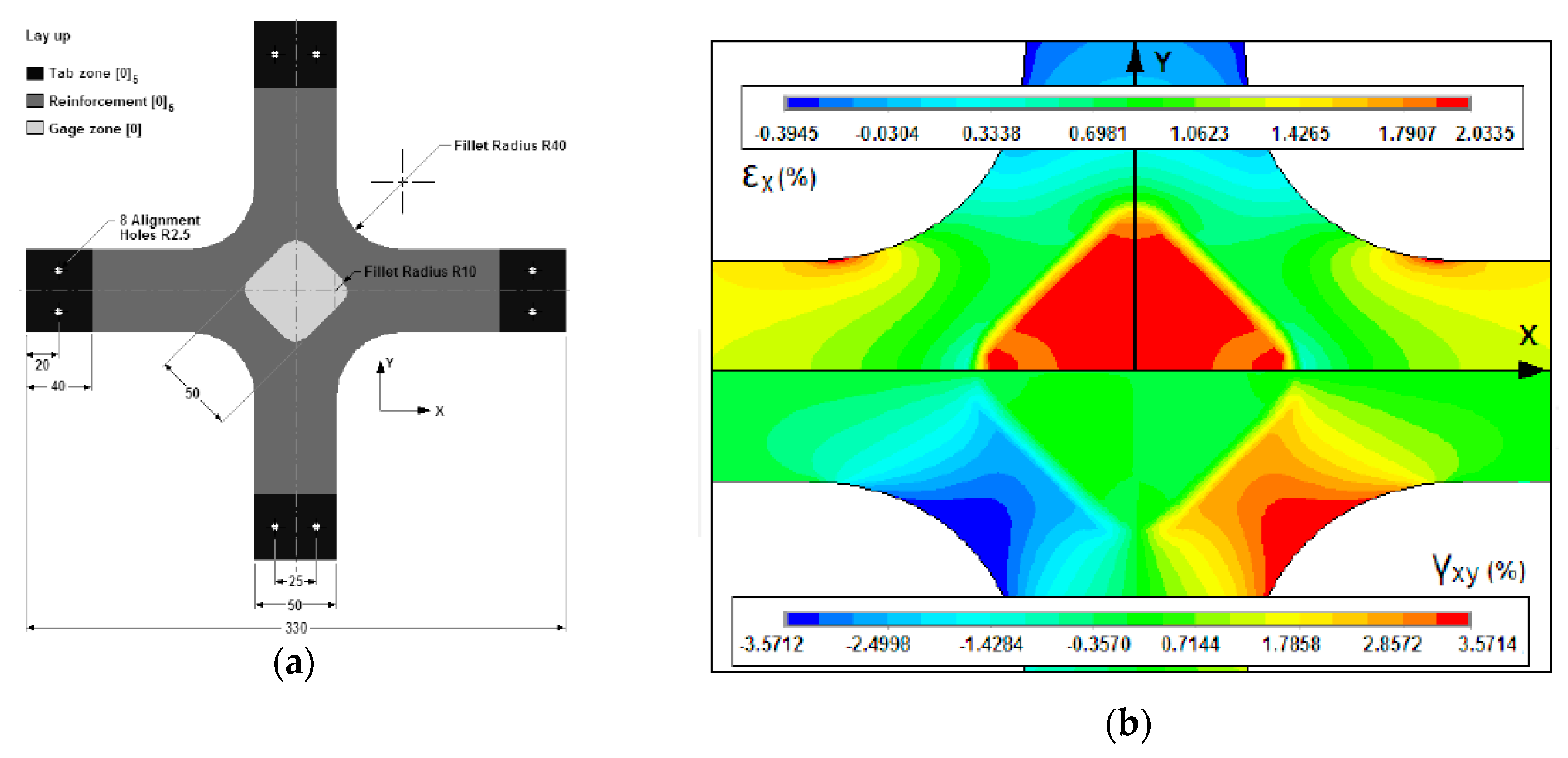
3.3.3. Cruciform Biaxial Specimens
- To maximise the stress level recorded in the central part of the specimen;
- To reduce the stress concentration in the arms of the specimen.
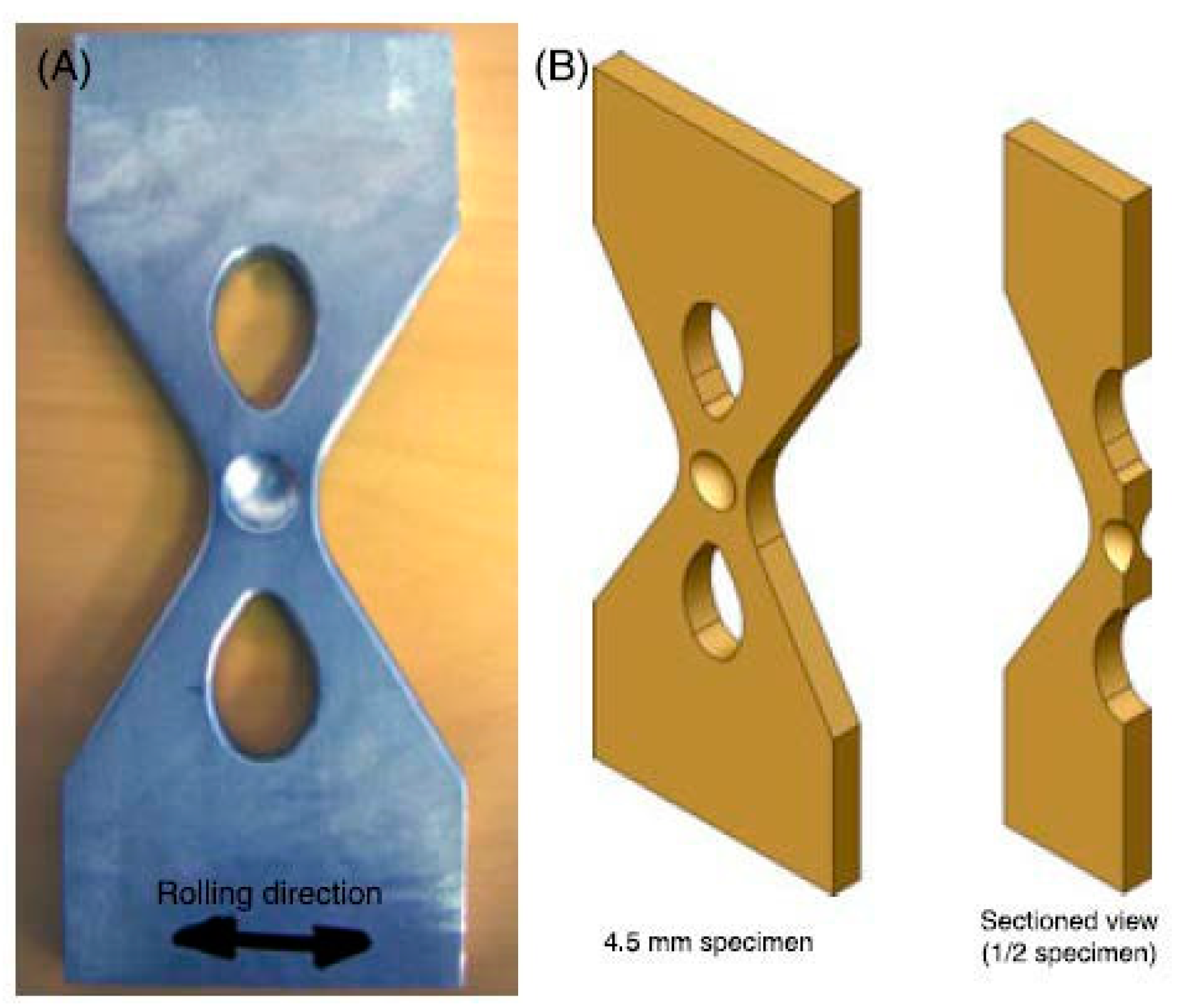
3.3.4. Biaxial Specimens for Uniaxial Machines
4. Multiaxial Fatigue Testing at Very High Number of Cycles
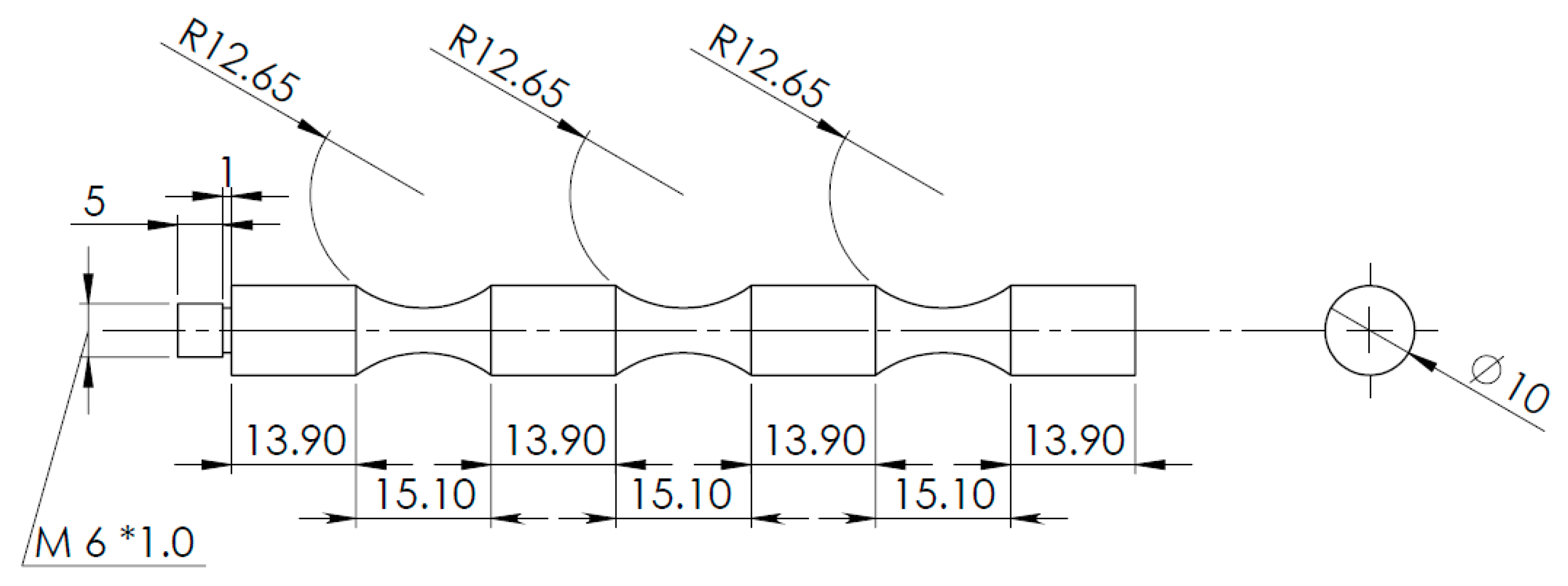
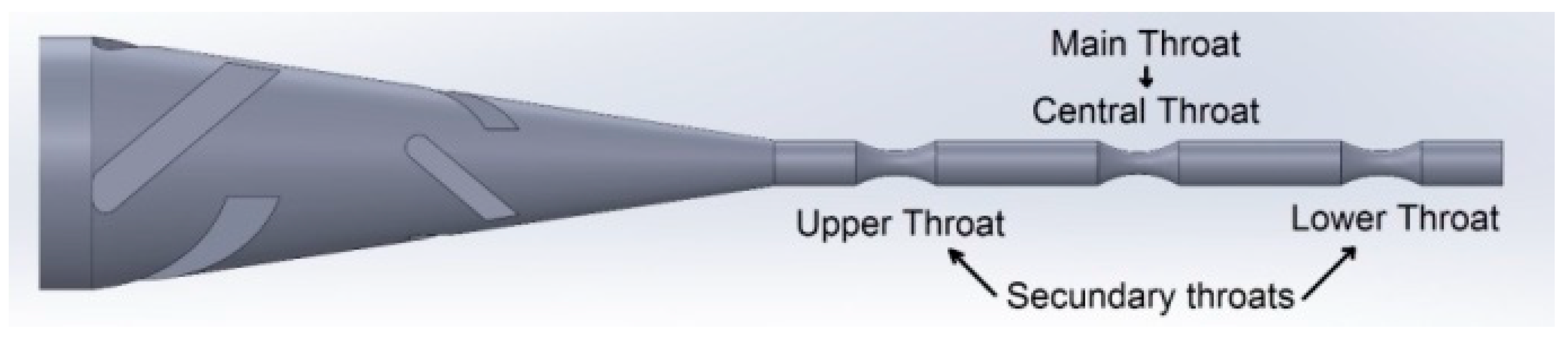
4.1. Tension/Torsion Ultrasonic Fatigue Testing
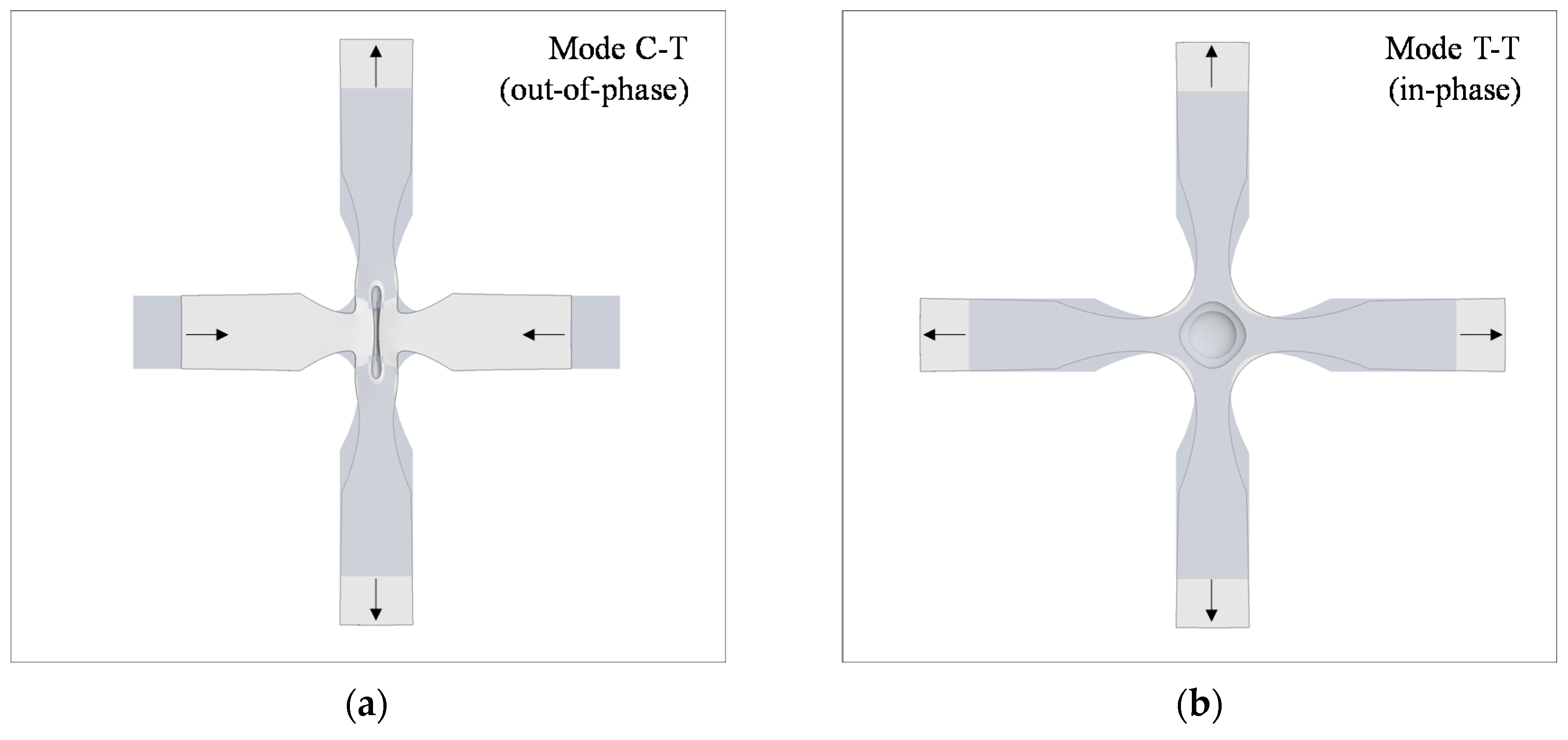
4.2. Tension/Tension Ultrasonic Fatigue Testing (Cruciform Specimens)
4.2.1. Tuning with a Global Dimensional Scale Factor
4.2.2. Tuning by Changing the Specimen’s Arms’ Dimensions
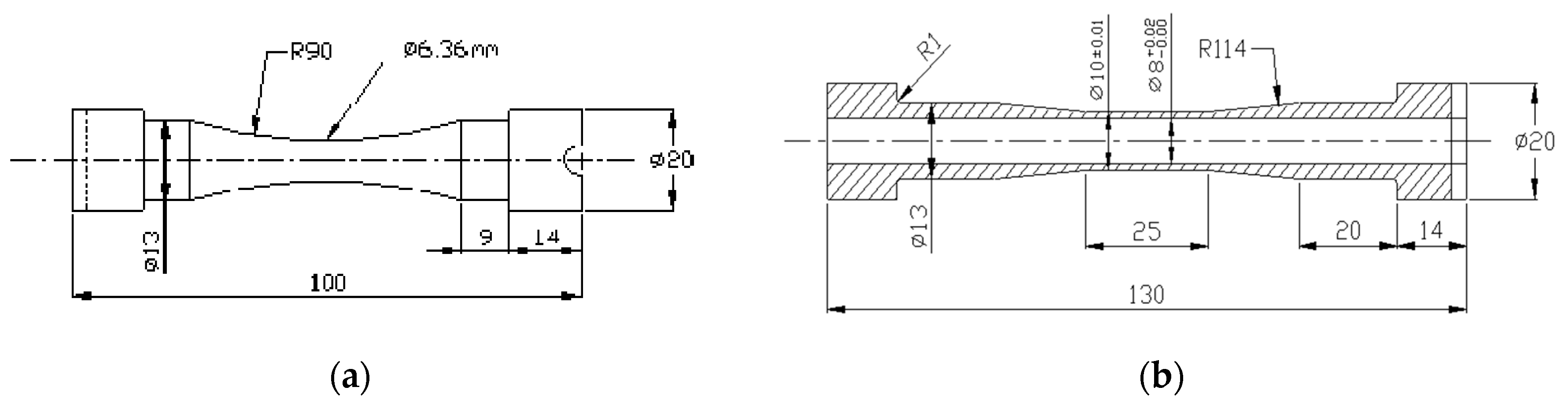
4.3. Tension/Tension Ultrasonic Fatigue Testing (Teardrop Specimens)
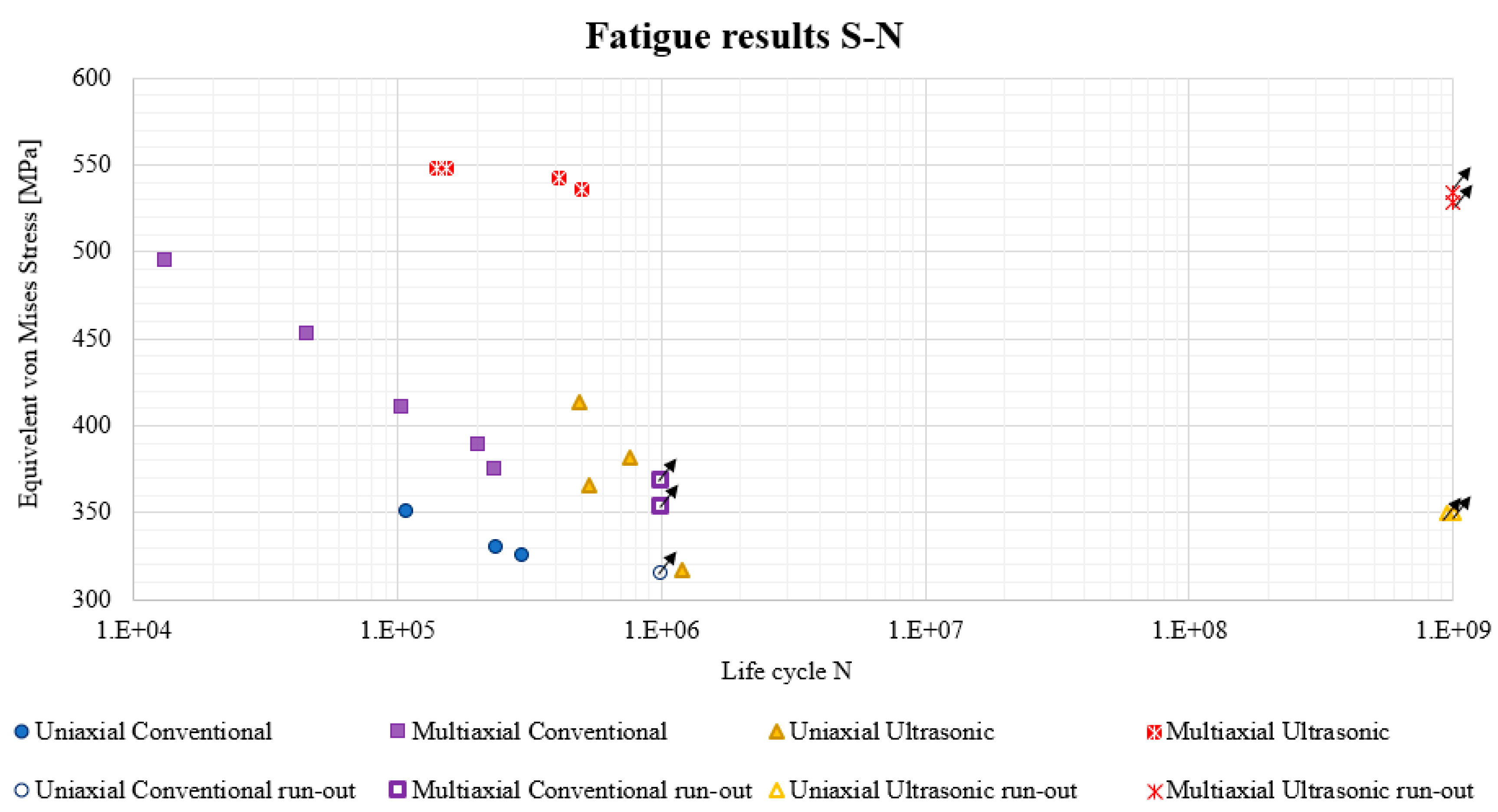
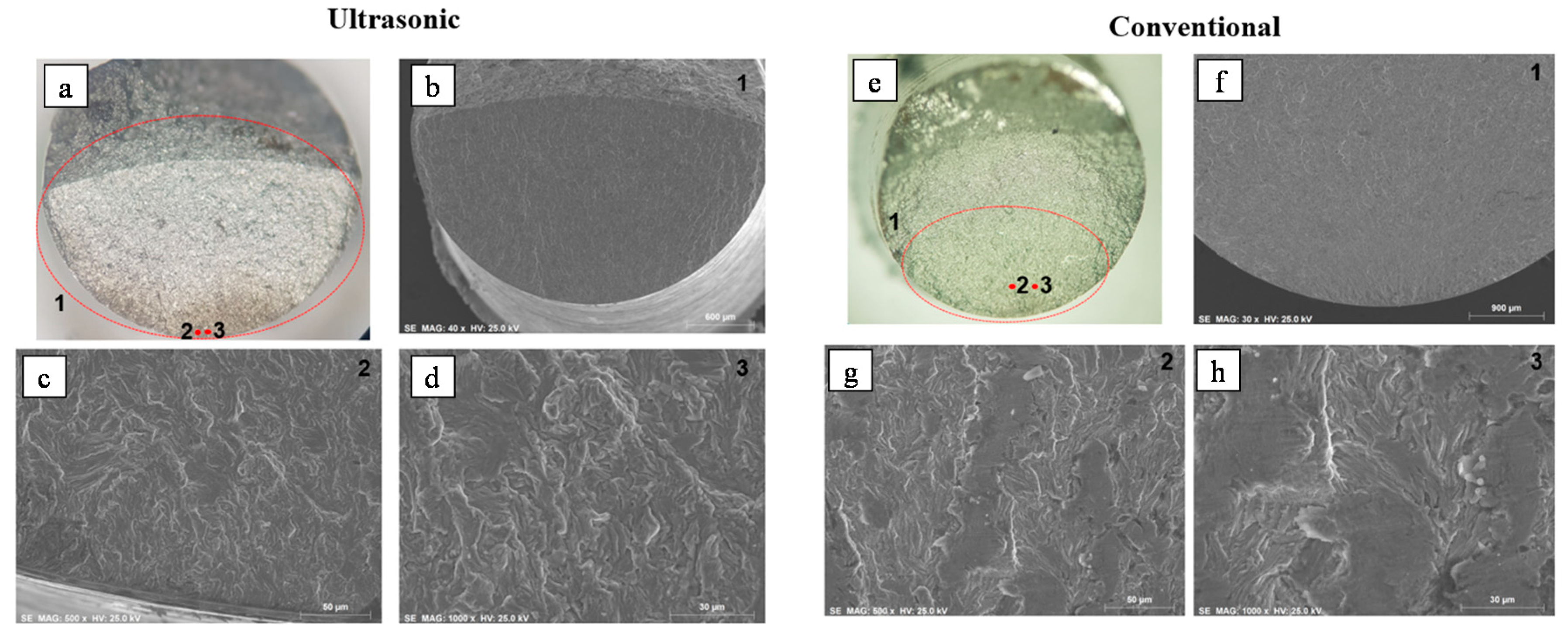
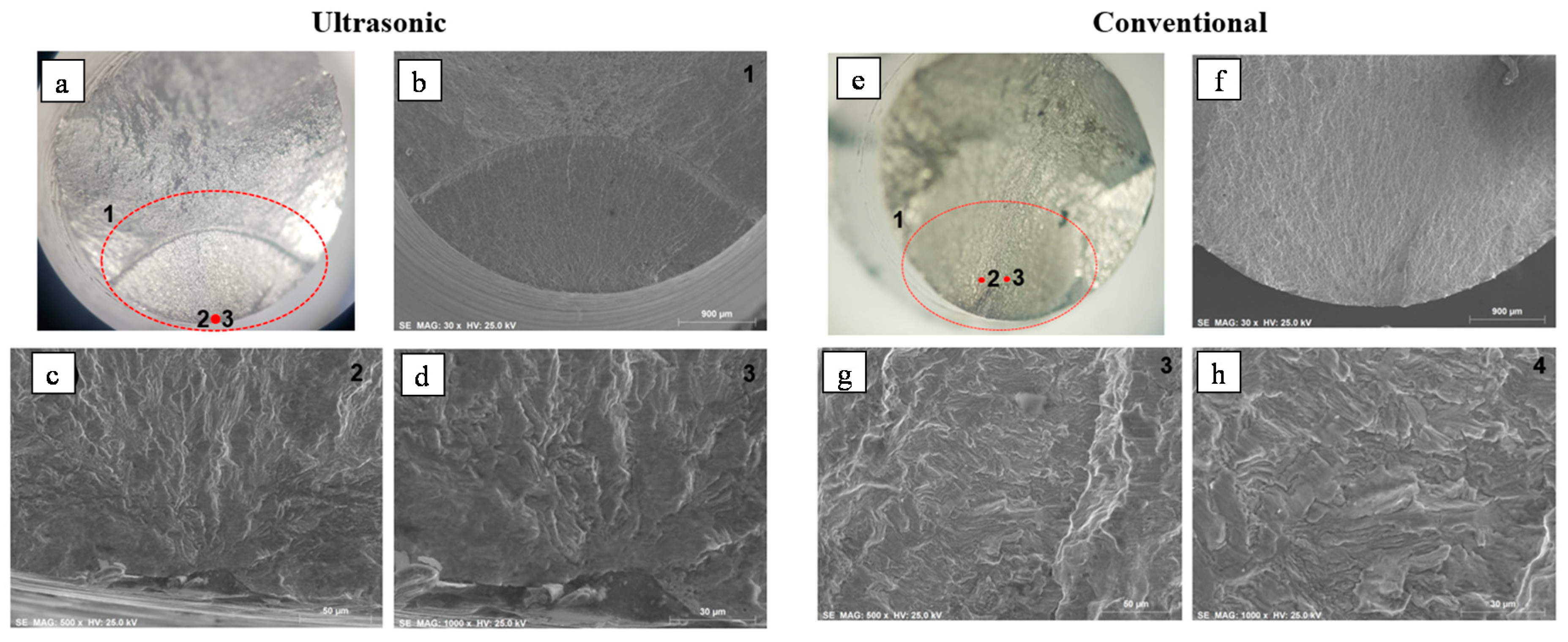
5. Performance of Biaxial Specimens Based on Experimental Evidence
5.1. Tension/Torsion Ultrasonic Fatigue Testing
5.2. Tension/Tension Ultrasonic Fatigue Testing (Cruciform Specimens)
6. Conclusions
Author Contributions
Funding and Acknowledgments
Conflicts of Interest
References
- Suryanarayana, C. Experimental Techniques in Materials and Mechanics; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Freitas, M. Multiaxial fatigue: From materials testing to life prediction. Theor. Appl. Fract. Mech. 2017, 92, 360–372. [Google Scholar] [CrossRef]
- Anes, V.; Montalvao, D.; Ribeiro, A.; Freitas, M.; Fonte, M. Design and instrumentation of an ultrasonic fatigue testing machine. In Proceedings of the VHCF5—5th International Conference on Very High Cycle Fatigue, Berlin, Germany, 28–30 June 2011. [Google Scholar]
- Davies, P. Long-Haul Spaceship Travel ‘Could Soon Become Mainstream’. Available online: https://www.travelweekly.co.uk/articles/327137/long-haul-spaceship-travel-could-soon-become-mainstream (accessed on 12 May 2020).
- Freitas, M.; Anes, V.; Montalvao, D.; Reis, L.; Ribeiro, A. Design and assembly of an ultrasonic fatigue testing machine. In Proceedings of the XXVIII GEF—Encuentro del Grupo Español de Fractura (Anales de Mecânica de la Fractura), Gijón, Spain, 6–8 April 2011. [Google Scholar]
- Kok, Y.; Tan, X.P.; Wang, P.; Nai, M.L.; Loh, N.H.; Liu, E.; Tor, S.B. Anisotropy and heterogeneity of microstructure and mechanical properties in metal additive manufacturing: A critical review. Mater. Des. 2018, 139, 565–586. [Google Scholar] [CrossRef]
- Lage, Y.; Cachão, H.; Reis, L.; Fonte, M.; de Freitas, M.; Ribeiro, A. A damage parameter for HCF and VHCF based on hysteretic damping. Int. J. Fatigue 2014, 62, 2–9. [Google Scholar] [CrossRef]
- Bathias, C. There is no infinite fatigue life in metallic materials. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 559–566. [Google Scholar] [CrossRef]
- Pyttel, B.; Schwerdt, D.; Berger, C. Very high cycle fatigue–Is there a fatigue limit? Int. J. Fatigue 2011, 33, 49–58. [Google Scholar] [CrossRef]
- Lage, Y.; Ribeiro, A.; Montalvão, D.; Reis, L.; Freitas, M. Automation in strain and temperature control on VHCF with an ultrasonic testing facility. J. ASTM Int. 2014, 1571, 80–100. [Google Scholar]
- Bathias, C. Piezoelectric fatigue testing machines and devices. Int. J. Fatigue 2006, 28, 1438–1445. [Google Scholar] [CrossRef]
- Freitas, M.; Reis, L.; Li, B.; Guelho, I.; Antunes, V.; Maia, J.; Cláudio, R. In-Plane Biaxial Fatigue Testing Machine Powered by Linear Iron-Core Motors. J. ASTM Int. 2014, 1571, 63–79. [Google Scholar]
- Montalvão, D.; Shengwen, Q.; Freitas, M. A study on the influence of Ni–Ti M-Wire in the flexural fatigue life of endodontic rotary files by using Finite Element Analysis. Mater. Sci. Eng. C 2014, 40, 172–179. [Google Scholar] [CrossRef] [Green Version]
- Reis, L.; Li, B.; Freitas, M. A multiaxial fatigue approach to Rolling Contact Fatigue in railways. Int. J. Fatigue 2014, 67, 191–202. [Google Scholar] [CrossRef]
- Costa, P.; Vieira, M.; Reis, L.; Ribeiro, A.; de Freitas, M. New specimen and horn design for combined tension and torsion ultrasonic fatigue testing in the very high cycle fatigue regime. Int. J. Fatigue 2017, 103, 248–257. [Google Scholar] [CrossRef]
- Baptista, R.; Claudio, R.A.; Reis, L.; Guelho, I.; Freitas, M.; Madeira, J.F.A. Design optimization of cruciform specimens for biaxial fatigue loading. Frat. Integrità Strutt. 2014, 8, 118–126. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.Y.; Liu, H.Q.; Wang, H.M.; Wagner, D.; Khan, M.K.; Wang, Q.Y. Effect of stress ratio on VHCF behavior for a compressor blade titanium alloy. Int. J. Fatigue 2016, 93, 232–237. [Google Scholar] [CrossRef]
- Kovacs, S.; Beck, T.; Singheiser, L. Influence of mean stresses on fatigue life and damage of a turbine blade steel in the VHCF-regime. Int. J. Fatigue 2013, 49, 90–99. [Google Scholar] [CrossRef]
- Sander, M.; Stäcker, C.; Müller, T. Experimental and numerical investigations on crack initiation and crack growth under constant and variable amplitude loadings in the VHCF regime. In Fatigue of Materials at Very High Numbers of Loading Cycles: Experimental Techniques, Mechanisms, Modeling and Fatigue Life Assessment; Christ, H.-J., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2018; pp. 273–293. [Google Scholar]
- Nikitin, A.; Bathias, C.; Palin-Luc, T. A new piezoelectric fatigue testing machine in pure torsion for ultrasonic gigacycle fatigue tests: Application to forged and extruded titanium alloys. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 1294–1304. [Google Scholar] [CrossRef] [Green Version]
- Mayer, H.; Schuller, R.; Karr, U.; Irrasch, D.; Fitzka, M.; Hahn, M.; Bacher-Höchst, M. Cyclic torsion very high cycle fatigue of VDSiCr spring steel at different load ratios. Int. J. Fatigue 2015, 70, 322–327. [Google Scholar] [CrossRef]
- Marines-Garcia, I.; Doucet, J.-P.; Bathias, C. Development of a new device to perform torsional ultrasonic fatigue testing. Int. J. Fatigue 2007, 29, 2094–2101. [Google Scholar] [CrossRef]
- Vieira, M.; de Freitas, M.; Reis, L.; Ribeiro, A.M.R. Development of a Very High Cycle Fatigue (VHCF) multiaxial testing device. Frat. Integrità Strutt. 2016, 10, 131–137. [Google Scholar] [CrossRef] [Green Version]
- Costa, P.R.; Montalvão, D.; Freitas, M.; Baxter, R.; Reis, L. Cruciform specimens’ experimental analysis in ultrasonic fatigue testing. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 2496–2508. [Google Scholar] [CrossRef]
- Montalvão, D.; Wren, A. Redesigning axial-axial (biaxial) cruciform specimens for very high cycle fatigue ultrasonic testing machines. Heliyon 2017, 3, e00466. [Google Scholar] [CrossRef]
- Montalvão, D.; Blaskovics, A.; Costa, P.; Reis, L.; Freitas, M. Numerical analysis of VHCF cruciform test specimens with non-unitary biaxiality ratios. Int. J. Comput. Methods Exp. Meas. 2019, 7, 327–339. [Google Scholar] [CrossRef] [Green Version]
- Brugger, C.; Palin-Luc, T.; Osmond, P.; Blanc, M. Gigacycle fatigue behavior of a cast aluminum alloy under biaxial bending: Experiments with a new piezoelectric fatigue testing device. Procedia Struct. Integr. 2016, 2, 1173–1180. [Google Scholar] [CrossRef] [Green Version]
- Kazymyrovych, V. Very High Cycle Fatigue of Engineering Materials: A Literature Review; Karlstad University: Karlstad, Sweden, 2009. [Google Scholar]
- Kazymyrovych, V. Very High Cycle Fatigue of Tool Steels. Ph.D. Thesis, Karlstad University, Karlstad, Sweden, 2010. [Google Scholar]
- Bathias, C.; Paris, P.C. Gigacycle Fatigue in Mechanical Practice; CRC Press: New York, NY, USA, 2004. [Google Scholar]
- Stanzl-Tschegg, S.E.; Schönbauer, B. Mechanisms of strain localization, crack initiation and fracture of polycrystalline copper in the VHCF regime. Int. J. Fatigue 2010, 32, 886–893. [Google Scholar] [CrossRef] [Green Version]
- Green, C.H. Stress amplitude analysis in a generalized ultrasonic fatigue dumbbell specimen. J. Phys. D Appl. Phys. 1991, 24, 469–477. [Google Scholar] [CrossRef]
- Cho, I.-S.; Shin, C.-S.; Kim, J.-Y.; Jeon, Y.-H. Accelerated ultrasonic fatigue testing applications and research trends. Trans. Korean Soc. Mech. Eng. A 2012, 36, 707–712. [Google Scholar] [CrossRef] [Green Version]
- Marines, I.; Dominguez, G.; Baudry, G.; Vittori, J.F.; Rathery, S.; Doucet, J.P.; Bathias, C. Ultrasonic fatigue tests on bearing steel AISI-SAE 52100 at frequency of 20 and 30 kHz. Int. J. Fatigue 2003, 25, 1037–1046. [Google Scholar] [CrossRef]
- Ribeiro, A.; Montalvao, D.; Azinheira, J.; Freitas, M.; Reis, L.; Fontul, M. Hysteretic Damping as an Energy Parameter in Gigacycle Fatigue. In Proceedings of the 5th International Conference on Very High Cycle Fatigue, Berlin, Germany, 28–30 June 2011; DVM: Berlin, Germany, 2011. [Google Scholar]
- Delmotte, E.; Micone, N.; De Waele, W. Testing methodologies for corrosion fatigue. Int. J. Sustain. Constr. Des. 2015, 6, 10. [Google Scholar] [CrossRef] [Green Version]
- Cavalieri, F.; Bathias, C.; Ranc, N.; Cardona, A.; Risso, J. Ultrasonic fatigue analysis on an austenitic steel at high temperature. Mecánica Comput. 2008, 27, 1205–1224. [Google Scholar]
- Shyam, A.; Torbet, C.J.; Jha, S.K.; Larsen, J.M.; Caton, M.J.; Szczepanski, C.J.; Pollock, T.M.; Jones, J.W. Development of ultrasonic fatigue for rapid, high temperature fatigue studies in turbine engine materials. Superalloys 2004 2004, 259–268. [Google Scholar] [CrossRef]
- Müller, T.; Sander, M. On the use of ultrasonic fatigue testing technique – Variable amplitude loadings and crack growth monitoring. Ultrasonics 2013, 53, 1417–1424. [Google Scholar] [CrossRef]
- Atkinson, R.; Norris, G.; Winkworth, W. Behaviour of Skin Fatigue Cracks at the Corners of Windows in a Comet I Fuselage; HM Stationery Office: London, UK, 1960.
- Cohen, B.; Farren, W.; Duncan, W.; Wheeler, A. Report of the Court of Inquiry into the Accidents to Comet G-ALYP on 10 January 1954 and Comet G-ALYY on 8 April 1954; Her Majesty Station of Office: London, UK, 1955.
- Lage, Y.; Freitas, M.; Montalvao, D.; Ribeiro, A.; Reis, L. Ultrasonic fatigue analysis on steel specimen with temperature control: Evaluation of variable temperature effect. In Proceedings of the the XIII Portuguese Conference on Fracture, Coimbra, Portugal, 2–3 February 2012. [Google Scholar]
- Galliot, C.; Luchsinger, R.H. Uniaxial and biaxial mechanical properties of ETFE foils. Polym. Test. 2011, 30, 356–365. [Google Scholar] [CrossRef]
- Koster, M.; Wagner, G.; Eifler, D. Ultrasonic fatigue of a high strength steel. J. Phys. Conf. Ser. 2010, 240, 012044. [Google Scholar] [CrossRef]
- Tridello, A. VHCF Response of Two AISI H13 Steels: Effect of Manufacturing Process and Size-Effect. Metals 2019, 9, 133. [Google Scholar] [CrossRef] [Green Version]
- McDiarmid, D.L. A new analysis of fatigue under combined bending and twisting. Aeronaut. J. 2016, 78, 325–329. [Google Scholar]
- Kurath, P. Multiaxial fatigue criteria for spot welds. Prog. Technol. 1997, 67, 143–154. [Google Scholar]
- Manfredi, E.; Cumbo, F.; Hippoliti, R. Computer Assisted Fatigue Life Prediction of Spot Welded Frames. In Proceedings of the 10th International Conference on Machine Design and Production, Cappadocia, Turkey, 4–6 September 2002. [Google Scholar]
- Quaak, G. Biaxial Testing of Sheet Metal: An Experimental-Numerical Analysis. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2008. [Google Scholar]
- Brieu, M.; Diani, J.; Bhatnagar, N. A New Biaxial Tension Test Fixture for Uniaxial Testing Machine—A Validation for Hyperelastic Behavior of Rubber-like Materials. J. Test. Eval. 2007, 35, 364–372. [Google Scholar]
- Bold, P.E. Multiaxial Fatigue Crack Growth in Rail Steel. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 1990. [Google Scholar]
- Hua, G.; Alagok, N.; Brown, M.W.; Miller, K.J. Growth of Fatigue Cracks Under Combined Mode I and Mode II Loads. In Multiaxial Fatigue; Miller, K.J., Brown, M.W., Eds.; ASTM International: West Conshohocken, PA, USA, 1985; pp. 184–202. [Google Scholar]
- Tomlinson, R.A.; Marsavina, L. Thermoelastic investigations for fatigue life assessment. Exp. Mech. 2004, 44, 487–494. [Google Scholar] [CrossRef]
- Pereira, A.B.; Fernandes, F.A.; Morais, A.B.; Carvalhoso, P. Development of a Delamination Fatigue Testing Machine for Composite Materials. Machines 2019, 7, 27. [Google Scholar] [CrossRef] [Green Version]
- Baptista, R.; Claudio, R.A.; Reis, L.; Madeira, J.F.A.; Guelho, I.; Freitas, M. Optimization of cruciform specimens for biaxial fatigue loading with direct multi search. Theor. Appl. Fract. Mech. 2015, 80, 65–72. [Google Scholar] [CrossRef]
- Baptista, R.; Cláudio, R.A.; Reis, L.; Madeira, J.F.A.; Freitas, M. Numerical study of in-plane biaxial fatigue crack growth with different phase shift angle loadings on optimal specimen geometries. Theor. Appl. Fract. Mech. 2016, 85, 16–25. [Google Scholar] [CrossRef]
- Iadicola, M.A.; Creuziger, A.A.; Foecke, T. Advanced Biaxial Cruciform Testing at the NIST Center for Automotive Lightweighting. In Residual Stress, Thermomechanics & Infrared Imaging, Hybrid Techniques and Inverse Problems; Springer International Publishing: Cham, Switzerland, 2014; Volume 8. [Google Scholar]
- Hannon, A.; Tiernan, P. A review of planar biaxial tensile test systems for sheet metal. J. Mater. Process. Technol. 2008, 198, 1–13. [Google Scholar] [CrossRef]
- Welsh, J.S.; Adams, D.F. Development of an electromechanical triaxial test facility for composite materials. Exp. Mech. 2000, 40, 312–320. [Google Scholar] [CrossRef]
- Soden, P.D.; Hinton, M.J.; Kaddour, A.S. Chapter 2.2—Biaxial test results for strength and deformation of a range of E-glass and carbon fibre reinforced composite laminates: Failure exercise benchmark data. In Failure Criteria in Fibre-Reinforced-Polymer Composites; Hinton, M.J., Kaddour, A.S., Soden, P.D., Eds.; Elsevier: Oxford, UK, 2004; pp. 52–96. [Google Scholar]
- Escárpita, D.A.A.; Cárdenas, D.; Elizalde, H.; Ramirez, R.; Probst, O. Biaxial tensile strength characterization of textile composite materials. In Composites and Their Properties; IntechOpen: Rijeka, Croatia, 2012; pp. 83–106. [Google Scholar]
- Smits, A.; Van Hemelrijck, D.; Philippidis, T.P.; Cardon, A. Design of a cruciform specimen for biaxial testing of fibre reinforced composite laminates. Compos. Sci. Technol. 2006, 66, 964–975. [Google Scholar] [CrossRef]
- Makris, A.; Ramault, C.; Van Hemelrijck, D.; Clarke, A.; Williamson, C.; Gower, M.; Shaw, R.; Mera, R.; Lamkanfi, E.; Van Paepegem, W. A review of biaxial test methods for composites. In Experimental Analysis of Nano and Engineering Materials and Structures; Gdoutos, E.E., Ed.; Springer: Dordrecht, The Netherlands, 2007; pp. 933–940. [Google Scholar]
- Swanson, S.R.; Christoforou, A.P.; Colvin, G.E. Biaxial testing of fiber composites using tubular specimens. Exp. Mech. 1988, 28, 238–243. [Google Scholar] [CrossRef]
- Francis, P.H.; Walrath, D.E.; Sims, D.F.; Weed, D.N. Biaxial Fatigue Loading of Notched Composites. J. Compos. Mater. 1977, 11, 488–501. [Google Scholar] [CrossRef]
- Razmjoo, G.R.; Tubby, P.J. Fatigue of Welded Joints Under Complex Loading. In European Structural Integrity Society; Marquis, G., Solin, J., Eds.; Elsevier: Edinburgh, UK, 1997; Volume 22, pp. 153–164. [Google Scholar]
- Madhavan, R. On the Collapse of Long Thick-Walled Circular Tubes under Biaxial Loading. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1988. [Google Scholar]
- Quaresimin, M.; Carraro, P.A. On the investigation of the biaxial fatigue behaviour of unidirectional composites. Compos. Part B Eng. 2013, 54, 200–208. [Google Scholar] [CrossRef]
- Makris, A.; Vandenbergh, T.; Ramault, C.; Van Hemelrijck, D.; Lamkanfi, E.; Van Paepegem, W. Shape optimisation of a biaxially loaded cruciform specimen. Polym. Test. 2010, 29, 216–223. [Google Scholar] [CrossRef]
- Guelho, I.; Reis, L.; Freitas, M.; Li, B.; Madeira, J.; Cláudio, R. Optimization of cruciform specimen for low capacity biaxial testing machine. In Proceedings of the 10th International Conference on Multiaxial Fatigue (ICMFF10), Kyoto, Japan, 3–6 June 2013. [Google Scholar]
- Hopperstad, O.S.; Langseth, M.; Remseth, S. Cyclic stress-strain behaviour of alloy AA6060 T4, part II: Biaxial experiments and modelling. Int. J. Plast. 1995, 11, 741–762. [Google Scholar] [CrossRef]
- Ghiotti, A.; Bruschi, S.; Bariani, P.F. Determination of yield locus of sheet metal at elevated temperatures: A novel concept for experimental set-up. Key Eng. Mater. 2007, 344, 97–104. [Google Scholar] [CrossRef]
- Lebedev, A.A.; Muzyka, N.R. Design of cruciform specimens for fracture toughness tests in biaxial tension (Review). Strength Mater. 1998, 30, 243–254. [Google Scholar] [CrossRef]
- Mönch, E.; Galster, D. A method for producing a defined uniform biaxial tensile stress field. Br. J. Appl. Phys. 1963, 14, 810–812. [Google Scholar] [CrossRef]
- Terry, G. The biaxial tensile strain field from a conventional load-splitting tree. Strain 1977, 13, 110–112. [Google Scholar] [CrossRef]
- Vieira, M.; Reis, L.; de Freitas, M.; Ribeiro, A. Preliminary evaluation of the loading characteristics of biaxial tests at low and very high frequencies. Procedia Struct. Integr. 2016, 1, 205–211. [Google Scholar] [CrossRef] [Green Version]
- Abu-Farha, F.; Hector, L.G.; Khraisheh, M. Cruciform-shaped specimens for elevated temperature biaxial testing of lightweight materials. JOM 2009, 61, 48–56. [Google Scholar] [CrossRef]
- Cláudio, R.A.; Reis, L.; Freitas, M. Biaxial high-cycle fatigue life assessment of ductile aluminium cruciform specimens. Theor. Appl. Fract. Mech. 2014, 73, 82–90. [Google Scholar] [CrossRef]
- Cláudio, R.; Freitas, M.; Reis, L.; Li, B.; Guelho, I. Multiaxial Fatigue Behaviour of 1050 H14 Aluminium Alloy by a Biaxial Cruciform Specimen Testing Method. In Proceedings of the 10th International Conference on Multiaxial Fatigue & Fracture (ICMFF10), Kyoto, Japan, 3–6 June 2013. [Google Scholar]
- Lyadova, K.A.; Shadrin, V.V.; Kovtanyuk, L.V.; Ustinova, A.S. Shape optimization of a biaxially loaded specimen. In Proceedings of the XLI International Summer School Conference on “Advanced Problems in Mechanics”, St. Petersburg, Russia, 2–6 July 2013. [Google Scholar]
- Kuwabara, T.; Ikeda, S.; Kuroda, K. Measurement and analysis of differential work hardening in cold-rolled steel sheet under biaxial tension. J. Mater. Process. Technol. 1998, 80–81, 517–523. [Google Scholar] [CrossRef]
- Smith, E.W.; Pascoe, K.J. Fatigue Crack Initiation and Growth in a High-Strength Ductile Steel Subject to In-Plane Biaxial Loading. In Multiaxial Fatigue; Miller, K.J., Brown, M.W., Eds.; ASTM International: West Conshohocken, PA, USA, 1985; pp. 111–134. [Google Scholar]
- Corbin, C. The Design of Cruciform Test Specimens for Planar Biaxial Testing of Fabrics for Inflatable Aerodynamic Decelerators. Earth Space 2012, 2012, 763–772. [Google Scholar]
- Sawert, W. Verhalten der Baustähle bei wechselnder mehrachsiger Beanspruchung. Z. Ver. Deut. Ing. 1943, 87, 39–40. [Google Scholar]
- Lebedev, A.; Mouzuika, N. Ukrainian Patent. SU 769 399 A1, 7 October 1980. [Google Scholar]
- Clay, S.B. Biaxial Testing Apparatus. U.S. Patent 5,905,205, 18 May 1999. [Google Scholar]
- Bellett, D.; Morel, F.; Morel, A.; Lebrun, J.-L. A Biaxial Fatigue Specimen for Uniaxial Loading. Strain 2011, 47, 227–240. [Google Scholar] [CrossRef] [Green Version]
- Mura, T. Micromechanics of Defects in Solids; Springer Science & Business Media: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Soares, H.; Costa, P.; Freitas, M.; Reis, L. Fatigue life assessment of a railway wheel material under HCF and VHCF conditions. MATEC Web. Conf. 2018, 165, 09003. [Google Scholar] [CrossRef] [Green Version]
- Soares, H.; Costa, P.; Vieira, M.; Freitas, M.; Reis, L. Characterization and Evaluation of a Railway Wheel Steel in the HCF and VHCF Regimes. In Proceedings of the 17th International Conference on New Trends in Fatigue and Fracture (NT2F19), Cancun, Mexico, 25–27 October 2017; Springer: Cancun, Mexico, 2017. [Google Scholar]
- Costa, P.R.; Soares, H.; Reis, L.; Freitas, M. Ultrasonic fatigue testing under multiaxial loading on a railway steel. Int. J. Fatigue 2020, 136, 105581. [Google Scholar] [CrossRef]
- Montalvão, D.; Ribeiro, A.M.R.; Duarte-Silva, J.A.B. Experimental Assessment of a Modal-Based Multi-Parameter Method for Locating Damage in Composite Laminates. Exp. Mech. 2011, 51, 1473–1488. [Google Scholar] [CrossRef] [Green Version]
- Montalvão, D.; Karanatsis, D.; Ribeiro, A.M.; Arina, J.; Baxter, R. An experimental study on the evolution of modal damping with damage in carbon fiber laminates. J. Compos. Mater. 2015, 49, 2403–2413. [Google Scholar] [CrossRef] [Green Version]
- Mitsheal, A.; Daerefa-a Diogo, M.; Opukuro, D.-W.; George, H. A Review of Structural Health Monitoring Techniques as Applied to Composite Structures. Struct. Durab. Health Monit. 2017, 11, 91–147. [Google Scholar]
- Montalvão, D.; Silva, J.M.M. An alternative method to the identification of the modal damping factor based on the dissipated energy. Mech. Syst. Signal Process. 2015, 54–55, 108–123. [Google Scholar]
- Maia, N.M.M.; Ribeiro, A.M.R.; Fontul, M.; Montalvão, D.; Sampaio, R.P.C. Using the Detection and Relative Damage Quantification Indicator (DRQ) with Transmissibility. Key Eng. Mater. 2007, 347, 455–460. [Google Scholar] [CrossRef]
- Montalvão, D.; Freitas, M.; Reis, L.; Fonte, M. Design of Cruciform Test Specimens with different Biaxiality ratios for VHCF Fatigue. In Proceedings of the 8th International Conference on Engineering Failure Analysis (ICEFA VIII), Budapest, Hungary, 8–11 July 2018. [Google Scholar]
- Nwawe, R.; Grasso, M.; Chen, Y.; Klusak, J.; Rosiello, V. Optimisation of a gigacycle biaxial fatigue specimen for ultrasonic testing. In Proceedings of the Engineering and Computer Science Research Conference, Hatfield, UK, 17 April 2019. [Google Scholar]
- Bach, J.; Göken, M.; Höppel, H.-W. Fatigue of low alloyed carbon steels in the HCF/VHCF-regimes. In Fatigue of Materials at Very High Numbers of Loading Cycles: Experimental Techniques, Mechanisms, Modeling and Fatigue Life Assessment; Christ, H.-J., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2018; pp. 1–23. [Google Scholar]
- Grigorescu, A.; Hilgendorff, P.M.; Zimmermann, M.; Fritzen, C.-P.; Christ, H.-J. Fatigue behaviour of austenitic stainless steels in the VHCF regime. In Fatigue of Materials at Very High Numbers of Loading Cycles: Experimental Techniques, Mechanisms, Modeling and Fatigue Life Assessmenet; Christ, H.-J., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2018; pp. 49–71. [Google Scholar]
- Hilgendorff, P.M.; Grigorescu, A.C.; Zimmermann, M.; Fritzen, C.-P.; Christ, H.-J. Simulation of the VHCF deformation of austenitic stainless steels and its effect on the resonant behaviour. In Fatigue of Materials at Very High Numbers of Loading Cycles: Experimental Techniques, Mechanisms, Modeling and Fatigue Life Assessment; Christ, H.-J., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2018; pp. 73–94. [Google Scholar]
- Dönges, B.; Fritzen, C.-P.; Christ, H.-J. Fatigue mechanism and its modeling of an austenitic-ferritic duplex stainless steel under HCF and VHCF loading conditions. In Fatigue of Materials at Very High Numbers of Loading Cycles: Experimental Techniques, Mechanisms, Modeling and Fatigue Life Assessment; Christ, H.-J., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2018; pp. 111–131. [Google Scholar]
- Tsutsumi, N.; Murakami, Y.; Doquet, V. Effect of test frequency on fatigue strength of low carbon steel. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 473–483. [Google Scholar] [CrossRef]
- Nonaka, I.; Setowaki, S.; Ichikawa, Y. Effect of load frequency on high cycle fatigue strength of bullet train axle steel. Int. J. Fatigue 2014, 60, 43–47. [Google Scholar] [CrossRef]
- Guennec, B.; Ueno, A.; Sakai, T.; Takanashi, M.; Itabashi, Y.; Ota, M. Dislocation-based interpretation on the effect of the loading frequency on the fatigue properties of JIS S15C low carbon steel. Int. J. Fatigue 2015, 70, 328–341. [Google Scholar] [CrossRef]
- Soares, H. Avaliação e Caracterização em Fadiga Multiaxial do Aço de uma Roda Ferroviária de Aplicabilidade ao Transporte de Passageiros. Ph.D. Thesis, Instituto Superior Técnico, University of Lisbon, Lisboa, Portugal, 2019. (In Portuguese). [Google Scholar]







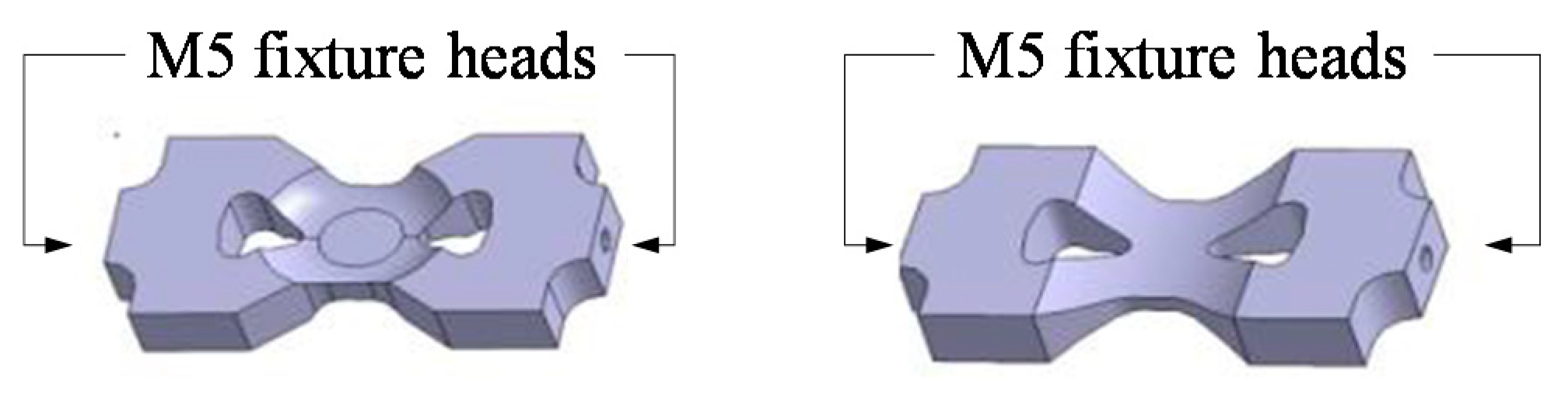



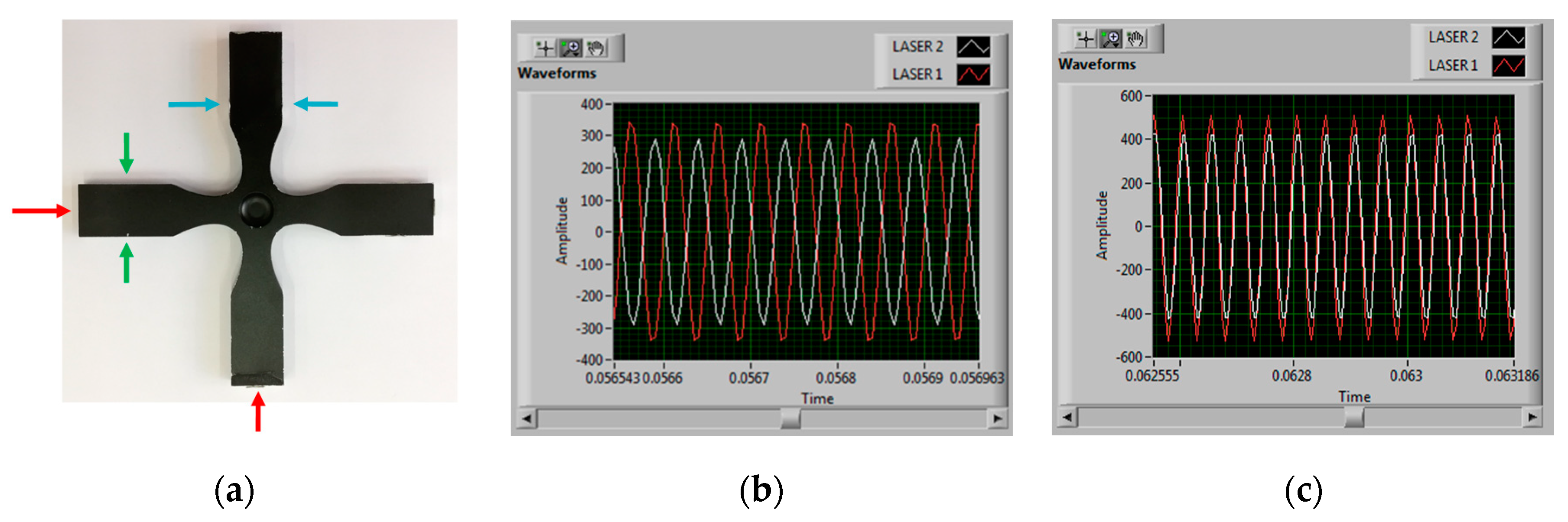
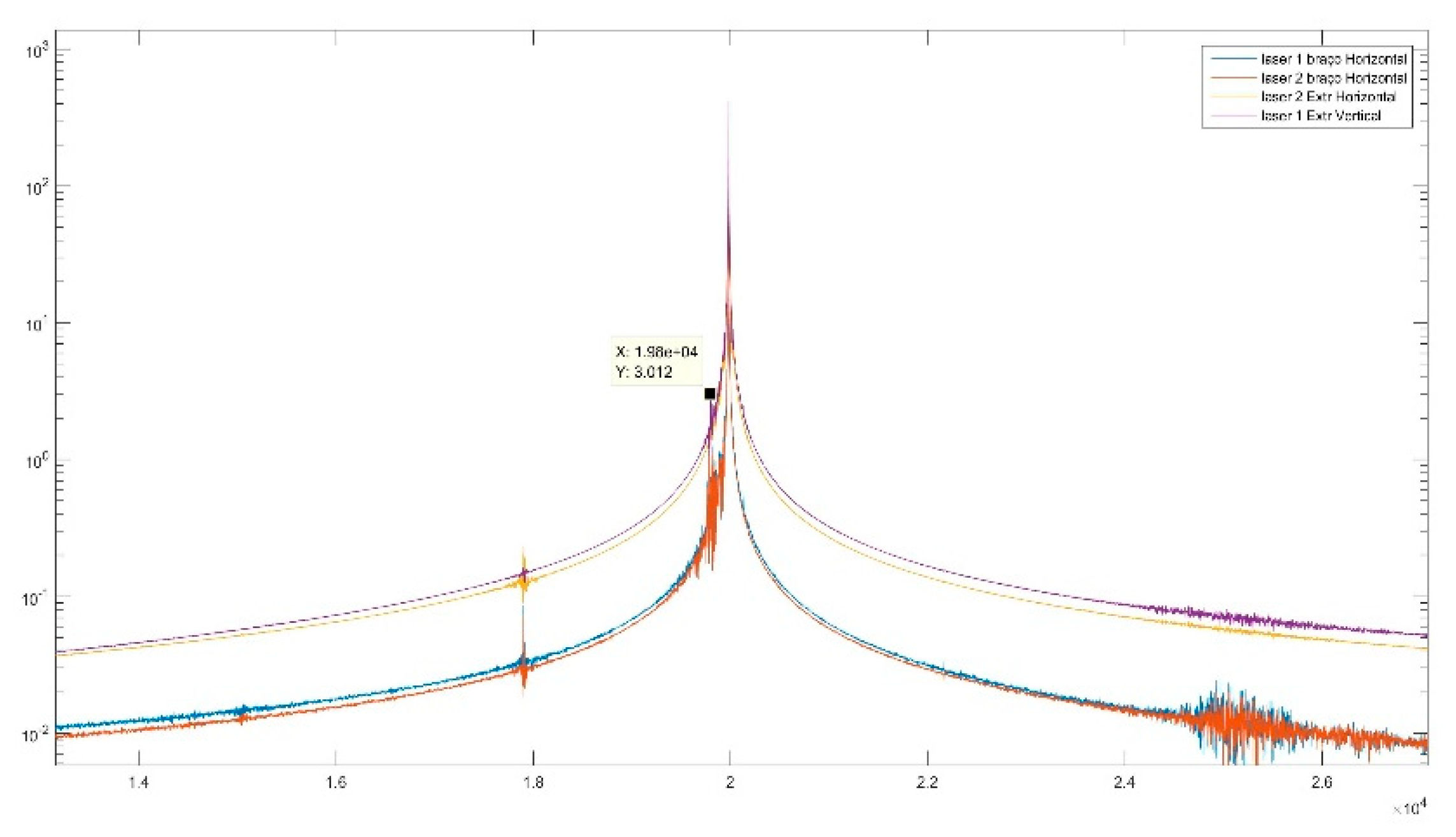
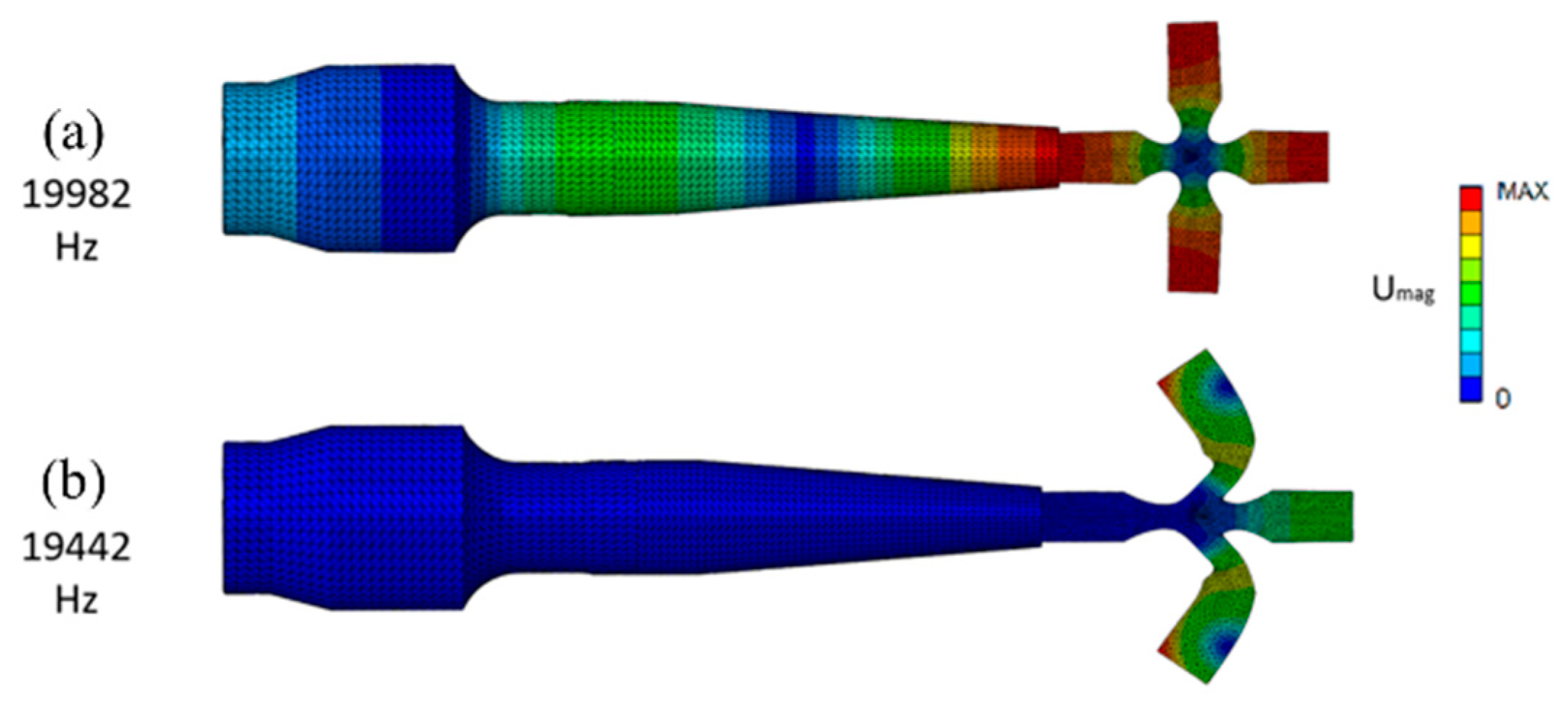
| Number of Cycles | Ultrasonic (20 kHz) | Resonance (150 Hz) | Rotating Bending (30 Hz) | |||
|---|---|---|---|---|---|---|
| 107 | 8.5 | min | 1 | days | 4 | days |
| 108 | 1.5 | h | 1 | weeks | 1.5 | months |
| 109 | 0.5 | days | 2.5 | months | 1 | years |
| 1010 | 1 | weeks | 2 | years | 1 | decades |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, P.; Nwawe, R.; Soares, H.; Reis, L.; Freitas, M.; Chen, Y.; Montalvão, D. Review of Multiaxial Testing for Very High Cycle Fatigue: From ‘Conventional’ to Ultrasonic Machines. Machines 2020, 8, 25. https://doi.org/10.3390/machines8020025
Costa P, Nwawe R, Soares H, Reis L, Freitas M, Chen Y, Montalvão D. Review of Multiaxial Testing for Very High Cycle Fatigue: From ‘Conventional’ to Ultrasonic Machines. Machines. 2020; 8(2):25. https://doi.org/10.3390/machines8020025
Chicago/Turabian StyleCosta, Pedro, Richard Nwawe, Henrique Soares, Luís Reis, Manuel Freitas, Yong Chen, and Diogo Montalvão. 2020. "Review of Multiaxial Testing for Very High Cycle Fatigue: From ‘Conventional’ to Ultrasonic Machines" Machines 8, no. 2: 25. https://doi.org/10.3390/machines8020025
APA StyleCosta, P., Nwawe, R., Soares, H., Reis, L., Freitas, M., Chen, Y., & Montalvão, D. (2020). Review of Multiaxial Testing for Very High Cycle Fatigue: From ‘Conventional’ to Ultrasonic Machines. Machines, 8(2), 25. https://doi.org/10.3390/machines8020025