An Analytical Method for Generating Determined Torque Ripple in Synchronous Machines with Surface Magnets by Harmonic Current Injection
Abstract
:1. Introduction
2. Fundamentals
2.1. Machine Equations for Synchronous Machines with Surface-Mounted Permanent Magnets
2.2. Power Supply System
2.3. Back EMF
2.4. Formulation of the Electromagnetic Torque Resulting from the Lorentz Force
3. Approach
3.1. Formulation of the System of Linear Equations
3.2. Solvability of the Linear System of Equations
4. Validation
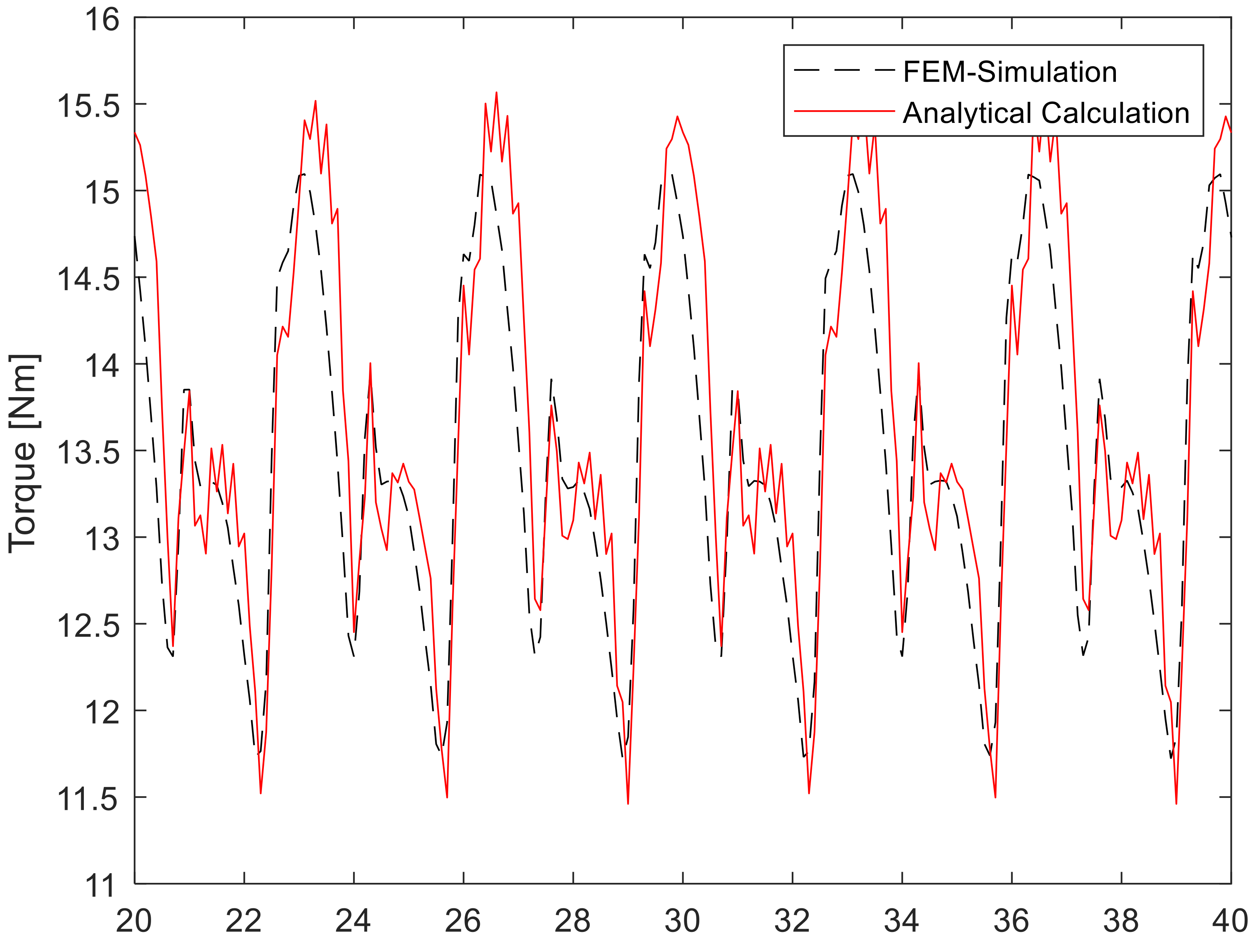
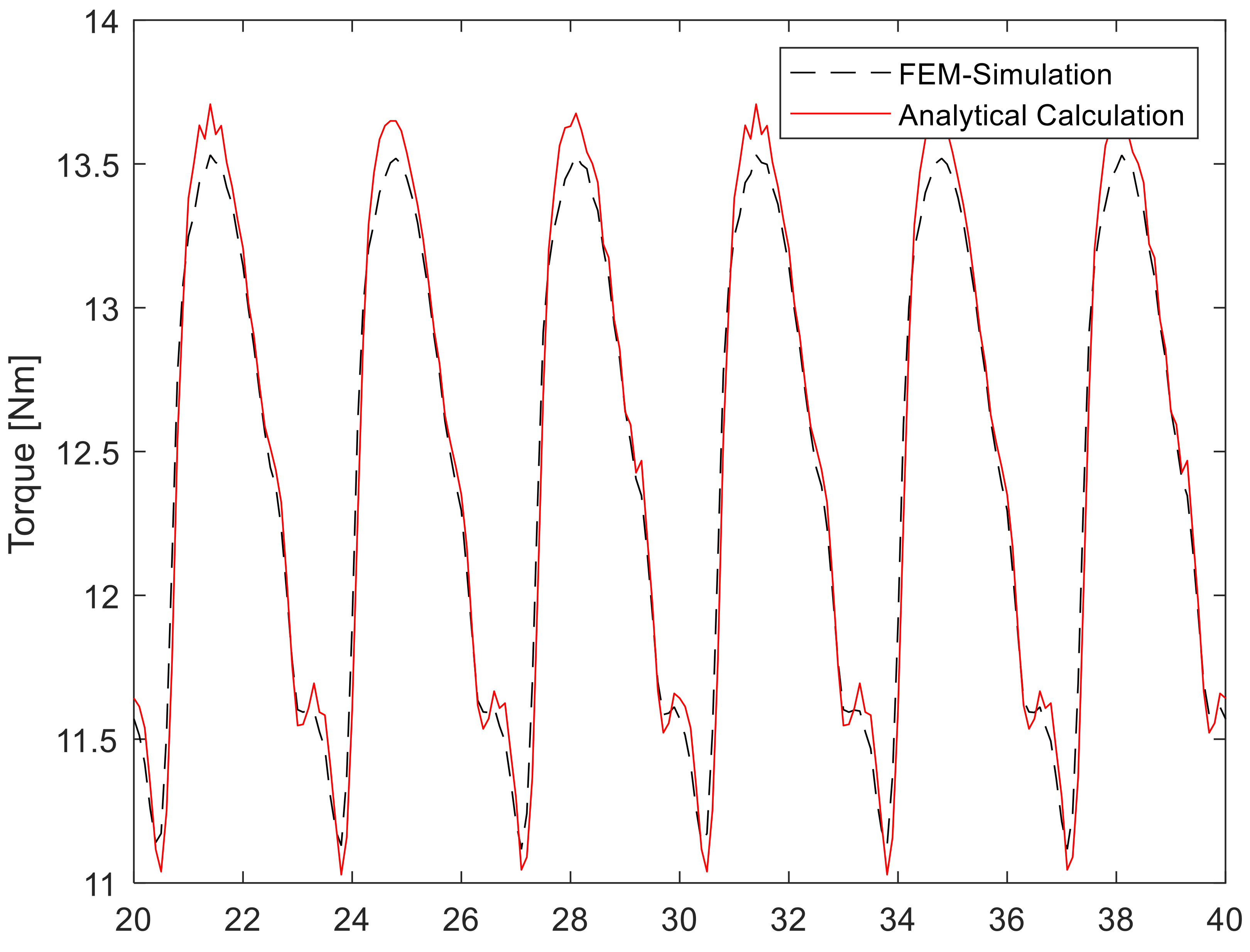
4.1. Machine Parameters and Validation of the Torque Calculation Method
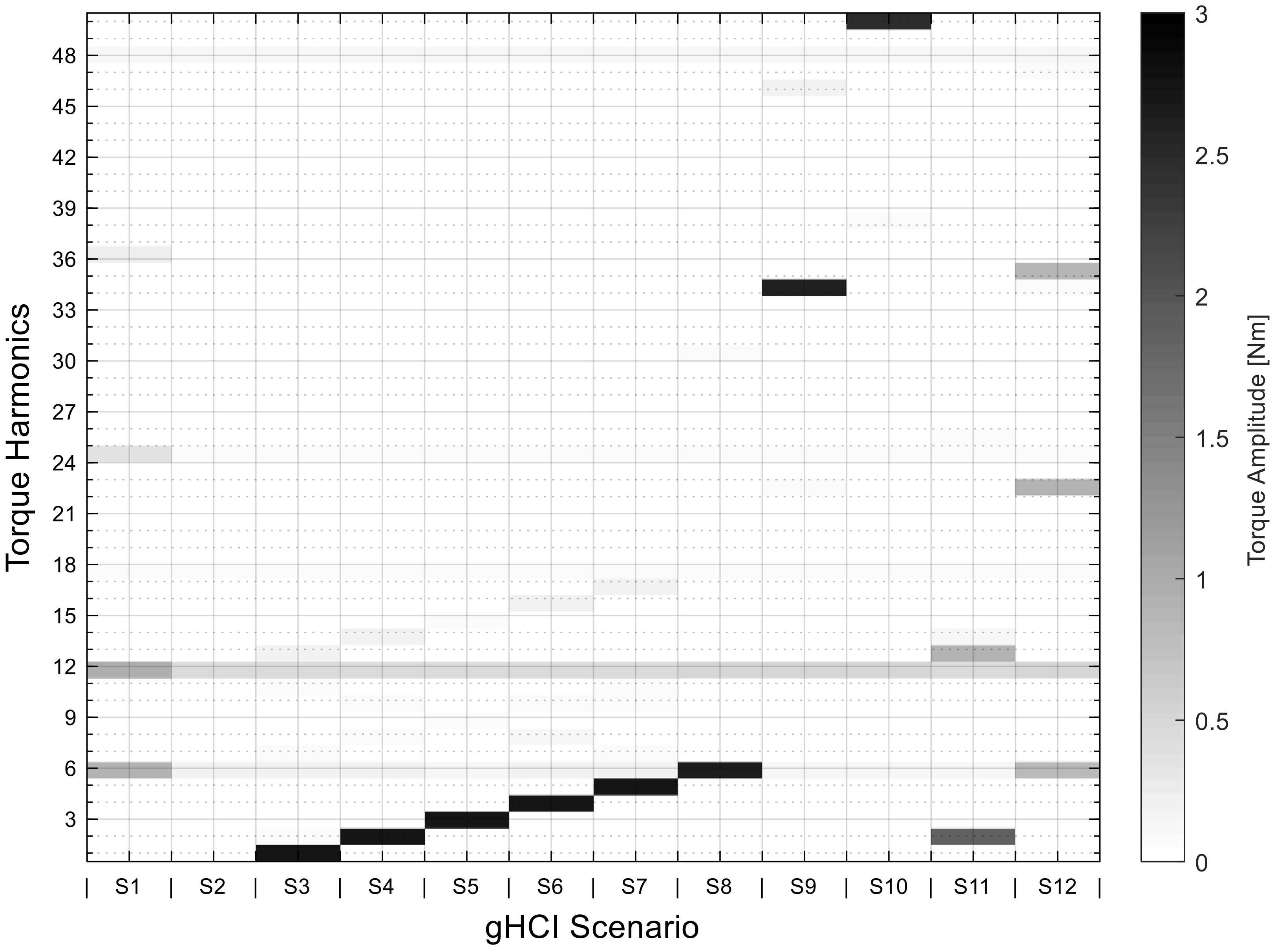
4.2. Validation of Generative Harmonic Current Injection
5. Conclusions
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zeraoulia, M.; Benbouzid, M.E.H.; Diallo, D. Electric Motor Drive Selection Issues for HEV Propulsion Systems: A Comparative Study. IEEE Trans. Veh. Technol. 2006, 55, 1756–1764. [Google Scholar] [CrossRef] [Green Version]
- Kimura, T.; Saitou, R.; Kubo, K.; Nakatsu, K.; Ishikawa, H.; Sasaki, K. High-power-density inverter technology for hybrid and electric vehicle applications. Hitachi Rev. 2014, 63, 42–47. [Google Scholar]
- Holtz, J.; Springob, L. Identification and compensation of torque ripple in high-precision permanent magnet motor drives. IEEE Trans. Ind. Electron. 1996, 43, 309–320. [Google Scholar] [CrossRef] [Green Version]
- Magnussen, F.; Thelin, P.; Sadarangani, C. Performance evaluation of permanent magnet synchronous machines with concentrated and distributed windings including the effect of field-weakening. In Proceedings of the Second International Conference on Power Electronics, Machines and Drives (PEMD 2004), Edinburgh, UK, 31 March–2 April 200; p. v2-679. [CrossRef]
- Bianchi, N.; Bolognani, S.; Pre, M.D.; Grezzani, G. Design considerations for fractional-slot winding configurations of synchronous machines. IEEE Trans. Ind. Appl. 2006, 42, 997–1006. [Google Scholar] [CrossRef]
- Chung, D.-W.; You, Y.-M. Cogging Torque Reduction in Permanent-Magnet Brushless Generators for Small Wind Turbines. J. Magn. 2015, 20, 176–185. [Google Scholar] [CrossRef] [Green Version]
- Favre, E.; Cardoletti, L.; Jufer, M. Permanent-magnet synchronous motors: A comprehen-sive approach to cogging torque suppression. IEEE Trans. Ind. Appl. 1993, 29, 1141–1149. [Google Scholar] [CrossRef]
- Najmabadi, A.; Xu, W.; Degner, M. A Sensitivity Analysis on the Fifth and the Seventh Harmonic Current Injection for Sixth Order Torque Ripple Reduction. In Proceedings of the IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–8. [Google Scholar]
- Zhu, Z.Q.; Wu, L.J.; Xia, Z.P. An Accurate Subdomain Model for Magnetic Field Computation in Slotted Surface-Mounted Permanent-Magnet Machines. IEEE Trans. Magn. 2010, 46, 1100–1115. [Google Scholar] [CrossRef]
- Hanselman, D. Brushless Permanent Magnet Motor Design; Magna Physics Pub: Lebanon, OH, USA, 2006. [Google Scholar]
- Pyrhönen, J.; Hrabovcová, V.; Jokinen, T.; Niemelä, H. Design of Rotating Electrical Machines; Reprinted; Wiley: Chichester, UK, 2010. [Google Scholar]
- Schröder, D. Elektrische Antriebe–Grundlagen. Mit Durchgerechneten Übungs- und Prüfungsaufgaben; 5., erw. Aufl.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Farshadnia, M. Advanced Theory of Fractional-Slot Concentrated-Wound Permanent Magnet Synchronous Machines; Springer: Singapore, 2018. [Google Scholar]
- Chen, Z.; Li, Z.; Ma, H. A harmonic current injection method for electromagnetic torque ripple suppression in permanent-magnet synchronous machines. Int. J. Appl. Electromagn. Mech. 2017, 53, 327–336. [Google Scholar] [CrossRef]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D.; Pekarek, S. Analysis of Electric Machinery and Drive Systems, 3rd ed.; Wiley IEEE Press: Hoboken, NJ, USA, 2013. [Google Scholar]
- Schröder, D. Elektrische Antriebe–Regelung von Antriebssystemen; 4. Auflage; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]



| n | ||
|---|---|---|
| 1 | 10 | 0 |
| 2 | 2 | |
| 4 | 1 | 0 |
| 5 | 0.5 | 0 |
| 7 | 0.25 | |
| 8 | 0.125 | |
| 10 | 0.0625 | 0 |
| Machine A | Machine B | |
|---|---|---|
| Number of Poles | 4 | 4 |
| Number of Stator Slots | 24 | 12 |
| Outer Diameter of Stator | 120 mm | 100 mm |
| Inner Diameter of Stator | 75 mm | 50 mm |
| Length of Stator Core | 65 mm | 100 mm |
| Minimum Air Gap | 0.5 mm | 0.5 mm |
| Residual Flux Density | 0.96 Tesla | 0.96 Tesla |
| excitation frequency | |
| phase angle | 0.2 |
| current amplitude | 12 A |
| Amplitude in V | ||
|---|---|---|
| Machine A | Machine B | |
| 21.93 | 111.53 | |
| −5.02 | 13.39 | |
| 4.80 | 3.39 | |
| −8.10 | −2.10 | |
| −1.61 | −2.07 | |
| Amplitude in Nm | Phase in Rad | ||||
|---|---|---|---|---|---|
| Machine A | Machine B | Machine A | Machine B | ||
| 0.0021 | 0.0000 | 1.22 | 0.00 | ||
| 0.3102 | 0.2246 | 1.76 | 1.76 | ||
| 0.0031 | 0.0374 | −1.57 | −1.29 | ||
| 0.3702 | 0.1402 | −1.19 | −1.19 | ||
| 0.0011 | 0.0691 | 1.88 | −1.10 | ||
| 0.2470 | 0.0000 | 2.15 | 0.00 | ||
| 0.0000 | 0.0241 | 0.00 | 2.23 | ||
| Scenario | Required Torque Ripple | Injected Harmonics |
|---|---|---|
| 1 | First reference scenario: simple sinusoidal current, without HCI | |
| 2 | Second reference scenario:pure compensation of all harmonics in torque | |
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vollat, M.; Hartmann, D.; Gauterin, F. An Analytical Method for Generating Determined Torque Ripple in Synchronous Machines with Surface Magnets by Harmonic Current Injection. Machines 2020, 8, 32. https://doi.org/10.3390/machines8020032
Vollat M, Hartmann D, Gauterin F. An Analytical Method for Generating Determined Torque Ripple in Synchronous Machines with Surface Magnets by Harmonic Current Injection. Machines. 2020; 8(2):32. https://doi.org/10.3390/machines8020032
Chicago/Turabian StyleVollat, Matthias, Daniel Hartmann, and Frank Gauterin. 2020. "An Analytical Method for Generating Determined Torque Ripple in Synchronous Machines with Surface Magnets by Harmonic Current Injection" Machines 8, no. 2: 32. https://doi.org/10.3390/machines8020032





