Tool Wear Prediction in Single-Sided Lapping Process
Abstract
:1. Introduction
2. Related Work
2.1. Physics-Based Models
2.2. Data-Driven Models
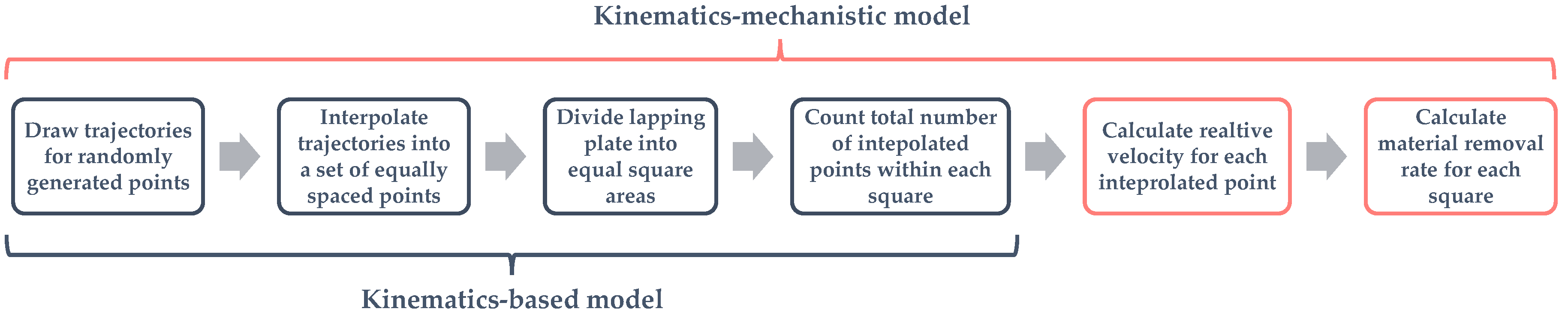
3. Physics-Based Model
3.1. Analysis of the Angular Velocities of the Conditioning Ring and the Lapping Plate
- -
- For k1 < 0, generated trajectories are epicycloids, initially stretched and then interlaced.
- -
- For k1 > 1, generated trajectories are hypocycloids, initially stretched and then interlaced.
- -
- For 0 < k1 < 1, generated trajectories are pericycloids.
3.2. Analysis of the Radial Position of Conditioning Rings
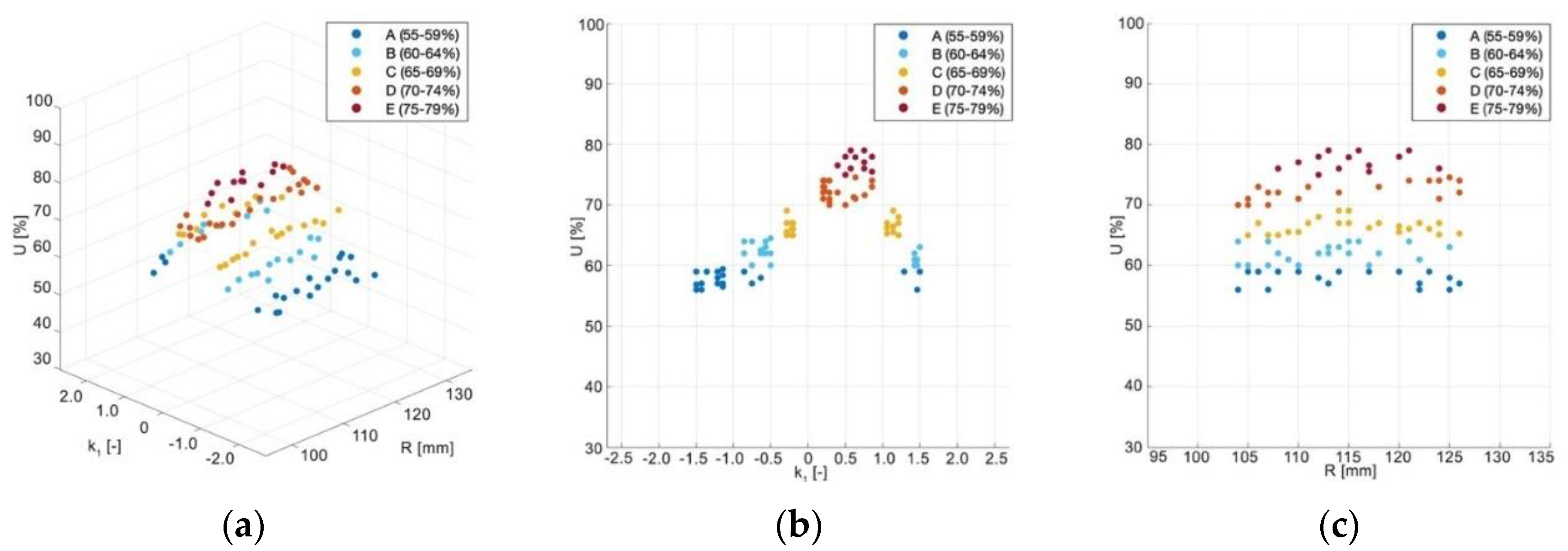
3.3. Tool Wear Uniformity Prediction
4. Data-Driven Model
5. Conclusions
Funding
Conflicts of Interest
List of Abbreviations and Symbols
| A | contact area of the lapping plate (m2) |
| CMP | chemical-mechanical polishing |
| H | lapping plate wear removal rate (μm/min) |
| k | number of nearest neighbors |
| kNN | k-Nearest Neighbors algorithm |
| K | Preston’s coefficient |
| k1 | speed ratio of the conditioning ring and the lapping plate |
| MRR | material removal rate |
| nt | rotational speeds of the lapping plate (rpm) |
| ns | rotational speeds of the conditioning ring (rpm) |
| p | contact pressure (MPa) |
| R | radial position of the condition rings (mm) |
| RD | radius of the lapping plate (mm) |
| SD | standard deviation of the trajectory density |
| t | simulation time (s) |
| T | time of cycle, when generated trajectories are closed curves (s) |
| Tc | time of one cycle in v(t) function (s) |
| U | lapping plate wear uniformity (%) |
| v | relative velocity of the analyzed point P (m/s) |
| vsr | average relative velocity (m/s) |
| ωt | angular velocity of the lapping plate (rad/s) |
| ωs | angular velocity of the conditioning ring (rad/s) |
References
- Deaconescu, A.; Deaconescu, T. Experimental and statistical parametric optimisation of surface roughness and machining productivity by lapping. Trans. FAMENA 2015, 39, 65–78. [Google Scholar]
- Uhlmann, E.; Ardelt, T.G. Influence of kinematics on the face grinding process on lapping machines. CIRP Ann. 1999, 48, 281–284. [Google Scholar] [CrossRef]
- Kasai, T.; Horio, K.; Karaki-Doy, T.; Kobayashi, A. Improvement of Conventional Polishing Conditions for Obtaining Super Smooth Surfaces of Glass and Metal Works. CIRP Ann. 1990, 39, 321–324. [Google Scholar] [CrossRef]
- Marinescu, I.D.; Uhlmann, E.; Doi, T. Handbook of Lapping and Polishing; Taylor & Francis Publishing House: New York, NY, USA, 2007. [Google Scholar]
- Marinescu, I.D.; Rowe, W.B.; Dimitrov, B.; Inasaki, I. Tribology of Abrasive Machining Processes; William Andrew Publishing Ltd.: Norwich, UK, 2004. [Google Scholar]
- Feld, M.; Barylski, A. Lappen ebener Flachen mit Zweimetall-Scheiben. Werks. u. Betr. 1990, 123, 933–936. [Google Scholar]
- Deja, M. Correlation between shape errors in flat grinding. J. Vibroeng. 2012, 14, 520–527. [Google Scholar]
- Liu, H.K.; Chen, C.A.; Chen, W.C. Diamond lapping of sapphire wafer with addition of graphene in slurry. Procedia Eng. 2017, 184, 156–162. [Google Scholar] [CrossRef]
- Lu, L.Y.; Fang, C.F.; Shen, J.Y.; Lu, J.; Xu, X.P. Analysis of path distribution in lapping and polishing with single fixed abrasive. Key Eng. Mater. 2014, 589, 475–479. [Google Scholar] [CrossRef]
- Deja, M.; List, M.; Lichtschlag, L.; Uhlmann, E. Thermal and technological aspects of double face grinding of Al2O3 ceramic materials. Ceram. Int. 2019, 45, 19489–19495. [Google Scholar] [CrossRef]
- Chang, Y.P.; Hashimura, M.M.; Dornfeld, D.A. An investigation of material removal mechanisms in lapping with grain size transition. J. Manuf. Sci. Eng. 2000, 122, 413–419. [Google Scholar] [CrossRef]
- Kling, J.; Matthias, E. Workpiece material removal and lapping wheel wear in plane and plane-parallel lapping. CIRP Ann. 1986, 35, 219–222. [Google Scholar] [CrossRef]
- Nguyen, N.Y.; Zhong, Z.W.; Tian, Y. An analytical investigation of pad wear caused by the conditioner in fixed abrasive chemical–mechanical polishing. Int. J. Adv. Manuf. Technol. 2015, 77, 897–905. [Google Scholar] [CrossRef]
- Barylski, A.; Deja, M. Wear of a tool in double-disk lapping of silicon wafers. In Proceedings of the 5th International Manufacturing Science and Engineering Conference (MSEC 2010), Erie, PA, USA, 12–15 October 2010; pp. 301–307. [Google Scholar]
- Lee, H.; Jeong, H. A Wafer-Scale Material Removal Rate Profile Model for Copper Chemical Mechanical Planarization. Int. J. Mach. Tools Manuf. 2011, 51, 395–403. [Google Scholar] [CrossRef]
- Wang, P.; Gao, R.X.; Yan, R. A deep learning-based approach to material removal rate prediction in polishing. CIRP Ann. 2017, 66, 429–432. [Google Scholar] [CrossRef]
- Jia, X.; Di, Y.; Feng, J.; Yang, Q.; Dai, H.; Lee, J. Adaptive Virtual Metrology for Semiconductor Chemical Mechanical Planarization Process Using GMDH-Type Polynomial Neural Networks. J. Process Control 2018, 62, 44–54. [Google Scholar] [CrossRef]
- Yu, T.; Li, Z.; Wu, D. Predictive modeling of material removal rate in chemical mechanical planarization with physics-informed machine learning. Wear 2019, 426, 1430–1438. [Google Scholar] [CrossRef]
- Barylski, A.; Piotrowski, N. Non-conventional approach in single-sided lapping process: Kinematic analysis and parameters optimization. Int. J. Adv. Manuf. Technol. 2019, 100, 589–598. [Google Scholar] [CrossRef] [Green Version]
- Evans, J.; Paul, E.; Dornfeld, D.; Lucca, D.; Byrne, G.; Tricard, M.; Klocke, F.; Dambon, O.; Mullany, B. Material Removal Mechanisms in Lapping and Polishing; University of California: Berkeley, CA, USA, 2003; pp. 611–633. [Google Scholar]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Li, Z.; Wu, D.; Yu, T. Prediction of Material Removal Rate for Chemical Mechanical Planarization Using Decision Tree-Based Ensemble Learning. J. Manuf. Sci. Eng. 2019, 141, 031003. [Google Scholar] [CrossRef] [Green Version]
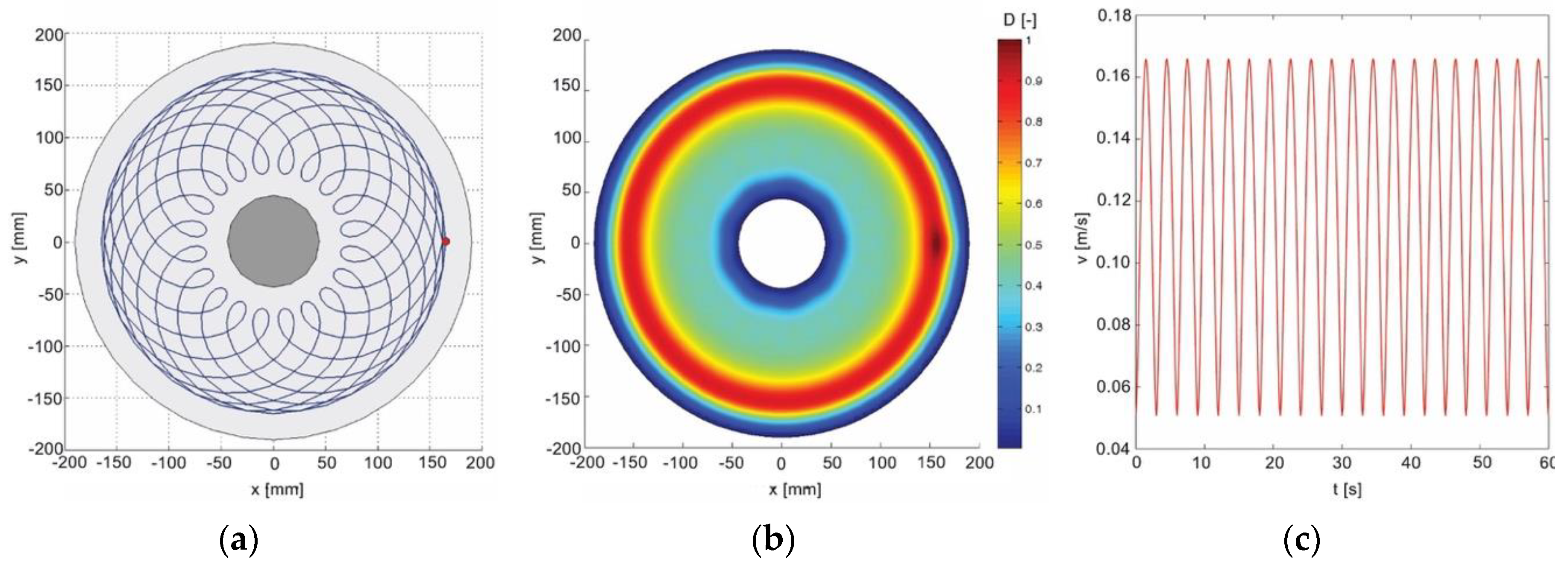

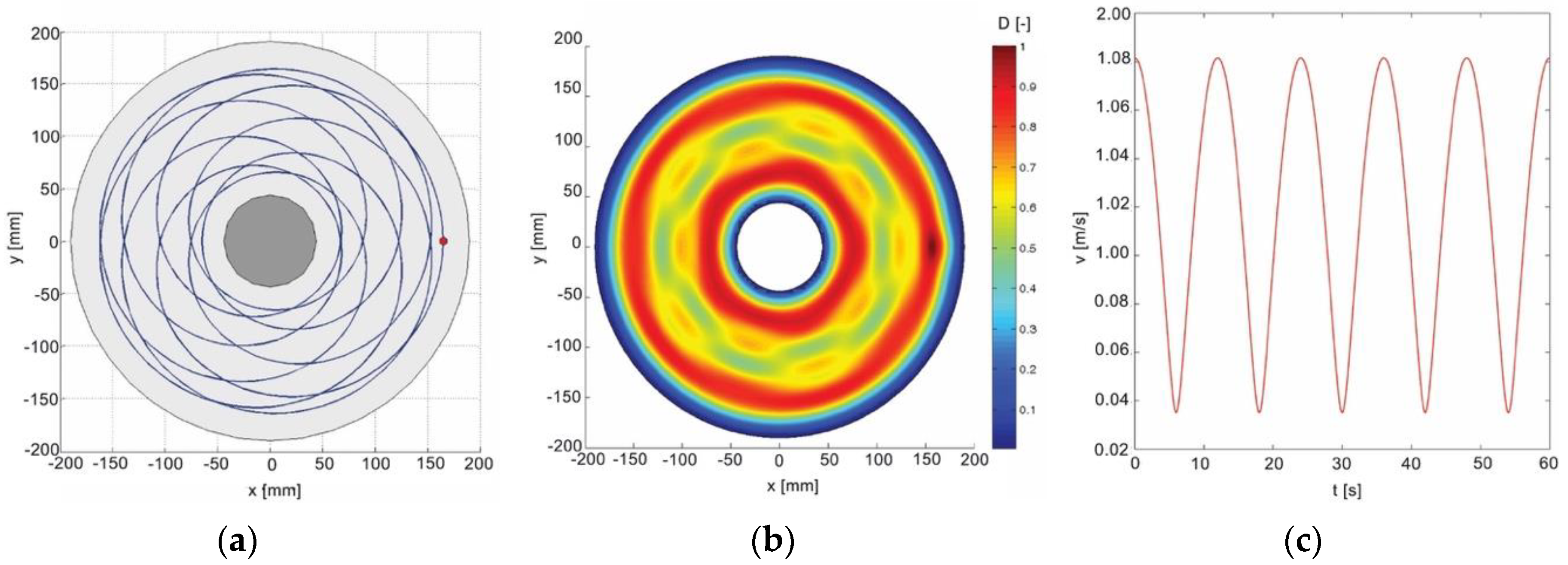
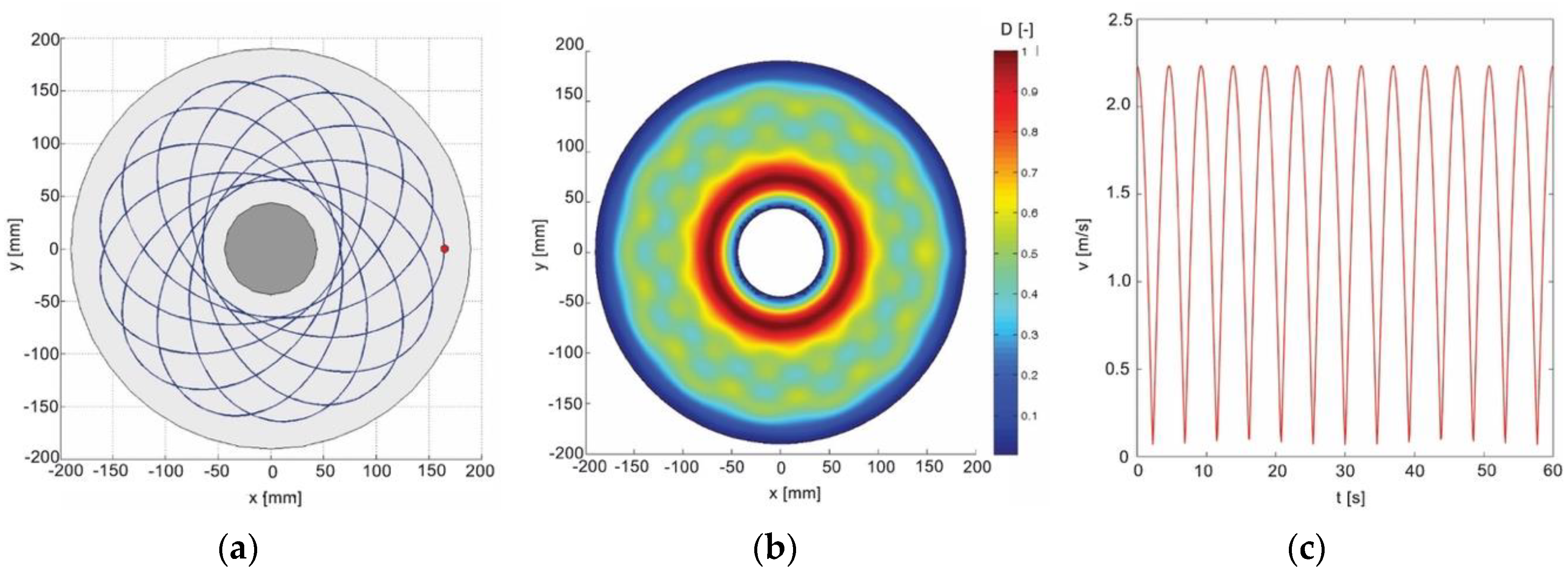



| k1 | −20/9 | −5/9 | 5/9 | 13/9 |
| Tc (s) | 3 | 12 | 12 | 4.62 |
| Class | A | B | C | D | E |
|---|---|---|---|---|---|
| U | 55–59% | 60–64% | 65–69% | 70–74% | 75–79% |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piotrowski, N. Tool Wear Prediction in Single-Sided Lapping Process. Machines 2020, 8, 59. https://doi.org/10.3390/machines8040059
Piotrowski N. Tool Wear Prediction in Single-Sided Lapping Process. Machines. 2020; 8(4):59. https://doi.org/10.3390/machines8040059
Chicago/Turabian StylePiotrowski, Norbert. 2020. "Tool Wear Prediction in Single-Sided Lapping Process" Machines 8, no. 4: 59. https://doi.org/10.3390/machines8040059
APA StylePiotrowski, N. (2020). Tool Wear Prediction in Single-Sided Lapping Process. Machines, 8(4), 59. https://doi.org/10.3390/machines8040059





