Figure 1.
A typical multi-layer perceptron (MLP) neural network used in the study.
Figure 1.
A typical multi-layer perceptron (MLP) neural network used in the study.
Figure 2.
Schematic of the experimental rig.
Figure 2.
Schematic of the experimental rig.
Figure 3.
Experimental mode shapes: (a) 50.66 Hz, vertical direction dominant; (b) 56.76 Hz, horizontal direction dominant.
Figure 3.
Experimental mode shapes: (a) 50.66 Hz, vertical direction dominant; (b) 56.76 Hz, horizontal direction dominant.
Figure 4.
A typical mounting arrangement of an accelerometer at a bearing housing.
Figure 4.
A typical mounting arrangement of an accelerometer at a bearing housing.
Figure 5.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x velocity spectra values for the healthy condition at 1800 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 5.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x velocity spectra values for the healthy condition at 1800 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
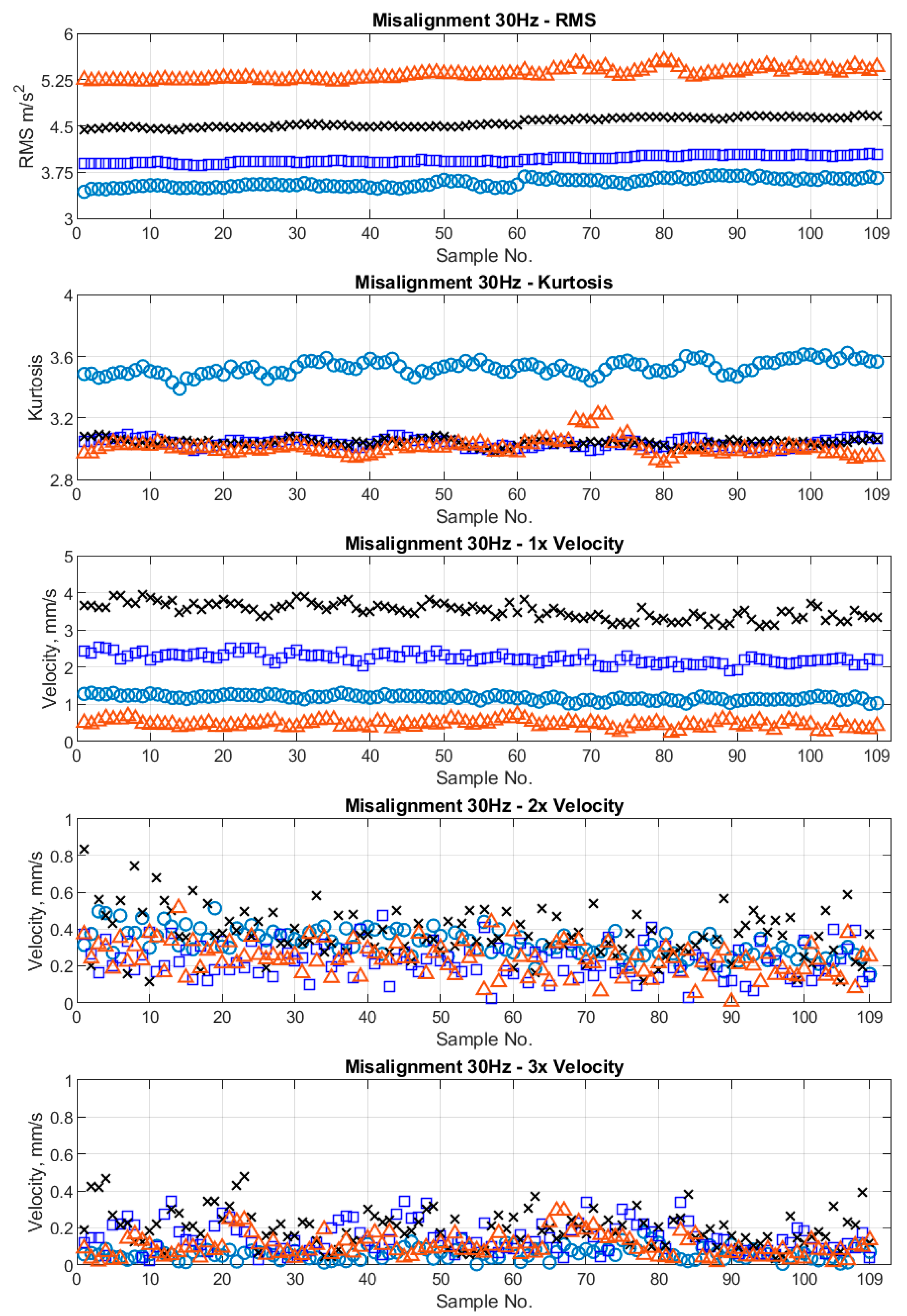
Figure 6.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the misalignment condition at 1800 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 6.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the misalignment condition at 1800 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 7.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the looseness condition at 1800 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 7.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the looseness condition at 1800 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 8.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the shaft bow condition at 1800 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 8.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the shaft bow condition at 1800 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 9.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the shaft rub condition at 1800 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 9.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the shaft rub condition at 1800 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 10.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x velocity spectra values for the healthy condition at 2400 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 10.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x velocity spectra values for the healthy condition at 2400 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 11.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the misalignment condition at 2400 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 11.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the misalignment condition at 2400 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 12.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the looseness condition at 2400 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 12.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the looseness condition at 2400 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 13.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the shaft bow condition at 2400 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 13.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the shaft bow condition at 2400 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 14.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the shaft rub condition at 2400 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Figure 14.
Estimated RMS and Kurtosis from the measured acceleration signals and their 1x, 2x, 3x velocity spectra values for the shaft rub condition at 2400 RPM (B1, circle; B2, square; B3, cross; and B4, triangle).
Table 1.
A summary of few machine learning (ML) studies for the vibration-based faults diagnosis (VFD) in rotating machines.
Table 1.
A summary of few machine learning (ML) studies for the vibration-based faults diagnosis (VFD) in rotating machines.
| Ref. No. | Defects/Faults | ML Method |
|---|
| [3,4] | Several rotor-related defects separately tested at a few different machine speeds and different machine foundations | Principal Component Analysis (PCA) method used to develop the diagnostic model for each speed, each foundation and their combination |
| [7] | Roller bearing outer race defect only | Probabilistic principal component analysis (PCA) |
| [8] | Different bearing faults (outer, inner race, rolling element) separately and combined tested at three different machine speeds | PCA and broad learning methods are used for diagnosis. Separate model is used for each speed |
| [9] | Outer race bearing defect at three different severities, tested at two machine speeds | PCA and ANN methods are used separately. Separate model developed for each speed. ANN performance found to be much better compared to PCA |
| [10] | Different bearing faults (outer, inner race, rolling element) separately | Support vector regression machines (SVRMs) |
| [11] | Rolling bearings fault (inner race, outer race, ball, and some combinations) | Convolutional neural network |
| [12] | Several bearing-related faults at different operational conditions (fault size, motor load, rotor speed) | Transfer learning in ANN |
| [13] | Roller bearing defects (outer, inner race, rolling element) in low-speed rotating machinery. Different operational speeds, separately | Supervised decision tree |
| [14] | Bearing faults and bevel gear, separately | Twin support vector machine (TWSVM) |
| [15] | Planetary gearbox and motor bearings faults, separately | Deep learning neural network |
| [16] | Bearing faults and gearbox faults, separately | Convolutional neural network |
| [17] | Gear crack with different severities | PCA and sequential probability ratio test |
| [18] | Gearbox healthy and three faults types tested at four machine speeds | Support Vectors Machine (SVM) method used, but all speed data are used together for the development of the model |
| [19] | High and low imbalance in high-pressure cylinder of synthetic ammonia compressor | k-nearest neighbour (kNN) |
| [20] | Impeller cracks and blockage in pumps | SVM |
| [21] | Blockages and cavitation in centrifugal pumps | SVM |
| [22] | Unbalance localisation, two-plane balancing at two different speed | ANN method used separately for each speed |
| [23] | Rotor crack | ANN |
| [24] | Several defects through different machines | ANN method used separately for different machines |
Table 2.
Data samples per rotor condition and operational speed.
Table 2.
Data samples per rotor condition and operational speed.
| Rotor Condition | No. of Data Sets (Runs) per Rotor Speed |
|---|
| 1800 RPM (30 Hz) | 2400 RPM (40 Hz) |
|---|
| Healthy (residual unbalance) | 66 | 44 |
| Misalignment | 109 | 119 |
| Shaft bow | 202 | 183 |
| Looseness in pedestal | 190 | 87 |
| Rotor rub | 112 | 114 |
Table 3.
Blind application performance (%) at 2400 RPM of approach 1: time domain feature-based ML model.
Table 3.
Blind application performance (%) at 2400 RPM of approach 1: time domain feature-based ML model.
| Actual | Healthy | Misalignment | Bow | Looseness | Rub |
|---|
| Diagnosis |
|---|
| Healthy | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Misalignment | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Bow | 0.0 | 67.1 | 100.0 | 0.0 | 0.0 |
| Looseness | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 |
| Rub | 0.0 | 32.9 | 0.0 | 0.0 | 100.0 |
Table 4.
Blind application performance (%) at 2400 RPM of approach 2: time–frequency feature-based ML model.
Table 4.
Blind application performance (%) at 2400 RPM of approach 2: time–frequency feature-based ML model.
| Actual | Healthy | Misalignment | Bow | Looseness | Rub |
|---|
| Diagnosis |
|---|
| Healthy | 15.9 | 0.0 | 0.0 | 0.0 | 0.0 |
| Misalignment | 0.0 | 5.9 | 0.0 | 0.0 | 0.0 |
| Bow | 0.0 | 0.0 | 10.8 | 0.0 | 0.0 |
| Looseness | 0.0 | 0.0 | 0.0 | 1.1 | 0.0 |
| Rub | 84.1 | 94.1 | 89.2 | 98.9 | 100.0 |
Table 5.
Blind application performance (%) at 2400 RPM of the proposed vibration-based machine learning (VML) model.
Table 5.
Blind application performance (%) at 2400 RPM of the proposed vibration-based machine learning (VML) model.
| Actual | Healthy | Misalignment | Bow | Looseness | Rub |
|---|
| Diagnosis |
|---|
| Healthy | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Misalignment | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| Bow | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 |
| Looseness | 0.0 | 0.0 | 0.0 | 98.9 | 0.0 |
| Rub | 0.0 | 0.0 | 0.0 | 1.1 | 100.0 |
Table 6.
CPU time by different VML models.
Table 6.
CPU time by different VML models.
| Approaches | Total Training CPU Time (Seconds) | Blind Diagnosis CPU Time (Seconds/Sample) |
|---|
| Approach 1: only time domain features [25] | 104.5156 | 0.1396 |
| Approach 2: time domain and frequency domain features [26] | 95.1250 | 0.1218 |
| Proposed approach: optimised features | 91.8125 | 0.1123 |