Calculating Power Parameters of Rolling Mill Based on Model of Deformation Zone with Four-Roll Passes
Abstract
:1. Introduction
- In the deformation zone, a pattern of all-round compression of the workpiece at high hydrostatic pressure is created, which increases the plasticity of the processed material, also providing for better one-time deformations;
- The pattern of the deformed state is changing, which makes it possible to eliminate the crossflow of the material, for better one-time deformations, in order to increase one-time draw-downs;
- Intensive all-round compression of the workpiece leads to a higher density, better physical and mechanical properties and structure of the product.
2. Problem Formulation
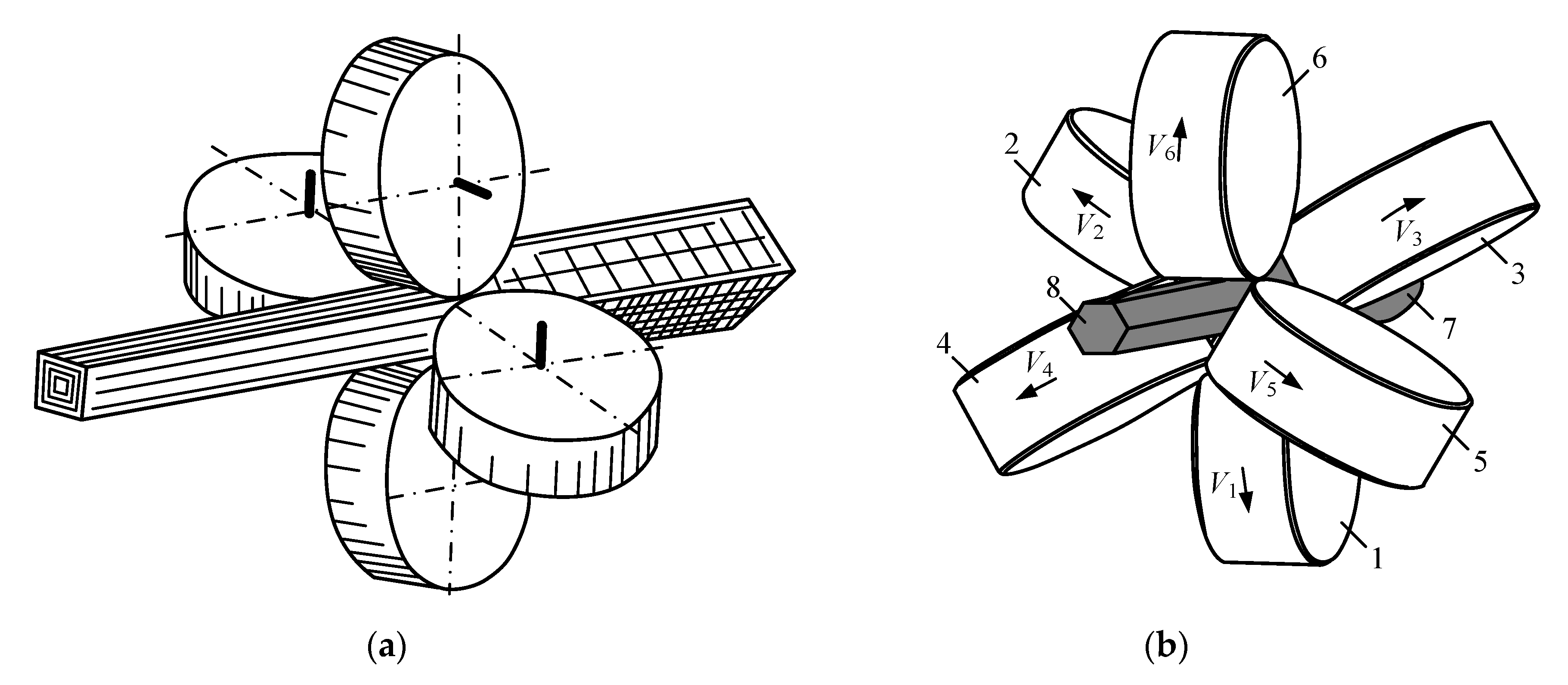
2.1. Study Object Properties
2.2. Rationale for Model Development
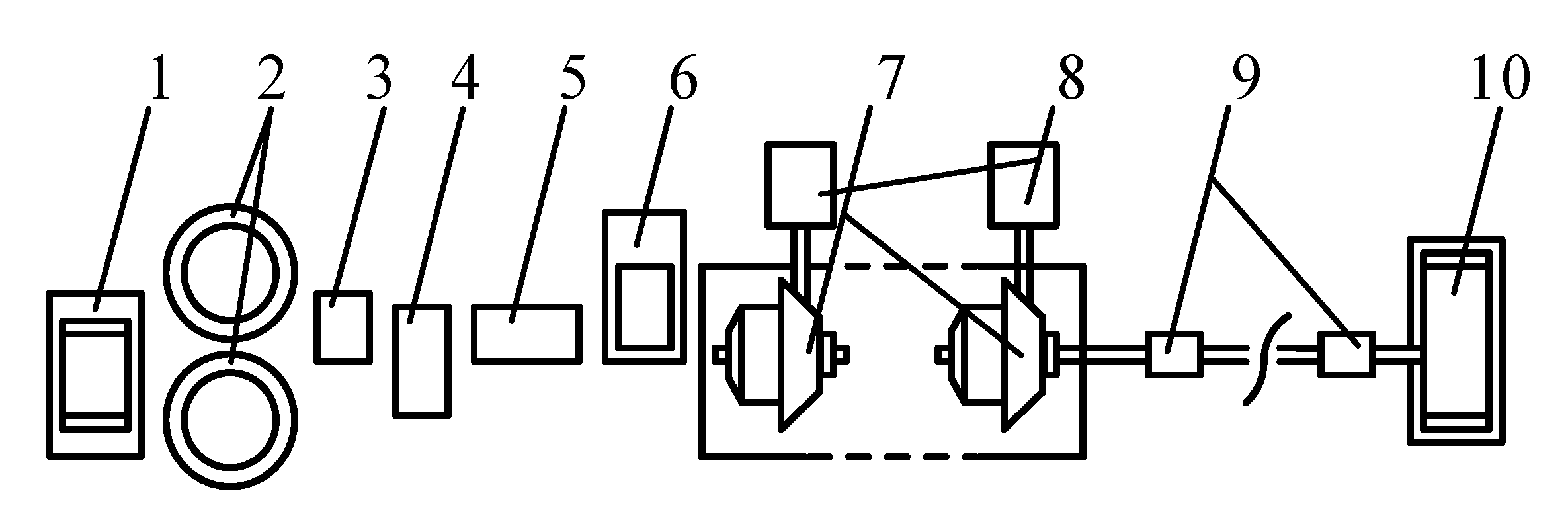
3. Materials and Methods
- Improvement of the method applied to calculate the metal rolling pressure, moment and power of the drive motor.
- Making up a methodological base to simulate the rolling process at promising multi-stand mills, taking into account the electromechanical system interaction via metal.
- The hypothesis of plane sections, experimentally confirmed by many studies, is accepted as a working hypothesis.
- The relationship between normal and shear stresses is described either by the Amonton–Coulomb dry friction law or by Siebel’s law.
- The hardening curve is approximated as a straight line.
- The friction coefficient along the contact arc is considered constant.
- The distribution of specific pressure over the groove width is assumed to be uniform.
- The contact arc is replaced by a chord.
- —for drawing-down in neutral sectionwhere ; ; ; ; ; ; ; ; —hardening module; —co-sign coefficient of ; —coefficient given by Equation (2).
- —for calculating the average specific pressure of the metal on the rollswhere —integration constants: ;
- —for mill torqueWhen deriving Equations (6)–(8), Siebel’s law of friction was used. Metal forward slip in the deformation zone:
4. Implementation
4.1. Digital Model for Deformation Zone of Stand with Four-Roll Pass
- −
- in the backward slip zone
- −
- in the forward slip zonewhere , —elementary forces applied to the site :
- −
- in the backward slip zone
- −
- in the forward slip zone, —indexes of lags in backward and forward slip zones.
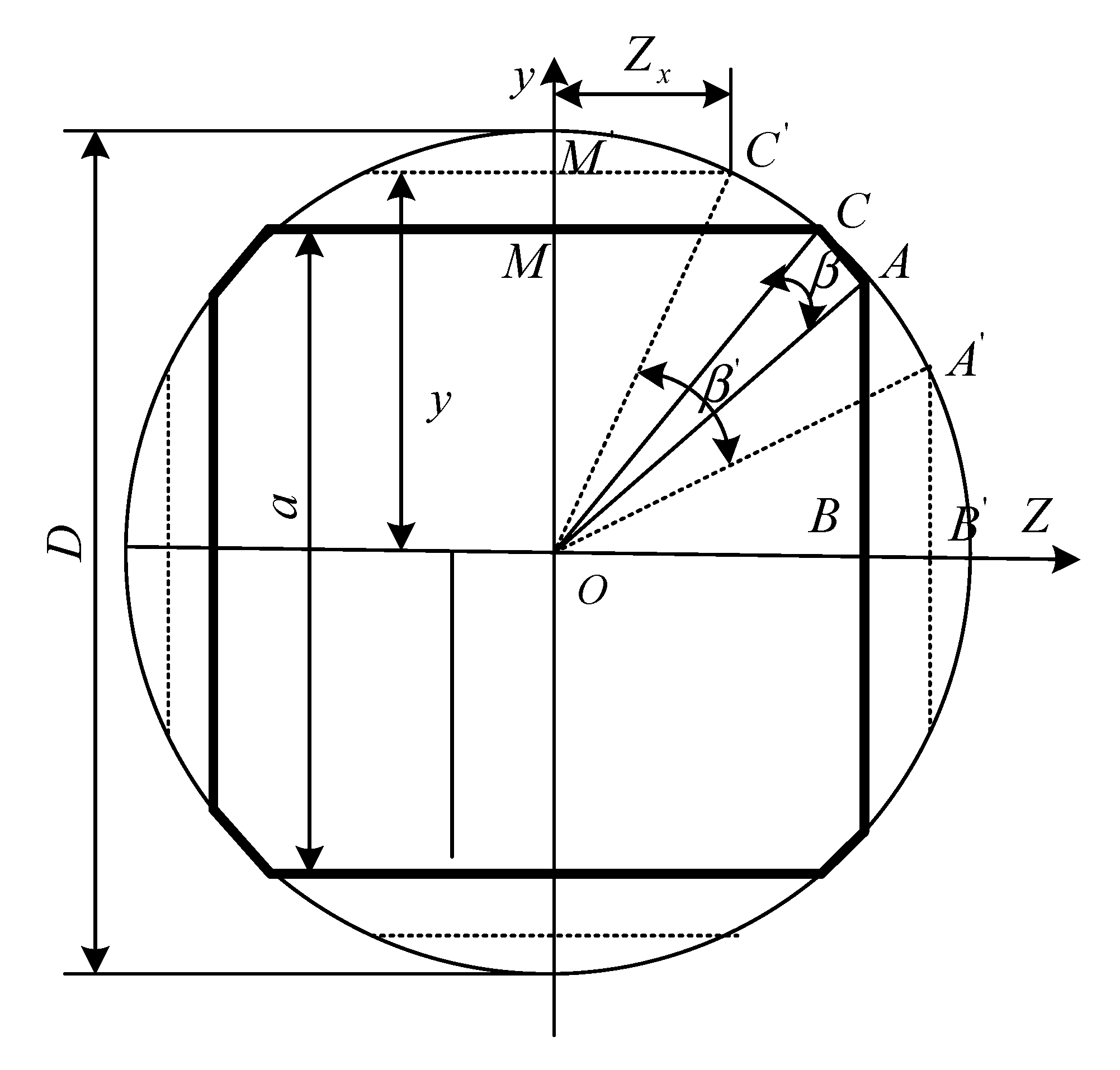
4.2. Groove System “Circle—Incomplete Square” (First Stand)
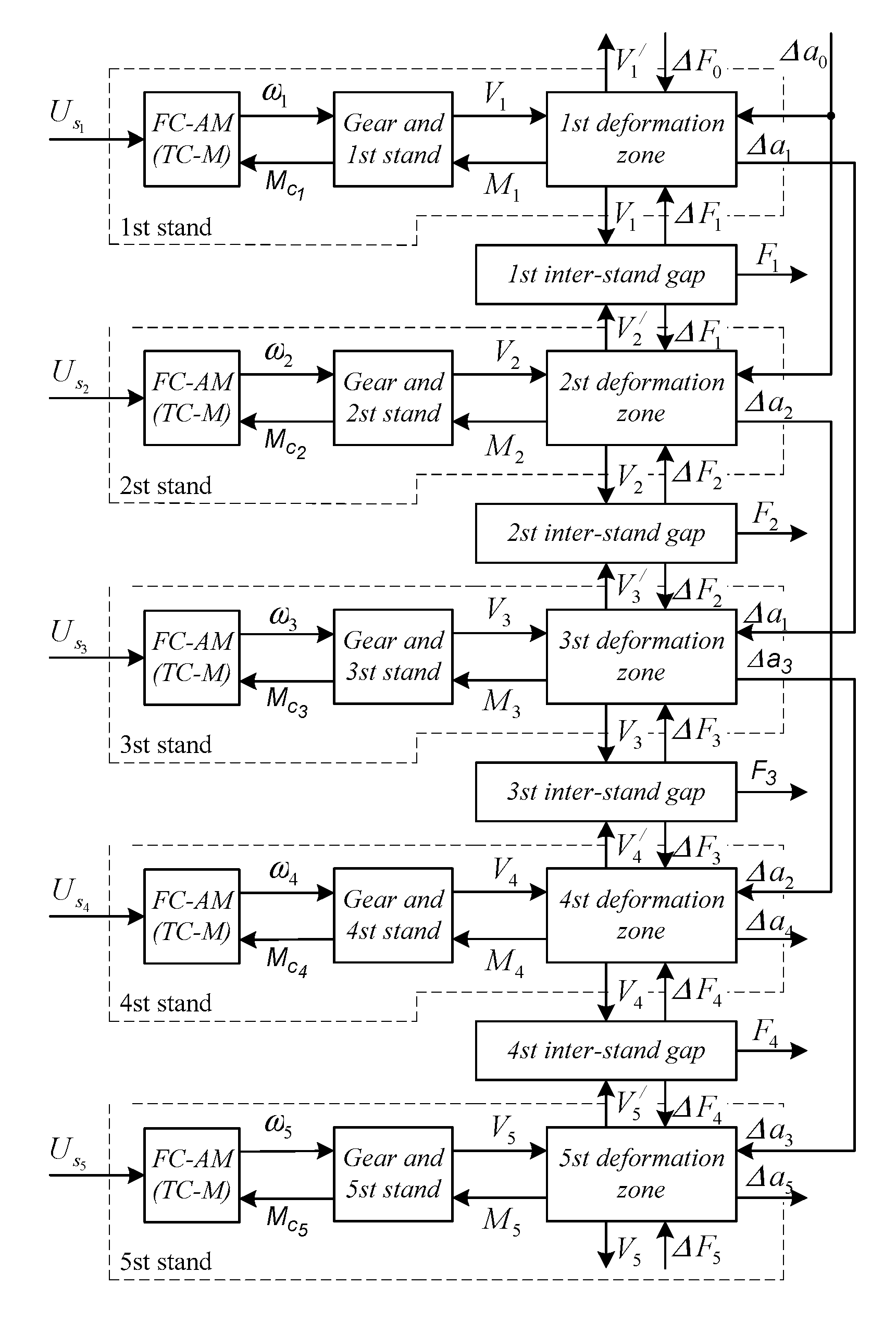
4.3. Structure of a Digital Model for a Five-Stand Mill
5. Experimental Research Conduct Method
5.1. Initial Rolling Product Range
5.2. Measuring Energy and Force Rolling Parameters
- Defining the deformation of measuring pins installed in the chock body under roll bearing. Operating and compensating sensors were put on the pin polished edges; the sensors were connected in a half-bridge circuit, four sensors in each leg.
- Stand housing deformation measurement. To do this, the authors measured deformations occurring in the roll base and determined the reactions occurring in the bearing assembly. For this purpose, tension meters were put on the bases. They were intended to measure the resulting force of rolling pressure and its horizontal component. The calibration of pressure meters was conducted in the stands with special hydraulic devices allowing for the simultaneous loading of all rolls with equal forces simulating rolling pressure.
- The rotating moment was obtained by the motor armature current (at the experimental plant DC current motors are applied). To measure the tension in the interstand space, two methods were used at continuous rolling: measurement of stand movement from the axial force acting on the strip side and tension measurement with the help of a roller type sensor.
- Sample temperature at cool and hot rolling was measured by a double-electrode thermocouple with information record. The temperature of rolled stock surface at continuous rolling measured by a photoelectric pyrometer (non-contact method).
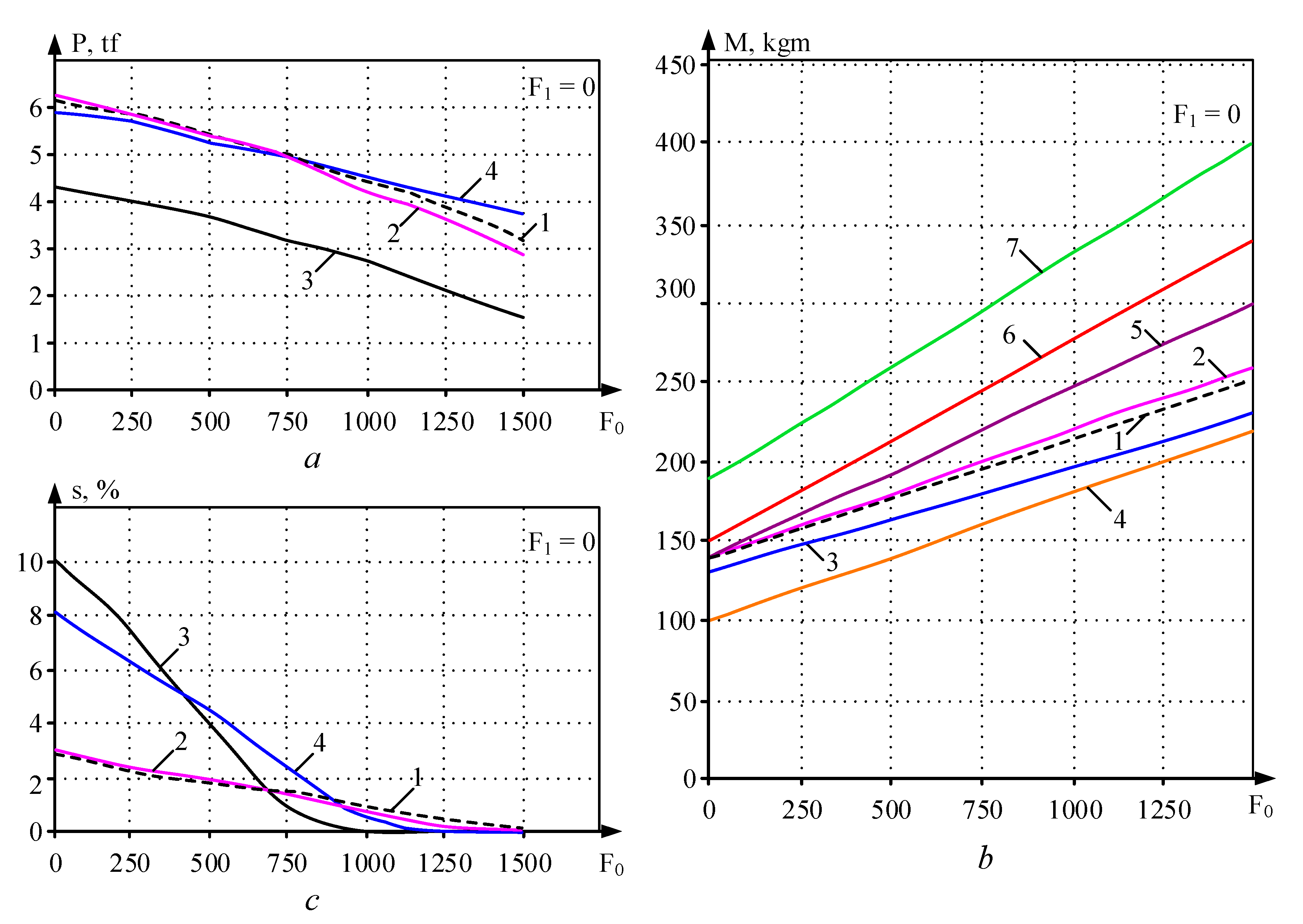
6. Results
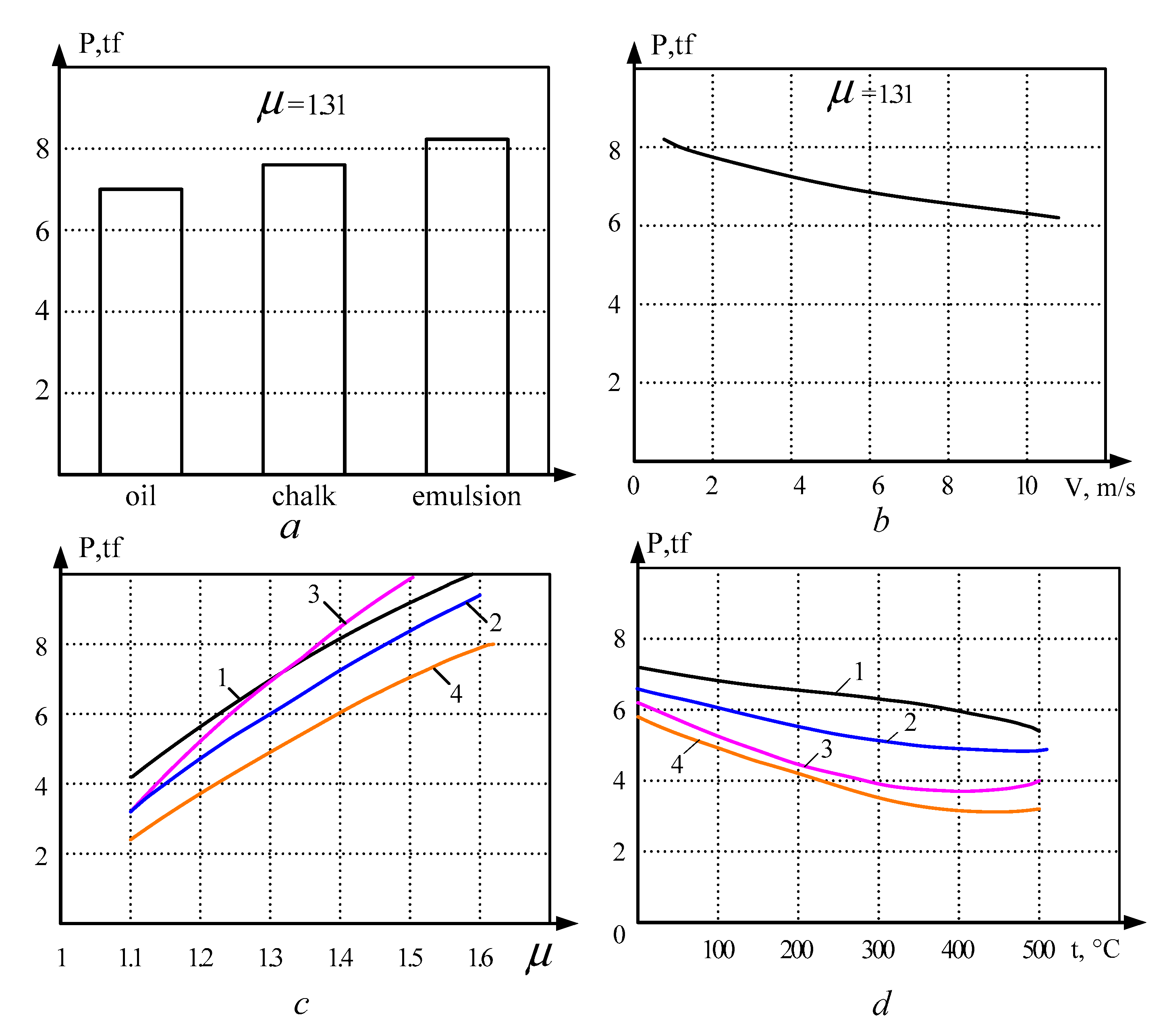
6.1. Experimental Research Results
6.2. Mathematic Simulation Result
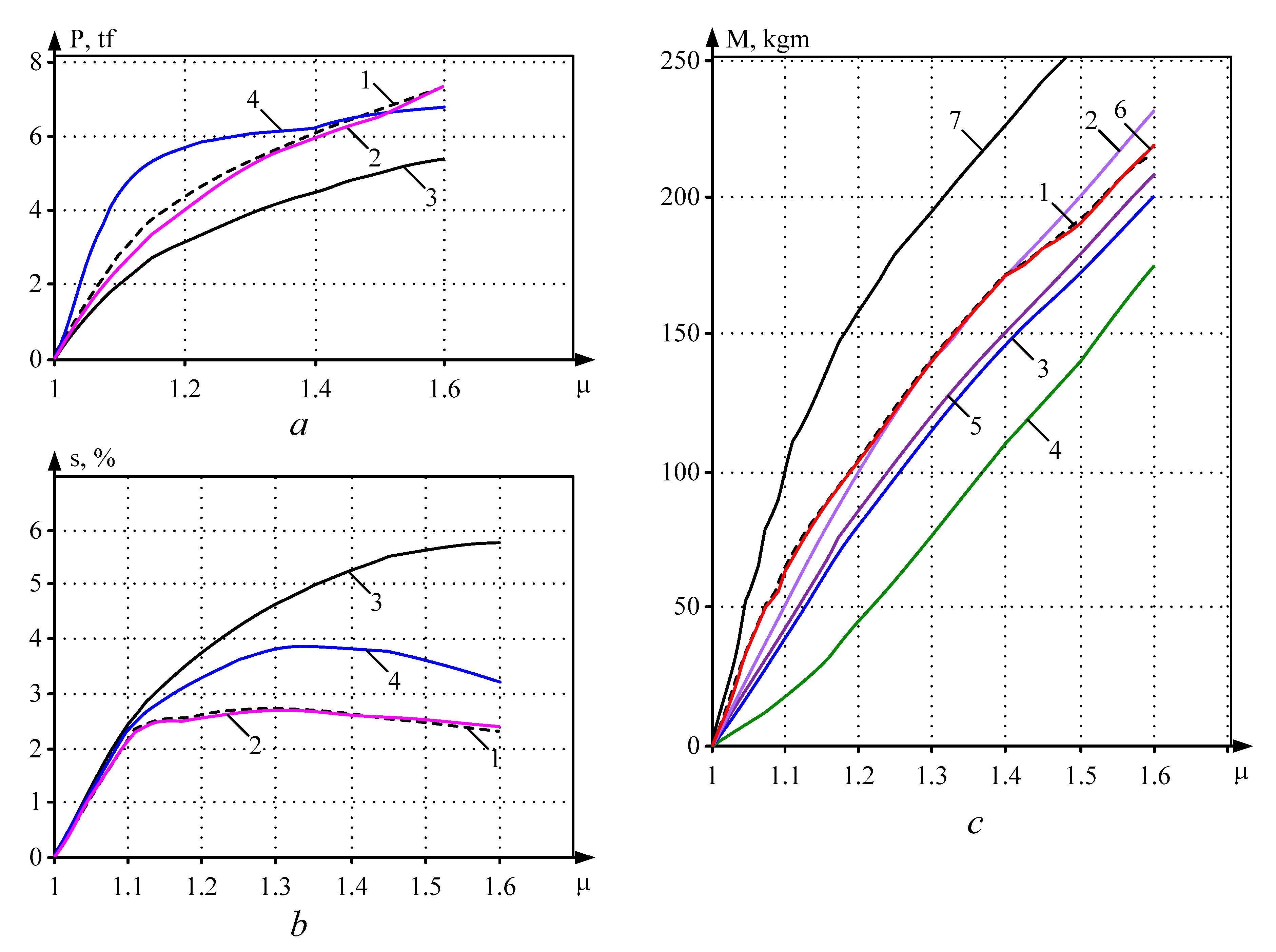
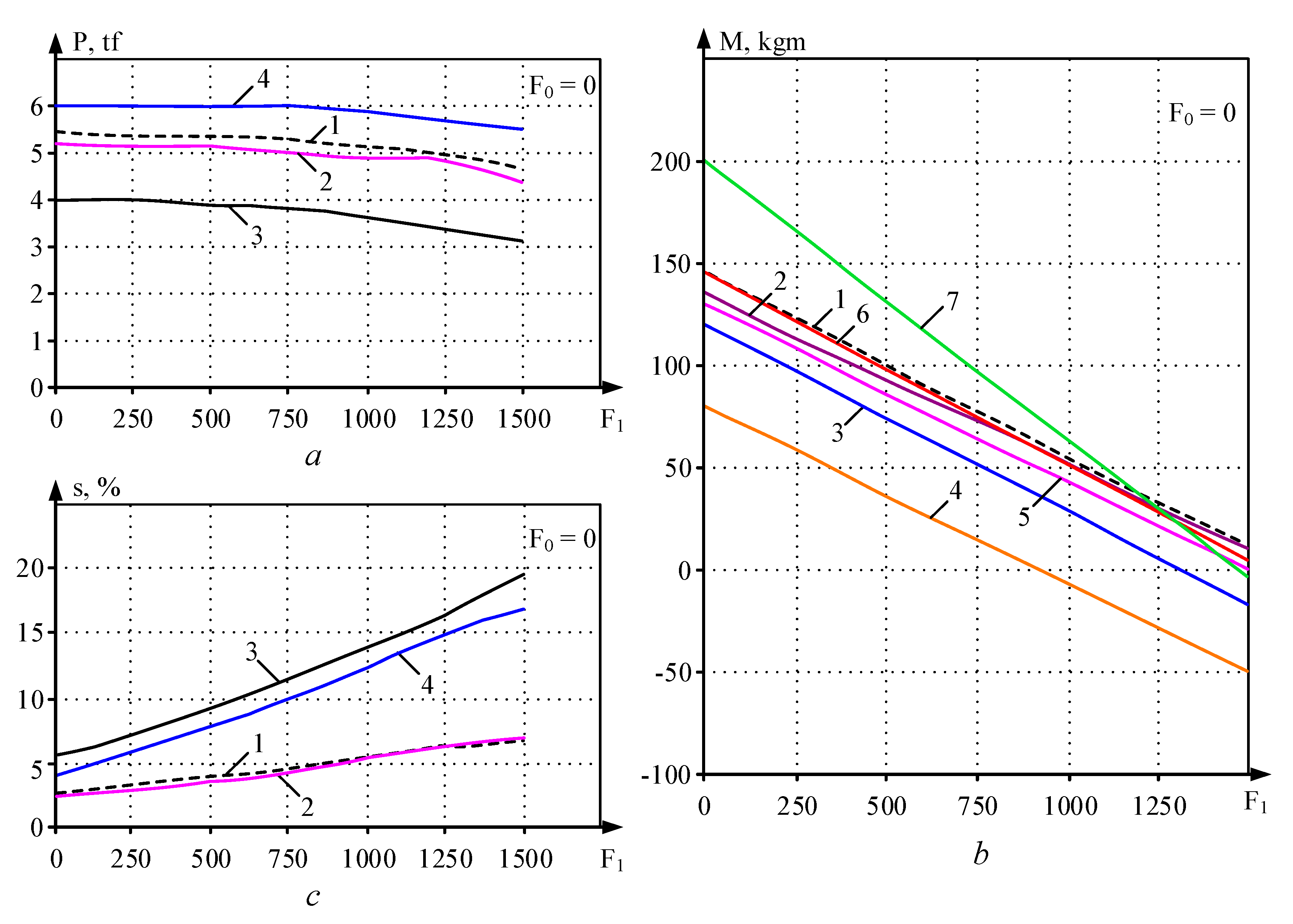
- The considered analytical expressions and the developed digital model reliably reflect the patterns of the metal deformation process in a multi-roll groove. By the nature of the change, they correspond to the results of experimental studies. However, the degree of impact of the process parameters on the rolling pressure, the mill torque and the metal flow are different.
- The closest coincidence of the calculated and experimental data is provided by the mathematical model. In the assessed cases, the discrepancy ceiling is 10–15%.
- From the analytical dependencies considered above, Equation (10) can be recommended for determining the mill torque. It provides acceptable results (the discrepancy at µ = 1.3–1.5 does not exceed 20%) and requires minimal calculations.
- It is advisable to calculate the metal flow in the deformation zone using the mathematical model only. The use of analytical formulas gives a result that is inflated by 2–5 times.
7. Discussion of the Results
8. Conclusions
- The authors carried out a complex of theoretical and experimental studies of power parameters for rolling mills with four-roll pass stands. The obtained results can be used as the initial data for development of new assortments for rolled products or in the design of new mills. The paper analyses the accuracy of determining the power parameters by the known analytical dependences, giving recommendations for their application in calculations.
- The developed digital model of the deformation zone provides more accurate calculations in comparison with analytical expressions. The discrepancy between the results from the model and from the experimental data does not exceed 10–15%.
- When calculating the power of actuating units, the mill torque should be defined using the digital model. For approximate calculations, it is advisable to use Equation (10) as it provides results with acceptable precision while requiring the least amount of calculations.
- The results of experimental research are recommended for the application to optimize drafting, and define energy and power and kinematic parameters and the temperature mode impact at the rolling of the extended range of billets at the existing multi-roll mills.
- The developed model and program for calculating power parameters are recommended for use in studies of rolling on “conventional” cold rolling mills.
Author Contributions
Funding
Conflicts of Interest
References
- Barkov, L.A.; Samodurova, M.N.; Latfulina, Y.S. Processes of obtaining semi-finished products and rods from titanium alloys by pressing and rolling in multi-roll groove. Stock Mater. Mech. Eng. 2016, 11, 3541. [Google Scholar]
- Barkov, L.A.; Samodurova, M.N.; Latfulina, Y.S. Universal mills with multi-roll passes designed by SUSU and their roller assemblies. Russ. Internet J. Ind. Eng. 2017, 5, 11–17. [Google Scholar]
- Barkov, L.A.; Samodurova, M.N. Equipment and technology for pressure treatment of hard-to-deform compacted materials. Bull. South Ural State Univ. Ser. Mech. Eng. 2006, 8, 155–161. [Google Scholar]
- Pesin, A.; Chukin, M.; Pustovoytov, D. Finite element analysis of symmetric and asymmetric three-roll rolling process. In Proceedings of the MATEC Web Conference, Chengdu, China, 23–24 July 2015; Volume 26. [Google Scholar] [CrossRef] [Green Version]
- Barkov, L.A.; Vydrin, V.N.; Pastukhov, V.V. Rolling of Low-Ductility Metals with Multisided Drafting; Metallurgy: Moscow, Russia, 1988; Volume 304. [Google Scholar]
- Polyakov, M.G.; Nikiforov, B.A.; Gun, G.S. Metal Strain in Multi-Roll Passes; Metallurgy: Moscow, Russia, 1979; Volume 240. [Google Scholar]
- Pesin, A.M.; Pustovoitov, V.O.; Kharitonov, V.A. Method of Cold Rolling of Metal Profiles. RF Patent No. 2617191, B21B 1/28, 21 May 2017. [Google Scholar]
- Pesin, A.; Chukin, M.; Korchunov, A.; Pustovoytov, D. Finite element modelling of shear strain in asymmetric and symmetric rolling in multi-roll grooves. Procedia Eng. 2014, 81, 2469–2474. [Google Scholar] [CrossRef]
- Pesin, A.; Chukin, M.; Korchunov, A.; Pustovoytov, D. Finite element modelling of shear strain in rolling with velocity asymmetry in multi-roll grooves. Key Eng. Mater. 2014, 622–623, 912–918. [Google Scholar] [CrossRef]
- Brauer, H. Kocks rolling mill for tungsten and molybdenum. Metall. Met. Form. 1971, 38, 273. [Google Scholar]
- Vydrin, V.N.; Barkov, L.A.; Komarovskiy, I.I. Cold rolling of titanium profiles in multi-roll grooves [Kholodnaya prokatka titanovykh profiley v mnogovalkovykh kalibrakh], Aviatsionnaya promyshlennost. Aircr. Ind. 1978, 3, 54–55. [Google Scholar]
- Vydrin, V.N.; Barkov, L.A.; Pastukhov, V.V. Cold rolling of hexagonal profiles from hard alloys [Kholodnaya prokatka shestigrannykh profiley iz trudnodeformiruemykh splavov], Byulleten “Chernaya metallurgiya”. Bull. Ferr. Metall. 1978, 11, 41–43. [Google Scholar]
- Selivanov, I.A.; Petukhova, O.I.; Bodrov, E.E.; Suzdalev, I.V. Automated Electric Drive of Continuous Rolling Mills with Multi-Roll Passes; MGTU: Magnitogorsk, Russia, 2008; Volume 252. [Google Scholar]
- Karandaev, A.S.; Yakimov, I.A.; Petukhova, O.I.; Antropova, L.I.; Khramshina, E.A. Power parameters of electric drives of five-stand wire rod mill with four-roll passes. In Proceedings of the EIConRus, Moscow, Russia, 1–3 February 2017. [Google Scholar]
- Kharitonov, V.A.; Taranin, I.V. Analysis of the stress-strain state in the deformation zone for wire-rod milling in various groove systems based on modelling by the Finite Element method. News High. Educ. Instit. Ferr. Metall. 2013, 2, 26–30. [Google Scholar]
- Tretyakov, A.V.; Zyuzin, V.I. Mechanical Properties of Metal Alloys During Pressure Treatment; Metallurgy: Moscow, Russia, 1973; Volume 224. [Google Scholar]
- Vydrin, V.N.; Dukmasov, V.G. New in Precision Metal Rolling; South-Urals Publishing House: Chelyabinsk, Russia, 1970; Volume 107. [Google Scholar]
- Vydrin, V.N.; Dukmasov, V.G. Precise Rolling of High-Quality Metal; South-Urals Publishing House: Chelyabinsk, Russia, 1965; p. 120. [Google Scholar]
- Kharitonov, V.A.; Taranin, I.V. Study of the stress state and failure of metal in wire production by various methods of metal working process. Process. Solid Layer. Mater. 2013, 113–120. [Google Scholar]
- Haritonov, V.A.; Taranin, I.V. Modelling of lengthwise rolling in grooves by the finite- elements method. Blank Prod. Mech. Eng. 2013, 7, 36–38. [Google Scholar]
- Joo, H.S.; Hwang, S.K.; Baek, H.M.; Im, Y.; Son, I.; Bae, C.M. The effect of a non-circular drawing sequence on spheroidization of medium carbon steel wires. J. Mater. Process. Technol. 2015, 216, 348–356. [Google Scholar] [CrossRef]
- Li, Y.H.; Park, J.J.; Kim, W.J. Finite element analysis of severe deformation in Mg–3Al–1Zn sheets through differential-speed rolling with a high-speed ratio. Mater. Sci. Eng. A 2007, 454–455, 570–574. [Google Scholar]
- Barkov, L.A.; Vydrin, V.N.; Soloviev, A.V. Power at rolling simple sections in multi-roll passes, rolling theory and technology. In Collection of Research Papers of Chelyabinsk Polytechnic Institute; ChPI: Chelyabinsk, Russian, 1976. [Google Scholar]
- Vydrin, V.N.; Barkov, L.A.; Soloviev, A.V. Torque and power at rolling in forming multi-roll passes. Bull. High. Sch. Iron Steel Ind. 1969, 3, 70–73. [Google Scholar]
- Vydrin, V.N.; Serdyaga, Y.L.; Nagarnov, V.S. Engineering method of rolling power determination. Bull. High. Sch. Iron Steel Ind. 1972, 3, 115–118. [Google Scholar]
- Serdyaga, Y.L.; Vydrin, V.N. Torque and power at rolling in multi-roll passes. In Rolling Theory and Technology. Collection of Research Papers of Chelyabinsk Polytechnic Institute; ChPI: Chelyabinsk, Russian, 1971; Volume 76, pp. 80–85. [Google Scholar]
- Eggertsen, P.; Mattiasson, K. On the modelling of the bending–unbending behaviour for accurate springback predictions. Int. J. Mech. Sci. 2009, 51, 547–563. [Google Scholar] [CrossRef]
- Eggertsen, P.; Mattiasson, K. On the identification of kinematic hardening material parameters for accurate springback predictions. Int. J. Mater. Form. 2011, 4, 103–120. [Google Scholar] [CrossRef]
- Tselikov, A.I.; Grishkov, A.I. Rolling Theory; Metallurgy: Moscow, Russia, 1970; 358p. [Google Scholar]
- Radionov, A.A.; Karandaev, A.S.; Evdokimov, A.S.; Andryushin, I.Y.; Gostev, A.N.; Shubin, A.G. Mathematical modeling of electromechanical systems interconnected continuous-subgroup rolling stands. Part 1: Development of a mathematical model. Bull. South Ural State Univ. Ser. Power Eng. 2015, 15, 59–73. [Google Scholar]
- Selivanov, I.A.; Salganik, V.M.; Gun, I.G.; Petukhova, O.I.; Mamleeva, Y.I. Control Systems of Continuous Rolling Mills. Bull. High. Inst. Electromech. 2011, 4, 36–40. [Google Scholar]
- Shreyner, R.T. Mathematical Modeling ac Electric Drives with Semiconductor Frequency Converters; Ural Branch of the Russian Academy of Sciences: Ekaterinburg, Russia, 2000; p. 654. [Google Scholar]
- Certificate on Official Registration of Software Application No. 2009616950. Simulation of Static and Dynamic Modes of Operation of Four-Roll Pass Wire Rolling Mill; Applicant and patent holder GOU VPO Nosov Magnitogorsk State Technical University; No. 2009615980; Petukhova, O.I., Radionov, A.A., Malakhov, O.S., Linkov, S.A., Eds.; Magnitogorsk State Technical University: Magnitogorsk, Russia, 2009. [Google Scholar]
- Grudnev, A.P. External Friction at Rolling; Metallurgy: Moscow, Russia, 1971; Volume 215. [Google Scholar]
- Benyakovsky, M.A.; Brovman, M.Y. Tensometry Application in Rolling; Metallurgy: Moscow, Russia, 1965; Volume 144. [Google Scholar]
- Zagirov, N.N.; Konstantinov, I.L.; Ivanov, E.V. Fundamentals of Calculations of the Processes of Obtaining Long Metal Products by Methods of Pressure-Based Metal Treatment; Siberian Federal University: Krasnoyarsk, Russia, 2011; Volume 312. [Google Scholar]
- Nekit, V.A.; Platov, S.I.; Kurbakov, I.A.; Golev, A.D. Experimental study of advancing and lagging in rolling. Bull. Nosov Magnitogorsk State Tech. Univ. 2015, 1, 52–54. [Google Scholar]
- Selivanov, I.A.; Petukhova, O.I.; Radionov, A.A.; Suzdalev, I.V. Synthesis of systems of subordinate monitoring of processes at continuous mills. Izv. vuzov. Electromech. 2009, 1, 21–24. [Google Scholar]
- Selivanov, I.A.; Petukhova, O.I.; Radionov, A.A.; Suzdalev, I.V. Mathematical modelling of control system for continuous mill when driven stand is powered from power source. Izv. Vuzov. Electromech. 2009, 1, 25–27. [Google Scholar]
- Selivanov, I.A.; Petukhova, O.I.; Bodrov, E.Y.; Suzdalev, I.V. Synthesis of control systems for continuous mills with multi-roll calibers. Bull. South Ural State Univ. 2009, 15, 60–63. [Google Scholar]
- Andryushin, I.Y.; Galkin, V.V.; Gostev, A.N.; Kazakov, I.V.; Evdokimov, S.A.; Karandaev, A.S.; Khramshin, V.R.; Khramshin, R.R. Method for Automatic Coil Tension Control in the Roughing Group of Continuous Mill Stands. RF Patent No. 2494828, 10 October 2013. [Google Scholar]
- Khramshin, V.R.; Karandaev, A.S.; Khramshin, R.R.; Andryushin, I.Y.; Gostev, A.N. Device for Automatic Metal Tension Control in Two Inter-Stand Spaces of Roughing Group of Hot Rolling Mill. RF Patent No. 147042, MPK B21B 37/52, 27 October 2014. [Google Scholar]
- Radionov, A.A.; Karandaev, A.S.; Khramshin, V.R.; Andryushin, I.Y.; Gostev, A.N. Speed and load modes of rolling hollow billet at the wide-strip rolling mill. In Proceedings of the MEACS, Tomsk, Russia, 16–18 October 2014. [Google Scholar]
- Khramshin, V.R.; Karandaev, A.S.; Evdokimov, S.A.; Andryushin, I.Y.; Shubin, A.G.; Gostev, A.N. Reduction of the dynamic loads in the universal stands of a rolling mill. Metallurgist 2015, 59, 315–323. [Google Scholar] [CrossRef]
- Khramshin, V.R.; Evdokimov, S.A.; Karandaev, A.S.; Andryushin, I.Y.; Shubin, A.G. Algorithm of No-Pull Control in the Continuous Mill Train. In Proceedings of the SIBCON, Omsk, Russia, 21–23 May 2015. [Google Scholar]
- Andryushin, I.Y.; Shubin, A.G.; Gostev, A.N.; Radionov, A.A.; Karandaev, A.S.; Gasiyarov, V.R.; Khramshin, V.R. Automatic tension control in the continuous roughing train of a wide-strip hot-rolling mill. Metallurgist 2017, 61, 366–374. [Google Scholar] [CrossRef]
- Radionov, A.A.; Maklakov, A.S.; Gasiyarov, V.R.; Maklakova, E.A. Research of electric drive at load impact on hot plate mill 5000. In Proceedings of the MEACS, Tomsk, Russia, 1–4 December 2015. [Google Scholar]
- Gasiyarov, V.R.; Karandaev, A.S.; Radionov, A.A.; Khramshin, V.R.; Maklakov, A.S. Correcting electric motor drive speed of plate mill stand in profiled sheet rolling. In Proceedings of the PEDES, Chennai, India, 18–21 December 2018. [Google Scholar]
- Gasiyarov, V.R.; Radionov, A.A.; Karandaev, A.S.; Loginov, B.M.; Khramshin, V.R.; Maklakov, A.S. Coordinating the modes of the axial roll shifting and roll bending systems of a roll mill stand. In Proceedings of the IECON, Lisbon, Portugal, 14–17 October 2019; pp. 330–335. [Google Scholar]

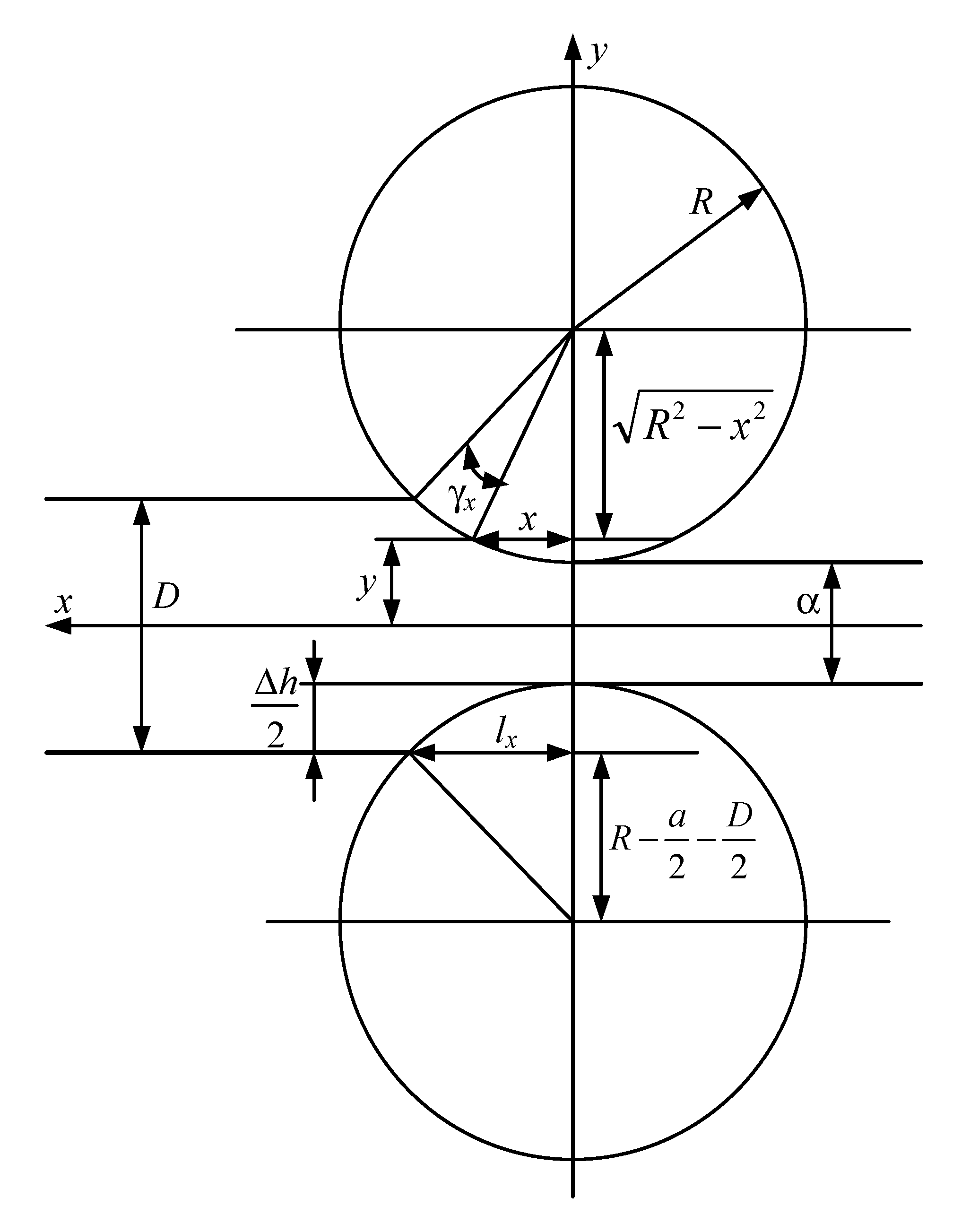
| Description | Diagram | Draw-Down Ratio |
|---|---|---|
| Circle–square |  | µ = 1.57 |
| Circle–octagon |  | µ = 1.11 |
| Octagon–square |  | µ = 1.66 |
| Octagon–octagon |  | µ = 1.17 |
| Octagon–circle |  | µ = 1.05 |
| Material | Original Rod Wire Diameter, mm | Initial Billet Heat Treatment | |
|---|---|---|---|
| Characteristics | Grade | ||
| Pearlite high carbon steel | ShKh15 | 5.5–8 | Oxidizing annealing in chamber furnaces |
| Ledeburite chisel rapid steel | R6M5 RI8 | 5.5–8 | Oxidizing annealing in chamber furnaces |
| Ferritic and martensite stainless corrosion-resistant steel | IKhI3 | 5.5–8 | Annealing in the furnaces with a blanketing atmosphere |
| Austenitic stainless corrosion-resistant steel | KhI8N9T | 5.5–8 | Annealing in the furnaces with a blanketing atmosphere |
| Ferritic scale-proof steel | 0Kh23Yu5A 0Kh27Yu5A | 8 | Annealing in the furnaces with a blanketing atmosphere |
| Austenitic heat-resistant nickel-based alloys | KhN568MTYuR KhN678MTYu | 6.5 | Hardening 1200 °C outside |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samodurova, M.N.; Karandaeva, O.I.; Khramshin, V.R.; Liubimov, I.V. Calculating Power Parameters of Rolling Mill Based on Model of Deformation Zone with Four-Roll Passes. Machines 2020, 8, 73. https://doi.org/10.3390/machines8040073
Samodurova MN, Karandaeva OI, Khramshin VR, Liubimov IV. Calculating Power Parameters of Rolling Mill Based on Model of Deformation Zone with Four-Roll Passes. Machines. 2020; 8(4):73. https://doi.org/10.3390/machines8040073
Chicago/Turabian StyleSamodurova, Marina N., Olga I. Karandaeva, Vadim R. Khramshin, and Ivan V. Liubimov. 2020. "Calculating Power Parameters of Rolling Mill Based on Model of Deformation Zone with Four-Roll Passes" Machines 8, no. 4: 73. https://doi.org/10.3390/machines8040073
APA StyleSamodurova, M. N., Karandaeva, O. I., Khramshin, V. R., & Liubimov, I. V. (2020). Calculating Power Parameters of Rolling Mill Based on Model of Deformation Zone with Four-Roll Passes. Machines, 8(4), 73. https://doi.org/10.3390/machines8040073







