Cooling Performance Analysis of Outside Fins of the Closed Circuit Axial Piston Transmission
Abstract
:1. Introduction
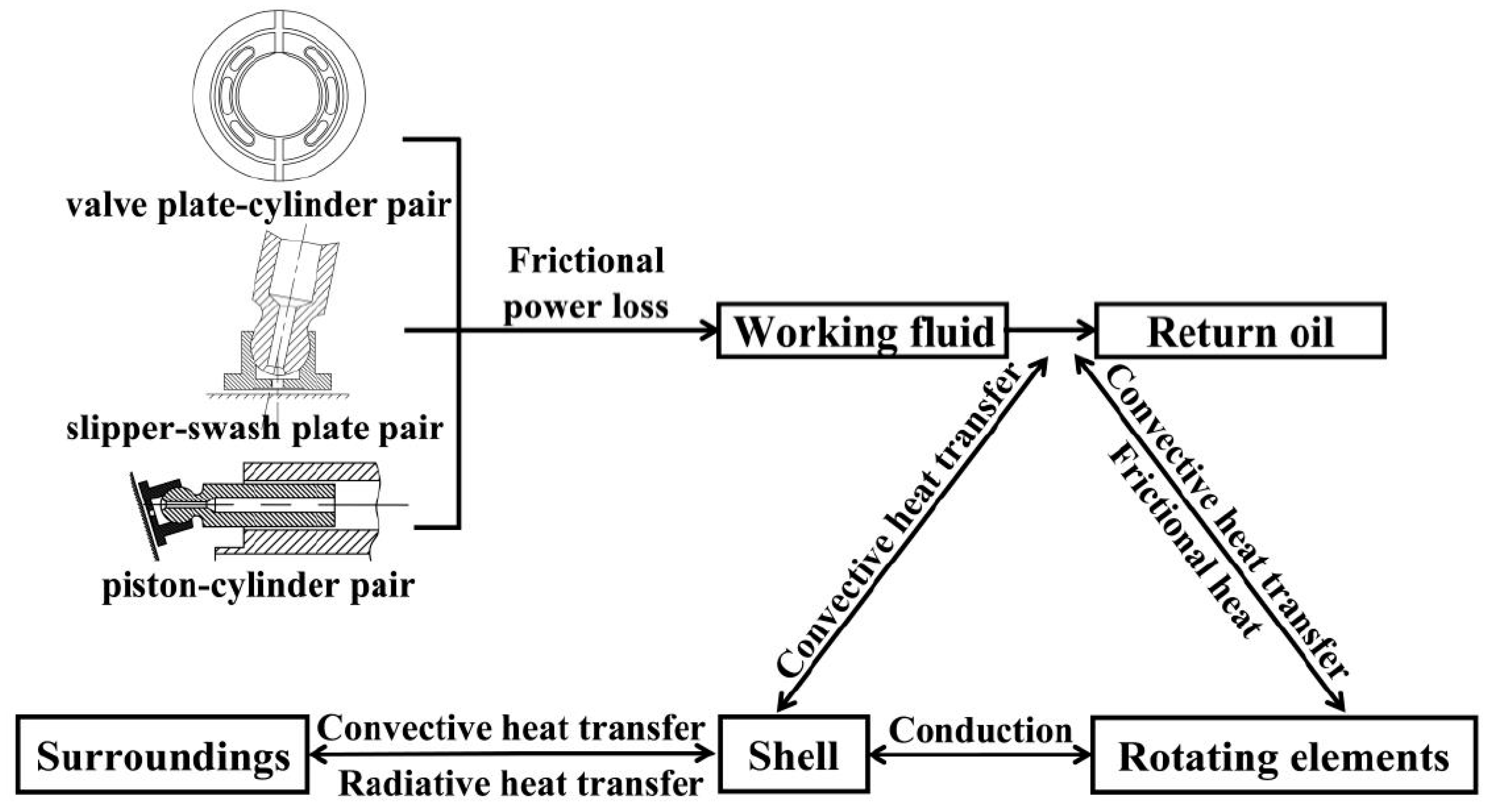
2. Analysis and Modeling
2.1. Geometrical Model
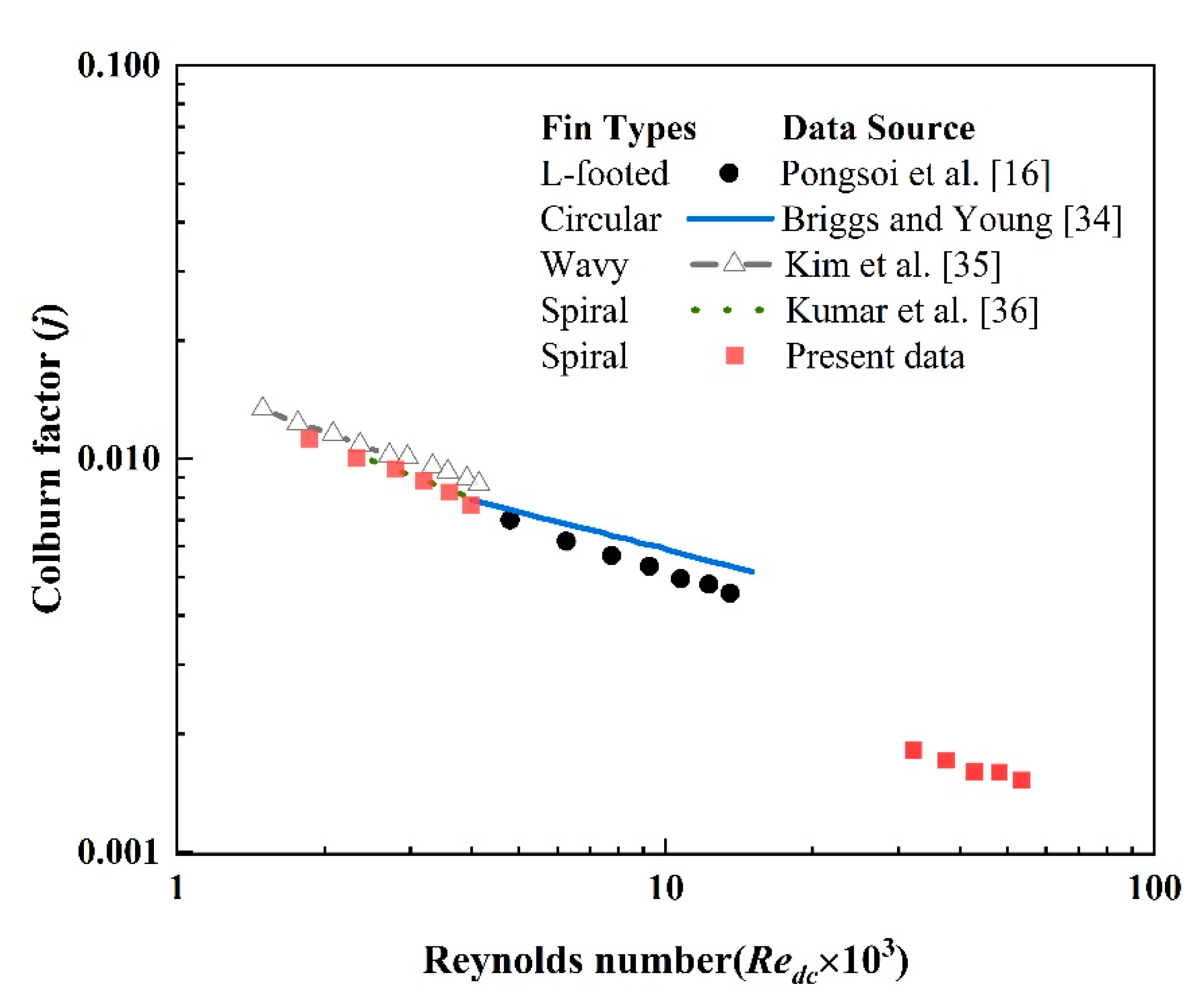
2.2. Data Reduction
2.3. Mesh and Boundary Conditions
- (1)
- The CCAPT operates under the steady state, which means the volume loss and the mechanical loss are constant during the simulation.
- (2)
- Neglect the temperature differences between the shell and the internal rotating elements.
- (3)
- Take no account of the variance of the ambient temperature.
- (4)
- Leave out the pressure pulsation inside the CCAPT.
3. Results and Discussion
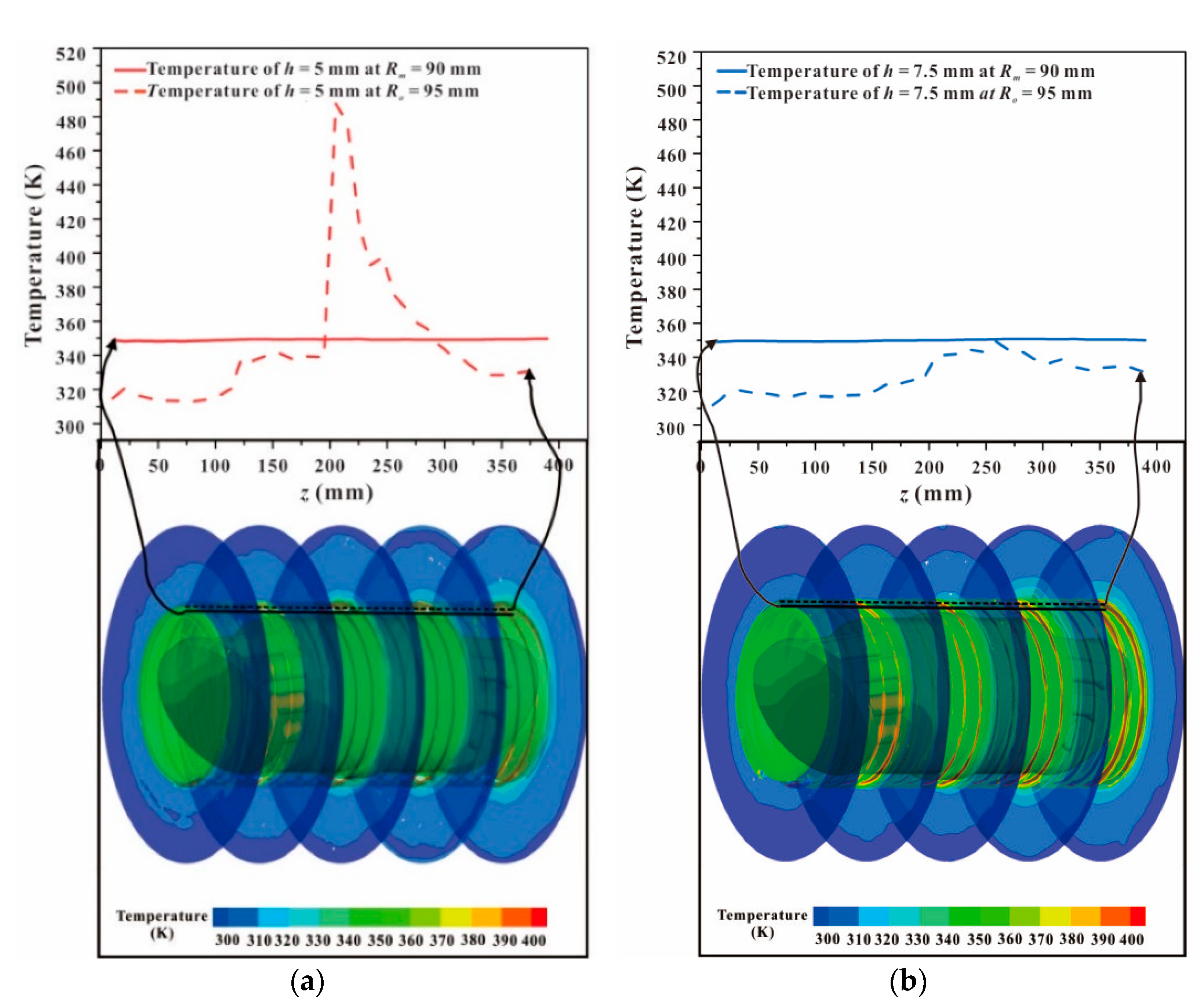
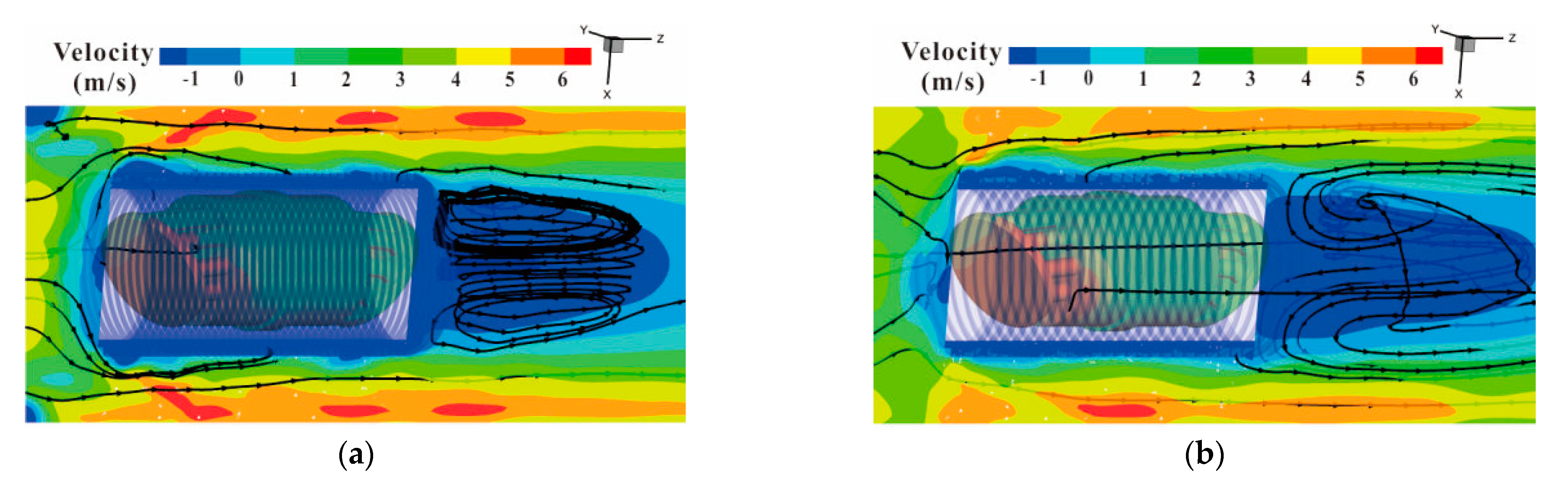
3.1. Temperature Distribution Inside the CCAPT
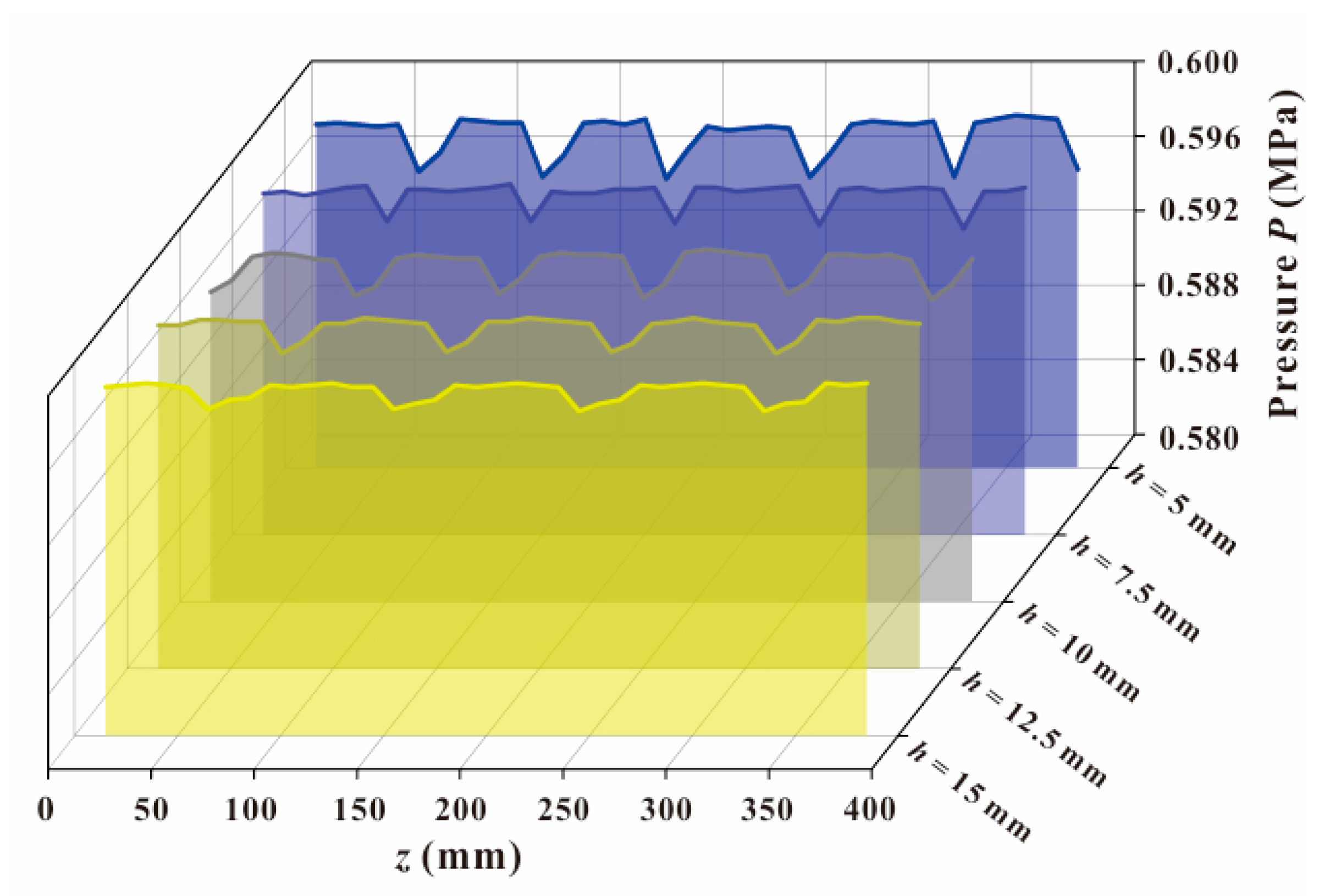
3.2. Effect of Fin Height h
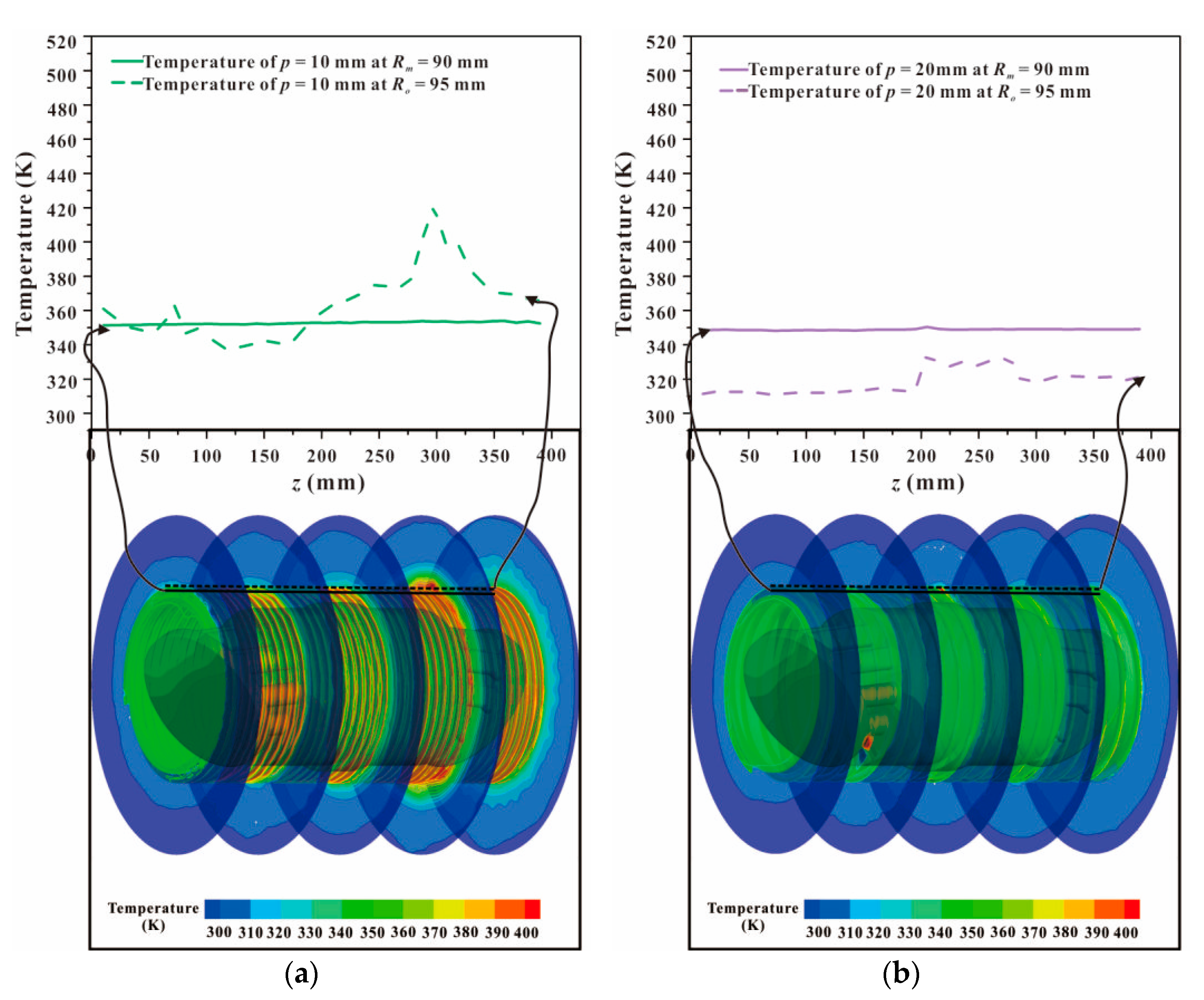
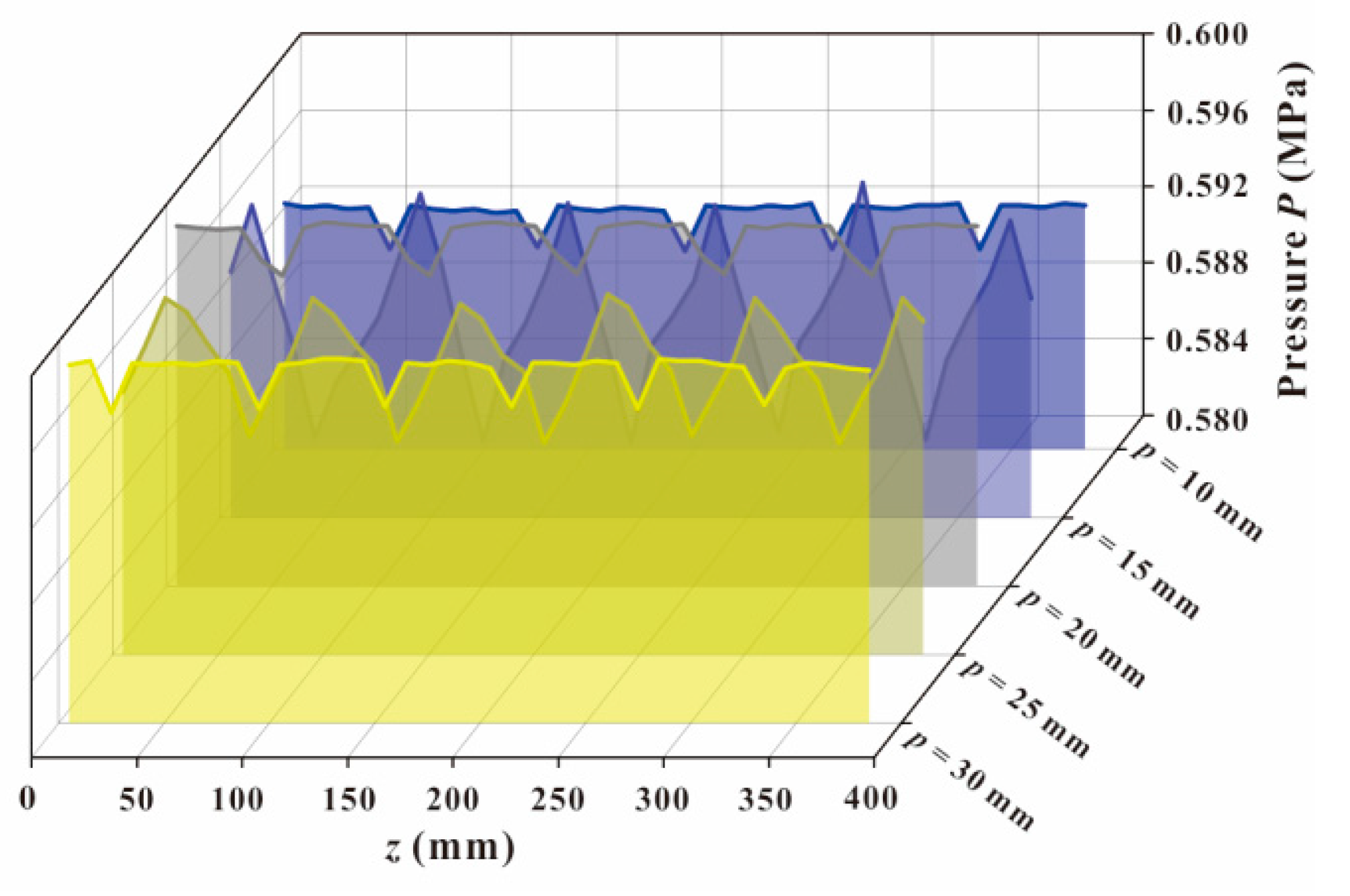
3.3. Effect of Fin Pitch p
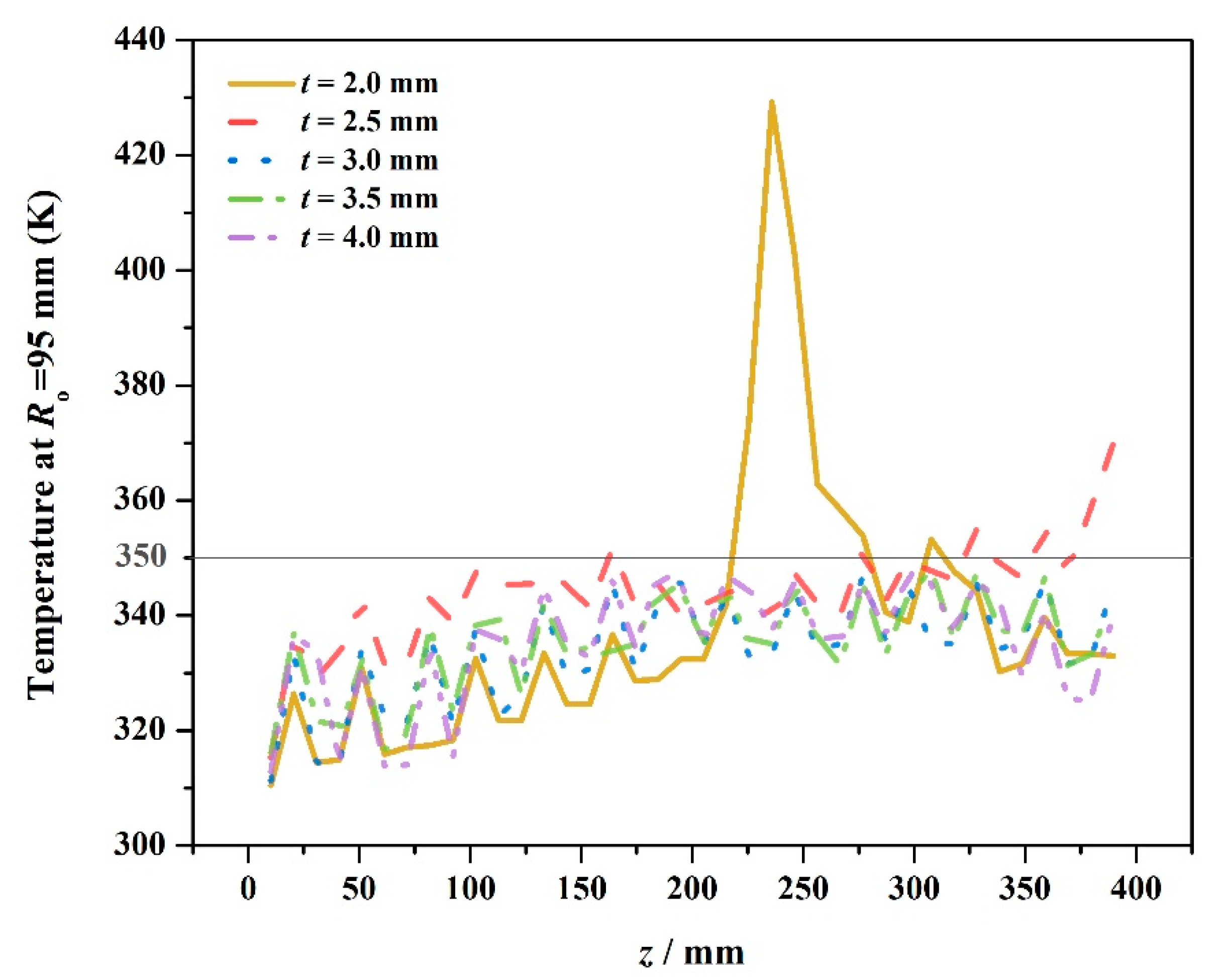
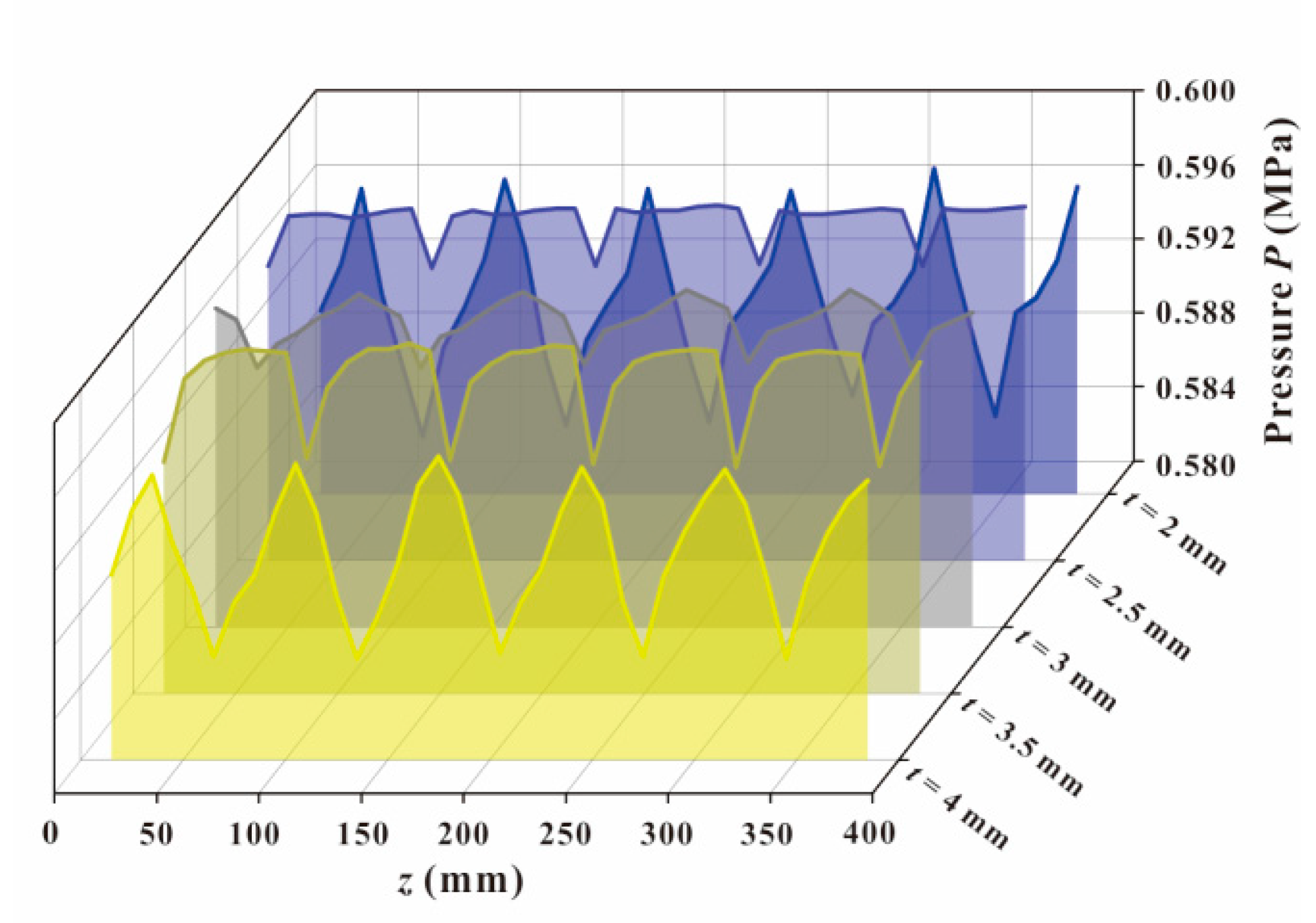
3.4. Effect of Fin Thickness t
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Aa | Total heat transfer area | mm2 |
| Acf | Heat transfer area between the shell and fluids | mm2 |
| Ach | Heat transfer area between the shell and environments | mm2 |
| Acs | Contact area between rotating area and the shell | mm2 |
| Af | Area of the fin structure | mm2 |
| Asf | Heat transfer area between rotating element and fluid | mm2 |
| Cp | Specific heat capacity | J·kg−1·K−1 |
| dcf | Characteristic diameter of the inner surface | mm |
| Gr | Grashof number | |
| h | Fin height | mm |
| hi | Heat transfer coefficient | W·m−2·K−1 |
| hc | Thickness of pump shell | mm |
| j | Colburn factor | |
| kf | Thermal conductivity of the material of the fin structure | W·m−2·K−1 |
| l | Half the length of the fin height | mm |
| Nu | Nusselt number | |
| Nux | Local Nusselt number | |
| p | Pitch | mm |
| P | Pressure | Pa |
| Pr | Prandtl number | |
| Q | Heat transfer quantity | J |
| Convective heat transfer rate between the shell and fluids | W | |
| Convective heat transfer rate between the shell and surroundings | W | |
| Heat transfer rate of thermal conduction between rotating element and system | W | |
| Radiative heat transfer rate between the shell and ambient environment | W | |
| Heat transfer rate of forced convection between the rotating element and fluid | W | |
| Re | Reynolds number | |
| Tcn | Temperature of inner surface | K |
| Tcw | Temperature of outer surface | K |
| Tf | Temperature of fluid | K |
| Th | Temperature of environment | K |
| Ts | Surface temperature of rotating element | K |
| t | Fin thickness | mm |
| u | Velocity | m·s−1 |
| Greek symbols | ||
| ε | Blackness of shell material | |
| αcf | Convection coefficient between the shell and fluids | W·m−2·K−1 |
| αchf | Convection coefficient between the shell and surroundings | W·m−2·K−1 |
| αsf | Convective heat transfer coefficient between rotating elements and fluid | W·m−2·K−1 |
| η0 | Surface coefficient of the fin | |
| ηf | Fin efficiency | |
| λ | Thermal conductivity | W·m−1·K−1 |
| ρ | Density | kg/m3 |
| σ | The Stefan-Boltzmann constant | W·m−2·K−4 |
| ΔP | Pressure difference | Pa |
| ΔTLMTD | Logarithm mean temperature difference | K |
References
- Wang, Z.W.; Wang, L.; Ma, A.H.; Liang, K.F.; Song, Z.; Feng, L.W. Performance evaluation of ground water-source heat pump system with a fresh air pre-conditioner using ground water. Energy Convers. Manag. 2019, 188, 250–261. [Google Scholar] [CrossRef]
- Sergey, A. System of energy-saving optimal control of metal heating process in heat treatment furnaces of rolling mills. Machines 2019, 7, 60. [Google Scholar]
- Harish, S.; Simone, B. A novel modelling approach for condensing boilers based on hybrid dynamical systems. Machines 2016, 4, 10. [Google Scholar]
- Muhammad, S.U.Z.; Raza, H.; Syed, B.A.B.; Hafiz, M.A.; Chul-Hwan, K. Impacts of responsive loads and energy storage system on frequency response of a multi-machine power system. Machines 2019, 7, 1–15. [Google Scholar]
- Gao, D.R.; Zhang, Z.Y.; Sun, Y.N.; Xu, S.H.; Liu, J.C.; Zhang, Y. Numerical simulation and analysis of temperature and flow field of high-speed axial piston motor pump. J. Eng. 2019, 13, 127–131. [Google Scholar] [CrossRef]
- Chen, H.; Peng, Y.H.; Wang, Y.L.; Zhang, J. Thermodynamic analysis of hybrid cooling system integrated with waste heat reusing and peak load shifting for data center. Energy Convers. Manag. 2019, 183, 427–439. [Google Scholar] [CrossRef]
- Chan, M.A.; Yap, C.R.; Ng, K.C. Modeling and testing of an advanced compact two-phase cooler for electronics cooling. Int. J. Heat Mass Transf. 2009, 52, 3456–3463. [Google Scholar] [CrossRef]
- Alexey, N.; Innokentiy, S.; Igor, S. The setup design for selective laser sintering of high-temperature polymer materials with the alignment control system of layer deposition. Machines 2018, 6, 11. [Google Scholar]
- Amber, K.P.; Akram, W.; Bashir, M.A.; Muhammad, S.K.; Anila, K. Experimental performance analysis of two different passive cooling techniques for solar photovoltaic installations. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Pongsoi, P.; Pikulkajorn, S.; Wang, C.C.; Wongwises, S. Effect of number of tube rows on the air-side performance of crimped spiral fin-and-tube heat exchangers with a multipass parallel and counter cross-flow configuration. Int. J. Heat Mass Transf. 2012, 55, 1403–S1411. [Google Scholar] [CrossRef]
- Dezan, D.J.; Yanagihara, J.I.; Jenovencio, G.; Leandro, O.S. Parametric investigation of heat transfer enhancement and pressure loss in louvered fins with longitudinal vortex generators. Int. J. Therm. Sci. 2019, 135, 533–545. [Google Scholar] [CrossRef]
- Kim, N.H. Airside performance of fin-and-tube heat exchangers having nonrepeating nonsymmetrical slit fins under wet condition. Int. J. Air-Cond. Refrig. 2019, 27, 1950033. [Google Scholar] [CrossRef]
- Shadlaghani, A.; Farzaneh, M.; Shahabadi, M. Numerical investigation of serrated fins on natural convection from concentric and eccentric annuli with different cross sections. J. Therm. Anal. Calorim. 2018, 135, 1429–1442. [Google Scholar] [CrossRef]
- Alsallami, W.; Aldamook, A.; Thompson, H.M. A numerical investigation of the thermal-hydraulic characteristics of perforated plate fin heat sinks. Int. J. Therm. Sci. 2017, 121, 266–277. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.; Kang, T.; Kim, Y. Air-side heat transfer characteristics of spiral-type circular fin-tube heat exchangers. Int. J. Refrig. 2010, 33, 313–320. [Google Scholar] [CrossRef]
- Kim, N. An experimental investigation on the airside performance of fin-and-tube heat exchangers having radial slit fins under wet condition. Int. J. Therm. Sci. 2016, 11, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Pongsoi, P.; Promoppatum, P.; Pikulkajorn, S.; Wongwises, S. Effect of fin pitches on the air-side performance of L-footed spiral fin-and-tube heat exchangers. Int. J. Heat Mass Transf. 2013, 59, 75–82. [Google Scholar] [CrossRef]
- Nørgård, J. Thermodynamic determination of power loss in hydraulic components. J. Fluids Eng. 1973, 95, 2–7. [Google Scholar] [CrossRef]
- Olems, L. Investigations of the Temperature behaviour of the piston cylinder assembly in axial piston pumps. Int. J. Fluid Power 2000, 1, 27–39. [Google Scholar] [CrossRef]
- Iboshi, N.; Yamaguchi, A. Characteristics of a slipper bearing for swash plate type axial piston pumps and motors: 1st report, theoretical-analysis. JSME Int. J. Ser. B-Fluids Therm. Eng. 1982, 25, 1921–1930. [Google Scholar] [CrossRef] [Green Version]
- Iboshi, N. Characteristics of a slipper bearing for swash plate type axial piston pumps and motors: 2nd report, experiment. JSME Int. J. Ser. B-Fluids Therm. Eng. 1983, 26, 1583–1589. [Google Scholar] [CrossRef] [Green Version]
- Iboshi, N.; Yamaguchi, A. Characteristics of a slipper bearing for swash plate type axial piston pumps and motors: 3rd report, design method for a slipper with a minimum power loss in fluid lubrication. JSME Int. J. Ser. B-Fluids Therm. Eng. 1986, 29, 2529–2538. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Wang, Q.N.; Zhang, J.H. Effect of case drain pressure on slipper/swashplate pair within axial piston pump. J. Zhejiang Univ.-Sci. A 2015, 16, 1001–1014. [Google Scholar] [CrossRef]
- Wieczorek, U.; Monika, I. Computer aided optimization of bearing and sealing gaps in hydrostatic machines—the simulation tool caspar. Int. J. Fluid Power 2002, 3, 7–20. [Google Scholar] [CrossRef]
- Li, D.L.; Li, G.Q.; Han, J.H.; Liu, Y.S.; Wu, D.F. Thermodynamic characteristics research of a water lubricating axial piston pump. Proc. Inst. Mech. Eng. C-J. Mech. 2020. [Google Scholar] [CrossRef]
- Xu, B.; Hu, M.; Zhang, J.H.; Mao, Z.B. Distribution characteristics and impact on pump’s efficiency of hydro-mechanical losses of axial piston pump over wide operating ranges. Cent. South Univ. 2017, 24, 609–624. [Google Scholar] [CrossRef]
- Xu, B.; Hu, M.; Zhang, J.H.; Su, Q. Characteristics of volumetric losses and efficiency of axial piston pump with respect to displacement conditions. J. Zhejiang Univ.-Sci. A 2016, 17, 186–201. [Google Scholar] [CrossRef] [Green Version]
- Ye, S.; Zhang, J.; Xu, B.; Zhu, S.; Xiang, J.; Tang, H. Theoretical investigation of the contributions of the excitation forces to the vibration of an axial piston pump. Mech. Syst. Signal Process. 2019, 129, 201–217. [Google Scholar] [CrossRef]
- Ye, S.; Zhang, J.; Xu, B.; Hou, L.; Xiang, J.; Tang, H. A theoretical dynamic model to study the vibration response characteristics of an axial piston pump. Mech. Syst. Signal Process. 2021, 150, 107237. [Google Scholar] [CrossRef]
- Amiri, H.A.; Shafaghat, R.; Alamian, R.; Taheri, S.M.; Shadloo, M.S. Study of horizontal axis tidal turbine performance and investigation on the optimum fixed pitch angle using CFD. Int. J. Numer. Method Heart 2020, 30, 206–227. [Google Scholar] [CrossRef]
- Alavi, S.M.A.; Safaei, M.R.; Mahian, O.; Goodarzi, M.; Yarmand, H.; Dahari, M.; Wongwises, S. A hybrid finite-element/finite-difference scheme for solving the 3-d energy equation in transient nonisothermal fluid flow over a staggered tube bank. Numer. Heat Transf. B-Fundam. 2015, 68, 169–183. [Google Scholar] [CrossRef] [Green Version]
- Roberto, M. Pollutant emission validation of a heavy-duty gas turbine burner by CFD modeling. Machines 2013, 1, 81–97. [Google Scholar]
- Nemati, H.; Moghimi, M.A.; Sapin, P.; Markides, C.N. Shape optimisation of air-cooled finned-tube heat exchangers. Int. J. Therm. Sci. 2020, 150, 106233. [Google Scholar] [CrossRef]
- Briggs, D.E.; Young, E.H. Convective heat transfer and pressure drop of air flowing across triangular pitch banks of finned tubes. Chem. Prog. Eng. Symp. Ser. 1963, 59, 1–10. [Google Scholar]
- Kim, N.H.; Ham, J.H.; Cho, J.P. Experimental investigation on the airside performance of fin-and-tube heat exchangers having herringbone wave fins and proposal of a new heat transfer and pressure drop correlation. J. Mech. Sci. Technol. Convers. Manag. 2008, 22, 545–555. [Google Scholar] [CrossRef]
- Kumar, A.; Joshi, J.B.; Nayak, A.K. A comparison of thermal-hydraulic performance of various fin patterns using 3D CFD simulations. Int. J. Heat Mass Transf. 2017, 109, 336–356. [Google Scholar] [CrossRef]






| Material | Pump Housing | Motor Housing |
|---|---|---|
| 40Cr | ZL105 | |
| Density/(kg m−3) | 7820 | 2680 |
| Specific heat capacity/(J kg−1 K−1) | 460 | 837 |
| Thermal conductivity/(W m−1 K−1) | 32.6 | 163.3 |
| Fin Height (mm) | Nu | j (10−3) |
|---|---|---|
| 5.0 | 89.02 | 1.77 |
| 7.5 | 108.27 | 1.81 |
| 10.0 | 93.75 | 1.79 |
| 12.5 | 81.02 | 1.77 |
| 15.0 | 74.61 | 1.73 |
| without fin structure | 51.76 | - |
| Fin Pitch (mm) | Nu | j (10−3) |
|---|---|---|
| 10 | 83.75 | 1.72 |
| 15 | 87.13 | 1.75 |
| 20 | 93.75 | 1.79 |
| 25 | 99.42 | 1.80 |
| 30 | 105.73 | 1.83 |
| without fin structure | 51.76 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Yu, L.-j.; Zhang, J.; Qian, J.-y. Cooling Performance Analysis of Outside Fins of the Closed Circuit Axial Piston Transmission. Machines 2021, 9, 17. https://doi.org/10.3390/machines9010017
Yang C, Yu L-j, Zhang J, Qian J-y. Cooling Performance Analysis of Outside Fins of the Closed Circuit Axial Piston Transmission. Machines. 2021; 9(1):17. https://doi.org/10.3390/machines9010017
Chicago/Turabian StyleYang, Chen, Long-jie Yu, Junhui Zhang, and Jin-yuan Qian. 2021. "Cooling Performance Analysis of Outside Fins of the Closed Circuit Axial Piston Transmission" Machines 9, no. 1: 17. https://doi.org/10.3390/machines9010017
APA StyleYang, C., Yu, L.-j., Zhang, J., & Qian, J.-y. (2021). Cooling Performance Analysis of Outside Fins of the Closed Circuit Axial Piston Transmission. Machines, 9(1), 17. https://doi.org/10.3390/machines9010017







