Thermal Analysis of Low-Power Three-Phase Induction Motors Operating under Voltage Unbalance and Inter-Turn Short Circuit Faults

Abstract

Three-phase induction motors are considered to be the workhorse of industry. Therefore, induction motor faults are not only the cause of users’ frustrations but they also drive up the costs related to unexpected breakdowns, repair actions, and safety issues. One of the most critical faults in three-phase induction motors is related to the occurrence of inter-turn short circuits, due to its devastating consequences. The topic of inter-turn short-circuit faults in three-phase induction motors has been discussed over recent decades by several researchers. These studies have mainly dealt with early fault detection to avoid dramatic consequences. However, they fall short of addressing the potential burnout of the induction motor before the detection step. Furthermore, the cumulative action played by an inevitable degree of unbalanced supply voltages may exacerbate such consequences. For that reason, in deep detail, this paper delves into the thermal analysis of the induction motor when operating under these two harsh conditions: unbalanced supply voltages and the presence of the most incipient type of inter-turn short-circuit condition—a short-circuit between two turns only. In this work, the finite element method has been applied to create the faulty scenarios, and a commercial software (Flux2D) has been used in order to simulate the electromagnetic and thermal behavior of the machine for various degrees of severity of the aforementioned faulty modes. The obtained results confirm that the diagnostic tools reported in the literature might not be effective, failing to warrant the required lead time so that suitable actions can be taken to prevent permanent damage to the machine.

1. Introduction

The induction motor (IM) is widely used in industry because it provides good performance as well as high reliability and durability [1,2]. IMs can be found in many applications which create, in turn, potentially stressed conditions. Working under these conditions adversely affects IMs performance [3].

IMs fault diagnosis is very important, as it avoids dramatic consequences to the machine itself and to the surrounding environment. The major faults that can affect the operation of electrical machines, are broadly classified as: (1) stator faults, resulting from the opening or shorting of one or more turns; (2) abnormal connection of the stator windings; (3) broken rotor bars or cracked rotor end-rings; (4) static and/or dynamic air-gap eccentricity; (5) bent shaft (akin to dynamic eccentricity) which can result in a rub between the rotor and stator, causing serious damage to the stator core and windings; (6) shorted rotor field winding; (7) bearings and gearbox failures [4].

This paper focuses on the stator faults, which are due to several different stresses, mainly grouped into four categories [5]:

(1)

Thermal: aging, overloading, cycling.

(2)

Electrical: dielectric, tracking, transients.

(3)

Mechanical: coil movement, rotor strike, miscellaneous.

(4)

Environmental: moisture, chemical, abrasion.

The voltage unbalance is one of the electrical supply conditions that cannot be completely avoided. In recent years, this issue has gained much importance [6]. Over long time intervals, the abnormal supply causes aging of the stator windings’ insulation, and weak turns insulation lead to 80% of all the electrical failures in the stator [7]. This might cause a coil-to-coil short-circuit in the same phase or between two phases. Later, these faults can be developed into another severe short-circuit fault, known as a phase-to-ground fault [8,9]. 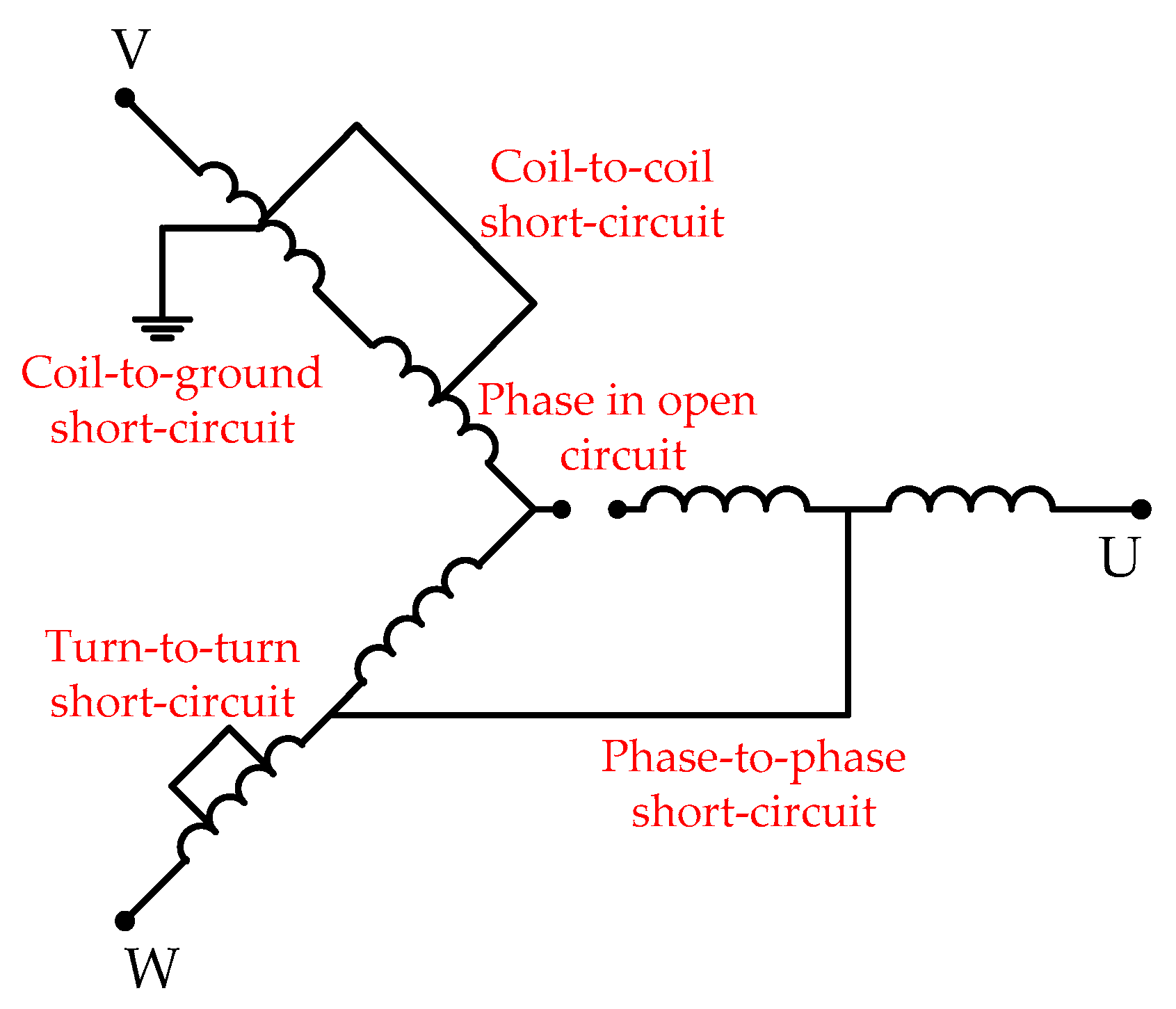Figure 1 summarizes the different possible short- or open-circuit faults that may happen in the stator windings.

The inter-turn short-circuit generates an abnormal IMs behavior under closed loop control. A qualitative analysis of direct torque control (DTC) drives proves that the flux and torque hysteresis controllers tend to introduce a significant third harmonic component in the stator currents [11]. Furthermore, the occurrence of an inter-turn short circuit in the stator windings of an induction motor introduces a negative sequence component in the motor supply currents. As well as the production of the negative sequence component mentioned before, this failure introduces an additional term in the positive sequence component of the motor supply current at the fundamental supply frequency [12]. Consequently, a large faulty current, higher than the healthy one, will be circulating in the short-circuit, therefore adversely affecting the stator insulation. In the literature, many papers consider the diagnosis of the insulation fault [7]. If this weakness is detected at an early stage, the motor can be repaired, and the lifetime of the machine can be prolonged.

Many researchers have discussed the topic of inter-turn short-circuit faults in IMs. Different diagnostic techniques have been proposed, which may be classified into signal-based, model-based, and data-driven approaches. The proposed strategies aim to detect rapidly and accurately the faults, in order to avoid drastic consequences. However, they fall short of addressing the potential burnout of the induction motor before the detection step.

This paper focuses on IM thermal analysis at a very early stage of the inter-turn short-circuit occurrence (only two shorted turns). Besides the aforementioned faulty condition, a squirrel-cage delta-connected IM fed by an unbalanced voltage is also considered. In this study, the finite element method (FEM) provides the transient and the steady-state temperatures in different locations of the IM.

The rest of the paper is divided into four sections: the motivation for the conducted work is firstly presented; after, the finite element method is proposed to simulate the different intended scenarios, and in the following section, the results are presented and discussed. Finally, the main conclusions are presented, and some perspectives of future work are also suggested.

2. Motivation

According to several studies under the auspices of the Institute of Electrical and Electronics Engineers (IEEE) and the Electric Power Research Institute (EPRI), stator winding faults account for 35% of IM failures. Hence, the researchers classified it as a major fault [10,13].

To handle the stator faults and especially inter-turn short-circuit faults, the researchers typically use diagnostic techniques, trying to ensure an early detection. However, to the authors’ best knowledge, there are no other studies in the published literature dealing with such a small degree of severity of fault—a short-circuit between two turns, only—as it remains undetectable by the existing fault diagnostic techniques. Therefore, despite the very interesting published studies on this topic, they fall short of addressing the potential burnout of IMs before the detection step.

Furthermore, the cumulative action played by an inevitable degree of unbalanced supply voltages may introduce further complexity to the diagnostics process.

Therefore, this paper presents analysis of the IM thermal behavior under the presence of several scenarios: (a) healthy conditions—characterized by the simultaneous absence of inter-turn short-circuits and unbalanced supply voltages; (b) absence of inter-turn short-circuits but under unbalanced supply voltage conditions; and (c) simultaneous occurrence of inter-turn short-circuits and unbalanced supply voltages. However, it has to be clearly stated that the purpose of this work is not to propose any fault diagnostic strategy, but rather to evaluate to what extent the available fault diagnostic strategies are ineffective in preventing permanent damages to induction machines.

2.1. Unbalance Voltage

The electrical grid is described by international standard definitions. When at least one of the supply characteristics (amplitude and/or phase angle) deviates from the standards, the electrical grid is affected by the unbalance voltage [14].

Let us denote $U_{UV}$, $U_{VW}$, and $U_{WU}$ as the three phase-to-phase voltages which feed the IM. Based on the National Electrical Manufacturers Association (NEMA) standard definition [15], a denominated indicator “Percent of Voltage Unbalance” (PVU) is used to compute the unbalance severity. Equation (1) to (3) give details about the computing procedure:

$$PVU=\frac{MVD}{U_{avg}}\times 100$$

(1)

$$MVD=\max \left[\left(U_{UV}-U_{avg}\right),\left(U_{VW}-U_{avg}\right),\left(U_{WU}-U_{avg}\right)\right]$$

(2)

$$U_{avg}=\frac{U_{UV}+U_{VW}+U_{WU}}{3}$$

(3)

where $MVD$ is the Maximum Voltage Deviation and $U_{avg}$ is the average value of the voltage [14].

2.2. Inter-Turn Short-Circuits

The short-circuit fault has a tremendous impact on the insulation systems. However, this impact depends on the insulation system classes.

Table 1. Insulation system classes, according to the NEMA and IEC 60085 classification [15,16].

IEC60085 Thermal Class [16]	Old IEC 60085 Thermal Class [16]	NEMA Class [17]	NEMA/UL Letter Class	Maximum Hotspot Temperature Allowed [°C]	Relative Thermal Endurance Index (°C) [16]
90	Y			90	>90–105
105	A	105	A	105	>105–120
120	E			120	>120–130
130	B	130	B	130	>130–155
155	F	155	F	155	>155–180
180	H	180	H	180	>180–200
200			N	200	>200–220
220		220	R	220	>220–250
			S	240
250				250	>250

introduces the different categories of the insulation systems according to the NEMA and IEC 60085 standards [15,16].

In this study, the class F is chosen. A thermal description of this class is depicted in Figure 2. In this case, the maximum hotspot temperature allowed is 155 °C. Hence, when the temperature is higher than that value, the lifetime of the insulation starts to decrease significantly, and rapidly. Actually, the life of the insulation system decreases by about 50% whenever the operating temperature exceeds by 10 °C its rating temperature [10], i.e., 165 °C in this case [17]. Figure 3 illustrates the percentage of life vs. temperature for the insulation system classes A, B, F, and H.

3. Finite Element Method

FEM is an efficient numerical tool, widely used for induction motors electromagnetic and thermal analyses, envisioning design optimization [18,19], performance analysis [20], and fault diagnosis [21,22] among others.

In this study, a commercial software (Flux2D—version 12.1) has been used in order to simulate the IM electromagnetic and thermal behaviors. The geometry is composed of 627,690 face elements, 621 faces, and 83 faces regions. The coefficient of mesh density is 0.5. The horizon time of the electromagnetic simulation is equal to 0.3 s.

3.1. Transient Electromagnetic Analysis

The transient electromagnetic behavior (Figure 4) is firstly simulated, because it provides the different losses, mainly the Joule losses and the iron losses, which are mandatory for the thermal analysis. At this stage, a coupling between the electrical circuit and the 2D IM geometry is required. An appropriate electrical circuit is chosen (Figure 5) based on the windings map. It is composed of three phases, connected in delta, each of them composed of 8 coils. Each coil belongs to {C4, C5, C6, C7, C8, C12, C13, C14, C15, C16, C20, C21, C22, C23, and C24} and embraces 36 turns.

The couple of coils (C1, C9), (C2, C10), and (C3, C11) embrace, respectively, 6, 9, and 21 turns. Regarding the coils C17 and C18, each one embraces 17 turns. Only the coil C19 embraces 2 turns.

The three phases, described in

Table 2. Supply voltage description.

Phase U (V)	$\left(\frac{230}{\sqrt{3}}\times \sqrt{2}+10\right)\times \sin \left(\omega t\right)$
Phase V (V)	$\frac{230}{\sqrt{3}}\times \sqrt{2}\times \sin \left(\omega t-\frac{2\pi }{3}\right)$
Phase W (V)	$\frac{230}{\sqrt{3}}\times \sqrt{2}\times \sin \left(\omega t+\frac{2\pi }{3}\right)$

, are affected by a realistic voltage unbalance of 1.8%. Furthermore, the scenarios are simulated at a half-load condition (7 Nm) that corresponds to 50% of the rated load torque.

To create the inter-turns short-circuit, a resistance (Rf) is connected in parallel to the coil C19. Its value reflects the faulty severity (as the Rf value decreases, the severity increases). Therefore, the healthy mode of operation (Rf is supposed infinite) is simulated, and the voltage supply is considered balanced. Then, an unbalance voltage is created. Regarding fault occurrence, two different inter-turns short-circuit scenarios (Rf equal to 0.001 and 0.0001 Ω) are tested. It should be noted that the resistor Rf of the equivalent electric circuit is assigned, in the FEM model, to the geometric region of the stator slots where the shorted turns are allocated. Therefore, the FEM model is able to accurately model the Joule losses, induced by the short-circuit condition, taking place inside the stator slots allocating the shorted turns.

Once the transient electromagnetic study is concluded, the Joule losses and the iron losses of the different regions are post calculated. The Loss Surface Method (LS) is chosen to compute the iron losses of the stator, the rotor, and the shaft. Later, these losses will be used as inputs for the thermal analysis.

3.2. Thermal Analysis

The transient thermal study uses the same 2D IM geometry. Figure 6 shows the transient thermal application flowchart. In the used commercial software (Flux2D), the basic relation treated is the heat conduction equation:

$$div(\overrightarrow{\phi })+\rho C_p\frac{\partial T}{\partial t}=q\left(4\right)$$

(4)

where

• $\overrightarrow{\phi }$ is the heat flux density (W/m²) and is expressed using Fourier’s law ($\overrightarrow{\phi }=-\left[k\right].\overrightarrow{grad}T$);
• $\left[k\right]$ is the tensor of the thermal conductivity (W/m/K);
• $\rho C_p$ is the volumetric heat capacity (J/m³/K);
• $q$ is the volume density of power of the heat sources (W/m³).

The different IM specifications and technical parameters are presented in

Table 3. Induction motor specifications and technical parameters.

General	Power [kW]	2.2
	Speed [rpm]	1435
	Frequency [Hz]	50
	Torque [Nm]	14.6
	Voltage [V]	400, star connection
	Current [A]	4.56, star connection
	Number of poles	4
	Cooling	Closed motor with external ventilation—IC 411
Stator	Turns per phase	216
	Inner diameter [mm]	100
	Outer diameter [mm]	160
	Number of slots	36
Rotor	Inner diameter [mm]	35
	Outer diameter [mm]	99.4
	Number of bars	28
	Conductor gauge [mm]	0.8/0.7
Winding	Pitch	1:8:10/1:8
	Layer	Single
	Per phase resistance [Ω]	2.1 (at 20 °C)
	Insulation class	F

. After defining the properties of the used materials (

Table 4. Induction motor (IM) materials’ thermal properties.

Face Region	Material	Thermal Conductivity (W/m/°C)
Stator windings	Cooper	388
Rotor bars	Aluminum	210
Stator	Silicon steel	39
Airgap	Air	0.03
Copper insulation	Insulation	0.083

), the post computed losses are allocated to the corresponding regions. Furthermore, the initial conditions and the boundary conditions at the surface of the solid component are added. In fact, the 2D geometry regions are initially set to 20 °C. Once the thermal scenario is implemented, the post processing procedure provides the temperature distribution (local quantities) and the transient temperature in specific points is measured using sensors. In this work, both local and global quantities are presented and discussed.

4. Results and Discussion

Non-destructive experimental validation of the operation scenarios considered in this study is not feasible. Indeed, experimental testbeds used to validate the fault diagnostic tools proposed in the literature impose controlled short-circuit conditions, resorting to a current limiting resistor, placed outside the stator frame of the machine. This resistor “transfers” a significant share of the heat generated by the short-circuit condition to the external part of the motor. Therefore, the literature adopts means of experimental verification which are far from replicating, with precision and consistency, the inter-turn short-circuit fault, particularly in what concerns the thermal aspects of this type of fault.

Therefore, validation of the results is performed through the adoption of alternative analytical thermal models.

4.1. Simulation Results: Two Inter-Turns Short-Circuit

The iron losses are not dependent on the currents. Actually, they mainly depend on the voltages. Hence, the iron losses during all the simulations are roughly equal.

Table 5. Joule losses in the inter-turn short-circuited coil.

	Without Unbalance Voltage	With Unbalance Voltage
Rf (Ω)	Infinite	Infinite	0.001	0.0001
JC19 (W)	0.1734	0.2188	214.32385	232.09490

presents the Joule losses of the C19 coil under healthy behavior and when it is subjected to the unbalance voltage and short-circuit fault. It is noted that these losses increase progressively with the decrease in the resistance Rf. The Joule losses measured for a critical situation (Rf = 0.0001 Ω) reach more than 230 W.

Figure 7 illustrates the temperature distribution during the presence and the absence of the inter-turns short-circuits and the unbalance voltage. A uniform temperature distribution is observed in Figure 7a. However, a nonuniform distribution is detected in Figure 7b (when the resistance Rf is supposed as infinite, the induction motor is solely working under the unbalanced voltage condition). Besides the previous scenarios, two inter-turns short-circuit severities are simulated. Figure 7c,d present the steady-state temperature distribution when Rf is equal to 0.001 and 0.0001Ω, respectively.

To enhance the observations, Figure 8 depicts the transient and steady-state values of the temperature in the four sensors that were used to measure the temperatures in the stator core, insulator, stator teeth, and short-circuited C19 coil.

4.2. Discussion

Understanding the thermal behavior of the faulted coil is one of the keys to evaluate IM performance. Generally, the heat generated by the different components of the machine and dissipated to the surrounding ambient is considered as losses. This paper focuses on the thermal behavior of an IM working under two harsh conditions: unbalanced supply voltages and the presence of the most incipient type of inter-turn short-circuit condition—a short-circuit between two turns only. The different results illustrated in Figure 7 and Figure 8 show the thermal behavior of the IM regarding its healthy operation and also, for different severities of the fault. At first, the considered unbalanced voltage does not seem to be critical because an increase of just 2 °C is detected. However, a nonuniform distribution is clearly observed, which decreases the reliability of the IM and accelerates its aging.

For a realistic unbalance voltage (MVD equal to 1.8%) and based only on the thermal behavior, the IM presents for a two inter-turn short-circuit fault an overheating condition that may cause its burnout (

Table 6. IM steady-state temperature values (°C) under the occurrence of two inter-turns short-circuit.

		Healthy	With Unbalanced Supply Voltage
	Rf (Ω)	Rf = inf	Rf = inf	Rf = 0.001	Rf = 0.0001
Region
Stator core		37.87	40.75	112.33	118.04
Insulator		39.03	41.65	128.33	135.25
Stator Teeth		39.52	42.99	136.99	144.54
Winding		39.51	42.87	155.88	164.92

). Indeed, the temperature in a critical scenario (Rf set to 0.0001 Ω) reaches more than 160 ºC, which is well above the maximum permissible temperature for the class F insulation system (155 °C) (Figure 2 and Figure 3).

5. Conclusions

The presence of some degree of unbalance voltage in the supply is unavoidable in practice. Hence, it becomes mandatory to take into account this abnormal behavior in all studies. The thermal behavior of a low-power, three-phase, IM working under two harsh conditions (unbalanced supply voltage and two inter-turns short-circuit) was discussed in this paper. Different scenarios, according to the severity of the fault, were considered. It has been proven that during a realistic short-circuit condition, for which Rf tends to be zero, low-power, three-phase, induction motors will most probably burn before some of the diagnostic tools available in the literature can provide any useful warning in due time.

Provided that the simulated operating scenarios considered the IM operation in derated mode, far more severe consequences should be experienced if the motor is operated close to the nominal load torque. Much faster warming of the stator windings will shorten the already very narrow window of chance for the diagnosis of this fault even more.

Further insight into the multiple parameters impacting the severity of the fault is vital in establishing a concise evaluation to confirm the effectiveness of the state-of-the-art inter-turn SC fault diagnostic algorithms.

The use of Computational Fluid Dynamics techniques is envisaged in future research work, providing a gold standard for comparison and validation of FEM analysis.