PSIC-Net: Pixel-Wise Segmentation and Image-Wise Classification Network for Surface Defects
Abstract
:1. Introduction
2. Related Work
3. Methods
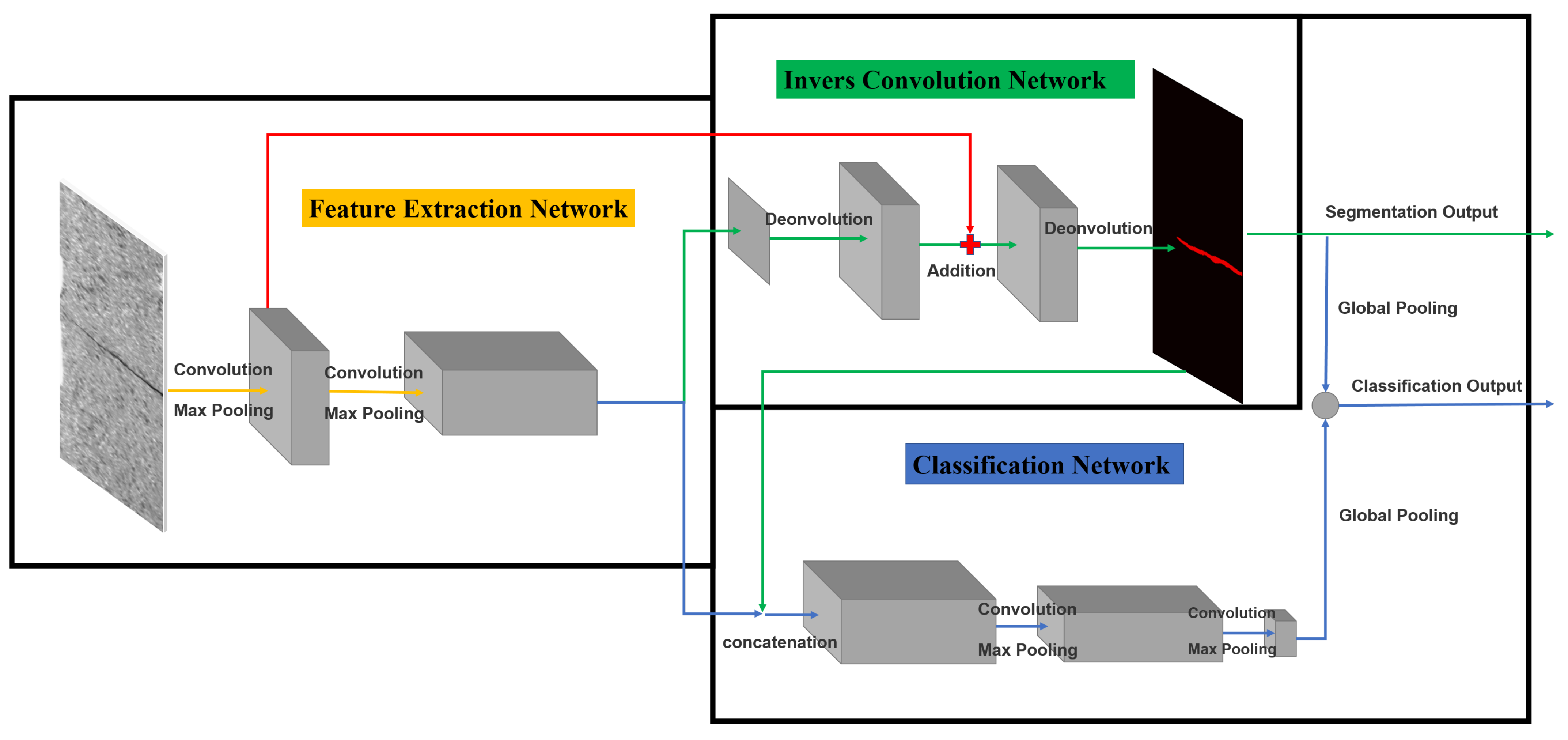
3.1. Network Framework
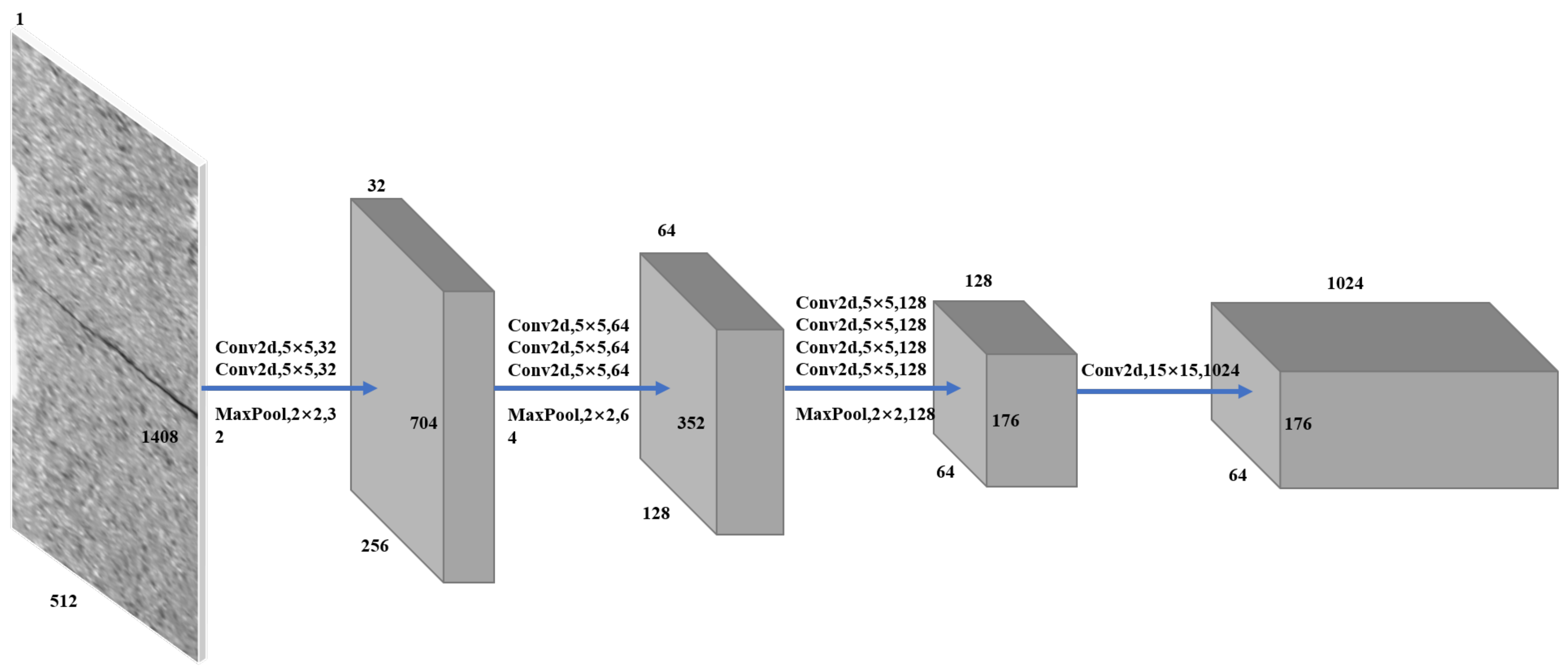
3.1.1. Feature Extraction Network
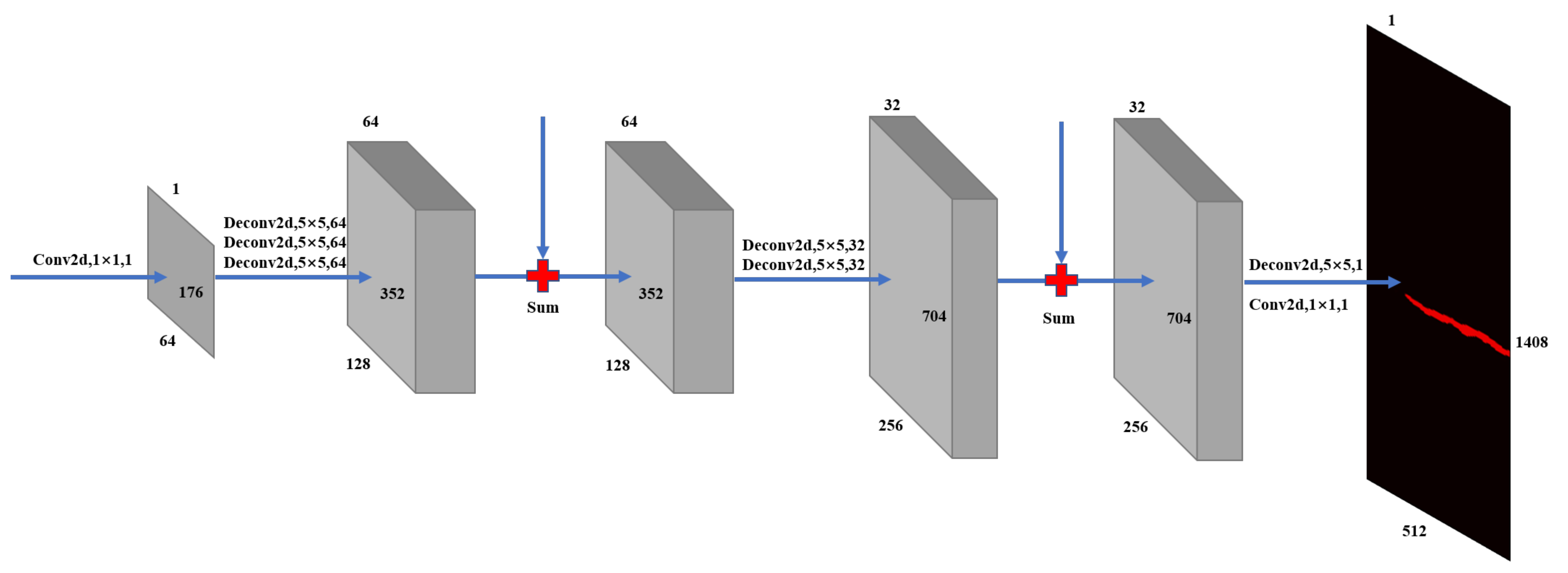
3.1.2. Invers Convolution Network
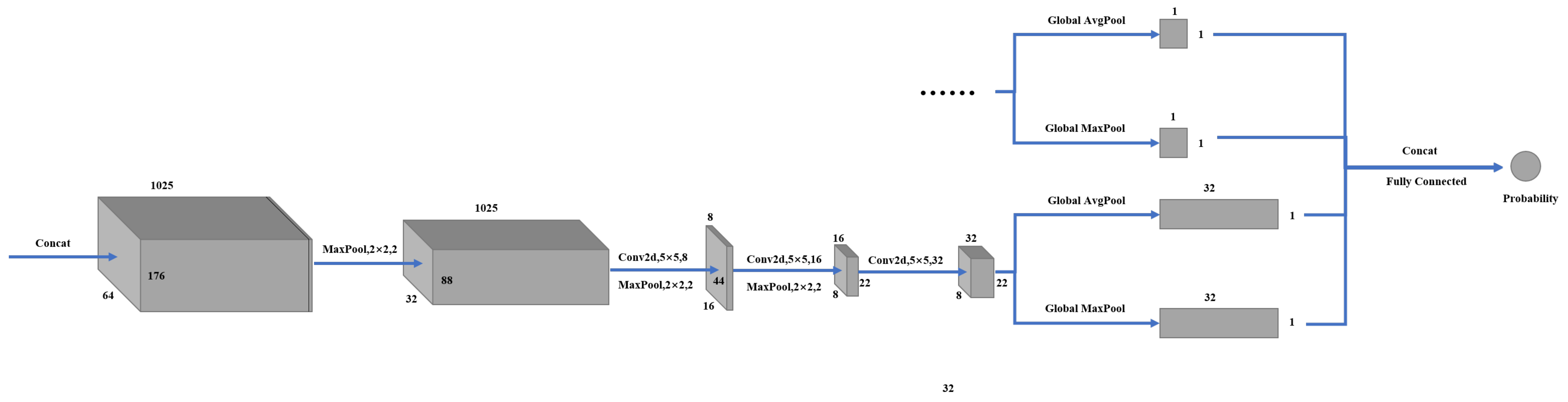
3.1.3. Classification Network
3.2. Training
3.3. Inference
4. Experiments and Results
4.1. Datasets
4.2. Experiment Settings
4.3. Performance Metrics
4.4. Experiment Results
4.4.1. Experiment Results of Defect Segmentation
4.4.2. Experiment Results of Defect Image Classification
4.4.3. Time Cost of Training and Inference
5. Discussion
- The network is sensitive to data, and the results may fluctuate slightly even if the data remain unchanged. Making the network more stable during training is needed.
- The guidance of the segmentation network results to the classification network needs to be improved. In the experiment, it is found that a small number of defect data successfully segmented by the segmentation network are not successfully classified by the classification network. Strengthening the synergy of the two networks to improve the accuracy of the classification network also needs to be further explored.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PSIC-Net | Pixel-wise Segmentation and Image-wise Classification Network |
| LBP | Local Binary Patterns |
| CASAE | Cascaded Autoencoder |
| CNN | Convolutional Neural Network |
| FCN | Fully Convolutional Networks |
| BN | Batch Normalization |
| ReLU | Rectified Linear Unit |
| IoU | Intersection over Union |
| mIoU | mean Intersection over Union |
| AP | Average Precision |
| mAP | mean Average Precision |
| ROC | Receiver Operating Characteristic Curve |
| AUC | Area Under ROC Curve |
| Nomenclature | Full Name | Brief Introduction |
| BN | Batch Normalization | Data standardization |
| ReLU | Rectified Linear Unit | Activation function |
| IoU | Intersection over Union | Measure the accuracy of segmentation |
| mIoU | mean Intersection over Union | Measure the accuracy of segmentation |
| AP | Average Precision | Measure the accuracy of classification |
| mAP | Mean Average Precision | Measure the accuracy of classification |
| ROC | Receiver Operating Characteristic Curve | Measure the accuracy of 2-class classification |
| AUC | Area Under ROC Curve | Measure the ability to distinguish +/− examples |
References
- Guo, X.; Tang, C.; Zhang, H.; Chang, Z. Automatic thresholding for defect detection. ICIC Express Lett. 2012, 6, 159–164. [Google Scholar]
- Oliveira, H.; Correia, P.L. Automatic Road Crack Segmentation Using Entropy and Image Dynamic Thresholding. In Proceedings of the 2009 17th European Signal Processing Conference, Scotland, UK, 24–28 August 2009. [Google Scholar]
- Jia, C.; Wang, Y. Edge detection of crack defect based on wavelet multi-scale multiplication. Comput. Eng. Appl. 2011, 47, 219–221. [Google Scholar]
- Xi, Y.; Qi, D.; Li, X. Multi-scale Edge Detection of Wood Defect Images Based on the Dyadic Wavelet Transform. In Proceedings of the International Conference on Machine Vision & Human-Machine Interface, Kaifeng, China, 24–25 April 2010. [Google Scholar]
- Kanopoulos, N.; Vasanthavada, N.; Baker, R.L. Design of an image edge detection filter using the Sobel operator. IEEE J. Solid-State Circuits 1988, 23, 358–367. [Google Scholar] [CrossRef]
- Li, E.S.; Zhu, S.L.; Zhu, B.S.; Zhao, Y.; Song, L.H. An Adaptive Edge-Detection Method Based on the Canny Operator. In Proceedings of the International Conference on Environmental Science & Information Application Technology, Wuhan, China, 4–5 July 2009. [Google Scholar]
- Wang, D.; Zhou, S.S. Color Image Recognition Method Based on the Prewitt Operator. In Proceedings of the International Conference on Computer Science & Software Engineering, Wuhan, China, 19–20 December 2009; pp. 170–173. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution Gray-Scale and Rotation Invariant Texture Classification with Local Binary Patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Lei, L.J.; Sun, S.L.; Xiang, Y.K.; Zhang, Y.; Liu, H.K. bottleneck issues of computer vision in intelligent manufacturing. J. Image Graph. 2020, 25, 1330–1343. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Jeon, Y.J.; Choi, D.c.; Yun, J.P.; Park, C.; Kim, S.W. Detection of scratch defects on slab surface. In Proceedings of the 2011 11th International Conference on Control, Automation and Systems, Gyeonggi, Korea, 26–29 October 2011; pp. 1274–1278. [Google Scholar]
- Neogi, N.; Mohanta, D.K.; Dutta, P.K. Review of vision-based steel surface inspection systems. EURASIP J. Image Video Process. 2014, 2014, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Bhatt, P.M.; Malhan, R.K.; Rajendran, P.; Shah, B.C.; Gupta, S.K. Image-Based Surface Defect Detection Using Deep Learning: A Review. J. Comput. Inf. Sci. Eng. 2021, 21, 1–23. [Google Scholar] [CrossRef]
- Pan, S.J.; Qiang, Y. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Oquab, M.; Bottou, L.; Laptev, I.; Sivic, J. Learning and Transferring Mid-level Image Representations Using Convolutional Neural Networks. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1717–1724. [Google Scholar] [CrossRef] [Green Version]
- Xian, T.; Wei, H.; De, X. D. A survey of surface defect detection methods based on deep learning. Acta Autom. Sin. 2021, 47, 1017–1034. [Google Scholar] [CrossRef]
- Tabernik, D.; Šela, S.; Skvarč, J.; Skočaj, D. Segmentation-based deep-learning approach for surface-defect detection. J. Intell. Manuf. 2019, 31, 759–776. [Google Scholar] [CrossRef] [Green Version]
- Božič, J.; Tabernik, D.; Skočaj, D. Mixed supervision for surface-defect detection: From weakly to fully supervised learning. Comput. Ind. 2021, 129, 103459. [Google Scholar] [CrossRef]
- Weimer, D.; Scholz-Reiter, B.; Shpitalni, M. Design of deep convolutional neural network architectures for automated feature extraction in industrial inspection. CIRP Ann. 2016, 65, 417–420. [Google Scholar] [CrossRef]
- Gfa, B.; Psa, B.; Wza, B.; Jya, B.; Yca, B.; Myy, C.; Yca, B. A deep-learning-based approach for fast and robust steel surface defects classification. Opt. Lasers Eng. 2019, 121, 397–405. [Google Scholar]
- Maestro-Watson, D.; Balzategui, J.; Eciolaza, L.; Arana-Arexolaleiba, N. Deep Learning for Deflectometric Inspection of Specular Surfaces. In Proceedings of the 13th International Conference on Soft Computing Models in Industrial and Environmental Applications, San Sebastian, Spain, 6–8 June 2018. [Google Scholar]
- Khumaidi, A.; Yuniarno, E.M.; Purnomo, M.H. Welding defect classification based on convolution neural network (CNN) and Gaussian kernel. In Proceedings of the 2017 International Seminar on Intelligent Technology and Its Applications (ISITIA), Surabaya, Indonesia, 28–29 August 2017; pp. 261–265. [Google Scholar] [CrossRef]
- Wang, T.; Chen, Y.; Qiao, M.; Snoussi, H. A fast and robust convolutional neural network-based defect detection model in product quality control. Int. J. Adv. Manuf. Technol. 2018, 94, 3465–3471. [Google Scholar] [CrossRef]
- Xu, X.; Zheng, H.; Guo, Z.; Wu, X.; Zheng, Z. SDD-CNN: Small Data-Driven Convolution Neural Networks for Subtle Roller Defect Inspection. Appl. Sci. 2019, 9, 1364. [Google Scholar] [CrossRef] [Green Version]
- Ren, R.; Hung, T.; Tan, K.C. A Generic Deep-Learning-Based Approach for Automated Surface Inspection. IEEE Trans. Cybern. 2018, 48, 929–940. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, W.; Pan, J. Deformable Patterned Fabric Defect Detection With Fisher Criterion-Based Deep Learning. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1256–1264. [Google Scholar] [CrossRef]
- He, Z.; Liu, Q. Deep Regression Neural Network for Industrial Surface Defect Detection. IEEE Access 2020, 8, 35583–35591. [Google Scholar] [CrossRef]
- Xu, L.; Lv, S.; Deng, Y.; Li, X. A Weakly Supervised Surface Defect Detection Based on Convolutional Neural Network. IEEE Access 2020, 8, 42285–42296. [Google Scholar] [CrossRef]
- Ding, R.; Dai, L.; Li, G.; Liu, H. TDD-net: A tiny defect detection network for printed circuit boards. CAAI Trans. Intell. Technol. 2019, 2, 110–116. [Google Scholar]
- Di, H.; Ke, X.; Peng, Z.; Dongdong, Z. Surface defect classification of steels with a new semi-supervised learning method. Opt. Lasers Eng. 2019, 117, 40–48. [Google Scholar] [CrossRef]
- Dong, H.; Song, K.; He, Y.; Xu, J.; Yan, Y.; Meng, Q. PGA-Net: Pyramid Feature Fusion and Global Context Attention Network for Automated Surface Defect Detection. IEEE Trans. Ind. Inform. 2020, 16, 7448–7458. [Google Scholar] [CrossRef]
- Mujeeb, A.; Dai, W.; Erdt, M.; Sourin, A. One class based feature learning approach for defect detection using deep autoencoders. Adv. Eng. Inform. 2019, 42, 100933. [Google Scholar] [CrossRef]
- Liong, S.T.; Gan, Y.S.; Huang, Y.C.; Yuan, C.A.; Chang, H.C. Automatic Defect Segmentation on Leather with Deep Learning. arXiv 2019, arXiv:1903.12139. [Google Scholar]
- Tao, X.; Zhang, D.; Ma, W.; Liu, X.; Xu, D. Automatic Metallic Surface Defect Detection and Recognition with Convolutional Neural Networks. Appl. Sci. 2018, 8, 1575. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Li, H.; Wang, H. Pixel-Wise Crack Detection Using Deep Local Pattern Predictor for Robot Application. Sensors 2018, 18, 3042. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Božič, J.; Tabernik, D.; Skočaj, D. End-to-end training of a two-stage neural network for defect detection. arXiv 2020, arXiv:2007.07676. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Amhaz, R.; Chambon, S.; Idier, J.; Baltazart, V. Automatic crack detection on 2D pavement images: An algorithm based on minimal path selection. IEEE Trans. Intell. Transp. Syst 2015, 17, 2718–2729. [Google Scholar] [CrossRef] [Green Version]
- Song, K.; Yan, Y. A noise robust method based on completed local binary patterns for hot-rolled steel strip surface defects. Appl. Surf. Sci. 2013, 285, 858–864. [Google Scholar] [CrossRef]
- Huang, Y.; Qiu, C.; Yuan, K. Surface defect saliency of magnetic tile. Vis. Comput. 2020, 36, 85–96. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature Pyramid and Hierarchical Boosting Network for Pavement Crack Detection. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1525–1535. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning Deconvolution Network for Semantic Segmentation. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1520–1528. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.; Tu, Z. Holistically-Nested Edge Detection. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Xing, Z.; Xia, X.; Lo, D.; Wang, X.; Grundy, J. Neural Network-based Detection of Self-Admitted Technical Debt: From Performance to Explainability. ACM Trans. Softw. Eng. Methodol. 2019, 28, 1–45. [Google Scholar] [CrossRef] [Green Version]
- Cheng, B.; Girshick, R.; Dollár, P.; Berg, A.C.; Kirillov, A. Boundary IoU: Improving Object-Centric Image Segmentation Evaluation. arXiv 2021, arXiv:2103.16562. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Qiu, L.; Wu, X.; Yu, Z. A High-Efficiency Fully Convolutional Networks for Pixel-Wise Surface Defect Detection. IEEE Access 2019, 7, 15884–15893. [Google Scholar] [CrossRef]
- Kim, S.; Kim, W.; Noh, Y.K.; Park, F.C. Transfer learning for automated optical inspection. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 2517–2524. [Google Scholar] [CrossRef]
- Racki, D.; Tomazevic, D.; Skocaj, D. A Compact Convolutional Neural Network for Textured Surface Anomaly Detection. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1331–1339. [Google Scholar] [CrossRef]
- Lin, Z.; Ye, H.; Zhan, B.; Huang, X. An Efficient Network for Surface Defect Detection. Appl. Sci. 2020, 10, 6085. [Google Scholar] [CrossRef]
- Huang, Y.; Qiu, C.; Wang, X.; Wang, S.; Yuan, K. A Compact Convolutional Neural Network for Surface Defect Inspection. Sensors 2020, 20, 1974. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Yuan, Y.; Balta, C.; Liu, J. A Light-Weight Deep-Learning Model with Multi-Scale Features for Steel Surface Defect Classification. Materials 2020, 13, 4629. [Google Scholar] [CrossRef]
- Dong, X.; Cootes, T. Defect Detection and Classification by Training a Generic Convolutional Neural Network Encoder. IEEE Trans. Signal Process. 2020, 68, 6055–6069. [Google Scholar] [CrossRef]
- Liu, G.; Yang, N.; Guo, L.; Guo, S.; Chen, Z. A One-Stage Approach for Surface Anomaly Detection with Background Suppression Strategies. Sensors 2020, 20, 1829. [Google Scholar] [CrossRef] [PubMed] [Green Version]




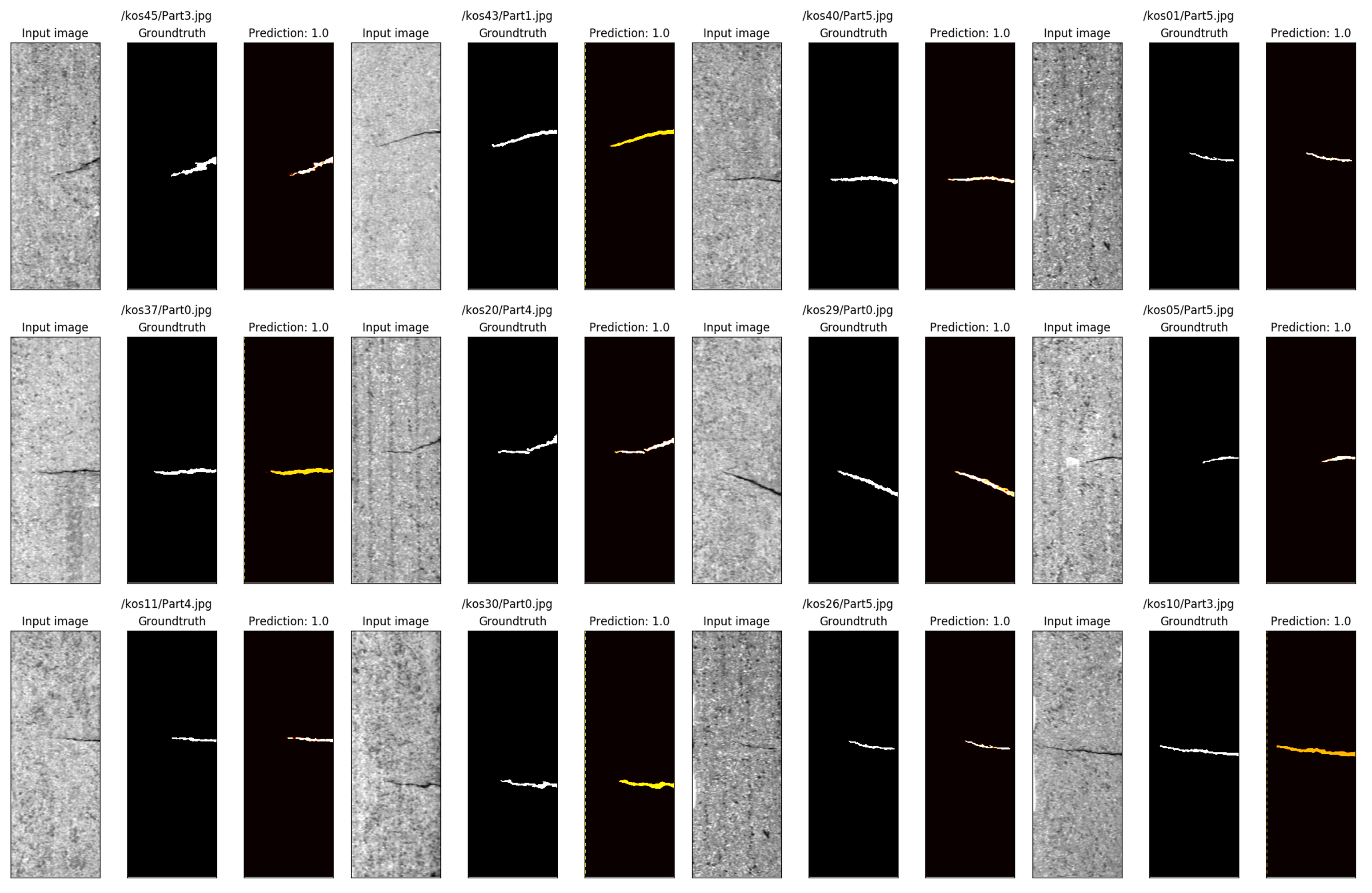
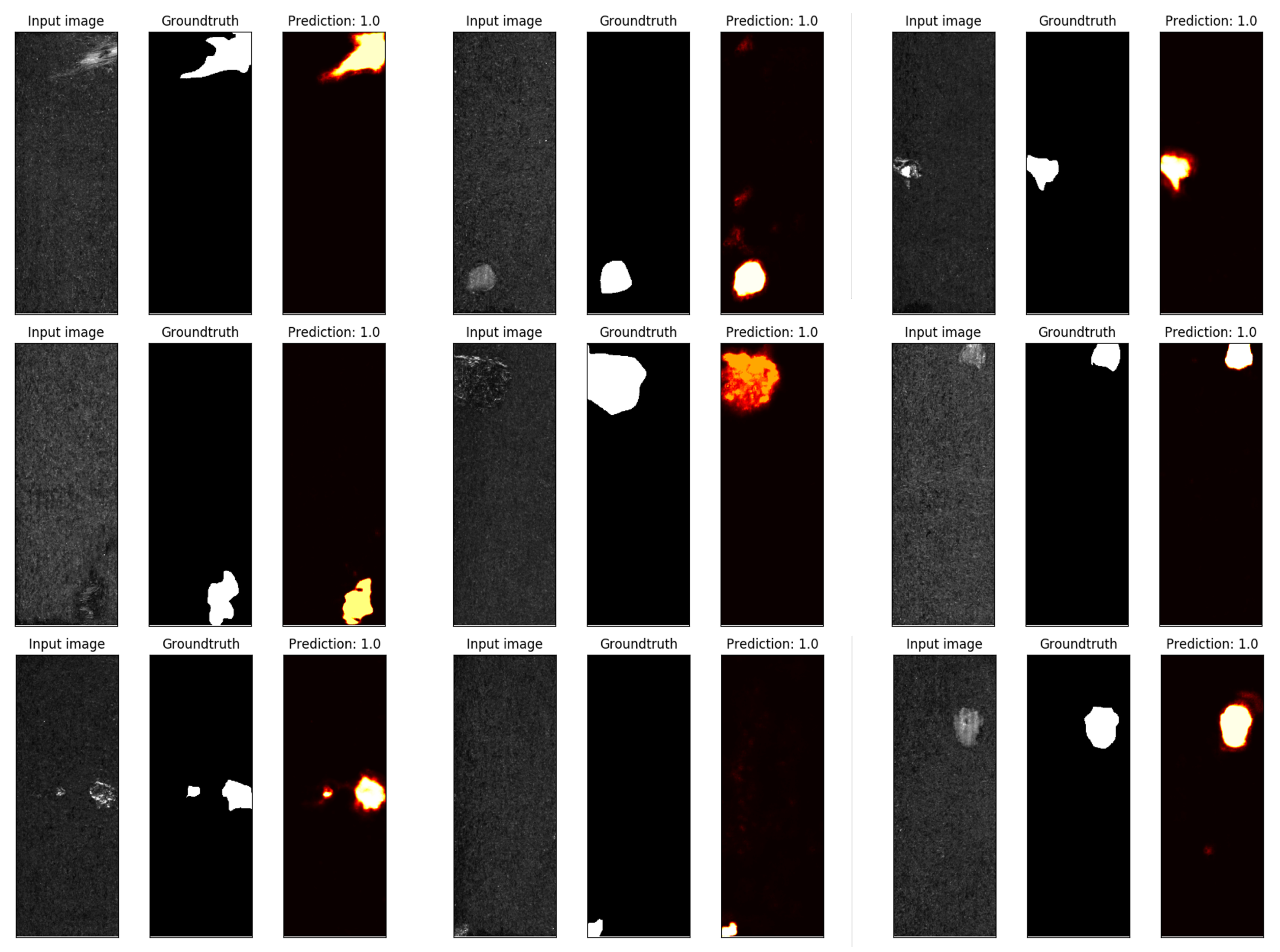


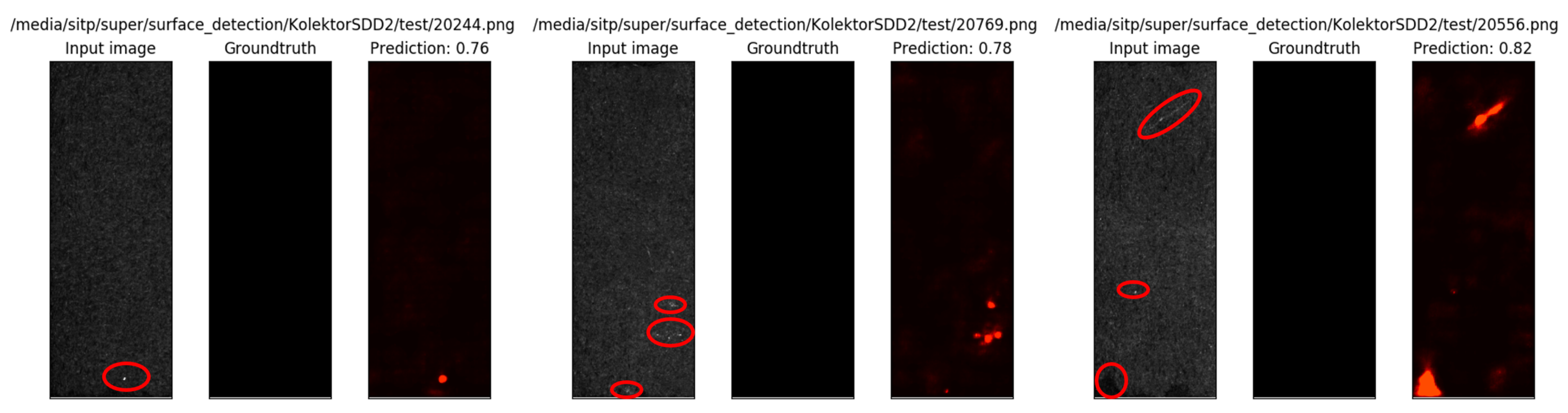

| Datasets | Mask mIoU (%) | Max Mask IoU (%) | Min Mask IoU (%) | Boundary mIoU (%) | Max Boundary IoU (%) | Min Boundary IoU (%) |
|---|---|---|---|---|---|---|
| KolektorSDD | 88.49 | 89.25 | 86.88 | 73.99 | 80.63 | 69.46 |
| KolektorSDD2 | 86.13 | 87.79 | 83.05 | 70.98 | 73.99 | 65.98 |
| DAGM | 89.10 | 89.93 | 87.01 | 82.55 | 88.21 | 77.56 |
| Methods | Datasets | Mask mIoU (%) | Boundary mIoU (%) |
|---|---|---|---|
| FCN [42] | DAGM | 73.86 | - |
| DeepLab [47] | DAGM | 74.61 | - |
| [27] | DAGM | 84.50 | - |
| [48] | DAGM | 73.56 | - |
| [31] | DAGM | 74.78 | - |
| [18,36] | KolektorSDD | 76.21 | - |
| KolektorSDD2 | 71.69 | - | |
| DAGM | 79.46 | - | |
| [17] | KolektorSDD | 87.77 | 71.23 |
| KolektorSDD2 | 84.20 | 63.59 | |
| DAGM | 87.79 | 77.13 | |
| PSIC-Net(ours) | KolektorSDD | 88.49 | 73.99 |
| KolektorSDD2 | 86.13 | 70.98 | |
| DAGM | 89.10 | 82.55 |
| Datasets | AUC (%) | mAP (%) | Accuracy (%) |
|---|---|---|---|
| KolektorSDD | 98.05 | 96.43 | 98.53 |
| KolektorSDD2 | 96.34 | 93.27 | 97.50 |
| DAGM | 100 | 100 | 100 |
| Methods | Datasets | AUC (%) | mAP (%) | Accuracy (%) |
|---|---|---|---|---|
| [49] | DAGM | - | - | 99.90 |
| [50] | DAGM | 99.60 | - | 99.40 |
| [19] | DAGM | - | - | 99.20 |
| [51] | DAGM | 99.00 | - | 99.80 |
| [23] | DAGM | - | - | 99.40 |
| [52] | DAGM | - | - | 99.80 |
| [53] | DAGM | - | - | 99.90 |
| [54] | KolektorSDD | - | 98.80 | - |
| [55] | KolektorSDD | - | 100 | - |
| [36] | KolektorSDD | - | 97.36 | 98.12 |
| DAGM | - | 100 | 100 | |
| [18] | KolektorSDD | - | 97.36 | 98.12 |
| KolektorSDD2 | - | 95.40 | - | |
| DAGM | - | 100 | 100 | |
| [17] | KolektorSDD | 88.49 | 89.24 | 87.41 |
| KolektorSDD2 | 83.86 | 68.65 | 86.67 | |
| DAGM | 100 | 100 | 100 | |
| PSIC-Net(ours) | KolektorSDD | 98.05 | 96.43 | 98.53 |
| KolektorSDD2 | 96.34 | 93.27 | 97.50 | |
| DAGM | 100 | 100 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, L.; Sun, S.; Zhang, Y.; Liu, H.; Xu, W. PSIC-Net: Pixel-Wise Segmentation and Image-Wise Classification Network for Surface Defects. Machines 2021, 9, 221. https://doi.org/10.3390/machines9100221
Lei L, Sun S, Zhang Y, Liu H, Xu W. PSIC-Net: Pixel-Wise Segmentation and Image-Wise Classification Network for Surface Defects. Machines. 2021; 9(10):221. https://doi.org/10.3390/machines9100221
Chicago/Turabian StyleLei, Linjian, Shengli Sun, Yue Zhang, Huikai Liu, and Wenjun Xu. 2021. "PSIC-Net: Pixel-Wise Segmentation and Image-Wise Classification Network for Surface Defects" Machines 9, no. 10: 221. https://doi.org/10.3390/machines9100221
APA StyleLei, L., Sun, S., Zhang, Y., Liu, H., & Xu, W. (2021). PSIC-Net: Pixel-Wise Segmentation and Image-Wise Classification Network for Surface Defects. Machines, 9(10), 221. https://doi.org/10.3390/machines9100221







