Time-Delay Luenberger Observer Design for Sliding Mode Control of Nonlinear Markovian Jump Systems via Event-Triggered Mechanism
Abstract
:1. Introduction
2. Model Establishing and Problem Statement
3. Main Results
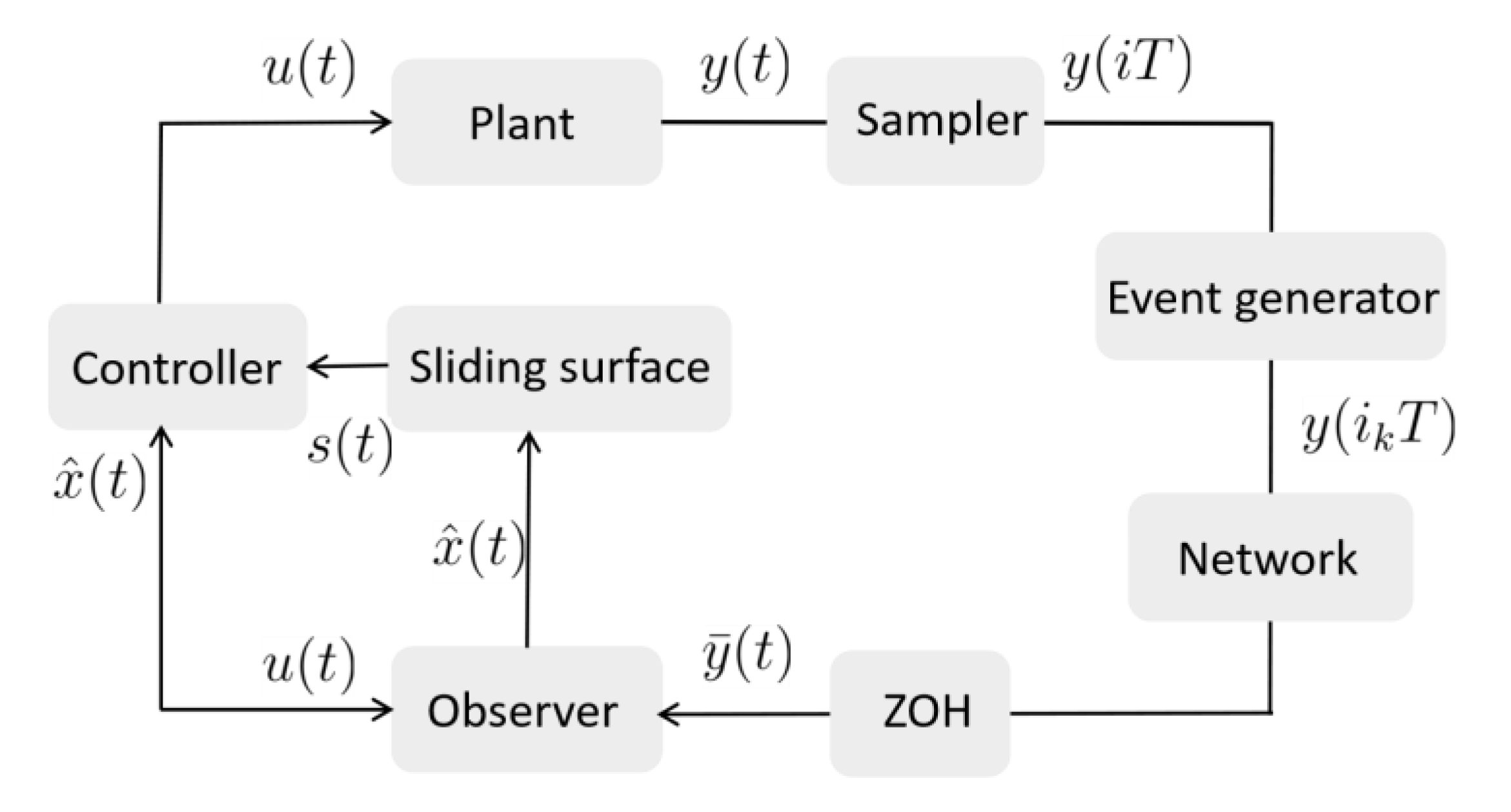
3.1. Network and ZOH
3.2. Luenberger State Observer Design
3.3. Sliding Surface Design
- It is stochastically stable for system (17) with w(t) = 0 and the sliding mode dynamics (21).
- The measurement of H∞ performance with the condition of zero-initial will be satisfied as follows:where is a positive constant.
3.4. Stochastic Stability and H∞ Performance Analysis
- 1.
- andforare known, that isare known, that is;
- 2.
- andforare partially known, that iswhileis also not empty;
- 3.
- andforare partially known, that iswhileis also not empty;
- 4.
- andforare all unknown, that is.
3.5. Reachability of Sliding Surface
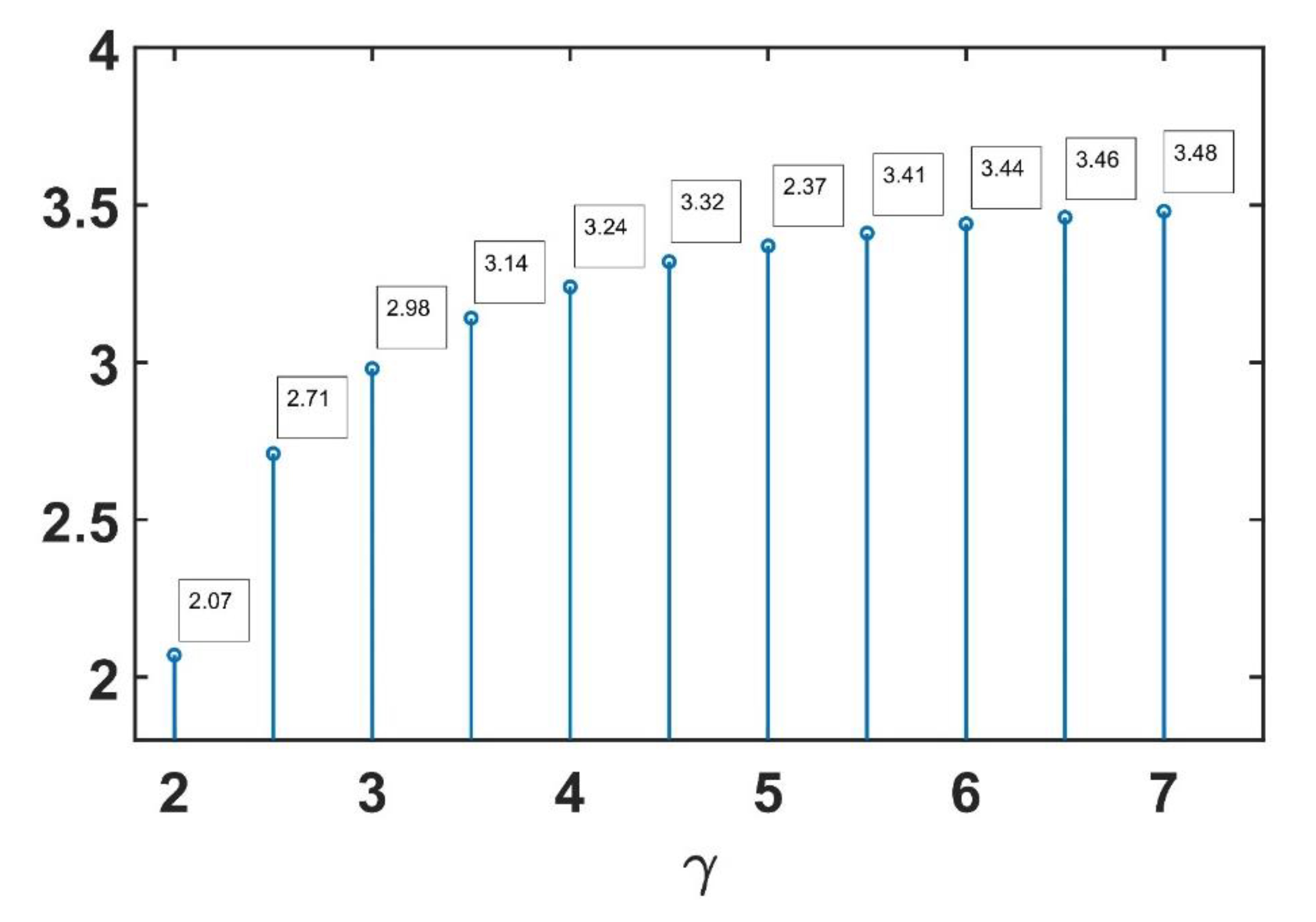
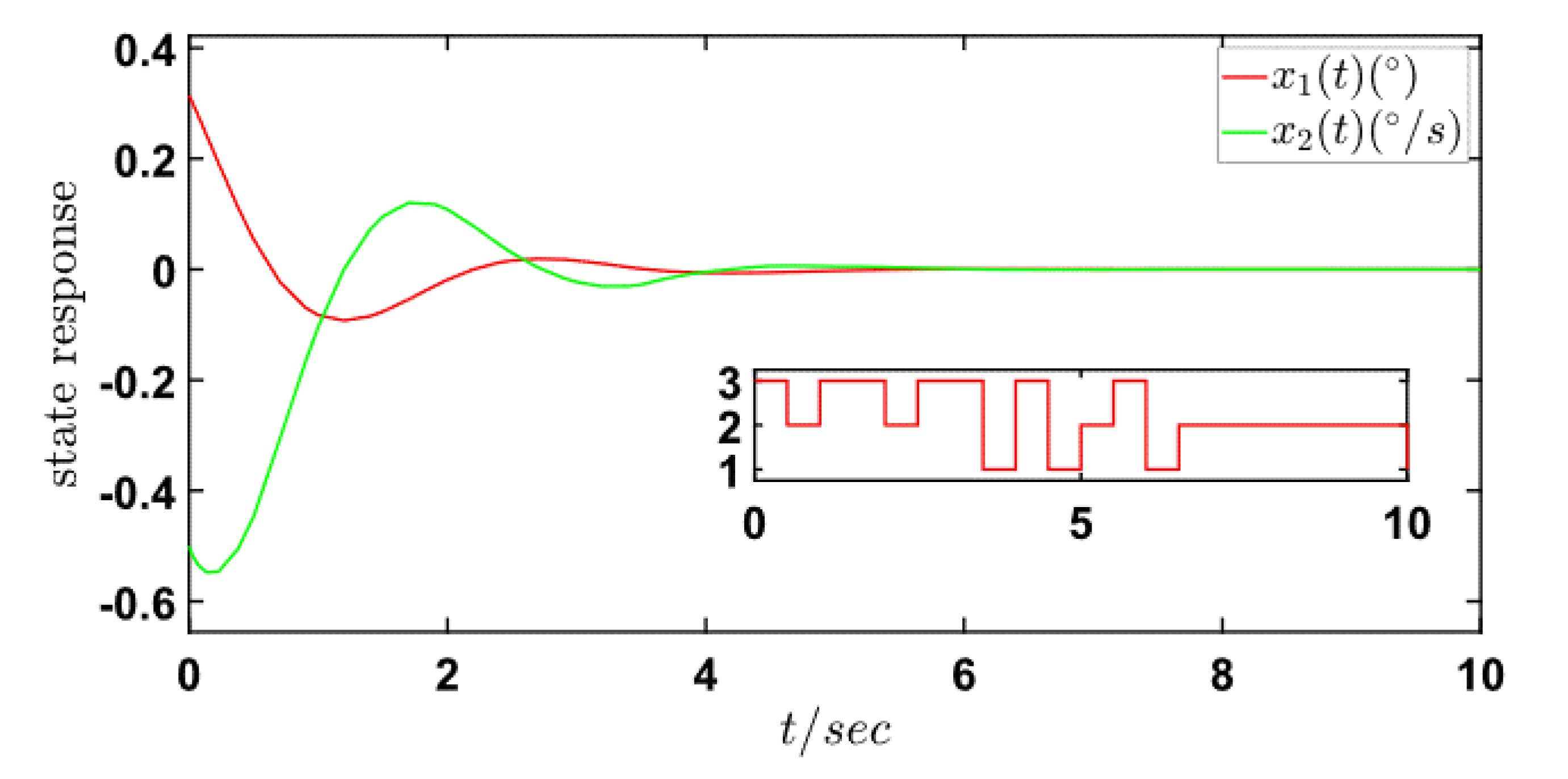
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krasovskii, N.M.; Lidskii, E.A. Analytical design of controllers in systems with random attributes. Autom. Remote Control 1961, 22, 1021–2025. [Google Scholar]
- Ugrinovskii, V.; Pota, H.R. Decentralized control of power systems via robust control of uncertain Markov jump parameter systems. Int. J. Control 2005, 78, 662–677. [Google Scholar] [CrossRef]
- Andrieu, C.; Davy, M.; Doucet, A. Efficient particle filtering for jump Markov systems. Application to time-varying autoregressions. IEEE Trans. Signal Process. 2003, 51, 1762–1770. [Google Scholar] [CrossRef] [Green Version]
- Wallace, V.L.; Rosenberg, R.S. Markovian models and numerical analysis of computer system behavior. In Proceedings of the Spring Joint Computer Conference, Boston, MA, USA, 26–28 April 1966; pp. 141–148. [Google Scholar] [CrossRef]
- Ellis, R.S. Large deviations for the empirical measure of a Markov chain with an application to the multivariate empirical measure. Ann. Probab. 1988, 16, 1496–1508. [Google Scholar] [CrossRef]
- Souza, C.E.D. Robust stability and stabilization of uncertain discrete-time Markovian jump linear systems. IEEE Trans. Autom. Control 2006, 51, 836–841. [Google Scholar] [CrossRef]
- Gao, H.; Lam, J.; Xu, S.; Wang, C. Stabilization and H∞ control of two-dimensional Markovian jump systems. IMA J. Math. Control Inf. 2004, 21, 377–392. [Google Scholar] [CrossRef]
- Mao, X.; Yuan, C. Stochastic Differential Equations with Markovian Switching; Imperial College Press: London, UK, 2006. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Shi, P.; Gao, H.; Wang, C. H∞ filtering for 2D Markovian jump systems. Automatica 2008, 44, 1849–1858. [Google Scholar] [CrossRef]
- Xu, S.; Lam, J.; Mao, X. Delay-dependent H∞ control and filtering for uncertain Markovian jump systems with time-varying delays. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 2070–2077. [Google Scholar] [CrossRef]
- Fei, Z.; Gao, H.; Shi, P. New results on stabilization of Markovian jump systems with time delay. Automatica 2009, 45, 2300–2306. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, B.; Lam, J. H∞ model reduction of Markovian jump linear systems. Syst. Control Lett. 2003, 50, 103–118. [Google Scholar] [CrossRef]
- Jilkov, V.P.; Li, X.R. Online Bayesian estimation of transition probabilities for Markovian jump systems. IEEE Trans. Signal Process. 2004, 52, 1620–1630. [Google Scholar] [CrossRef]
- Wu, Z.; Su, H.; Chu, J. H∞ filtering for singular Markovian jump systems with time delay. Int. J. Robust Nonlinear Control 2010, 20, 939–957. [Google Scholar] [CrossRef]
- Costa, O.L.V.; Guerra, S. Stationary filter for linear minimum mean square error estimator of discrete-time Markovian jump systems. IEEE Trans. Autom. Control 2002, 47, 1351–1356. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, Y.; Shen, H.; Zhou, P. SMC design for robust stabilization of nonlinear Markovian jump singular systems. IEEE Trans. Autom. Control 2018, 63, 219–224. [Google Scholar] [CrossRef]
- Saravanakumar, R.; Ali, M.S.; Karimi, H.R. Robust H∞ control of uncertain stochastic Markovian jump systems with mixed time-varying delays. Int. J. Syst. Sci. 2017, 48, 862–872. [Google Scholar] [CrossRef]
- Park, I.S.; Kwon, N.K.; Park, P. H∞ control for Markovian jump fuzzy systems with partly unknown transition rates and input saturation. J. Frankl. Inst. 2018, 355, 2498–2514. [Google Scholar] [CrossRef]
- Shen, H.; Li, F.; Yan, H.; Karimi, H.R.; Lam, H. Finite-time event-triggered H∞ control for T–S fuzzy Markov jump systems. IEEE Trans. Fuzzy Syst. 2018, 26, 3122–3135. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Wu, Z.; Pan, Y.; Su, H.; Liu, Y. Hidden-Markov-model-based asynchronous filter design of nonlinear Markov jump systems in continuous-time domain. IEEE Trans. Cybern. 2019, 49, 2294–2304. [Google Scholar] [CrossRef]
- Zhang, L.; Boukas, E.-K. Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities. Automatica 2009, 45, 463–468. [Google Scholar] [CrossRef]
- Xiong, L.; Tian, J.; Liu, X. Stability analysis for neutral Markovian jump systems with partially unknown transition probabilities. J. Frankl. Inst. 2012, 349, 2193–2214. [Google Scholar] [CrossRef]
- Kao, Y.; Xie, J.; Wang, C. Stabilization of singular Markovian jump systems with generally uncertain transition rates. IEEE Trans. Autom. Control 2014, 59, 2604–2610. [Google Scholar] [CrossRef]
- Wei, Y.; Qiu, J.; Karimi, H.R. Quantized filtering for continuous-time Markovian jump systems with deficient mode information. Asian J. Control 2015, 17, 1914–1923. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, L.; Shi, P.; Zhao, Y. Sliding mode control of continuous-time Markovian jump systems with digital data transmission. Automatica 2017, 80, 200–209. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Shi, Y. Robust H∞ sliding-mode control for Markovian jump systems subject to intermittent observations and partially known transition probabilities. Syst. Control Lett. 2013, 62, 1114–1124. [Google Scholar] [CrossRef]
- Song, J.; Niu, Y.; Zou, Y. Asynchronous sliding mode control of Markovian jump systems with time-varying delays and partly accessible mode detection probabilities. Automatica 2018, 93, 33–41. [Google Scholar] [CrossRef]
- Li, H.; Shi, P.; Yao, D.; Wu, L. Observer-based adaptive sliding mode control for nonlinear Markovian jump systems. Automatica 2016, 64, 133–142. [Google Scholar] [CrossRef]
- Liu, M.; Shi, P.; Zhang, L.; Zhao, X. Fault-tolerant control for nonlinear Markovian jump systems via proportional and derivative sliding mode observer technique. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 2755–2764. [Google Scholar] [CrossRef]
- Jiang, B.; Karimi, H.R.; Yang, S.; Gao, C.; Kao, Y. Observer-based adaptive sliding mode control for nonlinear stochastic Markov jump systems via T–S fuzzy modeling: Applications to robot arm model. IEEE Trans. Ind. Electron. 2021, 68, 466–477. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, J. Non-fragile observer-based adaptive control of uncertain nonlinear stochastic Markovian jump systems via sliding mode technique. Nonlinear Anal. Hybrid Syst. 2020, 38, 100931. [Google Scholar] [CrossRef]
- Karimi, H.R. A sliding mode approach to H∞ synchronization of master-slave time-delay systems with Markovian jumping parameters and nonlinear uncertainties. J. Frankl. Inst. 2012, 349, 1480–1496. [Google Scholar] [CrossRef] [Green Version]
- Zohrabi, N.; Reza Momeni, H.; Hossein Abolmasoumi, A. Sliding mode control of Markovian jump systems with partly unknown transition probabilities. IFAC Proc. Vol. 2013, 46, 947–952. [Google Scholar] [CrossRef]
- Yue, D.; Tian, E.; Han, Q. A delay system method for designing event-triggered controllers of networked control systems. IEEE Trans. Autom. Control 2013, 58, 475–481. [Google Scholar] [CrossRef]
- Su, X.; Liu, X.; Shi, P.; Song, Y.-D. Sliding mode control of hybrid switched systems via an event-triggered mechanism. Automatica 2018, 90, 294–303. [Google Scholar] [CrossRef]
- Peng, C.; Han, Q.; Yue, D. To transmit or not to transmit: A discrete event-triggered communication scheme for networked Takagi–Sugeno fuzzy systems. IEEE Trans. Fuzzy Syst. 2013, 21, 164–170. [Google Scholar] [CrossRef]
- Behera, A.K.; Bandyopadhyay, B.; Yu, X. Periodic event-triggered sliding mode control. Automatica 2018, 96, 61–72. [Google Scholar] [CrossRef]
- Dimarogonas, D.V.; Frazzoli, E.; Johansson, K.H. Distributed event-triggered control for multi-agent systems. IEEE Trans. Autom. Control 2012, 57, 1291–1297. [Google Scholar] [CrossRef]
- Cheng, J.; Park, J.H.; Zhang, L.; Zhu, Y. An asynchronous operation approach to event-triggered control for fuzzy Markovian jump systems with general switching policies. IEEE Trans. Fuzzy Syst. 2018, 26, 6–18. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Wei, G.; Alsaadi, F.E. Finite-time state estimation for recurrent delayed neural networks with component-based event-triggering protocol. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1046–1057. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Gao, Y.; Liu, J.; Li, H. Event-triggered sliding mode control of stochastic systems via output feedback. Automatica 2017, 82, 79–92. [Google Scholar] [CrossRef]
- Huai-Ning, W.; Kai-Yuan, C. Mode-independent robust stabilization for uncertain Markovian jump nonlinear systems via fuzzy control. IEEE Trans. Syst. Man Cybern. Part B 2006, 36, 509–519. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, K.; Kosaki, T. Design of a stable fuzzy controller for an articulated vehicle. IEEE Trans. Syst. Man Cybern. Part B 1997, 27, 552–558. [Google Scholar] [CrossRef] [PubMed]
- Meyn, S.P.; Tweedie, R.L. Markov Chains and Stochastic Stability; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Boukas, K. Stabilization of stochastic nonlinear hybrid systems. Int. J. Innov. Comput. Inf. Control 2005, 1, 131–141. [Google Scholar] [CrossRef]
- Xiong, J.; Lam, J. Robust H2 control of Markovian jump systems with uncertain switching probabilities. Int. J. Syst. Sci. 2009, 40, 255–265. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Gao, C. Decentralized adaptive sliding mode control of large-scale semi-Markovian jump interconnected systems with dead-zone input. IEEE Trans. Autom. Control 2021. [Google Scholar] [CrossRef]



| Symbol | Meaning |
|---|---|
| angle position of the robot arm | |
| the input of control | |
| coefficient of viscous friction | |
| length of the arm | |
| moment of inertia | |
| mass of the pay load | |
| the acceleration of gravity |
| Mode m | Parameter M | Parameter J |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1.5 | 2 |
| 3 | 2 | 2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, M.; Zhang, C.; Qiu, J.; Wu, Z.; Gao, Q. Time-Delay Luenberger Observer Design for Sliding Mode Control of Nonlinear Markovian Jump Systems via Event-Triggered Mechanism. Machines 2021, 9, 259. https://doi.org/10.3390/machines9110259
Cheng M, Zhang C, Qiu J, Wu Z, Gao Q. Time-Delay Luenberger Observer Design for Sliding Mode Control of Nonlinear Markovian Jump Systems via Event-Triggered Mechanism. Machines. 2021; 9(11):259. https://doi.org/10.3390/machines9110259
Chicago/Turabian StyleCheng, Min, Chunyang Zhang, Jin Qiu, Zhengtian Wu, and Qing Gao. 2021. "Time-Delay Luenberger Observer Design for Sliding Mode Control of Nonlinear Markovian Jump Systems via Event-Triggered Mechanism" Machines 9, no. 11: 259. https://doi.org/10.3390/machines9110259
APA StyleCheng, M., Zhang, C., Qiu, J., Wu, Z., & Gao, Q. (2021). Time-Delay Luenberger Observer Design for Sliding Mode Control of Nonlinear Markovian Jump Systems via Event-Triggered Mechanism. Machines, 9(11), 259. https://doi.org/10.3390/machines9110259







