Mechanism Design and Experiment of a Bionic Turtle Dredging Robot
Abstract
:1. Introduction
2. Mechanism Analysis and Solution Method
2.1. The Overall Bionic Design of the Dredging Robot
2.2. Outrigger Mechanism Modeling and Positive Kinematics Analysis Method
2.3. Inverse Kinematics of Outrigger Mechanism and Method of Solving Body Pose
3. Gait Analysis and Trajectory Planning of the Bionic Turtle Robot
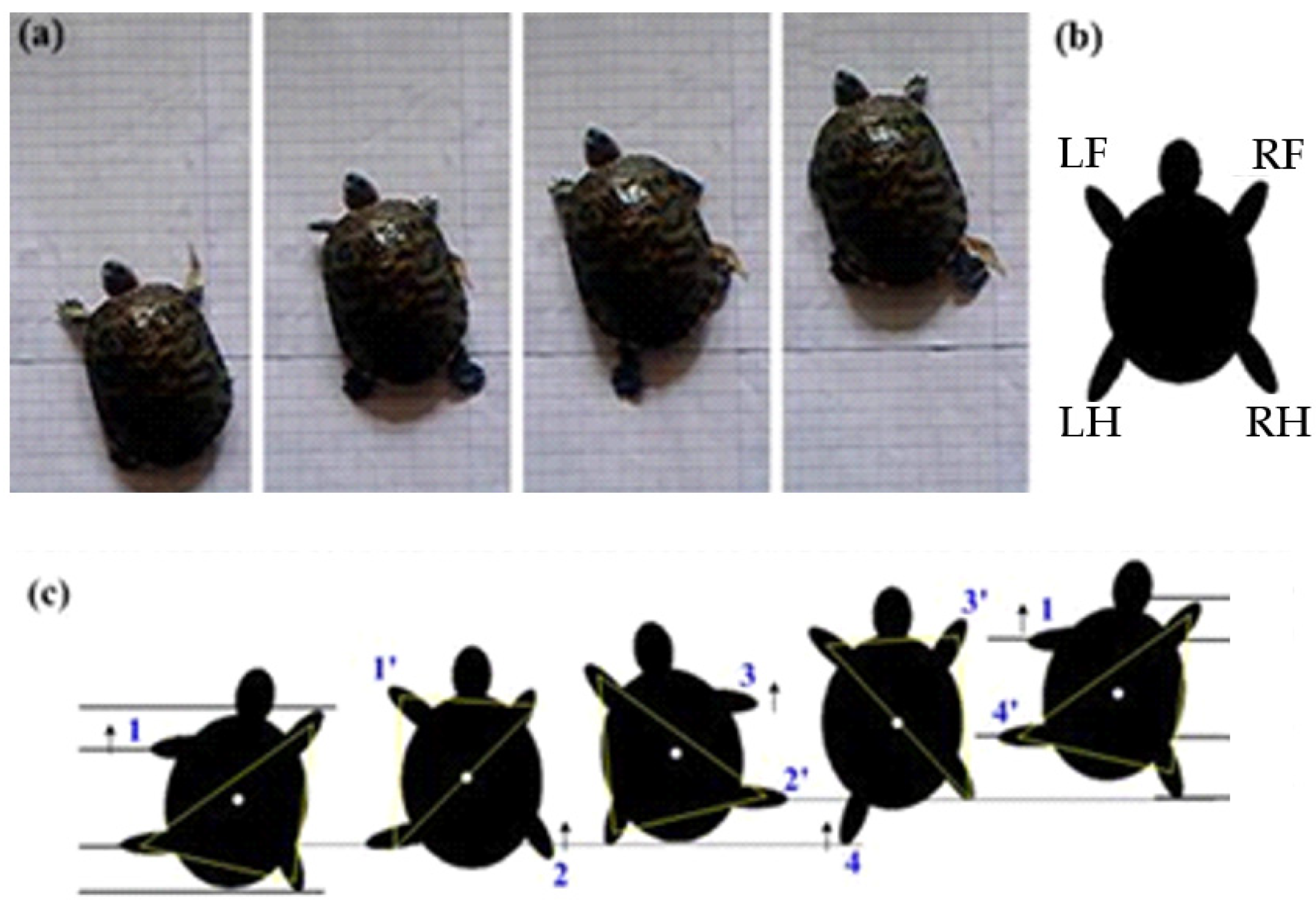
3.1. Turtle Crawling Mechanism
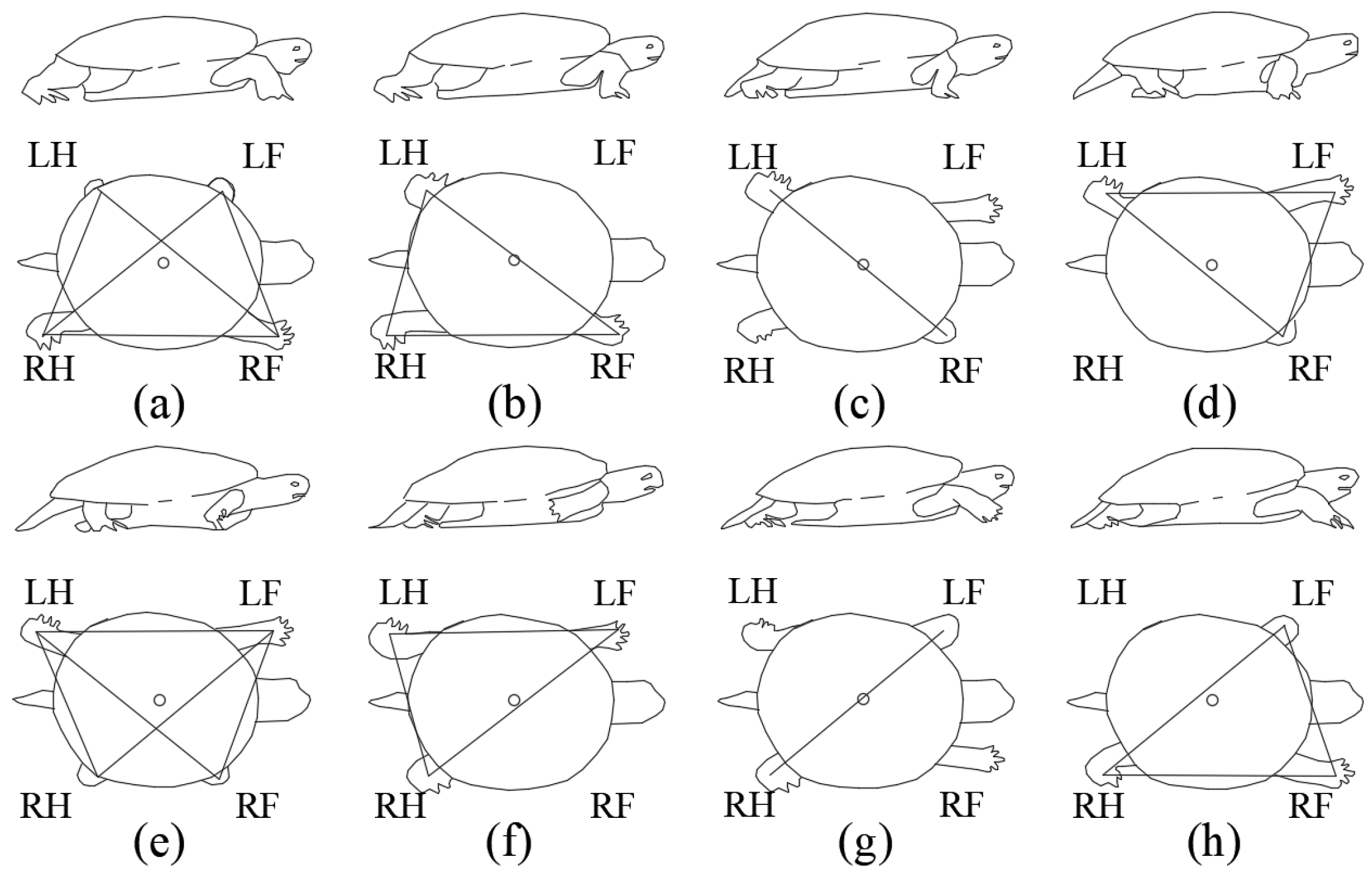
3.2. Gait Analysis of the Bionic Turtle Robot
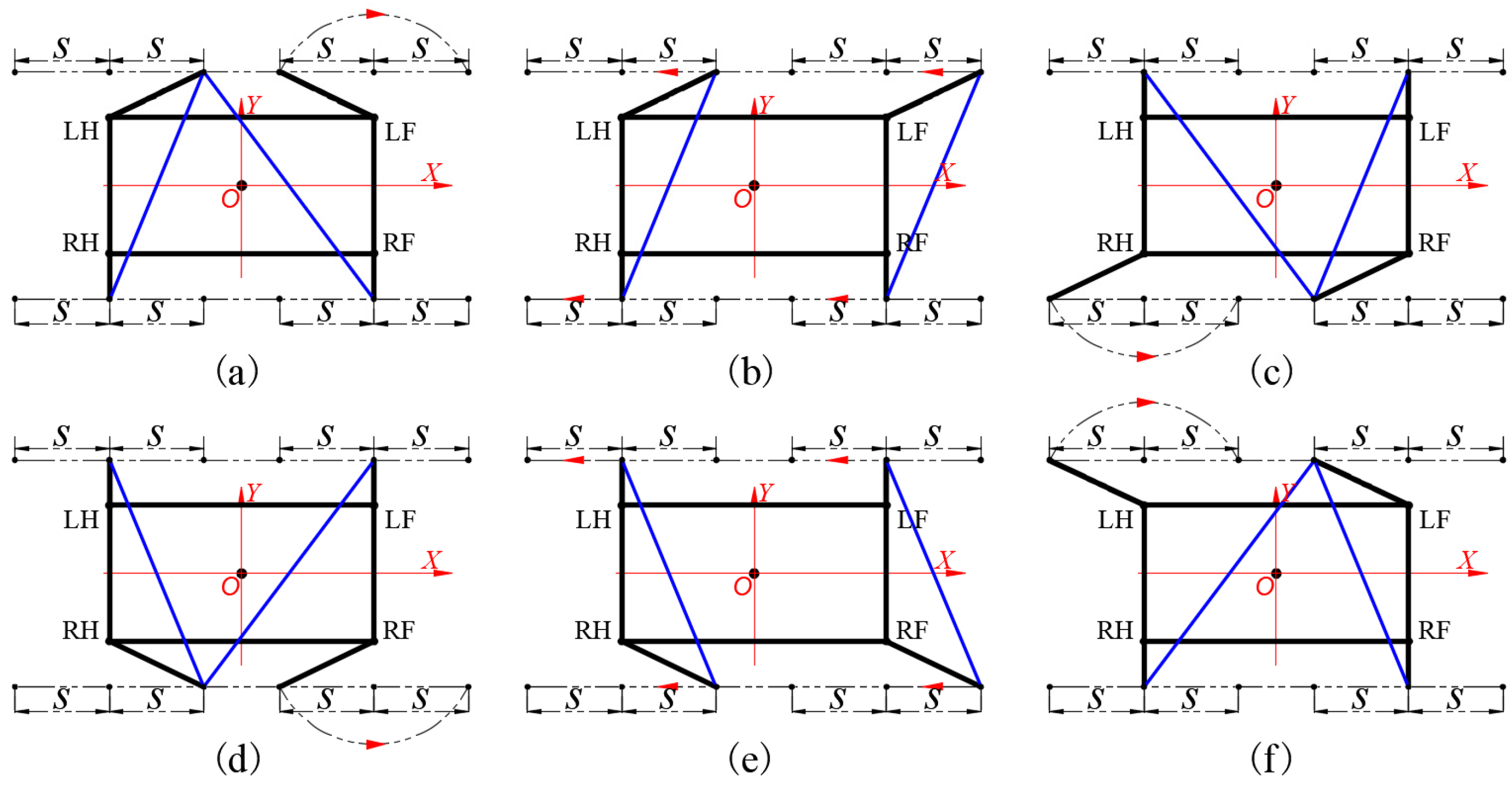
3.2.1. Gait Sequence Design
3.2.2. Three Kinds of Movement Gait of Dredging Robot
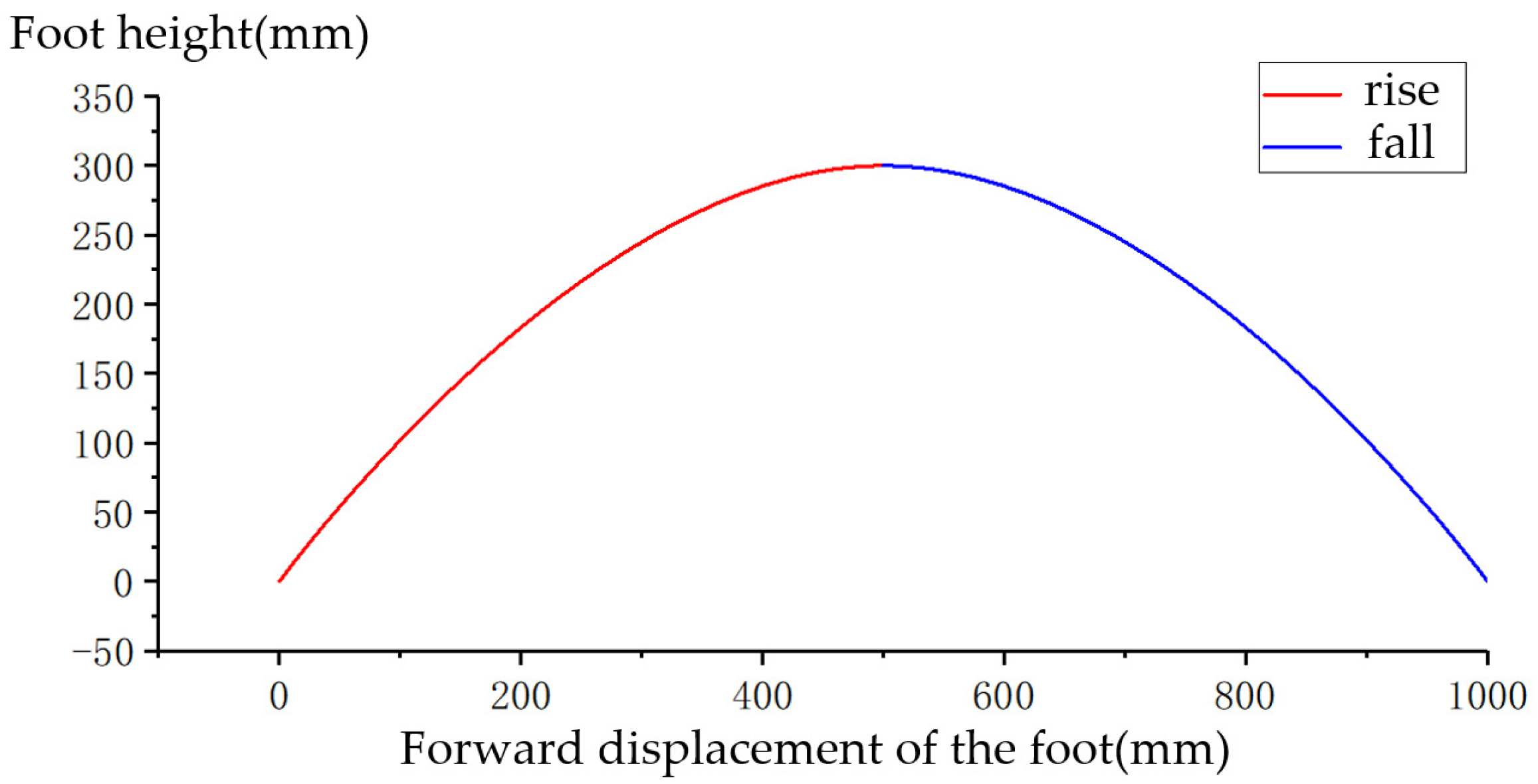
3.3. Motion Track Design
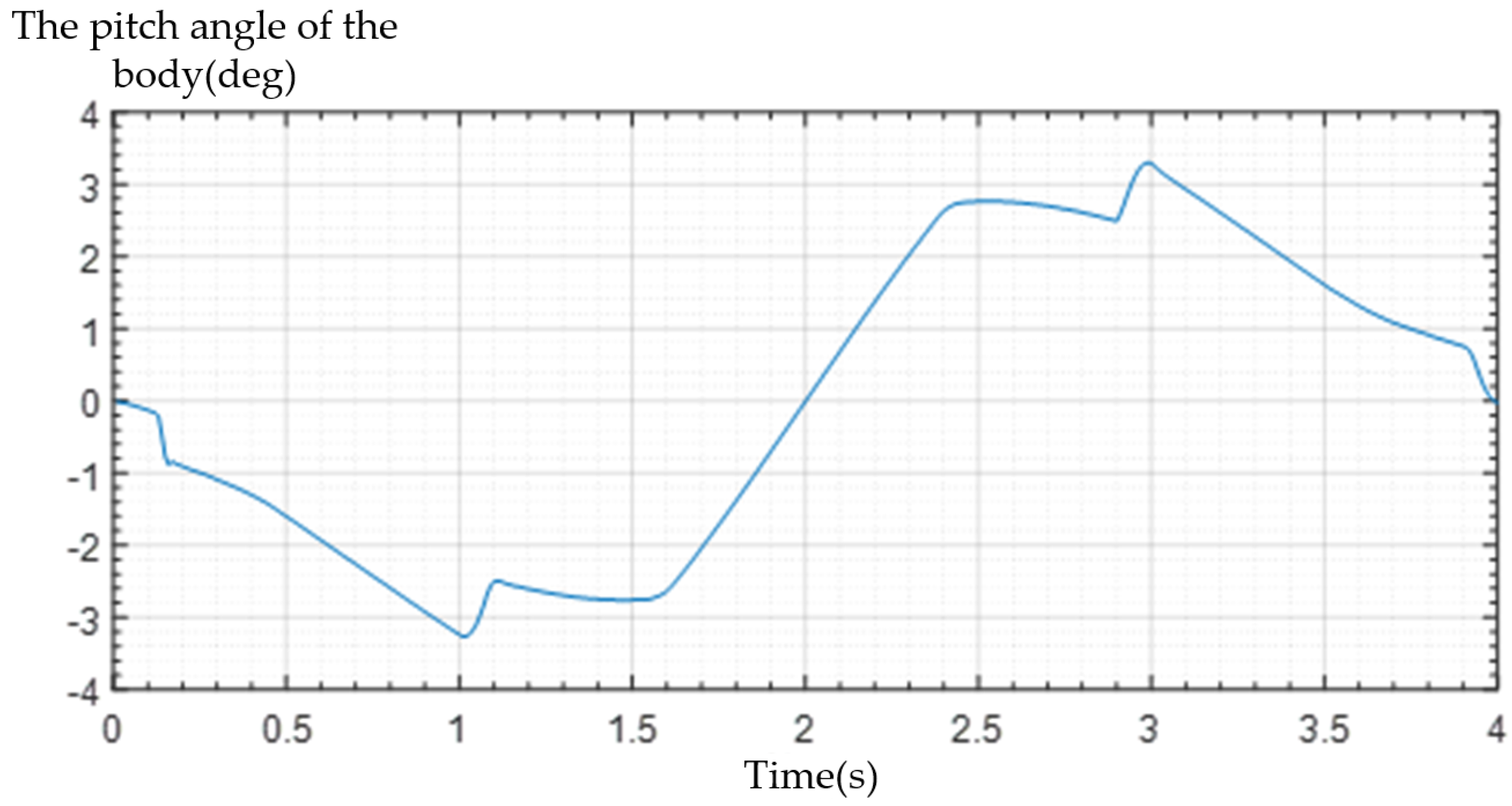
4. Gait Experiment of Dredging Robot
4.1. Coordinated Gait Experiment
4.2. Intermittent Gait Experiment
4.3. Mixed Gait Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, H.Q.; Zhou, J.J. Development and prospect of dredging at water conservancy works in China. J. Sedim. Res. 2011, 5, 67–72. [Google Scholar]
- Manap, N.; Voulvoulis, N. Environmental management for dredging sediments—The requirement of developing nations. J. Environ. Manag. 2015, 147, 338–348. [Google Scholar] [CrossRef] [PubMed]
- Seagren, E.H. Latest Developments in Small Hydraulic Dredges for Contaminated Sediment Removal in the USA. In Proceedings of the Third Specialty Conference on Dredging and Dredged Material Disposal, Orlando, FL, USA, 5–8 May 2002. [Google Scholar]
- Wang, H.X.; Wang, C.L.; Wang, C.Z. The Development of Boat-loaded Flushing-winching Submarine Dredging Machine. Mod. Manuf. Technol. Equip. 2009, 6, 32–34. [Google Scholar]
- Cha, Y.H.; Sun, S.M. The actuality and developing trend of clearing silt technology and machine for lake and pond in china. Chin. Agric. Mech. 2005, 2, 27–30. [Google Scholar]
- Ren, Z.X. Discussion on Silt Clearing and Silt Treatment in Middle and Small River. China Water Transp. 2020, 20, 180–181. [Google Scholar]
- Liao, W.Q.; Luo, Z.Y.; Xu, S.M. Research Status and Development Trend of Underwater Cleaning Robot. Mech. Electr. Eng. Technol. 2016, 45, 12–14. [Google Scholar]
- Xie, B.; Chen, C.; Zhang, G.X. Research and Implementation of Underwater Dredging Equipment Control System. Ship Eng. 2017, 39, 180–182. [Google Scholar]
- Zhao, L. On Selection and Configuration of Dredging Construction Machinery. Value Eng. 2017, 13, 141–143. [Google Scholar]
- Bao, J.P.; Zhu, W.; Min, J.H. Technology of dredging and sludge treatment in small and medium-sized river regulation. Water Resour. Protect. 2015, 31, 56–62. [Google Scholar]
- Bruzzone, P.; Quaglia, L. Review article: Locomotion systems for ground mobile robots in unstructured environments. Mech. Sci. 2012, 2, 49–62. [Google Scholar] [CrossRef] [Green Version]
- Hijdra, R.M.J.; Harst, S.V.D. Design of an Autonomous Underwater Maintenance Dredger: A teaser to the maritime industry. J. Phys. Conf. Ser. 2019, 1357, 012001. [Google Scholar] [CrossRef]
- Raibert, M.; Blankespoor, K.; Nelson, G. BigDog, the rough-terrain quadruped robot. In Proceedings of the 17th World Congress on the International Federation of Automatic Control, Seoul, Korea, 6 July 2008. [Google Scholar]
- Semini, C.; Barasuol, V.; Boaventura, T. Towards versatile legged robots through active impedance control. Int. J. Robot. Res. 2015, 34, 1003–1020. [Google Scholar] [CrossRef]
- Meng, J.; Liu, J.C.; Rong, X.W. Development status and prospect of quadruped robots. Sci. Technol. Rev. 2015, 33, 59–63. [Google Scholar]
- Gonzalez, D.S.; Pablo, G.; Elena, E. Quadrupedal Locomotion. An Introduction to the Control of Four-Legged Robots; Springer: London, UK, 2006; pp. 50–92. [Google Scholar]
- Zeng, N.; Hang, G.R.; Cao, G.H. Present State and Tendency of Bionic Underwater Robot. Mech. Eng. 2006, 04, 18–21. [Google Scholar]
- Chen, Y.H.; Tan, Y.G.; Li, Z. Method of Gait Generating for Quadruped Robot Walking on Rough Terrain. Comput. Meas. Control 2016, 24, 262–267. [Google Scholar]
- Boussema, C.; Powell, M.; Bledt, G. Online Gait Transitions and Disturbance Recovery for Legged Robots via the Feasible Impulse Set. IEEE Robot. Auto. Lett. 2019, 04, 1611–1618. [Google Scholar] [CrossRef]
- Koray, K.A.; Adams, G.G. Modeling and simulation of an artificial muscle and its application to biomimetic robot posture control. Robot. Auto. Syst. 2002, 41, 225–243. [Google Scholar]
- Kim, J.Y.; Jun, B.H. Design of six-legged walking robot, Little Crabster for underwater walking and operation. Adv. Robot. 2014, 28, 77–89. [Google Scholar] [CrossRef]
- Mao, S.; Dong, E.; Zhou, L. Design and Gait Analysis of a Tortoise-Like Robot with Soft Limbs. In Proceedings of the 18th International Conference on CLAWAR, HangZhou, China, 6–9 September 2015; Assistive Robotics, Printed in Singapore. pp. 215–223. [Google Scholar]
- Wang, D.; Li, H.; Lin, X. Study on the motion design and control algorithm of the tortoise robot. J. Phys. Conf. Ser. 2019, 1345, 042066. [Google Scholar] [CrossRef]


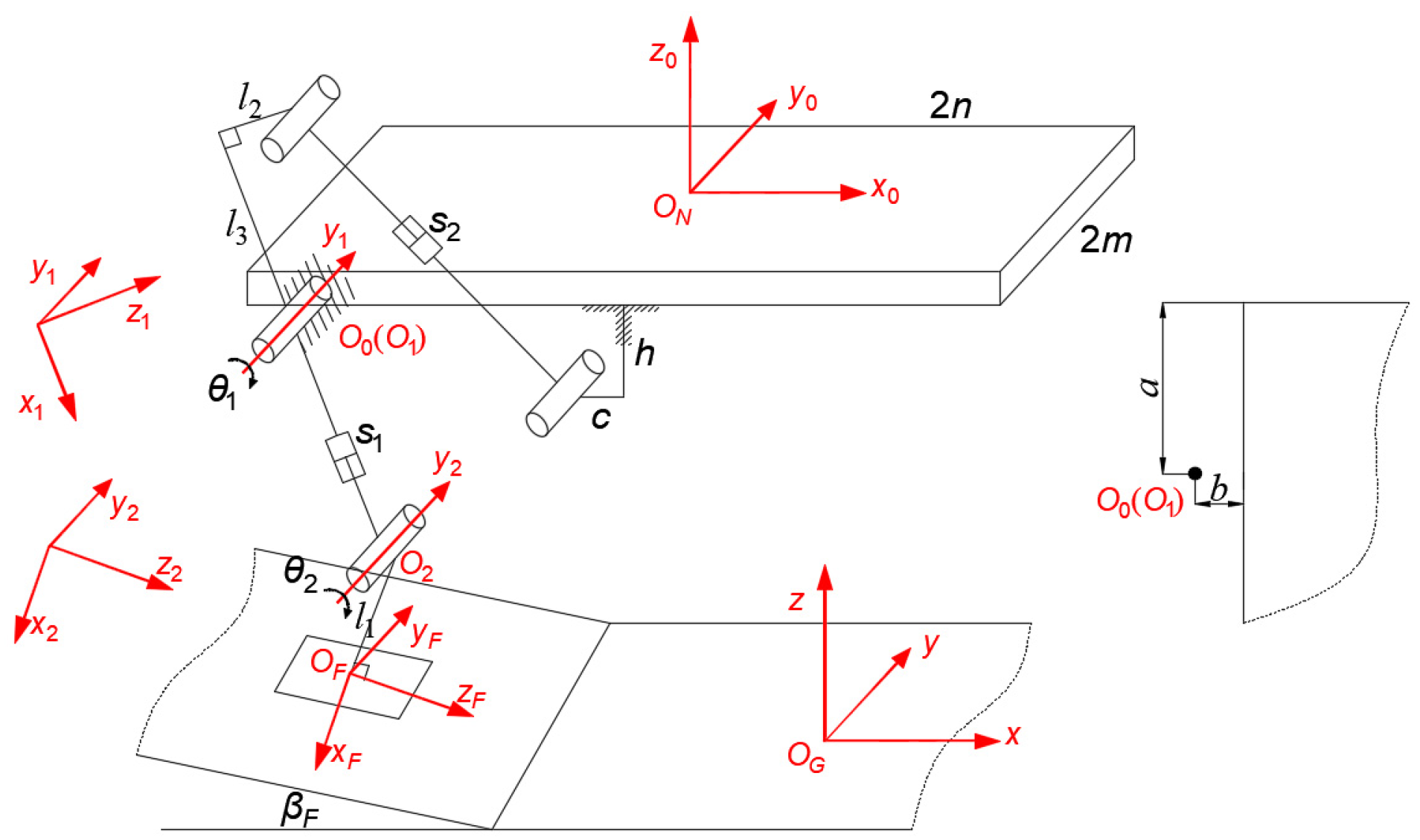
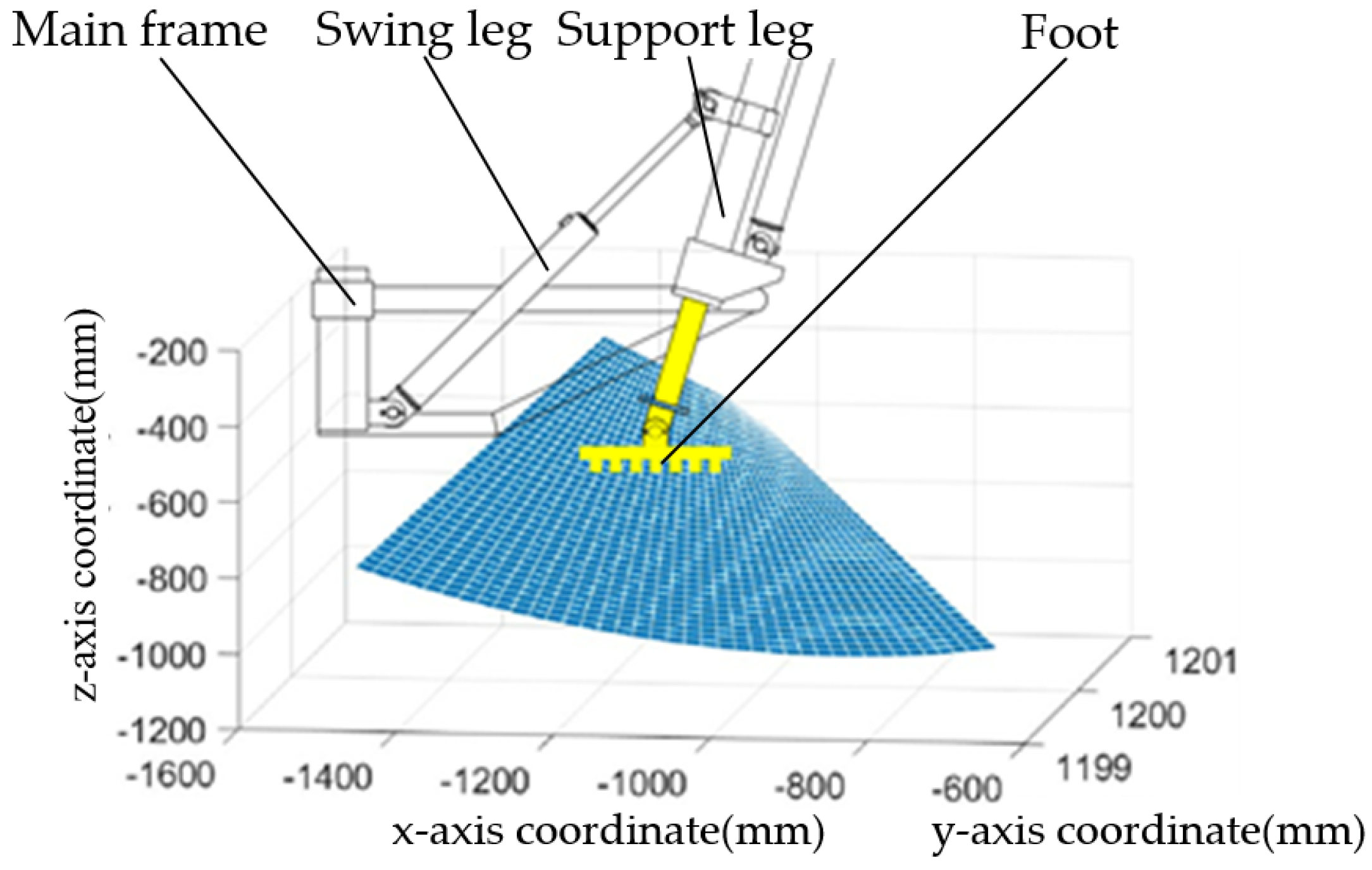
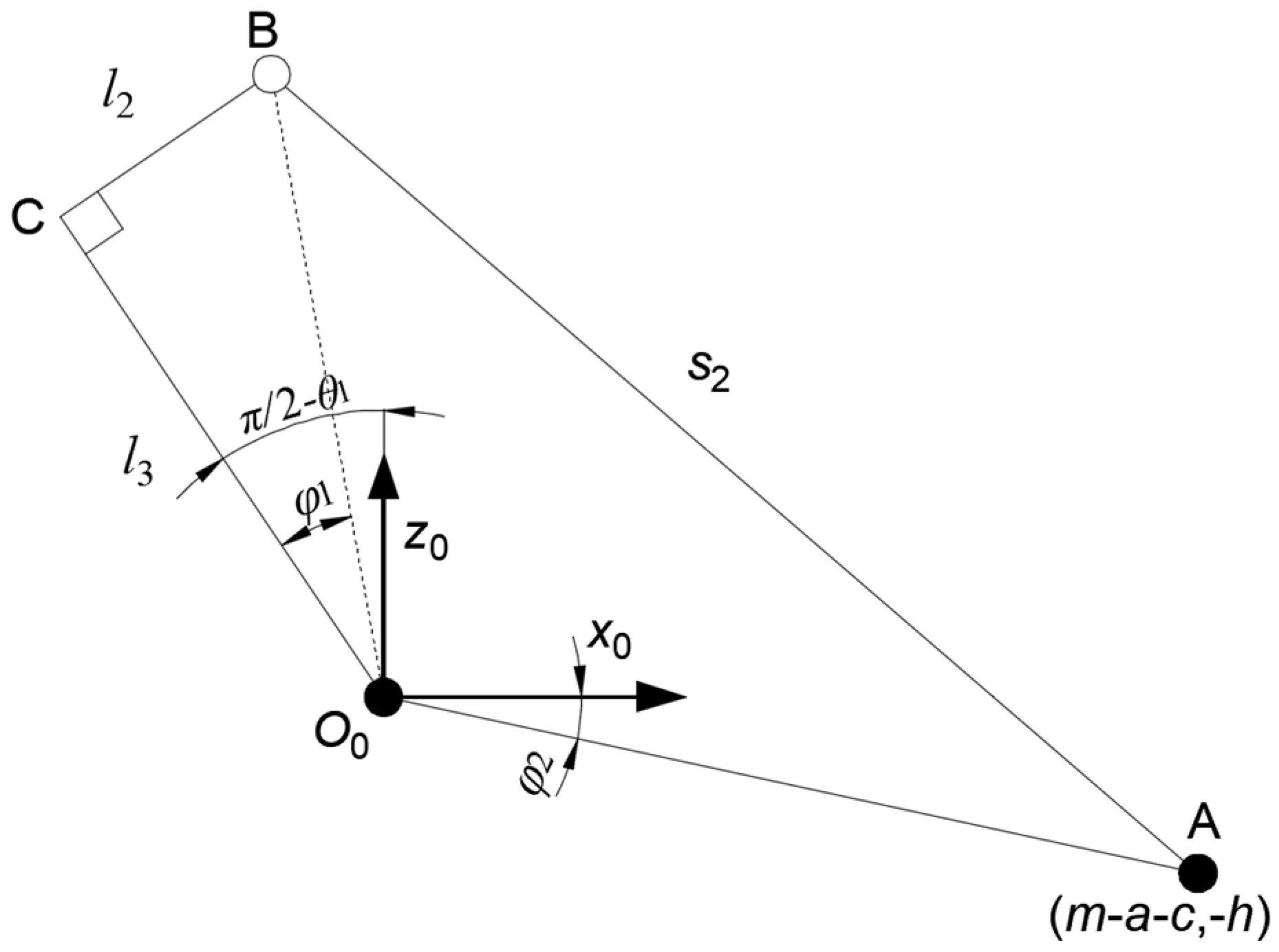
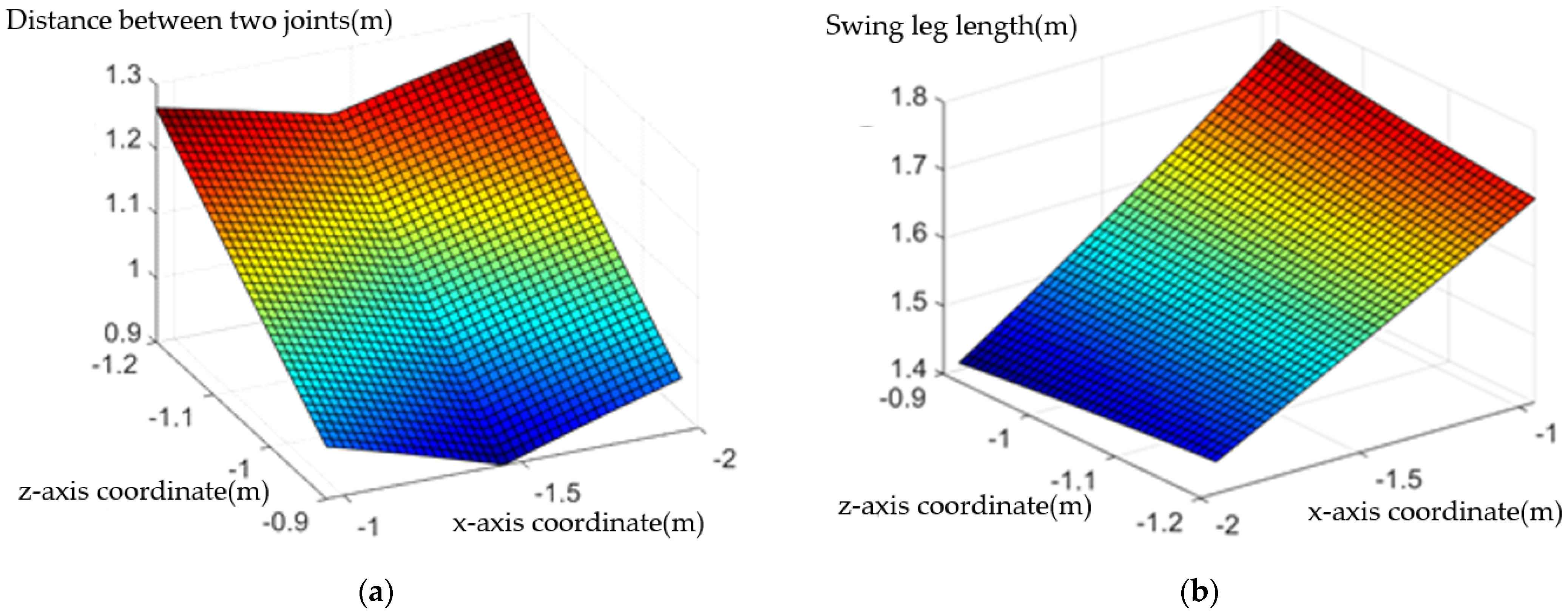








| Parameter Symbol | Parameter Meaning | Value |
|---|---|---|
| l1 | Vertical distance between ankle joint and foot plane | 160 mm |
| l2 | The distance between the hinge point of the swing leg and the support leg and the hip joint in the vertical support leg | 220 mm |
| l3 | The distance between the hinge point of the swing leg and the supporting leg and the hip joint along the supporting leg | 510 mm |
| h | The vertical distance between the hinge point of the swing leg and the body and the plane of the body | 450 mm |
| c | The vertical distance between the hinge point of the swing leg and the body and the center cross section of the body | 100 mm |
| a | The distance between the hip joint and the short side of the body | 250 mm |
| b | The distance between the hip joint and the long side of the body | 130 mm |
| m | Half of the body length | 1700 mm |
| n | Half of the body width | 1200 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Wang, Z.; Zhang, B. Mechanism Design and Experiment of a Bionic Turtle Dredging Robot. Machines 2021, 9, 86. https://doi.org/10.3390/machines9050086
Wang T, Wang Z, Zhang B. Mechanism Design and Experiment of a Bionic Turtle Dredging Robot. Machines. 2021; 9(5):86. https://doi.org/10.3390/machines9050086
Chicago/Turabian StyleWang, Tao, Zhuo Wang, and Bo Zhang. 2021. "Mechanism Design and Experiment of a Bionic Turtle Dredging Robot" Machines 9, no. 5: 86. https://doi.org/10.3390/machines9050086
APA StyleWang, T., Wang, Z., & Zhang, B. (2021). Mechanism Design and Experiment of a Bionic Turtle Dredging Robot. Machines, 9(5), 86. https://doi.org/10.3390/machines9050086





