Multi-Objective Lightweight Optimization of Parameterized Suspension Components Based on NSGA-II Algorithm Coupling with Surrogate Model
Abstract
1. Introduction
2. Parametric Modeling of Control Arm and Torsion Beam
2.1. Mesh Morphing Technology
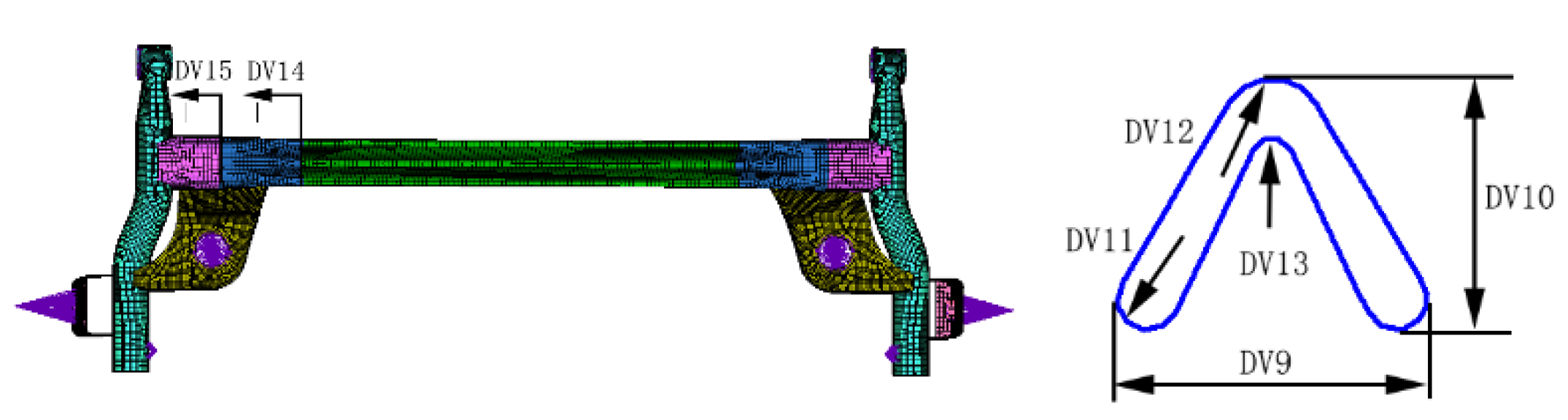
2.2. Parametric Modeling
3. Establishment of Vehicle Rigid–Flexible Coupling Model
3.1. Flexible Body Models of Control Arm and Torsion Beam
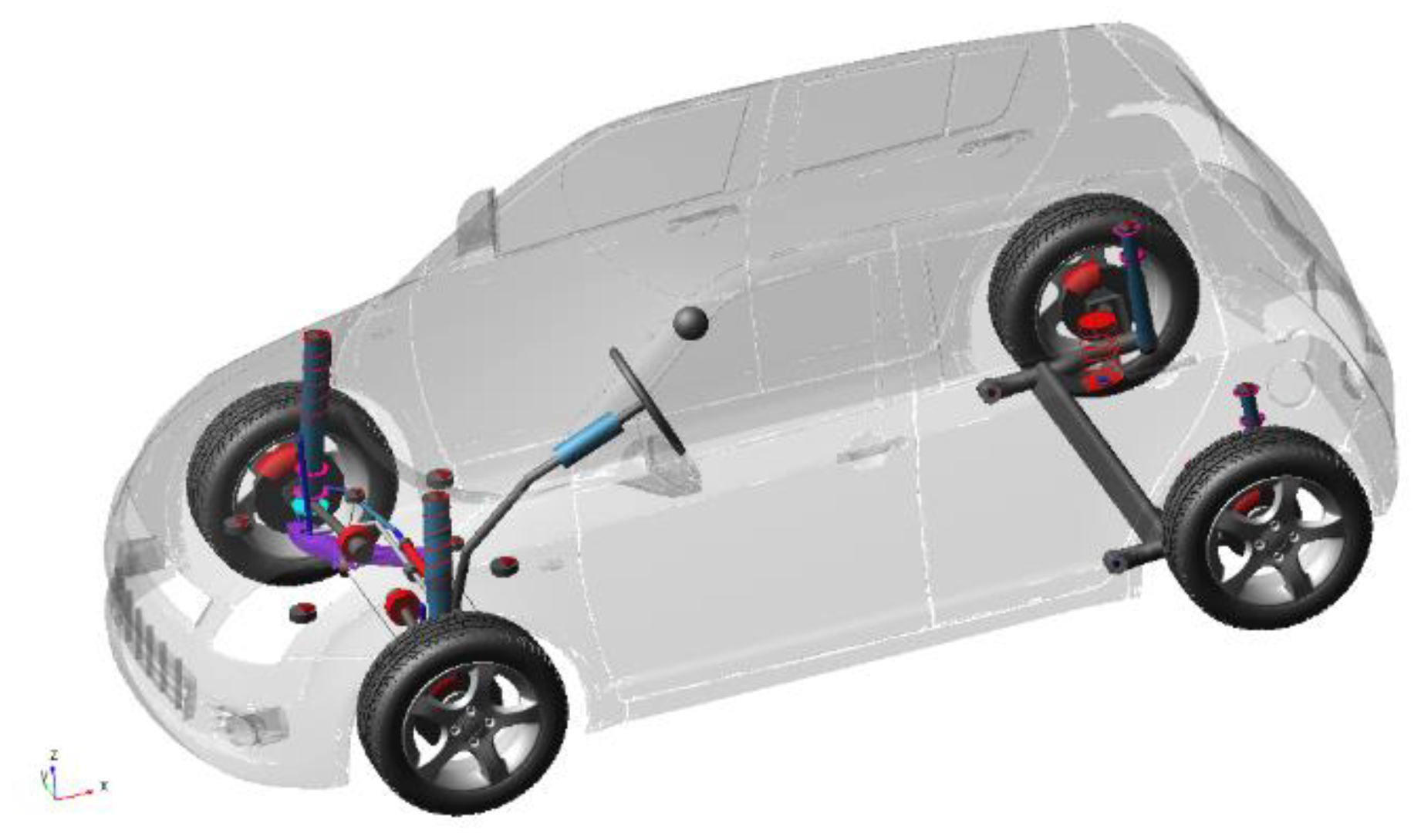
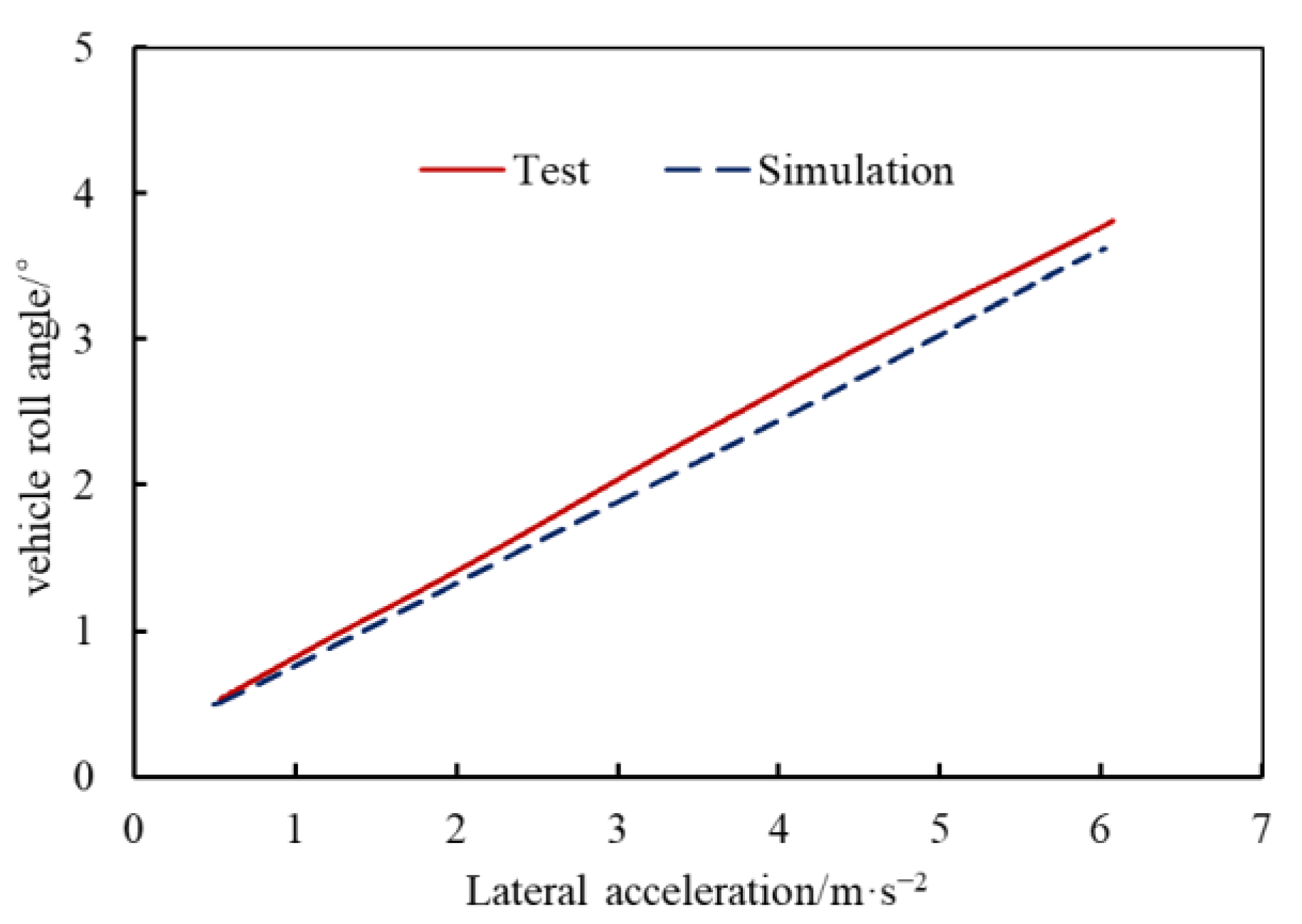
3.2. Establishment and Verification of Rigid–Flexible Coupling Vehicle Model
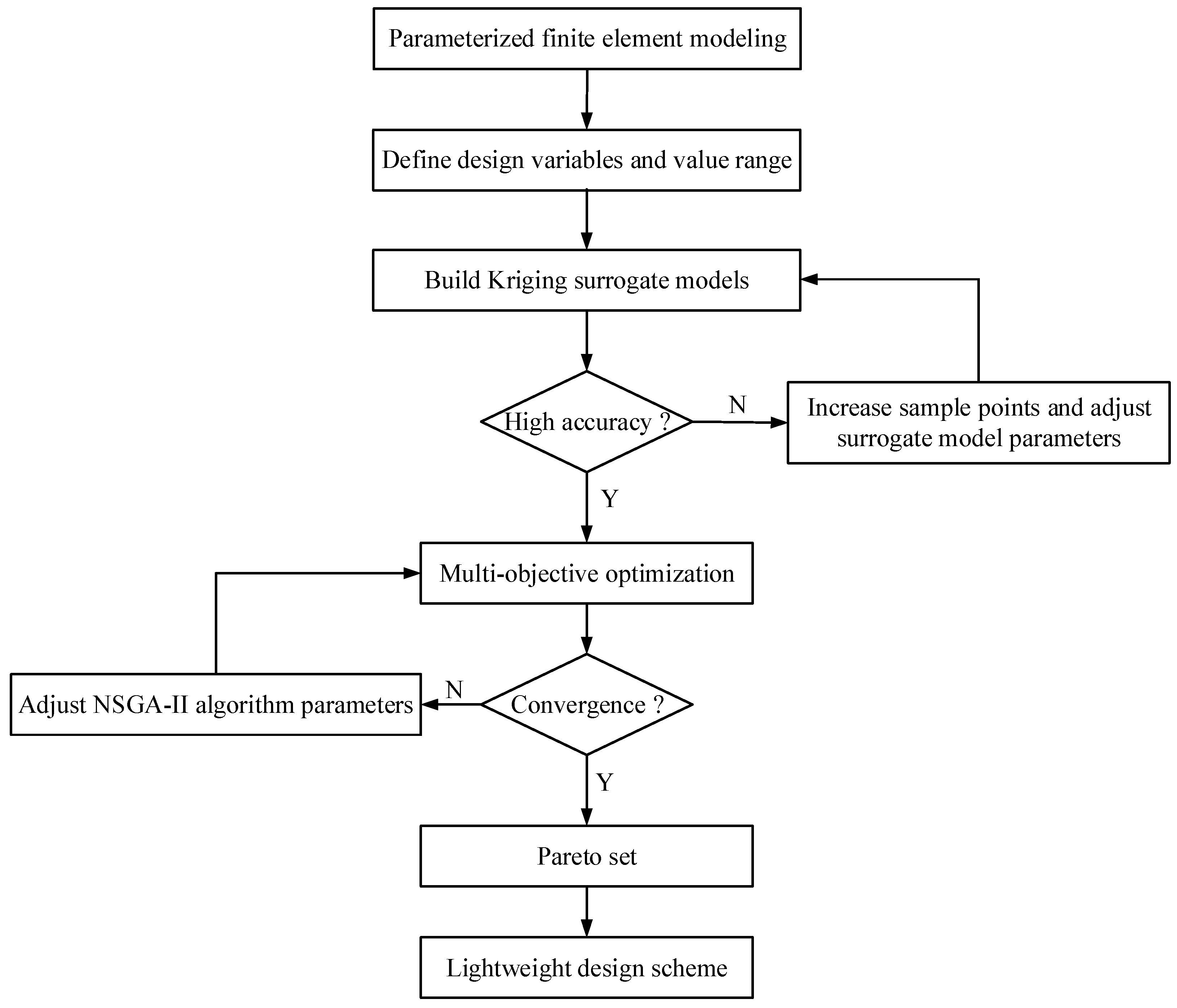
4. Lightweight Design of Control Arm and Torsion Beam
4.1. Optimization Formulation
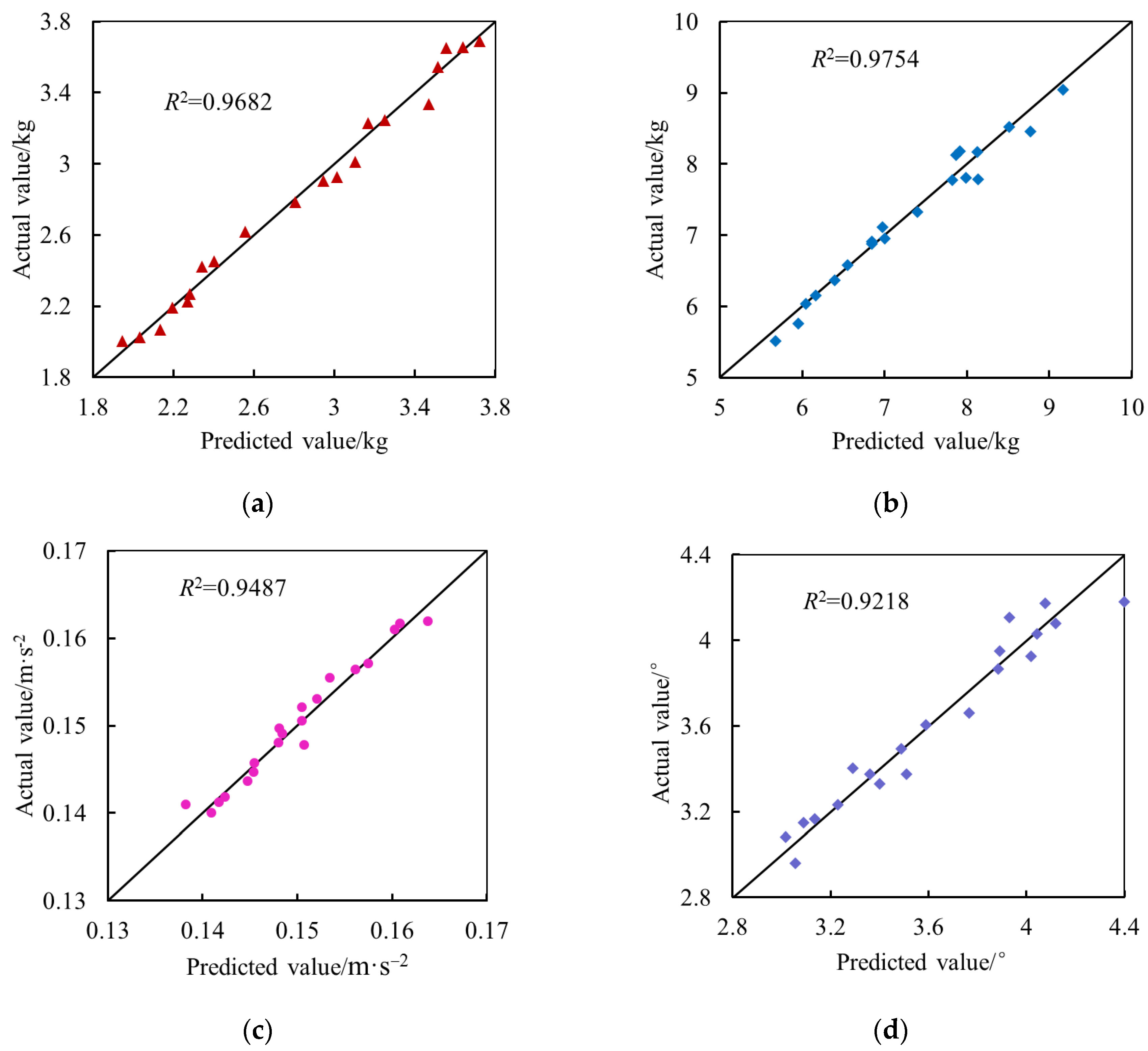
4.2. Surrogate Model
4.3. Multi-Objective Optimization Based on NSGA-II Algorithm
5. Results and Discussion
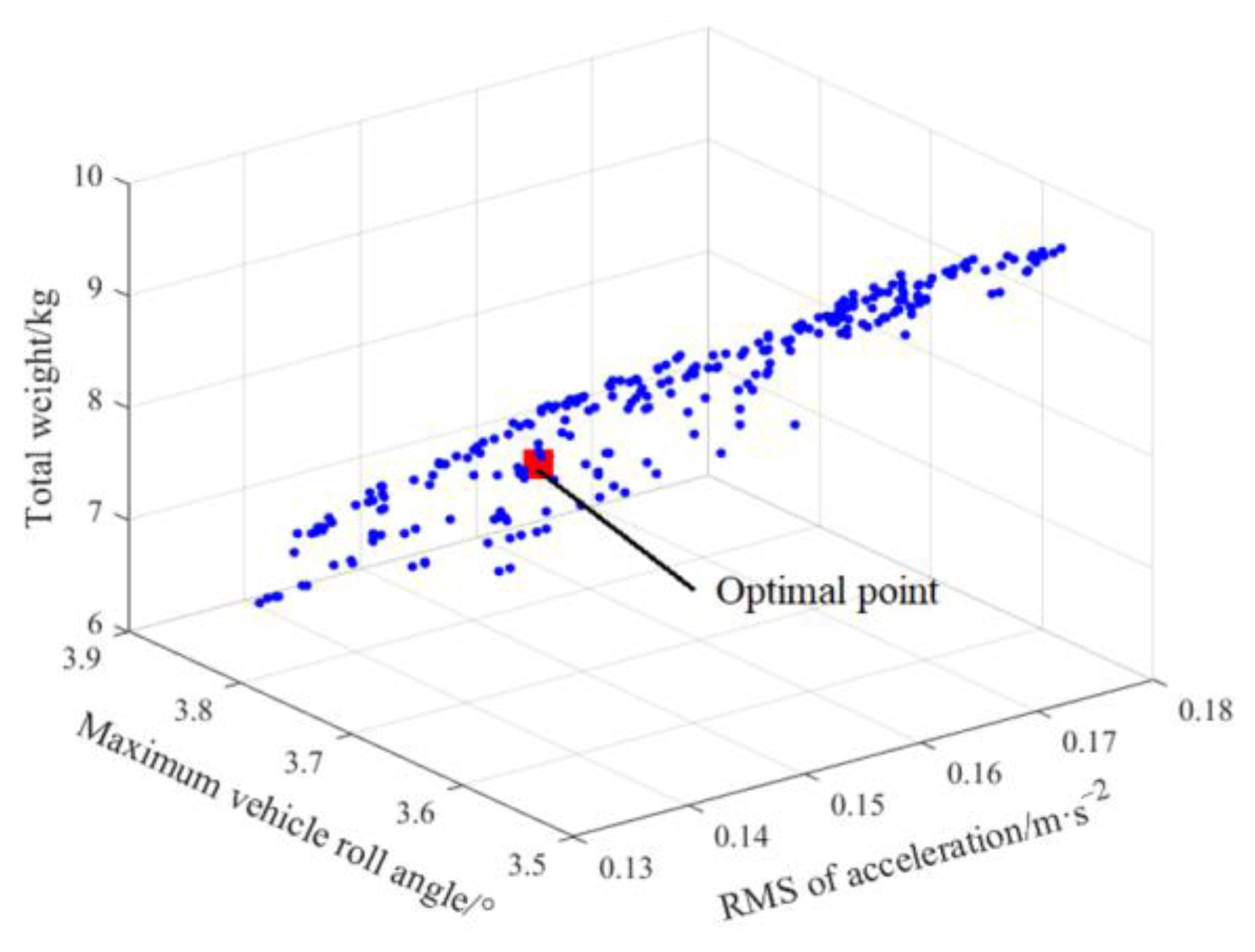
5.1. Optimization Results
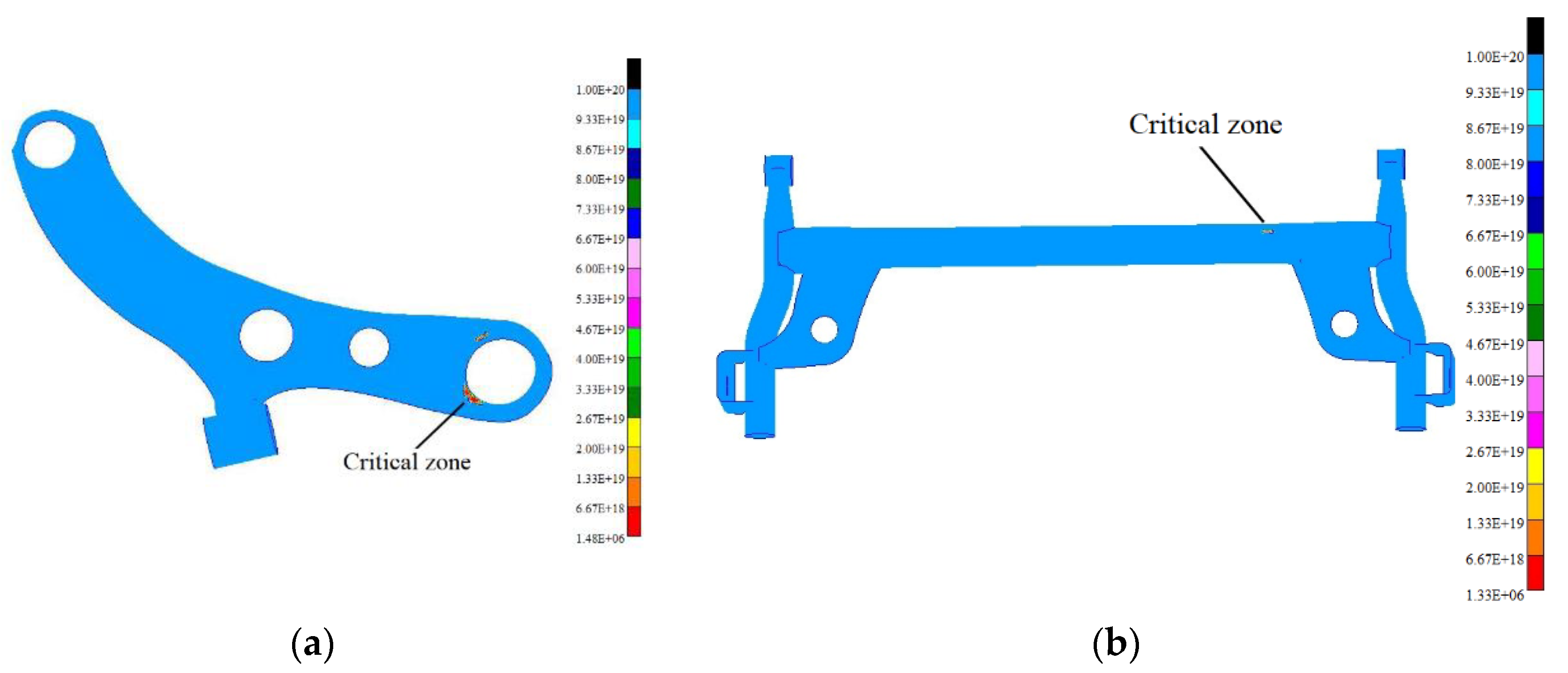
5.2. Structural Performance of Control Arm and Torsion Beam
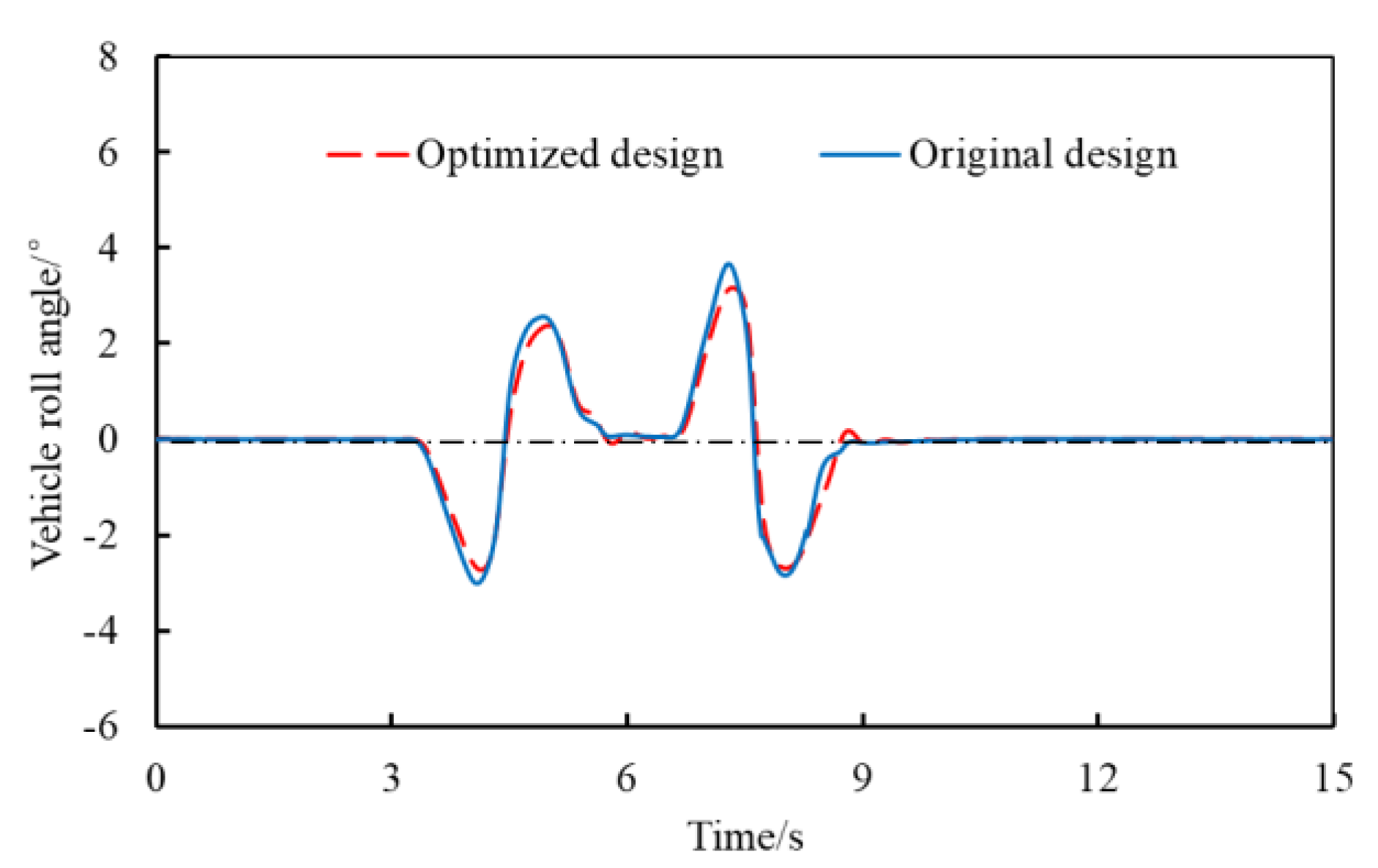
5.3. Vehicle Dynamic Performance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Cavazzuti, M.; Baldini, A.; Bertocchi, E.; Costi, D.; Torricelli, E.; Moruzzi, P. High performance automotive chassis design: A topology optimization based approach. Struct. Multidiscip. Optim. 2011, 44, 45–56. [Google Scholar] [CrossRef]
- Ozcanli, M.; Yilmaz, M. Effect of foam application in bus structure for conservation of residual space during rollovers. Int. J. Heavy Veh. Syst. 2014, 21, 56–63. [Google Scholar] [CrossRef]
- Del Pero, F.; Berzi, L.; Antonacci, A.; Delogu, M. Automotive Lightweight Design: Simulation Modeling of Mass-Related Consumption for Electric Vehicles. Machines 2020, 8, 51. [Google Scholar] [CrossRef]
- Yu, L.; Gu, X.; Qian, L.; Jiang, P.; Wang, W.; Yu, M. Application of tailor rolled blanks in optimum design of pure electric vehicle crashworthiness and lightweight. Thin Wall. Struct. 2021, 161, 107410. [Google Scholar] [CrossRef]
- Miao, B.R.; Luo, Y.X.; Peng, Q.M.; Qiu, Y.Z.; Chen, H.; Yang, Z.K. Multidisciplinary design optimization of lightweight carbody for fatigue assessment. Mater. Des. 2020, 194, 108910. [Google Scholar] [CrossRef]
- Jiang, R.; Zhang, T.; Sun, H.; Liu, D.; Chen, H.; Wang, D. Study on lightweighting of CFRP bumper beam using entropy-based TOPSIS approach. Automot. Eng. 2021, 43, 421–428. [Google Scholar]
- Paz, J.; Díaz, J.; Romera, L.; Costas, M. Crushing analysis and multi-objective crashworthiness optimization of GFRP honeycomb-filled energy absorption devices. Finite Elem. Anal. Des. 2014, 91, 30–39. [Google Scholar] [CrossRef]
- Velea, M.N.; Wennhage, P.; Zenkert, D. Multi-objective optimisation of vehicle bodies made of FRP sandwich structures. Compos. Struct. 2014, 111, 75–84. [Google Scholar] [CrossRef]
- Duan, L.; Li, G.; Cheng, A.; Sun, G.; Song, K. Multi-objective system reliability-based optimization method for design of a fully parametric concept car body. Eng. Optimiz. 2017, 49, 1247–1263. [Google Scholar] [CrossRef]
- Li, Z.; Yu, Q.; Zhao, X.; Chen, J.; Fan, Q. Crashworthiness and lightweight optimization for frontal structure of automobile under low-speed impact. China J. Highw. Transp. 2016, 29, 149–158. [Google Scholar]
- Wang, D.; Mao, A.; Niu, Y.; Wei, J.; Shi, X. Lightweight multi-objective optimization design for body frame of pure electric large bus based on topology optimization. China J. Highw. Transp. 2017, 30, 136–143. [Google Scholar]
- Sharma, B. CAE driven multi disciplinary optimization of vehicle systems and sub systems. SAE Tech. Pap. 2014, 2014, 0804. [Google Scholar]
- Wang, D.; Jiang, R.; Wu, Y. A hybrid method of modified NSGA-II and TOPSIS for lightweight design of parameterized passenger car sub-frame. J. Mech. Sci. Technol. 2016, 30, 4909–4917. [Google Scholar] [CrossRef]
- Lian, Z. Study on Multi-Objective Optimization of a Coach Retrofit Design Based on the Mesh Morphing Method. Master’s Thesis, Jilin University, Changchun, China, 2015. [Google Scholar]
- Fang, J.; Gao, Y.; Wang, J.; Wang, Y. Multi-objective shape optimization of body-in-white based on mesh morphing technology. Chin. J. Mech. Eng. 2013, 48, 119–126. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, J.; Wang, J.; Tian, L. A research on the application of mesh morphing technology to car body retrofit design. Automot. Eng. 2012, 34, 847–851. [Google Scholar]
- Park, J.H.; Kim, K.J.; Lee, J.W.; Yoon, J.K. Light-weight design of automotive suspension link based on design of experiment. Int. J. Automot. Technol. 2015, 16, 67–71. [Google Scholar] [CrossRef]
- Gu, Z.; Mi, C.; Wang, Y.; Jiang, J. A-type frame fatigue life estimation of a mining dump truck based on modal stress recovery method. Eng. Fail. Anal. 2012, 26, 89–99. [Google Scholar] [CrossRef]
- Van der Auweraer, H.; Van Langenhove, T.; Brughmans, M.; Bosmans, I.; El Masri, N.; Donders, S. Application of mesh morphing technology in the concept phase of vehicle development. Int. J. Veh. Des. 2007, 43, 281–305. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, D.; Qin, M.; Jiang, Y. Lightweight design of twist beam of rear suspension of passenger car based on fatigue life. J. Jilin Univ. (Eng. Technol. Ed.) 2016, 46, 35–42. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Huang, W.; Huang, J.; Yin, C. Optimal Design and Control of a Two-Speed Planetary Gear Automatic Transmission for Electric Vehicle. Appl. Sci. 2020, 10, 6612. [Google Scholar] [CrossRef]






| Variables | Description | Deformation Mode | Initial Value | Upper Limit | Lower Limit |
|---|---|---|---|---|---|
| DV1/mm | Side height | Free-form | 0 | −5.0 | 5.0 |
| DV2 | Scaling of front width | Control block | 1.0 | 0.90 | 1.1 |
| DV3 | Scaling of rear width | Control block | 1.0 | 0.90 | 1.1 |
| DV4 | Scaling of small hole diameter | Free-form | 1.0 | 0.90 | 1.1 |
| DV5 | Scaling of big hole diameter | Free-form | 1.0 | 0.90 | 1.1 |
| DV6 | Scaling of groove length | Control block | 1.0 | 0.95 | 1.05 |
| DV7/mm | Groove depth | Free-form | 0 | −5.0 | 5.0 |
| DV8/mm | Thickness | 4.0 | 2.0 | 6.0 |
| Variables | Description | Deformation Mode | Initial Values | Upper Limit | Lower Limit |
|---|---|---|---|---|---|
| DV9 | Scaling of beam width | Control block | 1.0 | 0.90 | 1.1 |
| DV10 | Scaling of beam height | Control block | 1.0 | 0.90 | 1.1 |
| DV11 | Scaling of bottom circle arc | Free-form | 1.0 | 0.95 | 1.05 |
| DV12 | Scaling of outer circle arc | Free-form | 1.0 | 0.95 | 1.05 |
| DV13 | Scaling of inner circle arc | Free-form | 1.0 | 0.95 | 1.05 |
| DV14 | V-beam length | Control block | 0 | −10.0 | 10.0 |
| DV15/mm | Transition zone length | Control block | 0 | −10.0 | 10.0 |
| DV16/mm | Thickness | 3.0 | 2.0 | 4.0 |
| Order | Control Arm/Hz | Relative Error | Torsion Beam/Hz | Relative Error | ||
|---|---|---|---|---|---|---|
| Simulation | Test | Simulation | Test | |||
| 1 | 212.0 | 204.7 | 3.4% | 40.6 | 42.1 | 3.7% |
| 2 | 246.1 | 235.7 | 4.2% | 65.7 | 68.5 | 4.3% |
| 3 | 396.9 | 378.8 | 4.6% | 99.0 | 99.9 | 0.9% |
| 4 | 715.6 | 674.1 | 5.8% | 102.3 | 106.1 | 3.7% |
| 5 | 928.4 | 909.5 | 2.0% | 137.2 | 139.8 | 1.9% |
| 6 | 994.9 | 970.2 | 2.5% | 169.1 | 167.2 | 1.1% |
| Design Variable | Optimal Results | Modified Value |
|---|---|---|
| DV1/mm | 3.3577 | 3.4 |
| DV2 | 0.9109 | 0.91 |
| DV3 | 1.0579 | 1.06 |
| DV4 | 1.0894 | 1.09 |
| DV5 | 1.0387 | 1.04 |
| DV6 | 0.9914 | 0.99 |
| DV7/mm | −2.3306 | −2.3 |
| DV8/mm | 3.5374 | 3.5 |
| DV9 | 1.0227 | 1.02 |
| DV10 | 0.9657 | 0.97 |
| DV11 | 0.9878 | 0.99 |
| DV12 | 1.0291 | 1.03 |
| DV13 | 1.0328 | 1.03 |
| DV14/mm | −9.1089 | −9.1 |
| DV15/mm | 3.0972 | 3.1 |
| DV16/mm | 2.5329 | 2.5 |
| Stiffness | Original | Optimum | Variation | |
|---|---|---|---|---|
| Control arm | Longitudinal stiffness(kN/mm) | 3.76 | 3.05 | −0.71 |
| Lateral stiffness(kN/mm) | 40.60 | 34.84 | −5.76 | |
| Torsion beam | Torsional stiffness(N·m/°) | 40.8 | 42.1 | +1.3 |
| Mode | Control Arm/Hz | Torsion Beam/Hz | ||||
|---|---|---|---|---|---|---|
| Original | Optimum | Variation | Original | Optimum | Variation | |
| 1 | 212.0 | 224.7 | +12.7 | 40.6 | 44.1 | +3.5 |
| 2 | 246.1 | 328.4 | +82.3 | 65.7 | 86.8 | +21.1 |
| 3 | 396.9 | 502.6 | +105.7 | 99.0 | 130.6 | +31.6 |
| 4 | 715.6 | 878.1 | +162.5 | 102.3 | 202.6 | +100.3 |
| 5 | 928.4 | 1024.1 | +95.7 | 137.2 | 260.1 | +122.9 |
| 6 | 994.9 | 1227.4 | +232.5 | 169.1 | 335.4 | +166.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, R.; Jin, Z.; Liu, D.; Wang, D. Multi-Objective Lightweight Optimization of Parameterized Suspension Components Based on NSGA-II Algorithm Coupling with Surrogate Model. Machines 2021, 9, 107. https://doi.org/10.3390/machines9060107
Jiang R, Jin Z, Liu D, Wang D. Multi-Objective Lightweight Optimization of Parameterized Suspension Components Based on NSGA-II Algorithm Coupling with Surrogate Model. Machines. 2021; 9(6):107. https://doi.org/10.3390/machines9060107
Chicago/Turabian StyleJiang, Rongchao, Zhenchao Jin, Dawei Liu, and Dengfeng Wang. 2021. "Multi-Objective Lightweight Optimization of Parameterized Suspension Components Based on NSGA-II Algorithm Coupling with Surrogate Model" Machines 9, no. 6: 107. https://doi.org/10.3390/machines9060107
APA StyleJiang, R., Jin, Z., Liu, D., & Wang, D. (2021). Multi-Objective Lightweight Optimization of Parameterized Suspension Components Based on NSGA-II Algorithm Coupling with Surrogate Model. Machines, 9(6), 107. https://doi.org/10.3390/machines9060107






