Passive Gravity Balancing with a Self-Regulating Mechanism for Variable Payload
Abstract
:1. Introduction
2. Balancing a Single DOF Link: Force Analysis
3. Self-Regulating Mechanism
- -
- Bring the link to the position (Figure 4a)
- -
- Connect the link to the pulley with radius and release the slider, which will not move because of Equation (10) (Figure 4b)
- -
- Add the new payload to the link, and add the same amount to the counterweight (Figure 4c)
- -
- Lock the slider to the link and the pulley with radius to the frame
- -
- The link is now in indifferent equilibrium with the new payload, and can move where required (Figure 4d)
4. Remarks and Simulation Results
- I.
- The link (in indifferent equilibrium since ), with no payload, is at for 4 s.
- II.
- Some payload needs to be added. The link moves to the configuration in 10 s.
- III.
- The link is connected to the pulley with radius the slider is released and the new payload, kg, is added. The mass of the counterweight is increased by the same amount. As a result, the slider moves to mm. All of this takes 3 s.
- IV.
- The slider is locked and the pulley with radius is disconnected—this takes another 3 s.
- V.
- The link is then required to reach the configuration in 10 s, and then it stays in that position for a while.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Keung, G.; Chen, C. Novel Design of an Adjustable Constant Force Mechanism Based on Cam and Spring. In IFToMM World Congress on Mechanism and Machine Science; Springer International Publishing: Cham, Switzerland, 2019; pp. 1481–1490. [Google Scholar]
- Lenzo, B.; Zanotto, D.; Vashista, V.; Frisoli, A.; Agrawal, S. A new Constant Pushing Force Device for human walking analysis. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 3 May 2014; pp. 6174–6179. [Google Scholar]
- Ou, M.; Qi, L.; Jesse, M.; Ken, R. Concepts Study of a Passive Reduced-Gravity Simulator for Training Astronauts. In Proceedings of the ASME Design Engineering Technical Conference, Montreal, QC, Canada, 15–18 August 2010. [Google Scholar]
- Banala, S.K.; Agrawal, S.K.; Fattah, A.; Rudolph, K.; Scholz, J. A gravity balancing leg orthosis for robotic rehabilitation. In Proceedings of the IEEE Conference (ICRA 2004), New Orleans, LA, USA, 26 April–1 May 2004. [Google Scholar]
- French, M.J.; Widden, M.B. The spring-and-lever balancing mechanism, George Carwardine and the Anglepoise lamp. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2000, 214, 501–508. [Google Scholar] [CrossRef] [Green Version]
- Herder, J.L.; Tuijthof, G.J.M. Two Spatial Gravity Equilibrators. In Proceedings of the ASME Design Engineering Technical Conference, MECH-14120, Baltimore, MD, USA, 10–13 September 2000. [Google Scholar]
- Lenzo, B.; Fontana, M.; Marcheschi, S.; Salsedo, F.; Frisoli, A.; Bergamasco, M. Trackhold: A novel passive arm-support device. J. Mech. Robot. 2016, 8, 021007. [Google Scholar] [CrossRef] [Green Version]
- Lee, G.; Lee, D.; Oh, Y. One-piece gravity compensation mechanism using cam mechanism and compression spring. Int. J. Precis. Eng. Manuf.-Green Technol. 2018, 5, 415–420. [Google Scholar] [CrossRef]
- Chheta, Y.R.; Joshi, R.M.; Gotewal, K.K.; Manoah, S.M. A Review on Passive Gravity Compensation. In Proceedings of the International Conference on Electronics, Communication and Aerospace Technology (ICECA 2017), Coimbatore, India, 20–22 April 2017. [Google Scholar]
- Agrawal, S.; Fattah, A. Gravity-balancing of spatial robotic manipulators. Mech. Mach. Theory 2004, 39, 1331–1344. [Google Scholar] [CrossRef]
- Franco, J.A.; Gallego, J.A.; Herder, J.L. Static Balancing of Four-Bar Compliant Mechanisms with Torsion Springs by Exerting Negative Stiffness Using Linear Spring at the Instant Center of Rotation. J. Mech. Robot. 2021, 13, 031010. [Google Scholar] [CrossRef]
- Barents, R.; Schenk, M.; van Dorsser, W.D.; Wisse, B.M.; Herder, J.L. Spring-to-spring balancing as energy-free adjustment method in gravity equilibrators. J. Mech. Des. 2011, 133, 061010. [Google Scholar] [CrossRef]
- Agrawal, A.; Agrawal, S.K. Design of gravity balancing leg orthosis using non-zero free length springs. Mech. Mach. Theory 2005, 40, 693–709. [Google Scholar] [CrossRef]
- Zhang, Y.; Arakelian, V.; Le Baron, J.P. Linkage Design for Gravity Balancing by Means of Non-zero Length Springs. In ROMANSY 22-Robot Design, Dynamics and Control; Springer International Publishing: Cham, Switzerland, 2019; pp. 163–170. [Google Scholar]
- Delissen, A.A.; Radaelli, G.; Herder, J.L. Design and optimization of a general planar zero free length spring. Mech. Mach. Theory 2017, 117, 56–77. [Google Scholar] [CrossRef] [Green Version]
- Lenzo, B.; Frisoli, A.; Salsedo, F.; Bergamasco, M. New gravity balancing technique and hybrid actuation for spatial serial manipulators. In Advances in Robot Kinematics; Springer International Publishing: Cham, Switzerland, 2014; pp. 419–427. [Google Scholar]
- Rahman, T.; Ramanathan, R.; Seliktar, R.; Harwin, W. A Simple Technique to Passively Gravity-Balance Articulated Mechanisms. J. Mech. Des. 1995, 117, 655–658. [Google Scholar] [CrossRef]
- Lenzo, B. Gravity balancing of a spatial serial 4-dof arm without auxiliary links using minimum number of springs. In Proceedings of the AIMETA XXIII Conference-The Italian Association of Theoretical and Applied Mechanics, Salerno, Italy, 4–7 September 2017. [Google Scholar]
- Deepak, S.R.; Ananthasuresh, G.K. Static balancing of spring-loaded planar revolute-joint linkages without auxiliary links. In Proceedings of the 14th National Conference on Machines and Mechanism (NaCoMM09), Durgapur, India, 18 December 2009. [Google Scholar]
- Wisse, B.M.; Van Dorsser, W.D.; Barents, R.; Herder, J.L. Energy-free adjustment of gravity equilibrators using the virtual spring concept. In Proceedings of the 2007 IEEE 10th International Conference on Rehabilitation Robotics, Noordwijk, The Netherlands, 13–15 June 2007; pp. 742–750. [Google Scholar]
- Van Der Wijk, V.; Herder, J.L. Force balancing of variable payload by active force-balanced reconfiguration of the mechanism. In Proceedings of the 2009 ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots, London, UK, 22–24 June 2009; pp. 323–330. [Google Scholar]
- Takesue, N.; Ikematsu, T.; Murayama, H.; Fujimoto, H. Design and prototype of variable gravity compensation mechanism (VGCM). J. Robot. Mechatron. 2011, 23, 249–257. [Google Scholar] [CrossRef]
- Shieh, W.B.; Chen, C.K. Conceptual Design of a Two-Stage Variable Gravity Compensated Mechanism. In IFToMM World Congress on Mechanism and Machine Science; Springer International Publishing: Cham, Switzerland, 2019; pp. 1535–1543. [Google Scholar]
- Chew, D.X.; Wood, K.L.; Tan, U. Design of a passive self-regulating gravity compensator for variable payloads. J. Mech. Des. 2019, 141. [Google Scholar] [CrossRef]
- Nguyen, V.L.; Lin, C.-Y.; Kuo, C.-H. Gravity compensation design of planar articulated robotic arms using the gear-spring modules. J. Mech. Robot. 2020, 12, 031014. [Google Scholar] [CrossRef]
- Nguyen, V.L.; Lin, C.-Y.; Kuo, C.-H. Gravity compensation design of Delta parallel robots using gear-spring modules. Mech. Mach. Theory 2020, 154, 104046. [Google Scholar] [CrossRef]
- Gatti, G.; Carbone, G. Gravity Compensation of Robotic Manipulators Using Non-linear Spring Configurations, Mechanisms and Machine Science 91; Springer: Cham, Switzerland, 2021; pp. 310–317. [Google Scholar]
- Woo, J.; Seo, J.T.; Yi, B.J. A static balancing method for variable payloads by combination of a counterweight and spring and its application as a surgical platform. Appl. Sci. 2019, 9, 3955. [Google Scholar] [CrossRef] [Green Version]
- Chiang, W.H.; Chen, D.Z. Design of planar variable-payload balanced articulated manipulators with actuated linear ground-adjacent adjustment. Mech. Mach. Theory 2017, 109, 296–312. [Google Scholar] [CrossRef]
- Chu, Y.L.; Kuo, C.H. A single-degree-of-freedom self-regulated gravity balancer for adjustable payload. J. Mech. Robot. 2017, 9, 021006. [Google Scholar] [CrossRef]
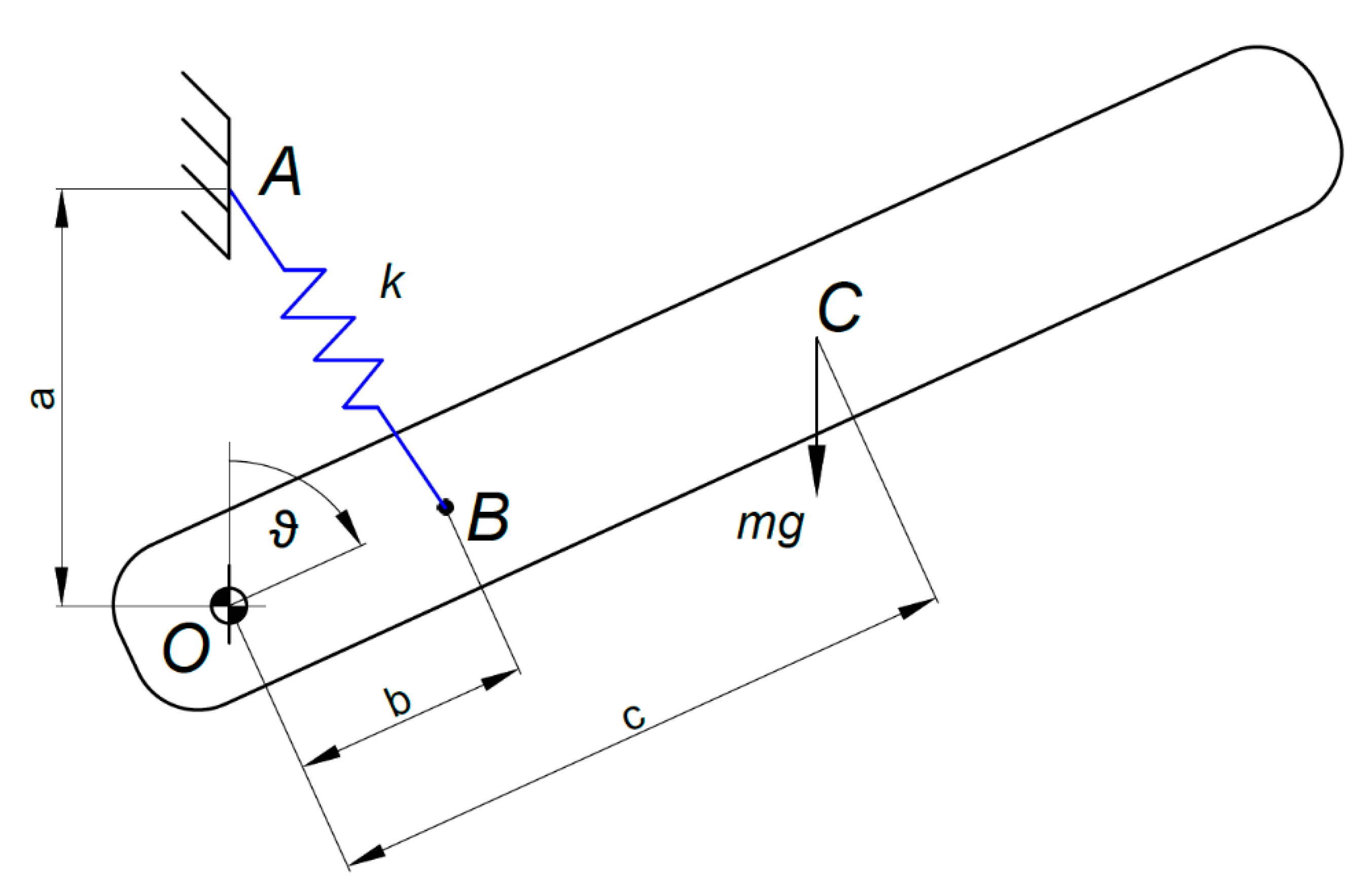
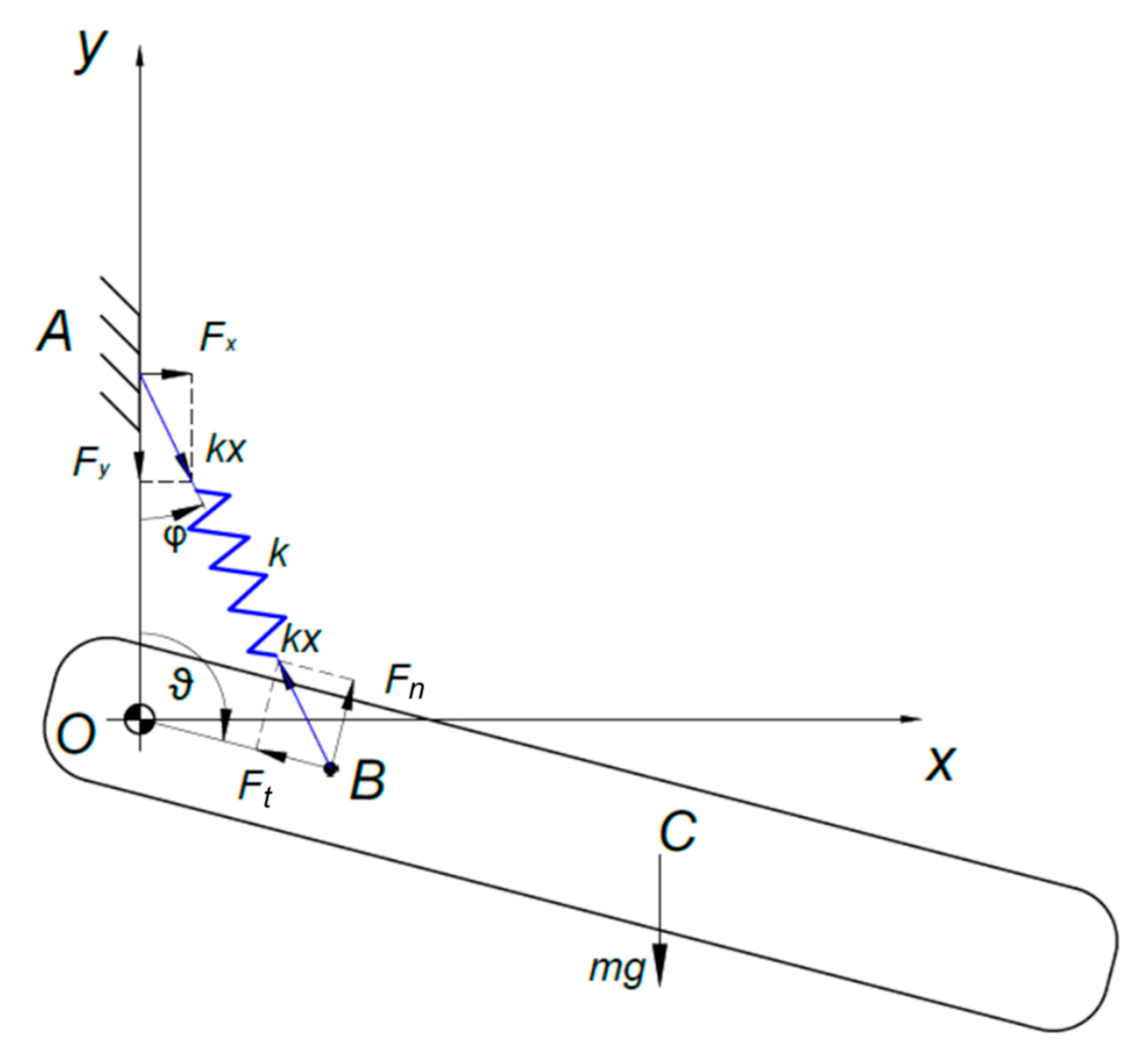
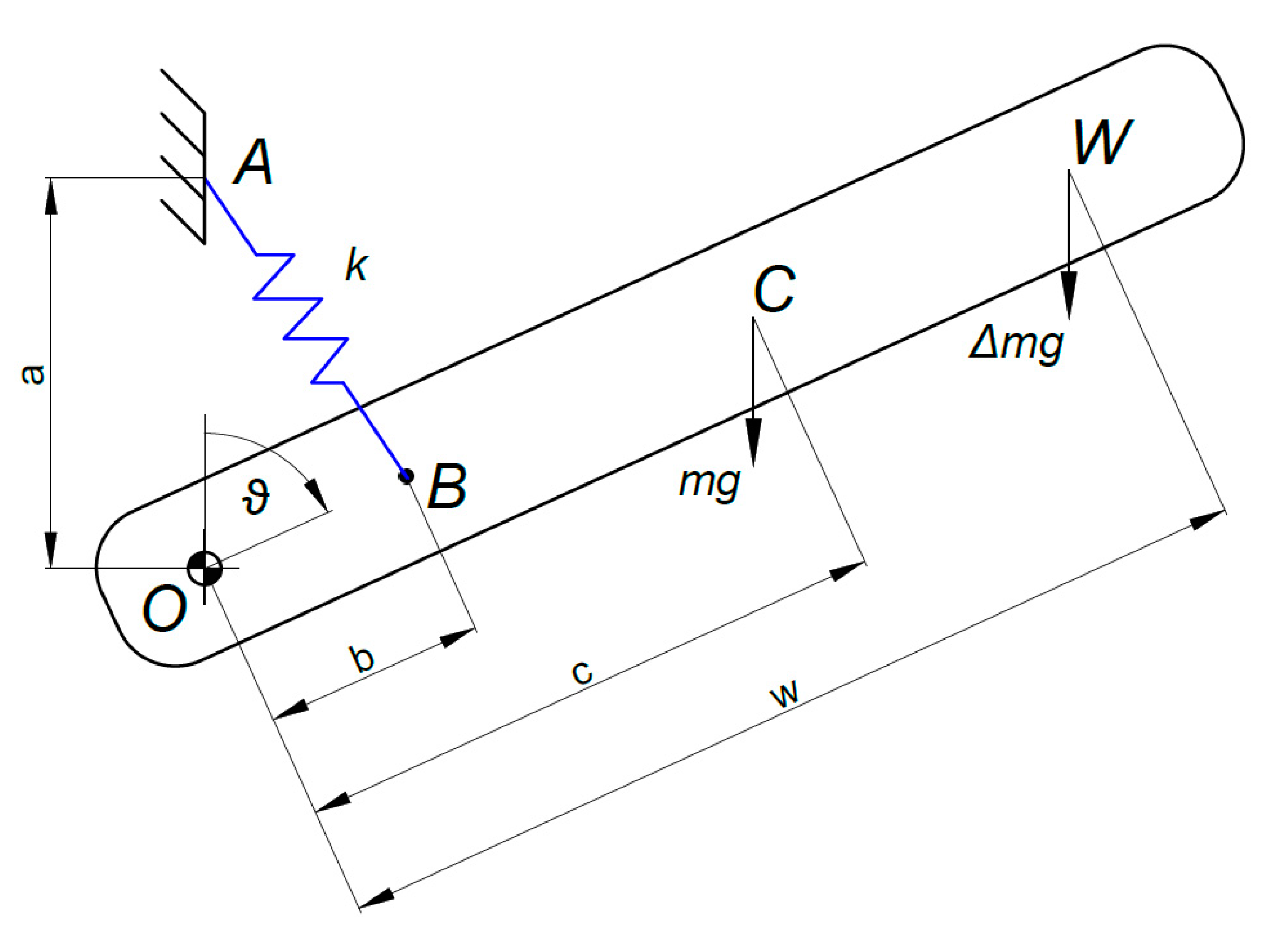


| Quantity | Symbol | Value and Unit |
|---|---|---|
| Mass of the link | 3 kg | |
| Distance between point O and W | 0.35 m | |
| Distance between points O and A | 0.1 m | |
| Distance between points O and B | 0.06 m | |
| Distance between O and C | 0.2 m | |
| Radius of pulley integral with the frame | 0.035 m | |
| Radius of the pulley integral with the link | 0.01 m | |
| Spring stiffness | 981 N/m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franchetti, D.; Boschetti, G.; Lenzo, B. Passive Gravity Balancing with a Self-Regulating Mechanism for Variable Payload. Machines 2021, 9, 145. https://doi.org/10.3390/machines9080145
Franchetti D, Boschetti G, Lenzo B. Passive Gravity Balancing with a Self-Regulating Mechanism for Variable Payload. Machines. 2021; 9(8):145. https://doi.org/10.3390/machines9080145
Chicago/Turabian StyleFranchetti, Diego, Giovanni Boschetti, and Basilio Lenzo. 2021. "Passive Gravity Balancing with a Self-Regulating Mechanism for Variable Payload" Machines 9, no. 8: 145. https://doi.org/10.3390/machines9080145
APA StyleFranchetti, D., Boschetti, G., & Lenzo, B. (2021). Passive Gravity Balancing with a Self-Regulating Mechanism for Variable Payload. Machines, 9(8), 145. https://doi.org/10.3390/machines9080145








