Evaluation of the Ability to Accurately Produce Angular Details by 3D Printing of Plastic Parts
Abstract
:1. Introduction
2. Hypotheses
- -
- The values of certain dimensions that characterize the shape of the sample surfaces to be produced (the presence of some intersections made by small values of the intersection angles or the connection radii, the thickness of the sample, the coefficient of the slenderness of some areas of the sample, etc.);
- -
- Characteristics of the wire/filament generated by the printer nozzle (diameter of the deposition filament, corresponding to the diameter of the nozzle hole) and of the filament material (melting temperature, viscosity, specific heat and thermal conductivity, thermal shrinkage, the adhesion capacity between the deposited layers, etc.);
- -
- Elements of thermal conditions of operation of some components/subassemblies of the printer (heating temperature of the nozzle, temperature of the plate on which the deposition takes place, ventilation cooling, etc.);
- -
- Parameters that characterize the deposition conditions (travel speed between nozzle and printer table, the thickness of the deposited layer, etc.);
- -
- The degree of filling of the spaces between the walls of the sample, etc.
3. Materials and Methods
4. Results
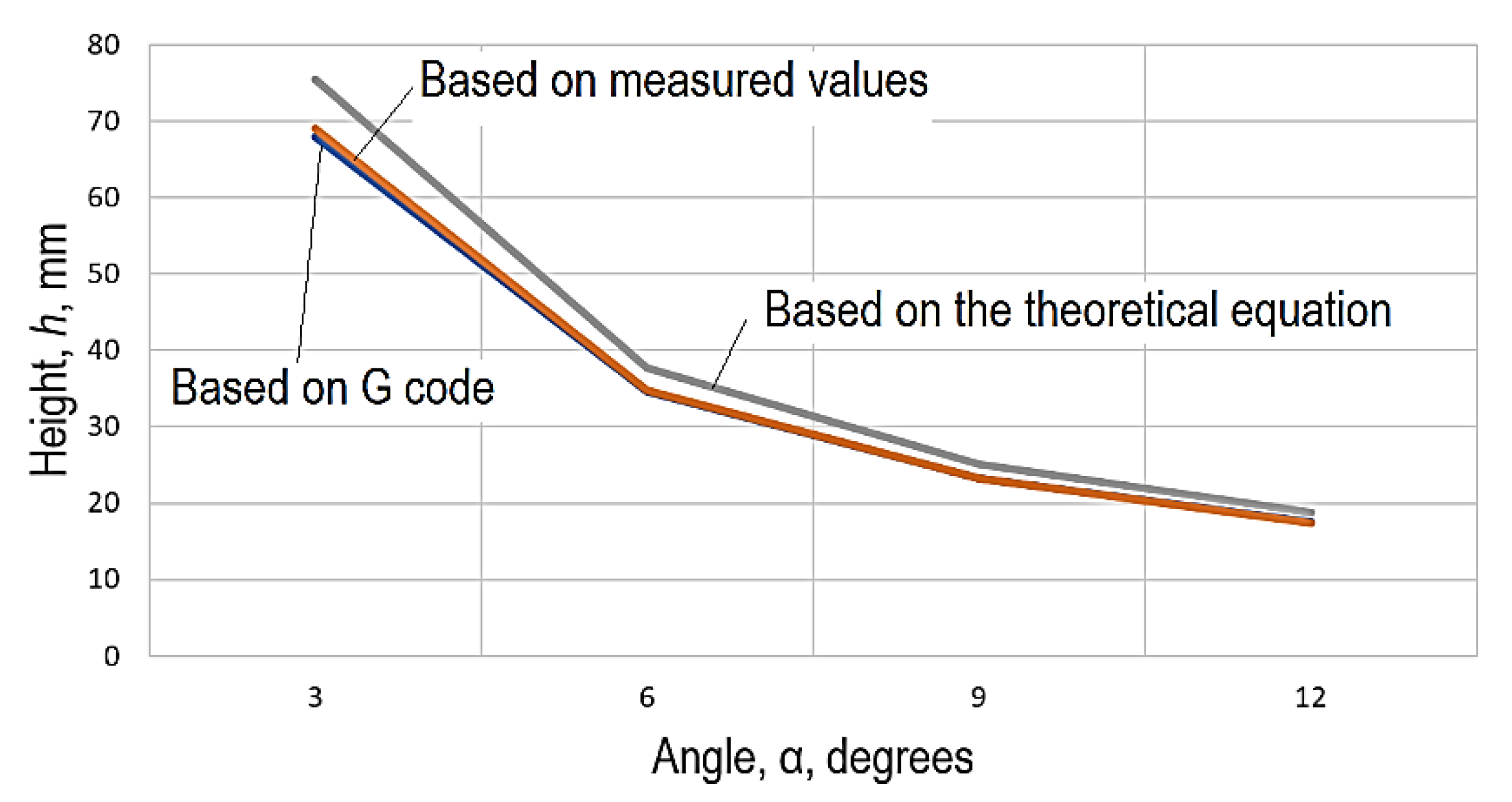
5. Discussion
- -
- For the height determined by using G code:
- -
- By using the experimental results:
- -
- For the theoretical variation of the height h of the triangles, Equation (2) remains valid;
- -
- For the variation of the height h of the triangles determined by taking into account the G code:
- -
- By taking into account the experimental results:
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Brischetto, S.; Maggiore, P.; Ferro, C.G. (Eds.) Additive Manufacturing Technologies and Applications; MDPI: Basel, Switzerland, 2017; pp. 1–180. [Google Scholar] [CrossRef] [Green Version]
- Ponis, S.; Aretoulaki, E.; Maroutas, T.N.; Plakas, G.; Dimogiorgi, K. A systematic literature review on additive manufacturing in the context of circular economy. Sustainability 2021, 13, 6007. [Google Scholar] [CrossRef]
- Mehrpouya, M.; Dehghanghadikolaei, A.; Fotovvati, B.; Vosooghnia, A.; Emamian, S.S.; Gisario, A. The potential of additive manufacturing in the smart factory industrial 4.0: A review. Appl. Sci. 2019, 9, 3865. [Google Scholar] [CrossRef] [Green Version]
- Asnaf, N. Metal Additive Manufacturing—State of the Art 2020. Metals 2021, 11, 867. [Google Scholar] [CrossRef]
- Arefin, A.M.E.; Khatri, N.R.; Kulkarni, N.; Egan, P.F. Polymer 3D Printing Review: Materials, Process, and Design Strategies for Medical Applications. Polymers 2021, 13, 1499. [Google Scholar] [CrossRef]
- Azad, M.A.; Olawuni, D.; Kimbell, G.; Badruddoza, A.Z.M.; Hossain, M.S.; Sultana, T. Polymers for extrusion-based 3D printing of pharmaceuticals: A holistic materials–process perspective. Pharmaceutics 2020, 12, 124. [Google Scholar] [CrossRef] [Green Version]
- Bagalkot, A.; Pons, D.; Symons, D.; Clucas, D. Analysis of raised feature failures on 3D printed injection moulds. Polymers 2021, 13, 1541. [Google Scholar] [CrossRef] [PubMed]
- Gwamuri, J.; Franco, D.; Khan, K.Y.; Gauchia, L.; Pearce, J.M. High-efficiency solar-powered 3-D printers for sustainable development. Machines 2016, 4, 3. [Google Scholar] [CrossRef]
- Mantelli, A.; Romani, A.; Suriano, R.; Diani, M.; Colledani, M.; Sarlin, E.; Turri, S.; Levi, M. UV-Assisted 3D printing of polymer composites from thermally and mechanically recycled carbon fibers. Polymers 2021, 13, 726. [Google Scholar] [CrossRef] [PubMed]
- Nath, S.D.; Nilufar, S. An Overview of Additive Manufacturing of Polymers and Associated Composites. Polymers 2020, 12, 2719. [Google Scholar] [CrossRef] [PubMed]
- Ziółkowski, M.; Dyl, T. Possible Applications of Additive Manufacturing Technologies in Shipbuilding: A Review. Machines 2020, 8, 84. [Google Scholar] [CrossRef]
- Amza, C.G.; Zapciu, A.; Constantin, G.; Baciu, F.; Vasile, M.I. Enhancing mechanical properties of polymer 3D printed parts. Polymers 2021, 13, 562. [Google Scholar] [CrossRef] [PubMed]
- Avdeev, A.; Shvets, A.; Gushchin, I.; Torubarov, I.; Drobotov, A.; Makarov, A.; Plotnikov, A.; Serdobintsev, Y. Strength increasing additive manufacturing fused filament fabrication technology, based on spiral toolpath material deposition. Machines 2019, 7, 57. [Google Scholar] [CrossRef] [Green Version]
- Calignano, F.; Lorusso, M.; Roppolo, I.; Minetola, P. Investigation of the Mechanical Properties of a Carbon Fibre-Reinforced Nylon Filament for 3D Printing. Machines 2020, 8, 52. [Google Scholar] [CrossRef]
- Ferrari, F.; Corcione, C.E.; Montagna, F.; Maffezzoli, A. 3D printing of polymerwaste for improving people’s awareness about marine litter. Polymers 2020, 12, 1738. [Google Scholar] [CrossRef]
- Mazzanti, V.; Malagutti, L.; Mollica, F. FDM 3D printing of polymers containing natural fillers: A review of their mechanical properties. Polymers 2019, 11, 1094. [Google Scholar] [CrossRef] [Green Version]
- Pezzana, L.; Riccucci, G.; Spriano, S.; Battegazzore, D.; Sangermano, M.; Chiappone, A. 3D printing of PDMS-like polymer nanocomposites with enhanced thermal conductivity: Boron nitride based photocuring system. Nanomaterials 2021, 11, 373. [Google Scholar] [CrossRef]
- Ritzen, L.; Montano, V.; Garcia, S.J. 3D printing of a self-healing thermoplastic polyurethane through fdm: From polymer slab to mechanical assessment. Polymers 2021, 13, 305. [Google Scholar] [CrossRef]
- Wickramasinghe, S.; Do, T.; Tran, P. FDM-based 3D printing of polymer and associated composite: A review on mechanical properties, defects and treatments. Polymers 2020, 12, 1529. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.; Straub, J. Concepts for 3D printing-based self-replicating robot command and coordination techniques. Machines 2017, 5, 12. [Google Scholar] [CrossRef] [Green Version]
- Straub, J. Initial Work on the Characterization of Additive Manufacturing (3D Printing) Using Software Image Analysis. Machines 2015, 3, 55–71. [Google Scholar] [CrossRef] [Green Version]
- Msallem, B.; Sharma, N.; Cao, S.; Halbeisen, F.S.; Zeilhofer, H.F.; Thieringer, F.M. Evaluation of the dimensional accuracy of 3d-printed anatomical mandibular models using FFF, SLA, SLS, MJ, and BJ printing technology. J. Clin. Med. 2020, 9, 817. [Google Scholar] [CrossRef] [Green Version]
- Yoo, S.-Y.; Kim, S.-K.; Heo, S.-J.; Koak, J.-Y.; Kim, J.-G. Dimensional accuracy of dental models for three-unit prostheses fabricated by various 3d printing technologies. Materials 2021, 14, 1550. [Google Scholar] [CrossRef]
- Dorweiler, B.; Baqué, P.E.; Chaban, R.; Ghazy, A.; Salem, O. Quality control in 3D printing: Accuracy analysis of 3D-printed models of patient-specific anatomy. Materials 2021, 14, 1021. [Google Scholar] [CrossRef]
- Lee, S.; Squelch, A.; Sunm, Z. Quantitative assessment of 3D printed model accuracy in delineating congenital heart disease. Biomolecules 2021, 11, 270. [Google Scholar] [CrossRef]
- Czajkowska, M.; Walejewska, E.; Zadrozny, Ł.; Wieczorek, M.; Swieszkowski, W.; Wagner, L.; Mijiritsky, E.; Markowski, J. Comparison of dental stone models and their 3D printed acrylic replicas for the accuracy and mechanical properties. Materials 2020, 13, 4066. [Google Scholar] [CrossRef] [PubMed]
- Budzik, G.; Wozniak, J.; Paszkiewicz, A.; Przeszłowski, Ł.; Dziubek, T.; Debski, M. Methodology for the quality control process of additive manufacturing products made of polymer materials. Materials 2021, 14, 2202. [Google Scholar] [CrossRef]
- Slătineanu, L.; Dodun, O.; Nagit, G.; Coteață, M.; Bosoancă, G.; Beșliu, I. Fine details obtained by 3D printing and using polymers. Mater. Plast. 2018, 55, 474–477. [Google Scholar] [CrossRef]
- Boca, M.-A.; Sover, A.; Slătineanu, L. The dimensional accuracy of the test parts made of various plastic materials by the fused filament fabrication process. IOP Conf. Ser. Mater. Sci. Eng. 2020, 997, 012021. [Google Scholar] [CrossRef]
- Kaschwich, M.; Horn, M.; Matthiensen, S.; Stahlberg, E.; Behrendt, C.A.; Matysiak, F.; Bouchagiar, J.; Dell, A.; Ellebrecht, D.; Bayer, A.; et al. Accuracy evaluation of patient-specific 3D-printed aortic anatomy. Ann. Anat. 2021, 234. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, Q.; Tang, L.; Zhang, L.; Sun, Y.; Xie, Q. Accuracy of a chairside fused deposition modeling 3D-printed single-tooth surgical template for implant placement: An in vitro comparison with a light cured template. J. Cranio Maxillofac. Surg. 2019, 47, 1216–1221. [Google Scholar] [CrossRef]
- Herpel, C.; Tasaka, A.; Higuchi, S.; Finke, D.; Kühle, R.; Odaka, K.; Rues, S.; Lux, C.-J.; Yamashita, S.; Rammelsberg, P.; et al. Accuracy of 3D printing compared with milling—A multi-center analysis of try-in dentures. J. Dent. 2021, 110, 103681. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Fan, G. An overview of tailoring strain delocalization for strength-ductility synergy. Prog. Mater. Sci. 2020, 113, 100675. [Google Scholar] [CrossRef]
- Chapter 2 Introduction to Taguchi Method. University of Massachusetts Amherst. Available online: http://www.ecs.umass.edu/mie/labs/mda/fea/sankar/chap2.html (accessed on 16 July 2021).
- Crețu, G. Fundamentals of Experimental Research; “Gheorghe Asachi” Technical University of Iasi: Iasi, Romania, 1992. (In Romanian) [Google Scholar]
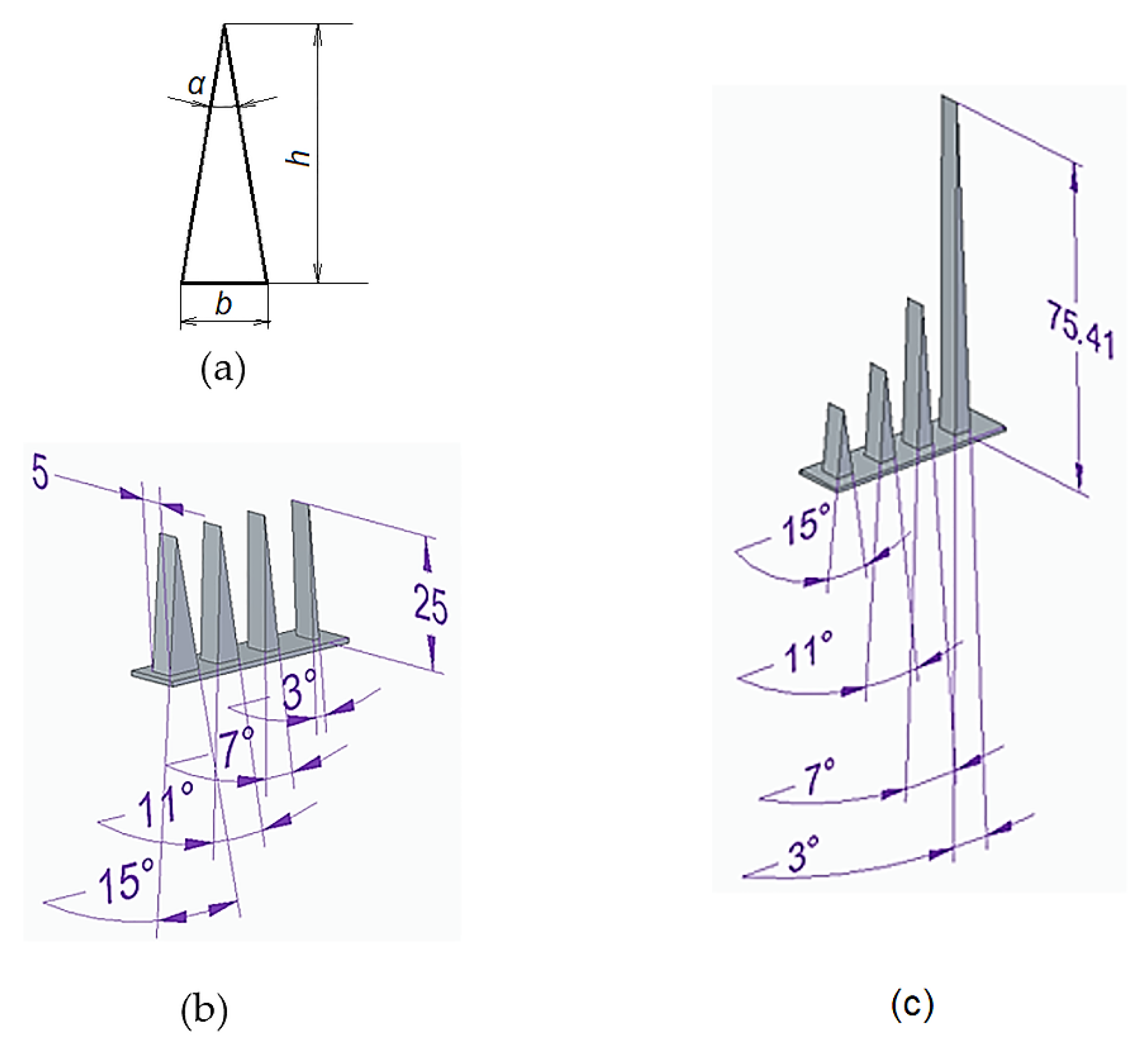
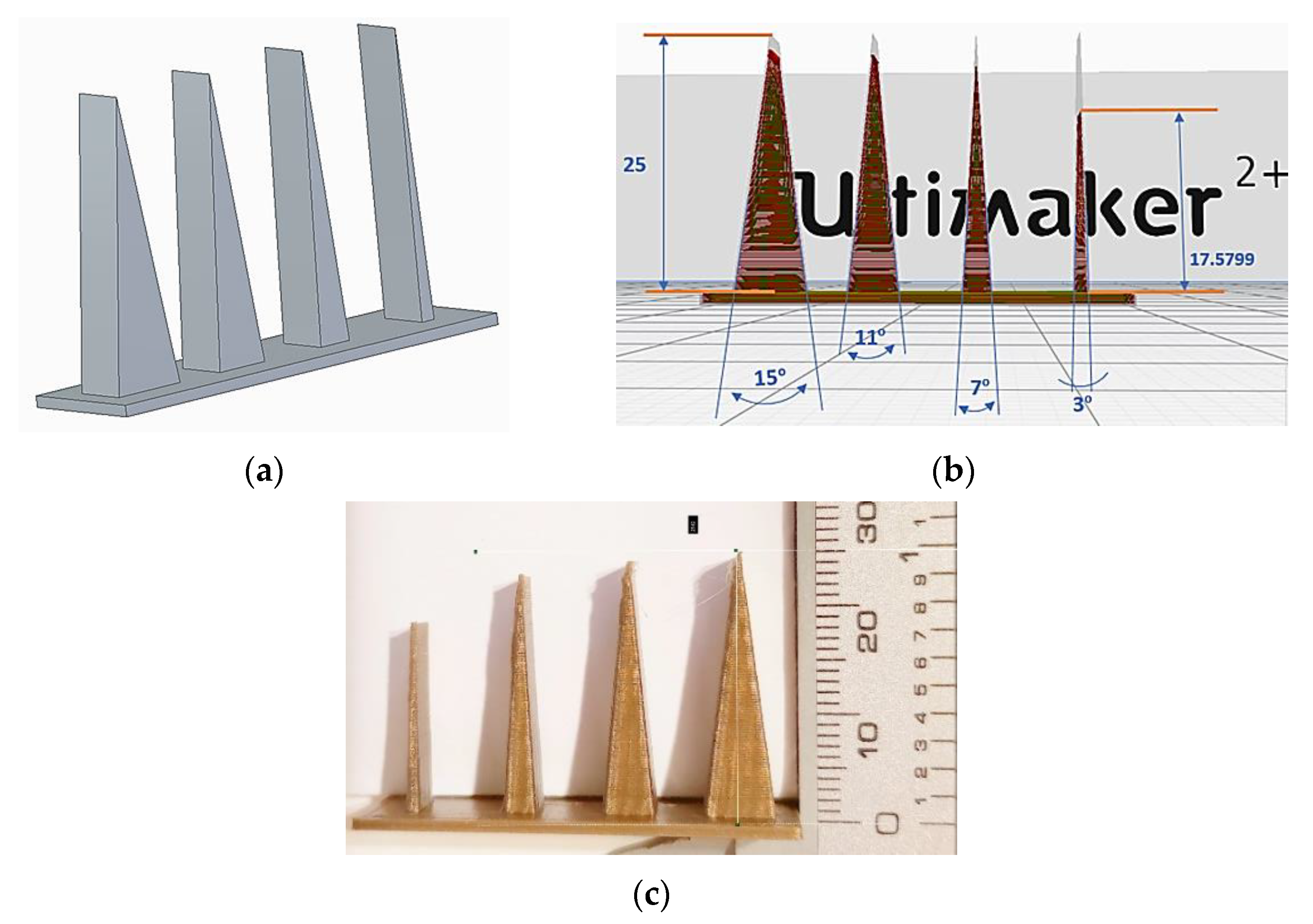


| Exp. No. | Values of the Input Factors | Achievable Height h of the Triangle, mm, by Considering G Code/Real Height of the Triangle, mm, for Vertex Angle α, o, of: | Deviation, Δ, mm | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Deposited Layer Thickness tl, mm | Printing Speed v, mm/s | Cooling c, % | Infill i, % | Sample Thickness ts, mm | 15 | 11 | 7 | 3 | ||
| 1 | 0.06 | 50 | 0 | 22 | 5 | 23.9343/ 23.8 | 23.2522/ 23.4 | 21.9121/ 22.2 | 17.3723/ 17.8 | 0.7568 |
| 2 | 0.06 | 55 | 50 | 20 | 7.5 | 23.8254/ 24 | 23.1613/ 23.5 | 22.0139/ 22.1 | 17.5799/ 17.8 | 0.5568 |
| 3 | 0.06 | 60 | 100 | 18 | 10 | 23.815/ 23.9 | 23.4581/ 23.4 | 22.1120/ 22.2 | 18.4442/ 17.8 | 0.6568 |
| 4 | 0.1 | 50 | 50 | 18 | 5 | 23.8652/ 24 | 23.2738/ 23.4 | 22.5883/ 22.2 | 17.9017/ 17.7 | 0.5568 |
| 5 | 0.1 | 55 | 100 | 22 | 7.5 | 23.8883/ 24 | 23.4691/ 23.4 | 22.0833/ 22.2 | 17.6337/ 17.7 | 0.5568 |
| 6 | 0.1 | 60 | 0 | 20 | 10 | 23.8816/ 23.9 | 23.4008/ 23.4 | 21.9920/ 22.2 | 17.6675/ 17.7 | 0.6568 |
| 7 | 0.15 | 50 | 100 | 20 | 5 | 23.8882/ 24 | 23.3956/ 23.4 | 21.9474/ 22.3 | 17.4919/ 17.7 | 0.5568 |
| 8 | 0.15 | 55 | 0 | 18 | 7.5 | 23.8784/ 23.9 | 23.1641/ 23.4 | 22.2486/ 22.2 | 17.5280/ 17.7 | 0.6568 |
| 9 | 0.15 | 60 | 50 | 22 | 10 | 23.8670/ 23.9 | 23.4079/ 23.4 | 22.1936/ 22.1 | 17.7187/ 17.8 | 0.6568 |
| Exp. No. | Values of the Input Factors | Intended Height of the Triangle, mm, by Considering the G Code/Real Height of the Triangle, mm, for Vertex Angle α, °, of: | Deviation Δ, mm | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Deposited Layer Thickness tl, mm | Printing Speed v, mm/s | Coo- ling c, % | Infill i, % | Sample Thickness, ts, mm | 15 | 11 | 7 | 3 | ||
| 1 | 0.06 | 50 | 0 | 22 | 5 | 13.9293/ 13.8 | 18.7728/ 18.8 | 29.1808/ 29.5 | 67.8049/ 71 | 0.9416 |
| 2 | 0.06 | 55 | 50 | 20 | 7.5 | 13.8192/ 13.9 | 19.2261/ 19 | 29.2671/ 29.6 | 67.8508/ 68.5 | 0.8416 |
| 3 | 0.06 | 60 | 100 | 18 | 10 | 13.9112/ 13.9 | 18.9852/ 19.1 | 29.4398/ 29.5 | 67.8559/ 68.4 | 0.8416 |
| 4 | 0.10 | 50 | 50 | 18 | 5 | 13.8178/ 14 | 19.7232/ 19 | 29.9709/ 29.6 | 68.1037/ 68.8 | 0.7416 |
| 5 | 0.10 | 55 | 100 | 22 | 7.5 | 13.8361/ 14 | 18.7852/ 18.9 | 29.4599/ 29.5 | 68.246/ 68.5 | 0.7416 |
| 6 | 0.10 | 60 | 0 | 20 | 10 | 13.8679/ 14 | 19.125/ 18.8 | 30.0142/ 29.6 | 68.0931/ 68.5 | 0.7416 |
| 7 | 0.15 | 50 | 100 | 20 | 5 | 13.9187/ 14 | 20.1006/ 19 | 29.5744/ 29.5 | 67.8714/ 68.5 | 0.7416 |
| 8 | 0.15 | 55 | 0 | 18 | 7.5 | 13.919/ 14 | 19.161/ 19 | 29.6599/ 29.5 | 68.0868/ 69.4 | 0.7416 |
| 9 | 0.15 | 60 | 50 | 22 | 10 | 14.3825/ 14 | 19.4766/ 19 | 30.1188/ 29.5 | 68.0014/ 68.8 | 0.7416 |
| Theoretical height h of the isosceles triangle, mm, taking into account a base length b = 3.95 mm and distinct values of the vertex angle α | 14.7416 | 20.3209 | 32.1701 | 75.3704 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihalache, A.M.; Nagîț, G.; Slătineanu, L.; Hrițuc, A.; Markopoulos, A.; Dodun, O. Evaluation of the Ability to Accurately Produce Angular Details by 3D Printing of Plastic Parts. Machines 2021, 9, 150. https://doi.org/10.3390/machines9080150
Mihalache AM, Nagîț G, Slătineanu L, Hrițuc A, Markopoulos A, Dodun O. Evaluation of the Ability to Accurately Produce Angular Details by 3D Printing of Plastic Parts. Machines. 2021; 9(8):150. https://doi.org/10.3390/machines9080150
Chicago/Turabian StyleMihalache, Andrei Marius, Gheorghe Nagîț, Laurențiu Slătineanu, Adelina Hrițuc, Angelos Markopoulos, and Oana Dodun. 2021. "Evaluation of the Ability to Accurately Produce Angular Details by 3D Printing of Plastic Parts" Machines 9, no. 8: 150. https://doi.org/10.3390/machines9080150
APA StyleMihalache, A. M., Nagîț, G., Slătineanu, L., Hrițuc, A., Markopoulos, A., & Dodun, O. (2021). Evaluation of the Ability to Accurately Produce Angular Details by 3D Printing of Plastic Parts. Machines, 9(8), 150. https://doi.org/10.3390/machines9080150









