Robust and Accurate Mandible Segmentation on Dental CBCT Scans Affected by Metal Artifacts Using a Prior Shape Model
Abstract
:1. Introduction
2. Methodology
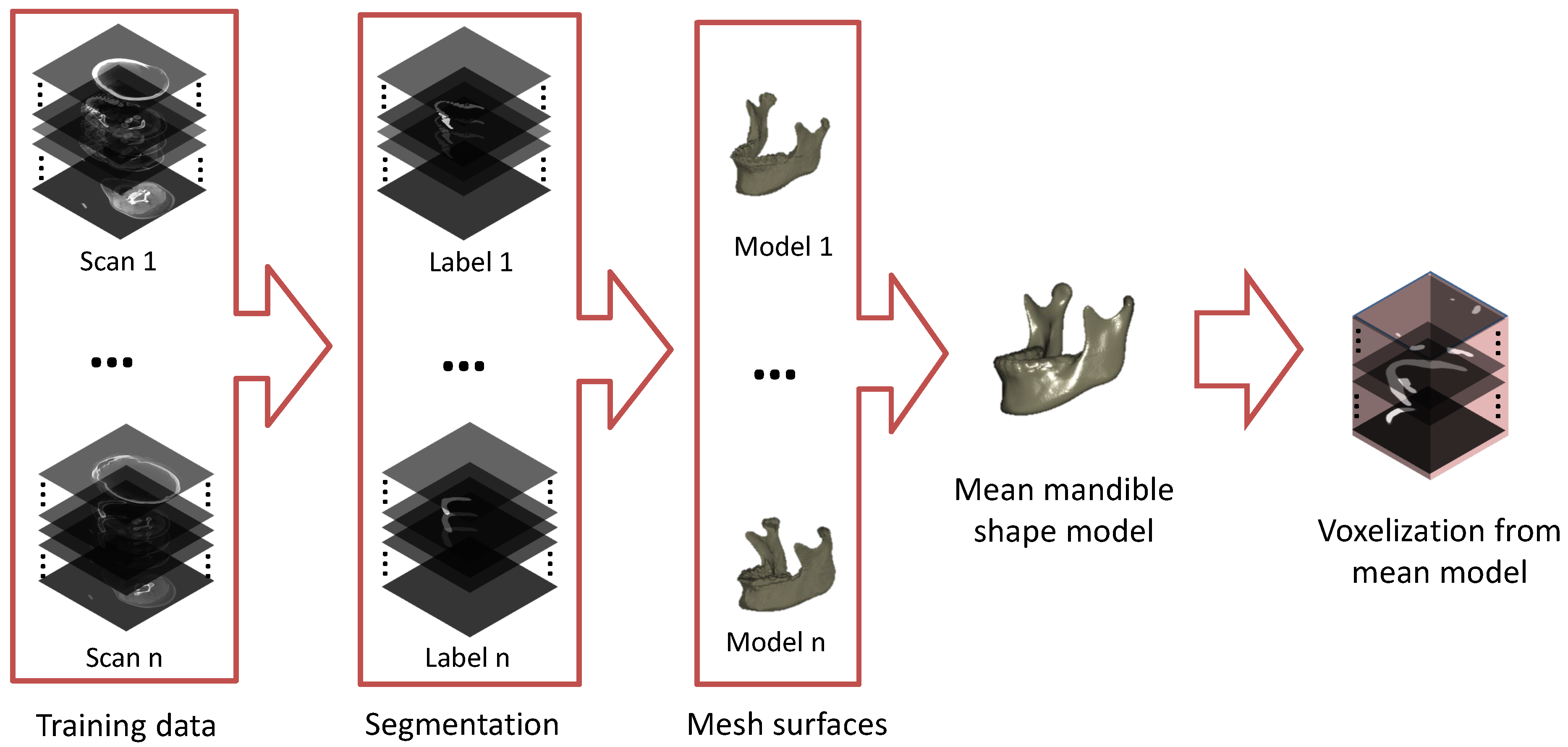
2.1. Building a Mean Mandible Shape Model
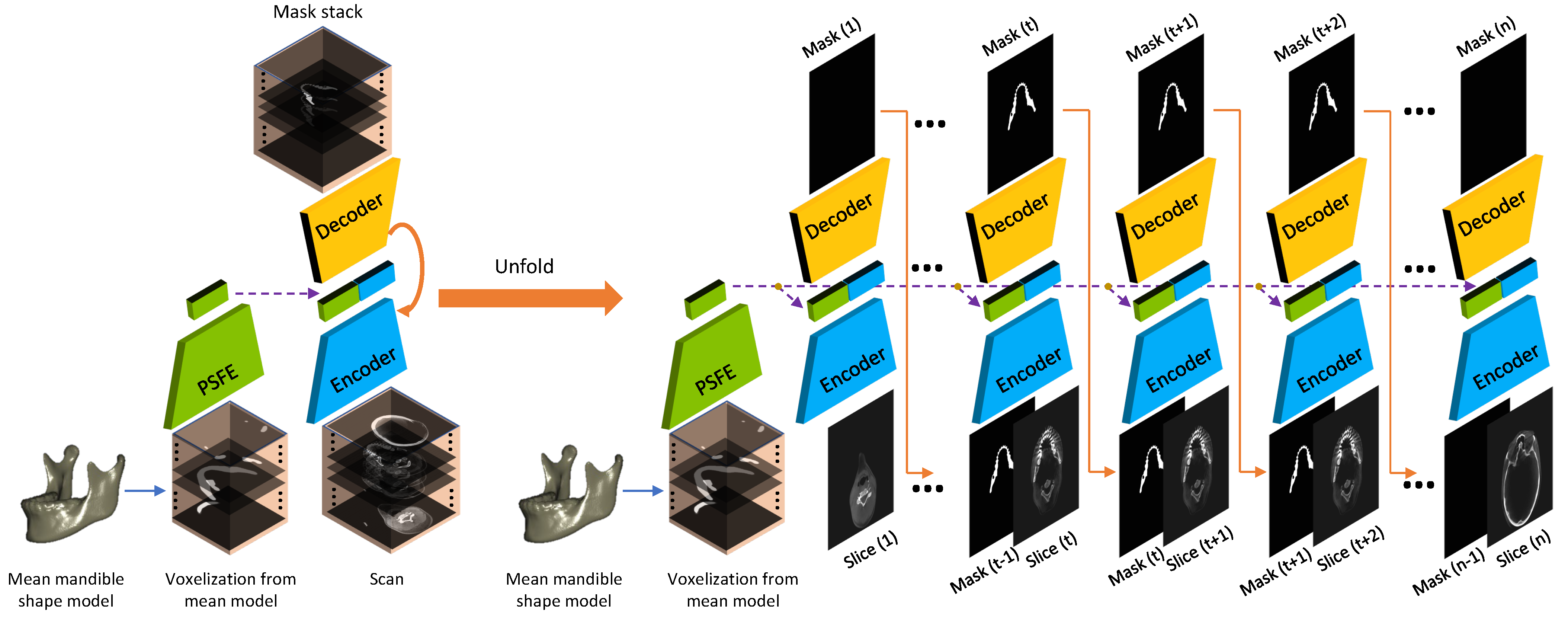
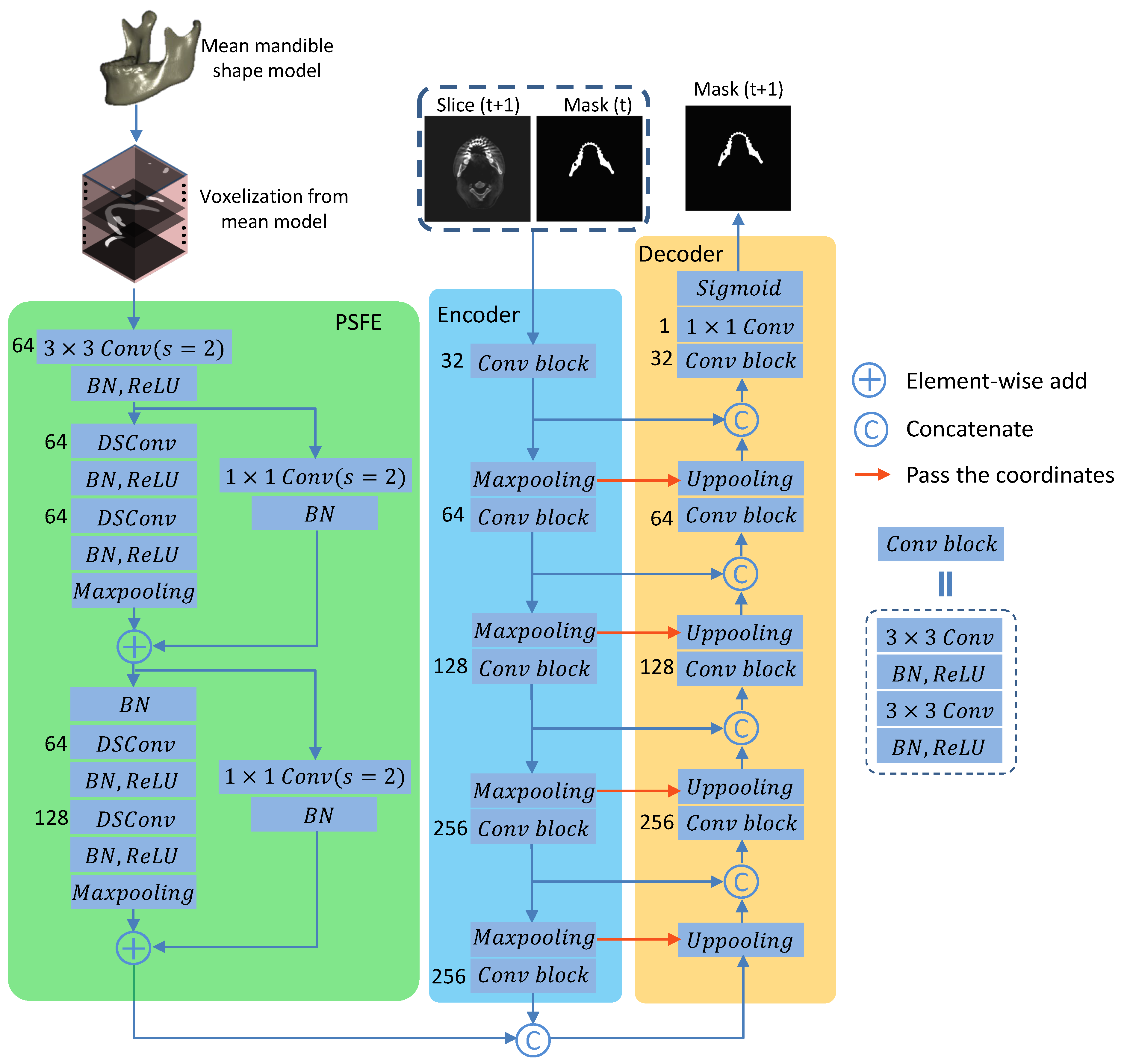
2.2. Prior Shape Feature Extractor (PSFE)
2.3. Recurrent Convolutional Neural Networks for Segmentation
2.4. Combo Loss Function
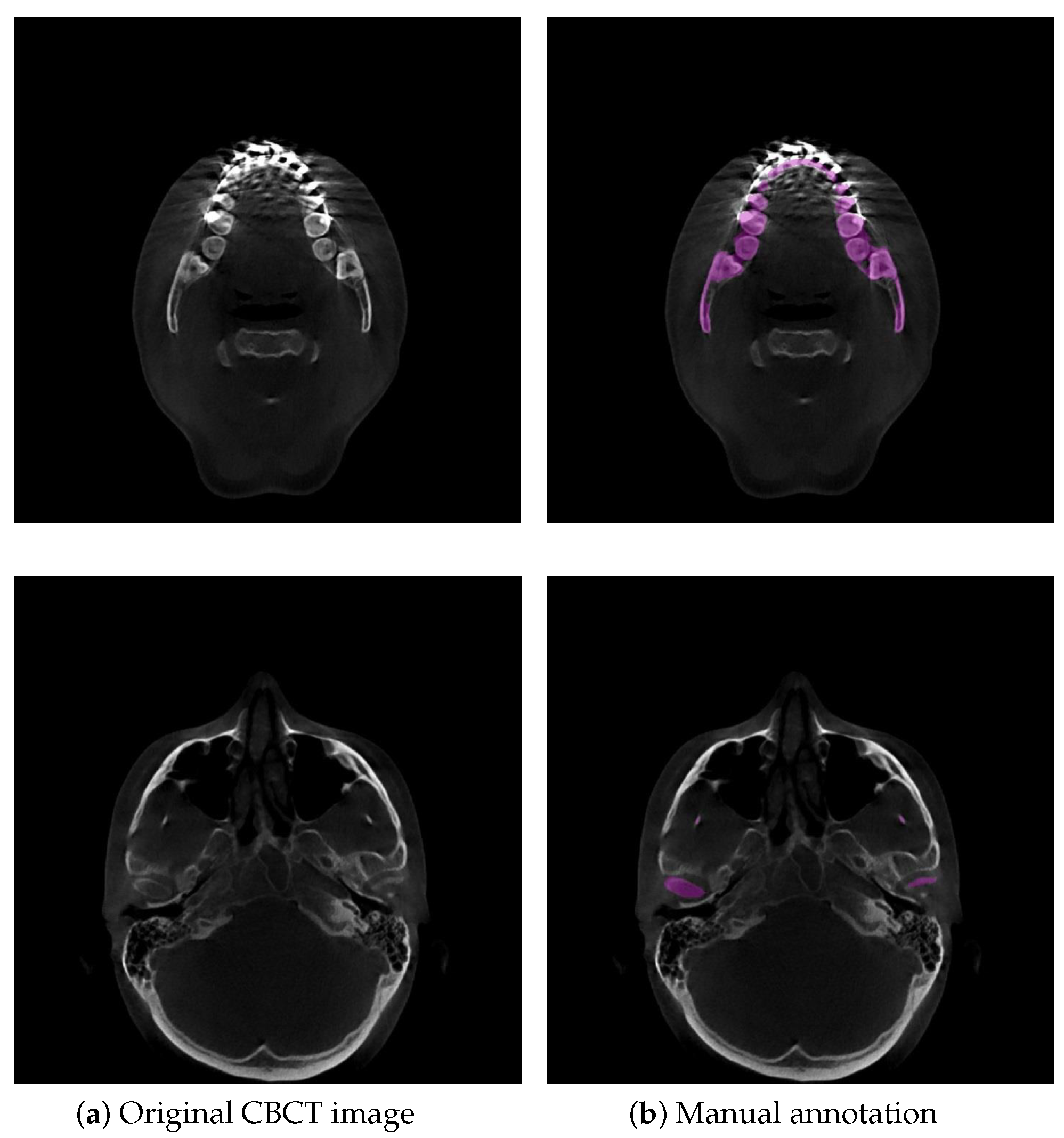
2.5. Dataset
2.6. Evaluation Metrics
2.7. Implementation Details
3. Results
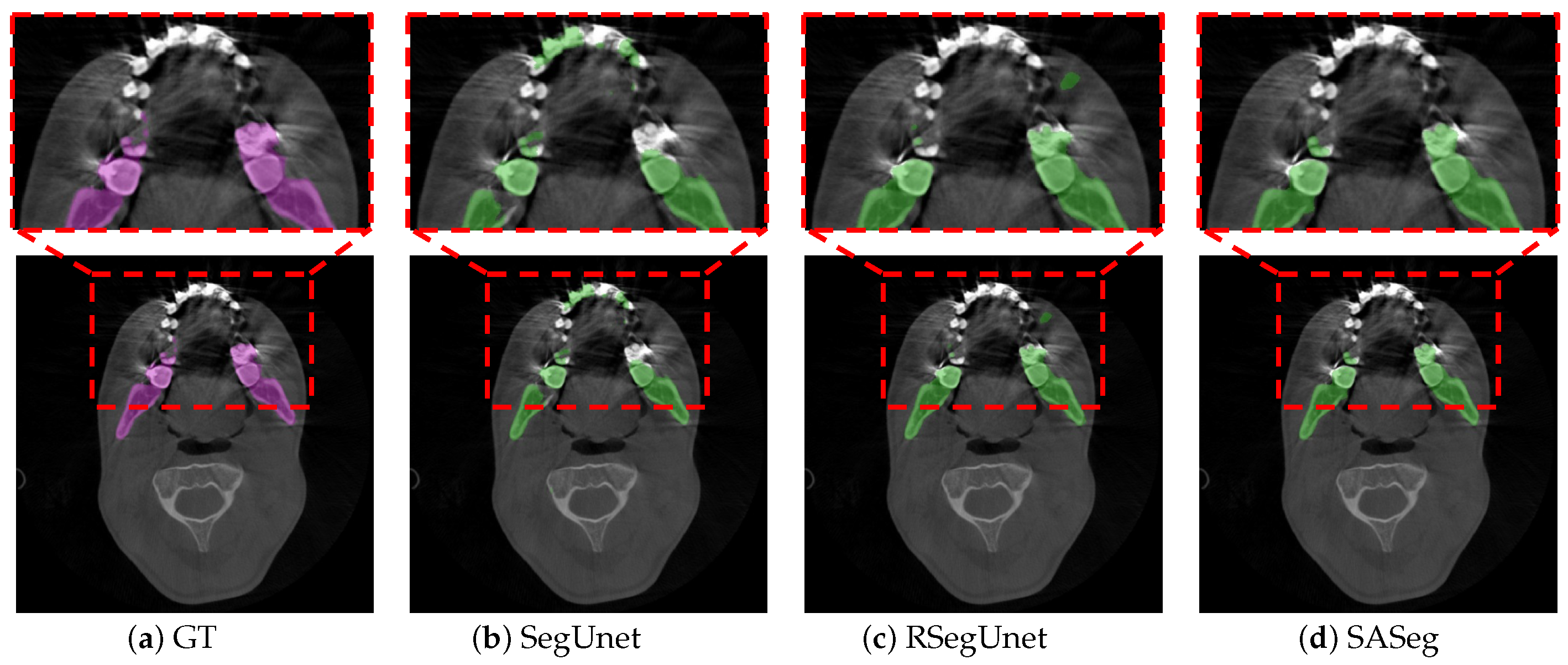
3.1. Method Comparison
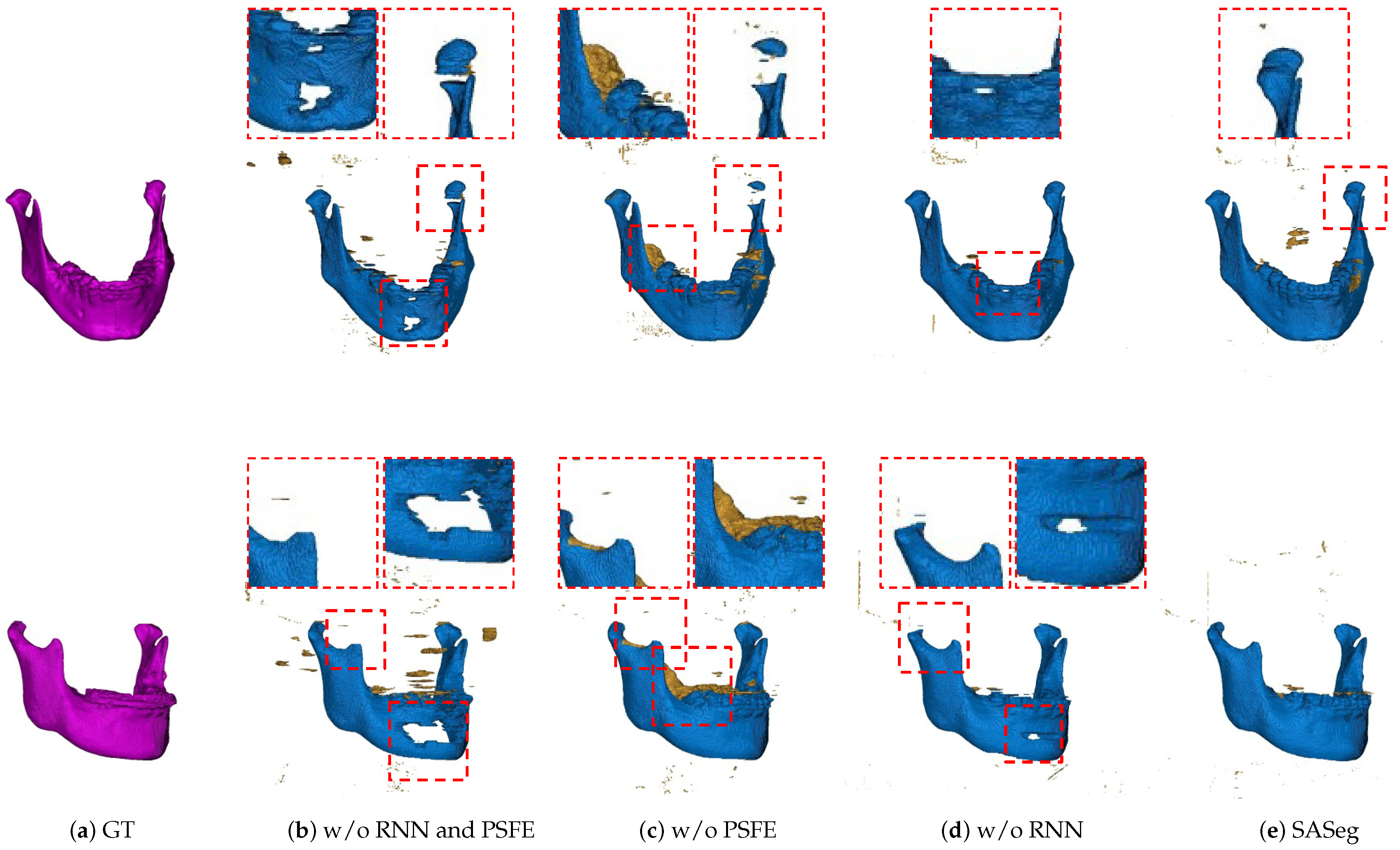
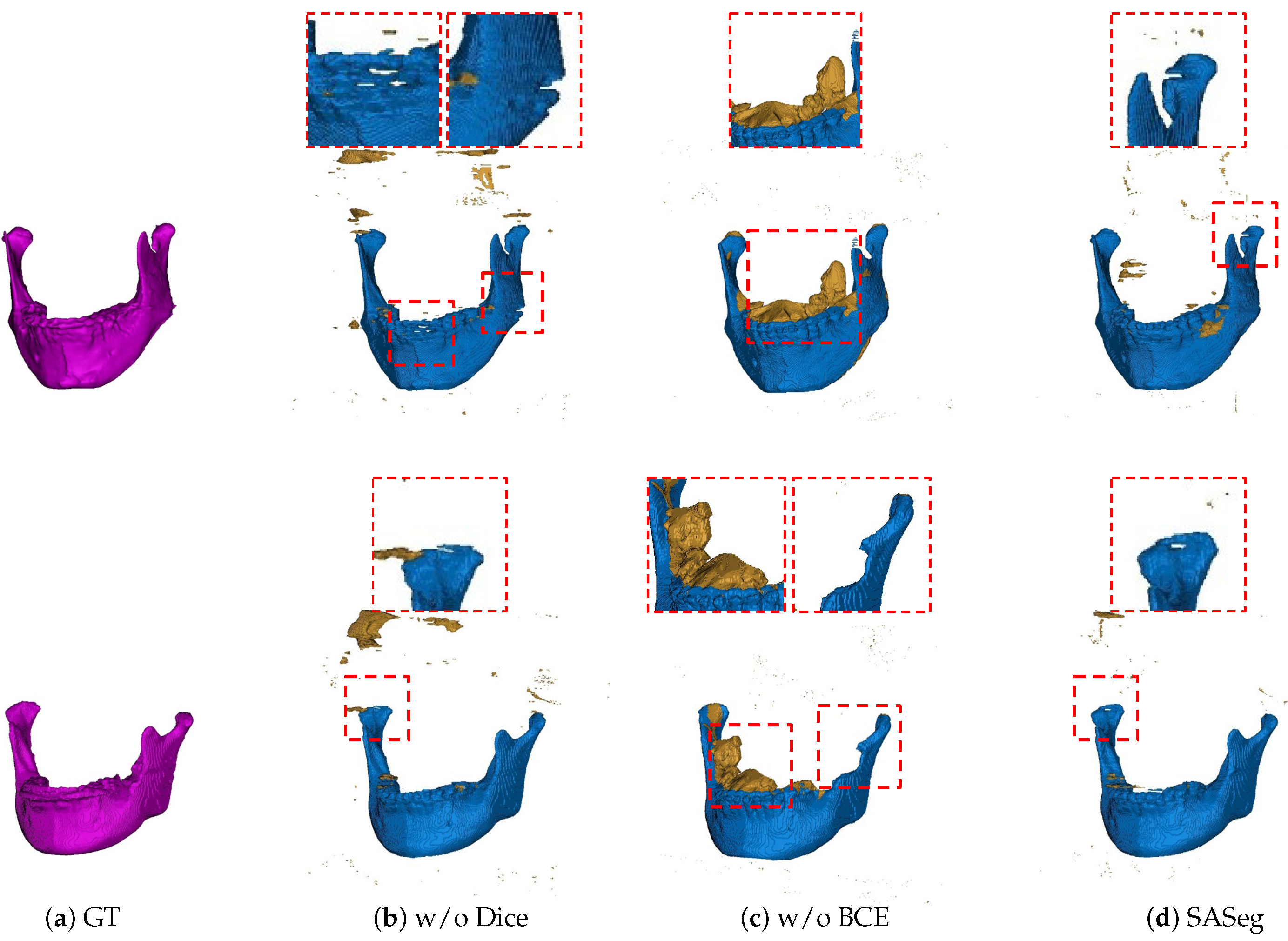
3.2. Ablation Experiments
3.2.1. Ablation Analysis of the PSFE Module
3.2.2. Ablation Analysis of the Loss Functions
3.3. Reliability Analysis
3.4. Experiments on the PDDCA Dataset
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kraeima, J. Three Dimensional Virtual Surgical Planning for Patient Specific Osteosynthesis and Devices in Oral In addition, Maxillofacial Surgery. A New Era. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2019. [Google Scholar]
- Fourie, Z.; Damstra, J.; Schepers, R.H.; Gerrits, P.O.; Ren, Y. Segmentation process significantly influences the accuracy of 3D surface models derived from cone beam computed tomography. Eur. J. Radiol. 2012, 81, e524–e530. [Google Scholar] [CrossRef]
- Vaitiekūnas, M.; Jegelevičius, D.; Sakalauskas, A.; Grybauskas, S. Automatic Method for Bone Segmentation in Cone Beam Computed Tomography Data Set. Appl. Sci. 2020, 10, 236. [Google Scholar] [CrossRef] [Green Version]
- Hirschinger, V.; Hanke, S.; Hirschfelder, U.; Hofmann, E. Artifacts in orthodontic bracket systems in cone-beam computed tomography and multislice computed tomography. J. Orofac. Orthop. Kieferorthopädie 2015, 76, 152–163. [Google Scholar] [CrossRef] [PubMed]
- Wallner, J.; Mischak, I.; Egger, J. Computed tomography data collection of the complete human mandible and valid clinical ground truth models. Sci. Data 2019, 6, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Chen, K.C.; Gao, Y.; Shi, F.; Liao, S.; Li, G.; Shen, S.G.; Yan, J.; Lee, P.K.; Chow, B.; et al. Automated bone segmentation from dental CBCT images using patch-based sparse representation and convex optimization. Med. Phys. 2014, 41, 043503. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Beare, R.; Matthews, H.; Schneider, P.; Kilpatrick, N.; Clement, J.; Claes, P.; Penington, A.; Adamson, C. Marker-based watershed transform method for fully automatic mandibular segmentation from CBCT images. Dentomaxillofacial Radiol. 2019, 48, 20180261. [Google Scholar] [CrossRef] [PubMed]
- Gollmer, S.T.; Buzug, T.M. Fully automatic shape constrained mandible segmentation from cone-beam CT data. In Proceedings of the IEEE 9th International Symposium on Biomedical Imaging, Barcelona, Spain, 2–5 May 2012; pp. 1272–1275. [Google Scholar] [CrossRef]
- Linares, O.C.; Bianchi, J.; Raveli, D.; Neto, J.B.; Hamann, B. Mandible and skull segmentation in cone beam computed tomography using super-voxels and graph clustering. Vis. Comput. 2019, 35, 1461–1474. [Google Scholar]
- Wang, L.; Gao, Y.; Shi, F.; Li, G.; Chen, K.C.; Tang, Z.; Xia, J.J.; Shen, D. Automated segmentation of dental CBCT image with prior-guided sequential random forests. Med. Phys. 2016, 43, 336–346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nosrati, M.S.; Hamarneh, G. Incorporating prior knowledge in medical image segmentation: A survey. arXiv 2016, arXiv:1607.01092. [Google Scholar]
- Qiu, B.; Guo, J.; Kraeima, J.; Glas, H.H.; Borra, R.J.H.; Witjes, M.J.H.; van Ooijen, P.M.A. Automatic segmentation of the mandible from computed tomography scans for 3D virtual surgical planning using the convolutional neural network. Phys. Med. Biol. 2019, 64, 175020. [Google Scholar] [CrossRef] [PubMed]
- Minnema, J.; van Eijnatten, M.; Hendriksen, A.A.; Liberton, N.; Pelt, D.M.; Batenburg, K.J.; Forouzanfar, T.; Wolff, J. Segmentation of dental cone-beam CT scans affected by metal artifacts using a mixed-scale dense convolutional neural network. Med. Phys. 2019, 46, 5027–5035. [Google Scholar] [CrossRef] [PubMed]
- Pauwels, R.; Araki, K.; Siewerdsen, J.; Thongvigitmanee, S.S. Technical aspects of dental CBCT: State of the art. Dentomaxillofacial Radiol. 2015, 44, 20140224. [Google Scholar] [CrossRef] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar] [CrossRef] [Green Version]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder–decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning where to look for the pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- O’Mahony, N.; Campbell, S.; Carvalho, A.; Harapanahalli, S.; Hernandez, G.V.; Krpalkova, L.; Riordan, D.; Walsh, J. Deep learning vs. traditional computer vision. In Proceedings of the Science and Information Conference, Las Vegas, NV, USA, 25–26 April 2019; pp. 128–144. [Google Scholar]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; pp. 424–432. [Google Scholar] [CrossRef] [Green Version]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Huang, Y.; Tang, H.; Qian, Z.; Du, N.; Fan, W.; Xie, X. AnatomyNet: Deep 3D Squeeze-and-excitation U-Nets for fast and fully automated whole-volume anatomical segmentation. arXiv 2018, arXiv:1808.05238. [Google Scholar]
- Wang, C.; MacGillivray, T.; Macnaught, G.; Yang, G.; Newby, D. A two-stage 3D Unet framework for multi-class segmentation on full resolution image. arXiv 2018, arXiv:1804.04341. [Google Scholar]
- Mortazi, A.; Burt, J.; Bagci, U. Multi-planar deep segmentation networks for cardiac substructures from MRI and CT. In Proceedings of the International Workshop on Statistical Atlases and Computational Models of the Heart, Quebec City, QC, Canada, 10–14 September 2017; pp. 199–206. [Google Scholar] [CrossRef] [Green Version]
- Novikov, A.A.; Major, D.; Wimmer, M.; Lenis, D.; Bühler, K. Deep sequential segmentation of organs in volumetric medical scans. IEEE Trans. Med. Imaging 2018, 38, 1207–1215. [Google Scholar] [CrossRef] [Green Version]
- Ghavami, N.; Hu, Y.; Bonmati, E.; Rodell, R.; Gibson, E.; Moore, C.; Barratt, D. Integration of spatial information in convolutional neural networks for automatic segmentation of intraoperative transrectal ultrasound images. J. Med. Imaging 2018, 6, 011003. [Google Scholar] [CrossRef] [Green Version]
- Qiu, B.; Guo, J.; Kraeima, J.; Glas, H.H.; Borra, R.J.; Witjes, M.J.; Ooijen, P.M.V. Recurrent convolutional neural networks for mandible segmentation from computed tomography. arXiv 2020, arXiv:2003.06486. [Google Scholar]
- Kamal, U.; Tonmoy, T.I.; Das, S.; Hasan, M.K. Automatic Traffic Sign Detection and Recognition Using SegU-Net and a Modified Tversky Loss Function With L1-Constraint. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1467–1479. [Google Scholar] [CrossRef]
- Chen, F.; Yu, H.; Hu, R.; Zeng, X. Deep learning shape priors for object segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1870–1877. [Google Scholar]
- Duan, Y.; Feng, J.; Lu, J.; Zhou, J. Context aware 3D fully convolutional networks for coronary artery segmentation. In Proceedings of the International Workshop on Statistical Atlases and Computational Models of the Heart, Granada, Spain, 16 September 2018; pp. 85–93. [Google Scholar]
- Tong, N.; Gou, S.; Yang, S.; Ruan, D.; Sheng, K. Fully automatic multi-organ segmentation for head and neck cancer radiotherapy using shape representation model constrained fully convolutional neural networks. Med. Phys. 2018, 45, 4558–4567. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cootes, T.F.; Taylor, C.J.; Cooper, D.H.; Graham, J. Active shape models-their training and application. Comput. Vis. Image Underst. 1995, 61, 38–59. [Google Scholar] [CrossRef] [Green Version]
- Ambellan, F.; Lamecker, H.; von Tycowicz, C.; Zachow, S. Statistical shape models: Understanding and mastering variation in anatomy. In Biomedical Visualisation; Springer: Berlin/Heidelberg, Germany, 2019; pp. 67–84. [Google Scholar]
- Zheng, G.; Li, S.; Szekely, G. Statistical Shape and Deformation Analysis: Methods, Implementation and Applications; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Krzanowski, W. Principles of Multivariate Analysis; OUP Oxford: Oxford, UK, 2000; Volume 23. [Google Scholar]
- Manu. NonrigidICP. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/41396-nonrigidicp (accessed on 23 February 2021).
- Saito, A.; Nawano, S.; Shimizu, A. Joint optimization of segmentation and shape prior from level-set-based statistical shape model, and its application to the automated segmentation of abdominal organs. Med. Image Anal. 2016, 28, 46–65. [Google Scholar] [CrossRef]
- Grosgeorge, D.; Petitjean, C.; Dacher, J.N.; Ruan, S. Graph cut segmentation with a statistical shape model in cardiac MRI. Comput. Vis. Image Underst. 2013, 117, 1027–1035. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Taghanaki, S.A.; Zheng, Y.; Zhou, S.K.; Georgescu, B.; Sharma, P.; Xu, D.; Comaniciu, D.; Hamarneh, G. Combo loss: Handling input and output imbalance in multi-organ segmentation. Comput. Med. Imaging Graph. 2019, 75, 24–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raudaschl, P.F.; Zaffino, P.; Sharp, G.C.; Spadea, M.F.; Chen, A.; Dawant, B.M.; Albrecht, T.; Gass, T.; Langguth, C.; Lüthi, M.; et al. Evaluation of segmentation methods on head and neck CT: Auto-segmentation challenge 2015. Med. Phys. 2017, 44, 2020–2036. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Xiang, L.; Nie, D.; Shao, Y.; Zhang, H.; Shen, D.; Wang, Q. Interleaved 3D-CNN s for joint segmentation of small-volume structures in head and neck CT images. Med. Phys. 2018, 45, 2063–2075. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghafoorian, M.; Karssemeijer, N.; Heskes, T.; Uden, I.W.; Sanchez, C.I.; Litjens, G.; Leeuw, F.E.; Ginneken, B.; Marchiori, E.; Platel, B. Location sensitive deep convolutional neural networks for segmentation of white matter hyperintensities. Sci. Rep. 2017, 7, 5110. [Google Scholar] [CrossRef] [PubMed]
- Huttenlocher, D.P.; Rucklidge, W.J.; Klanderman, G.A. Comparing images using the Hausdorff distance under translation. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Champaign, IL, USA, 15–18 June 1992; pp. 654–656. [Google Scholar] [CrossRef]
- Taha, A.A.; Hanbury, A. Metrics for evaluating 3D medical image segmentation: Analysis, selection, and tool. BMC Med. Imaging 2015, 15, 29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Chen, A.; Dawant, B. A multi-atlas approach for the automatic segmentation of multiple structures in head and neck CT images. In Proceedings of the Head and Neck Auto-Segmentation Challenge (MICCAI), Munich, Germany, 9 October 2015. [Google Scholar]
- Mannion-Haworth, R.; Bowes, M.; Ashman, A.; Guillard, G.; Brett, A.; Vincent, G. Fully automatic segmentation of head and neck organs using active appearance models. In Proceedings of the Head and Neck Auto-Segmentation Challenge (MICCAI), Munich, Germany, 9 October 2015. [Google Scholar]
- Albrecht, T.; Gass, T.; Langguth, C.; Lüthi, M. Multi atlas segmentation with active shape model refinement for multi-organ segmentation in head and neck cancer radiotherapy planning. In Proceedings of the Head and Neck Auto-Segmentation Challenge (MICCAI), Munich, Germany, 9 October 2015. [Google Scholar]
- Ibragimov, B.; Xing, L. Segmentation of organs-at-risks in head and neck CT images using convolutional neural networks. Med. Phys. 2017, 44, 547–557. [Google Scholar] [CrossRef] [Green Version]
- Orbes-Arteaga, M.; Pea, D.; Dominguez, G. Head and neck auto segmentation challenge based on non-local generative models. In Proceedings of the Head and Neck Auto-Segmentation Challenge (MICCAI), Munich, Germany, 9 October 2015. [Google Scholar]
- Kodym, O.; Španěl, M.; Herout, A. Segmentation of Head and Neck Organs at Risk Using CNN with Batch Dice Loss. In Proceedings of the German Conference on Pattern Recognition, Stuttgart, Germany, 9–12 October 2018; pp. 105–114. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wei, L.; Wang, L.; Gao, Y.; Chen, W.; Shen, D. Hierarchical vertex regression-based segmentation of head and neck CT images for radiotherapy planning. IEEE Trans. Image Process. 2017, 27, 923–937. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, L.; Song, Z.; Wang, M. Organ at Risk Segmentation in Head and Neck CT Images by Using a Two-Stage Segmentation Framework Based on 3D U-Net. arXiv 2018, arXiv:1809.00960. [Google Scholar] [CrossRef]
- Liang, S.; Thung, K.; Nie, D.; Zhang, Y.; Shen, D. Multi-view Spatial Aggregation Framework for Joint Localization and Segmentation of Organs at risk in Head and Neck CT Images. IEEE Trans. Med. Imaging 2020, 39, 2794–2805. [Google Scholar] [CrossRef] [PubMed]

| Methods | (%) | (mm) | (mm) | #Params (M) |
|---|---|---|---|---|
| U-Net | 94.79 (±1.77) | 2.0698 (±0.6137) | 32.6401 (±22.0779) | 3.35 |
| SegNet | 94.93 (±1.74 ) | 1.7762 (±1.5937) | 15.9851 (±26.5286) | 2.96 |
| SegUnet | 91.27 (±5.13) | 3.1436 (±3.6049) | 26.3569 (±34.9539) | 3.35 |
| AttUnet | 93.34 (±3.79) | 3.9705 (±4.6460) | 35.1859 (±42.3474) | 8.73 |
| SASeg | 95.35 (±1.54) | 0.9908 (±0.4128) | 2.5723 (±4.1192) | 3.80 |
| RNN | PSFE | (%) | (mm) | (mm) |
|---|---|---|---|---|
| 93.78 (±2.50) | 1.5851 (±1.0680) | 17.2517 (±24.2681) | ||
| ✓ | 92.26 (±5.66) | 1.3133 (±0.7276) | 7.2442 (±8.9275) | |
| ✓ | 95.09 (±1.47) | 1.2083 (±0.3354) | 4.7629 (±8.1762) | |
| ✓ | ✓ | 95.35 (±1.54) | 0.9908 (±0.4128) | 2.5723 (±4.1192) |
| BCE | Dice | (%) | (mm) | (mm) |
|---|---|---|---|---|
| ✓ | 95.45 (±1.39) | 1.3934 (±0.6228) | 10.6093 (±20.8654) | |
| ✓ | 83.75 (±15.59) | 3.2537 (±3.4075) | 16.7939 (±23.4980) | |
| ✓ | ✓ | 95.35 (±1.54) | 0.9908 (±0.4128) | 2.5723 (±4.1192) |
| (%) | (mm) | (mm) | |
|---|---|---|---|
| Intraobserver | 98.76 (±0.96) | 0.0690 (±0.534) | 0.6347 (±0.6176) |
| Interobserver | 91.56 (±4.45) | 0.3555 (±0.1701) | 2.0780 (±1.1699) |
| SASeg | 95.35 (±1.54) | 0.9908 (±0.4128) | 2.5723 (±4.1192) |
| Methods | (%) | (mm) | (mm) |
|---|---|---|---|
| Multiatlas [49] | 91.7 (±2.34) | - | 2.4887 (±0.7610) |
| AAM [50] | 92.67 (±1) | - | 1.9767 (±0.5945) |
| ASM [51] | 88.13 (±5.55) | - | 2.832 (±1.1772) |
| CNN [52] | 89.5 (±3.6) | - | - |
| NLGM [53] | 93.08 (±2.36) | - | - |
| AnatomyNet [21] | 92.51 (±2) | - | 6.28 (±2.21) |
| FCNN [30] | 92.07 (±1.15) | 0.51 (±0.12) | 2.01 (±0.83) |
| FCNN+SRM [30] | 93.6 (±1.21) | 0.371 (±0.11) | 1. 5 (±0.32) |
| CNN+BD [54] | 94.6 (±0.7) | 0.29 (±0.03) | - |
| HVR [55] | 94.4 (± 1.3) | 0.43 (± 0.12) | - |
| Cascade 3D U-Net [56] | 93 (±1.9) | - | 1.26 (±0.5) |
| Multiplanar [12] | 93.28 (±1.44) | - | 1.4333 (±0.5564) |
| Multiview [57] | 94.1 (±0.7) | 0.28 (±0.14) | - |
| RSegUnet [26] | 95.10 (±1.21) | 0.1367 (±0.0382) | 1.3560 (±0.4487) |
| SASeg | 95.29 (±1.16) | 0.1353 (±0.0481) | 1.3054 (±0.3195) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, B.; van der Wel, H.; Kraeima, J.; Hendrik Glas, H.; Guo, J.; Borra, R.J.H.; Witjes, M.J.H.; van Ooijen, P.M.A. Robust and Accurate Mandible Segmentation on Dental CBCT Scans Affected by Metal Artifacts Using a Prior Shape Model. J. Pers. Med. 2021, 11, 364. https://doi.org/10.3390/jpm11050364
Qiu B, van der Wel H, Kraeima J, Hendrik Glas H, Guo J, Borra RJH, Witjes MJH, van Ooijen PMA. Robust and Accurate Mandible Segmentation on Dental CBCT Scans Affected by Metal Artifacts Using a Prior Shape Model. Journal of Personalized Medicine. 2021; 11(5):364. https://doi.org/10.3390/jpm11050364
Chicago/Turabian StyleQiu, Bingjiang, Hylke van der Wel, Joep Kraeima, Haye Hendrik Glas, Jiapan Guo, Ronald J. H. Borra, Max Johannes Hendrikus Witjes, and Peter M. A. van Ooijen. 2021. "Robust and Accurate Mandible Segmentation on Dental CBCT Scans Affected by Metal Artifacts Using a Prior Shape Model" Journal of Personalized Medicine 11, no. 5: 364. https://doi.org/10.3390/jpm11050364
APA StyleQiu, B., van der Wel, H., Kraeima, J., Hendrik Glas, H., Guo, J., Borra, R. J. H., Witjes, M. J. H., & van Ooijen, P. M. A. (2021). Robust and Accurate Mandible Segmentation on Dental CBCT Scans Affected by Metal Artifacts Using a Prior Shape Model. Journal of Personalized Medicine, 11(5), 364. https://doi.org/10.3390/jpm11050364








