Framework for Testing Robustness of Machine Learning-Based Classifiers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Overview of Methods
2.2. Robustness Framework
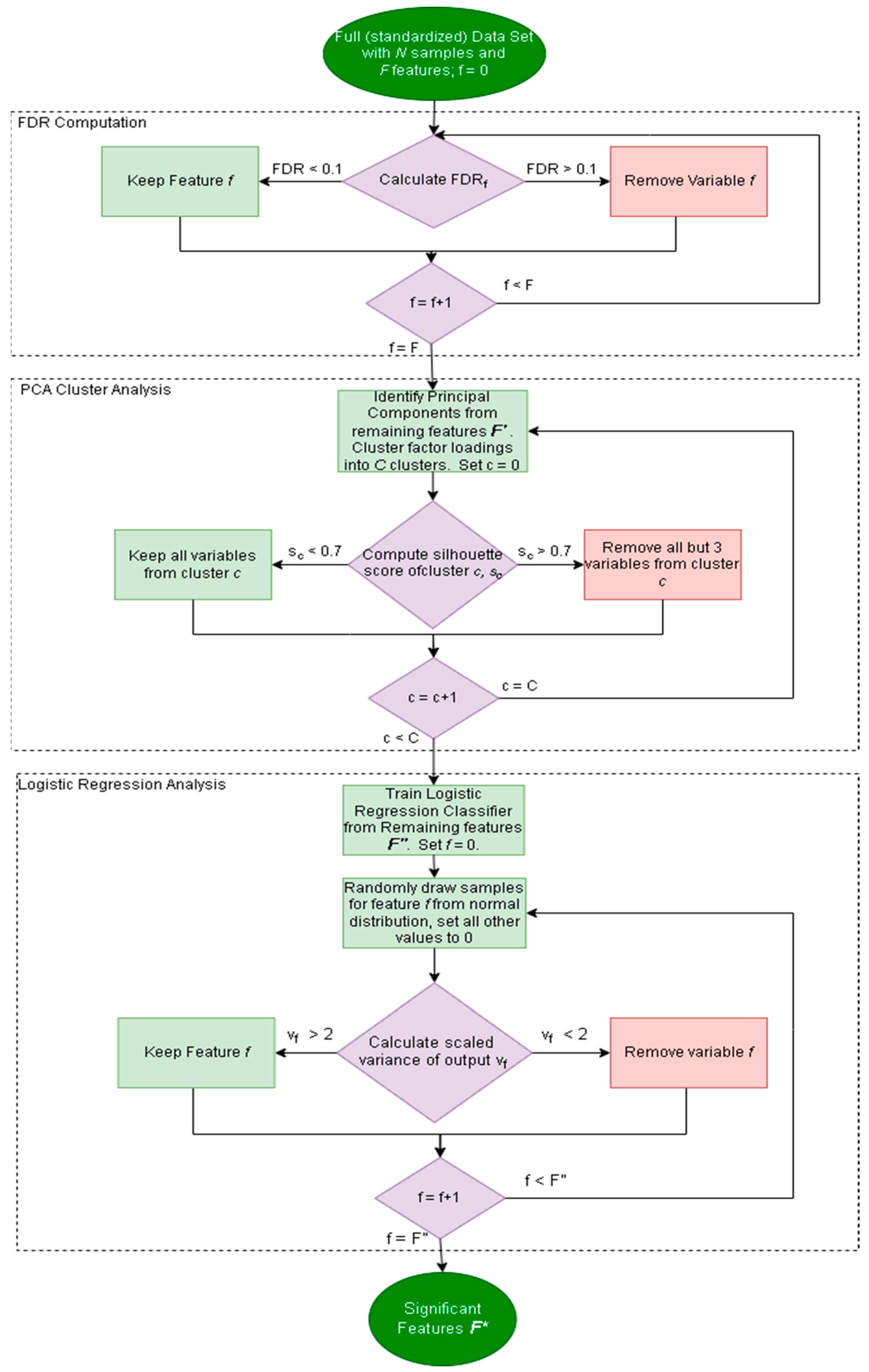
2.2.1. Factor Analysis Procedure
2.2.2. Noise Corruption
| Algorithm 1: Replacement Noise Algorithm |
| Input: Dataset D with N samples and F features |
| Output: D’, a corrupted dataset with N samples and F features |
| 1: Define noise term p, the proportion of values to replace |
| 2: For each |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: Randomly remove v values from column |
| 8: Replace each value with a randomly sampled value from N |
| 9: End for loop |
2.2.3. Severity of Noise
| Algorithm 2: Gaussian Noise Algorithm |
| Input: Dataset D with N samples and F features |
| Output: Noisy dataset D’ with N samples and F features |
| 1: Define noise term s, which scales the standard deviation of the noise distribution |
| 2: For each |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: End for loop |
2.2.4. Monte Carlo Data Splitting
2.3. Dataset
2.4. Classifiers
2.4.1. Classifier Overview
2.4.2. Classification Algorithms
Linear Discriminant Analysis
Support Vector Machine
Random Forest
Partial Least Squares-Discriminant Analysis
Logistic Regression
Multilayer Perceptron
2.4.3. Classifier Construction
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- LDA: Linear Discriminant Analysis (
- ○
- n_components = 1,
- ○
- solver = ‘eigen’)
- SVC (
- ○
- C = 0.1,
- ○
- kernel = ‘linear’)
- Random Forest Classifier (
- ○
- n_components = 16,
- ○
- max_features = ‘auto’,
- ○
- max_depth = 5,
- ○
- min_samples_split = 2,
- ○
- min_samples_leaf = 5,
- ○
- random_state = 42,
- ○
- n_jobs = −1)
- PLS Regression (n_components = 1)
- Logistic Regression (
- ○
- C = 0.1,
- ○
- solver = ‘saga’,
- ○
- random_state = 42)
- MLP Classifier (
- ○
- hidden_layer_sizes = ((32,16)),
- ○
- solver = ‘adam’,
- ○
- activation = ‘relu’,
- ○
- learning_rate = ‘constant’,
- ○
- learning_rate_init = 0.01,
- ○
- alpha = 1 × 10−5,
- ○
- random_state = 1,
- ○
- tol = 1× 10−3,
- ○
- n_iter_no_change = 5)
Appendix B




Appendix C



References
- Biomarkers, EndpointS, and Other Tools Resource. Available online: https://www.ncbi.nlm.nih.gov/books/NBK326791 (accessed on 25 February 2022).
- Krassowski, M.; Das, V.; Sahu, S.K.; Misra, B.B. State of the field in multi-omics research: From computational needs to data mining and sharing. Front. Genet. 2020, 11, 610798. [Google Scholar] [CrossRef] [PubMed]
- Liebal, U.W.; Phan, A.N.; Sudhakar, M.; Raman, K.; Blank, L.M. Machine learning applications for mass spectrometry-based metabolomics. Metabolites 2020, 10, 243. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, T.; Zhang, W.; Ghosh, D.; Kechris, K. Predictive modeling for Metabolomics Data. In Computational Methods and Data Analysis for Metabolomics; Humana: New York, NY, USA, 2020; pp. 313–336. [Google Scholar]
- Not-CA-22-037: Notice of Special Interest (NOSI): Validation of Digital Health and Artificial Intelligence Tools for Improved Assessment in Epidemiological, Clinical, and Intervention Research. Available online: https://grants.nih.gov/grants/guide/notice-files/NOT-CA-22-037.html (accessed on 11 February 2022).
- Wu, E.; Wu, K.; Daneshjou, R.; Ouyang, D.; Ho, D.E.; Zou, J. How medical AI devices are evaluated: Limitations and recommendations from an analysis of FDA approvals. Nat. Med. 2021, 27, 582–584. [Google Scholar] [CrossRef] [PubMed]
- Determan, C.E., Jr. Optimal algorithm for Metabolomics classification and feature selection varies by dataset. Int. J. Biol. 2014, 7, 100. [Google Scholar]
- Mendez, K.M.; Reinke, S.N.; Broadhurst, D.I. A comparative evaluation of the generalised predictive ability of eight machine learning algorithms across ten clinical metabolomics data sets for binary classification. Metabolomics 2019, 15, 150. [Google Scholar] [CrossRef] [PubMed]
- Harper, P.R. A review and comparison of classification algorithms for medical decision making. Health Policy 2005, 71, 315–331. [Google Scholar] [CrossRef] [PubMed]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef] [PubMed]
- Antonelli, J.; Claggett, B.L.; Henglin, M.; Kim, A.; Ovsak, G.; Kim, N.; Deng, K.; Rao, K.; Tyagi, O.; Watrous, J.D.; et al. Statistical Workflow for Feature Selection in Human Metabolomics Data. Metabolites 2019, 9, 143. [Google Scholar] [CrossRef] [PubMed]
- Tötsch, N.; Hoffmann, D. Classifier uncertainty: Evidence, potential impact, and probabilistic treatment. PeerJ Comp. Sci. 2021, 7, e398. [Google Scholar] [CrossRef] [PubMed]
- Mervin, L.H.; Johansson, S.; Semenova, E.; Giblin, K.A.; Engkvist, O. Uncertainty quantification in drug design. Drug Discov. Today 2021, 26, 474–489. [Google Scholar] [CrossRef] [PubMed]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A review of uncertainty quantification in Deep learning: Techniques, applications and challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Mishra, S.; Dutta, S.; Long, J.; Magazzeni, D. A Survey on the Robustness of Feature Importance and Counterfactual Explanations. arXiv 2021, arXiv:2111.00358. [Google Scholar] [CrossRef]
- Qureshi, F.; Adams, J.; Coleman, D.; Quig, D.; Hahn, J. Urinary essential elements of young children with autism spectrum disorder and their mothers. Res. Autism Spectr. Disord. 2020, 72, 101518. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- O’connor, B.P. SPSS and SAS programs for determining the number of components using parallel analysis and Velicer’s map test. Behav. Res. Methods Instrum. Comput. 2000, 32, 398–402. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global K-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Hubert, L.; Arabie, P. Comparing Partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Vinh, N.X.; Epps, J.; Bailey, J. Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance. J. Mach. Learn. Res. 2010, 11, 2837–2854. [Google Scholar]
- Birodkar, V.; Mobahi, H.; Bengio, S. Semantic Redundancies in Image-Classification Datasets: The 10% You Don’t Need. arXiv 2019, arXiv:1901.11409. [Google Scholar] [CrossRef]
- Altman, D.G.; Bland, J.M. Standard deviations and standard errors. BMJ 2005, 331, 903. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, J.L.; Manski, C.F. Identification and robustness with contaminated and corrupted data. Econometrics 1995, 63, 281. [Google Scholar] [CrossRef]
- Redestig, H.; Fukushima, A.; Stenlund, H.; Moritz, T.; Arita, M.; Saito, K.; Kusano, M. Compensation for Systematic Cross-Contribution Improves Normalization of Mass Spectrometry Based Metabolomics Data. Anal. Chem. 2009, 19, 7974–7980. [Google Scholar] [CrossRef] [PubMed]
- Broadhurst, D.; Goodacre, R.; Reinke, S.N.; Kuligowski, J.; Wilson, I.D.; Lewis, M.R.; Dunn, W.B. Guidelines and considerations for the use of system suitability and quality control samples in mass spectrometry assays applied in untargeted clinical metabolomics studies. Metabolomics 2018, 14, 72. [Google Scholar] [CrossRef]
- Xu, Y.; Goodacre, R. On splitting training and validation set: A comparative study of cross-validation, bootstrap and systematic sampling for estimating the generalization performance of supervised learning. J. Anal. Test. 2018, 2, 249–262. [Google Scholar] [CrossRef]
- Frye, R.E.; Vassali, S.; Kaur, G.; Lewis, C.; Karim, M.; Rossignol, D. Emerging biomarkers in autism spectrum disorder: A systematic review. Ann. Transl. Med. 2019, 7, 792. [Google Scholar] [CrossRef]
- Howsmon, D.P.; Kruger, U.; Melnyk, S.; James, S.J.; Hahn, J. Classification and adaptive behavior prediction of children with autism spectrum disorder based upon multivariate data analysis of markers of oxidative stress and DNA methylation. PLoS Comp. Biol. 2017, 13, e1005385. [Google Scholar] [CrossRef] [PubMed]
- Rao, C.R. The utilization of multiple measurements in problems of biological classification. J. R. Stat. Soc. Ser. B 1948, 10, 159–193. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees, 1st ed.; Routledge: New York, NY, USA, 1984. [Google Scholar]
- Höskuldsson, A. PLS regression methods. J. Chemom. 1988, 2, 211–228. [Google Scholar] [CrossRef]
- Rospial, R.; Kramer, N. Overview and Recent Advances in Partial Least Squares. In International Statistical and Optimization Perspectives Workshop “Subspace, Latent Structure and Feature Selecion”; Springer: Berlin/Heidelberg, Germany, 2005; pp. 34–51. [Google Scholar]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression, 3rd ed.; John Wiley and Sons: Hoboken, NY, USA, 2013. [Google Scholar]
- Defazio, A.; Bach, F.; Lacoste-Julien, S. A fast incremental gradient method with support for non-strongly convex composite objectives. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; pp. 1646–1654. [Google Scholar]
- Hinton, G.E. Connectionist learning procedures. Artif. Intell. 1989, 40, 185–234. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Duchesnay, E. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Grissa, D.; Pétéra, M.; Brandolini, M.; Napoli, A.; Comte, B.; Pujos-Guillot, E. Feature selection methods for early predictive biomarker discovery using untargeted Metabolomic Data. Front. Mol. Biosci. 2016, 3, 30. [Google Scholar] [CrossRef] [PubMed]
- Qureshi, F.; Hahn, J. Towards the Development of a Diagnostic Test for Autism Spectrum Disorder: Big Data Meets Metabolomics. Can. J. Chem. Eng. 2022, in press. [Google Scholar] [CrossRef]
- Wanichthanarak, K.; Fahrmann, J.F.; Grapov, D. Genomic, Proteomic, and Metabolomic Data Integration Strategies. Biomark. Insights 2015, 10, 1–6. [Google Scholar] [CrossRef]
- Barla, A.; Jurman, G.; Riccadonna, S.; Merler, S.; Chierici, M.; Furlanello, C. Machine Learning methods for predictive proteomics. Brief. Bioinform. 2008, 9, 119–128. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, Y.; Li, Y.; Luo, Y. Statistical and machine learning methods for spatially resolved transcriptomics data analysis. Genome Biol. 2022, 23, 83. [Google Scholar] [CrossRef]
- Parmar, C.; Barry, J.D.; Hosny, A.; Quackenbush, J.; Aerts, H.J.W.L. Data Analysis Strategies in Medical Imaging. Clin. Cancer Res. 2018, 24, 3492–3499. [Google Scholar] [CrossRef]
- Kaviani, S.; Han, K.J.; Sohn, I. Adversarial attacks and defenses on AI in medical imaging informatics: A survey. Expert Syst. Appl. 2022, 198, 116815. [Google Scholar] [CrossRef]










| Algorithm | Feature 1 | Feature 2 | Feature 3 | Feature 4 | Feature 5 | # From F.A. |
|---|---|---|---|---|---|---|
| LDA | % DNA Meth. | 8-OHG | Glu-Cys | fCystine/fCysteine | % oxid. Glut. | 5 |
| SVM | % DNA Meth. | 8-OHG | Glu-Cys | fGSH/GSSG | fCystine/fCysteine | 4 |
| RF | Methionine | % DNA Meth. | tGSH | fGSH/GSSG | fCystine/fCysteine | 2 |
| PLS-DA | % DNA Meth. | 8-OHG | Glu-Cys | fGSH/GSSG | fCystine/fCysteine | 4 |
| LOG | % DNA Meth. | 8-OHG | Glu-Cys | fCystine/fCysteine | % oxid. Glut. | 5 |
| MLP | % DNA Meth. | 8-OHG | Glu-Cys | fCystine/fCysteine | % oxid. Glut. | 5 |
| Classifier | Accuracy No Noise | Accuracy p = 1 | Variance p = 1 | Accuracy s = 1 | Variance s = 1 | Accuracy MC Split | Variance MC Split | Runtime MC Split |
|---|---|---|---|---|---|---|---|---|
| LDA | 93.8% | 50.4% | 4.88 × 10−3 | 94.4% | 1.78 × 10−4 | 96.4% | 1.40 × 10−4 | 2.80 min |
| SVM | 93.8% | 50.6% | 4.30 × 10−3 | 93.8% | 1.35 × 10−4 | 95.4% | 1.93 × 10−4 | 2.77 min |
| RF | 91.7% | 50.4% | 4.99 × 10−3 | 84.7% | 2.67 × 10−3 | 92.0% | 3.71 × 10−4 | 36.95 min |
| PLS-DA | 93.8% | 50.5% | 4.91 × 10−3 | 91.1% | 2.18 × 10−3 | 96.3% | 1.43 × 10−4 | 2.56 min |
| LOG | 95.8% | 50.6% | 4.79 × 10−3 | 95.4% | 3.38 × 10−4 | 96.0% | 1.33 × 10−4 | 3.46 min |
| MLP | 95.8% | 50.3% | 5.17 × 10−3 | 95.1% | 3.65 × 10−4 | 95.2% | 3.13 × 10−4 | 46.60 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuah, J.; Kruger, U.; Wang, G.; Yan, P.; Hahn, J. Framework for Testing Robustness of Machine Learning-Based Classifiers. J. Pers. Med. 2022, 12, 1314. https://doi.org/10.3390/jpm12081314
Chuah J, Kruger U, Wang G, Yan P, Hahn J. Framework for Testing Robustness of Machine Learning-Based Classifiers. Journal of Personalized Medicine. 2022; 12(8):1314. https://doi.org/10.3390/jpm12081314
Chicago/Turabian StyleChuah, Joshua, Uwe Kruger, Ge Wang, Pingkun Yan, and Juergen Hahn. 2022. "Framework for Testing Robustness of Machine Learning-Based Classifiers" Journal of Personalized Medicine 12, no. 8: 1314. https://doi.org/10.3390/jpm12081314
APA StyleChuah, J., Kruger, U., Wang, G., Yan, P., & Hahn, J. (2022). Framework for Testing Robustness of Machine Learning-Based Classifiers. Journal of Personalized Medicine, 12(8), 1314. https://doi.org/10.3390/jpm12081314








