Evaluating the Potential of Younger Cases and Older Controls Cohorts to Improve Discovery Power in Genome-Wide Association Studies of Late-Onset Diseases
Abstract
1. Introduction
2. Materials and Methods
2.1. The Simulation Design Summary and Conceptual Foundations
2.2. Simulations and Analysis of the Youngest Possible Cases and Older Controls Cohorts Scenario
2.3. GWASs Association Analysis and Effect-Size Adjustment for Younger Cases and Older Controls Cohorts
2.4. Data Sources, Programming, And Equipment
2.5. Statistical Analysis
3. Results
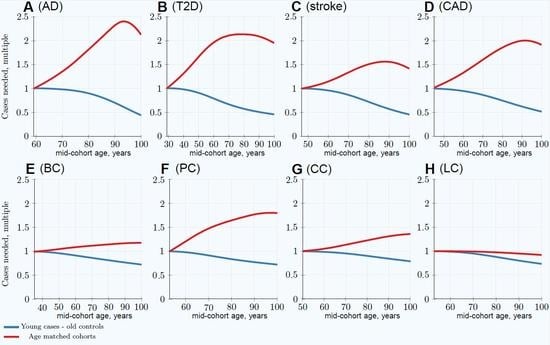
3.1. Impairment of GWASs’ Statistical Discovery Power with Progressively Older Age-Matched Cohorts
3.2. Advantage of Using Youngest Possible Cases and Oldest Controls in GWASs LOD Cohorts
3.3. Characterizing and Adjusting for Effect Size in the Younger Cases and Older Controls GWASs
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Alzheimer’s disease |
| CAD | coronary artery disease |
| GWAS | genome-wide association study |
| LOD | late-onset disease |
| MAF | minor allele frequency; customarily implying the “effect allele frequency” |
| OR | odds ratio |
| PRS | polygenic risk score |
| SNP | single nucleotide polymorphism; in context of this study used synonymously with the term ‘allele’ |
| T2D | type 2 diabetes |
References
- Franceschi, C.; Garagnani, P.G.; Morsiani, C.; Conte, M.; Santoro, A.; Grignolio, A.; Monti, D.; Capri, M.; Salvioli, S. The continuum of aging and age-related diseases: Common mechanisms but different rates. Front. Med. 2018, 5, 61. [Google Scholar] [CrossRef] [PubMed]
- Jager, R.D.; Mieler, W.F.; Miller, J.W. Age-related macular degeneration. N. Engl. J. Med. 2008, 358, 2606–2617. [Google Scholar] [CrossRef] [PubMed]
- Manolio, T.A.; Collins, F.S.; Cox, N.J.; Goldstein, D.B.; Hindorff, L.A.; Hunter, D.J.; McCarthy, M.I.; Ramos, E.M.; Cardon, L.R.; Chakravarti, A. Finding the missing heritability of complex diseases. Nature 2009, 461, 747–753. [Google Scholar] [CrossRef] [PubMed]
- Sobrin, L.; Ripke, S.; Yu, Y.; Fagerness, J.; Bhangale, T.R.; Tan, P.L.; Souied, E.H.; Buitendijk, G.H.; Merriam, J.E.; Richardson, A.J. Heritability and genome-wide association study to assess genetic differences between advanced age-related macular degeneration subtypes. Ophthalmology 2012, 119, 1874–1885. [Google Scholar] [CrossRef] [PubMed]
- Shendure, J.; Findlay, G.M.; Snyder, M.W. Genomic MedicineâEUR”Progress, Pitfalls, and Promise. Cell 2019, 177, 45–57. [Google Scholar] [CrossRef] [PubMed]
- OMIM. Available online: http://omim.org/statistics/geneMap (accessed on 2 June 2019).
- Murphy, S.L.; Xu, J.; Kochanek, K.D.; Curtin, S.C.; Arias, E. Mortality in the United States, 2016. NCHS Data Brief 2017, 293, 1–8. [Google Scholar]
- Visscher, P.M.; Wray, N.R.; Zhang, Q.; Sklar, P.; McCarthy, M.I.; Brown, M.A.; Yang, J. 10 years of GWAS discovery: Biology, function, and translation. Am. J. Hum. Genet. 2017, 101, 5–22. [Google Scholar] [CrossRef] [PubMed]
- Clarke, A.J.; Cooper, D.N. GWAS: Heritability missing in action? Eur. J. Hum. Genet. 2010, 18, 859. [Google Scholar] [CrossRef]
- Kumar, S.K.; Feldman, M.W.; Rehkopf, D.H.; Tuljapurkar, S. Limitations of GCTA as a solution to the missing heritability problem. Proc. Natl. Acad. Sci. USA 2016, 113, E61–E70. [Google Scholar] [CrossRef] [PubMed]
- Zaitlen, N.; Kraft, P. Heritability in the genome-wide association era. Hum. Genet. 2012, 131, 1655–1664. [Google Scholar] [CrossRef]
- Brookmeyer, R.; Gray, S.; Kawas, C. Projections of Alzheimer’s disease in the United States and the public health impact of delaying disease onset. Am. J. Public Health 1998, 88, 1337–1342. [Google Scholar] [CrossRef] [PubMed]
- Fuchsberger, C.; Flannick, J.; Teslovich, T.M.; Mahajan, A.; Agarwala, V.; Gaulton, K.J.; Ma, C.; Fontanillas, P.; Moutsianas, L.; McCarthy, D.J.; et al. The genetic architecture of type 2 diabetes. Nature 2016, 536, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Aparicio, H.J.; Seshadri, S. Familial Occurrence and Heritability of Stroke. In Stroke Genetics; Springer: Cham, Switzerland, 2017; pp. 9–20. [Google Scholar]
- Nielsen, M.; Andersson, C.; Gerds, T.A.; Andersen, P.K.; Jensen, T.B.; Køber, L.; Gislason, G.; Torp-Pedersen, C. Familial clustering of myocardial infarction in first-degree relatives: A nationwide study. Eur. Heart J. 2013, 34, 1198–1203. [Google Scholar] [CrossRef] [PubMed]
- Möller, S.; Mucci, L.A.; Harris, J.R.; Scheike, T.; Holst, K.; Halekoh, U.; Adami, H.O.; Czene, K.; Christensen, K.; Holm, N.V.; et al. The heritability of breast cancer among women in the Nordic Twin Study of Cancer. Cancer Epidemiol. Prev. Biomark. 2016, 25, 145–150. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Gu, J. Heritability of prostate cancer: A tale of rare variants and common single nucleotide polymorphisms. Ann. Transl. Med. 2016, 4. [Google Scholar] [CrossRef]
- Graff, R.E.; Möller, S.; Passarelli, M.N.; Witte, J.S.; Skytthe, A.; Christensen, K.; Tan, Q.; Adami, H.O.; Czene, K.; Harris, J.R. Familial risk and heritability of colorectal cancer in the nordic twin study of cancer. Clin. Gastroenterol. Hepatol. 2017, 15, 1256–1264. [Google Scholar] [CrossRef] [PubMed]
- Kanwal, M.; Ding, X.J.; Cao, Y. Familial risk for lung cancer. Oncol. Lett. 2017, 13, 535–542. [Google Scholar] [CrossRef]
- Eyre-Walker, A. Genetic architecture of a complex trait and its implications for fitness and genome-wide association studies. Proc. Natl. Acad. Sci. USA 2010, 107, 1752–1756. [Google Scholar] [CrossRef]
- Yang, J.; Ferreira, T.; Morris, A.P.; Medland, S.E.; Madden, P.A.; Heath, A.C.; Martin, N.G.; Montgomery, G.W.; Weedon, M.N.; Loos, R.J. Conditional and joint multiple-SNP analysis of GWAS summary statistics identifies additional variants influencing complex traits. Nat. Genet. 2012, 44, 369–375. [Google Scholar] [CrossRef]
- Thornton, K.R.; Foran, A.J.; Long, A.D. Properties and modeling of GWAS when complex disease risk is due to non-complementing, deleterious mutations in genes of large effect. PLoS Genet. 2013, 9, e1003258. [Google Scholar] [CrossRef]
- Agarwala, V.; Flannick, J.; Sunyaev, S.; Altshuler, D.; Consortium, G. Evaluating empirical bounds on complex disease genetic architecture. Nat. Genet. 2013, 45, 1418–1427. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, D.B. Common genetic variation and human traits. N. Engl. J. Med. 2009, 360, 1696. [Google Scholar] [CrossRef] [PubMed]
- Dickson, S.P.; Wang, K.; Krantz, I.; Hakonarson, H.; Goldstein, D.B. Rare variants create synthetic genome-wide associations. PLoS Biol. 2010, 8, e1000294. [Google Scholar] [CrossRef] [PubMed]
- North, T.L.; Beaumont, M. Complex trait architecture: The pleiotropic model revisited. Sci. Rep. 2015, 5, 9351. [Google Scholar] [CrossRef] [PubMed]
- Park, J.H.; Gail, M.H.; Weinberg, C.R.; Carroll, R.J.; Chung, C.C.; Wang, Z.; Chanock, S.J.; Fraumeni, J.F.; Chatterjee, N. Distribution of allele frequencies and effect sizes and their interrelationships for common genetic susceptibility variants. Proc. Natl. Acad. Sci. USA 2011, 108, 18026–18031. [Google Scholar] [CrossRef]
- Anderson, C.A.; Soranzo, N.; Zeggini, E.; Barrett, J.C. Synthetic associations are unlikely to account for many common disease genome-wide association signals. PLoS Biol. 2011, 9, e1000580. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Bakshi, A.; Zhu, Z.; Hemani, G.; Vinkhuyzen, A.A.; Lee, S.H.; Robinson, M.R.; Perry, J.R.; Nolte, I.M.; van Vliet-Ostaptchouk, J.V. Genetic variance estimation with imputed variants finds negligible missing heritability for human height and body mass index. Nat. Genet. 2015, 47, 1114. [Google Scholar] [CrossRef]
- Warner, S.C.; Valdes, A.M. The genetics of osteoarthritis: A review. J. Funct. Morphol. Kinesiol. 2016, 1, 140–153. [Google Scholar] [CrossRef]
- Zaitlen, N.; Lindström, S.; Pasaniuc, B.; Cornelis, M.; Genovese, G.; Pollack, S.; Barton, A.; Bickeböller, H.; Bowden, D.W.; Eyre, S.; et al. Informed conditioning on clinical covariates increases power in case-control association studies. PLoS Genet. 2012, 8, e1003032. [Google Scholar] [CrossRef]
- Thompson, J.R.; Attia, J.; Minelli, C. The meta-analysis of genome-wide association studies. Brief. Bioinf. 2011, 12, 259–269. [Google Scholar] [CrossRef]
- Mefford, J.; Witte, J.S. The Covariate’s Dilemma. PLoS Genet. 2012, 8, e1003096. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Meyre, D. Challenges in reproducibility of genetic association studies: Lessons learned from the obesity field. Int. J. Obes. 2013, 37, 559. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.Y.; Tao, R.; Kalsbeek, W.D.; Zeng, D.; Gonzalez, F., II; Fernández-Rhodes, L.; Graff, M.; Koch, G.G.; North, K.E.; Heiss, G. Genetic association analysis under complex survey sampling: The Hispanic Community Health Study/Study of Latinos. Am. J. Hum. Genet. 2014, 95, 675–688. [Google Scholar] [CrossRef]
- Bjørnland, T.; Bye, A.; Ryeng, E.; Wisløff, U.; Langaas, M. Powerful extreme phenotype sampling designs and score tests for genetic association studies. Stat. Med. 2018, 37, 4234–4251. [Google Scholar] [CrossRef] [PubMed]
- Oliynyk, R.T. Age-related late-onset disease heritability patterns and implications for genome-wide association studies. PeerJ 2019, 7, e7168. [Google Scholar] [CrossRef] [PubMed]
- Cox, D. Regression Models and Life-Tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–220. [Google Scholar] [CrossRef]
- Chatterjee, N.; Shi, J.; García-Closas, M. Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat. Rev. Genet. 2016, 17, 392. [Google Scholar] [CrossRef] [PubMed]
- Song, M.; Kraft, P.; Joshi, A.D.; Barrdahl, M.; Chatterjee, N. Testing calibration of risk models at extremes of disease risk. Biostatistics 2014, 16, 143–154. [Google Scholar] [CrossRef]
- Barrdahl, M.; Canzian, F.; Joshi, A.D.; Travis, R.C.; Chang-Claude, J.; Auer, P.L.; Gapstur, S.M.; Gaudet, M.; Diver, W.R.; Henderson, B.E.; et al. Post-GWAS gene–environment interplay in breast cancer: Results from the Breast and Prostate Cancer Cohort Consortium and a meta-analysis on 79,000 women. Hum. Mol. Genet. 2014, 23, 5260–5270. [Google Scholar] [CrossRef] [PubMed]
- Langenberg, C.; Sharp, S.J.; Franks, P.W.; Scott, R.A.; Deloukas, P.; Forouhi, N.G.; Froguel, P.; Groop, L.C.; Hansen, T.; Palla, L.; et al. Gene-lifestyle interaction and type 2 diabetes: The EPIC interact case-cohort study. PLoS Med. 2014, 11, e1001647. [Google Scholar] [CrossRef] [PubMed]
- Rudolph, A.; Milne, R.L.; Truong, T.; Knight, J.A.; Seibold, P.; Flesch-Janys, D.; Behrens, S.; Eilber, U.; Bolla, M.K.; Wang, Q.; et al. Investigation of gene-environment interactions between 47 newly identified breast cancer susceptibility loci and environmental risk factors. Int. J. Cancer 2015, 136, E685–E696. [Google Scholar] [CrossRef] [PubMed]
- Pawitan, Y.; Seng, K.C.; Magnusson, P.K. How many genetic variants remain to be discovered? PLoS ONE 2009, 4, e7969. [Google Scholar] [CrossRef] [PubMed]
- Noh, M.; Yip, B.; Lee, Y.; Pawitan, Y. Multicomponent variance estimation for binary traits in family-based studies. Genet. Epidemiol. 2006, 30, 37–47. [Google Scholar] [CrossRef] [PubMed]
- Vukcevic, D.; Hechter, E.; Spencer, C.; Donnelly, P. Disease model distortion in association studies. Genet. Epidemiol. 2011, 35, 278–290. [Google Scholar] [CrossRef] [PubMed]
- Luan, J.; Wong, M.; Day, N.; Wareham, N. Sample size determination for studies of gene-environment interaction. Int. J. Epidemiol. 2001, 30, 1035–1040. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chang, C.C.; Chow, C.C.; Tellier, L.C.; Vattikuti, S.; Purcell, S.M.; Lee, J.J. Second-generation PLINK: Rising to the challenge of larger and richer datasets. Gigascience 2015, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Purcell, S.; Chang, C. PLINK 1.9. Available online: www.cog-genomics.org/plink/1.9/ (accessed on 27 January 2019).
- Harrell, F.E., Jr. Package ‘rms’; Vanderbilt University: Nashville, TN, USA, 2018; p. 229. [Google Scholar]
- Chatterjee, N.; Chen, Y.H.; Breslow, N.E. A pseudoscore estimator for regression problems with two-phase sampling. J. Am. Stat. Assoc. 2003, 98, 158–168. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Social Security Administration (US). Available online: https://www.ssa.gov/oact/STATS/table4c6.html (accessed on 2 June 2019).
- Edland, S.D.; Rocca, W.A.; Petersen, R.C.; Cha, R.H.; Kokmen, E. Dementia and Alzheimer disease incidence rates do not vary by sex in Rochester, Minn. Arch. Neurol. 2002, 59, 1589–1593. [Google Scholar] [CrossRef] [PubMed]
- Kokmen, E.; Chandra, V.; Schoenberg, B.S. Trends in incidence of dementing illness in Rochester, Minnesota, in three quinquennial periods, 1960–1974. Neurology 1988, 38, 975–975. [Google Scholar] [CrossRef] [PubMed]
- Hebert, L.E.; Scherr, P.A.; Beckett, L.A.; Albert, M.S.; Pilgrim, D.M.; Chown, M.J.; Funkenstein, H.H.; Evans, D.A. Age-specific incidence of Alzheimer’s disease in a community population. JAMA 1995, 273, 1354–1359. [Google Scholar] [CrossRef] [PubMed]
- Boehme, M.W.; Buechele, G.; Frankenhauser-Mannuss, J.; Mueller, J.; Lump, D.; Boehm, B.O.; Rothenbacher, D. Prevalence, incidence and concomitant co-morbidities of type 2 diabetes mellitus in South Western Germany-a retrospective cohort and case control study in claims data of a large statutory health insurance. BMC Public Health 2015, 15, 855. [Google Scholar] [CrossRef] [PubMed]
- Rothwell, P.; Coull, A.; Silver, L.; Fairhead, J.; Giles, M.; Lovelock, C.; Redgrave, J.; Bull, L.; Welch, S.; Cuthbertson, F. Population-based study of event-rate, incidence, case fatality, and mortality for all acute vascular events in all arterial territories (Oxford Vascular Study). Lancet 2005, 366, 1773–1783. [Google Scholar] [CrossRef]
- Cancer Research UK. Available online: http://www.cancerresearchuk.org/health-professional/cancer-statistics-for-the-uk (accessed on 10 November 2018).
- Kuchenbaecker, K.B.; Hopper, J.L.; Barnes, D.R.; Phillips, K.A.; Mooij, T.M.; Roos-Blom, M.J.; Jervis, S.; Van Leeuwen, F.E.; Milne, R.L.; Andrieu, N. Risks of breast, ovarian, and contralateral breast cancer for BRCA1 and BRCA2 mutation carriers. JAMA 2017, 317, 2402–2416. [Google Scholar] [CrossRef] [PubMed]
- Hjelmborg, J.B.; Scheike, T.; Holst, K.; Skytthe, A.; Penney, K.L.; Graff, R.E.; Pukkala, E.; Christensen, K.; Adami, H.O.; Holm, N.V.; et al. The heritability of prostate cancer in the Nordic Twin Study of Cancer. Cancer Epidemiol. Prev. Biomarkers 2014, 23, 2303–2310. [Google Scholar] [CrossRef]
- Grönberg, H. Prostate cancer epidemiology. Lancet 2003, 361, 859–864. [Google Scholar] [CrossRef]
- Stringer, S.; Wray, N.R.; Kahn, R.S.; Derks, E.M. Underestimated effect sizes in GWAS: Fundamental limitations of single SNP analysis for dichotomous phenotypes. PLoS ONE 2011, 6, e27964. [Google Scholar] [CrossRef]
- Banerjee, S.; Zeng, L.; Schunkert, H.; Söding, J. Bayesian multiple logistic regression for case-control GWAS. PLoS Genet. 2018, 14, e1007856. [Google Scholar] [CrossRef]
- De Maturana, E.L.; Ye, Y.; Calle, M.L.; Rothman, N.; Urrea, V.; Kogevinas, M.; Petrus, S.; Chanock, S.J.; Tardón, A.; García-Closas, M.; et al. Application of multi-SNP approaches Bayesian LASSO and AUC-RF to detect main effects of inflammatory-gene variants associated with bladder cancer risk. PLoS ONE 2013, 8, e83745. [Google Scholar] [CrossRef]
- Duan, W.; Zhao, Y.; Wei, Y.; Yang, S.; Bai, J.; Shen, S.; Du, M.; Huang, L.; Hu, Z.; Chen, F. A fast algorithm for Bayesian multi-locus model in genome-wide association studies. Mol. Genet. Genom. 2017, 292, 923–934. [Google Scholar] [CrossRef]
- Zhu, X.; Stephens, M. Bayesian large-scale multiple regression with summary statistics from genome-wide association studies. Ann. Appl. Stat. 2017, 11, 1561. [Google Scholar] [CrossRef]
- Sham, P.C.; Purcell, S.M. Statistical power and significance testing in large-scale genetic studies. Nat. Rev. Genet. 2014, 15, 335. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, S.; Chatterjee, N.; Wheeler, W. An R package for analysis of case-control studies in genetic epidemiology. Package CGEN Vers. 3.20.0. Available online: https://rdrr.io/bioc/CGEN/ (accessed on 17 July 2019).
- SAS Institute Inc. SAS/Genetics(tm) 13.1 User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2013. [Google Scholar]
- Conomos, M.P.; Thornton, T. GENetic EStimation and inference in structured samples (GENESIS): Statistical methods for analyzing genetic data from samples with population structure and/or relatedness. Package GENESIS Vers. 2.14.1. Available online: https://rdrr.io/bioc/GENESIS/ (accessed on 17 July 2019).
- McCarthy, M.I.; Abecasis, G.R.; Cardon, L.R.; Goldstein, D.B.; Little, J.; Ioannidis, J.P.; Hirschhorn, J.N. Genome-wide association studies for complex traits: Consensus, uncertainty and challenges. Nat. Rev. Genet. 2008, 9, 356. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.J.; Seo, H.I.; Cha, H.Y.; Yang, Y.J.; Kwon, S.H.; Yang, S.J. Diabetes and Alzheimer’s Disease: Mechanisms and Nutritional Aspects. Clin. Nutr. Res. 2018, 7, 229–240. [Google Scholar] [CrossRef] [PubMed]
- Kendler, K.S.; Gardner, C.O.; Lichtenstein, P. A developmental twin study of symptoms of anxiety and depression: Evidence for genetic innovation and attenuation. Psychol. Med. 2008, 38, 1567–1575. [Google Scholar] [CrossRef] [PubMed]
- Wichers, M.; Gardner, C.; Maes, H.; Lichtenstein, P.; Larsson, H.; Kendler, K. Genetic innovation and stability in externalizing problem behavior across development: A multi-informant twin study. Behav. Genet. 2013, 43, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Lewis, G.; Plomin, R. Heritable influences on behavioural problems from early childhood to mid-adolescence: Evidence for genetic stability and innovation. Psychol. Med. 2015, 45, 2171–2179. [Google Scholar] [CrossRef] [PubMed]
- Van Dongen, J.; Nivard, M.G.; Willemsen, G.; Hottenga, J.J.; Helmer, Q.; Dolan, C.V.; Ehli, E.A.; Davies, G.E.; van Iterson, M.; Breeze, C.E.; et al. Genetic and environmental influences interact with age and sex in shaping the human methylome. Nat. Commun. 2016, 7, 11115. [Google Scholar] [CrossRef]
- Benayoun, B.A.; Pollina, E.A.; Brunet, A. Epigenetic regulation of ageing: Linking environmental inputs to genomic stability. Nat. Rev. Mol. Cell Biol. 2015, 16, 593–610. [Google Scholar] [CrossRef] [PubMed]
- Simino, J.; Shi, G.; Bis, J.C.; Chasman, D.I.; Ehret, G.B.; Gu, X.; Guo, X.; Hwang, S.J.; Sijbrands, E.; Smith, A.V.; et al. Gene-age interactions in blood pressure regulation: A large-scale investigation with the CHARGE, Global BPgen, and ICBP Consortia. Am. J. Hum. Genet. 2014, 95, 24–38. [Google Scholar] [CrossRef]
- Halladay, J.R.; Lenhart, K.C.; Robasky, K.; Jones, W.; Homan, W.F.; Cummings, D.M.; Cené, C.W.; Hinderliter, A.L.; Miller, C.L.; Donahue, K.E.; et al. Applicability of Precision Medicine Approaches to Managing Hypertension in Rural Populations. J. Pers. Med. 2018, 8. [Google Scholar] [CrossRef]




| Highly Prevalent LODs | Cancers | |||||||
|---|---|---|---|---|---|---|---|---|
| AD | T2D | Stroke | CAD | Breast | Prostate | Colorectal | Lung | |
| Heritability | 0.795 | 0.69 | 0.41 | 0.55 | 0.31 | 0.57 | 0.40 | 0.095 |
| SNP number | 3575 | 2125 | 625 | 1175 | 400 | 1250 | 600 | 100 |
| Highly Prevalent LODs | Cancers | |||||||
|---|---|---|---|---|---|---|---|---|
| AD | T2D | Stroke | CAD | Breast | Prostate | Colorectal | Lung | |
| LOD characteristics: | ||||||||
| Lifetime risk % | 10–20 | 55 | 25–30 | 32–49 | 12 | 12 | < 4.5 | <6.9 |
| Heritability % | 79–80 | 69 | 38–44 | 50–60 | 31 | 57 | 40 | 8–18 |
| Maximum yearly incidence % | > 20 | 2.5 | 4.4 | 3.6 | <0.5 | <0.8 | <0.6 | <0.6 |
| Cohort size multiple for: | ||||||||
| Age-matched at 80 years | 1.82 | 2.13 | 1.51 | 1.86 | 1.15 | 1.65 (1.36) | 1.25 | 0.98 |
| Youngest cases & controls at 80 years | 0.89 | 0.57 | 0.72 | 0.75 | 0.81 | 0.84 (0.82) | 0.90 | 0.88 |
| Relative advantage: 80-year-old controls | 2.04 | 3.74 | 2.10 | 2.48 | 1.42 | 1.96 (1.66) | 1.39 | 1.11 |
| Cohort size multiple for: | ||||||||
| Age-matched at 100 years | 2.12 | 1.95 | 1.42 | 1.91 | 1.19 | 1.80 (1.44) | 1.36 | 0.92 |
| Youngest cases & controls at 100 years | 0.43 | 0.46 | 0.46 | 0.52 | 0.72 | 0.72 (0.70) | 0.79 | 0.74 |
| Relative advantage: 100-year-old controls | 4.39 | 4.24 | 3.09 | 3.67 | 1.65 | 2.50 (2.06) | 1.72 | 1.24 |
| Highly Prevalent LODs | Cancers | |||||||
|---|---|---|---|---|---|---|---|---|
| AD | T2D | Stroke | CAD | Breast | Prostate | Colorectal | Lung | |
| Youngest cases mid-cohort age | 59 | 29 | 47 | 44 | 35 | 53 | 50 | 53 |
| GWAS Association SSE for (OR1.15): | ||||||||
| 100Y controls SSE raw | 0.00312 | 0.00311 | 0.00312 | 0.00311 | 0.00310 | 0.00310 | 0.00310 | 0.00310 |
| 100Y controls SSE adjusted | 0.00342 | 0.00345 | 0.00359 | 0.00336 | 0.00315 | 0.00314 | 0.0312 | 0.00314 |
| GWAS Association SSE for (OR1.05): | ||||||||
| 100Y controls SSE raw | 0.00283 | 0.00283 | 0.00283 | 0.00283 | 0.00283 | 0.00283 | 0.00283 | 0.00283 |
| 100Y controls SSE adjusted | 0.00310 | 0.00311 | 0.00321 | 0.00304 | 0.00288 | 0.00288 | 0.00285 | 0.00287 |
| Age bias adjustment—quadratic (): | ||||||||
| Slope coefficient | ||||||||
| Residual standard error | 0.029 | 0.026 | 0.0058 | 0.0039 | 0.0093 | 0.014 | 0.0050 | 0.0092 |
| p-value | ||||||||
| Age bias adjustment—best fit power (): | ||||||||
| Power | 3.2 | 1.4 | 2.1 | 2.0 | 1.4 | 1.2 | 1.6 | 1.7 |
| Slope coefficient | ||||||||
| Residual standard error | 0.0030 | 0.013 | 0.0057 | 0.0039 | 0.0036 | 0.0053 | 0.0025 | 0.0084 |
| p-value | ||||||||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliynyk, R.T. Evaluating the Potential of Younger Cases and Older Controls Cohorts to Improve Discovery Power in Genome-Wide Association Studies of Late-Onset Diseases. J. Pers. Med. 2019, 9, 38. https://doi.org/10.3390/jpm9030038
Oliynyk RT. Evaluating the Potential of Younger Cases and Older Controls Cohorts to Improve Discovery Power in Genome-Wide Association Studies of Late-Onset Diseases. Journal of Personalized Medicine. 2019; 9(3):38. https://doi.org/10.3390/jpm9030038
Chicago/Turabian StyleOliynyk, Roman Teo. 2019. "Evaluating the Potential of Younger Cases and Older Controls Cohorts to Improve Discovery Power in Genome-Wide Association Studies of Late-Onset Diseases" Journal of Personalized Medicine 9, no. 3: 38. https://doi.org/10.3390/jpm9030038
APA StyleOliynyk, R. T. (2019). Evaluating the Potential of Younger Cases and Older Controls Cohorts to Improve Discovery Power in Genome-Wide Association Studies of Late-Onset Diseases. Journal of Personalized Medicine, 9(3), 38. https://doi.org/10.3390/jpm9030038