TeV Instrumentation: Current and Future
Abstract
1. Introduction
2. Instrumentation
2.1. IACT Technique
2.2. SA and WCD Techniques
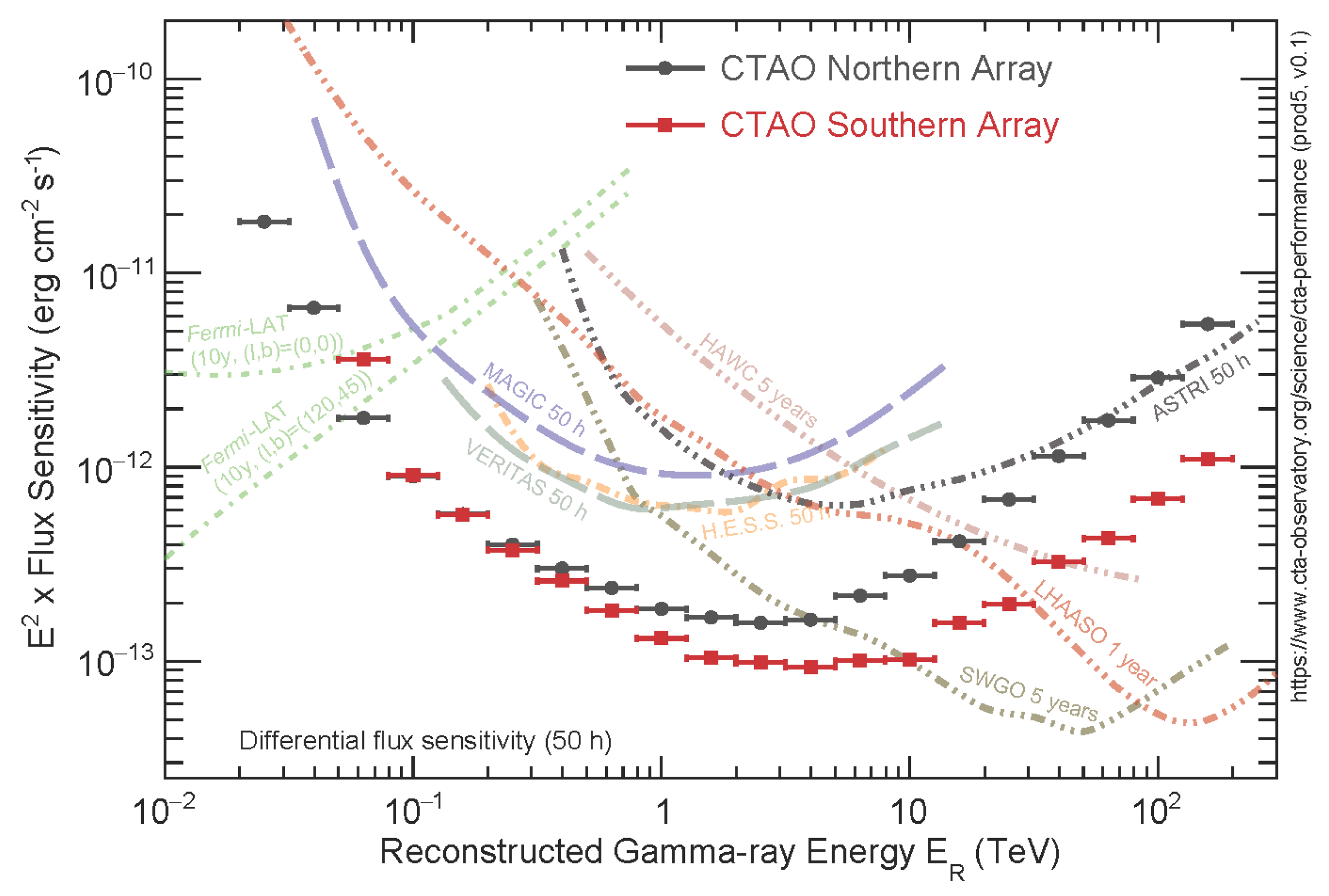
2.3. Comparison of Performance and Synergies
2.4. Hybrid Arrays
3. Future Instruments
4. Analysis Methods
4.1. Event Cleaning
4.2. Event Reconstruction and Background Rejection
4.3. Background Modeling
4.4. Largely Extended/Diffuse Emission
4.5. Energy Spectrum
4.6. Deep Learning Methods
4.7. Combination of Data from Different Instruments
5. Multi-Wavelength and Multi-Messenger Observations
TOO Observations with a Large Position Uncertainty
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Networks |
| CTA | Cherenkov Telescope Array |
| DL | Deep Learning |
| FOV | Field of View |
| HAWC | High-Altitude Water Cherenkov |
| H.E.S.S. | High-Energy Stereoscopic System |
| IACT | Imaging Atmospheric Cherenkov Telescope |
| LHAASO | Large High-Altitude Air Shower Observatory |
| LHAASO-WCDA | Water Cherenkov Detector Array |
| LHAASO-WFCTA | Wide-Field Air Cherenkov Telescope Array |
| LST | Large-Sized Telescope |
| MAGIC | Major Atmospheric Gamma-Ray Imaging Cherenkov |
| MC | Monte Carlo (Simulations) |
| MM | Multi-Messenger |
| MWL | Multi-Wavelength |
| PMT | Photomultiplier Tube |
| PSF | Point Spread Function |
| RNN | Recurrent Neural Networks |
| SA | Surface Array |
| SiPM | Silicon Photomultiplier |
| SWGO | Southern Wide-field Gamma-Ray Observatory |
| TOO | Target of Opportunity |
| VERITAS | Very Energetic Radiation Imaging Telescope Array System |
| VHE | Very High Energy |
| WCD | Water Cherenkov Detector |
| 1 | Various names are used for those types of detectors, including surface arrays, surface detectors, air shower arrays |
| 2 | Only at the highest energies for strong sources can the observations be considered background-free. |
| 3 | If the extension of the region is mainly in one direction, such as the inner part of the Galactic plane [74], it is still possible to use the adaptive ring method to evaluate the background. |
| 4 | In the case of IACTs also at large offset angles from the camera center |
References
- Takahashi, S.; Aoki, S.; Azuma, T.; Hayashi, H.; Iyono, A.; Karasuno, A.; Kato, T.; Kodama, K.; Komatani, R.; Komatsu, M.; et al. GRAINE precise γ-ray observations: Latest results on 2018 balloon-borne experiment and prospects on next/future scientific experiments. PoS 2021, ICRC2021, 654. [Google Scholar] [CrossRef]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The Large Area Telescope on the Fermi Gamma-Ray Space Telescope Mission. Astrophys. J. 2009, 697, 1071–1102. [Google Scholar] [CrossRef]
- Gottschall, D.; Förster, A.; Bonardi, A.; Santangelo, A.; Puehlhofer, G. The Mirror Alignment and Control System for CT5 of the H.E.S.S. experiment. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), The Hague, The Netherlands, 30 July–6 August 2015; Volume 34, p. 1017. [Google Scholar]
- Ahnen, M.L.; Baack, D.; Balbo, M.; Bergmann, M.; Biland, A.; Blank, M.; Bretz, T.; Bruegge, K.A.; Buss, J.; Domke, M.; et al. Bokeh mirror alignment for Cherenkov telescopes. Astropart. Phys. 2016, 82, 1–9. [Google Scholar] [CrossRef]
- Krähenbühl, T. nd Anderhub, H.; Backes, M.; Biland, A.; Boller, A.; Braun, I.; Bretz, T.; Commichau, V.; Djambazov, L.; Dorner, D.a.; et al. G-APDs in Cherenkov astronomy: The FACT camera. Nucl. Instrum. Methods Phys. Res. A 2012, 695, 96–99. [Google Scholar] [CrossRef]
- Hillas, A.M. Cerenkov Light Images of EAS Produced by Primary Gamma Rays and by Nuclei. In Proceedings of the 19th International Cosmic Ray Conference (ICRC19), San Diego, CA, USA, 11–23 August 1985; Volume 3, p. 445. [Google Scholar]
- Hofmann, W.; Jung, I.; Konopelko, A.; Krawczynski, H.; Lampeitl, H.; Pühlhofer, G. Comparison of techniques to reconstruct VHE gamma-ray showers from multiple stereoscopic Cherenkov images. Astropart. Phys. 1999, 12, 135–143. [Google Scholar] [CrossRef]
- Holder, J.; Atkins, R.W.; Badran, H.M.; Blaylock, G.; Bradbury, S.M.; Buckley, J.H.; Byrum, K.L.; Carter-Lewis, D.A.; Celik, O.; Chow, Y.C.K.; et al. The first VERITAS telescope. Astropart. Phys. 2006, 25, 391–401. [Google Scholar] [CrossRef]
- Aleksić, J.; Alvarez, E.A.; Antonelli, L.A.; Antoranz, P.; Asensio, M.; Backes, M.; Barrio, J.A.; Bastieri, D.; Becerra González, J.; Bednarek, W.; et al. Performance of the MAGIC stereo system obtained with Crab Nebula data. Astropart. Phys. 2012, 35, 435–448. [Google Scholar] [CrossRef]
- Ashton, T.; Backes, M.; Balzer, A.; Berge, D.; Bolmont, J.; Bonnefoy, S.; Brun, F.; Chaminade, T.; Delagnes, E.; Fontaine, G.; et al. A NECTAr-based upgrade for the Cherenkov cameras of the H.E.S.S. 12-meter telescopes. Astropart. Phys. 2020, 118, 102425. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barceló, M.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. The major upgrade of the MAGIC telescopes, Part I: The hardware improvements and the commissioning of the system. Astropart. Phys. 2016, 72, 61–75. [Google Scholar] [CrossRef]
- Krawczynski, H.; Prahl, J.; Arqueros, F.; Bradbury, S.; Cortina, J.; Deckers, T.; Eckmann, R.; Feigl, E.; Fernandez, J.; Fonseca, V.; et al. An optimized method for the reconstruction of the direction of air showers for scintillator arrays. Nucl. Instrum. Methods Phys. Res. A 1996, 383, 431–440. [Google Scholar] [CrossRef]
- Amenomori, M.; Ayabe, S.; Cao, P.Y.; Danzengluobu; Ding, L.K.; Feng, Z.Y.; Fu, Y.; Guo, H.W.; He, M.; Hibino, K.; et al. Observation of Multi-TEV Gamma Rays from the Crab Nebula using the Tibet Air Shower Array. Astrophys. J. Lett. 1999, 525, L93–L96. [Google Scholar] [CrossRef] [PubMed]
- Bartoli, B.; Bernardini, P.; Bi, X.J.; Bolognino, I.; Branchini, P.; Budano, A.; Calabrese Melcarne, A.K.; Camarri, P.; Cao, Z.; Cardarelli, R.; et al. TeV Gamma-Ray Survey of the Northern Sky Using the ARGO-YBJ Detector. Astrophys. J. 2013, 779, 27. [Google Scholar] [CrossRef]
- Yodh, G.B. Water Cherenkov Detectors: MILAGRO. Tev-Gamma-Ray Astrophys. 1996, 75, 199–212. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Solares, H.A.; Barber, A.S.; Baughman, B.; et al. The 2HWC HAWC Observatory Gamma-Ray Catalog. Astrophys. J. 2017, 843, 40. [Google Scholar] [CrossRef]
- Aharonian, F.; An, Q.; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; Cai, H.; Cai, J.T.; et al. Calibration of the air shower energy scale of the water and air Cherenkov techniques in the LHAASO experiment. Phys. Rev. D 2021, 104, 062007. [Google Scholar] [CrossRef]
- Aloisio, A.; Branchini, P.; Catalanotti, S.; Cavaliere, S.; Creti, P.; Marsella, G.; Mastroianni, S.; Parascandolo, P. The Trigger System of the ARGO-YBJ Experiment. IEEE Trans. Nucl. Sci. 2004, 51, 1835–1839. [Google Scholar] [CrossRef]
- Amenomori, M.; Ayabe, S.; Bi, X.J.; Chen, D.; Cui, S.W.; Ding, L.K.; Ding, X.H.; Feng, C.F.; Feng, Z.; Feng, Z.Y.; et al. Underground water Cherenkov muon detector array with the Tibet air shower array for gamma-ray astronomy in the 100 TeV region. Astrophys. Space Sci. 2007, 309, 435–439. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Ayala Solares, H.A.; Barber, A.S.; Baughman, B.; et al. Measurement of the Crab Nebula Spectrum Past 100 TeV with HAWC. Astrophys. J. 2019, 881, 134. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barceló, M.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. The major upgrade of the MAGIC telescopes, Part II: A performance study using observations of the Crab Nebula. Astropart. Phys. 2016, 72, 76–94. [Google Scholar] [CrossRef]
- Abdalla, H.; Abramowski, A.; Aharonian, F.; Ait Benkhali, F.; Angüner, E.O.; Arakawa, M.; Arrieta, M.; Aubert, P.; Backes, M.; Balzer, A.; et al. The H.E.S.S. Galactic plane survey. Astron. Astrophys. 2018, 612, A1. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Archer, A.; Aune, T.; Benbow, W.; Bird, R.; Brose, R.; Buchovecky, M.; Bugaev, V.; Cui, W.; Daniel, M.K.; et al. A Very High Energy γ-Ray Survey toward the Cygnus Region of the Galaxy. Astrophys. J. 2018, 861, 134. [Google Scholar] [CrossRef]
- Cao, Z.; Aharonian, F.A.; An, Q.; Axikegu; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; et al. Ultrahigh-energy photons up to 1.4 petaelectronvolts from 12 γ-ray Galactic sources. Nature 2021, 594, 33–36. [Google Scholar] [CrossRef] [PubMed]
- Abeysekara, A.U.; Archer, A.; Benbow, W.; Bird, R.; Brose, R.; Buchovecky, M.; Buckley, J.H.; Bugaev, V.; Chromey, A.J.; Connolly, M.P.; et al. VERITAS and Fermi-LAT Observations of TeV Gamma-Ray Sources Discovered by HAWC in the 2HWC Catalog. Astrophys. J. 2018, 866, 24. [Google Scholar] [CrossRef]
- Ahnen, M.L.; Ansoldi, S.; Antonelli, L.A.; Arcaro, C.; Baack, D.; Babić, A.; Banerjee, B.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; et al. MAGIC and Fermi-LAT gamma-ray results on unassociated HAWC sources. Mon. Not. R. Astron. Soc. 2019, 485, 356–366. [Google Scholar] [CrossRef]
- Abdalla, H.; Aharonian, F.; Ait Benkhali, F.; Angüner, E.O.; Arcaro, C.; Armand, C.; Armstrong, T.; Ashkar, H.; Backes, M.; Baghmanyan, V.; et al. TeV Emission of Galactic Plane Sources with HAWC and H.E.S.S. Astrophys. J. 2021, 917, 6. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Ayala Solares, H.A.; Barber, A.S.; Bautista-Elivar, N.; et al. The HAWC Real-time Flare Monitor for Rapid Detection of Transient Events. Astrophys. J. 2017, 843, 116. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.; Barrio, J.A.; Bernlöhr, K.; Börst, H.; Bojahr, H.; Bolz, O.; Contreras, J.L.; Cortina, J.; Denninghoff, S.; et al. Search for point sources of gamma radiation above 15 TeV with the HEGRA AIROBICC array. Astron. Astrophys. 2002, 390, 39–46. [Google Scholar] [CrossRef]
- Cao, Z. A future project at tibet: The large high altitude air shower observatory (LHAASO). Chin. Phys. C 2010, 34, 249–252. [Google Scholar] [CrossRef]
- Acharya, B.S.; Actis, M.; Aghajani, T.; Agnetta, G.; Aguilar, J.; Aharonian, F.; Ajello, M.; Akhperjanian, A.; Alcubierre, M.; Aleksić, J.; et al. Introducing the CTA concept. Astropart. Phys. 2013, 43, 3–18. [Google Scholar] [CrossRef]
- Cherenkov Telescope Array Consortium; Acharya, B.S.; Agudo, I.; Al Samarai, I.; Alfaro, R.; Alfaro, J.; Alispach, C.; Alves Batista, R.; Amans, J.P.; Amato, E.; et al. Science with the Cherenkov Telescope Array; World Scientific Publishing Co.: Singapore, 2019. [Google Scholar] [CrossRef]
- Lombardi, S.; Catalano, O.; Scuderi, S.; Antonelli, L.A.; Pareschi, G.; Antolini, E.; Arrabito, L.; Bellassai, G.; Bernlöhr, K.; Bigongiari, C.; et al. First detection of the Crab Nebula at TeV energies with a Cherenkov telescope in a dual-mirror Schwarzschild-Couder configuration: The ASTRI-Horn telescope. Astron. Astrophys. 2020, 634, A22. [Google Scholar] [CrossRef]
- Adams, C.B.; Alfaro, R.; Ambrosi, G.; Ambrosio, M.; Aramo, C.; Arlen, T.; Batista, P.I.; Benbow, W.; Bertucci, B.; Bissaldi, E.; et al. Detection of the Crab Nebula with the 9.7 m prototype Schwarzschild-Couder telescope. Astropart. Phys. 2021, 128, 102562. [Google Scholar] [CrossRef]
- Gould, R.J.; Schréder, G.P. Opacity of the Universe to High-Energy Photons. Phys. Rev. 1967, 155, 1408–1411. [Google Scholar] [CrossRef]
- Albert, A.; Alvarez, C.; Angeles Camacho, J.R.; Arteaga-Velázquez, J.C.; Arunbabu, K.P.; Avila Rojas, D.; Ayala Solares, H.A.; Baghmanyan, V.; Belmont-Moreno, E.; BenZvi, S.Y.; et al. A Survey of Active Galaxies at TeV Photon Energies with the HAWC Gamma-Ray Observatory. Astrophys. J. 2021, 907, 67. [Google Scholar] [CrossRef]
- Albert, A.; Alfaro, R.; Ashkar, H.; Alvarez, C.; Álvarez, J.; Arteaga-Velázquez, J.C.; Ayala Solares, H.A.; Arceo, R.; Bellido, J.A.; BenZvi, S.; et al. Science Case for a Wide Field-of-View Very-High-Energy Gamma-Ray Observatory in the Southern Hemisphere. arXiv 2019, arXiv:1902.08429. [Google Scholar]
- Werner, F.; Nellen, L. Technological options for the Southern Wide-field Gamma-ray Observatory (SWGO) and current design status. In Proceedings of the 37th International Cosmic Ray Conference—PoS(ICRC2021), Berlin, Germany, 12–23 July 2021; Volume 395, p. 714. [Google Scholar] [CrossRef]
- Kato, S.; Condori, C.A.H.; de la Fuente, E.; Gomi, A.; Hibino, K.; Hotta, N.; Toledano-Juarez, I.; Katayose, Y.; Kato, C.; Kawata, K.; et al. Detectability of southern gamma-ray sources beyond 100 TeV with ALPAQUITA, the prototype experiment of ALPACA. Exp. Astron. 2021, 52, 85–107. [Google Scholar] [CrossRef]
- Lombardi, S.; Antonelli, L.A.; Bigongiari, C.; Cardillo, M.; Gallozzi, S.; Green, J.G.; Lucarelli, F.; Saturni, F.G. Performance of the ASTRI Mini-Array at the Observatorio del Teide. In Proceedings of the 37th International Cosmic Ray Conference—PoS(ICRC2021), Berlin, Germany, 12–23 July 2021; Volume 395, p. 884. [Google Scholar] [CrossRef]
- CTA Observatory; CTA Consortium. CTAO Instrument Response Functions—Prod5 Version v0.1. 2021. Available online: https://zenodo.org/record/5499840#.YfIV5fgRVPY (accessed on 18 January 2022).
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Ayala Solares, H.A.; Barber, A.S.; Bautista-Elivar, N.; et al. Observation of the Crab Nebula with the HAWC Gamma-Ray Observatory. Astrophys. J. 2017, 843, 39. [Google Scholar] [CrossRef]
- Holler, M.; Berge, D.; van Eldik, C.; Lenain, J.P.; Marandon, V.; Murach, T.; de Naurois, M.; Parsons, R.D.; Prokoph, H.; Zaborov, D. Observations of the Crab Nebula with H.E.S.S. Phase II. arXiv 2015, arXiv:1509.02902. [Google Scholar]
- Bai, X.; Bi, B.Y.; Bi, X.J.; Cao, Z.; Chen, S.Z.; Chen, Y.; Chiavassa, A.; Cui, X.H.; Dai, Z.G.; della Volpe, D.; et al. The Large High Altitude Air Shower Observatory (LHAASO) Science White Paper. arXiv 2019, arXiv:1905.02773. [Google Scholar]
- Punch, M.; Akerlof, C.W.; Cawley, M.F.; Fegan, D.J.; Lamb, R.C.; Lawrence, M.A.; Lang, M.J.; Lewis, D.A.; Meyer, D.I.; O’Flaherty, K.S.; et al. Supercuts: An Improved Method of Selecting Gamma-rays. Int. Cosm. Ray Conf. 1991, 1, 464. [Google Scholar]
- Aliu, E.; Anderhub, H.; Antonelli, L.A.; Antoranz, P.; Backes, M.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; Becker, J.K.; et al. Improving the performance of the single-dish Cherenkov telescope MAGIC through the use of signal timing. Astropart. Phys. 2009, 30, 293–305. [Google Scholar] [CrossRef]
- Shayduk, M.; Consortium, C. Optimized Next-neighbour Image Cleaning Method for Cherenkov Telescopes. Int. Cosm. Ray Conf. 2013, 33, 3000. [Google Scholar]
- Maier, G.; Knapp, J. Cosmic-ray events as background in imaging atmospheric Cherenkov telescopes. Astropart. Phys. 2007, 28, 72–81. [Google Scholar] [CrossRef]
- Sitarek, J.; Sobczyńska, D.; Szanecki, M.; Adamczyk, K.; Cumani, P.; Moralejo, A. Nature of the low-energy, γ-like background for the Cherenkov Telescope Array. Astropart. Phys. 2018, 97, 1–9. [Google Scholar] [CrossRef]
- Greisen, K. Cosmic Ray Showers. Annu. Rev. Nucl. Part. Sci. 1960, 10, 63–108. [Google Scholar] [CrossRef]
- Kawata, K.; Sako, T.K.; Ohnishi, M.; Takita, M.; Nakamura, Y.; Munakata, K. Energy determination of gamma-ray induced air showers observed by an extensive air shower array. Exp. Astron. 2017, 44, 1–9. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Ayala Solares, H.A.; Barber, A.S.; Baughman, B.M.; Bautista-Elivar, N.; et al. Sensitivity of the high altitude water Cherenkov detector to sources of multi-TeV gamma rays. Astropart. Phys. 2013, 50, 26–32. [Google Scholar] [CrossRef]
- Aharonian, F.; An, Q.; Axikegu; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; Cai, H.; et al. Observation of the Crab Nebula with LHAASO-KM2A—A performance study. Chin. Phys. C 2021, 45, 025002. [Google Scholar] [CrossRef]
- Feng, Z.Y.; Zhang, Y.; Liu, C.; Fan, C.; Li, H.C.; Wang, B.; Wu, H.R.; Hu, H.B.; Lu, H.; Tan, Y.H. Study on the separation of 100 TeV γ-rays from cosmic rays for the Tibet ASγ experiment. Chin. Phys. C 2011, 35, 153–157. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Asensio, M.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; et al. Implementation of the Random Forest method for the Imaging Atmospheric Cherenkov Telescope MAGIC. Nucl. Instrum. Methods Phys. Res. A 2008, 588, 424–432. [Google Scholar] [CrossRef]
- Ohm, S.; van Eldik, C.; Egberts, K. γ/hadron separation in very-high-energy γ-ray astronomy using a multivariate analysis method. Astropart. Phys. 2009, 31, 383–391. [Google Scholar] [CrossRef]
- Krause, M.; Pueschel, E.; Maier, G. Improved γ/hadron separation for the detection of faint γ-ray sources using boosted decision trees. Astropart. Phys. 2017, 89, 1–9. [Google Scholar] [CrossRef]
- Capistrán, T.; Fan, K.L.; Linnemann, J.T.; Torres, I.; Saz Parkinson, P.M.; Yu, P.L.H. Use of Machine Learning for gamma/hadron separation with HAWC. arXiv 2021, arXiv:2108.00112. [Google Scholar]
- Atkins, R.; Benbow, W.; Berley, D.; Blaufuss, E.; Bussons, J.; Coyne, D.G.; Delay, R.S.; De Young, T.; Dingus, B.L.; Dorfan, D.E.; et al. Observation of TeV Gamma Rays from the Crab Nebula with Milagro Using a New Background Rejection Technique. Astrophys. J. 2003, 595, 803–811. [Google Scholar] [CrossRef]
- Le Bohec, S.; Degrange, B.; Punch, M.; Barrau, A.; Bazer-Bachi, R.; Cabot, H.; Chounet, L.M.; Debiais, G.; Dezalay, J.P.; Djannati-Atai, A.; et al. A new analysis method for very high definition imaging atmospheric Cherenkov telescopes as applied to the CAT telescope. Nucl. Instrum. Methods Phys. Res. A 1998, 416, 425–437. [Google Scholar] [CrossRef]
- de Naurois, M.; Rolland, L. A high performance likelihood reconstruction of γ-rays for imaging atmospheric Cherenkov telescopes. Astropart. Phys. 2009, 32, 231–252. [Google Scholar] [CrossRef]
- Parsons, R.D.; Hinton, J.A. A Monte Carlo template based analysis for air-Cherenkov arrays. Astropart. Phys. 2014, 56, 26–34. [Google Scholar] [CrossRef]
- Joshi, V.; Hinton, J.; Schoorlemmer, H.; López-Coto, R.; Parsons, R. A template-based γ-ray reconstruction method for air shower arrays. J. Cosmol. Astropart. Phys. 2019, 2019, 012. [Google Scholar] [CrossRef]
- Becherini, Y.; Djannati-Ataï, A.; Marandon, V.; Punch, M.; Pita, S. A new analysis strategy for detection of faint γ-ray sources with Imaging Atmospheric Cherenkov Telescopes. Astropart. Phys. 2011, 34, 858–870. [Google Scholar] [CrossRef]
- Fiasson, A.; Dubois, F.; Lamanna, G.; Masbou, J.; Rosier-Lees, S. Optimization of multivariate analysis for IACT stereoscopic systems. Astropart. Phys. 2010, 34, 25–32. [Google Scholar] [CrossRef]
- Fomin, V.P.; Stepanian, A.A.; Lamb, R.C.; Lewis, D.A.; Punch, M.; Weekes, T.C. New methods of atmospheric Cherenkov imaging for gamma-ray astronomy. I. The false source method. Astropart. Phys. 1994, 2, 137–150. [Google Scholar] [CrossRef]
- Aleksić, J.; Alvarez, E.A.; Antonelli, L.A.; Antoranz, P.; Asensio, M.; Backes, M.; Barrio, J.A.; Bastieri, D.; Becerra González, J.; Bednarek, W.; et al. Searches for dark matter annihilation signatures in the Segue 1 satellite galaxy with the MAGIC-I telescope. J. Cosmol. Astropart. Phys. 2011, 2011, 035. [Google Scholar] [CrossRef]
- Aleksić, J.; Alvarez, E.A.; Antonelli, L.A.; Antoranz, P.; Ansoldi, S.; Asensio, M.; Backes, M.; Barres de Almeida, U.; Barrio, J.A.; Bastieri, D.; et al. Discovery of VHE γ-rays from the blazar 1ES 1215+303 with the MAGIC telescopes and simultaneous multi-wavelength observations. Astron. Astrophys. 2012, 544, A142. [Google Scholar] [CrossRef]
- Archer, A.; Benbow, W.; Bird, R.; Buchovecky, M.; Buckley, J.H.; Bugaev, V.; Byrum, K.; Cardenzana, J.V.; Cerruti, M.; Chen, X.; et al. TeV Gamma-Ray Observations of the Galactic Center Ridge by VERITAS. Astrophys. J. 2016, 821, 129. [Google Scholar] [CrossRef]
- Vovk, I.; Strzys, M.; Fruck, C. Spatial likelihood analysis for MAGIC telescope data. From instrument response modelling to spectral extraction. Astron. Astrophys. 2018, 619, A7. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Antolini, E.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; et al. Fermi Large Area Telescope First Source Catalog. Astrophys. J. Suppl. Ser. 2010, 188, 405–436. [Google Scholar] [CrossRef]
- Abdo, A.A.; Allen, B.T.; Atkins, R.; Aune, T.; Benbow, W.; Berley, D.; Blaufuss, E.; Bonamente, E.; Bussons, J.; Chen, C.; et al. Observation and Spectral Measurements of the Crab Nebula with Milagro. Astrophys. J. 2012, 750, 63. [Google Scholar] [CrossRef]
- Huang, X.; Duan, K. A 3D Likelihood Analysis Tool for LHAASO-KM2A data. In Proceedings of the 37th International Cosmic Ray Conference—PoS(ICRC2021), Berlin, Germany, 12–23 July 2021; Volume 395, p. 769. [Google Scholar] [CrossRef]
- Abdalla, H.; Abramowski, A.; Aharonian, F.; Ait Benkhali, F.; Akhperjanian, A.G.; Andersson, T.; Angüner, E.O.; Arakawa, M.; Arrieta, M.; Aubert, P.; et al. Characterising the VHE diffuse emission in the central 200 parsecs of our Galaxy with H.E.S.S. Astron. Astrophys. 2018, 612, A9. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Anton, G.; Barres de Almeida, U.; Bazer-Bachi, A.R.; Becherini, Y.; Behera, B.; Bernlöhr, K.; Bochow, A.; Boisson, C.; et al. Probing the ATIC peak in the cosmic-ray electron spectrum with H.E.S.S. Astron. Astrophys. 2009, 508, 561–564. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Barrio, J.A.; Belgarian, A.S.; Bernlöhr, K.; Beteta, J.J.; Bojahr, H.; Bradbury, S.; Calle, I.; Contreras, J.L.; et al. Cosmic ray proton spectrum determined with the imaging atmospheric Cherenkov technique. Phys. Rev. 1999, 59, 092003. [Google Scholar] [CrossRef]
- Temnikov, P.; Verguilov, V.; Maneva, G.; Mirzoyan, R.; Baack, D.; Arbet-Engels, A.; Biland, A.; MAGIC Collaboration. Protons Spectrum from MAGIC Telescopes data. In Proceedings of the 37th International Cosmic Ray Conference—PoS(ICRC2021), Berlin, Germany, 12–23 July 2021; Volume 395, p. 231. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Ayala Solares, H.A.; Barber, A.S.; et al. Extended gamma-ray sources around pulsars constrain the origin of the positron flux at Earth. Science 2017, 358, 911–914. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Arceo, R.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Belmont-Moreno, E.; BenZvi, S.Y.; Brisbois, C.; Capistrán, T.; et al. All-sky Measurement of the Anisotropy of Cosmic Rays at 10 TeV and Mapping of the Local Interstellar Magnetic Field. Astrophys. J. 2019, 871, 96. [Google Scholar] [CrossRef]
- Amenomori, M.; Bao, Y.W.; Bi, X.J.; Chen, D.; Chen, T.L.; Chen, W.Y.; Chen, X.; Chen, Y.; Cirennima; Cui, S.W.; et al. First Detection of sub-PeV Diffuse Gamma Rays from the Galactic Disk: Evidence for Ubiquitous Galactic Cosmic Rays beyond PeV Energies. Phys. Rev. Lett. 2021, 126, 141101. [Google Scholar] [CrossRef] [PubMed]
- Chitnis, V.R.; Bhat, P.N. Čerenkov photon density fluctuations in extensive air showers. Astropart. Phys. 1998, 9, 45–63. [Google Scholar] [CrossRef][Green Version]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Asensio, M.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; et al. Unfolding of differential energy spectra in the MAGIC experiment. Nucl. Instrum. Methods Phys. Res. A 2007, 583, 494–506. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Measurement of the extragalactic background light using MAGIC and Fermi-LAT gamma-ray observations of blazars up to z = 1. Mon. Not. R. Astron. Soc. 2019, 486, 4233–4251. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Reynolds, P.T.; Fegan, D.J. Neural network classification of TeV gamma-ray images. Astropart. Phys. 1995, 3, 137–150. [Google Scholar] [CrossRef]
- Shilon, I.; Kraus, M.; Büchele, M.; Egberts, K.; Fischer, T.; Holch, T.L.; Lohse, T.; Schwanke, U.; Steppa, C.; Funk, S. Application of deep learning methods to analysis of imaging atmospheric Cherenkov telescopes data. Astropart. Phys. 2019, 105, 44–53. [Google Scholar] [CrossRef]
- Parsons, R.D.; Ohm, S. Background rejection in atmospheric Cherenkov telescopes using recurrent convolutional neural networks. Eur. Phys. J. C 2020, 80, 363. [Google Scholar] [CrossRef]
- Ohishi, M.; Arbeletche, L.; de Souza, V.; Maier, G.; Bernlöhr, K.; Olaizola, A.M.; Bregeon, J.; Arrabito, L.; Yoshikoshi, T. Effect of the uncertainty in the hadronic interaction models on the estimation of the sensitivity of the Cherenkov telescope array. J. Phys. G Nucl. Phys. 2021, 48, 075201. [Google Scholar] [CrossRef]
- Nieto Castaño, D.; Brill, A.; Kim, B.; Humensky, T.B. Exploring deep learning as an event classification method for the Cherenkov Telescope Array. In Proceedings of the 35th International Cosmic Ray Conference—PoS(ICRC2017), Busan, Korea, 12–20 July 2017; Volume 301, p. 809. [Google Scholar] [CrossRef]
- Steppa, C.; Holch, T.L. HexagDLy-Processing hexagonally sampled data with CNNs in PyTorch. SoftwareX 2019, 9, 193–198. [Google Scholar] [CrossRef]
- Vuillaume, T.; Jacquemont, M.; de Bony de Lavergne, M.; Sanchez, D.A.; Poireau, V.; Maurin, G.; Benoit, A.; Lambert, P.; Lamanna, G.; Project, C.L. Analysis of the Cherenkov Telescope Array first Large-Sized Telescope real data using convolutional neural networks. arXiv 2021, arXiv:2108.04130. [Google Scholar]
- Miener, T.; López-Coto, R.; Contreras, J.L.; Green, J.G.; Green, D.; Mariotti, E.; Nieto, D.; Romanato, L.; Yadav, S. IACT event analysis with the MAGIC telescopes using deep convolutional neural networks with CTLearn. arXiv 2021, arXiv:2112.01828. [Google Scholar]
- Spencer, S.; Armstrong, T.; Watson, J.; Mangano, S.; Renier, Y.; Cotter, G. Deep learning with photosensor timing information as a background rejection method for the Cherenkov Telescope Array. Astropart. Phys. 2021, 129, 102579. [Google Scholar] [CrossRef]
- Watson, I. Convolutional Neural Networks for Low Energy Gamma-Ray Air Shower Identification with HAWC. In Proceedings of the 37th International Cosmic Ray Conference—PoS(ICRC2021), Berlin, Germany, 12–23 July 2021; Volume 395, p. 770. [Google Scholar] [CrossRef]
- Zhang, F. Identification of proton and gamma in LHAASO-KM2A simulation data with deep learning algorithms. In Proceedings of the 37th International Cosmic Ray Conference—PoS(ICRC2021), Berlin, Germany, 12–23 July 2021; Volume 395, p. 741. [Google Scholar] [CrossRef]
- Armand, C.; Charles, E.; di Mauro, M.; Giuri, C.; Harding, J.P.; Kerszberg, D.; Miener, T.; Moulin, E.; Oakes, L.; Poireau, V.; et al. Combined dark matter searches towards dwarf spheroidal galaxies with Fermi-LAT, HAWC, H.E.S.S., MAGIC, and VERITAS. arXiv 2021, arXiv:2108.13646. [Google Scholar]
- Nigro, C.; Hassan, T.; Olivera-Nieto, L. Evolution of Data Formats in Very-High-Energy Gamma-Ray Astronomy. Universe 2021, 7, 374. [Google Scholar] [CrossRef]
- Nigro, C.; Deil, C.; Zanin, R.; Hassan, T.; King, J.; Ruiz, J.E.; Saha, L.; Terrier, R.; Brügge, K.; Nöthe, M.; et al. Towards open and reproducible multi-instrument analysis in gamma-ray astronomy. Astron. Astrophys. 2019, 625, A10. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Unraveling the Complex Behavior of Mrk 421 with Simultaneous X-Ray and VHE Observations during an Extreme Flaring Activity in 2013 April. Astrophys. J. Suppl. Ser. 2020, 248, 29. [Google Scholar] [CrossRef]
- The CHIME/FRB Collaboration; Andersen, B.C.; Bandura, K.; Berger, S.; Bhardwaj, M.; Boyce, M.M.; Boyle, P.J.; Brar, C.; Breitman, D.; Cassanelli, T.; et al. The First CHIME/FRB Fast Radio Burst Catalog. arXiv 2021, arXiv:2106.04352. [Google Scholar]
- Evans, P.A.; Beardmore, A.P.; Page, K.L.; Osborne, J.P.; O’Brien, P.T.; Willingale, R.; Starling, R.L.C.; Burrows, D.N.; Godet, O.; Vetere, L.; et al. Methods and results of an automatic analysis of a complete sample of Swift-XRT observations of GRBs. Mon. Not. R. Astron. Soc. 2009, 397, 1177–1201. [Google Scholar] [CrossRef]
- Barack, L.; Cardoso, V.; Nissanke, S.; Sotiriou, T.P.; Askar, A.; Belczynski, C.; Bertone, G.; Bon, E.; Blas, D.; Brito, R.; et al. Black holes, gravitational waves and fundamental physics: A roadmap. Class. Quantum Gravity 2019, 36, 143001. [Google Scholar] [CrossRef]
- Ashkar, H.; Zhu, S.; Brun, F.; Füßling, M.; Hoischen, C.; Konno, R.; Ohm, S.; Prokoph, H.; Reichherzer, P.; Schüssler, F.; et al. The H.E.S.S. Gravitational Wave Rapid Follow-up Program during O2 and O3. In Proceedings of the 37th International Cosmic Ray Conference—PoS(ICRC2021), Berlin, Germany, 12–23 July 2021; Volume 395, p. 936. [Google Scholar] [CrossRef]
- IceCube Collaboration; Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Andeen, K.; et al. Very high-energy gamma-ray follow-up program using neutrino triggers from IceCube. J. Instrum. 2016, 11, P11009. [Google Scholar] [CrossRef]
- Rolke, W.A.; López, A.M.; Conrad, J. Limits and confidence intervals in the presence of nuisance parameters. Nucl. Instrum. Methods Phys. Res. A 2005, 551, 493–503. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Al Samarai, I.; Altmann, D.; Andeen, K.; Anderson, T.; et al. Multiwavelength follow-up of a rare IceCube neutrino multiplet. Astron. Astrophys. 2017, 607, A115. [Google Scholar] [CrossRef]



| Characteristic | IACT | SA/WCD |
|---|---|---|
| Energy threshold | ∼ tens of GeV (for a few hundred m mirror dish) | ∼TeV |
| Duty cycle | ||
| Field of view | ∼ a few millisr | ∼ sr |
| Energy resolution | ||
| Angular resolution | ||
| Sensitivity | Crab Nebula flux in 25 h | a few % Crab Nebula flux in 5 yr |
| Main present instruments | H.E.S.S., MAGIC, VERITAS | Tibet AS-, HAWC, LHAASO-WCDA, LHAASO-KM2A |
| Future instruments | CTA | SWGO, ALPACA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sitarek, J. TeV Instrumentation: Current and Future. Galaxies 2022, 10, 21. https://doi.org/10.3390/galaxies10010021
Sitarek J. TeV Instrumentation: Current and Future. Galaxies. 2022; 10(1):21. https://doi.org/10.3390/galaxies10010021
Chicago/Turabian StyleSitarek, Julian. 2022. "TeV Instrumentation: Current and Future" Galaxies 10, no. 1: 21. https://doi.org/10.3390/galaxies10010021
APA StyleSitarek, J. (2022). TeV Instrumentation: Current and Future. Galaxies, 10(1), 21. https://doi.org/10.3390/galaxies10010021






